A Novel Dictionary-Based Method to Compress Log Files with Different Message Frequency Distributions
Abstract
:1. Introduction
2. Related Work
3. Concepts and Problems
3.1. Log Parsing
3.2. IPLoM
3.3. MoLFI
3.4. General Compressors
4. The Algorithm
5. Results
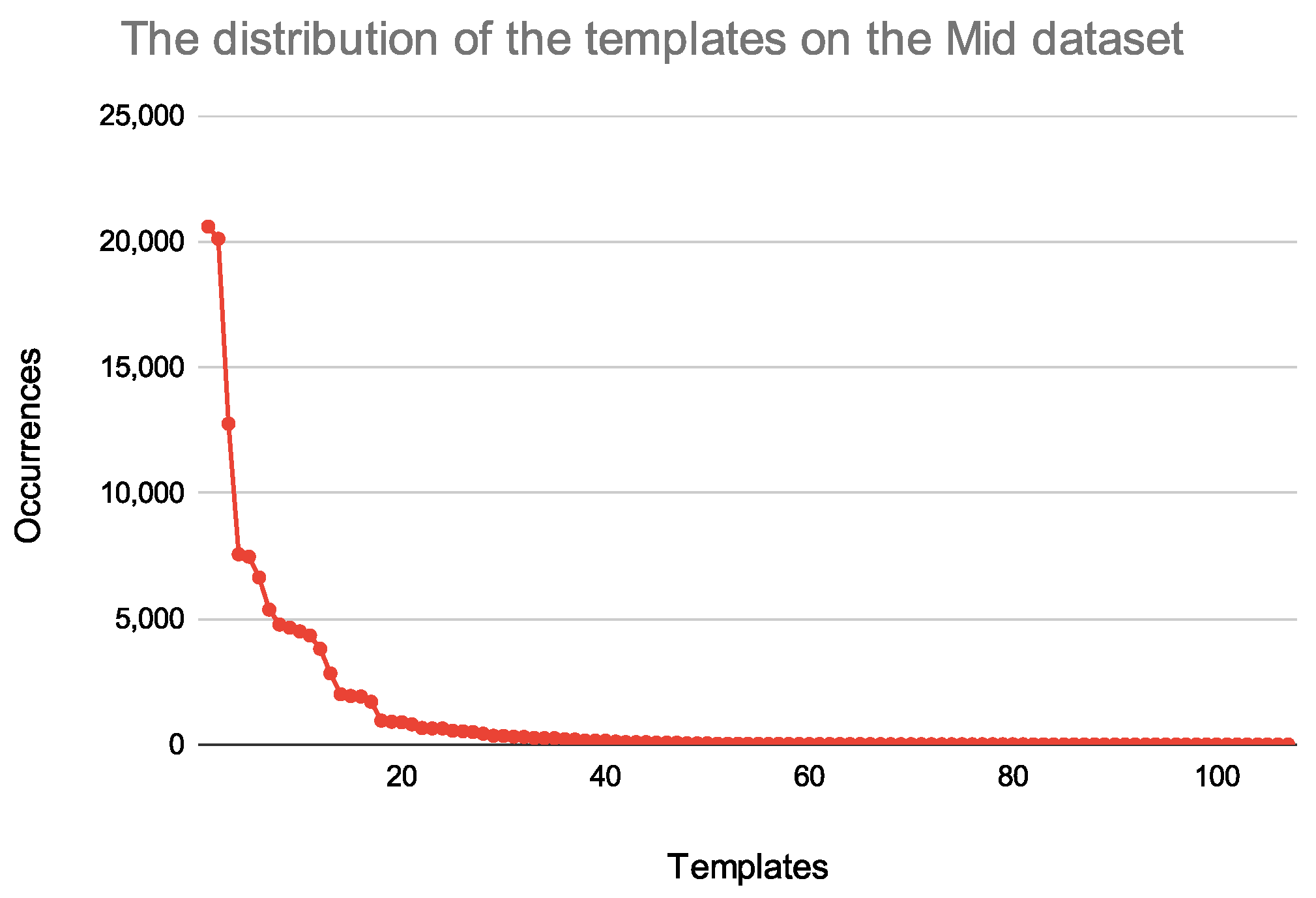
5.1. Data
5.2. Experimental Analysis
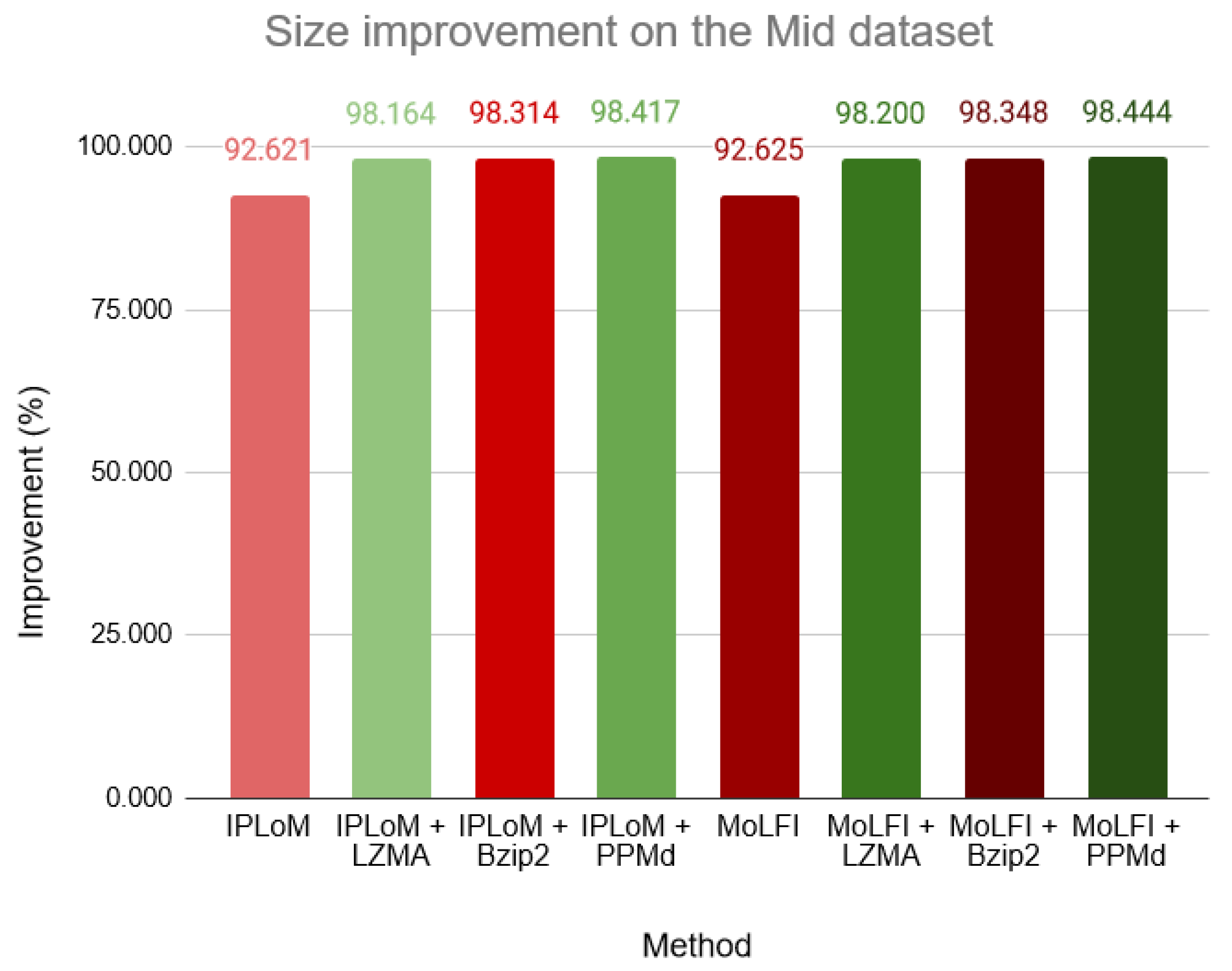
5.2.1. Experiment 1: Comparing the Compression Values Achieved by the Different Enhancements
5.2.2. Experiment 2: Comparing the Speeds of the Different Enhancements
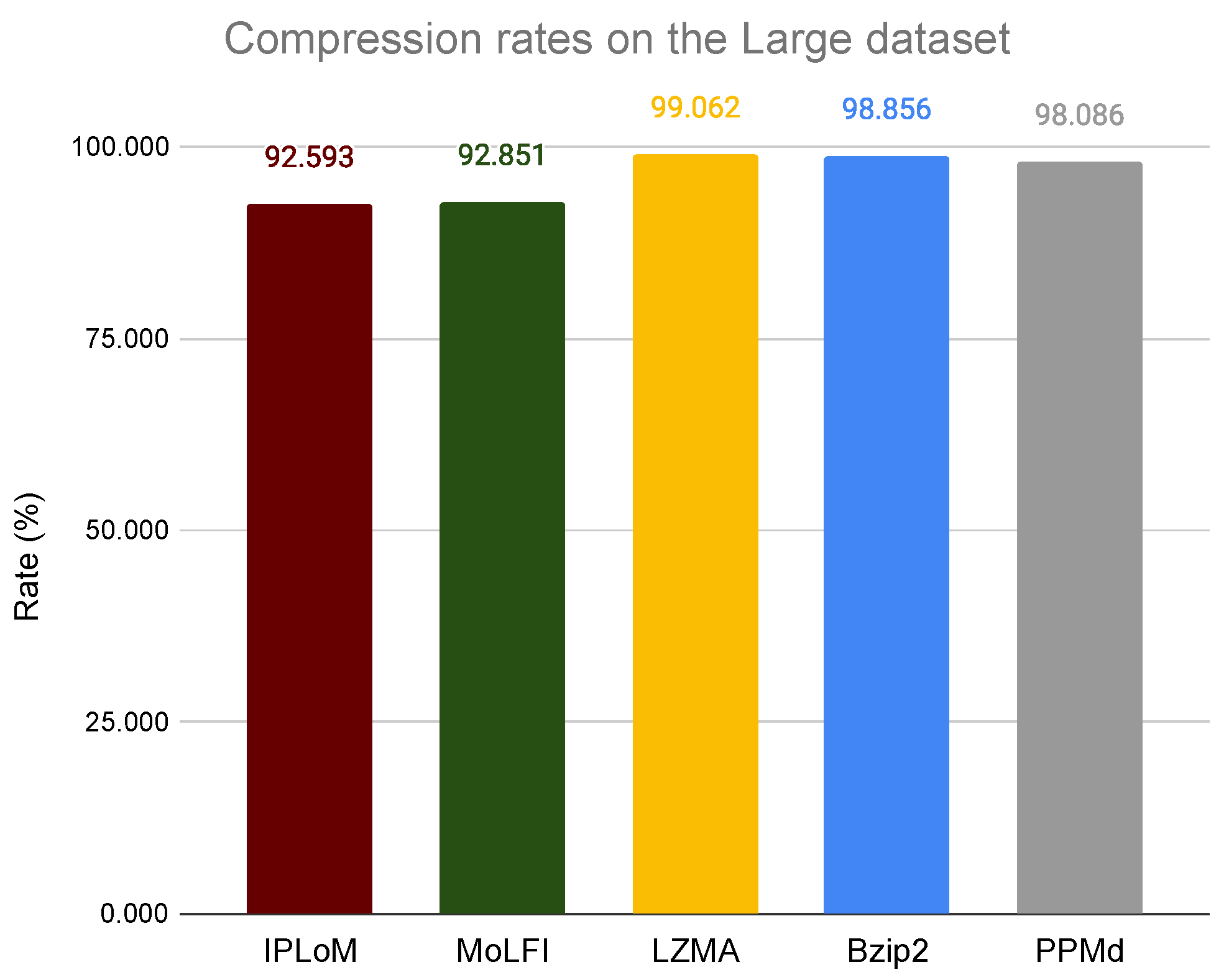
5.2.3. Experiment 3: Comparing the Compression Rates of the New Enhanced Algorithm and General Compressors
5.2.4. Experiment 4: Comparing the Speeds of the New Enhanced Algorithm and General Compressors
5.2.5. Experiment 5: Comparing the Compression Rates of the Joint Use of the New Enhanced Algorithm and General Compressors
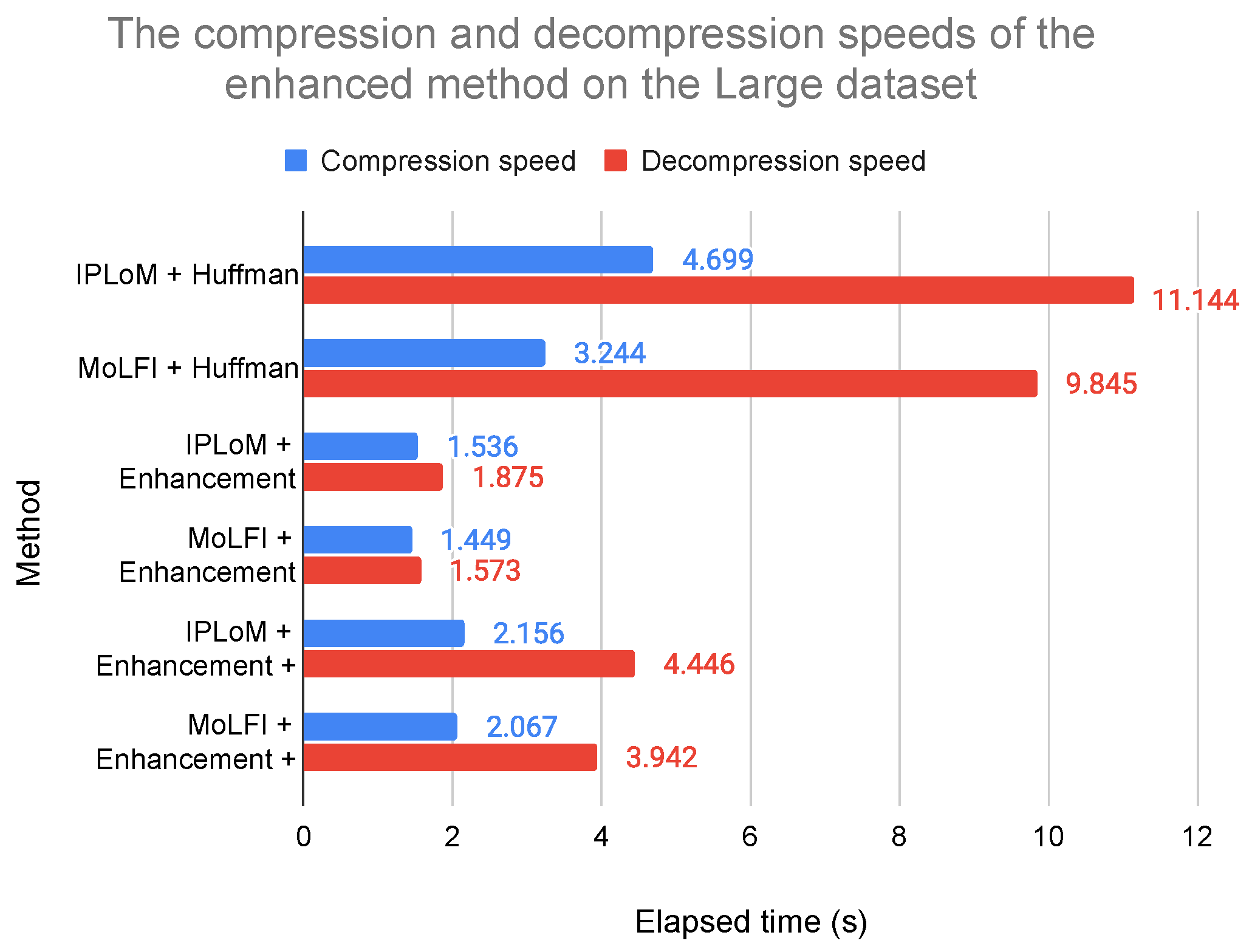
5.2.6. Experiment 6: Comparing the Speeds of the Joint Use of the New Enhanced Algorithm and General Compressors
5.2.7. Experiment 7: Comparing the Speeds and the Storage Sizes Needed to Retrieve All Instances of an Event Type by the New Enhanced Algorithm and General Compressors
5.2.8. Experiment 8: The Comparison of the Compression Rates Achieved by the Proposed Algorithm and Logzip
5.2.9. Experiment 9: Investigating the Memory Usage of the Proposed Algorithm and Logzip
5.2.10. Experiment 10: Generating Log Messages with Different Distributions and Evaluating the Compression Rates
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IPLoM | Iterative Partitioning Log Mining |
| MoLFI | Multi-objective Log message Format Identification |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| BWT | Burrows–Wheeler Transformation |
| LZMA | Lempel–Ziv–Markov-chain Algorithm |
| PPM | Prediction by Partial Matching |
| Enh | Enhanced version of our algorithm |
| Huff | Huffman coding |
| WPE | Without Parameter Encoding |
References
- Landauer, M.; Wurzenberger, M.; Skopik, F.; Settanni, G.; Filzmoser, P. Dynamic log file analysis: An unsupervised cluster evolution approach for anomaly detection. In Computers & Security; Elsevier: Amsterdam, The Netherlands, 2018; Volume 79, pp. 94–116. [Google Scholar] [CrossRef]
- Aivalis, C.; Boucouvalas, A.C. Log File Analysis of E-commerce Systems in Rich Internet Web 2.0 Applications. In Proceedings of the PCI 2011—15th Panhellenic Conference on Informatics, Kastoria, Greece, 30 September–2 October 2011; Volume 10, pp. 222–226. [Google Scholar] [CrossRef]
- Nagaraj, K.; Killian, C.; Neville, J. Structured comparative analysis of systems logs to diagnose performance problems. In Proceedings of the 9th USENIX Symposium on Networked Systems Design and Implementation, Jan Jose, CA, USA, 25–27 April 2012; pp. 353–366. [Google Scholar]
- Logothetis, D.; Trezzo, C.; Webb, K.C.; Yocum, K. In-situ MapReduce for log processing. In Proceedings of the USENIX ATC, Portland, OR, USA, 14–15 June 2011; Volume 11, p. 115. [Google Scholar]
- Li, H.; Shang, W.; Hassan, A.E. Which log level should developers choose for a new logging statement? In Empirical Software Engineering; Springer: New York, NY, USA, 2017; Volume 22, pp. 1684–1716. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, J.; Yao, B.; Guo, M.; Li, J. Cowic: A column-wise independent compression for log stream analysis. In Proceedings of the 2015 15th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Shenzhen, China, 4–7 May 2015; pp. 21–30. [Google Scholar] [CrossRef]
- Yao, K.; Li, H.; Shang, W.; Hassan, A.E. A study of the performance of general compressors on log files. In Empirical Software Engineering; Springer: New York, NY, USA, 2020; Volume 25, pp. 3043–3085. [Google Scholar] [CrossRef]
- Du, M.; Li, F. Spell: Streaming parsing of system event logs. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining, Barcelona, Spain, 12–15 December 2016; pp. 859–864. [Google Scholar] [CrossRef]
- Shima, K. Length matters: Clustering system log messages using length of words. arXiv 2016, arXiv:1611.03213. [Google Scholar]
- He, P.; Zhu, J.; Zheng, Z.; Lyu, M.R. Drain: An online log parsing approach with fixed depth tree. In Proceedings of the 2017 IEEE International Conference on Web Services (ICWS), Honolulu, HI, USA, 25–30 June 2017; pp. 33–40. [Google Scholar] [CrossRef]
- Christensen, R.; Li, F. Adaptive log compression for massive log data. In Proceedings of the SIGMOD Conference, New York, NY, USA, 22–27 June 2013; pp. 1283–1284. [Google Scholar]
- Feng, B.; Wu, C.; Li, J. MLC: An efficient multi-level log compression method for cloud backup systems. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 1358–1365. [Google Scholar] [CrossRef]
- Mell, P.; Harang, R.E. Lightweight packing of log files for improved compression in mobile tactical networks. In Proceedings of the 2014 IEEE Military Communications Conference, Baltimore, MD, USA, 6–8 October 2014; pp. 192–197. [Google Scholar] [CrossRef]
- Grabowski, S.; Deorowicz, S. Web log compression. Automatyka/Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie 2007, 11, 417–424. [Google Scholar]
- Lloyd, T.; Barton, K.; Tiotto, E.; Amaral, J.N. Run-length base-delta encoding for high-speed compression. In Proceedings of the 47th International Conference on Parallel Processing Companion, Eugene, OR, USA, 13–16 August 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, Z.; Zou, X.; Liao, Q.; Xia, W. Exploring the Potential of Fast Delta Encoding: Marching to a Higher Compression Ratio. In Proceedings of the 2020 IEEE International Conference on Cluster Computing (CLUSTER), Kobe, Japan, 14–17 September 2020; pp. 198–208. [Google Scholar] [CrossRef]
- Skibiński, P.; Swacha, J. Fast and efficient log file compression. In Proceedings of the CEUR Workshop, 11th East-European Conference on Advances in Databases and Information Systems, Varna, Bulgaria, 29 September–3 October 2007; pp. 56–69. [Google Scholar]
- Otten, F.; Irwin, B.; Thinyane, H. Evaluating text preprocessing to improve compression on maillogs. In Proceedings of the 2009 Annual Research Conference of the South African Institute of Computer Scientists and Information Technologists, Emfuleni, South Africa, 12–14 October 2009; pp. 44–53. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, J.; He, S.; He, P.; Zheng, Z.; Lyu, M.R. Logzip: Extracting hidden structures via iterative clustering for log compression. In Proceedings of the 2019 34th IEEE/ACM International Conference on Automated Software Engineering (ASE), San Diego, CA, USA, 11–15 November 2019; pp. 863–873. [Google Scholar] [CrossRef] [Green Version]
- Hätönen, K.; Boulicaut, J.F.; Klemettinen, M.; Miettinen, M.; Masson, C. Comprehensive log compression with frequent patterns. In International Conference on Data Warehousing and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2003; pp. 360–370. [Google Scholar] [CrossRef] [Green Version]
- Marjai, P.; Lehotay-Kéry, P.; Kiss, A. The Use of Template Miners and Encryption in Log Message Compression. Computers 2021, 10, 83. [Google Scholar] [CrossRef]
- He, P.; Zhu, J.; He, S.; Li, J.; Lyu, M.R. An evaluation study on log parsing and its use in log mining. In Proceedings of the 2016 46th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, Toulouse, France, 28 June–1 July 2016; pp. 654–661. [Google Scholar] [CrossRef]
- Makanju, A.; Zincir-Heywood, A.N.; Milios, E.E. A lightweight algorithm for message type extraction in system application logs. IEEE Trans. Knowl. Data Eng. 2011, 24, 1921–1936. [Google Scholar] [CrossRef]
- Messaoudi, S.; Panichella, A.; Bianculli, D.; Briand, L.; Sasnauskas, R. A search-based approach for accurate identification of log message formats. In Proceedings of the 26th Conference on Program Comprehension, Gothenburg, Sweden, 27 May–3 June 2018; pp. 167–177. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Sivanandam, S.N.; Deepa, S.N. Genetic algorithms. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–37. [Google Scholar] [CrossRef]
- Syswerda, G. Uniform crossover in genetic algorithms. In Proceedings of the Third International Conference on Genetic Algorithms; Morgan Kaufmann Publishers: Burlington, MA, USA, 1989; pp. 2–9. [Google Scholar]
- Branke, J.; Deb, K.; Dierolf, H.; Osswald, M. Finding knees in multi-objective optimization. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2004; pp. 722–731. [Google Scholar]
- Burrows, M.; Wheeler, D. A block-sorting lossless data compression algorithm. In Digital SRC Research Report; Digital Systems Research Center: Palo Alto, CA, USA, 1994. [Google Scholar]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef] [Green Version]
- Bell, T.; Witten, I.H.; Cleary, J.G. Modeling for text compression. ACM Comput. Surv. 1989, 21, 557–591. [Google Scholar] [CrossRef]
- Cleary, J.; Witten, I. Data compression using adaptive coding and partial string matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef] [Green Version]
- Huffman, D.A. A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Moffat, A.; Zobel, J.; Sharman, N. Text compression for dynamic document databases. IEEE Trans. Knowl. Data Eng. 1997, 9, 302–313. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Ferragina, P.; González, R.; Navarro, G.; Venturini, R. Compressed text indexes: From theory to practice. J. Exp. Algorithm. 2009, 13, 1.12–1.31. [Google Scholar] [CrossRef]
- Dahuffman Python Library. Available online: https://pypi.org/project/dahuffman/ (accessed on 22 September 2021).
- 7-Zip. Available online: https://www.7-zip.org/ (accessed on 1 October 2021).













































| Name | Number of Messages | Size in Kilobytes | Alphabet Size | Shannon Entropy |
|---|---|---|---|---|
| Small | 39,139 | 1152 KB | 76 | 5.08167 |
| Mid | 124,433 | 4607 KB | 76 | 5.08872 |
| Large | 280,002 | 10,198 KB | 74 | 5.05287 |
| Big | 637,369 | 22,840 KB | 71 | 5.00206 |
| A | 50,000,000 | 2,039,483 KB | 76 | 4.97789 |
| B | 130,000,000 | 5,303,394 KB | 76 | 4.97798 |
| C | 254,000,000 | 10,361,437 KB | 76 | 4.97781 |
| D | 1,264,000,000 | 51,562,601 KB | 76 | 4.89284 |
| IPLoM | Small Dataset | Mid Dataset | Large Dataset | Big Dataset |
| Huff | ||||
| Template dictionary | 2.981 KB | 4.266 KB | 4.24 KB | 4.293 KB |
| Huffman codec (WPE) | 1.158 KB | 1.179 KB | 1.203 KB | 1.197 KB |
| Compressed file | 409.426 KB | 1068.173 KB | 2674.835 KB | 5776.537 KB |
| Overall | 413.565 KB | 1073.618 KB | 2680.278 KB | 5782.027 KB |
| Enh | ||||
| Template dictionary | 2.981 KB | 4.266 KB | 4.24 KB | 4.293 KB |
| Parameter dictionary | 6.877 KB | 22.151 KB | 24.906 KB | 25.626 KB |
| Compressed file | 358.361 KB | 855.013 KB | 2004.595 KB | 4506.784 KB |
| Overall | 368.219 KB | 881.43 KB | 2033.741 KB | 4536.703 KB |
| Enh Huff | ||||
| Template dictionary | 2.981 KB | 4.266 KB | 4.24 KB | 4.293 KB |
| Parameter dictionary | 6.877 KB | 22.151 KB | 24.906 KB | 25.626 KB |
| Huffman codec | 0.362 KB | 0.362 KB | 0.362 KB | 0.362 KB |
| Compressed file | 132.147 KB | 306.09 KB | 725.813 KB | 1608.534 KB |
| Overall | 142.367 KB | 332.869 KB | 755.321 KB | 1638.815 KB |
| MoLFI | Small Dataset | Mid Dataset | Large Dataset | Big Dataset |
| Huff | ||||
| Template dictionary | 3.832 KB | 4.45 KB | 4.606 KB | 4.461 KB |
| Huffman codec (WPE) | 1.068 KB | 1.125 KB | 1.118 KB | 1.134 KB |
| Compressed file | 313.133 KB | 986.065 KB | 2455.239 KB | 5550.092 KB |
| Overall | 318.033 KB | 991.64 KB | 2460.963 KB | 5555.687 KB |
| Enh | ||||
| Template dictionary | 3.832 KB | 4.45 KB | 4.606 KB | 4.461 KB |
| Parameter dictionary | 6.348 KB | 21.743 KB | 24.448 KB | 25.206 KB |
| Compressed file | 288.102 KB | 854.308 KB | 1996.157 KB | 4522.154 KB |
| Overall | 298.282 KB | 880.501 KB | 2025.211 KB | 4551.821 KB |
| Enh Huff | ||||
| Template dictionary | 3.832 KB | 4.45 KB | 4.606 KB | 4.461 KB |
| Parameter dictionary | 6.348 KB | 21.743 KB | 24.448 KB | 25.206 KB |
| Huffman codec | 0.362 KB | 0.362 KB | 0.362 KB | 0.362 KB |
| Compressed file | 105.48 KB | 303.202 KB | 699.61 KB | 1606.879 KB |
| Overall | 116.022 KB | 329.757 KB | 729.026 KB | 1636.908 KB |
| Dataset | Proposed | LZMA | Bzip2 | PPMd |
|---|---|---|---|---|
| A | 94.652% | 92.931% | 95.823% | 95.542% |
| B | 94.782% | 92.931% | 95.823% | 95.543% |
| C | 94.650% | 92.932% | 95.823% | 95.543% |
| D | 94.682% | 92.931% | 95.823% | 95.543% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marjai, P.; Lehotay-Kéry, P.; Kiss, A. A Novel Dictionary-Based Method to Compress Log Files with Different Message Frequency Distributions. Appl. Sci. 2022, 12, 2044. https://doi.org/10.3390/app12042044
Marjai P, Lehotay-Kéry P, Kiss A. A Novel Dictionary-Based Method to Compress Log Files with Different Message Frequency Distributions. Applied Sciences. 2022; 12(4):2044. https://doi.org/10.3390/app12042044
Chicago/Turabian StyleMarjai, Péter, Péter Lehotay-Kéry, and Attila Kiss. 2022. "A Novel Dictionary-Based Method to Compress Log Files with Different Message Frequency Distributions" Applied Sciences 12, no. 4: 2044. https://doi.org/10.3390/app12042044
APA StyleMarjai, P., Lehotay-Kéry, P., & Kiss, A. (2022). A Novel Dictionary-Based Method to Compress Log Files with Different Message Frequency Distributions. Applied Sciences, 12(4), 2044. https://doi.org/10.3390/app12042044






