Characterization of Deburring by Abrasive Flow Machining for AL6061
Abstract
:1. Introduction
2. Abrasive Flow Machining
2.1. Deburring Mechanism
2.2. Objective Function
3. Preliminary Testing
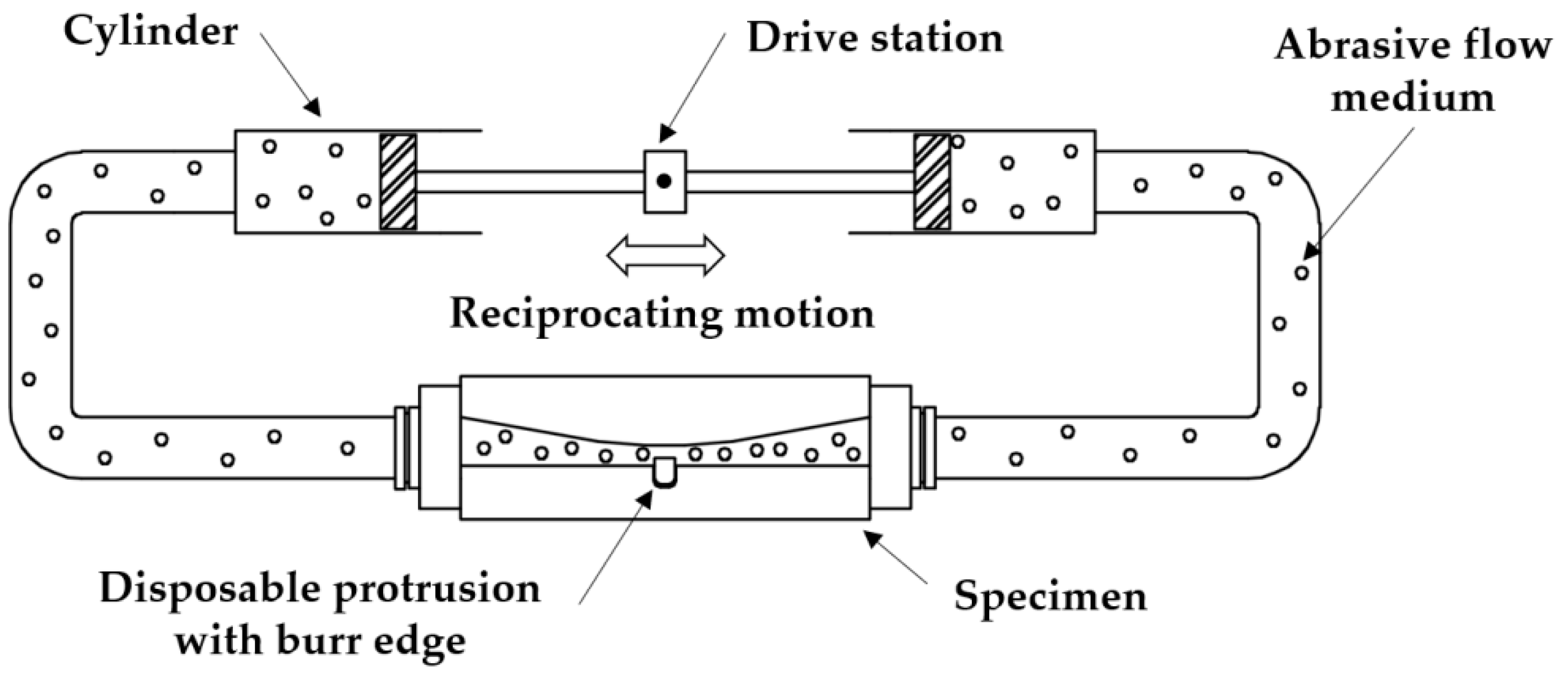
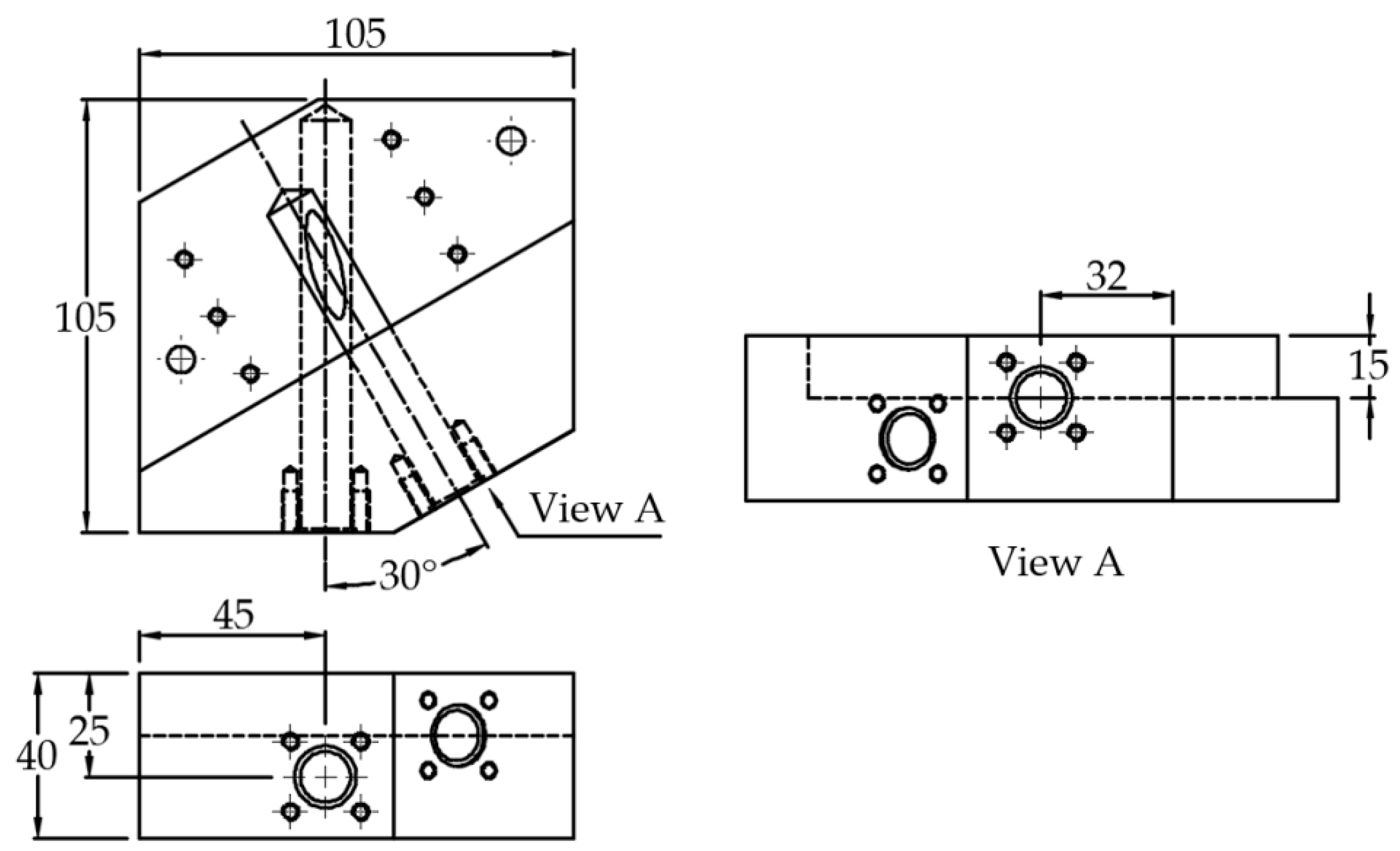
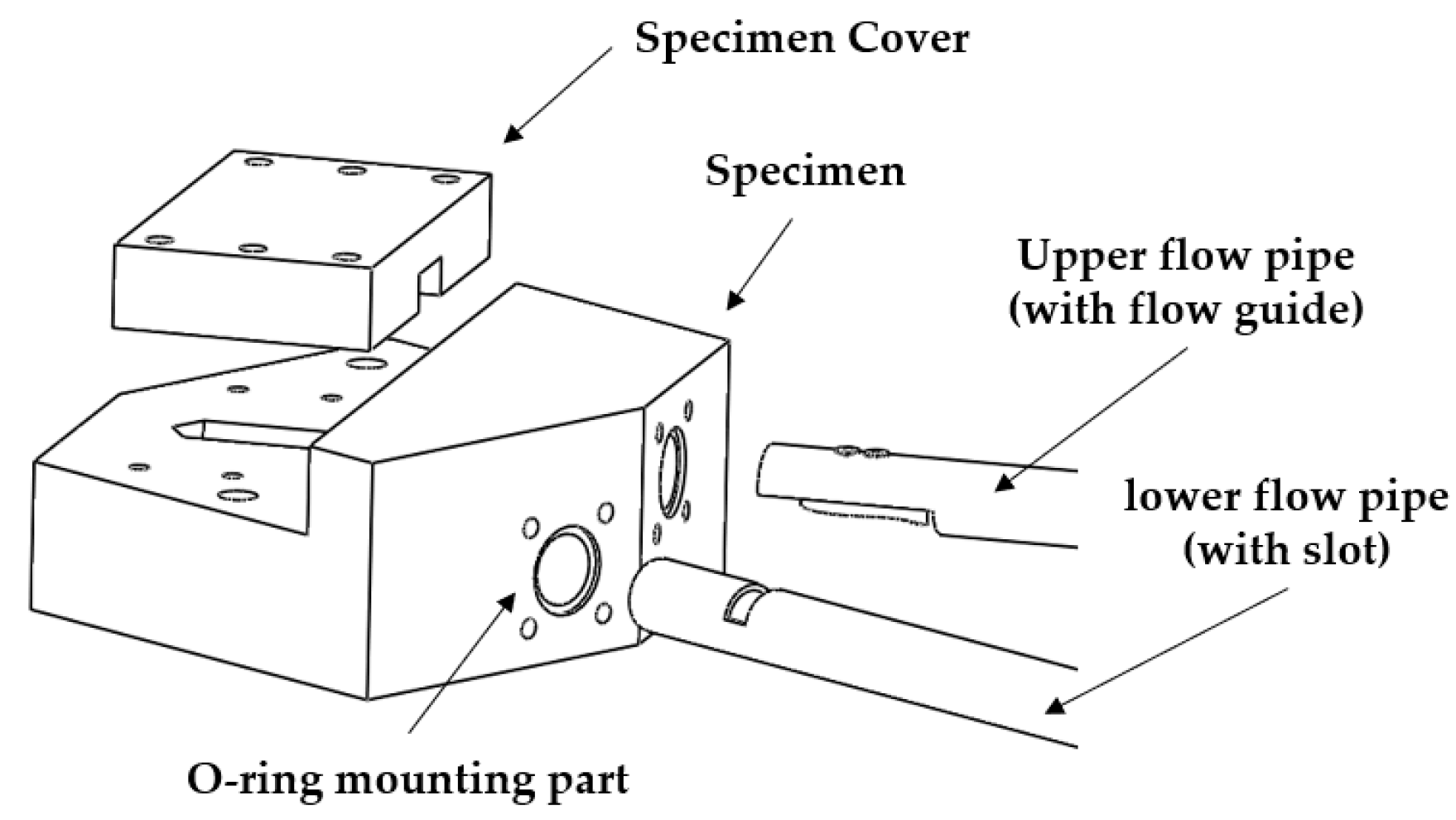
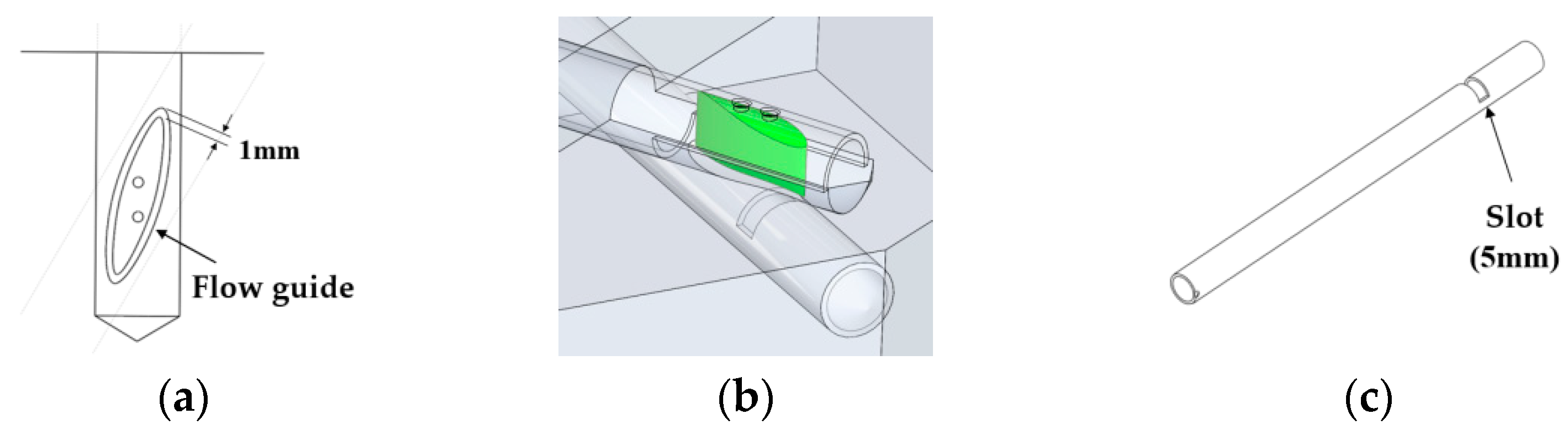
3.1. Deburring System
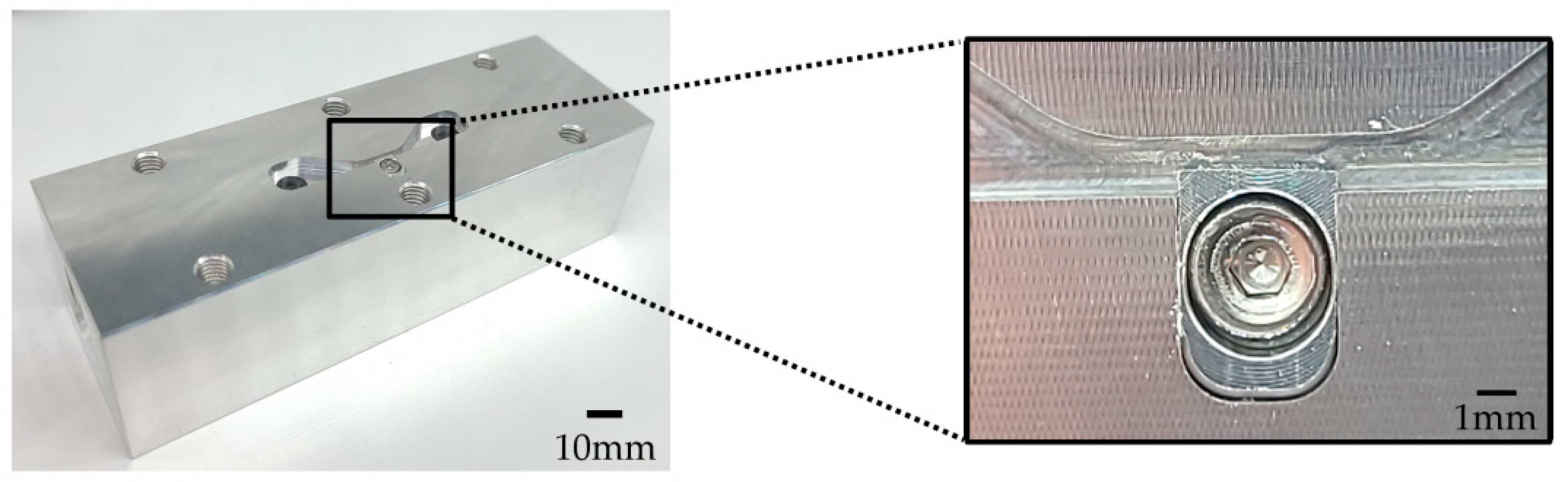
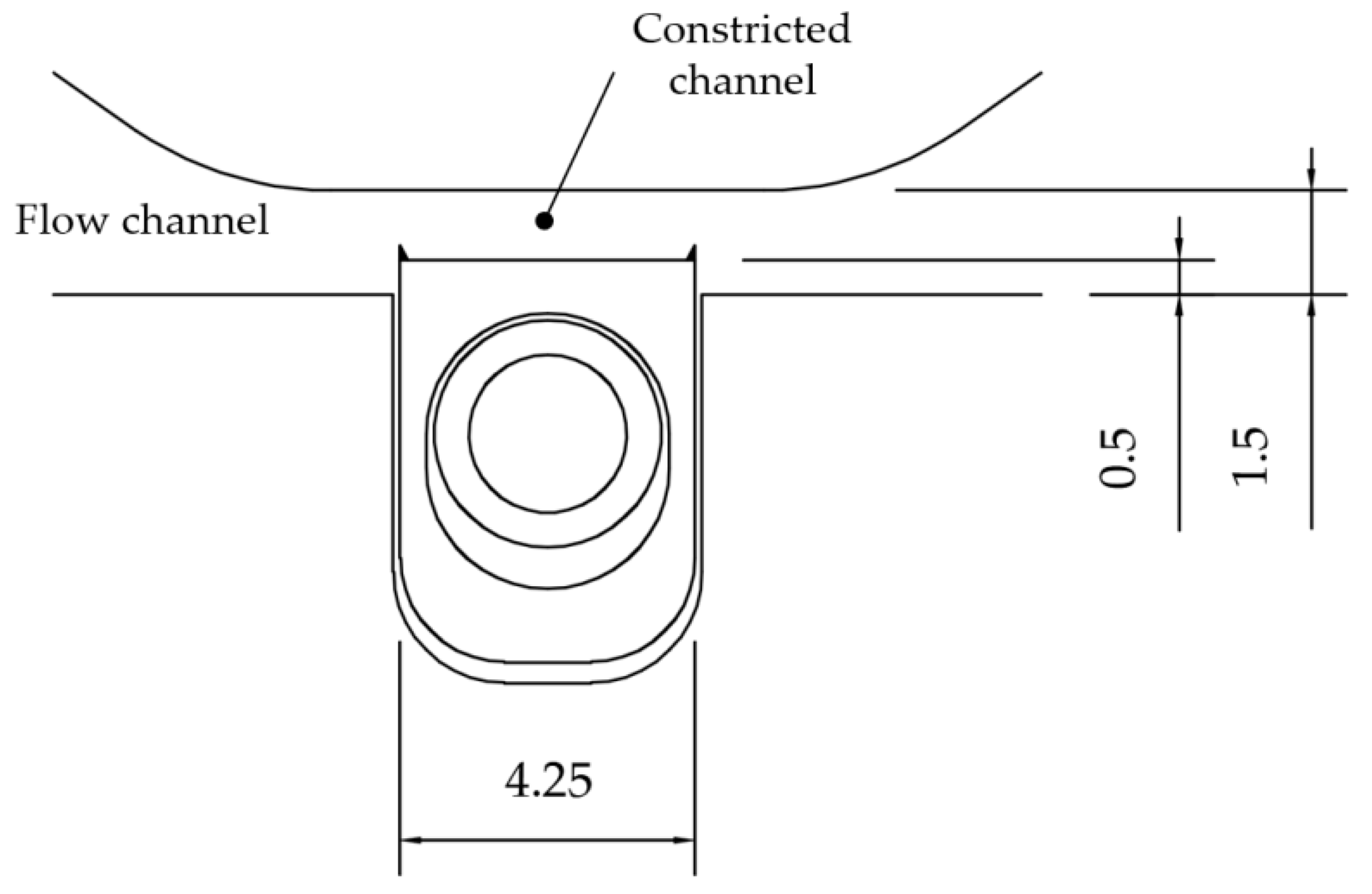
3.2. Test Setup (System and Abrasive Flow Medium)
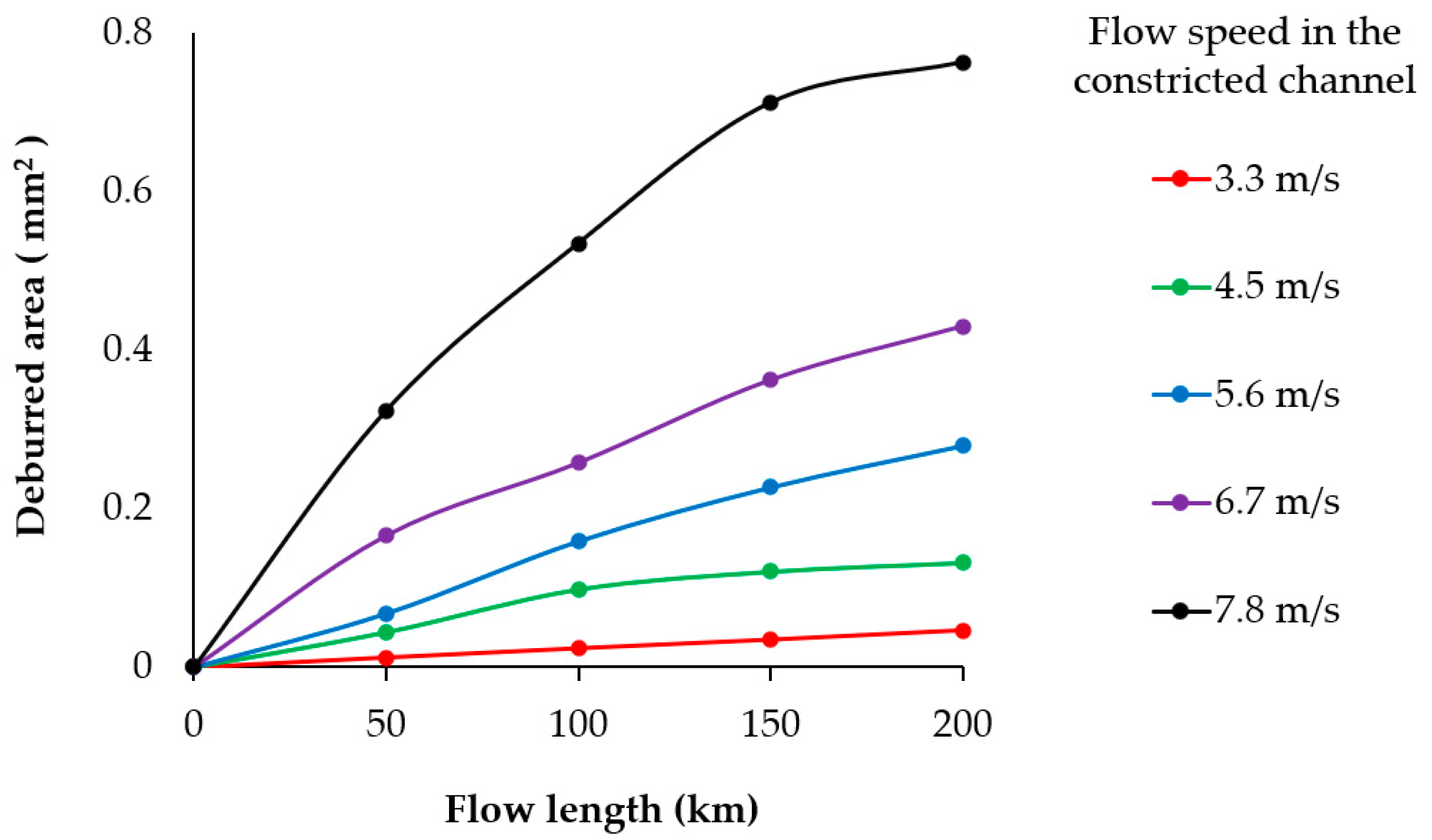
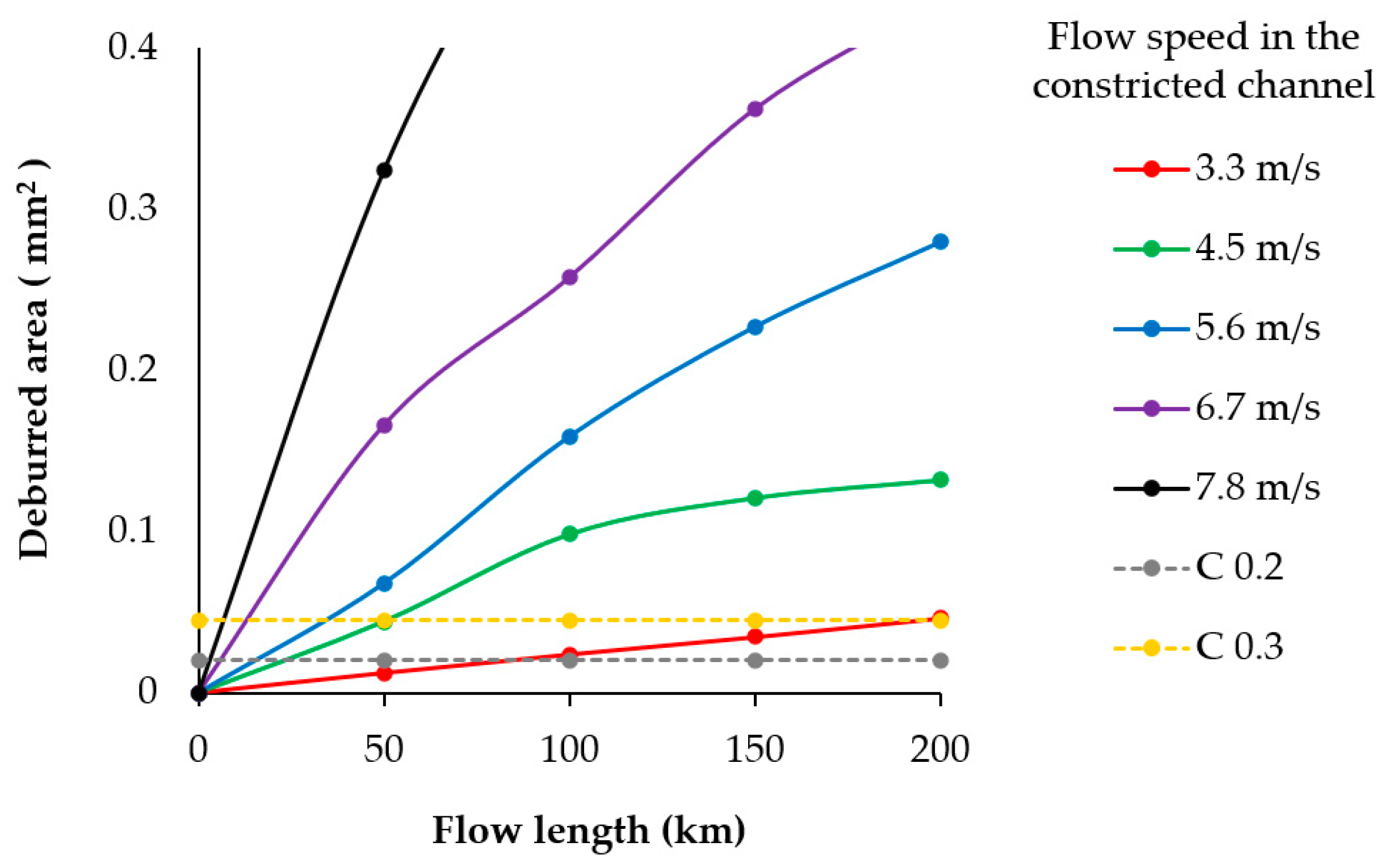
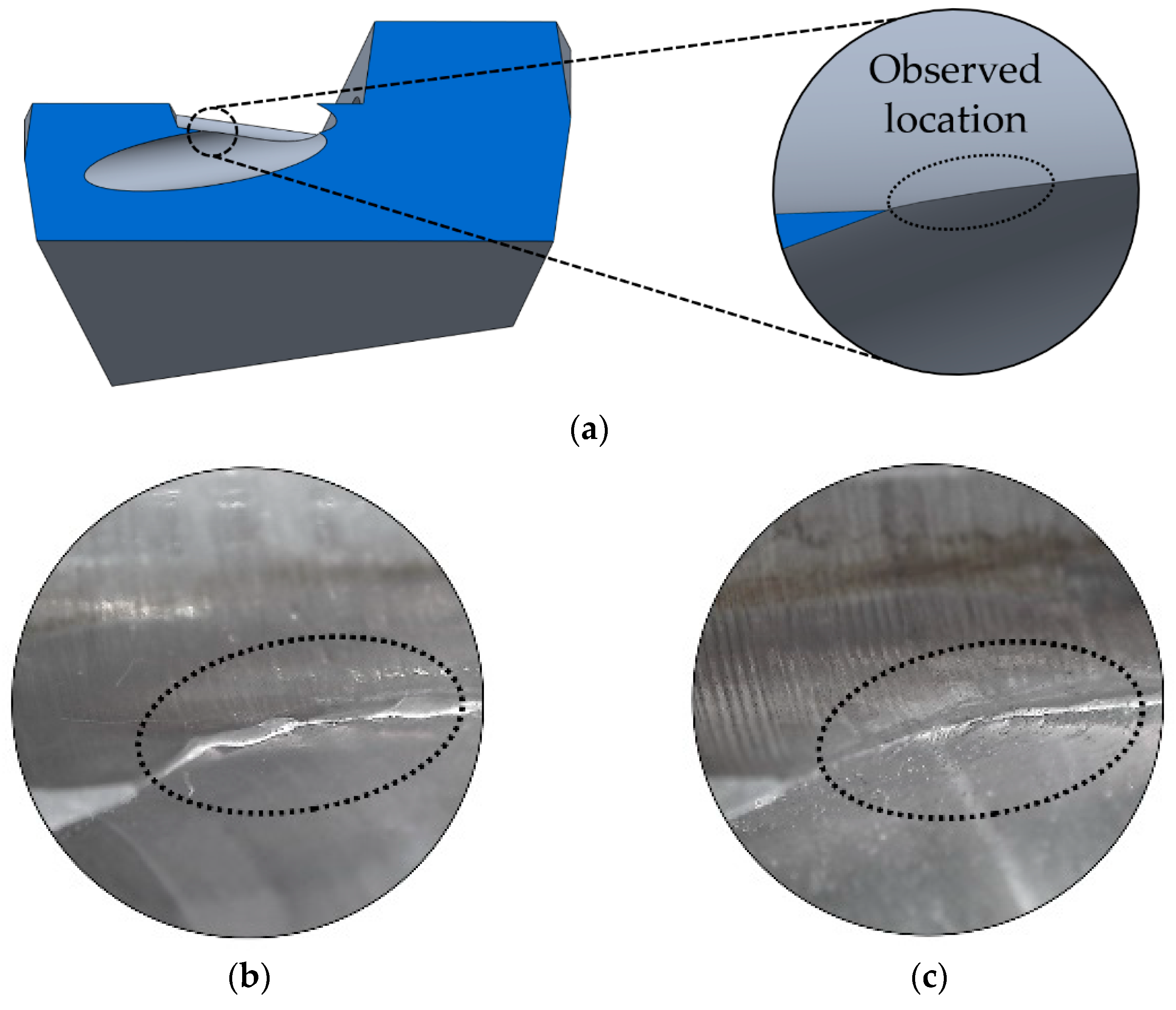
3.3. 200 km Flow Length Test and Results
3.4. Chamfering Test and Results
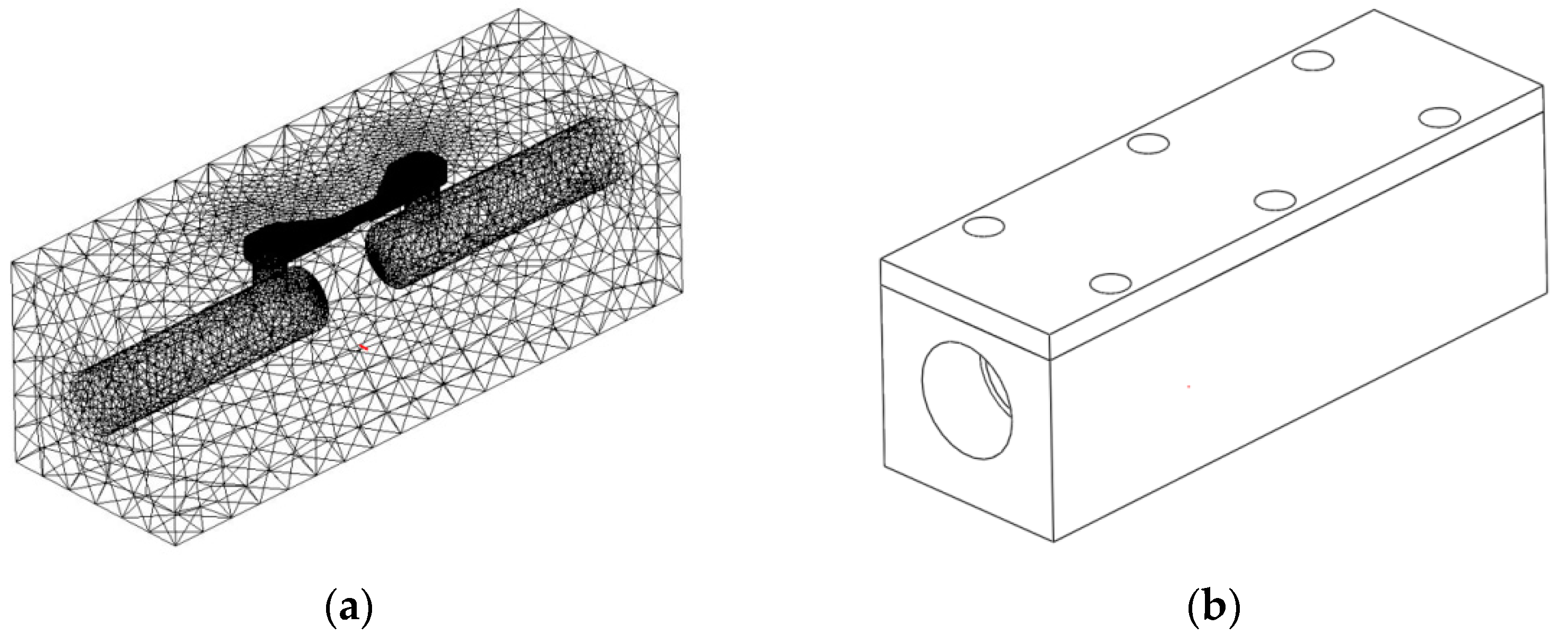
3.5. Computational Fluid Dynamics (CFD) Model
4. New Objective Function
4.1. Need for a New Objective Function
4.2. Suggestion for a New Objective Function
5. Validation of the New Objective Function
5.1. Deburring Test Setup
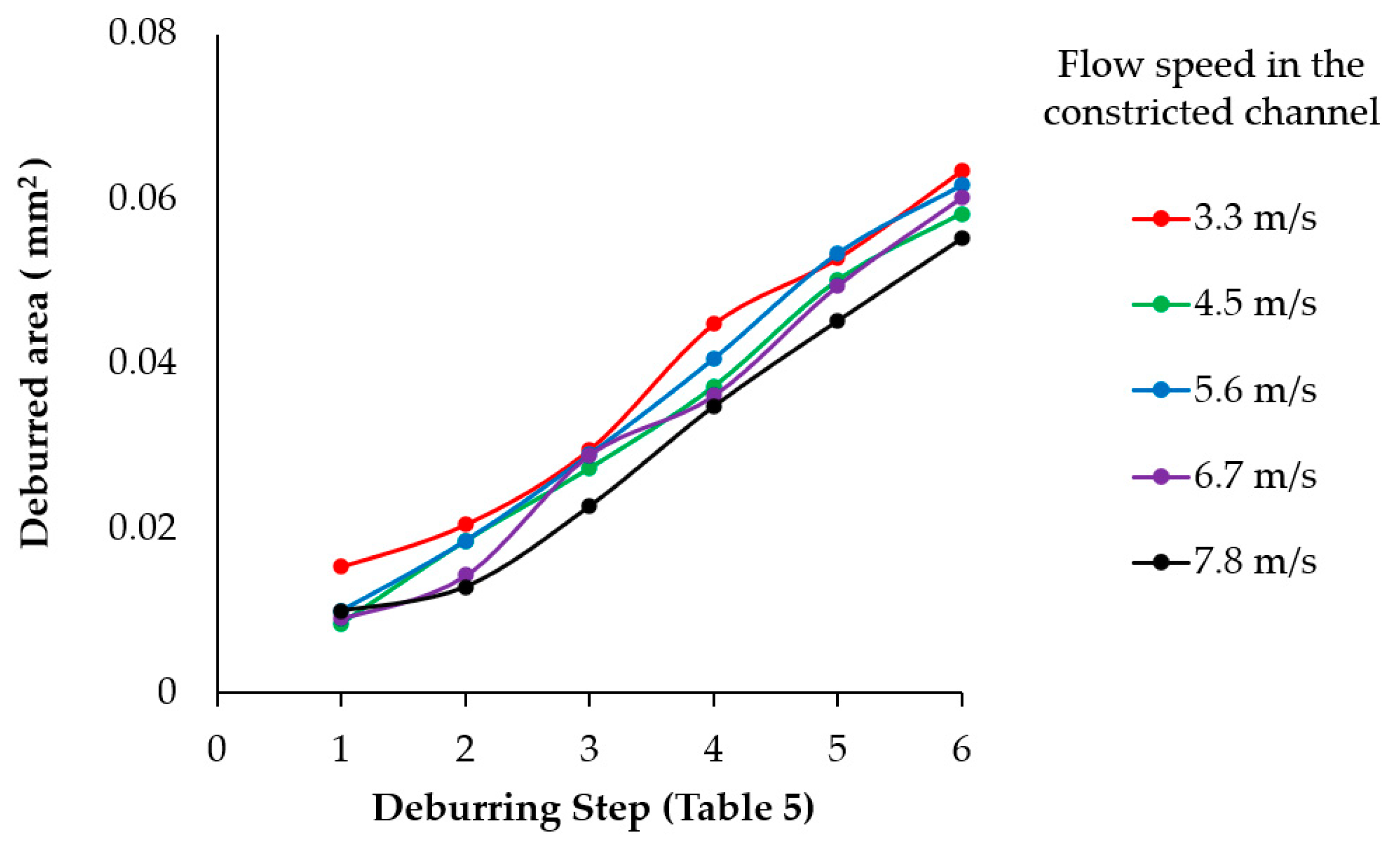
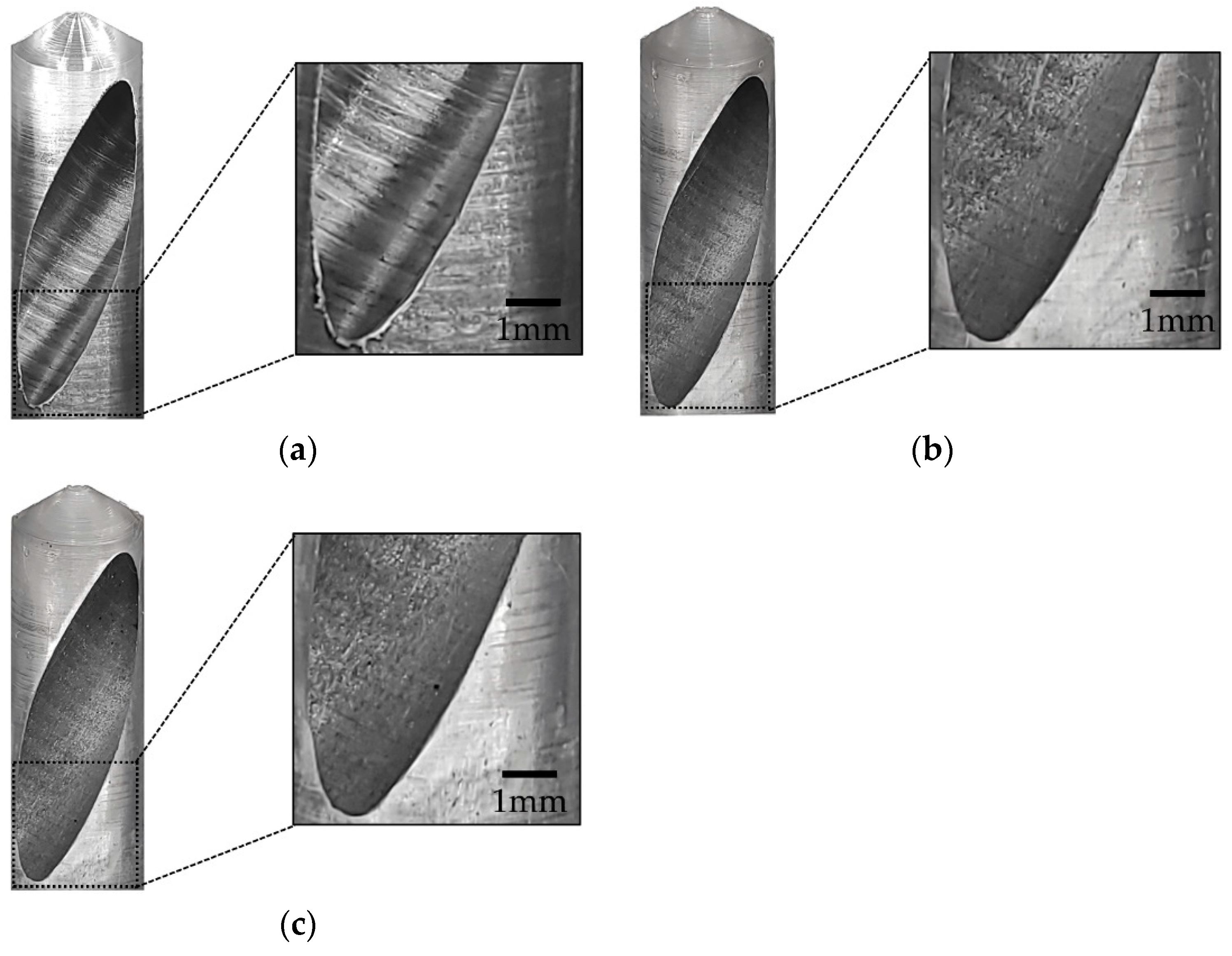
5.2. Deburring Test Results
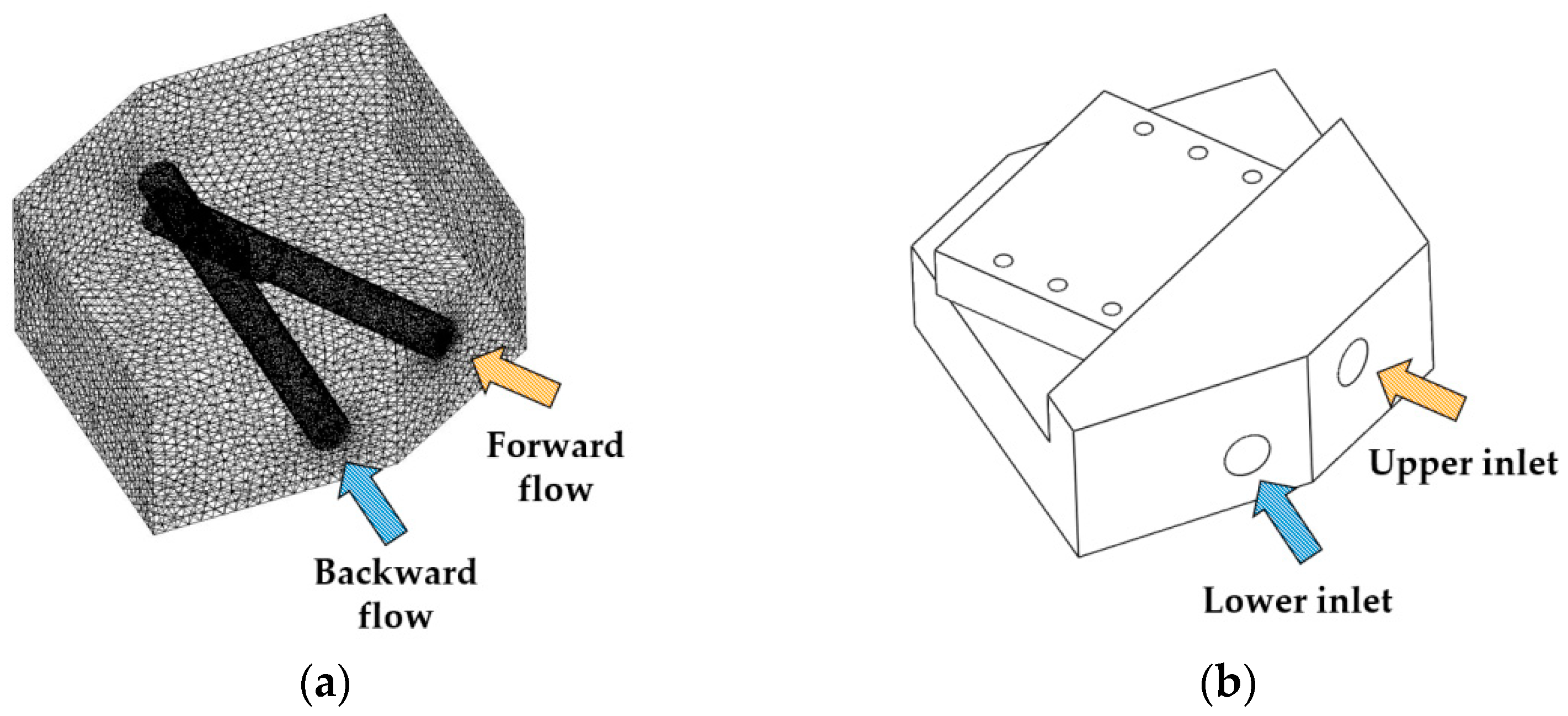
5.3. CFD Model
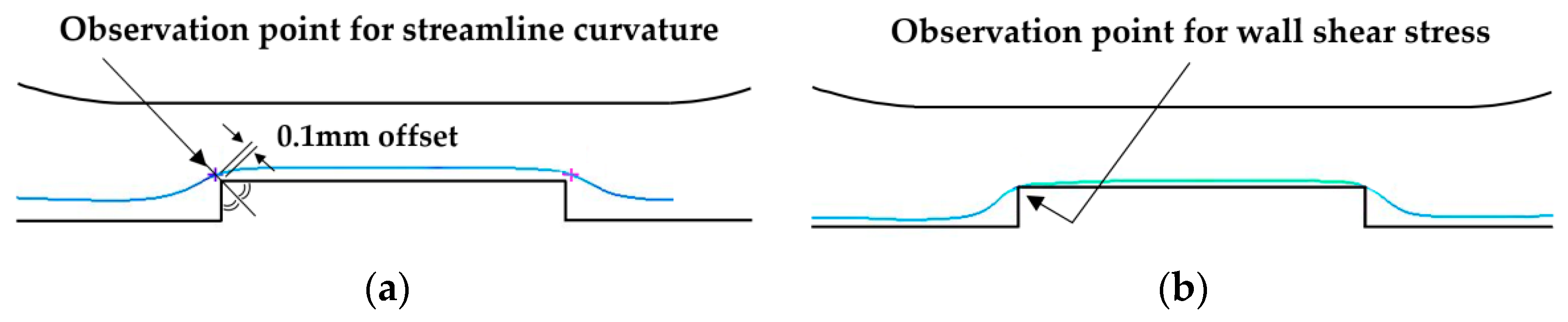
5.4. CFD Simulation and Validation of the New Objective Function
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gillespie, L.K. Deburring precision miniature parts. Precis. Eng. 1979, 1, 189–198. [Google Scholar] [CrossRef]
- Saptaji, K.; Triawan, F.; Sai, T.; Gebremariam, A. Deburring method of aluminum mold produced by milling process for microfluidic device fabrication. Indones. J. Sci. Technol. 2021, 6, 123–140. [Google Scholar] [CrossRef]
- Cho, C.H.; Kim, J.H.; Chae, S.W.; Kim, K.H. Improvement of a deburring tool for intersecting holes with reduced irregular cutting of burr edge. J. Eng. Manuf. 2013, 227, 1693–1703. [Google Scholar] [CrossRef]
- Kadam, S.P.; Mitra, S. Electrochemical deburring—A comprehensive review. Mater. Today Proc. 2021, 46, 141–148. [Google Scholar] [CrossRef]
- Kumar, A.S.; Deb, S.; Paul, S. Ultrasonic assisted abrasive micro-deburring of micromachined metallic alloys. J. Manuf. Process. 2021, 66, 595–607. [Google Scholar] [CrossRef]
- Balasubramaniam, R.; Krishnan, J.; Ramakrishnan, N. An experimental study on the abrasive jet deburring of cross-drilled holes. J. Mater. Process. Technol. 1999, 91, 178–182. [Google Scholar] [CrossRef]
- Jakub, M. Effect of ceramic brush treatment on the surface quality and edge condition of aluminum alloy after abrasive waterjet machining. Adv. Sci. Technol. Res. J. 2021, 15, 254–263. [Google Scholar]
- Yu, I.K. Improvement of the technological process of processing parts of coaxial radio components using thermal impulse deburring. J. Phys. Conf. Ser. 2021, 2032, 012066. [Google Scholar]
- Kwon, B.C.; Kim, K.H.; Kim, K.H.; Ko, S.L. New abrasive deburring method using suction for micro burrs at intersecting holes. CIRP Ann. 2016, 65, 145–148. [Google Scholar] [CrossRef]
- Sehijpal, S.; Shan, H.S. Development of magneto abrasive flow machining process. Int. J. Mach. Tools Manuf. 2002, 42, 953–959. [Google Scholar]
- Larry, R. Abrasive flow machining: A case study. J. Mater. Process. Technol. 1991, 28, 107–116. [Google Scholar]
- Dixit, N.; Sharma, V.; Kumar, P. Research trends in abrasive flow machining: A systematic review. J. Manuf. Process. 2021, 64, 1434–1461. [Google Scholar] [CrossRef]
- Kum, C.W.; Wu, C.H.; Wan, S.; Kang, C.W. Prediction and compensation of material removal for abrasive flow machining of additively manufactured metal components. J. Mater. Process. Technol. 2020, 282, 116704. [Google Scholar] [CrossRef]
- Choi, J.Y.; Kim, K.H. Research on the Deburring of Burr Edge at the Intersection of Small Holes. Master’s Thesis, Korea University, Seoul, Korea, 2015. [Google Scholar]
- Beom, J.K.; Kim, Y.G.; Kim, K.H. Study on the Deburring of Intersecting Holes with Abrasive Flow Machining. Master’s Thesis, Korea University, Seoul, Korea, 2018. [Google Scholar]
- Kim, K.J.; Kim, Y.G.; Kim, K.H. Deburring. Deburring of offset hole intersection with abrasive flow machining. Trans. Korean Soc. Mech. Eng. 2019, 43, 507–511. [Google Scholar] [CrossRef]
- Kim, D.W.; Kim, K.H. Removal of Drilling-Milling Composite Burrs by Abrasive Flow. Master’s Thesis, Korea University, Seoul, Korea, 2018. [Google Scholar]
- Kim, Y.G.; Kim, K.J.; Kim, K.H. Efficient Removal of milling Burrs by abrasive flow. Int. J. Precis. Eng. Manuf. 2021, 22, 441–451. [Google Scholar] [CrossRef]
- Uhlmann, E.; Mihotovic, V.; Szulczynski, H.; Kretzschmar, M. Developing a Process Model for Abrasive Flow Machining. In Burrs—Analysis, Control and Removal; Springer: Berlin/Heidelberg, Germany, 2010; pp. 73–78. [Google Scholar]
- Chen, X.; McLaury, B.S.; Shirazi, S.A. Numerical and experimental investigation of the relative erosion severity between plugged tees and elbows in dilute gas/solid two-phase flow. Wear 2006, 261, 715–729. [Google Scholar] [CrossRef]
- Edwards, J.K.; McLaury, B.S.; Shirazi, S.A. Modeling solid particle erosion in elbows and plugged tees. J. Energy Resour. Technol. 2001, 123, 277–284. [Google Scholar] [CrossRef]
- Wong, C.Y.; Solnordal, C.; Swallow, A.; Wu, J. Experimental and computational modelling of slid particle erosion in a pipe annular cavity. Wear 2013, 303, 109–129. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]














| Viscosity | 91.6 Poise | 63.5 Poise | 43.8 Poise | 30.2 Poise | 20.8 Poise |
|---|---|---|---|---|---|
| Flow speed 2.2 m/s | X 1 | X | X | X | X |
| Flow speed 4.5 m/s | O 2 | O | O | X | X |
| Flow speed 6.7 m/s | NA 3 | NA | O | O | O |
| Speed | 3.3 m/s | 4.5 m/s | 5.6 m/s | 6.7 m/s | 7.8 m/s | |
|---|---|---|---|---|---|---|
| Length | ||||||
| 50 km | 0.012 | 0.044 | 0.068 | 0.166 | 0.324 | |
| 100 km | 0.024 | 0.098 | 0.159 | 0.258 | 0.535 | |
| 150 km | 0.035 | 0.121 | 0.227 | 0.362 | 0.711 | |
| 200 km | 0.046 | 0.132 | 0.280 | 0.430 | 0.763 | |
| Chamfer | C0.2 | C0.3 | |
|---|---|---|---|
| Speed | |||
| 3.3 m/s | 83 km | 194 km | |
| 4.5 m/s | 23 km | 50 km | |
| 5.6 m/s | 16 km | 34 km | |
| 6.7 m/s | 6 km | 13 km | |
| 7.8 m/s | 3 km | 7 km | |
| Step | 3.3 m/s | 4.5 m/s | 5.6 m/s | 6.7 m/s | 7.8 m/s |
|---|---|---|---|---|---|
| 1 | 28 km | 8 km | 5 km | 2 km | 1 km |
| 2 | 56 km | 16 km | 10 km | 4 km | 2 km |
| 3 | 83 km | 23 km | 16 km | 6 km | 3 km |
| 4 | 120 km | 32 km | 22 km | 8 km | 4 km |
| 5 | 157 km | 41 km | 28 km | 10 km | 5 km |
| 6 | 194 km | 50 km | 34 km | 13 km | 7 km |
| Speed | 3.3 m/s | 4.5 m/s | 5.6 m/s | 6.7 m/s | 7.8 m/s | |
|---|---|---|---|---|---|---|
| Step of Deburring | ||||||
| Step 1 | 0.015 | 0.009 | 0.010 | 0.009 | 0.010 | |
| Step 2 | 0.021 | 0.019 | 0.019 | 0.014 | 0.013 | |
| Step 3 | 0.030 | 0.027 | 0.029 | 0.029 | 0.023 | |
| Step 4 | 0.044 | 0.037 | 0.041 | 0.036 | 0.035 | |
| Step 5 | 0.053 | 0.050 | 0.053 | 0.049 | 0.045 | |
| Step 6 | 0.063 | 0.058 | 0.062 | 0.060 | 0.055 | |
| 3.3 m/s | 4.5 m/s | 5.6 m/s | 6.7 m/s | 7.8 m/s | |
|---|---|---|---|---|---|
| τxy (kPa) | 14.05 | 18.46 | 22.62 | 26.72 | 30.58 |
| K (1/mm) | 1.28 | 1.28 | 1.29 | 1.29 | 1.30 |
| fob, Kim (N/m) | 10.7 | 14.1 | 17.2 | 20.2 | 23.1 |
| Deburred area (mm2) | 0.046 | 0.132 | 0.280 | 0.430 | 0.763 |
| 3.3 m/s | 4.5 m/s | 5.6 m/s | 6.7 m/s | 7.8 m/s | |
|---|---|---|---|---|---|
| fob, Kim (N/m) | 10.7 | 14.1 | 17.2 | 20.2 | 23.1 |
| fob, New (Nm/s2) | 10.2 | 23.6 | 44.5 | 75.1 | 115.1 |
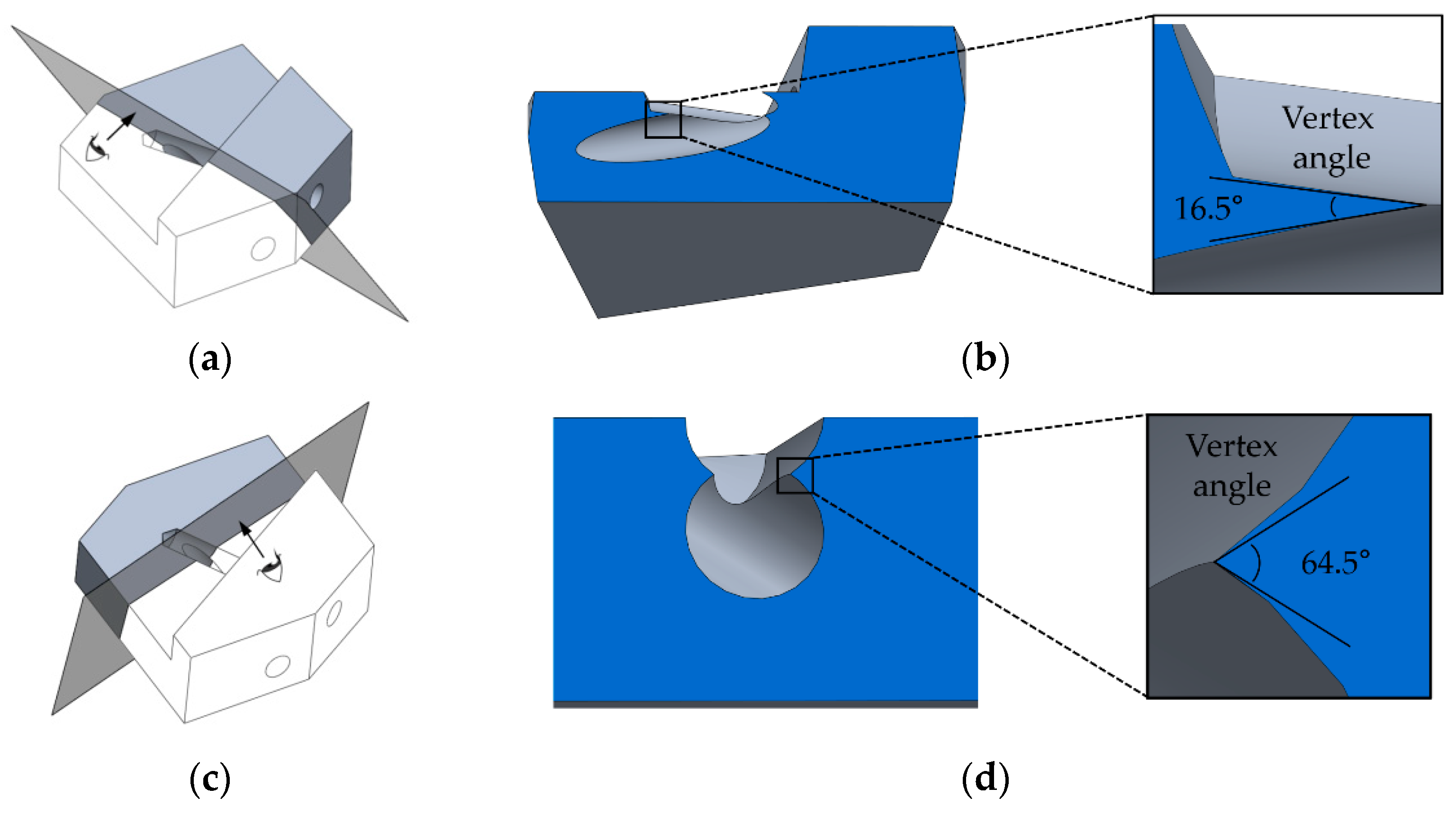
| Position | Vertex Angle | Position | Vertex Angle | Position | Vertex Angle |
|---|---|---|---|---|---|
| 1 | 16.5° | 5 | 60.9° | 9 | 60.9° |
| 2 | 50.3° | 6 | 50.6° | 10 | 64.5° |
| 3 | 60.7° | 7 | 16.5° | 11 | 60.7° |
| 4 | 64.5° | 8 | 50.6° | 12 | 50.2° |
| Length | Position 1 | Position 4 |
|---|---|---|
| 56 km | 0.033 | 0.022 |
| 112 km | 0.158 | 0.100 |
| Position | Forward (Nm/s2) | Backward (Nm/s2) | Average (Nm/s2) |
|---|---|---|---|
| 1 | 10,910.4 | 1662.9 | 6286.7 |
| 2 | 1124.7 | 458.4 | 791.6 |
| 3 | 3204 | 2197.6 | 2700.8 |
| 4 | 4595.4 | 3491.0 | 4043.2 |
| 5 | 11,027.9 | 5955.4 | 8491.7 |
| 6 | 16,173.9 | 15,396.9 | 15,785.4 |
| 7 | 6958.5 | 3962.9 | 5460.7 |
| 8 | 276 | 192.2 | 234.1 |
| 9 | 629.5 | 458.8 | 544.2 |
| 10 | 346.6 | 311.2 | 328.9 |
| 11 | 627.4 | 394.9 | 511.2 |
| 12 | 4736.2 | 2884.6 | 3810.4 |
| Average Objective Function Values | Deburred Area | |||
|---|---|---|---|---|
| fob, New (Nm/s2) | fob, Kim (N/m) | 56 km (mm2) | 112 km (mm2) | |
| Position 1 | 6286.7 | 22.4 | 0.033 | 0.158 |
| Position 4 | 4043.2 | 54.7 | 0.022 | 0.100 |
| Ratio (P1/P4) | 1.55 | 0.41 | 1.50 | 1.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.-J.; Kim, Y.-G.; Kim, K.-H. Characterization of Deburring by Abrasive Flow Machining for AL6061. Appl. Sci. 2022, 12, 2048. https://doi.org/10.3390/app12042048
Kim K-J, Kim Y-G, Kim K-H. Characterization of Deburring by Abrasive Flow Machining for AL6061. Applied Sciences. 2022; 12(4):2048. https://doi.org/10.3390/app12042048
Chicago/Turabian StyleKim, Kwang-Joon, Young-Gwan Kim, and Kwon-Hee Kim. 2022. "Characterization of Deburring by Abrasive Flow Machining for AL6061" Applied Sciences 12, no. 4: 2048. https://doi.org/10.3390/app12042048
APA StyleKim, K.-J., Kim, Y.-G., & Kim, K.-H. (2022). Characterization of Deburring by Abrasive Flow Machining for AL6061. Applied Sciences, 12(4), 2048. https://doi.org/10.3390/app12042048








