Joint Stiffness Influence on the First-Order Seismic Capacity of Dry-Joint Masonry Structures: Numerical DEM Investigations
Abstract
:Featured Application
Abstract
1. Introduction
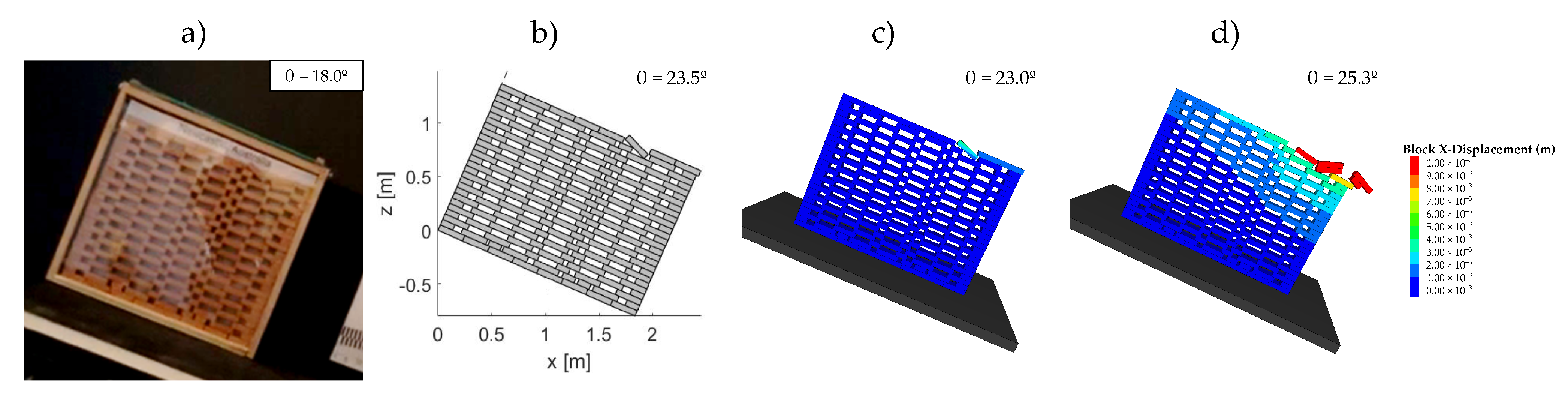
2. Tilting Tests on Perforated Dry-Masonry Walls
- Having unperforated external edges (two sides and top).
- Having at least 30% of voids inside the structure.
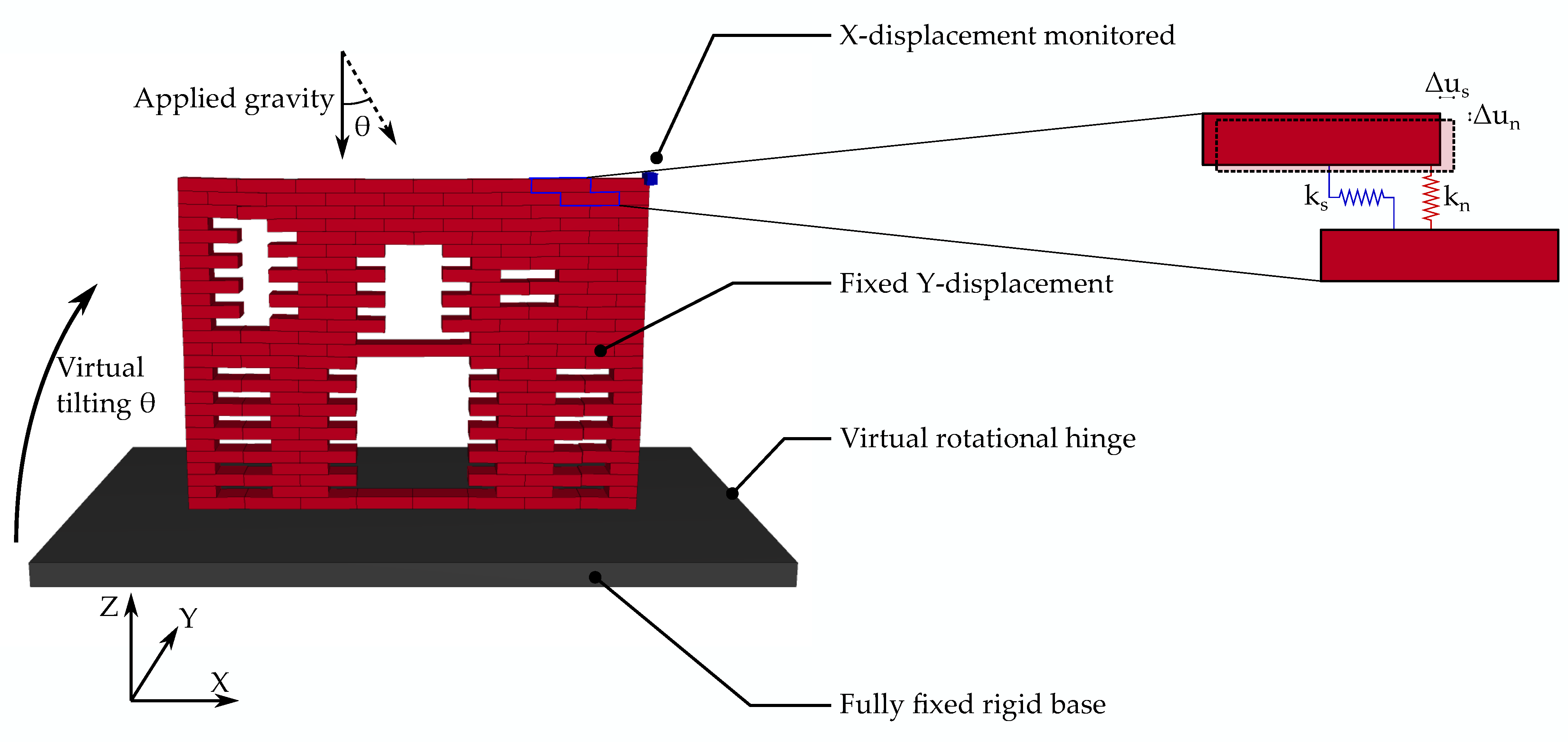
3. Numerical Discrete Element Method (DEM)
Δτ = ks ⋅ Δus = ks ⋅ [us(t + Δt) − us(t)].
vi(t + Δt/2) = vi(t − Δt/2) + ai(t) ⋅ Δt
ui(t + Δt) = ui(t) + vi(t + Δt/2) ⋅ Δt.
τ(t + Δt) = τ(t) + Δτ, |τ| < τmax = −σ ⋅ μ.
4. Results
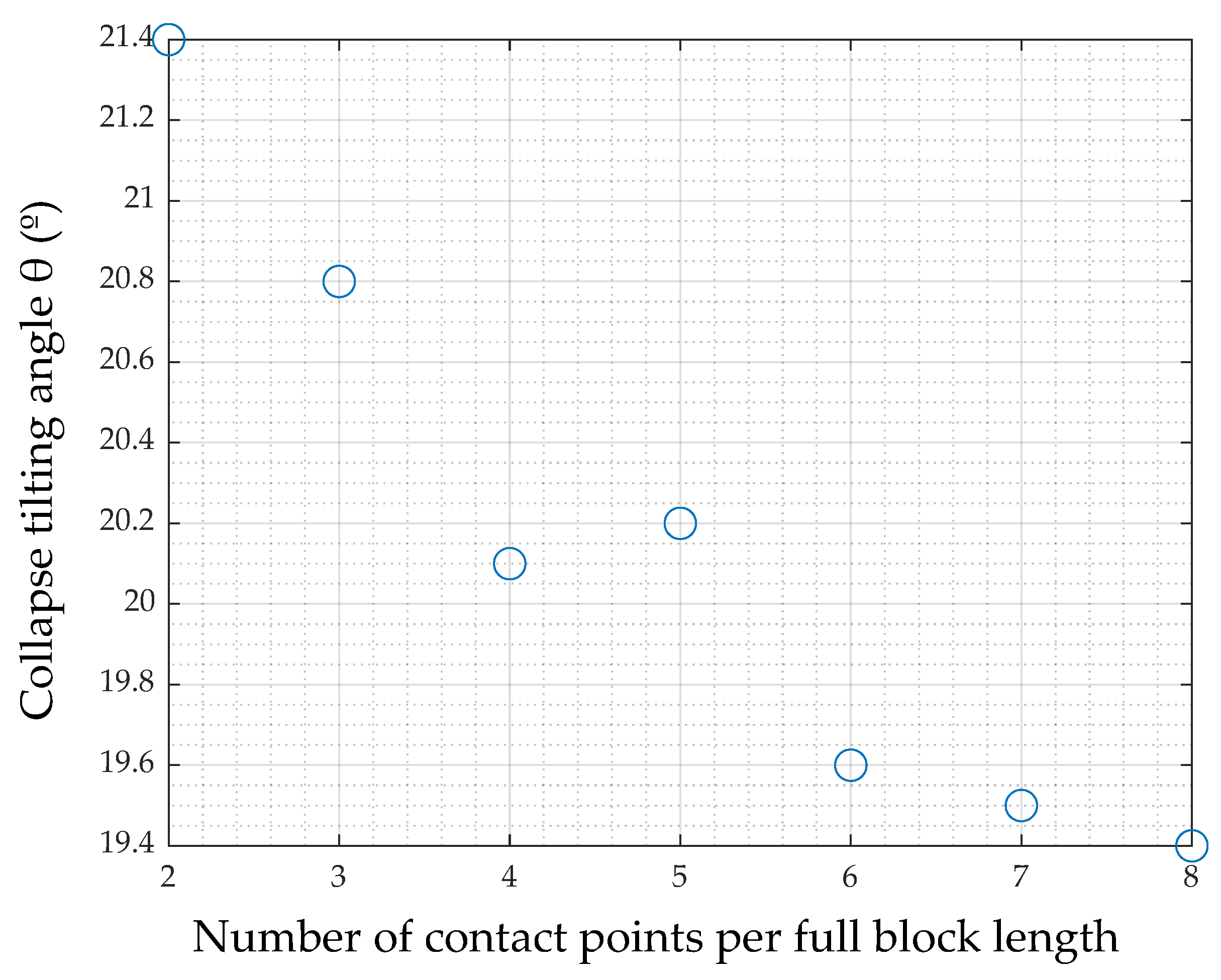
4.1. Mesh Sensitivity Analysis
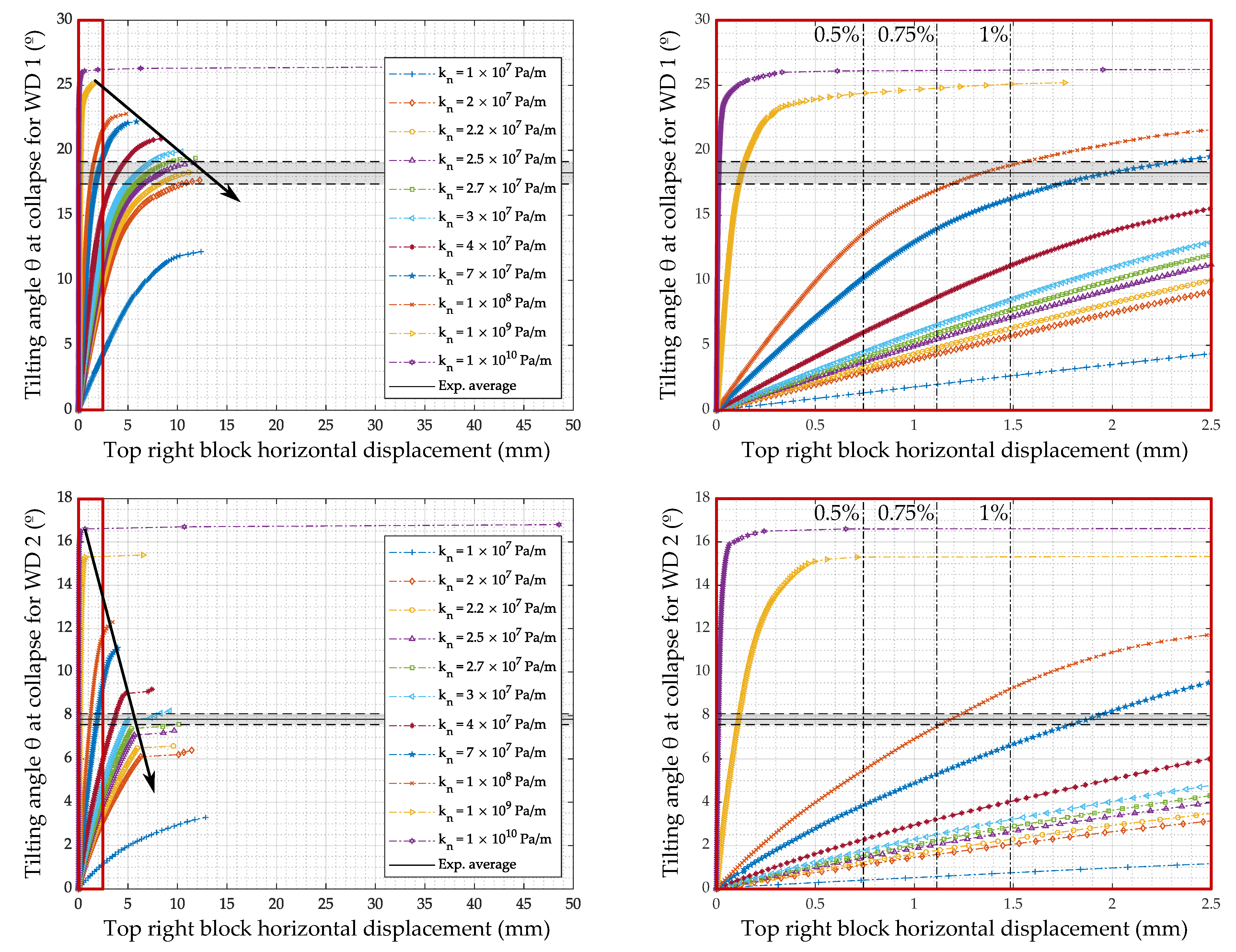
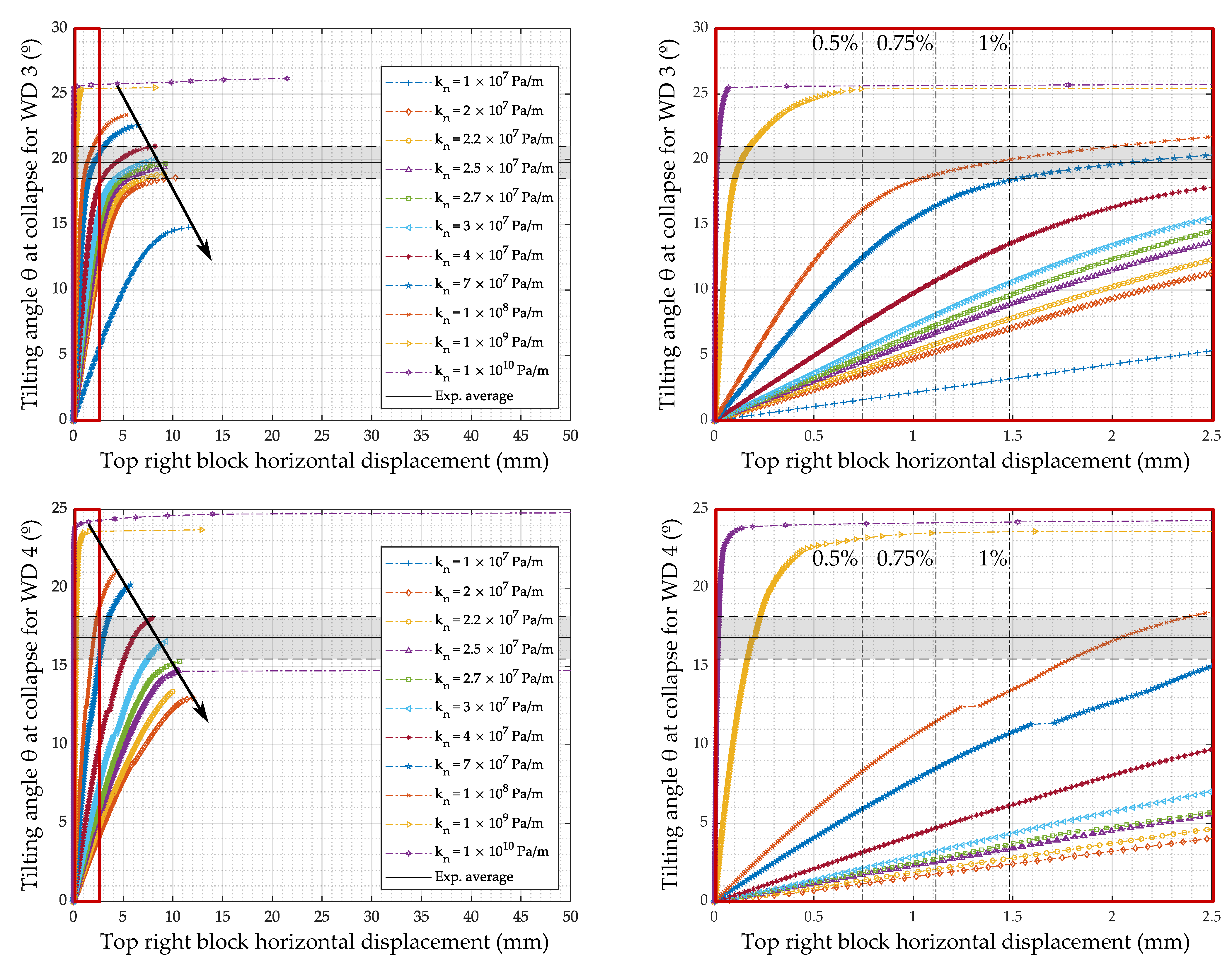
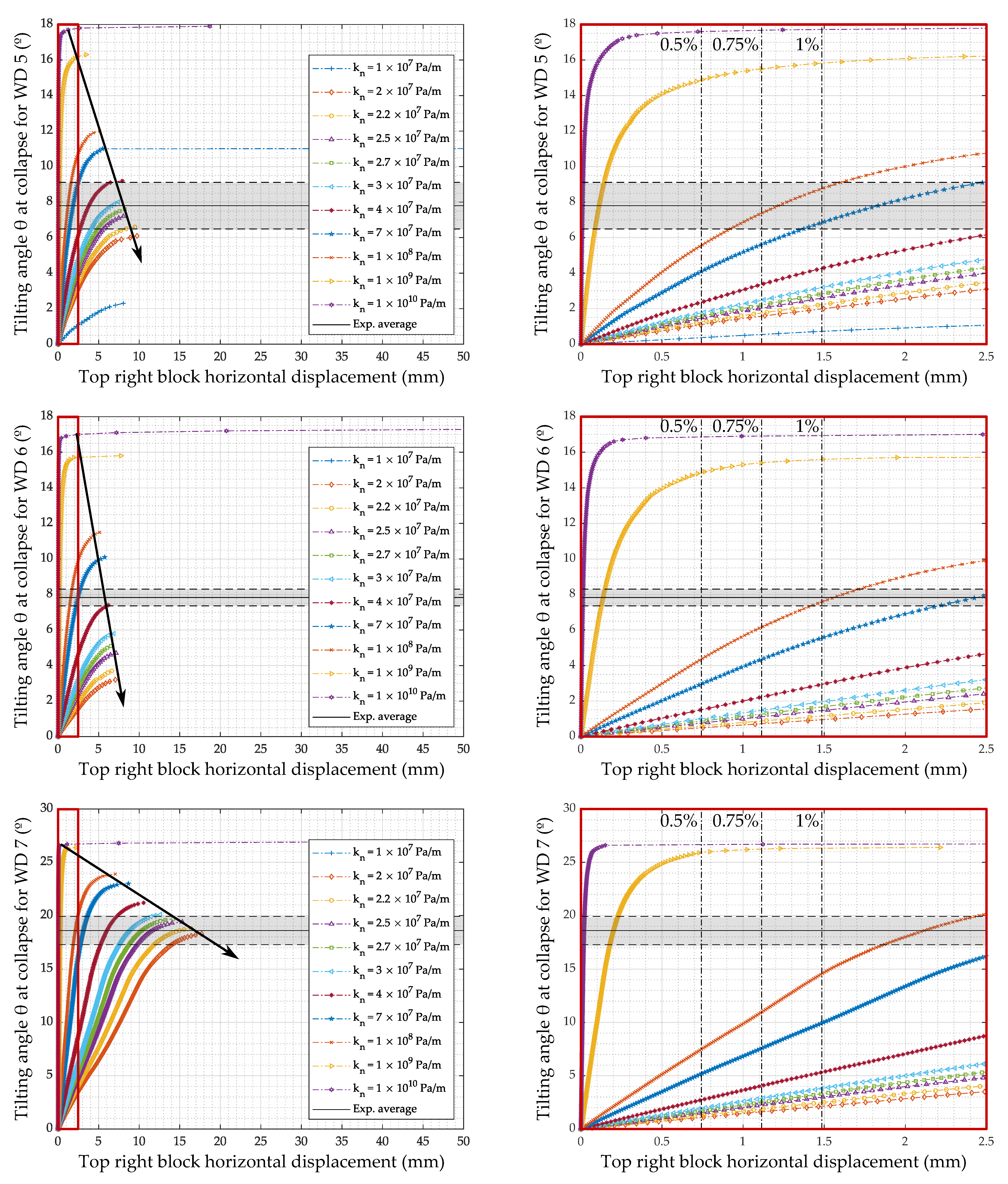
4.2. Simulations with Classical Joint Stiffness Values
- kn = ks = 1 × 109 Pa/m
- kn = ks = 1 × 1010 Pa/m.
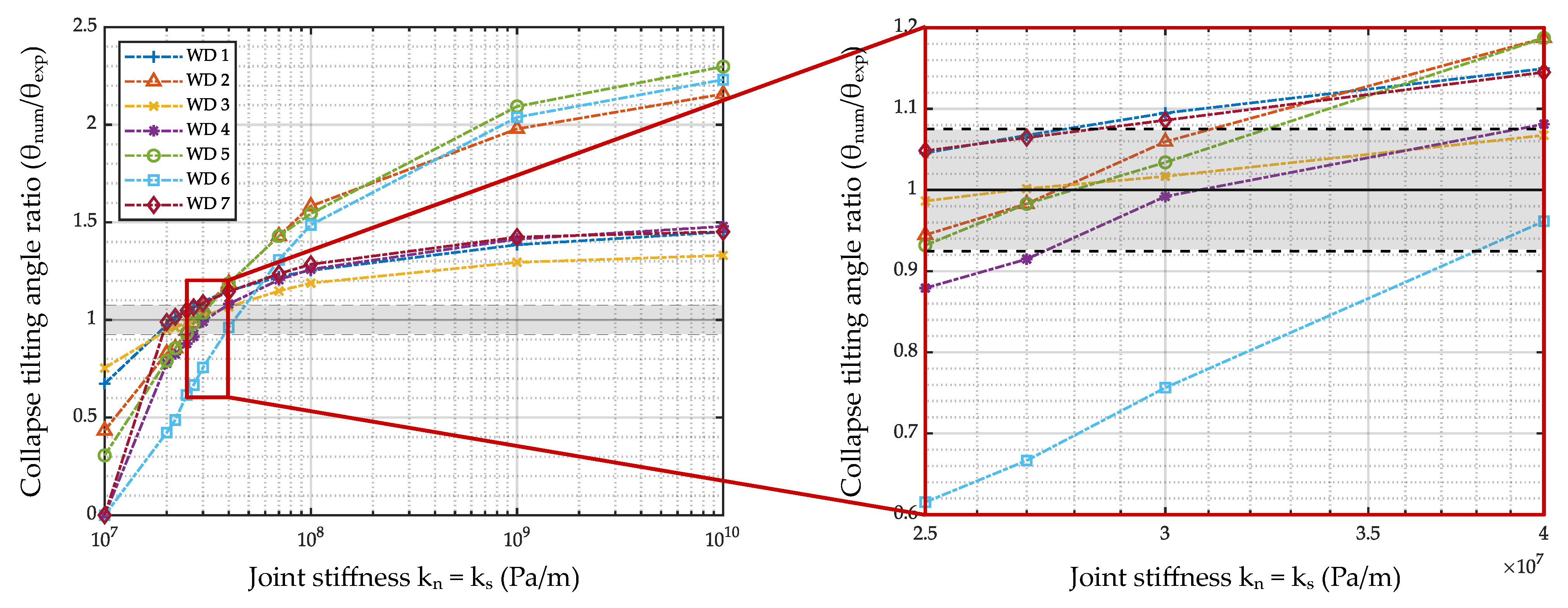
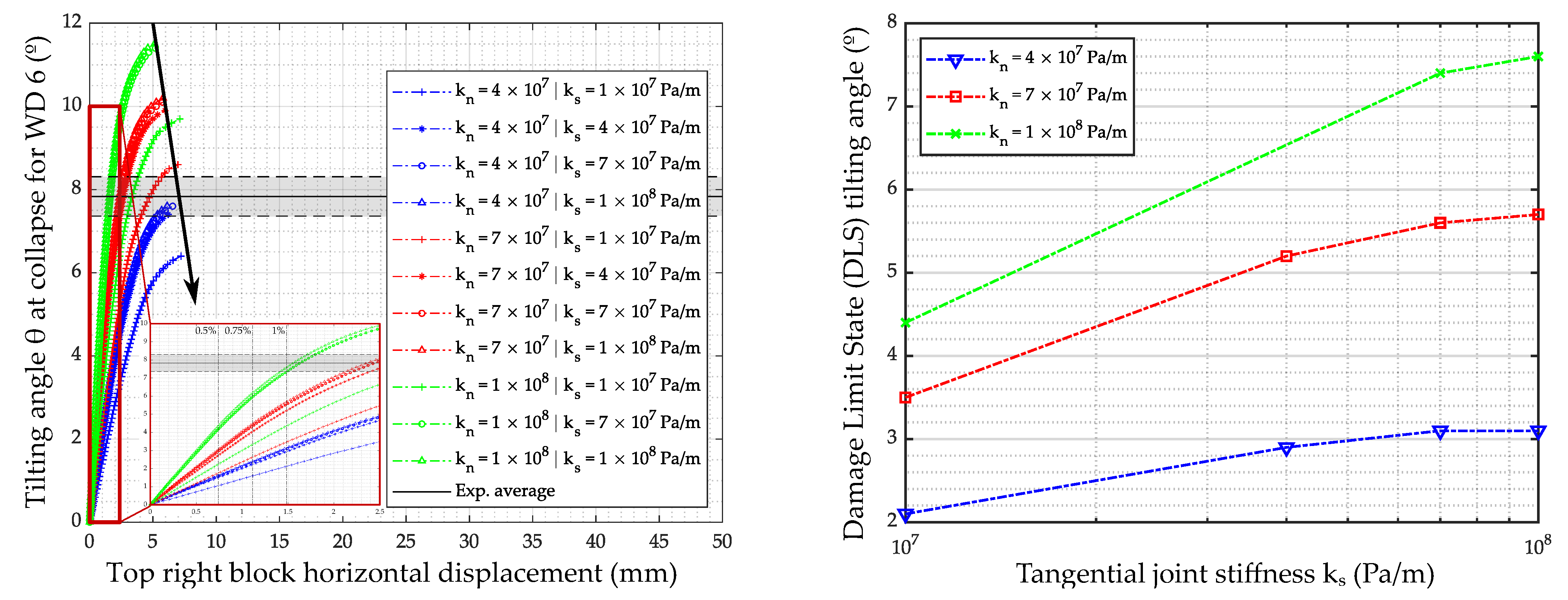
4.3. Influence of Low Joint Stiffness on the Simulation Results
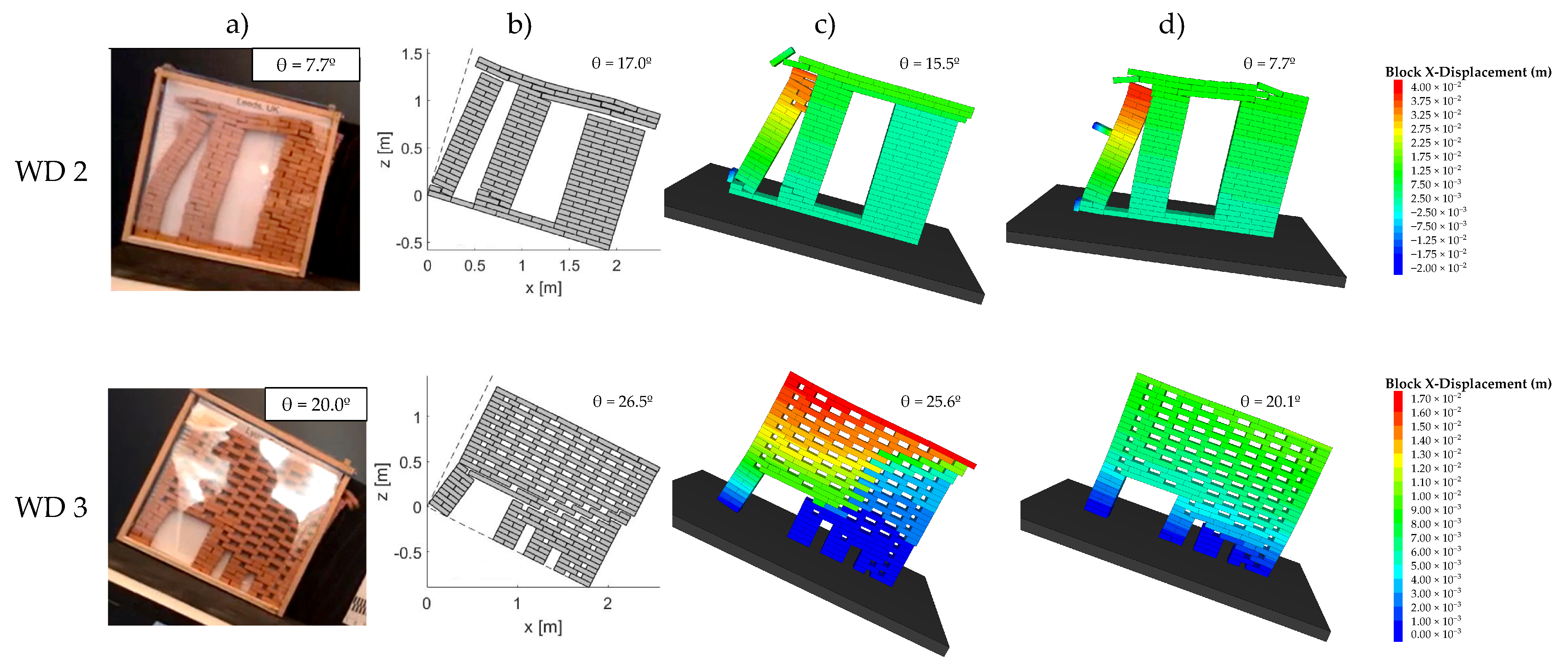
4.4. Validation of the Approach
- First, the joint stiffness of the studied block contacts must be evaluated. This can be done either using the proposed approach, i.e., calibrating the numerical value based on experiments conducted on structures (post-diction). Ideally, different structures should be investigated. Another option, which is even better, consists in characterising the joint stiffness itself, monitoring joints from a wall under vertical compression, as in [35]. The latter can be complemented by simpler joint closure tests [33]. Note that a combination of both experimental characterisation and numerical calibration/validation is ideal.
- Then, the numerical model with the calibrated parameters can be used in the engineering practice to assess every structure made of the same blocks (predictions).
5. Code Aspects and Masonry Structures with Soft Joints
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heyman, J. The Stone Skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
- Dejong, J.M.; Ochsendorf, A. Analysis of Vaulted Masonry Structures Subjected to Horizontal Ground Motion. In Proceedings of the 5th International Conference on Structural Analysis of Historical Constructions, New Delhi, India, 6–8 November 2006; pp. 973–980. [Google Scholar]
- Portioli, F.; Cascini, L. Assessment of masonry structures subjected to foundation settlements using rigid block limit analysis. Eng. Struct. 2016, 113, 347–361. [Google Scholar] [CrossRef]
- Bui, T.-T.; Limam, A.; Sarhosis, V.; Hjiaj, M. Discrete element modelling of the in-plane and out-of-plane behaviour of dry-joint masonry wall constructions. Eng. Struct. 2017, 136, 277–294. [Google Scholar] [CrossRef] [Green Version]
- Smoljanović, H.; Živaljić, N.; Nikolić, Ž.; Munjiza, A. Numerical Analysis of 3D Dry-Stone Masonry Structures by Combined Finite-Discrete Element Method. Int. J. Solids Struct. 2018, 136–137, 150–167. [Google Scholar] [CrossRef]
- Malena, M.; Portioli, F.; Gagliardo, R.; Tomaselli, G.; Cascini, L.; de Felice, G. Collapse mechanism analysis of historic masonry structures subjected to lateral loads: A comparison between continuous and discrete models. Comput. Struct. 2019, 220, 14–31. [Google Scholar] [CrossRef]
- Lemos, J.V. Discrete Element Modeling of the Seismic Behavior of Masonry Construction. Buildings 2019, 9, 43. [Google Scholar] [CrossRef] [Green Version]
- Pulatsu, B.; Gencer, F.; Erdogmus, E. Study of the Effect of Construction Techniques on the Seismic Capacity of Ancient Dry-Joint Masonry Towers Through DEM. Eur. J. Environ. Civ. Eng. 2020, 1–18. [Google Scholar] [CrossRef]
- Funari, M.; Mehrotra, A.; Lourenço, P. A Tool for the Rapid Seismic Assessment of Historic Masonry Structures Based on Limit Analysis Optimisation and Rocking Dynamics. Appl. Sci. 2021, 11, 942. [Google Scholar] [CrossRef]
- Casapulla, C.; Argiento, L.U.; Maione, A.; Speranza, E. Upgraded formulations for the onset of local mechanisms in multi-storey masonry buildings using limit analysis. Structures 2021, 31, 380–394. [Google Scholar] [CrossRef]
- Marmo, F. ArchLab: A MATLAB Tool for the Thrust Line Analysis of Masonry Arches. Curved Layer. Struct. 2021, 8, 26–35. [Google Scholar] [CrossRef]
- Gobbin, F.; de Felice, G.; Lemos, J.V. Numerical procedures for the analysis of collapse mechanisms of masonry structures using discrete element modelling. Eng. Struct. 2021, 246, 113047. [Google Scholar] [CrossRef]
- Portioli, F.; Cascini, L. Large displacement analysis of dry-jointed masonry structures subjected to settlements using rigid block modelling. Eng. Struct. 2017, 148, 485–496. [Google Scholar] [CrossRef]
- Restrepo Vélez, L.F.; Magenes, G.; Griffith, M.C. Dry Stone Masonry Walls in Bending—Part I: Static Tests. Int. J. Archit. Herit. 2014, 8, 1–28. [Google Scholar] [CrossRef]
- Shi, Y.; D’Ayala, D.; Prateek, J. Analysis of Out-of-Plane Damage Behaviour of Unreinforced Masonry Walls. In Proceedings of the 14th International Brick and Block Masonry Conference, The University of Newcastle, Sydney, Australia, 13–20 February 2008; pp. 02–17. [Google Scholar]
- Casapulla, C.; Maione, A. Experimental and Analytical Investigation on the Corner Failure in Masonry Buildings: Interaction between Rocking-Sliding and Horizontal Flexure. Int. J. Arch. Heritage 2018, 14, 208–220. [Google Scholar] [CrossRef]
- Giardina, G.; Marini, A.; Riva, P.; Giuriani, E. Analysis of a scaled stone masonry facade subjected to differential settlements. Int. J. Arch. Heritage 2020, 14, 1502–1516. [Google Scholar] [CrossRef]
- Gaetani, A.; Lourenco, P.; Monti, G.; Moroni, M. Shaking table tests and numerical analyses on a scaled dry-joint arch undergoing windowed sine pulses. Bull. Earthq. Eng. 2017, 15, 4939–4961. [Google Scholar] [CrossRef] [Green Version]
- Milani, G.; Rossi, M.; Calderini, C.; Lagomarsino, S. Tilting plane tests on a small-scale masonry cross vault: Experimental results and numerical simulations through a heterogeneous approach. Eng. Struct. 2016, 123, 300–312. [Google Scholar] [CrossRef]
- Stockdale, G.L.; Sarhosis, V.; Milani, G. Seismic capacity and multi-mechanism analysis for dry-stack masonry arches subjected to hinge control. Bull. Earthq. Eng. 2020, 18, 673–724. [Google Scholar] [CrossRef]
- Gagliardo, R.; Portioli, F.; Cascini, L.; Landolfo, R.; Lourenço, P. A rigid block model with no-tension elastic contacts for displacement-based assessment of historic masonry structures subjected to settlements. Eng. Struct. 2021, 229, 111609. [Google Scholar] [CrossRef]
- Grillanda, N.; Chiozzi, A.; Milani, G.; Tralli, A. Tilting plane tests for the ultimate shear capacity evaluation of perforated dry joint masonry panels. Part I: Experimental tests. Eng. Struct. 2021, 238, 112124. [Google Scholar] [CrossRef]
- Giamundo, V.; Sarhosis, V.; Lignola, G.; Sheng, Y.; Manfredi, G. Evaluation of different computational modelling strategies for the analysis of low strength masonry structures. Eng. Struct. 2014, 73, 160–169. [Google Scholar] [CrossRef] [Green Version]
- Ubertini, F.; Cavalagli, N.; Kita, A.; Comanducci, G. Assessment of a monumental masonry bell-tower after 2016 Central Italy seismic sequence by long-term SHM. Bull. Earthq. Eng. 2018, 16, 775–801. [Google Scholar] [CrossRef]
- Funari, M.F.; Hajjat, A.E.; Masciotta, M.G.; Oliveira, D.V.; Lourenço, P.B. A Parametric Scan-to-FEM Framework for the Digital Twin Generation of Historic Masonry Structures. Sustainability 2021, 13, 11088. [Google Scholar] [CrossRef]
- Oliveira, D.; Basilio, I.; Lourenco, P. Experimental Behavior of FRP Strengthened Masonry Arches. J. Compos. Constr. 2010, 14, 312–322. [Google Scholar] [CrossRef] [Green Version]
- Grillanda, N.; Chiozzi, A.; Milani, G.; Tralli, A. Tilting plane tests for the ultimate shear capacity evaluation of perforated dry joint masonry panels. Part II: Numerical analyses. Eng. Struct. 2021, 228, 111460. [Google Scholar] [CrossRef]
- Savalle, N.; Vincens, E.; Hans, S. Pseudo-static scaled-down experiments on dry stone retaining walls: Preliminary implications for the seismic design. Eng. Struct. 2018, 171, 336–347. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Mendes, N.; Ramos, L.; Oliveira, D. Analysis of Masonry Structures Without Box Behavior. Int. J. Arch. Heritage 2011, 5, 369–382. [Google Scholar] [CrossRef]
- de Felice, G.; De Santis, S.; Lourenço, P.B.; Mendes, N. Methods and Challenges for the Seismic Assessment of Historic Masonry Structures. Int. J. Arch. Heritage 2016, 11, 143–160. [Google Scholar] [CrossRef] [Green Version]
- Portioli, F.; Casapulla, C.; Gilbert, M.; Cascini, L. Limit analysis of 3D masonry block structures with non-associative frictional joints using cone programming. Comput. Struct. 2014, 143, 108–121. [Google Scholar] [CrossRef]
- Andreev, K.; Sinnema, S.; Rekik, A.; Allaoui, S.; Blond, E.; Gasser, A. Compressive behaviour of dry joints in refractory ceramic masonry. Constr. Build. Mater. 2012, 34, 402–408. [Google Scholar] [CrossRef] [Green Version]
- Kulatilake, P.H.S.W.; Shreedharan, S.; Sherizadeh, T.; Shu, B.; Xing, Y.; He, P. Laboratory Estimation of Rock Joint Stiffness and Frictional Parameters. Geotech. Geol. Eng. 2016, 34, 1723–1735. [Google Scholar] [CrossRef]
- Allaoui, S.; Rekik, A.; Gasser, A.; Blond, E.; Andreev, K. Digital Image Correlation measurements of mortarless joint closure in refractory masonries. Constr. Build. Mater. 2018, 162, 334–344. [Google Scholar] [CrossRef]
- Oliveira, R.L.; Rodrigues, J.P.C.; Pereira, J.M.; Lourenço, P.B.; Marschall, H.U. Normal and tangential behaviour of dry joints in refractory masonry. Eng. Struct. 2021, 243, 112600. [Google Scholar] [CrossRef]
- NF EN 1998-1:2005 (Eurocode 8); Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. National Standards Authority of Ireland Glasnevin: Dublin, Ireland, 2005; Volume 8.
- Itasca. 3 Dimensional Distinct Element Code (3DEC): Theory and Background, 7th ed.; Itasca Consulting Group: Minneapolis, MN, USA, 2019. [Google Scholar]
- Lourenco, P.; Ramos, L. Characterization of Cyclic Behavior of Dry Masonry Joints. J. Struct. Eng. 2004, 130, 779–786. [Google Scholar] [CrossRef]
- Rhinoceros3D. 2020. Available online: https://www.rhino3d.com/ (accessed on 28 January 2022).
- Savalle, N.; Lourenço, P.B. Numerical Simulation Files of Tilting Tests on Perforated Masonry Shear Walls. 2022. Available online: https://doi.org/10.5281/zenodo.5779099 (accessed on 28 January 2022).
- DeJong, M.J.; Vibert, C. Seismic response of stone masonry spires: Computational and experimental modeling. Eng. Struct. 2012, 40, 566–574. [Google Scholar] [CrossRef]
- Dell’Endice, A.; Iannuzzo, A.; DeJong, M.J.; Van Mele, T.; Block, P. Modelling imperfections in unreinforced masonry structures: Discrete element simulations and scale model experiments of a pavilion vault. Eng. Struct. 2021, 228, 111499. [Google Scholar] [CrossRef]
- Savalle, N.; Vincens, É.; Hans, S. Experimental and numerical studies on scaled-down dry-joint retaining walls: Pseudo-static approach to quantify the resistance of a dry-joint brick retaining wall. Bull. Earthq. Eng. 2020, 18, 581–606. [Google Scholar] [CrossRef]
- Quezada, J.C.; Vincens, E.; Mouterde, R.; Morel, J.-C. 3D failure of a scale-down dry stone retaining wall: A DEM modelling. Eng. Struct. 2016, 117, 506–517. [Google Scholar] [CrossRef] [Green Version]
- Funari, M.F.; Silva, L.C.; Savalle, N.; Lourenço, P.B. A concurrent micro/macro FE-model optimized with a limit analysis tool for the assessment of dry-joint masonry structures. Int. J. Multiscale Comput. Eng. 2021. [Google Scholar] [CrossRef]
- Naik, P.M.; Bhowmik, T.; Menon, A. Estimating joint stiffness and friction parameters for dry stone masonry constructions. Int. J. Mason. Res. Innov. 2021, 6, 232–254. [Google Scholar] [CrossRef]
- Oetomo, J.J.; Vincens, E.; Dedecker, F.; Morel, J.-C. Modeling the 2D behavior of dry-stone retaining walls by a fully discrete element method. Int. J. Numer. Anal. Methods Géoméch. 2016, 40, 1099–1120. [Google Scholar] [CrossRef]
- Santa-Cruz, S.; Daudon, D.; Tarque, N.; Zanelli, C.; Alcántara, J. Out-of-plane analysis of dry-stone walls using a pseudo-static experimental and numerical approach in scaled-down specimens. Eng. Struct. 2021, 245, 112875. [Google Scholar] [CrossRef]
- Powrie, W.; Harkness, R.M.; Zhang, X.; Bush, D.I. Deformation and failure modes of drystone retaining walls. Géotechnique 2002, 52, 435–446. [Google Scholar] [CrossRef]
- Griffith, M.C.; Lam, N.T.K.; Wilson, J.L.; Doherty, K. Experimental Investigation of Unreinforced Brick Masonry Walls in Flexure. J. Struct. Eng. 2004, 130, 423–432. [Google Scholar] [CrossRef] [Green Version]
- Lam, N.T.K.; Wilson, J.L.; Hutchinson, G.L. The seismic resistance of unreinforced masonry cantilever walls in low seismicity areas. Bull. N. Z. Soc. Earthq. Eng. 1995, 28, 179–195. [Google Scholar] [CrossRef] [Green Version]
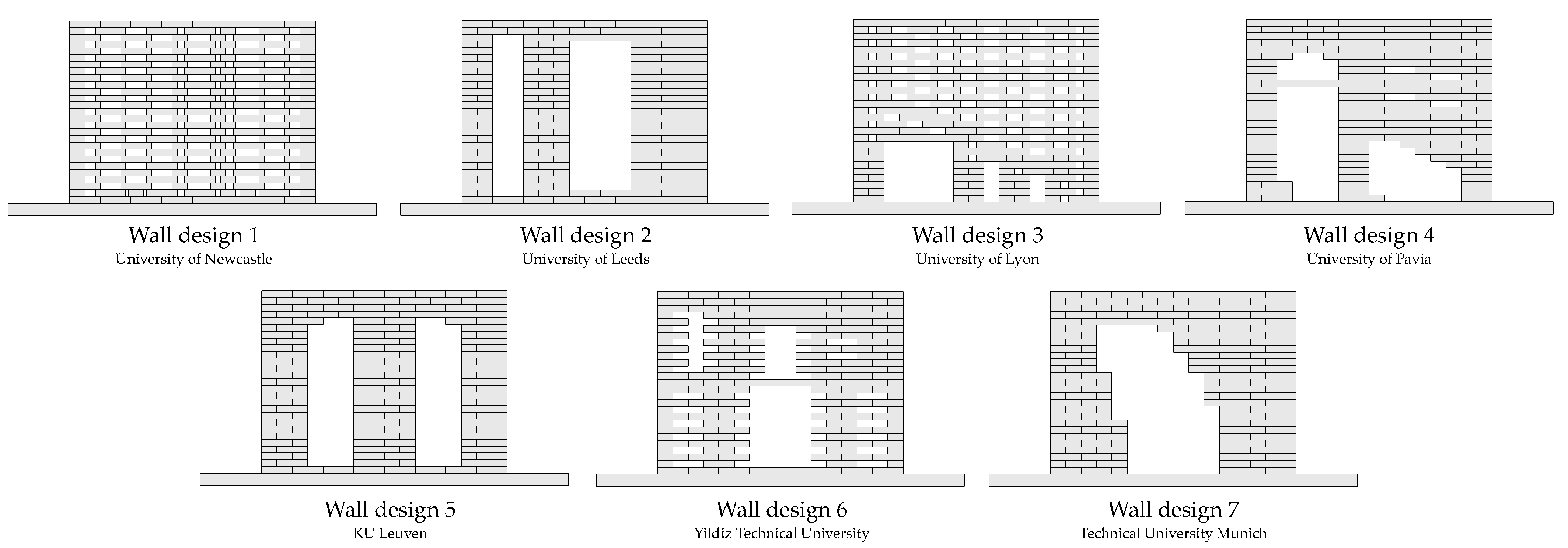



| WD 1 | WD 2 | WD 3 | WD 4 | WD 5 | WD 6 | WD 7 | |
|---|---|---|---|---|---|---|---|
| Collapse tilting angle θ (°) | 18.3 | 7.8 | 19.8 | 16.8 | 7.8 | 7.8 | 18.6 |
| Coefficient of Variation (%) | 4.7 | 3.2 | 6.2 | 8.1 | 16.8 | 6.0 | 7.1 |
| Exp [22] | LA-A [27] | LA-NA [27] | DEM (1 × 109) | DEM (1 × 1010) | |
|---|---|---|---|---|---|
| WD 1 (Newcastle) | 18.3° | 23.9° | 23.5° | 25.3° | 26.5° |
| WD 2 (Leeds) | 7.8° | 17.0° | 16.0° | 15.5° | 16.9° |
| WD 3 (Lyon) | 19.8° | 26.5° | 24.5° | 25.6° | 26.3° |
| WD 4 (Pavia) | 16.8° | 24.6° | 23.5° | 23.8° | 24.9° |
| WD 5 (Leuven) | 7.8° | 17.5° | 17.4° | 16.4° | 18.0° |
| WD 6 (Yildiz) | 7.8° | 18.3° | 17.1° | 15.9° | 17.4° |
| WD 7 (Munich) | 18.6° | 26.6° | 26.6° | 26.5° | 27.0° |
| αexp (°) | CoVexp (%) | αnum (°) | Rel. Error (%) | |
|---|---|---|---|---|
| WD 1 (Newcastle) | 18.3° | 4.7% | 20.0° | 9.5% |
| WD 2 (Leeds) | 7.8° | 3.2% | 8.3° | 6.0% |
| WD 3 (Lyon) | 19.8° | 6.2% | 20.1° | 1.7% |
| WD 4 (Pavia) | 16.8° | 8.1% | 16.7° | −0.8% |
| WD 5 (Leuven) | 7.8° | 16.8% | 8.1° | 3.8% |
| WD 6 (Yildiz) | 7.8° | 6.0% | 5.9° | −24.7% |
| WD 7 (Munich) | 18.6° | 7.1% | 20.2° | 8.6% |
| Abs average (%) | - | 7.5% | - | 7.9% |
| WD 1 | WD 2 | WD 3 | WD 4 | WD 5 | WD 6 | WD 7 | |
|---|---|---|---|---|---|---|---|
| Collapse tilting angle ratio | 1.3 | 1.9 | 1.3 | 1.4 | 2.0 | 2.7 | 2.0 |
| DLS tilting angle ratio | 3.0 | 4.8 | 2.4 | 5.5 | 4.9 | 7.8 | 6.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savalle, N.; Lourenço, P.B.; Milani, G. Joint Stiffness Influence on the First-Order Seismic Capacity of Dry-Joint Masonry Structures: Numerical DEM Investigations. Appl. Sci. 2022, 12, 2108. https://doi.org/10.3390/app12042108
Savalle N, Lourenço PB, Milani G. Joint Stiffness Influence on the First-Order Seismic Capacity of Dry-Joint Masonry Structures: Numerical DEM Investigations. Applied Sciences. 2022; 12(4):2108. https://doi.org/10.3390/app12042108
Chicago/Turabian StyleSavalle, Nathanaël, Paulo B. Lourenço, and Gabriele Milani. 2022. "Joint Stiffness Influence on the First-Order Seismic Capacity of Dry-Joint Masonry Structures: Numerical DEM Investigations" Applied Sciences 12, no. 4: 2108. https://doi.org/10.3390/app12042108
APA StyleSavalle, N., Lourenço, P. B., & Milani, G. (2022). Joint Stiffness Influence on the First-Order Seismic Capacity of Dry-Joint Masonry Structures: Numerical DEM Investigations. Applied Sciences, 12(4), 2108. https://doi.org/10.3390/app12042108








