Chinese Geomagnetic Reference Field 2020 by the Revised Surface Spline Method

Featured Application

We believe the paper may be of particular interest to the readers of your journal because in this paper, a simple but high-precision geomagnetic field modeling method is proposed. We also present Chinese Geomagnetic Reference Field 2020 (CGRF2020) as an example of this modeling method. Using CGRF2020, one can calculate high-precision geomagnetic field values in most of China and surrounding areas.

Abstract

We improved the surface spline method to make the centers of the base functions fixed. This improvement makes it meaningful to analyze the time series of coefficients. Based on the revised surface spline (RSS) method and 2382 geomagnetic data measured in mainland China, we built Chinese Geomagnetic Reference Field 2020 (CGRF2020) to describe the spatial distribution of the geomagnetic field in most of China and surrounding areas. The root mean square residual is 0.1318 degrees for D, 0.0857 degrees for I, 93.70 nT for F, 73.94 nT for X, 65.02 nT for Y, and 97.82 nT for Z. The values of F, X, Y, and Z are about 20 nT less than those by the SCH method and IGRF13. We also preliminarily analyzed the correlation between geomagnetic anomalies and geological structures.

1. Introduction

As a standard geomagnetic product, the geomagnetic reference field provides a higher-precision geomagnetic description field of the region. A geomagnetic reference field can easily provide the geomagnetic normal reference value of the target location so as to help identify whether the measurement data are abnormal and the magnitude of the anomaly. Therefore, in the field of energy and mineral resources, geomagnetic reference fields are needed to provide the normal distribution of the geomagnetic field so as to help accurately estimate the geomagnetic anomaly morphology and predict the mineral locations and reserves. By analyzing the precise geomagnetic field distribution provided by the geomagnetic reference field itself, the structure distribution of underground materials can be inferred, thus providing help in tectonic-geodynamic studies. The high-precision geomagnetic reference field also provides accurate and undisturbed navigation information for archaeological and environment investigations, military aviation, and other fields [1,2,3,4,5].

One important research problem with geomagnetism is how to describe the spatial and temporal distribution of the geomagnetic field as accurately as possible. To describe the global geomagnetic field and its secular variation, the International Association of Geomagnetism and Aeronomy (IAGA) has issued the International Geomagnetic Reference Field (IGRF) once every 5 years since 1968, with few exceptions [6]. The latest model, the thirteenth generation of IGRF, IGRF13, was issued in December 2019 [7]. While the IGRF is intended to describe the global geomagnetic field, its usefulness in characterizing the geomagnetic field over a regional area is limited due to its higher errors. Various countries, therefore, establish national geomagnetic charts or models according to the needs of the scientific community [8,9,10]. National geomagnetic charts, which describe the spatial–temporal variation in the regional geomagnetic field, tend to be country wide and are established or published every 5~10 years usually [11,12,13,14,15,16,17]. These charts or models describe the spatial distribution of the geomagnetic field of a region and are based on some absolute geomagnetic data. Efforts to develop such charts are faced with the technical challenge of describing the spatial distribution of the geomagnetic field with accuracy and proper resolution based on a large amount of spatially discrete data. Building a model and then calculating the regional geomagnetic field is an efficient method to resolve this technical problem. The first generation of the Chinese geomagnetic charts, i.e., China geomagnetic chart for 1950.0, was established in the 1950s. Seven generations of China geomagnetic charts were published during 1960~2000 (every 10 years). These charts were generated mainly using the Taylor polynomial method [18,19,20]. After that, China geomagnetic charts have been made using the spherical cap harmonic (SCH) method [21,22,23,24,25,26,27,28,29]. The SCH method is derived from the spherical harmonic method used in the International Geomagnetic Reference Field (IGRF) and meets the potential theory of the geomagnetic field while providing the three-dimensional structure of the field.

Despite the advantages of the SCH method, it has its own disadvantages. In addition to its being a little complex to calculate the non-integer-order Schmitt-Legendre functions, we find the non-integral-order Schmitt-Legendre function divergent oscillation when we increase the truncation order to improve the description precision. Qiu tried to use three sets of low-order spherical cap harmonic coefficients to describe the geomagnetic field in China to solve this problem [30]. However, it is necessary to first determine which set of coefficients should be chosen, according to the locations, and there are some complex steps to determine the geomagnetic field where the three models overlap.

Many kinds of modeling method are used to discuss various complex geophysical phenomena and processes [31,32,33]. The purpose of this paper is to propose a more convenient modeling method to express the regional geomagnetic field in most of China and surrounding areas. This method should have the following advantages: one formula and its coefficients for the whole target region; higher fitting accuracy; and a relatively independent form of basis function, which facilitates time series analysis. In this case, we propose a revised surface spline method to describe the regional geomagnetic field. This theory can be used to calculate the geomagnetic field distribution with a high spatial resolution by one easy-to-use formula and one set of coefficients.

2. Materials and Methods

2.1. Revised Surface Spline Method

The surface spline method was first applied in 1987 [34]. It can be expressed by Equation (1).

$$\left\{\begin{array}{c}P(x,y)=a_0+a_{1}x+a_{2}y+{\displaystyle \sum }_{i=1}^N{A}_i{r}_i^2\ln \left(r_i^2+\mathsf{\epsilon }\right)\\ r_i^2={\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2\\ {\displaystyle \sum }_{i=1}^N{A}_i={\displaystyle \sum }_{i=1}^N{x}_i{A}_i={\displaystyle \sum }_{i=1}^N{y}_i{A}_i=0\end{array}\right.$$

(1)

Here, x and y are the geographical longitude and latitude of the calculated position, respectively; x_i and y_i are the geographic longitude and latitude of the ith spatial position, respectively; P(x, y) is the value of an element of the geomagnetic field at position (x, y); a₀, a₁, a₂, and A_i are the fitting coefficients of the surface spline function; N is the amount of original data; r_i is the distance between the calculated position and the ith spatial position; and ε is the curvature factor and is usually 10⁻⁷.

From Equation (1), the traditional surface spline fitting formula consists of two parts. The first part is 1-order polynomials, and the second part includes some U-shaped waves centered on the base points. Because the base points are the field repeat stations in the traditional surface spline method, the geographical longitudes and latitudes of field repeat stations should be input when calculating geomagnetic data. Therefore, in practical use, we should not only know the fitting coefficients but also know the longitudes and latitudes of the repeat stations. In addition, the temporal characteristics of the geomagnetic field cannot be obtained by analyzing the time series of coefficients, due to the different centers of the basis function corresponding to the coefficients. This makes it inconvenient to extend and apply the surface spline method.

So, we redefine the centers of the U-shaped waves as a grid lattice distribution position in the second part. In addition, we increase the truncation order of polynomials in the first part to describe a more complex trend distribution of the geomagnetic field. Then the revised surface spline method can be expressed as:

$$\left\{\begin{array}{c}P(x,y)={\displaystyle \sum }_{i=0}^K{\displaystyle \sum }_{j=0}^i{a}_{ij}{x}^{i-j}{y}^j+{\displaystyle \sum }_{i=1}^N{A}_i{r}_i^2\ln \left(r_i^2+\mathsf{\epsilon }\right)\\ r_i^2={\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2\\ {\displaystyle \sum }_{i=1}^N{A}_i={\displaystyle \sum }_{i=1}^N{x}_i{A}_i={\displaystyle \sum }_{i=1}^N{y}_i{A}_i=\dots ={\displaystyle \sum }_{i=1}^N{x}_i{y}_i^{K-1}{A}_{\mathrm{i}}={\displaystyle \sum }_{i=1}^N{y}_i^K{A}_i=0\end{array}\right.$$

(2)

Here, K is the truncation order of polynomials; a_ij and A_i are the fitting coefficients of the revised surface spline function; x and y are the geographical longitude and latitude of the calculated position, respectively; x_i and y_i are the geographic longitude and latitude of the ith grid lattice distribution position, respectively; P(x, y) is the value of an element of the geomagnetic field at position (x, y); N is the number of the grid lattice distribution positions; r_i is the distance between the calculated position and the ith grid position; and ε is the curvature factor and usually is also 10⁻⁷.

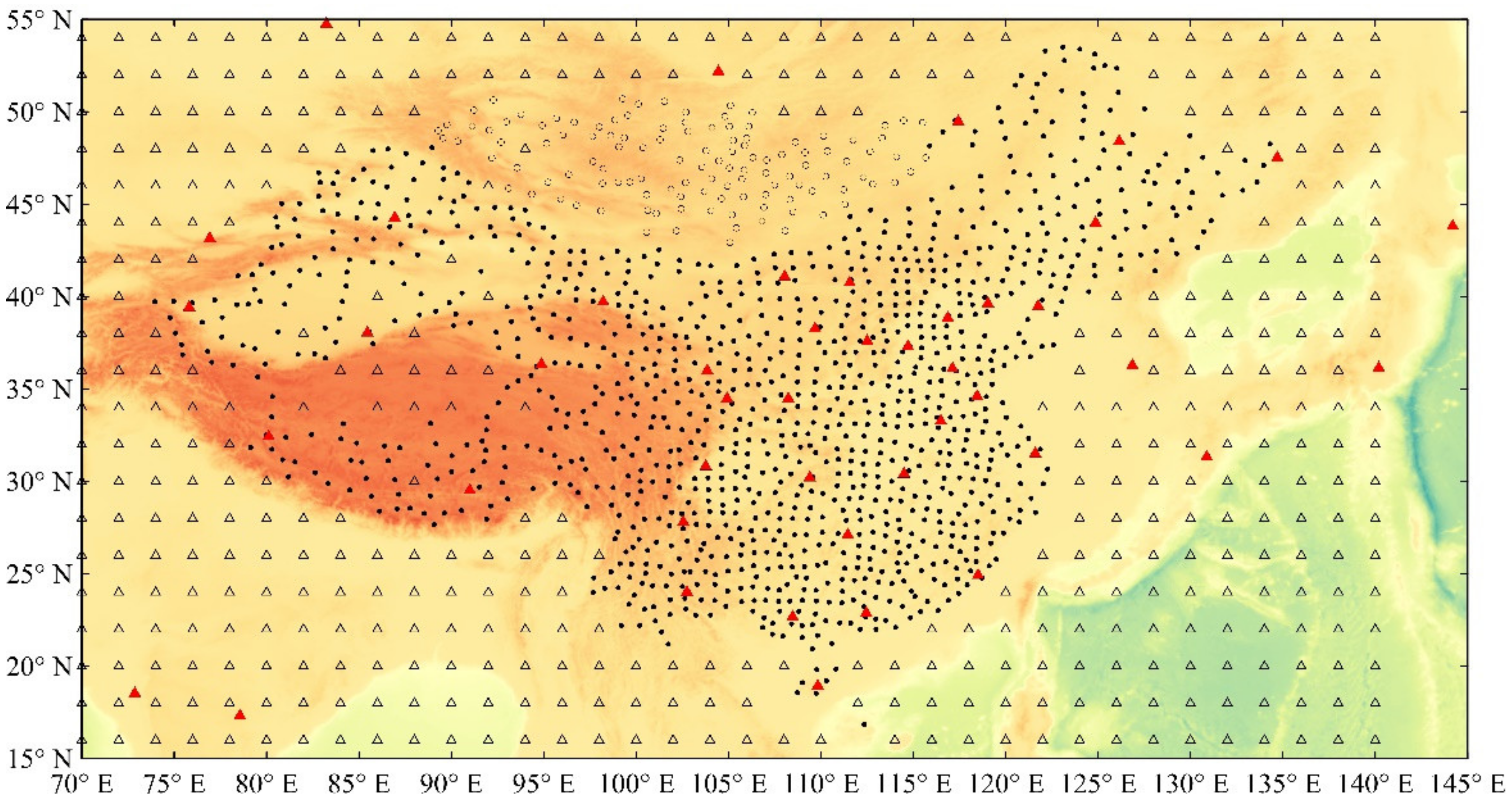
2.2. Source and Processing of the Geomagnetic Data

We collected three-component geomagnetic data for 2832 repeat stations, 1447 of them measured in 2019 and 1385 of them measured in 2020. The mean separation between two adjacent stations is about 70 km in most areas of China and is about 150 km in Tibet, China. All of the stations are located in a weak magnetic interference environment (e.g., far from man-made magnetic sources and with lower magnetic field gradients (less than 5 nT/m)). The measured geomagnetic elements are the geomagnetic declination (D), the inclination (I), and the total intensity (F). A GSM-19T proton magnetometer with a sensitivity of 0.05 nT and an accuracy of 0.2 nT was used to measure F. A CTM-DI magnetometer was used to measure D and I with a sensitivity of 0.1′ and an accuracy of 0.2′ [35]. A PM-100 GNSS system was used to measure the longitudes, latitudes, and elevations of stations and also provide the direction of geographical north, which is needed to determine the geomagnetic declination [36]. All geomagnetic elements (F, D, and I) of each station were measured in 6 sets. In each set, F was measure 10 times, D was measure 4 times, and I was measure 4 times to avoid operational mistakes.

All geomagnetic data of the three elements were calculated to 00:00~03:00 Beijing time on 1 January 2020 after reduction of the diurnal and secular variations. The reference data used in the reduction of the diurnal variations were the minute mean values of the nearest geomagnetic observatory to repeat stations [37]. The reference data used in the reduction of the secular variation were from a 6-order natural orthogonal component (NOC) model of the geomagnetic secular variation in China [38,39].

Then, we averaged the results of the same repeat stations in 2019 and 2020 with the preceding data, processing to further reduce the error and removing some data that were too close. In all, 1120 repeat stations remained for building the Chinese geomagnetic reference field. The spatial distribution of these repeat stations is shown in Figure 1. We also collected geomagnetic data at 45 geomagnetic observatories and at 118 stations in neighboring countries and calculated geomagnetic data by the enhanced magnetic model [40] for 419 positions. The spatial distribution of all four parts of these positions is shown in Figure 1.

3. Results

3.1. Parameter Determination

According to Equation (2), the main parameters that determine the accuracy of the revised surface spline model include the truncation order K and the number of grid lattice distribution positions N. Because the total number of grid positions is inversely proportional to the square of the grid interval (R; unit is degree), we calculated root mean square residuals, RMS σ, using several different truncation orders K and the grid interval R. Three elements, D, I, and F, are fitted; and X, Y, and Z are calculated by D, I, and F to compare with the results of previous studies. Although we obtained the fitting coefficients using the ordinary least squares method based on all four parts of the geomagnetic data, we focused on the geomagnetic field distribution in China. So we calculated the RMS σ based on the first two parts of the geomagnetic data and the data of 1120 repeat stations; the results are displayed in

Table 1. RMS of some elements with different K and R.

	R = 5	R = 4.5	R = 4	R = 3.5	R = 3	R = 2.5	R = 2
K = 1
Dσ (degree)	0.1539	0.1528	0.1503	0.1499	0.1453	0.1407	0.1317
Iσ (degree)	0.1010	0.0994	0.0986	0.0961	0.0946	0.0924	0.0857
Fσ (nT)	108.60	108.38	107.07	106.18	102.45	99.64	93.73
Xσ (nT)	87.28	86.27	85.50	83.63	81.69	80.36	73.98
Yσ (nT)	75.71	74.96	73.80	73.72	71.36	69.33	65.01
Zσ (nT)	113.23	112.70	111.44	110.13	106.98	103.57	97.86
K = 2
Dσ (degree)	0.1542	0.1529	0.1507	0.1498	0.14528	0.1407	0.1318
Iσ (degree)	0.0994	0.0987	0.0983	0.0956	0.0944	0.0923	0.0857
Fσ (nT)	108.66	108.38	107.24	106.18	102.46	99.60	93.74
Xσ (nT)	86.51	85.67	85.38	83.28	81.70	80.23	73.96
Yσ (nT)	75.55	74.94	73.89	73.67	71.36	69.33	65.03
Zσ (nT)	112.98	112.68	111.53	110.03	106.89	103.56	97.85
K = 3
Dσ (degree)	0.1535	0.1529	0.1505	0.1498	0.1453	0.1407	0.1318
Iσ (degree)	0.0990	0.0987	0.0982	0.0956	0.0944	0.0923	0.0857
Fσ (nT)	108.69	108.32	106.94	106.06	102.50	99.68	93.70
Xσ (nT)	86.06	85.74	85.09	83.24	81.71	80.31	73.94
Yσ (nT)	75.44	74.94	73.89	73.66	71.36	69.34	65.02
Zσ (nT)	112.97	112.61	111.35	109.97	106.90	103.60	97.82

.

When K > 4, the RMS sharply increased when R < 3 degrees; so this situation was not included in the consideration, and the values in this situation are not shown in Table 1. From Table 1, we can also see the advantages of the revised surface spline method. The lowest RMS values are 73.94 nT for X, 65.01 nT for Y, and 97.82 nT for Z. As a comparison, we also calculated the RMS residual of IGRF13; the results are 0.1858 degrees for D, 0.1089 degrees for I, and 117.48 nT for F. Usually, the estimated RMS errors of IGRF and WMM are 140–300 and 50–150 nT higher, respectively, in China [7,41,42]. In comparison, CGRF2010 by the spheric cap harmonic method has a higher value and a lower convergence rate of the RMS residual. The RMS values are about 101 nT for X, 80.5 nT for Y, and 122 nT for Z when the truncation order is 11, and the convergence rates are about 4 nT for X, 0.2 nT for Y, and 4 nT for Z when the order increases from 1 to 11 [29]. The errors will still increase to about 150 nT for X, 80 nT for Y, 180 nT for Z, and 250 nT for F when using the spheric cap harmonic method to build a 3D geomagnetic model [43]. We also calculated the RMS using the Taylor polynomial method, which can also be used to describe the geomagnetic field in the same area when the truncation order is 8. The RMS is 0.16 degrees for D, 0.10 degrees for I, and 111.31 nT for F. We chose a higher truncation order and a lower grid interval to describe the more complex geomagnetic field spatial structure. So K = 3 and R = 2 degrees were determined as the model parameters.

3.2. Maps and Coefficients of CGRF2020

Figure 2 shows the spatial distribution of the geomagnetic field described by CGRF2020-RSS and its difference from IGRF13. In most of China, the magnitude of geomagnetic anomalies can be up to 5′ for D and I; 100 nT for F, H, X, and Z; and 50 nT for Y.

After studying the right half of Figure 2 (the spatial distribution of seven elements of geomagnetic anomalies), we find the following:

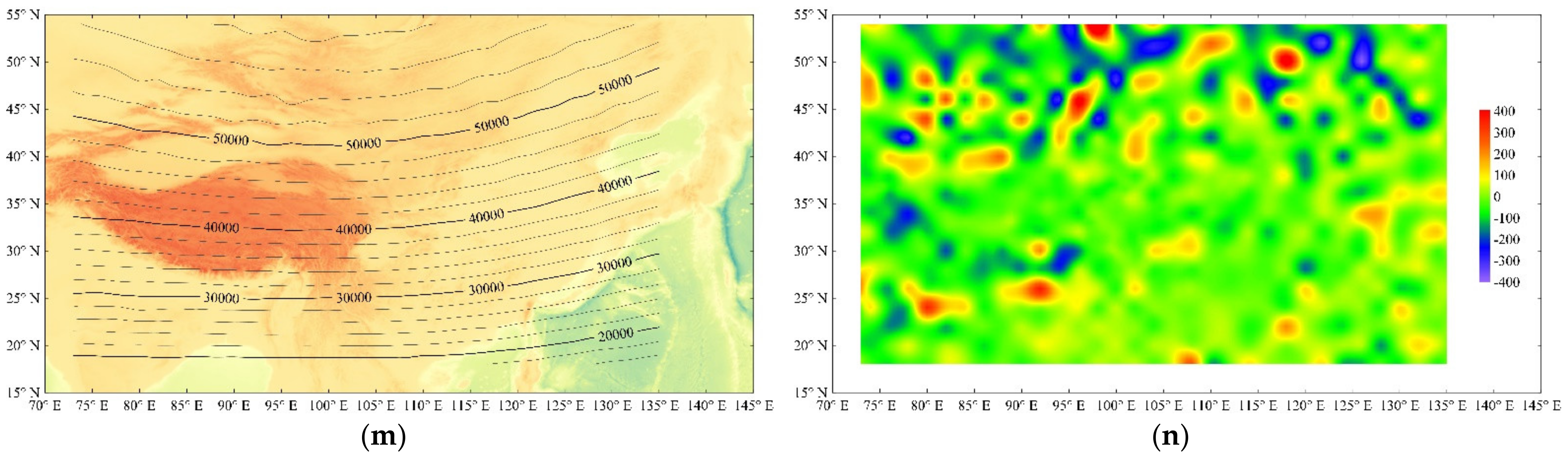
• The anomalies in the declination D and the east component Y are positive in most of North China and East China and are negative in most of West China. There are several positive anomalies located at (42° N, 118° E), (40° N, 107° E), (40° N, 83° E), and (35° N, 118° E), with the amplitude up to 10′ for D and up to 100 nT for Y; there are several negative anomalies centered near (42° N, 122° E), (40° N, 110° E), and (40° N, 80° E), with the amplitude up to −10′ for D and 100 nT for Y.
• The anomalies in the total intensity F and the vertical component Z are negative in most of China. Several old hard blocks correspond to the distribution of positive anomalies. For example, the anomaly over Sichuan Basin is a positive anomaly located at 28–33° N, 103–112° E, with the amplitude up to 100 nT for F and Z. There is also a positive anomaly (35–42° N, 75–88° E) near Tarim Basin, with the amplitude up to 150 nT for F and 200 nT for Z. There are three significant negative anomalies, the first one located in Qinling Mountains (30–35° N, 103–115° E), the second one located in Tianshan Mountains (38–42° N, 75–90° E), and the last one located in the south of Tibet (27–30° N, 78–100° E). Their amplitudes can be up to −100, 150, and −150 nT for F and Z, respectively.
• The spatial distributions of the anomalies in the horizontal component H and the north component X are almost the same. The amplitude of the anomalies is relatively weak in most areas of China, except for the three pairs of positive–negative anomalies. The first of them is located near Sichuan Basin and the west part of Qinling Mountains (27–33° N, 103–112° E), with the amplitude up to ±100 nT; the second pair is located near Tarim Basin and Tianshan Mountains (37–47° N, 73–87° E), with the amplitude up to ±150 nT; and the third is located near Southern Tibet or the Himalayas (25–32° N, 80–95° E), with the amplitude up to ±150 nT.
• The anomalies in the inclination I are negative in most parts of China. The centers of the negative anomalies are located in North China (37–45° N, 118–121° E) and Southeast China (23–32° N, 116–123° E), with the amplitude up to −8′. The centers of the positive anomalies are located in Sichuan Basin and Tarim Basin, with the amplitude up to 10′.

We have provided all the coefficients in Appendix A. Insert these coefficients into Equation (2) to calculate the geomagnetic fields of D, I, and F. The coefficients of the first part of Equation (2) are shown in

Table A1. The first part of the coefficients of the CGRF2020-RSS.

	a00	a10	a11	a20	a21	a22	a30	a31	a32	a33
D	−51.2926	1.5265	0.7781	−0.0144	−0.0134	0.0055	0.0000	0.0001	−0.0001	0.0001
I	−19.2891	0.2362	2.1605	−0.0056	0.0168	−0.0287	0.0000	−0.0001	0.0000	0.0001
F	56940.51	−514.85	−735.75	5.19	9.75	22.58	−0.01	−0.05	0.04	−0.23

,

Table A1. The second part of the coefficients of D.

Ai	16	18	20	22	24	26	28	30	32	34
72	0.0043	−0.0037	0.0183	−0.0074	−0.0233	0.0499	−0.0271	0.0064	0.0127	−0.0126
74	0.0136	−0.0417	0.0199	−0.0160	0.0056	−0.0303	0.0072	0.0191	−0.0445	0.0148
76	−0.0278	0.0576	−0.0261	0.0254	−0.0037	0.0533	−0.0591	0.0043	0.0517	−0.0140
78	0.0122	−0.0163	0.0071	−0.0384	0.0018	−0.0085	0.0125	0.0140	−0.0573	0.0325
80	0.0025	−0.0240	0.0235	0.0019	0.0103	0.0155	−0.0077	−0.0195	0.0466	−0.0188
82	0.0050	0.0010	0.0183	−0.0252	0.0022	−0.0134	−0.0003	0.0196	−0.0234	−0.0058
84	−0.0055	−0.0020	−0.0100	0.0203	0.0022	−0.0133	0.0112	−0.0060	−0.0108	0.0225
86	0.0009	0.0051	0.0008	−0.0281	0.0275	0.0096	−0.0113	0.0055	0.0060	−0.0050
88	−0.0039	0.0024	0.0020	0.0032	−0.0010	−0.0278	0.0129	−0.0047	−0.0077	−0.0017
90	0.0037	−0.0046	0.0092	−0.0159	0.0150	−0.0001	−0.0023	0.0224	−0.0011	0.0066
92	−0.0003	−0.0037	0.0001	0.0107	−0.0245	0.0313	−0.0070	−0.0501	0.0325	−0.0355
94	0.0003	0.0020	−0.0027	−0.0018	0.0204	−0.0345	0.0250	0.0097	0.0025	0.0013
96	0.0005	0.0056	−0.0051	0.0013	−0.0148	0.0341	−0.0263	−0.0005	0.0048	−0.0078
98	−0.0064	−0.0044	0.0009	0.0080	−0.0080	−0.0178	0.0126	0.0095	−0.0129	0.0103
100	0.0120	0.0001	0.0015	−0.0014	0.0014	0.0257	−0.0303	0.0044	0.0060	−0.0045
102	−0.0105	0.0025	−0.0048	0.0056	−0.0085	−0.0062	0.0243	0.0002	−0.0153	0.0159
104	0.0059	−0.0044	0.0105	−0.0187	0.0262	−0.0271	−0.0049	−0.0021	0.0103	−0.0169
106	0.0007	−0.0096	0.0075	0.0019	−0.0093	0.0194	0.0059	−0.0041	0.0107	−0.0016
108	0.0004	0.0175	−0.0124	0.0038	0.0038	−0.0190	0.0007	−0.0035	0.0027	−0.0133
110	−0.0165	0.0006	−0.0058	0.0034	−0.0083	0.0282	−0.0096	0.0080	−0.0234	0.0395
112	0.0247	−0.0010	−0.0033	−0.0012	0.0081	−0.0224	0.0108	−0.0109	0.0183	−0.0192
114	−0.0149	−0.0074	0.0171	−0.0050	−0.0111	0.0217	−0.0159	0.0187	−0.0192	0.0033
116	0.0089	0.0053	−0.0086	0.0042	0.0129	−0.0218	0.0110	−0.0142	0.0305	−0.0049
118	−0.0103	−0.0084	−0.0068	0.0097	−0.0230	0.0369	−0.0138	0.0016	−0.0206	−0.0192
120	0.0208	−0.0014	0.0134	0.0112	−0.0139	−0.0144	0.0052	0.0068	0.0228	−0.0044
122	−0.0288	0.0171	−0.0286	−0.0034	0.0031	0.0088	0.0197	−0.0457	0.0114	−0.0048
124	0.0272	−0.0092	−0.0005	0.0299	−0.0092	−0.0113	0.0004	0.0187	0.0030	−0.0061
126	−0.0141	−0.0019	0.0043	−0.0126	0.0047	0.0030	−0.0075	−0.0089	0.0069	−0.0052
128	−0.0071	0.0121	−0.0004	−0.0035	−0.0021	−0.0010	0.0067	0.0077	−0.0119	0.0058
130	0.0183	−0.0095	0.0011	−0.0141	0.0363	−0.0143	−0.0010	−0.0022	0.0079	0.0049
132	−0.0087	−0.0155	0.0113	0.0164	−0.0506	0.0180	0.0018	−0.0080	−0.0002	−0.0060
134	−0.0031	0.0255	−0.0224	0.0085	0.0132	0.0084	−0.0191	0.0246	−0.0064	−0.0077
136	0.0068	−0.0185	0.0207	−0.0171	0.0083	−0.0141	0.0173	−0.0192	0.0087	−0.0036
Ai	36	38	40	42	44	46	48	50	52	54
72	0.0125	−0.0127	−0.0084	0.0408	−0.0355	−0.0135	0.0129	0.0026	−0.0198	0.0136
74	0.0035	−0.0110	0.0096	−0.0050	−0.0208	0.0493	0.0383	−0.0404	0.0065	0.0059
76	−0.0046	−0.0004	0.0217	−0.0499	0.0747	−0.0726	−0.0586	0.0557	0.0250	−0.0757
78	−0.0172	0.0188	−0.0136	0.0427	−0.0376	0.0092	0.0744	−0.0369	−0.0590	0.1285
80	−0.0108	0.0353	−0.0584	−0.0133	0.0270	−0.0042	−0.0375	0.0139	0.0129	−0.0582
82	0.0294	−0.0702	0.0947	0.0107	−0.0597	0.0613	−0.0265	0.0156	0.0335	−0.0164
84	−0.0163	0.0463	−0.0602	−0.0266	0.0448	−0.0580	0.0460	−0.0481	−0.0199	0.0069
86	0.0099	−0.0510	0.0592	0.0071	0.0024	0.0297	−0.0466	0.0727	−0.0452	0.0635
88	0.0013	0.0225	−0.0377	0.0193	−0.0406	−0.0168	0.0589	−0.0565	0.0720	−0.1049
90	−0.0063	−0.0003	0.0068	−0.0156	0.0555	−0.0219	−0.0532	0.0250	−0.0608	0.0745
92	0.0260	−0.0073	0.0074	−0.0061	−0.0350	0.0420	0.0164	0.0947	−0.0708	0.0390
94	0.0046	−0.0129	0.0164	−0.0619	0.1380	−0.1504	0.0512	−0.1462	0.1112	−0.0701
96	0.0044	−0.0064	0.0072	0.0413	−0.1056	0.1712	−0.0955	0.1155	−0.0505	0.0244
98	−0.0053	0.0044	−0.0112	0.0265	−0.0796	0.0864	−0.2332	0.2231	−0.1287	0.0095
100	−0.0027	0.0048	−0.0103	−0.0032	0.0558	−0.0773	0.2071	−0.1435	0.0269	0.0512
102	−0.0042	0.0003	0.0102	0.0133	−0.0389	0.0505	−0.1525	0.1101	−0.0306	−0.0431
104	0.0027	0.0091	−0.0406	0.0472	−0.0621	0.0797	−0.0360	−0.0147	0.0223	0.0367
106	0.0155	−0.0338	0.0555	−0.0661	0.0468	−0.0241	0.0021	0.0873	−0.0554	−0.0478
108	−0.0108	0.0238	0.0044	−0.0007	0.0603	−0.1007	0.0863	−0.1403	0.1088	0.0375
110	−0.0054	0.0015	−0.0515	0.0318	−0.0650	0.0749	−0.0548	0.0614	−0.0627	−0.0619
112	−0.0158	0.0174	0.0093	0.0017	0.0194	−0.0219	0.0287	−0.0017	0.0253	0.0397
114	0.0132	−0.0121	0.0234	−0.0228	0.0257	−0.0609	0.0317	−0.0541	0.0254	−0.0303
116	−0.0024	−0.0051	−0.0254	0.0133	−0.0398	0.0934	−0.0607	0.1106	−0.0902	0.0528
118	0.0301	−0.0038	0.0214	0.0224	0.0182	−0.0694	0.0293	−0.0867	0.0830	−0.0455
120	−0.0027	−0.0266	0.0093	−0.0615	0.0430	0.0020	0.0176	0.0182	−0.0520	0.0310
122	0.0178	−0.0001	0.0289	−0.0154	−0.0046	−0.0133	0.0060	−0.0182	0.1013	−0.0730
124	−0.0168	−0.0021	−0.0171	0.0483	−0.0193	0.0535	−0.0782	0.1060	−0.1709	0.1076
126	0.0107	0.0183	−0.0201	−0.0318	−0.0014	−0.0381	0.0537	−0.1043	0.1000	−0.0547
128	−0.0086	0.0086	−0.0208	0.0891	−0.0551	0.0864	−0.0994	0.1962	−0.1374	0.0512
130	−0.0038	0.0008	−0.0038	−0.0503	0.0250	−0.0658	0.0907	−0.1544	0.0855	−0.0341
132	−0.0039	−0.0028	0.0347	−0.0282	0.0580	−0.0238	−0.0109	0.0396	−0.0062	0.0187
134	0.0200	−0.0044	−0.0219	0.0251	−0.0237	−0.0098	0.0298	−0.0395	0.0302	−0.0453
136	0.0064	−0.0155	0.0196	−0.0215	0.0191	−0.0094	0.0040	0.0114	−0.0266	0.0339

,

Table A3. The second part of the coefficients of I.

Ai	16	18	20	22	24	26	28	30	32	34
72	−0.0117	0.0249	−0.0167	0.0158	−0.0291	0.0126	0.0140	−0.0191	0.0093	−0.0036
74	−0.0152	0.0084	−0.0105	0.0068	0.0220	−0.0101	0.0154	−0.0288	0.0408	−0.0260
76	0.0133	−0.0103	0.0147	−0.0150	−0.0126	−0.0126	−0.0060	0.0166	−0.0266	0.0046
78	0.0188	−0.0402	0.0448	−0.0277	0.0065	0.0320	−0.0058	−0.0050	0.0218	−0.0205
80	−0.0103	0.0114	−0.0084	−0.0114	0.0478	−0.0448	0.0020	0.0130	−0.0124	0.0088
82	0.0029	0.0040	0.0058	−0.0220	−0.0026	0.0029	0.0186	−0.0436	0.0252	0.0034
84	−0.0091	0.0045	0.0050	0.0090	−0.0049	0.0163	−0.0110	0.0299	−0.0192	0.0030
86	−0.0036	0.0134	−0.0332	0.0160	0.0018	−0.0213	0.0093	−0.0276	0.0213	−0.0075
88	0.0010	0.0033	0.0093	−0.0014	−0.0130	0.0221	−0.0101	0.0167	−0.0001	−0.0034
90	0.0007	−0.0100	−0.0033	0.0112	−0.0103	0.0085	0.0036	−0.0336	0.0064	−0.0001
92	0.0095	−0.0041	0.0092	−0.0066	−0.0118	0.0311	−0.0470	0.0751	−0.0314	0.0139
94	−0.0145	0.0032	0.0007	0.0047	0.0002	−0.0134	0.0212	−0.0460	0.0112	0.0035
96	0.0174	−0.0118	0.0069	−0.0092	0.0065	−0.0007	0.0187	−0.0127	0.0168	−0.0081
98	−0.0145	0.0116	−0.0096	0.0123	−0.0186	0.0166	−0.0184	0.0098	−0.0095	0.0077
100	0.0060	−0.0050	0.0062	−0.0044	0.0089	−0.0117	−0.0010	0.0053	0.0035	−0.0029
102	−0.0094	0.0112	−0.0107	0.0092	−0.0090	0.0134	0.0048	−0.0076	−0.0057	0.0024
104	0.0143	−0.0125	0.0069	−0.0087	0.0031	−0.0043	−0.0092	0.0133	0.0002	−0.0008
106	−0.0051	−0.0079	0.0056	0.0009	0.0041	−0.0005	0.0067	−0.0193	0.0171	−0.0226
108	−0.0159	0.0392	−0.0154	−0.0007	−0.0057	0.0047	−0.0058	0.0036	0.0182	−0.0143
110	0.0307	−0.0377	0.0130	−0.0021	0.0075	−0.0043	0.0083	−0.0178	0.0146	−0.0159
112	−0.0326	0.0072	0.0036	−0.0016	−0.0003	−0.0018	−0.0033	0.0113	−0.0156	0.0022
114	0.0243	0.0084	−0.0047	−0.0047	0.0021	0.0021	−0.0026	−0.0015	0.0205	−0.0106
116	−0.0154	−0.0022	0.0001	0.0007	−0.0014	0.0057	0.0017	−0.0078	−0.0094	0.0050
118	0.0128	0.0003	−0.0133	0.0294	−0.0201	−0.0106	0.0146	−0.0055	0.0076	−0.0057
120	−0.0109	−0.0108	0.0025	−0.0022	−0.0056	0.0278	−0.0257	0.0116	0.0088	−0.0172
122	0.0187	0.0201	−0.0001	−0.0087	0.0159	−0.0165	0.0113	−0.0135	−0.0065	0.0190
124	−0.0234	−0.0220	0.0094	−0.0149	−0.0034	0.0051	−0.0057	0.0122	0.0023	0.0007
126	0.0509	−0.0272	0.0317	−0.0044	0.0205	−0.0149	0.0155	−0.0138	−0.0210	0.0211
128	−0.0543	0.0351	−0.0381	0.0147	−0.0341	0.0246	−0.0132	0.0126	0.0172	−0.0027
130	0.0326	−0.0221	0.0139	−0.0051	0.0333	−0.0341	0.0134	−0.0117	−0.0159	0.0032
132	−0.0144	0.0047	0.0176	−0.0218	0.0100	−0.0125	0.0206	0.0041	0.0113	−0.0189
134	0.0262	−0.0341	0.0199	−0.0127	0.0097	−0.0026	0.0008	−0.0292	0.0275	−0.0153
136	−0.0149	0.0209	−0.0216	0.0208	−0.0196	0.0159	−0.0118	0.0179	−0.0147	0.0028
Ai	36	38	40	42	44	46	48	50	52	54
72	0.0011	0.0022	−0.0086	0.0045	0.0070	−0.0040	−0.0299	0.0456	−0.0213	0.0005
74	0.0144	−0.0015	−0.0070	0.0082	−0.0113	0.0098	0.0175	−0.0138	0.0027	0.0042
76	0.0176	−0.0274	0.0370	−0.0146	−0.0053	0.0185	−0.0193	−0.0178	0.0140	−0.0053
78	−0.0093	−0.0022	0.0128	−0.0491	0.0299	−0.0261	0.0071	0.0028	0.0002	0.0071
80	0.0100	−0.0040	0.0393	−0.0347	0.0746	−0.0665	0.0778	−0.0194	−0.0049	−0.0112
82	−0.0102	−0.0149	−0.0092	0.0090	−0.0479	0.0427	−0.0491	−0.0065	0.0069	0.0113
84	−0.0083	0.0261	0.0066	−0.0166	0.0501	−0.0616	0.0511	0.0019	−0.0071	0.0047
86	0.0097	−0.0285	0.0098	−0.0039	−0.0283	0.0363	−0.0030	−0.0119	0.0027	−0.0247
88	0.0080	−0.0171	0.0376	−0.0053	−0.0018	0.0137	−0.0670	0.0543	−0.0107	0.0299
90	0.0004	0.0058	−0.0212	−0.0148	0.0270	−0.0351	0.0868	−0.0716	0.0114	−0.0092
92	−0.0092	0.0108	−0.0065	0.0254	−0.0271	0.0318	−0.0581	0.0498	−0.0131	−0.0105
94	−0.0030	−0.0127	0.0158	−0.0105	−0.0069	−0.0063	0.0205	−0.0275	0.0211	0.0136
96	−0.0013	0.0183	−0.0143	−0.0029	0.0122	0.0162	−0.0378	0.0498	−0.0372	−0.0132
98	−0.0082	−0.0025	0.0050	0.0042	−0.0075	−0.0074	0.0464	−0.0450	−0.0018	0.0440
100	0.0024	0.0045	−0.0069	−0.0185	0.0321	−0.0032	−0.0590	0.0491	0.0022	−0.0348
102	0.0079	−0.0209	0.0305	−0.0017	−0.0291	0.0004	0.0290	−0.0286	0.0255	−0.0067
104	−0.0068	0.0159	−0.0168	−0.0171	0.0762	−0.0455	0.0380	−0.0024	−0.0532	0.0350
106	0.0255	−0.0310	0.0206	0.0079	−0.0752	0.0517	−0.0724	0.0449	0.0200	−0.0148
108	0.0067	0.0058	0.0032	−0.0259	0.0754	−0.0539	0.0677	−0.0419	0.0093	−0.0105
110	0.0140	−0.0221	0.0281	−0.0205	−0.0068	0.0153	−0.0284	−0.0038	0.0068	0.0054
112	0.0038	0.0026	−0.0135	0.0091	0.0000	−0.0288	0.0453	−0.0301	0.0267	−0.0145
114	0.0037	−0.0025	0.0131	−0.0130	0.0097	0.0164	−0.0285	0.0519	−0.0431	0.0146
116	0.0031	−0.0048	−0.0214	0.0300	−0.0192	0.0049	−0.0084	−0.0337	0.0207	−0.0001
118	−0.0089	0.0246	0.0040	−0.0013	−0.0183	0.0253	−0.0134	0.0577	−0.0340	0.0044
120	0.0307	−0.0370	−0.0012	−0.0117	0.0310	−0.0332	0.0111	−0.0526	0.0341	−0.0087
122	−0.0304	0.0258	0.0136	−0.0081	0.0030	−0.0201	0.0488	0.0089	−0.0075	−0.0008
124	−0.0035	0.0057	−0.0226	0.0141	−0.0082	0.0414	−0.0734	0.0179	−0.0180	0.0109
126	−0.0103	0.0037	0.0118	−0.0103	0.0064	−0.0437	0.0687	−0.0304	0.0321	−0.0084
128	−0.0064	−0.0024	−0.0042	0.0012	−0.0133	0.0579	−0.0557	0.0057	−0.0106	−0.0008
130	0.0079	0.0076	−0.0022	0.0067	0.0061	−0.0374	0.0240	0.0021	0.0136	−0.0061
132	0.0103	−0.0192	0.0018	0.0005	−0.0075	0.0220	−0.0046	−0.0068	0.0006	−0.0029
134	0.0163	0.0040	−0.0078	0.0168	−0.0098	−0.0047	−0.0062	0.0080	0.0008	−0.0014
136	0.0033	−0.0132	0.0162	−0.0260	0.0252	−0.0124	0.0054	0.0027	−0.0120	0.0094

and

Table A4. The second part of the coefficients of F.

Ai	16	18	20	22	24	26	28	30	32	34
72	−14.6349	13.7592	−7.2368	16.7847	−51.4039	64.9940	−37.1171	−0.1891	11.4560	−9.3127
74	10.6347	−1.9384	1.2586	−12.5948	34.6707	−27.8421	13.1336	4.5755	−1.4905	−5.5042
76	−1.2869	−15.1666	1.5082	−2.7027	19.3015	−26.7798	17.4671	−8.9993	−5.6847	14.9245
78	−6.6708	42.5043	−20.1758	23.4548	−58.2267	32.8239	−11.1312	0.1198	2.0167	1.7611
80	5.1969	−37.1238	10.4947	−10.2332	41.1358	−7.4607	−9.6125	24.0920	−10.5866	−11.9769
82	2.9112	5.8836	18.1010	−23.0959	7.5271	−22.0457	12.3434	−9.9386	−14.1503	30.8439
84	−2.9171	3.5657	−3.4691	−16.4864	42.6278	−24.4700	17.9801	−3.1890	13.3405	−15.6858
86	6.2943	−20.8039	22.6271	−0.6962	−32.8713	19.5658	−21.0528	6.4805	−13.9210	12.8213
88	−3.4032	10.1920	−5.5591	−8.7708	21.6194	5.6233	4.1947	3.9910	−1.1427	2.2928
90	0.7563	−4.2991	−1.6159	8.6991	−14.9230	4.1343	−42.7192	27.7681	−16.7673	7.7860
92	4.8735	−4.7560	7.0941	−0.4393	−23.9449	62.8203	−19.5332	28.4429	−16.5018	−4.0118
94	−6.2815	5.4927	−4.9520	7.9354	−13.9294	8.1646	−45.2812	11.0199	−5.8203	13.9166
96	6.2837	−6.2564	2.9430	−4.2688	13.6180	−9.1942	28.9355	−14.6804	18.7779	−21.0134
98	−4.2468	5.1656	−7.0385	6.2189	−14.7397	12.1954	−5.5613	−5.8178	−0.0426	4.8654
100	6.1354	−6.1413	8.1017	−4.0519	15.1407	−19.9295	1.0231	6.0794	3.5981	−6.6333
102	−8.2728	6.8407	−7.9535	5.5245	−19.1472	26.6431	0.6804	−13.2343	2.9787	−2.1152
104	10.8701	−10.9272	15.1468	−10.5687	10.4264	−10.0029	−14.8287	28.4519	−17.8533	6.9129
106	−2.8819	−10.4081	−3.4031	6.3000	−5.1743	8.1854	−9.2933	15.5077	−22.0842	22.5702
108	−13.5480	46.0477	−18.0280	3.7190	−3.6025	8.9688	−14.9151	14.6006	1.2973	−15.6363
110	13.8667	−31.2848	4.2254	−0.0766	−2.0574	−0.5575	0.3229	5.2300	−16.4278	23.2953
112	−11.5528	11.0092	2.3718	7.9406	0.2783	−0.5420	−2.5247	1.5259	−4.1484	−5.1059
114	−1.1618	11.5883	−13.0790	−5.0932	2.5293	−2.3888	3.5583	1.2971	8.4702	3.7272
116	1.7154	−9.4996	17.7469	−18.7953	11.4076	−0.6741	−7.7922	5.8191	−19.7159	10.1240
118	5.7027	1.1162	−12.2477	25.7830	−12.6469	−6.8059	8.8340	8.9776	−2.1026	4.5643
120	−10.0626	−0.3263	3.0639	−10.0471	−0.2518	23.0213	−24.4916	−3.5038	7.1407	1.6889
122	10.9964	−2.1712	4.0445	2.5280	−2.2493	−5.3337	2.4238	18.2616	−21.6725	0.8413
124	0.8605	−18.7314	15.4017	−15.5972	6.6312	5.3215	−9.9649	1.1456	13.3540	−5.6655
126	9.4586	−1.7134	0.1001	8.0642	−7.3272	2.4939	7.4439	−13.6202	−10.7725	15.6161
128	−13.6334	12.7715	−5.8955	−2.1874	−3.3535	3.3510	−11.7776	22.4687	−5.1762	21.2140
130	7.2579	−12.1961	3.9581	−4.5075	15.3084	−2.6174	4.8517	−9.0343	−3.7837	−17.9162
132	0.3425	3.7098	0.8993	8.3591	−10.5178	−9.9437	1.5077	1.0401	5.4419	0.8753
134	−1.6012	−3.6495	0.3836	−3.4033	0.3153	11.5465	−0.7363	−4.8852	8.5154	−5.5271
136	2.1789	−0.6194	4.0557	−6.6561	7.6590	−10.7368	5.5924	−2.6753	3.5481	−9.9871
Ai	36	38	40	42	44	46	48	50	52	54
72	0.0011	0.0022	−0.0086	0.0045	0.0070	−0.0040	−0.0299	0.0456	−0.0213	0.0005
74	0.0144	−0.0015	−0.0070	0.0082	−0.0113	0.0098	0.0175	−0.0138	0.0027	0.0042
76	0.0176	−0.0274	0.0370	−0.0146	−0.0053	0.0185	−0.0193	−0.0178	0.0140	−0.0053
78	−0.0093	−0.0022	0.0128	−0.0491	0.0299	−0.0261	0.0071	0.0028	0.0002	0.0071
80	0.0100	−0.0040	0.0393	−0.0347	0.0746	−0.0665	0.0778	−0.0194	−0.0049	−0.0112
82	−0.0102	−0.0149	−0.0092	0.0090	−0.0479	0.0427	−0.0491	−0.0065	0.0069	0.0113
84	−0.0083	0.0261	0.0066	−0.0166	0.0501	−0.0616	0.0511	0.0019	−0.0071	0.0047
86	0.0097	−0.0285	0.0098	−0.0039	−0.0283	0.0363	−0.0030	−0.0119	0.0027	−0.0247
88	0.0080	−0.0171	0.0376	−0.0053	−0.0018	0.0137	−0.0670	0.0543	−0.0107	0.0299
90	0.0004	0.0058	−0.0212	−0.0148	0.0270	−0.0351	0.0868	−0.0716	0.0114	−0.0092
92	−0.0092	0.0108	−0.0065	0.0254	−0.0271	0.0318	−0.0581	0.0498	−0.0131	−0.0105
94	−0.0030	−0.0127	0.0158	−0.0105	−0.0069	−0.0063	0.0205	−0.0275	0.0211	0.0136
96	−0.0013	0.0183	−0.0143	−0.0029	0.0122	0.0162	−0.0378	0.0498	−0.0372	−0.0132
98	−0.0082	−0.0025	0.0050	0.0042	−0.0075	−0.0074	0.0464	−0.0450	−0.0018	0.0440
100	0.0024	0.0045	−0.0069	−0.0185	0.0321	−0.0032	−0.0590	0.0491	0.0022	−0.0348
102	0.0079	−0.0209	0.0305	−0.0017	−0.0291	0.0004	0.0290	−0.0286	0.0255	−0.0067
104	−0.0068	0.0159	−0.0168	−0.0171	0.0762	−0.0455	0.0380	−0.0024	−0.0532	0.0350
106	0.0255	−0.0310	0.0206	0.0079	−0.0752	0.0517	−0.0724	0.0449	0.0200	−0.0148
108	0.0067	0.0058	0.0032	−0.0259	0.0754	−0.0539	0.0677	−0.0419	0.0093	−0.0105
110	0.0140	−0.0221	0.0281	−0.0205	−0.0068	0.0153	−0.0284	−0.0038	0.0068	0.0054
112	0.0038	0.0026	−0.0135	0.0091	0.0000	−0.0288	0.0453	−0.0301	0.0267	−0.0145
114	0.0037	−0.0025	0.0131	−0.0130	0.0097	0.0164	−0.0285	0.0519	−0.0431	0.0146
116	0.0031	−0.0048	−0.0214	0.0300	−0.0192	0.0049	−0.0084	−0.0337	0.0207	−0.0001
118	−0.0089	0.0246	0.0040	−0.0013	−0.0183	0.0253	−0.0134	0.0577	−0.0340	0.0044
120	0.0307	−0.0370	−0.0012	−0.0117	0.0310	−0.0332	0.0111	−0.0526	0.0341	−0.0087
122	−0.0304	0.0258	0.0136	−0.0081	0.0030	−0.0201	0.0488	0.0089	−0.0075	−0.0008
124	−0.0035	0.0057	−0.0226	0.0141	−0.0082	0.0414	−0.0734	0.0179	−0.0180	0.0109
126	−0.0103	0.0037	0.0118	−0.0103	0.0064	−0.0437	0.0687	−0.0304	0.0321	−0.0084
128	−0.0064	−0.0024	−0.0042	0.0012	−0.0133	0.0579	−0.0557	0.0057	−0.0106	−0.0008
130	0.0079	0.0076	−0.0022	0.0067	0.0061	−0.0374	0.0240	0.0021	0.0136	−0.0061
132	0.0103	−0.0192	0.0018	0.0005	−0.0075	0.0220	−0.0046	−0.0068	0.0006	−0.0029
134	0.0163	0.0040	−0.0078	0.0168	−0.0098	−0.0047	−0.0062	0.0080	0.0008	−0.0014
136	0.0033	−0.0132	0.0162	−0.0260	0.0252	−0.0124	0.0054	0.0027	−0.0120	0.0094

lists the coefficients of the second part of Equation (2) for D. The first column provides the longitude of the ith position x_i in grid lattice distribution, the first action is the latitude y_i, and the data where the column and the action meet are the coefficient of A_i. Then we can calculate D on positions x and y using Equation (2). The coefficients for I and F can be used in the same way.

4. Discussion

We tried to use a simple method to achieve a high-precision spatial description of a regional geomagnetic field. The choice of the theoretical method for modeling is the first problem to be considered. The candidate modeling methods include the spherical cap harmonic method, the Taylor polynomial method, and the surface spline method. Because compared with the other two methods, the surface spline method can greatly improve the ability of model description [44], this theory is considered as an alternative to describe the detailed spatial structure of the geomagnetic field without boundary distortion. However, in practice, the theory needs to give not only the fitting coefficient but also the central position of the fundamental wave. We solved the problem by improving the surface spline method. The geomagnetic field of most of China and its surrounding areas can be calculated with a higher precision by a simple method based on the fitting coefficients.

The fundamental wave morphologies of three methods, the spherical cap harmonic method, the Taylor polynomial method, and the surface spline method, are compared. The fluctuations in the fundamental wave of the revised surface spline method on the calculated region boundary are less than the fluctuations in the spherical cap harmonic method and the Taylor polynomial method. So the expected boundary distortion by the surface spline method is smaller, with the same accuracy. This means that the revised surface spline method will be a convenient and useful theory for describing fields.

However, the revised surface spline method can be further improved in the future. For example, there are too many coefficients in the current model. We hope to unify the coefficients of the three elements by combining the surface spline fitting of the geomagnetic potential with spherical expansion in the future.

However, we find that the distribution of geomagnetic anomalies in Mongolia is complex. This may require testing of the geomagnetic field measurements we have collected in the area.

5. Conclusions

After improving the surface spline method, we propose the revised surface spline method based on grid lattice distribution positions. Because fundamental wave centers are fixed, it is possible to determine the time variation characteristics of a geomagnetic field by analyzing the time series of coefficients.

Based on geomagnetic field measurements in mainland China during 2019–2020, we set up Chinese Geomagnetic Reference Field 2020 to describe the geomagnetic field in most of China and surrounding areas. The RMS residual fitted by the RSS values are 0.1318 degrees for D, 0.0857 degrees for I, 93.70 nT for F, 73.94 nT for X, 65.02 nT for Y, and 97.82 nT for Z. The values of F, X, Y, and Z are about 20 nT less than those by the SCH method and IGRF13. So RSS can better reflect the spatial distribution of the geomagnetic field.

The spatial distribution of the geomagnetic field described by RSS shows that geomagnetic anomalies are spatially related to geological structures. Sichuan Basin and Tarim Basin are with positive geomagnetic anomalies for F, H, X, and Z. Qinling Mountains, Tianshan Mountains, and the south of Tibet are with negative geomagnetic anomalies for F, H, X, and Z.