Motion Simulation and Human–Computer Interaction System for Lunar Exploration
Abstract
:1. Introduction
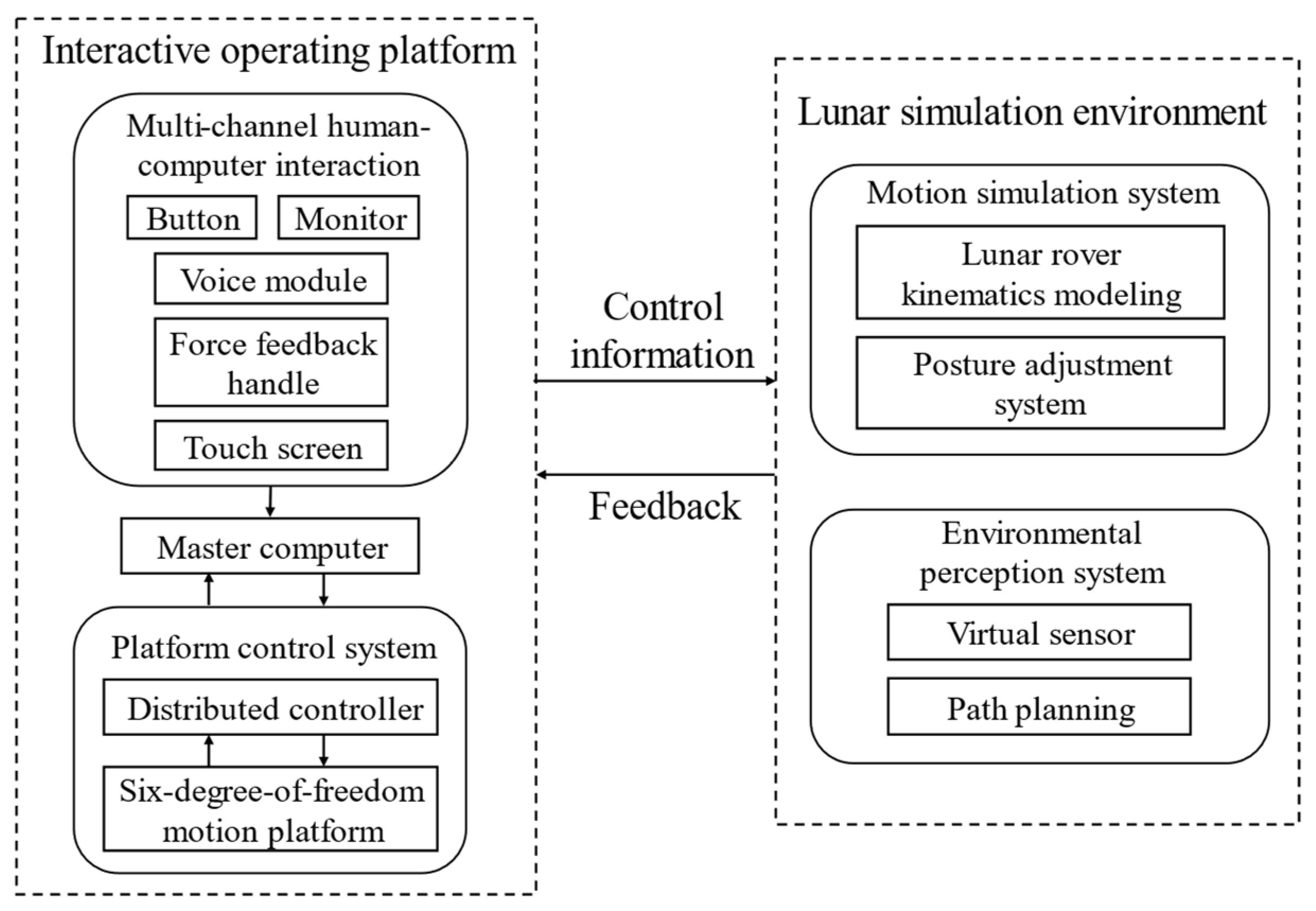
- We designed a motion simulation method based on a 6-DOF platform. We improved the somatosensory feedback algorithm to ensure that the platform can simulate the motion state of the rover over a limited motion range. This method enables training to be carried out in an environment with the physical characteristics of the lunar surface without the need for extensive physical testing.
- We designed a multi-channel human–computer interaction method. Natural and efficient interactions between the human and the rover were realized through the cooperation of five channels: vision, force feedback, body feeling, voice, and touch.
- We integrated multi-channel human-computer interaction methods and motion simulation methods, and designed mechanisms such as the 6-DOF platform to form a system. This system enables astronauts to master the driving skills for manned rovers and familiarize themselves with the lunar environment. Finally, the system realizes the interactive integration of astronauts’ actual operations and lunar rover operations in a virtual environment. Combining the above links, we have realized the innovative application of the hardware in the loop simulation system in the field of lunar rover simulation.
2. Materials and Methods
2.1. System Architecture and Interactive Operating Platform
2.2. Modeling of Lunar Environment and Rover
2.2.1. Lunar Environment Generation
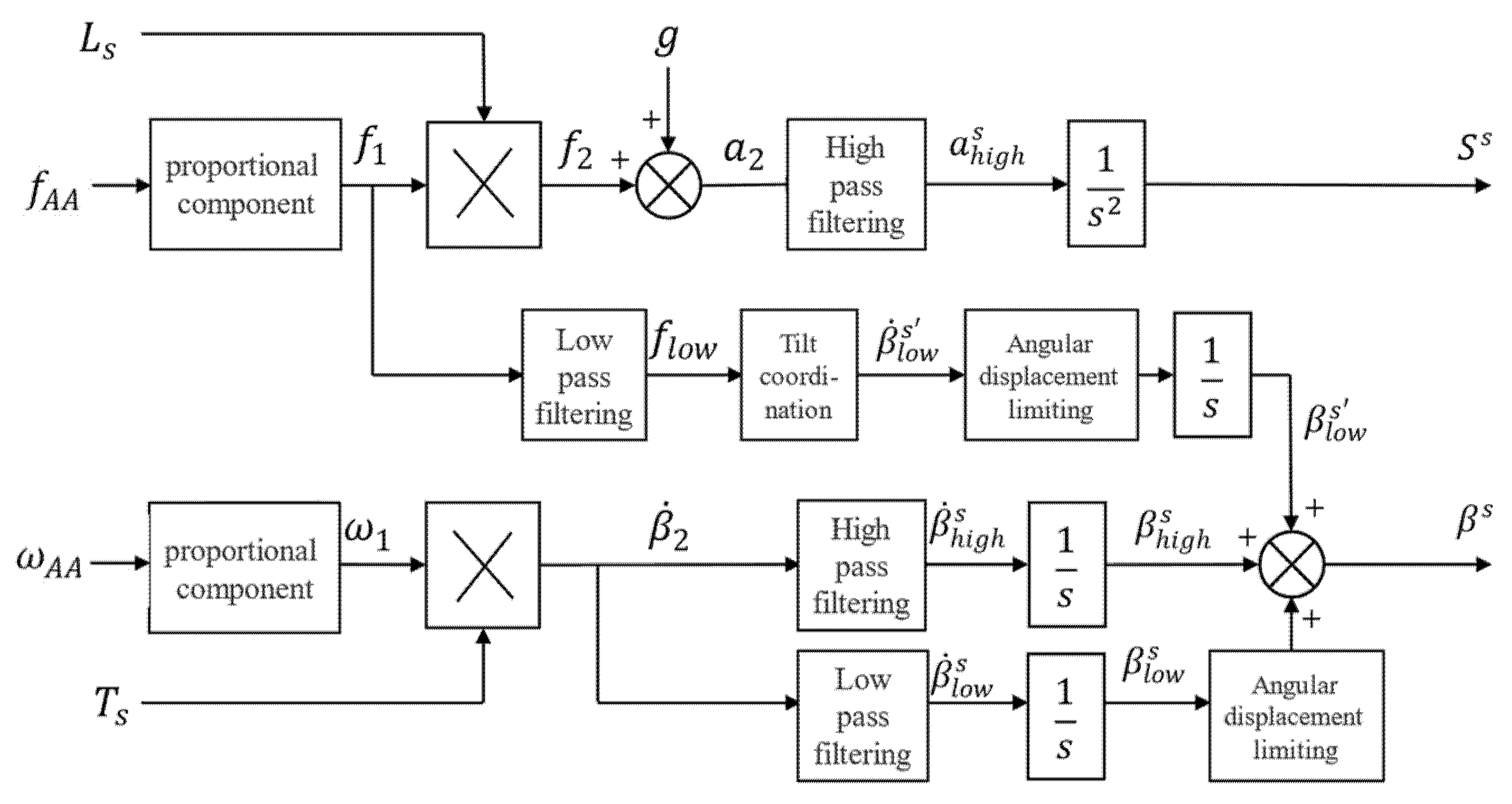
2.2.2. Motion Simulation of the Rover
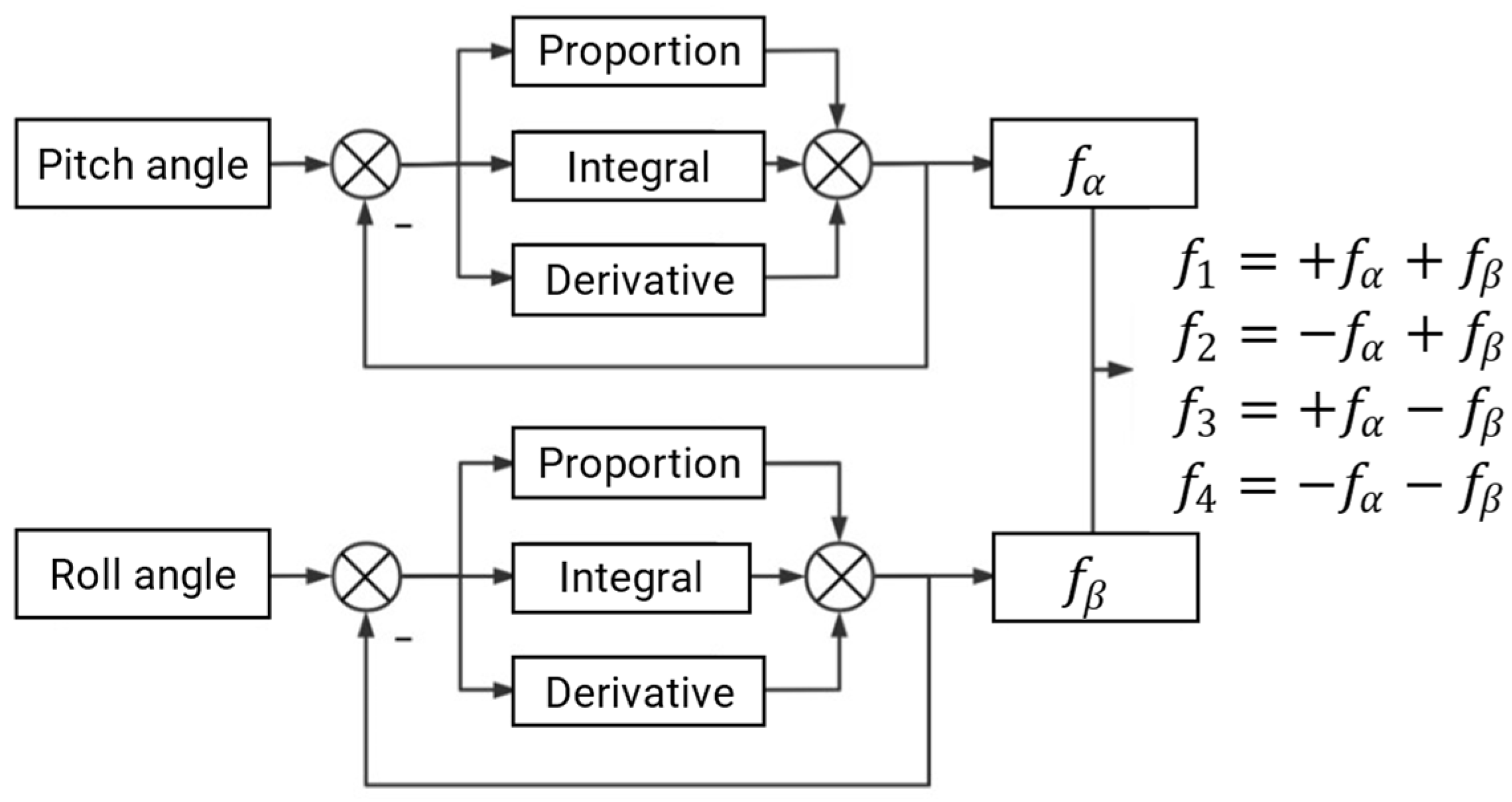
2.2.3. Posture Adjustment Module
2.2.4. Virtual Sensors and Driving Warning
2.3. Multi-Channel Human–Computer Interactions
3. Simulation Results
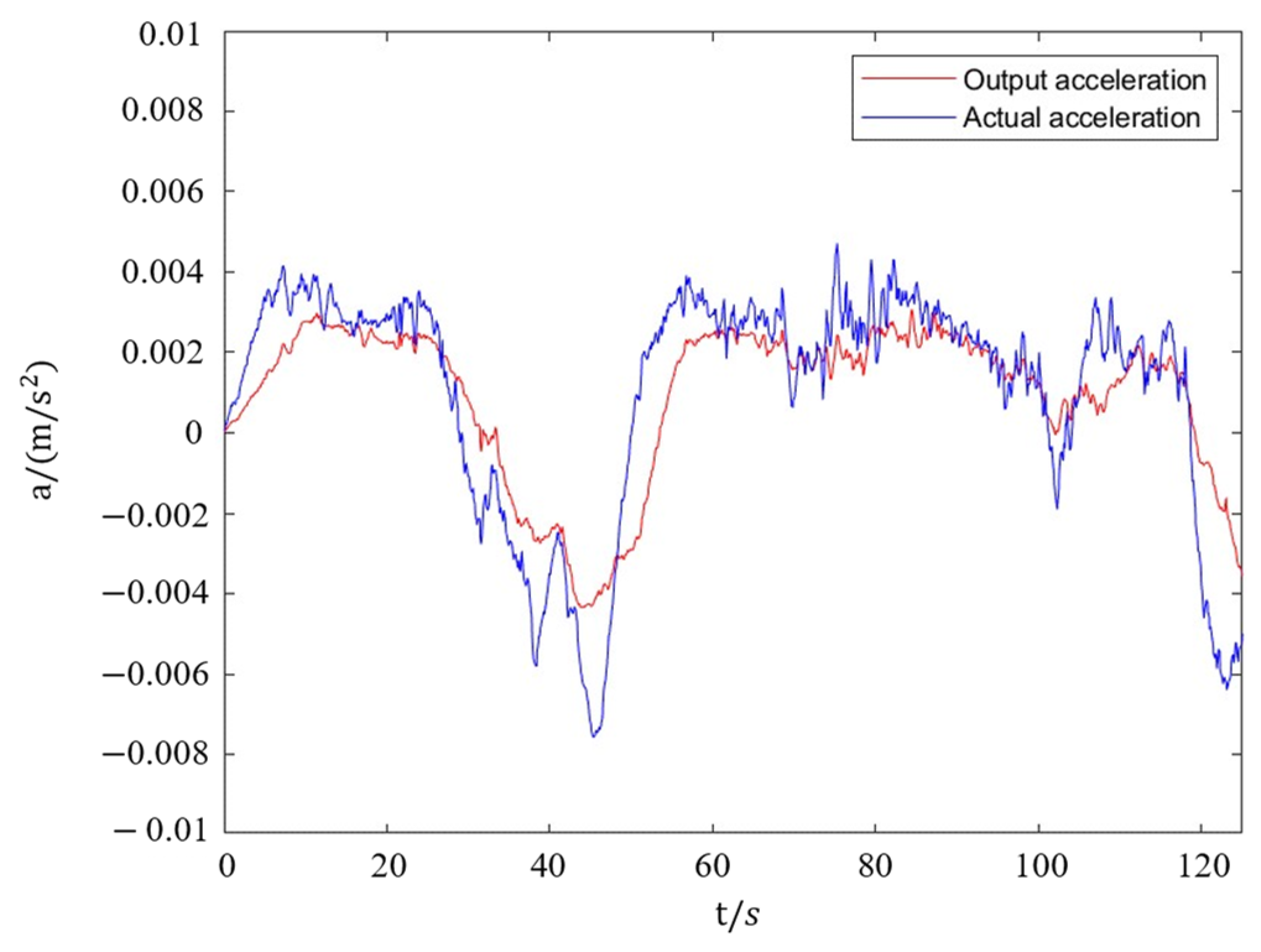
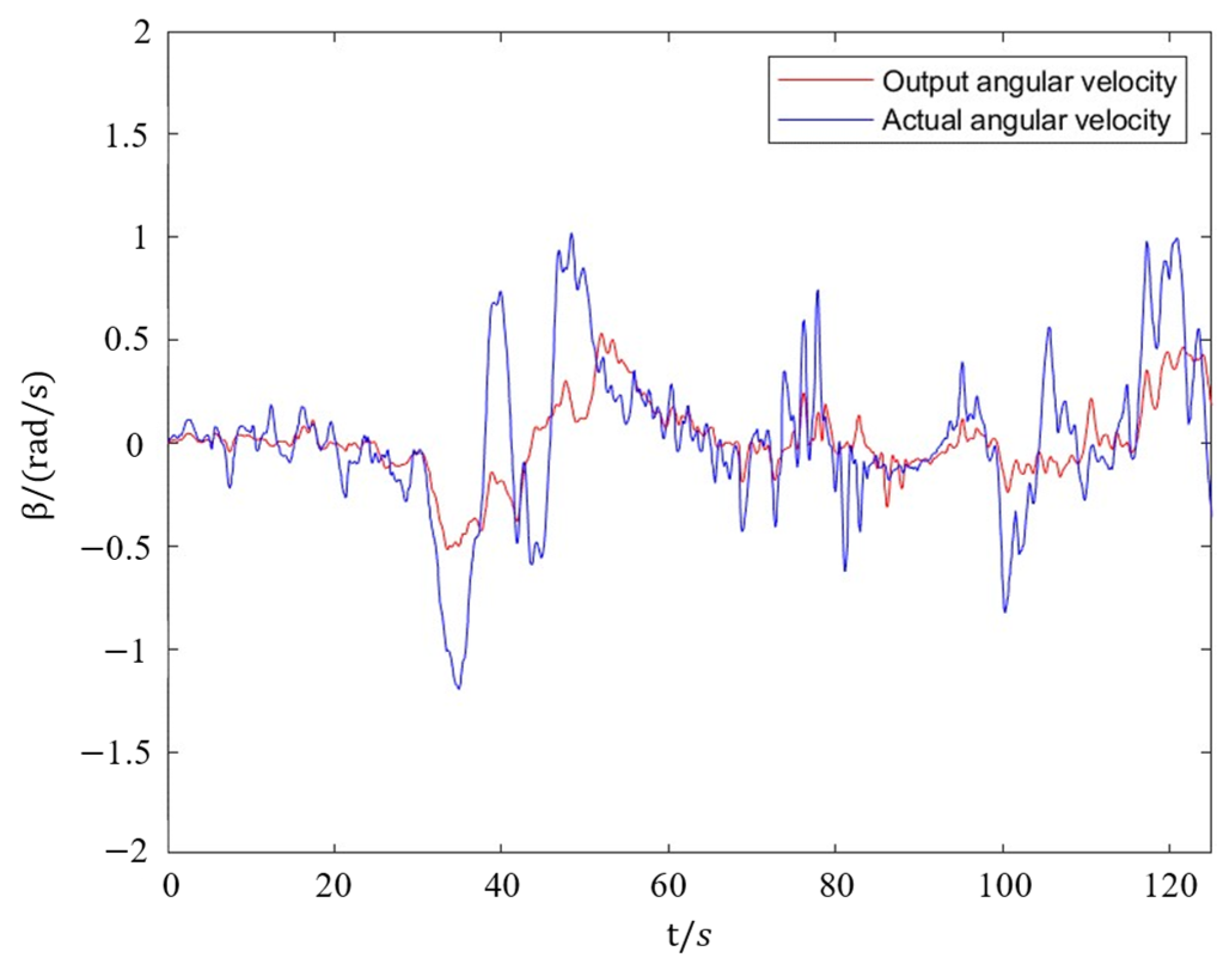
3.1. Real Time Capability of the System
3.2. Posture-Following Experiment
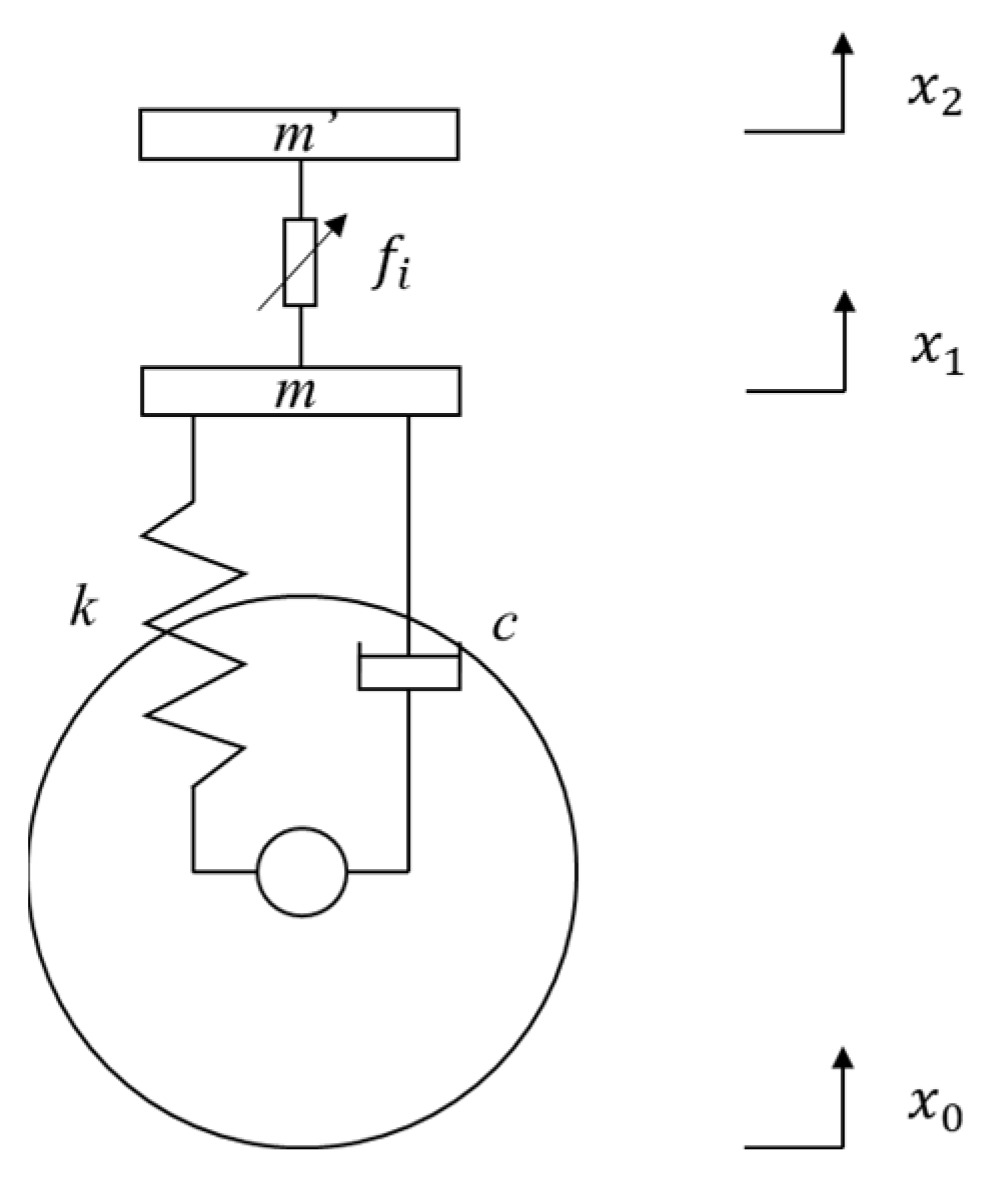
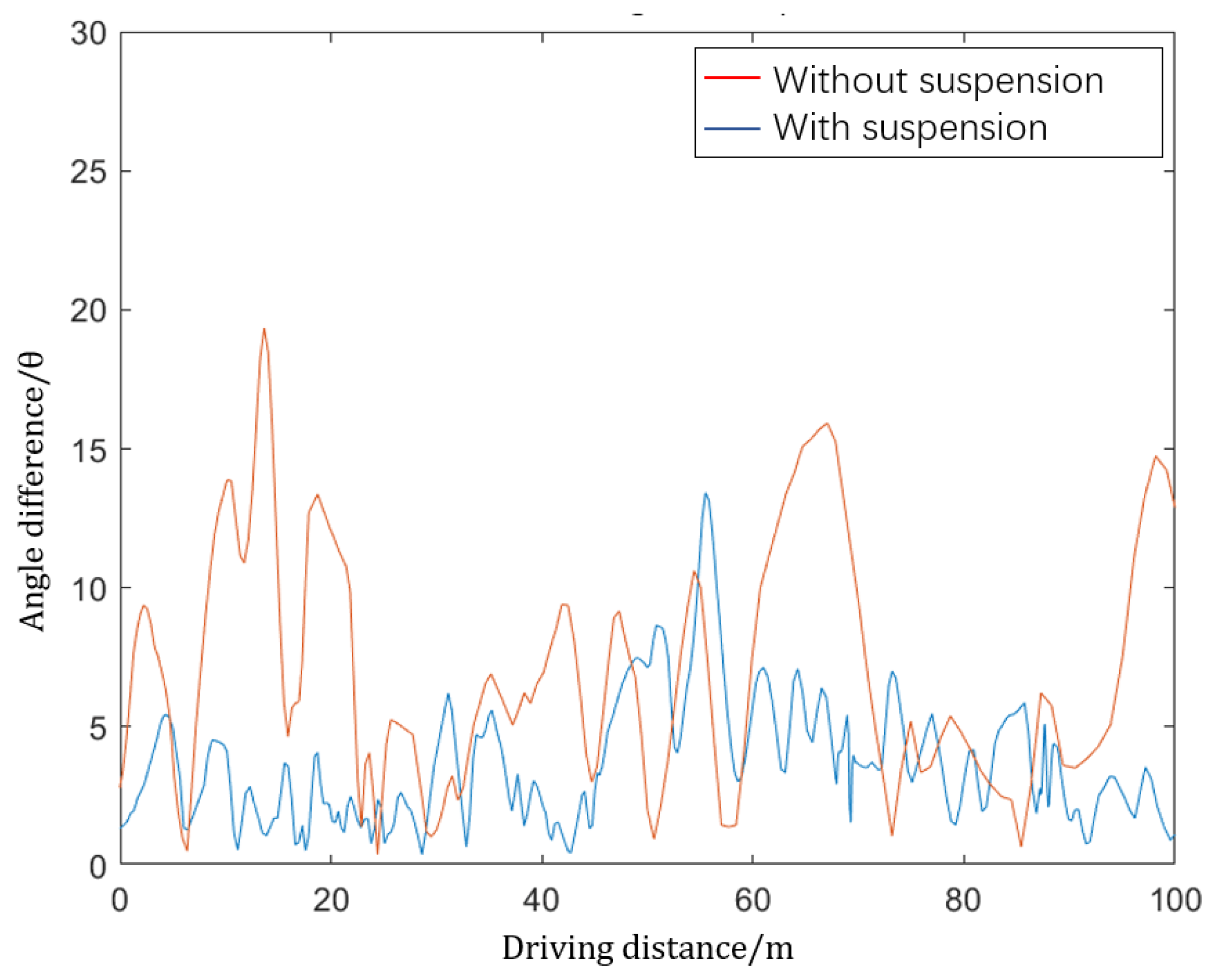
3.3. Suspension Effectiveness Test
3.4. Multi-Channel Interactive System Experiment
3.4.1. Visual and Force Interaction
3.4.2. Voice Control–Touch–Button Three-Channel Interactions
- Experiment 1: Starting the rover. The experimenter needed to complete the four operations of powering the console, turning on the attitude adjustment system, turning on the radar, and turning on the simulation system.
- Experiment 2: The experimenter turned on the radar and adjusted the suspension during driving.
- Control method: a. Button control; b. A combination of buttons, voice, and touch.
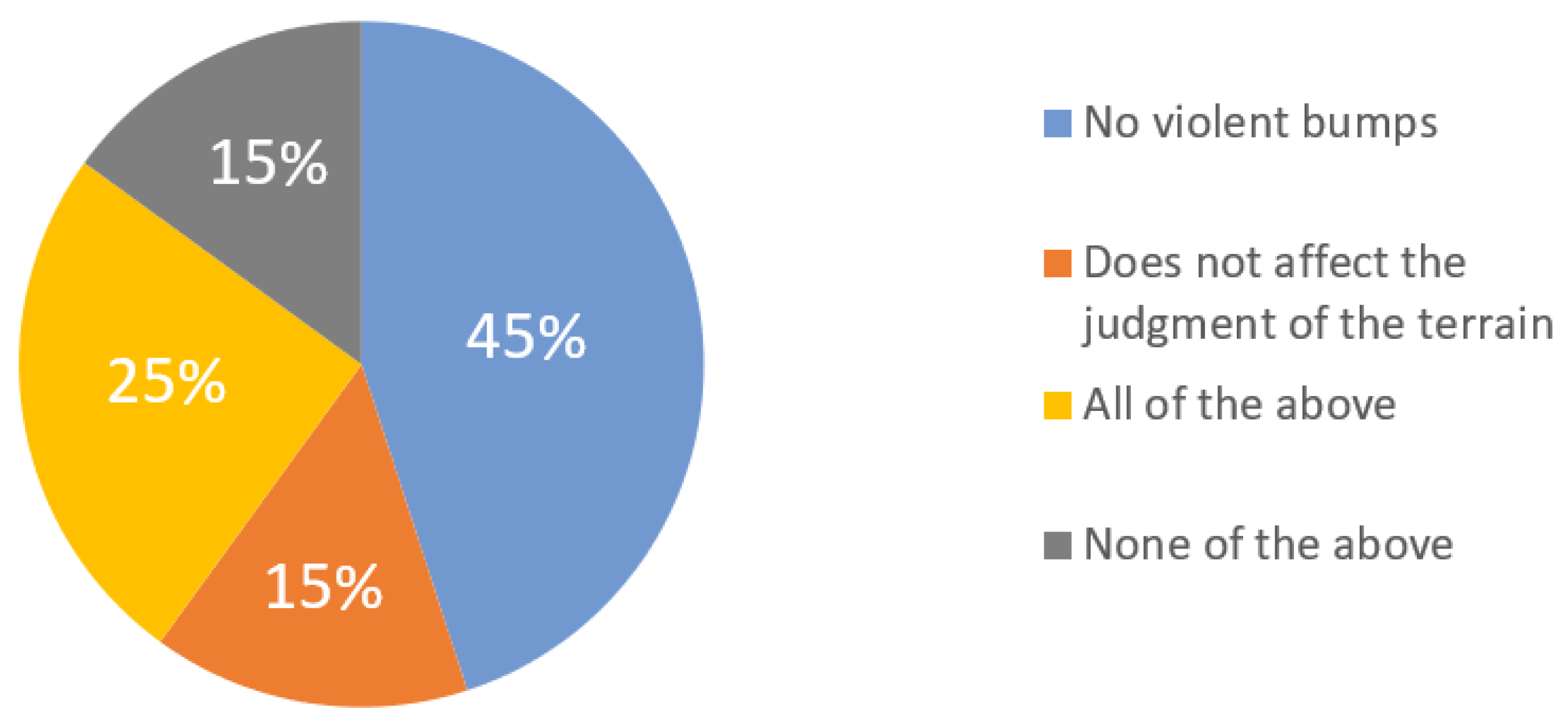
3.5. System Effectiveness Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trimble, J.; Carvalho, R. Lunar prospecting: Searching for volatiles at the south pole. In Proceedings of the SpaceOps 2016 Conference, Daejeon, Korea, 16–20 May 2016; pp. 2482–2490. [Google Scholar] [CrossRef] [Green Version]
- Andrews, D.; Colaprete, A.; Quinn, J.; Chavers, D.; Picard, M. Introducing the resource prospector (RP) mission. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 4–7 August 2014. [Google Scholar] [CrossRef]
- Hooey, B.L.; Toy, J.J.N.T.; Carvalho, R.E.; Fong, T.; Gore, B.F. Modeling operator workload for the resource prospector lunar rover mission. In Advances in Human Factors in Simulation and Modeling; Advances in Intelligent Systems and Computing; Springer: Los Angeles, CA, USA, 2018; pp. 183–194. [Google Scholar] [CrossRef]
- Hambuchen, K.; Roman, M.C.; Sivak, A.; Herblet, A.; Koenig, N.; Newmyer, D.; Ambrose, R. AIAA SPACE and Astronautics Forum and Exposition; SPACE: San Diego, CA, USA, 2017; pp. 5120–5129. [Google Scholar] [CrossRef]
- Allan, M.; Wong, U.; Furlong, P.M.; Rogg, A.; McMichael, S.; Welsh, T.; Chen, I.; Peters, S.; Gerkey, B.; Quigley, M.; et al. Planetary Rover Simulation for Lunar Exploration Missions. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–19. [Google Scholar] [CrossRef]
- Xie, Y.; Zhou, J.; Wang, Y. Environment modeling for mission planning of lunar rovers. Dongnan Daxue Xuebao (Ziran Kexue Ban)/J. Southeast Univ. (Nat. Sci. Ed.) 2010, 40, 292–296. [Google Scholar]
- Rao, N.S.; Appleby, M.H. The role of terrain modeling in lunar rover simulation. Simulation 1993, 61, 60–68. [Google Scholar] [CrossRef]
- Ju, H.H.; Tian, X.E. Real-time dynamics modeling and traction control for lunar rover. Yuhang Xuebao/J. Astronaut. 2014, 35, 743–752. [Google Scholar] [CrossRef]
- Tian, X.; Ju, H. Modeling and simulation for lunar rover based on terramechanics and multibody dynamics. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 8687–8692. [Google Scholar]
- Jain, A.; Balaram, J.; Cameron, J.; Guineau, J.; Lim, C.; Pomerantz, M.; Sohl, G. Recent developments in the ROAMS planetary rover simulation Environment. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 6–13 March 2004; Volume 2, pp. 861–876. [Google Scholar] [CrossRef]
- Neukum, G.; Ivanov, B.A.; Hartmann, W.K. Cratering records in the inner solar system in relation to the lunar reference system. Space Sci. Rev. 2001, 96, 55–86. [Google Scholar] [CrossRef]
- Shankar, U.J.; Shyong, W.J.; Criss, T.B.; Adams, D. Lunar terrain surface modeling for the ALHAT program. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar] [CrossRef]
- Goddard, E.N.; Halt, M.H.; Larson, K.K. Preliminary Geologic Investigation of the Apollo 12 Landing Site. Apollo 12-Preliminary Science Report, NASA-SP-235. 1970; p. 113. Available online: https://pubs.er.usgs.gov/publication/70044160 (accessed on 20 December 2021).
- Pike, R.J. Depth/diameter relations of fresh lunar craters: Revision from spacecraft data. Geophys. Res. Lett. 1974, 1, 291–294. [Google Scholar] [CrossRef]
- Zhang, H.H.; Liang, J.; Huang, X.Y. Chang’e 3 autonomous obstacle avoidance soft landing control technology. China Sci. Technol. Sci. 2014, 44, 559–568. [Google Scholar]
- Yoshida, K.; Hamano, H. Motion dynamics of a rover with slip-based traction model. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 3155–3160. [Google Scholar] [CrossRef]
- Asadi, H.; Mohammadi, A.; Mohamed, S.; Lim, C.P.; Khatami, A.; Khosravi, A.; Nahavandi, S. A Particle Swarm Optimization-based washout filter for improving simulator motion fidelity. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 1963–1968. [Google Scholar] [CrossRef]
- Guo, L.X.; Zhang, L.P. Constrained Active Suspension Control with Parameter Uncertainty for Non-stationary Running Based on LMI Optimization. J. Vib. Eng. Technol. 2018, 6, 441–451. [Google Scholar] [CrossRef]
- Chen, G.; Lv, S.; Dai, J. Study on pid control of vehicle semi-active suspension based on genetic algorithm. Int. J. Innov. Comput. Inf. Control 2019, 15, 1093–1114. [Google Scholar] [CrossRef]
- Carvajal, J.; Chen, G.; Ogmen, H. Fuzzy PID controller: Design, performance evaluation, and stability analysis. Inf. Sci. 2000, 123, 249–270. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.L.; Lin, H.C.; Ma, Z.; Zhao, J. Development of path planning approach using improved a-star algorithm in AGV system. J. Internet Technol. 2019, 20, 915–924. [Google Scholar] [CrossRef]
- Luo, J.; Su, B.; Chi, M.; Huang, S.H. Operational Effectiveness Evaluation of Unmanned Aerial Communication Platform Based on Improved ADC Model. Fire Control Command. Control 2021, 9, 83–88. [Google Scholar]














| Angle | Color | Explain |
|---|---|---|
| Less than −25° | Purple | Dangerous slope, no passage |
| From −25° to 110° | Blue | The brakes need to be applied |
| From −10° to 10° | Green | Safe passage |
| From 10° to 25° | Yellow | A certain pre-acceleration is required to pass |
| Greater than 25° | Red | Dangerous slope, no passage |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Vision | 37.2 | 32.6 | 40.5 | 39.2 | 33.6 | 31.3 | 42.3 | 35.5 |
| Vision and force perception | 39.2 | 34.1 | 44.1 | 37.8 | 35.6 | 36.1 | 42.9 | 34.8 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Time (s) | 9.8 | 10.5 | 11.1 | 8.5 | 8.9 | 9.5 | 7.7 | 10.7 |
| Evaluation of comfort | 6 | 7 | 7 | 9 | 7 | 8 | 8 | 7 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Time (s) | 8.3 | 7.2 | 9.5 | 8.7 | 7.4 | 7.9 | 7.5 | 6.9 |
| Evaluation of comfort | 8 | 9 | 8 | 8 | 8 | 10 | 8 | 8 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Time (s) | 24.7 | 23.4 | 19.8 | 21.6 | 19.9 | 22.3 | 26.2 | 18.8 |
| Evaluation of comfort | 6 | 6 | 7 | 5 | 6 | 5 | 5 | 6 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Time (s) | 23.4 | 23.0 | 20.7 | 20.6 | 18.3 | 19.5 | 23.6 | 18.5 |
| Evaluation of comfort | 7 | 9 | 7 | 8 | 10 | 9 | 8 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Tang, Z.; Song, A. Motion Simulation and Human–Computer Interaction System for Lunar Exploration. Appl. Sci. 2022, 12, 2312. https://doi.org/10.3390/app12052312
Xie Y, Tang Z, Song A. Motion Simulation and Human–Computer Interaction System for Lunar Exploration. Applied Sciences. 2022; 12(5):2312. https://doi.org/10.3390/app12052312
Chicago/Turabian StyleXie, Yuzhen, Zihan Tang, and Aiguo Song. 2022. "Motion Simulation and Human–Computer Interaction System for Lunar Exploration" Applied Sciences 12, no. 5: 2312. https://doi.org/10.3390/app12052312
APA StyleXie, Y., Tang, Z., & Song, A. (2022). Motion Simulation and Human–Computer Interaction System for Lunar Exploration. Applied Sciences, 12(5), 2312. https://doi.org/10.3390/app12052312







