Local Path-Planning Simulation and Driving Test of Electric Unmanned Ground Vehicles for Cooperative Mission with Unmanned Aerial Vehicles
Abstract
:Featured Application
Abstract
1. Introduction
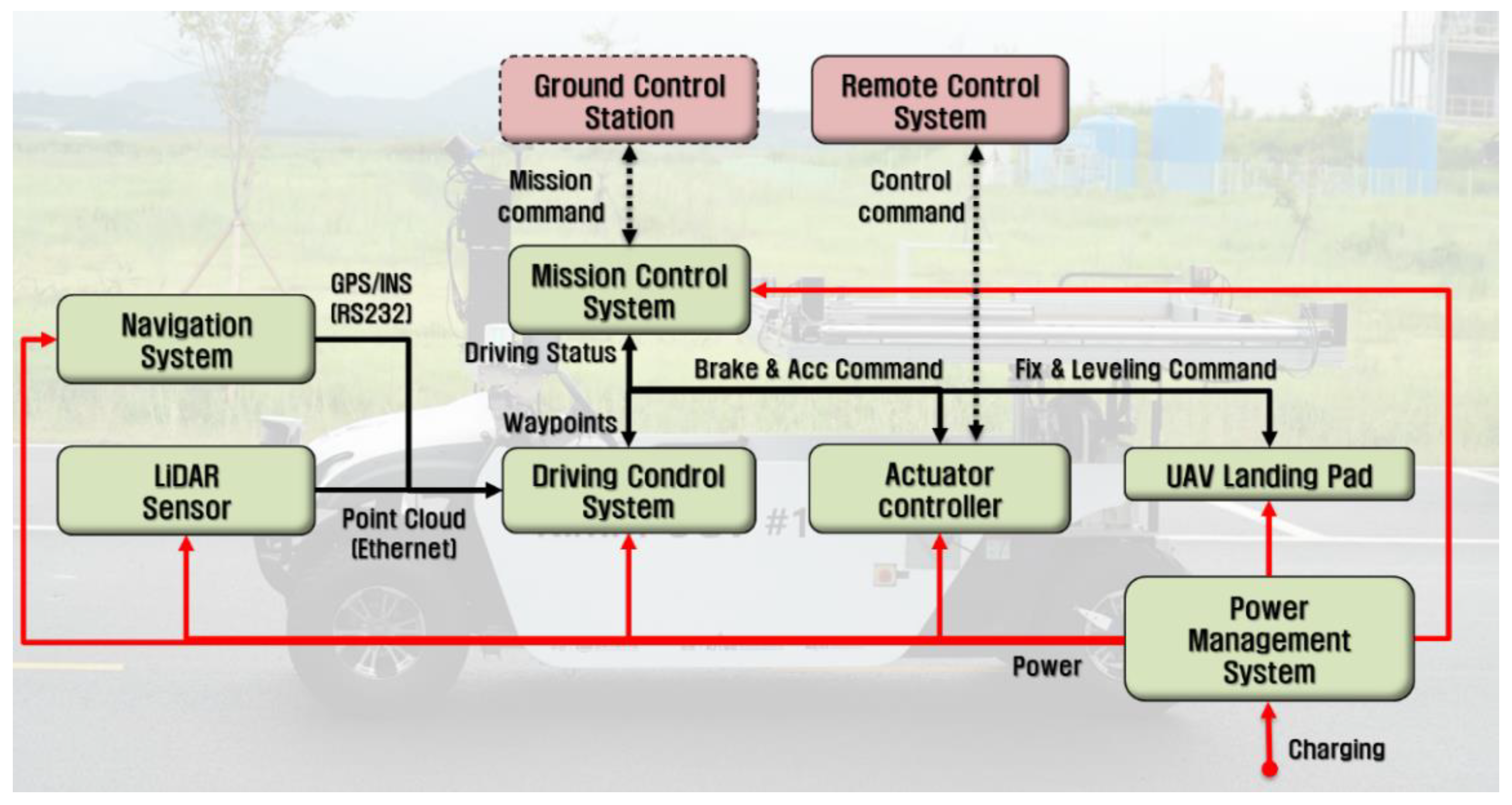
2. UGV System Configuration
3. Path Planning
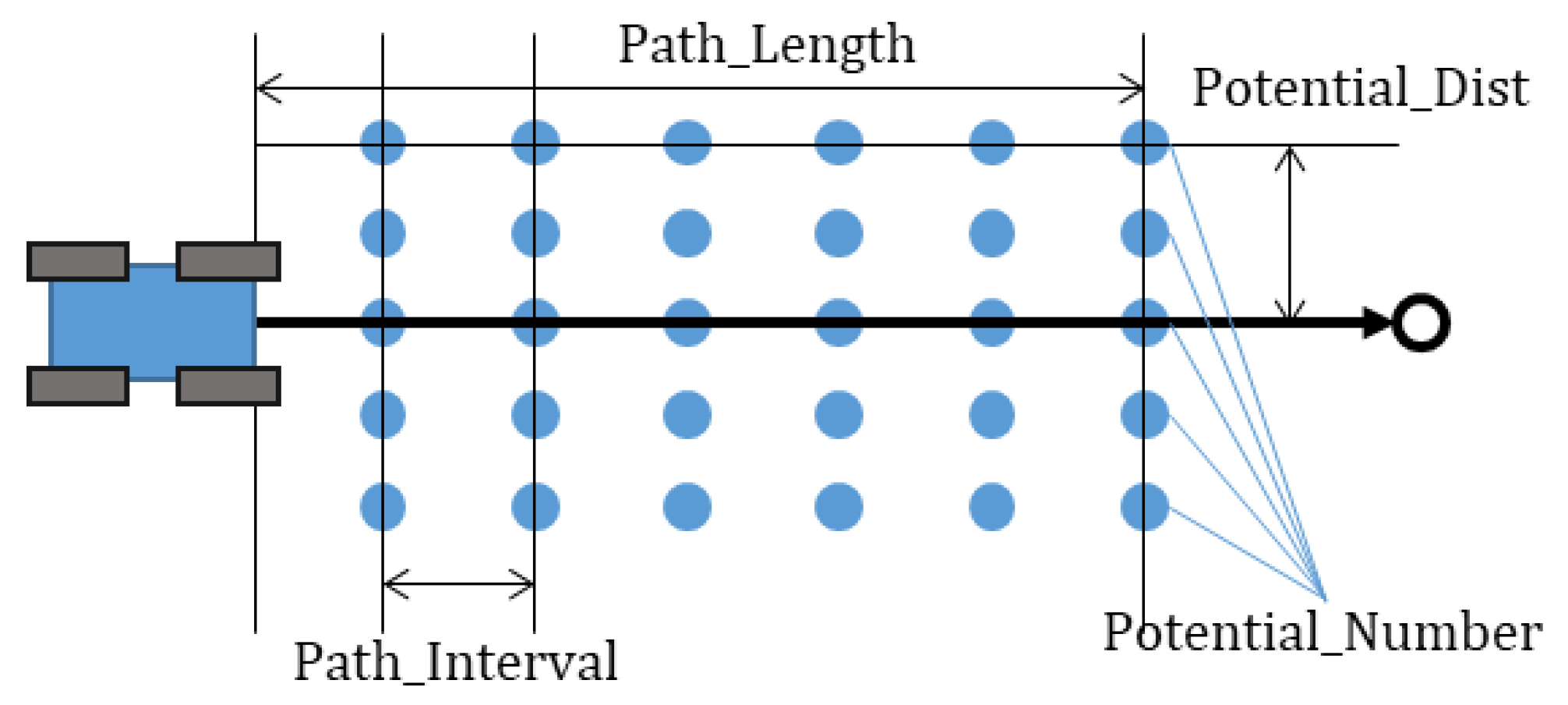
3.1. Potential Field Algorithm
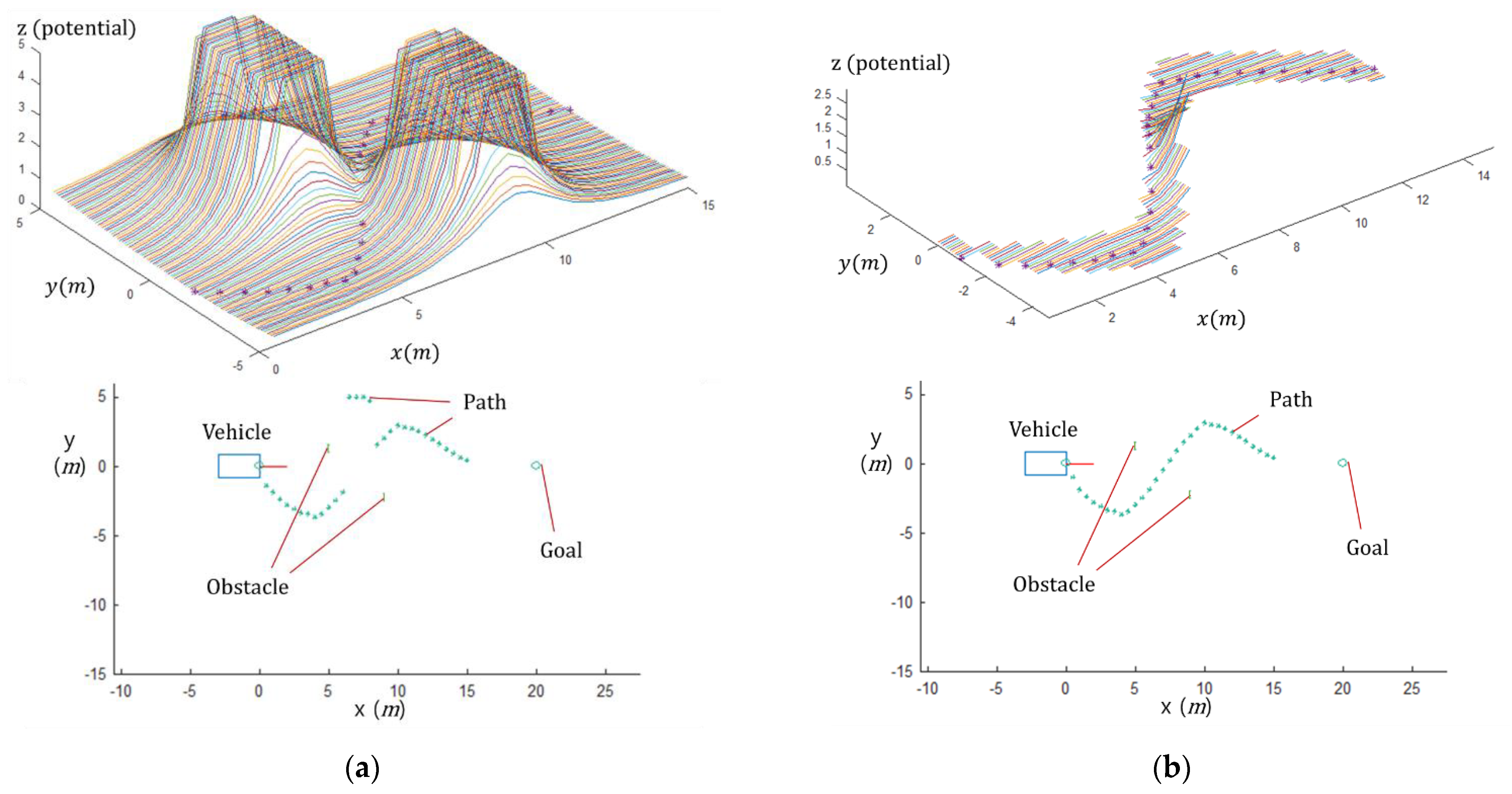
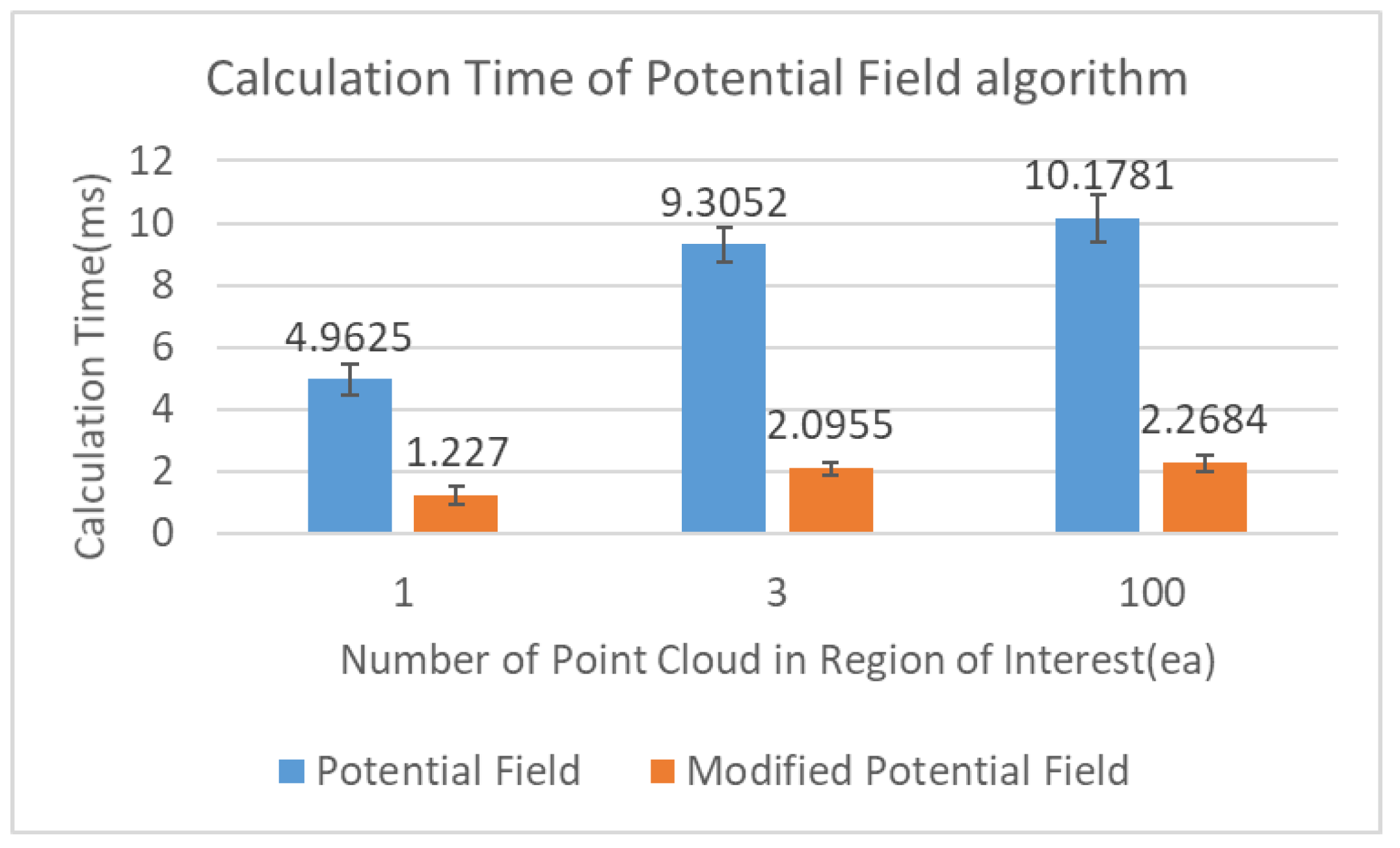
3.2. Potential Field Algorithm Simulation
| Algorithm 1: Pseudo code of modified potential field algorithm |
|
4. Driving Test
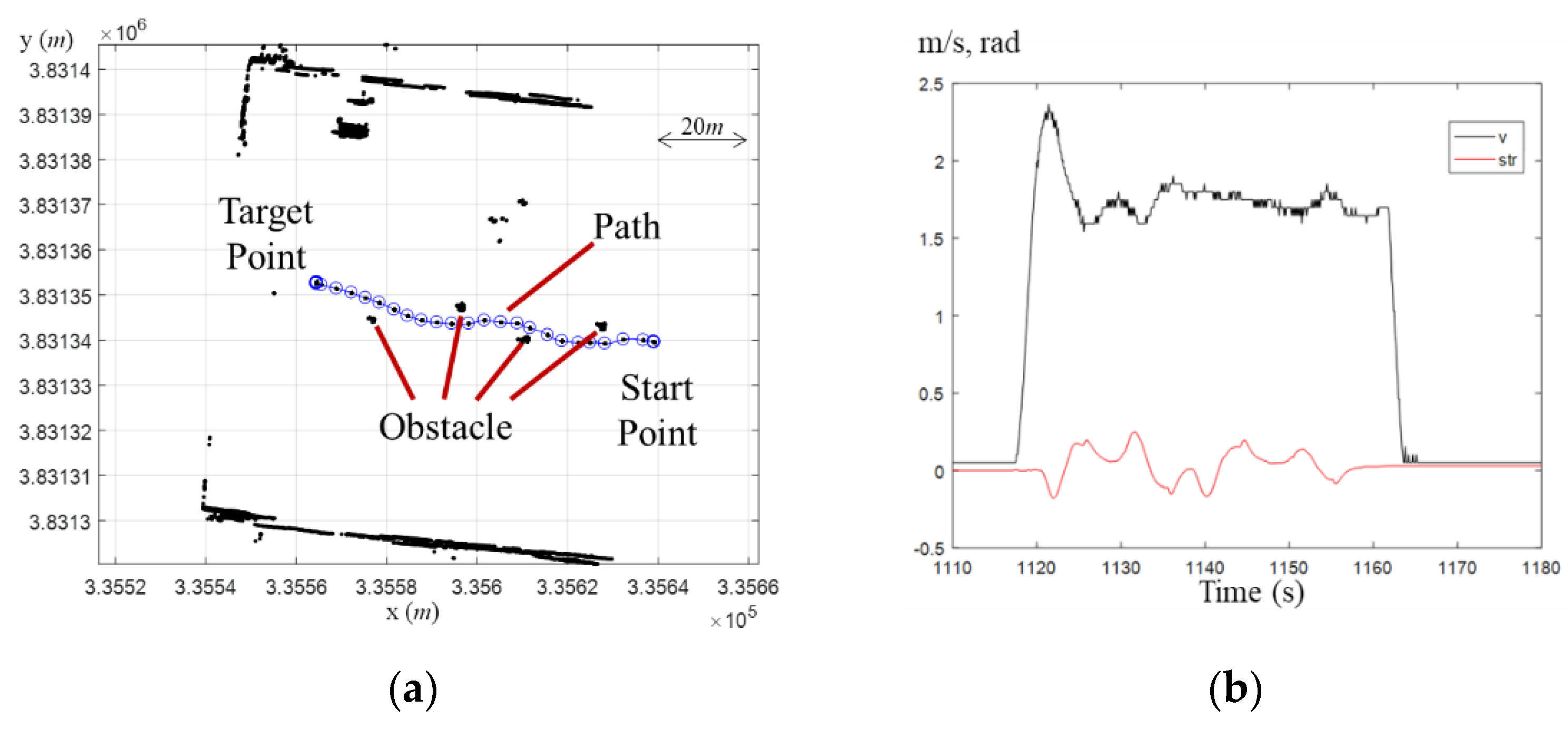
4.1. Multiple Obstacle Avoidance Experiment
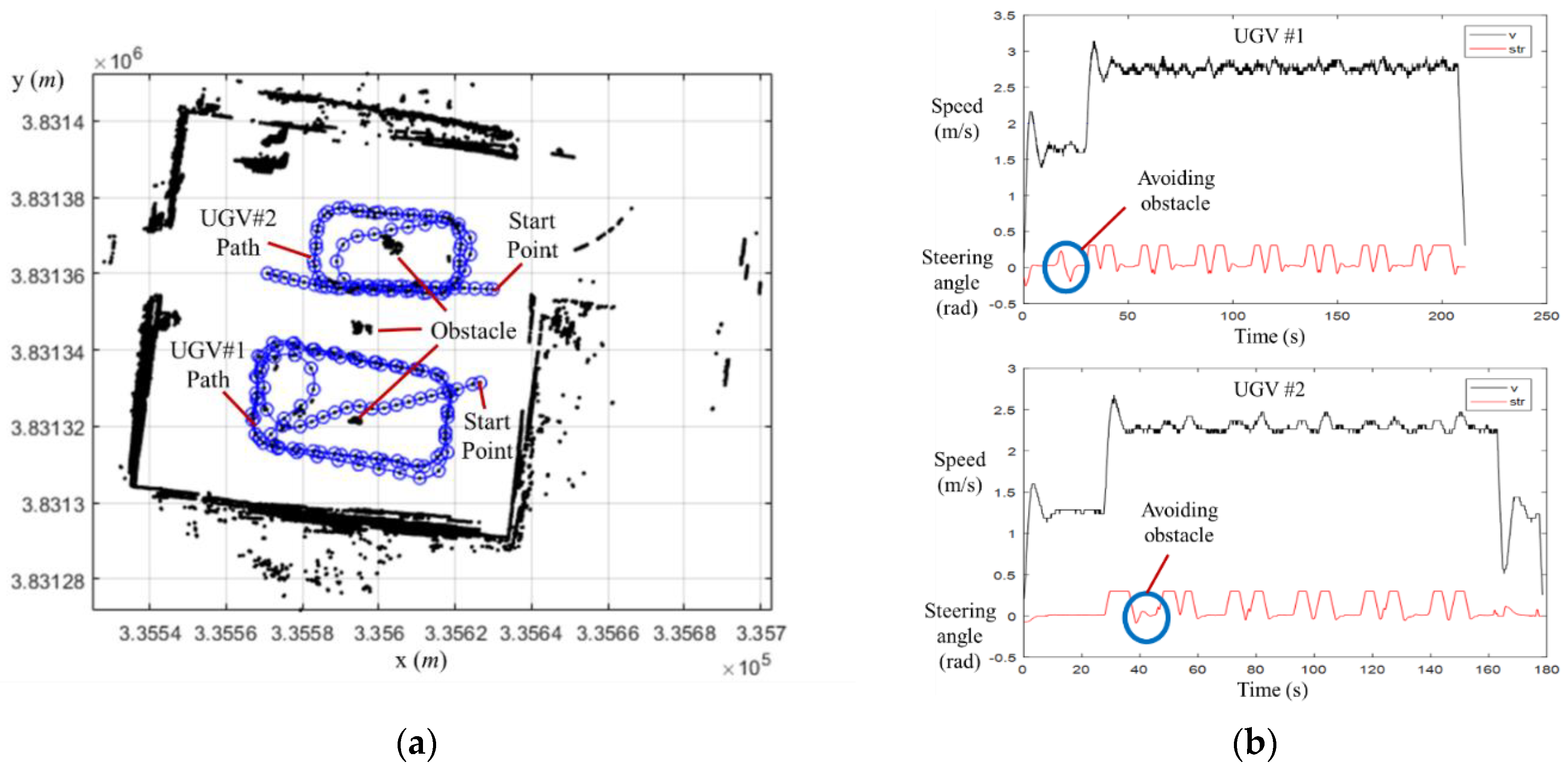
4.2. Multiple UGV/UAV Operation Test
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cantelli, L.; Presti, M.L.; Mangiameli, M.; Melita, C.D.; Muscato, G. Autonomous cooperation between UAV and UGV to improve navigation and environmental monitoring in rough environments. In Proceedings of the 10th International Symposium, HUDEM, Karnataka, India, 23–25 April 2013. [Google Scholar]
- Grocholsky, B.; Keller, J.; Kumar, V.; Pappas, G. Cooperative air and ground surveillance. IEEE Robot. Autom. Mag. 2006, 13, 16–25. [Google Scholar] [CrossRef] [Green Version]
- Mathew, N.; Smith, S.; Waslander, S. Multirobot Rendezvous Planning for Recharging in Persistent Tasks. IEEE Trans. Robot. 2015, 31, 128–142. [Google Scholar] [CrossRef]
- Ropero, F.; Muñoz, P.; R-Moreno, M.D. TERRA: A path planning algorithm for cooperative UGV–UAV exploration. Eng. Appl. Artif. Intell. 2019, 78, 260–272. [Google Scholar] [CrossRef]
- Gonzalez, D.; Perez, J.; Milanes, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 17, 1135–1145. [Google Scholar] [CrossRef]
- Lavalle, S.M. Planning Algorithms; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M. Sampling-Based Robot Motion Planning: A Review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.-C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Brezak, M.; Petrovic, I. Real-time Approximation of Clothoids With Bounded Error for Path Planning Applications. IEEE Trans. Robot. 2013, 30, 507–515. [Google Scholar] [CrossRef]
- Kim, J.-C.; Pae, D.-S.; Lim, M.-T. Obstacle Avoidance Path Planning based on Output Constrained Model Predictive Control. Int. J. Control Autom. Syst. 2019, 17, 2850–2861. [Google Scholar] [CrossRef]
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28. [Google Scholar] [CrossRef]
- Sfeir, J.; Saad, M.; Saliah-Hassane, H. An improved Artificial Potential Field approach to real-time mobile robot path planning in an unknown environment. In Proceedings of the 2011 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Montreal, QC, Canada, 17–18 September 2011; pp. 208–213. [Google Scholar]
- Kim, D.H. Escaping route method for a trap situation in local path planning. Int. J. Control Autom. Syst. 2009, 7, 495–500. [Google Scholar] [CrossRef]
- Kim, D.H.; Shin, S. Local path planning using a new artificial potential function configuration and its analytical design guidelines. Adv. Robot. 2006, 20, 115–135. [Google Scholar] [CrossRef]
- Lau, B.; Sprunk, C.; Burgard, W. Efficient grid-based spatial representations for robot navigation in dynamic environments. Robot. Auton. Syst. 2013, 61, 1116–1130. [Google Scholar] [CrossRef]
- Park, B.; Choi, J.; Chung, W.K. An efficient mobile robot path planning using hierarchical roadmap representation in indoor environment. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 180–186. [Google Scholar]
- Kim, J.; Kim, M.; Kim, Y.; Lee, G. Real-time 3D Mapping System in Multiple Autonomous Vehicle. In Proceedings of the KSME Spring and Autumn Conference, Daejoen, Korea, 25–26 April 2019. [Google Scholar]
- Koren, Y.; Borenstein, J. Potential field methods and their inherent limitations for mobile robot navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991. [Google Scholar]
- Kim, K. Predicted Potential Risk-Based Vehicle Motion Control of Automated Vehicles for Integrated Risk Management. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2016. [Google Scholar]
- Coulter, R.C. Implementation of the Pure Pursuit Path Tracking Algorithm; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 1992. [Google Scholar]
- Choset, H. Robotic Motion Planning: Potential Functions; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2010. [Google Scholar]
- Kim, M.; Yoo, S.; Kim, J.-C.; Lee, G.-H. Development of Electric Unmanned Ground Vehicle for Aerial-Ground Cooperative Missions. Trans. Korean Soc. Mech. Eng. A 2019, 43, 829–836. [Google Scholar] [CrossRef]
- Ryu, H.; Han, D.; Lee, J.; Jung, Y.; Kim, S. Test Scenario for Multiple Unmanned Vehicles Operation. In Proceedings of the KSAS Fall Conference, Jeju, Korea, 20–23 November 2019. [Google Scholar]











| Variables | |
|---|---|
| path_length | Length of local path generated by potential field algorithm |
| path_interval | Interval of global path (the shortest path) |
| K | Potential gain for obstacle |
| C | Potential gain for perpendicular distance from the global path |
| Q | Distance from obstacle to minimize potential |
| D_min | Distance from obstacle to maximize potential |
| Potential_Value_Max | Maximum potential value |
| potential_number | Number of potential calculation points |
| potential_dist | Perpendicular distance from global path to calculation potential |
| potential_dist_ratio | The ratio of distance in a normal direction to the driving direction to calculate potential |
| CPU | Intel® Core™ i7-8559U 2.70 GHz |
| RAM | 16 GB |
| OS | Windows 10 64 bit |
| Path_length | 15 m |
| Path_interval | 0.5 m |
| k | 10 |
| L | 10 m |
| Q | 10 m |
| D_min | 1.5 m |
| Potential_Value_Max | 5 |
| Potential_number | 100 |
| Potential_dist | 5 m |
| potential_dist_ratio | 2 |
| Path_length | 15 m |
| Path_interval | 0.5 m |
| k | 10 |
| L | 10 m |
| Q | 10 m |
| D_min | 1.5 m |
| Potential_Value_Max | 5 |
| Potential_number | 100 |
| Potential_dist | 5 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Yoo, S.; Lee, D.; Lee, G.-H. Local Path-Planning Simulation and Driving Test of Electric Unmanned Ground Vehicles for Cooperative Mission with Unmanned Aerial Vehicles. Appl. Sci. 2022, 12, 2326. https://doi.org/10.3390/app12052326
Kim M, Yoo S, Lee D, Lee G-H. Local Path-Planning Simulation and Driving Test of Electric Unmanned Ground Vehicles for Cooperative Mission with Unmanned Aerial Vehicles. Applied Sciences. 2022; 12(5):2326. https://doi.org/10.3390/app12052326
Chicago/Turabian StyleKim, Mingeuk, Seungjin Yoo, Dongwook Lee, and Geun-Ho Lee. 2022. "Local Path-Planning Simulation and Driving Test of Electric Unmanned Ground Vehicles for Cooperative Mission with Unmanned Aerial Vehicles" Applied Sciences 12, no. 5: 2326. https://doi.org/10.3390/app12052326
APA StyleKim, M., Yoo, S., Lee, D., & Lee, G.-H. (2022). Local Path-Planning Simulation and Driving Test of Electric Unmanned Ground Vehicles for Cooperative Mission with Unmanned Aerial Vehicles. Applied Sciences, 12(5), 2326. https://doi.org/10.3390/app12052326






