Dilatant Nature of Sand Shear Strength
Abstract
:1. Introduction
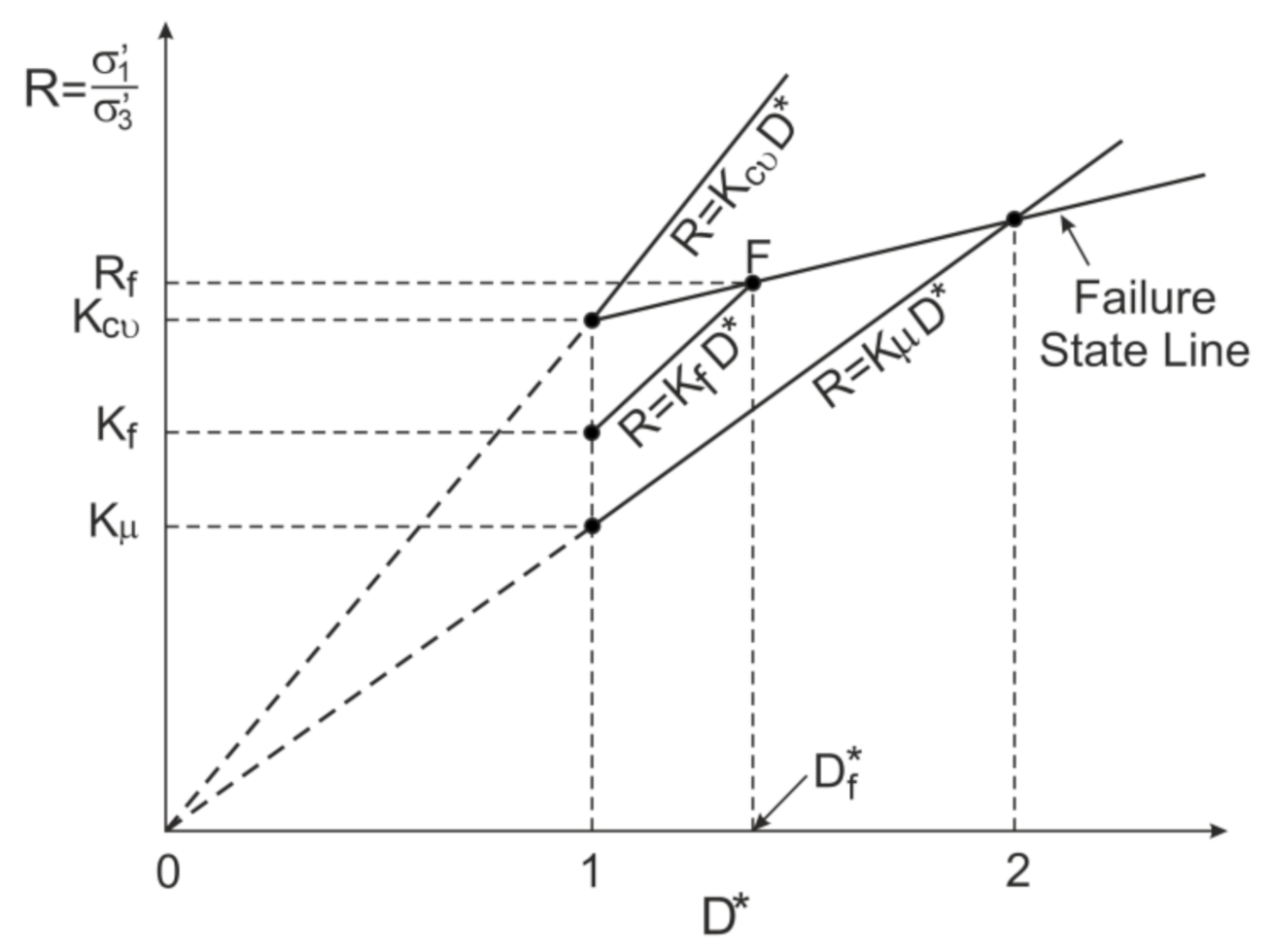
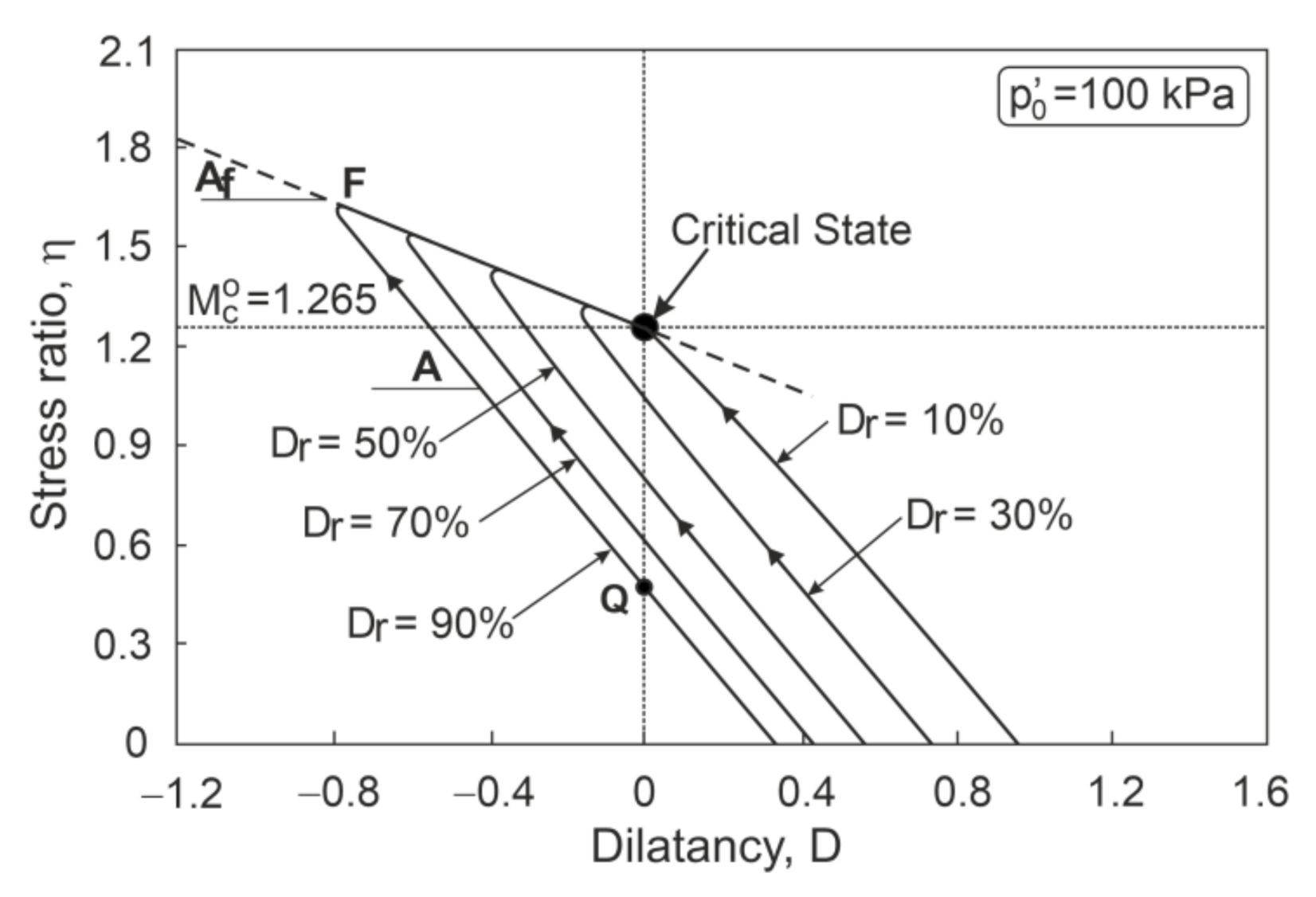
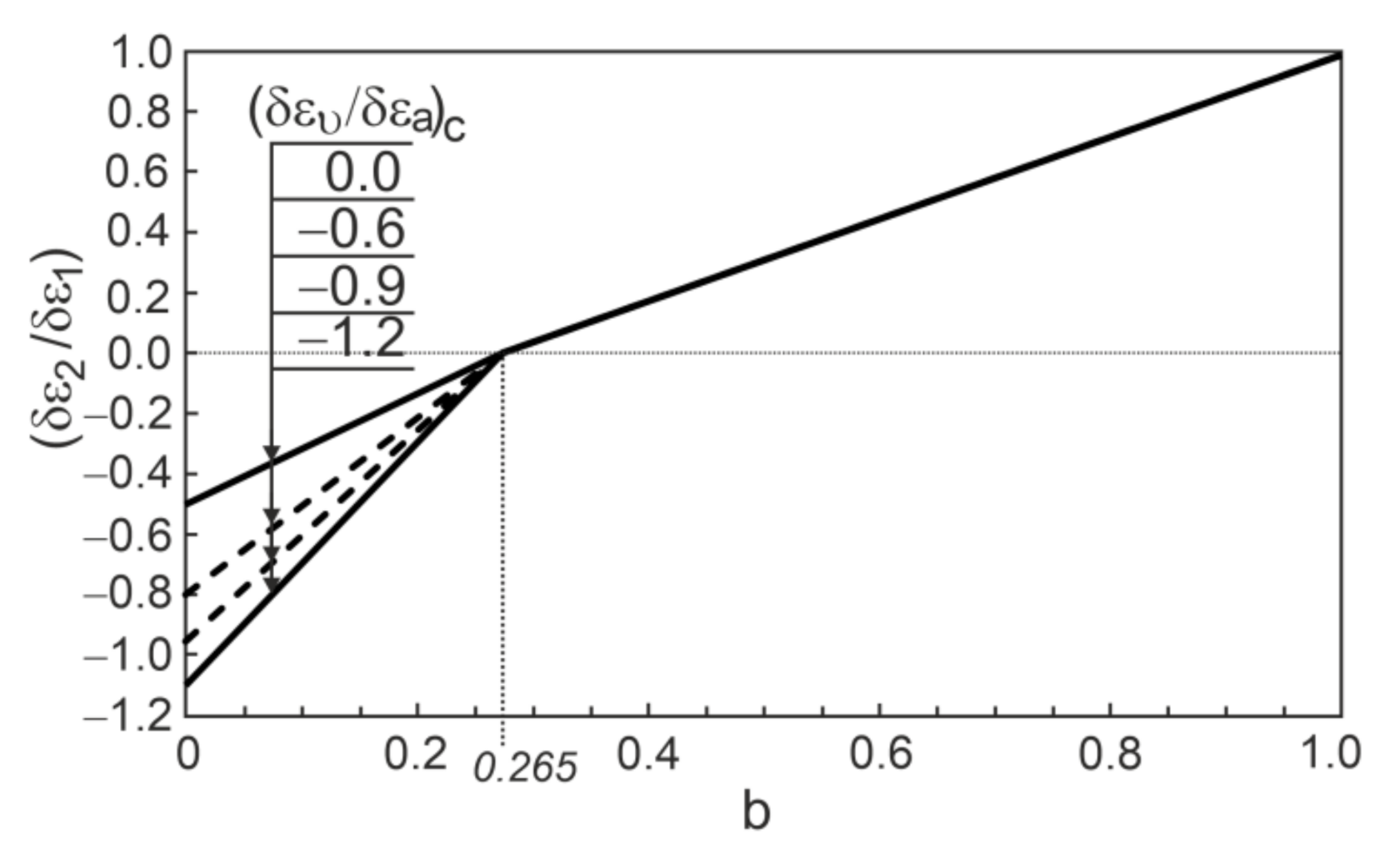
2. Stress–Dilatancy Relationships for Sand
3. Shear Strength of Sand for TXC, BXC, and TXE
3.1. Drained Triaxial Compression
3.2. Plane Strain Conditions
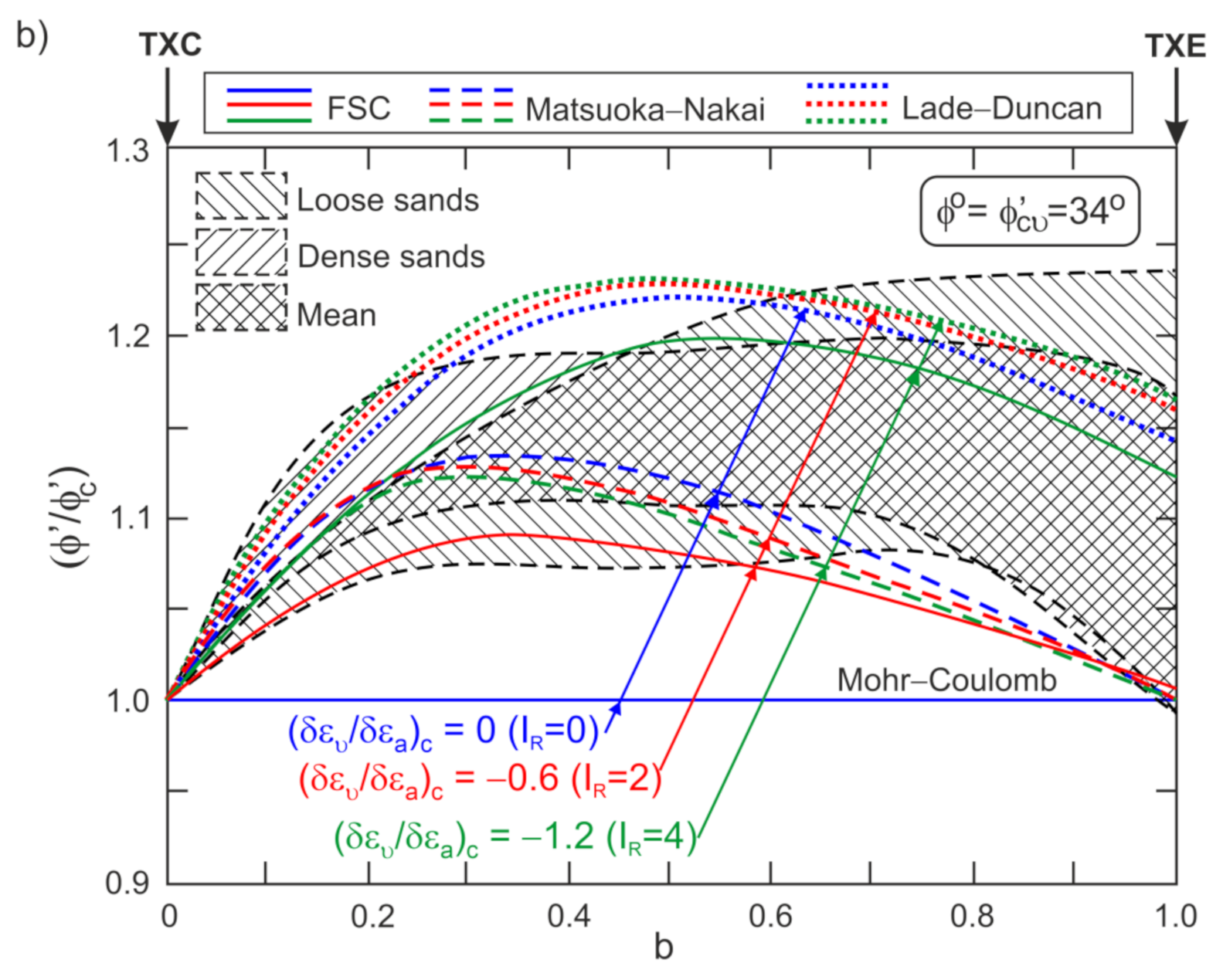
3.3. Drained Triaxial Extension
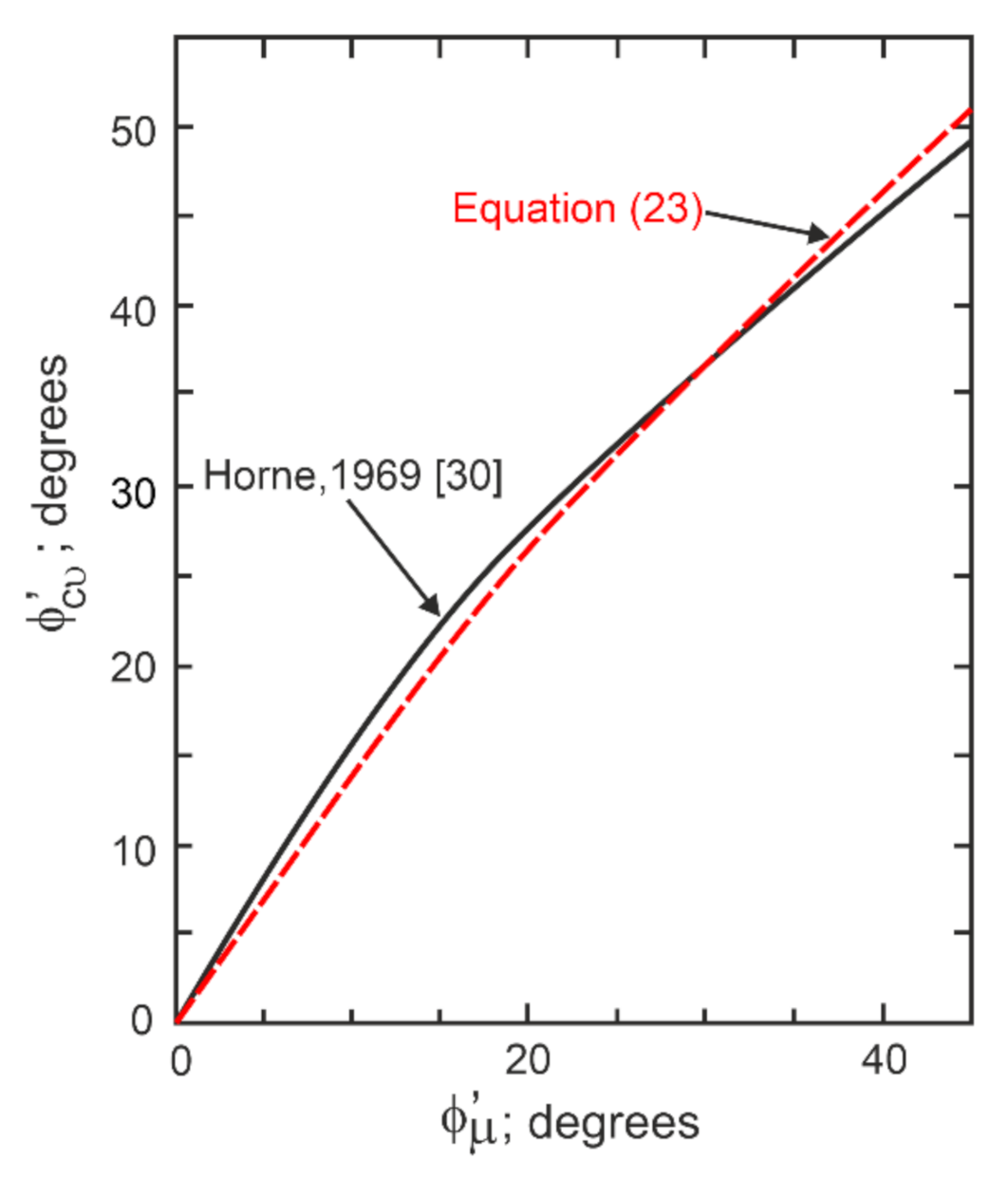
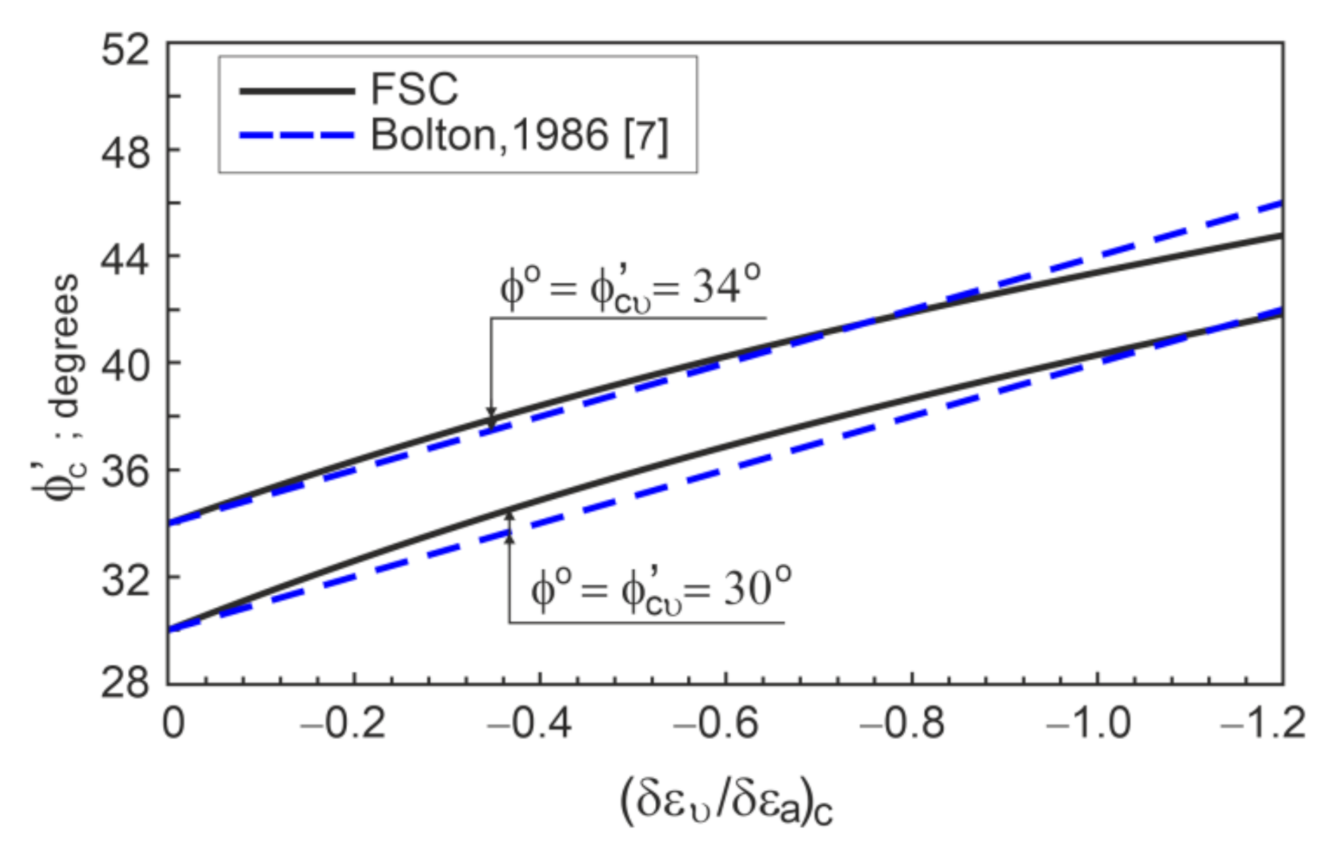
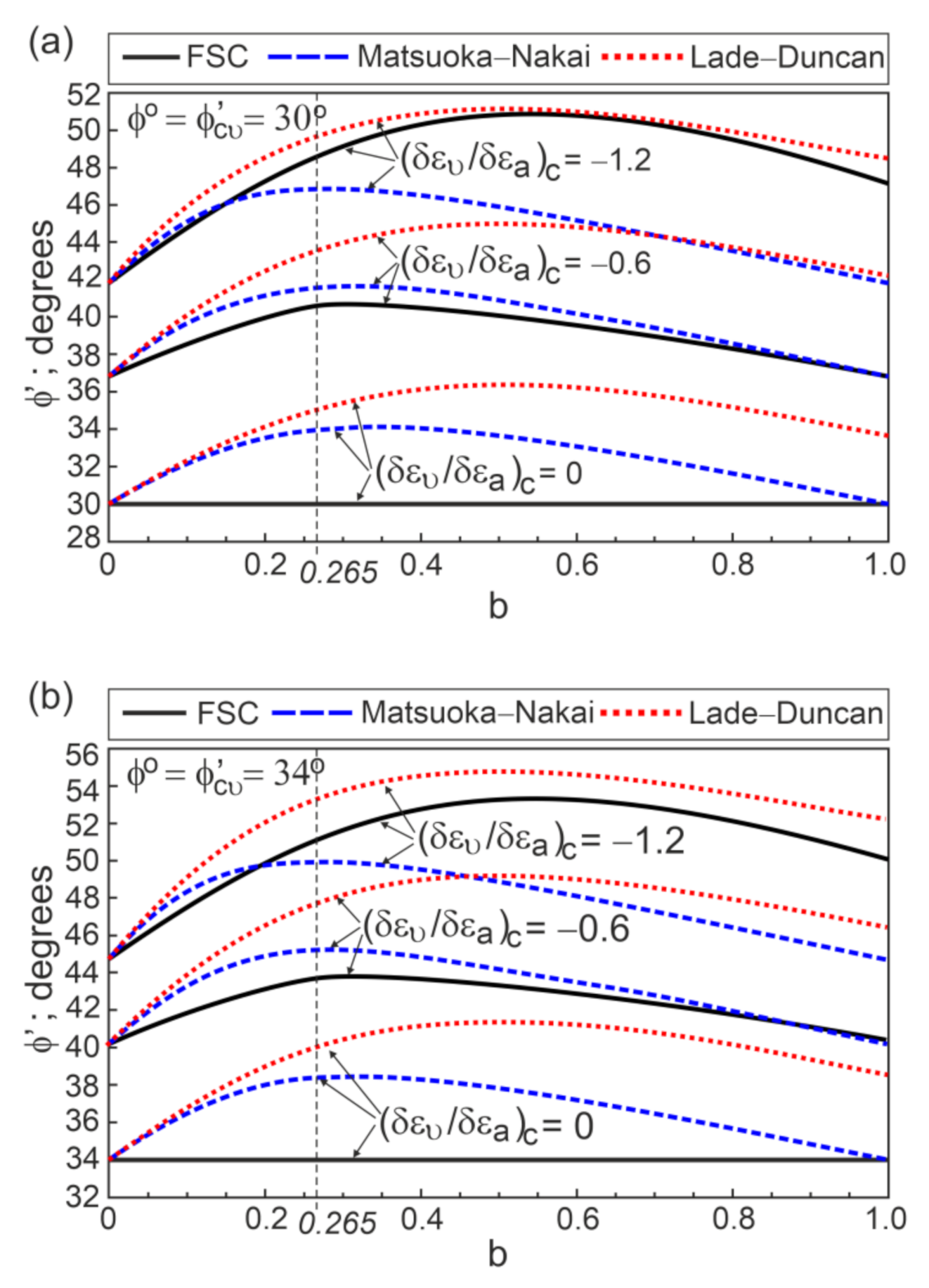
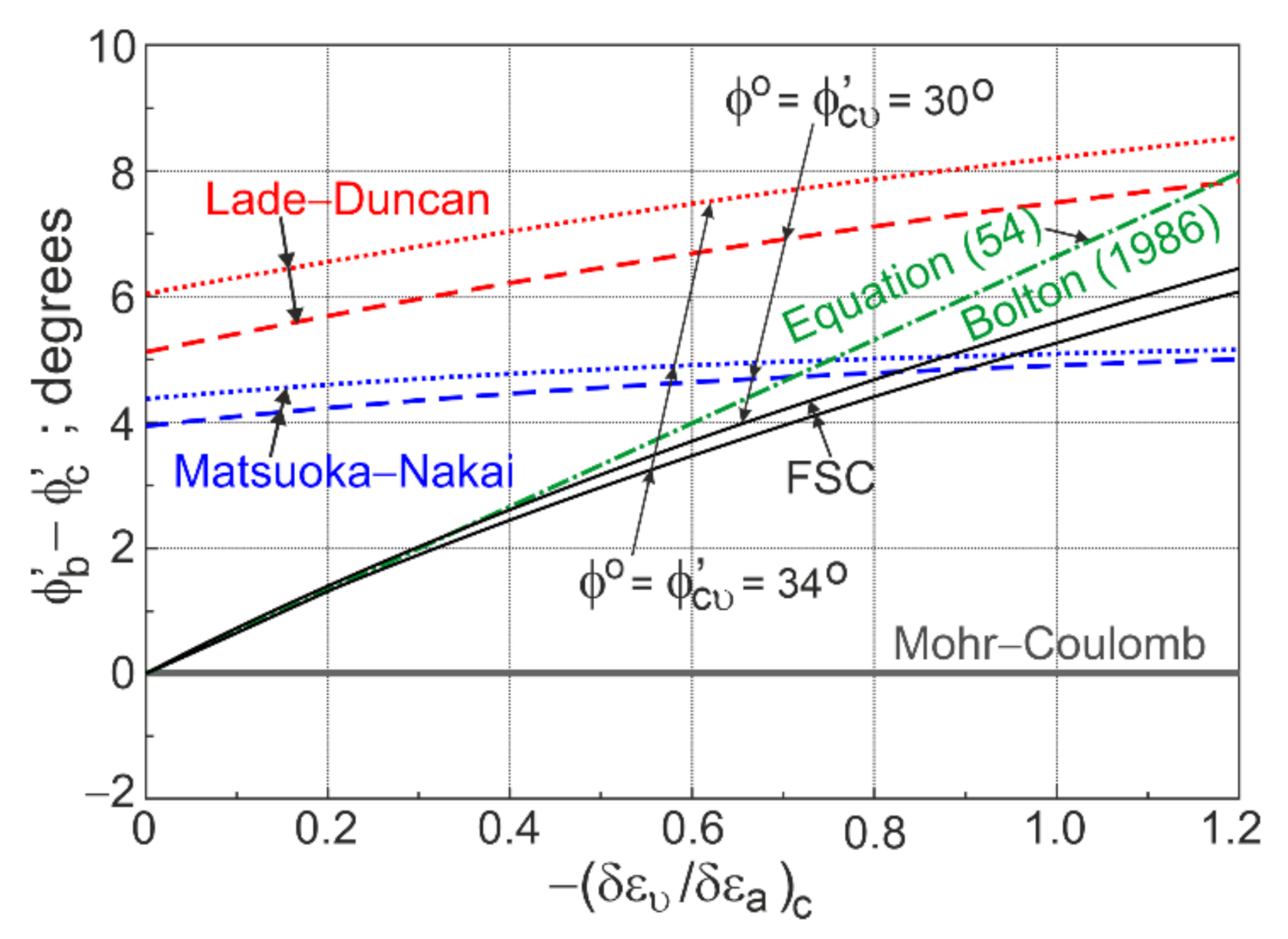
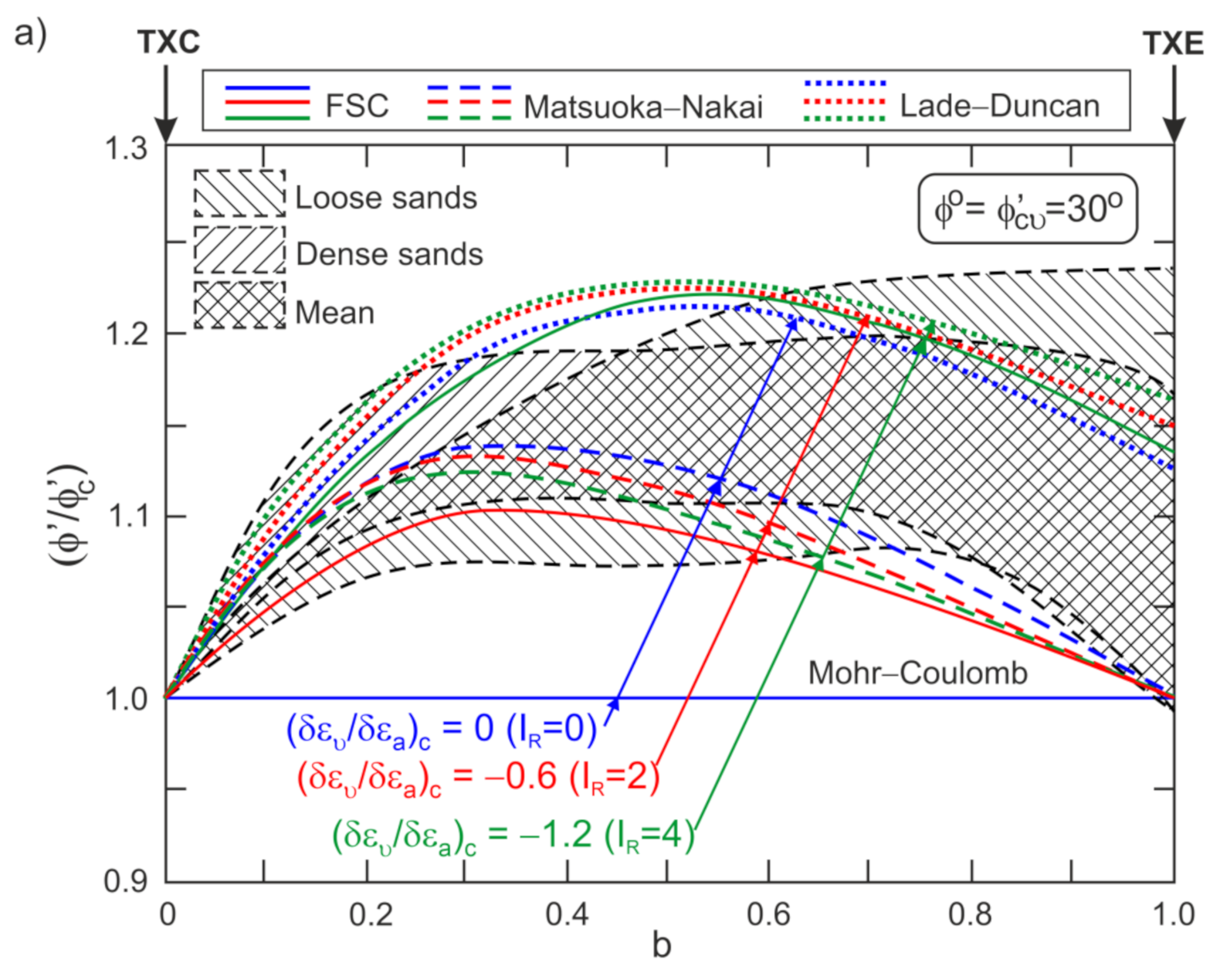
4. Shear Strength of Sand for the General Condition
- For TXC:
- For BXC:
- For TXE:
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atkinson, J. The Mechanics of Soils and Foundations, 2nd ed.; Taylor & Francis Group: London, UK, 2007. [Google Scholar] [CrossRef]
- Matsuoka, H.; Nakai, T. Stress-Deformations and Strength Characteristics of Soils under Three Different Principal Stresses; Japan Society of Civil Engineers: Tokyo, Japan, 1974; Volume 232, pp. 59–74. [Google Scholar] [CrossRef]
- Lade, P.V.; Duncan, J.M. Elastoplastic Stress-Strain Theory for Cohesionless Soil. J. Geotech. Eng. Div. 1975, 101, 1037–1053. [Google Scholar] [CrossRef]
- Lam, W.K.; Tatsuoka, F. Effects of Initial Anisotropic Fabric and σ2 on Strength and Deformation Characteristics of Sand. Soils Found. 1988, 28, 89–106. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.D.; Indraratna, B.N. General Strength Criterion for Geomaterials Including Anisotropic Effect. Int. J. Geomech. 2011, 11, 251–262. [Google Scholar] [CrossRef]
- Cao, W.; Wang, R.; Zhang, J.-M. Formulation of Anisotropic Strength Criteria for Cohesionless Granular Material. Int. J. Geomech. 2017, 17. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 35, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Cornforth, D.H. Some Experiments on the Influence of Strain Conditions on the Shear Strength of Sand. Géotechnique 1964, 14, 143–167. [Google Scholar] [CrossRef]
- Schanz, T.; Vermeer, P.A. Angles of friction and dilatancy of sand. Géotechnique 1996, 46, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Lade, P.V.; Lee, K.L. Engineering Properties of Soils; Report UCLA-ENG-7652; University of California: Los Angeles, CA, USA, 1976. [Google Scholar]
- Das, B.M. Advanced Soil Mechanics, 3rd ed.; Taylor & Francis Group: London, UK; New York, NY, USA, 2008. [Google Scholar]
- Lade, P.V. Assessment of test data for selection of 3-D failure criterion for sand. Int. J. Numer. Anal. Meth. Geomech. 2006, 30, 307–333. [Google Scholar] [CrossRef]
- Yamamuro, J.A.; Lade, P.V. Drained Sand Behaviour in Axisymmetric Tests at High Pressures. J. Geotech. Eng. 1996, 122, 109–119. [Google Scholar] [CrossRef]
- Corfdir, A. Sulem, J. Comparison of extension and compression triaxial tests for dense sand and sandstone. Acta Geotech. 2008, 3, 241. [Google Scholar] [CrossRef]
- Green, G.E.; Bishop, A.W. A Note on the Drained Strength of Sand Under Generalized Strain Conditions. Géotechnique 1969, 19, 144–149. [Google Scholar] [CrossRef]
- Mesdary, M.S.; Sutherland, H.B. Correspondence to “A Note on the Drained Strength of Sand Under Generalized Strain Conditions. Green, G.E., Bishop, A.W., Géotechnique 1969, 19, 144–149“. Géotechnique 1970, 20, 210–212. [Google Scholar] [CrossRef]
- Ko, H.Y.; Scott, R.F. Deformation of sand at failure. J. Soil Mech. Found. Div. 1968, 94, 883–898. [Google Scholar] [CrossRef]
- Ladd, C.C.; Foote, R.; Ishihara, K.; Schlosser, F.; Poulos, H.G. Stress-Deformation and Strength Characteristics. In Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering, Tokyo, Japan, 11 July 1977; Volume 2, pp. 421–494. [Google Scholar]
- Kulhawy, F.H.; Mayne, P.W. Manual on Estimating Soil Properties for Foundation Design; EL-6800 Research Project 1493-6; Cornell University: New York, NY, USA, 1990. [Google Scholar]
- Taylor, D.W. Fundamentals of Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1948. [Google Scholar]
- Rowe, P.W. The Relationship Between the Shear Strength of Sands in Triaxial Compression, Plane Strain and Direct Shear. Gèotechnique 1969, 19, 75–86. [Google Scholar] [CrossRef]
- Szypcio, Z. Stress-dilatancy for soils. Part I: The frictional state theory. Studia Geotech. Mech. 2016, 38, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Szypcio, Z. Stress-dilatancy for soils. Part II: Experimental validation for triaxial tests. Studia Geotech. Mech. 2016, 38, 59–65. [Google Scholar] [CrossRef] [Green Version]
- Szypcio, Z. Stress-Dilatancy for Soils. Part III: Experimental Validation for the Biaxial Condition. Studia Geotech. Mech. 2017, 3, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Szypcio, Z. Stress-Dilatancy for Soils. Part IV: Experimental Validation for Simple Shear Conditions. Studia Geotech. Mech. 2017, 39, 81–88. [Google Scholar] [CrossRef] [Green Version]
- Dołżyk-Szypcio, K. Stress-Dilatancy Relationship of Erksak Sand under Drained Triaxial Compression. Geosciences 2020, 10, 353. [Google Scholar] [CrossRef]
- Szypcio, Z. Stress-dilatancy of gravel for triaxial compression tests. Ann. Warsaw Univ. Life Sci. SGGW Land Reclam. 2018, 50, 119–128. [Google Scholar] [CrossRef]
- Dołżyk-Szypcio, K. Stress-dilatancy relationship for railway ballast. Studia Geotech. Mech. 2018, 40, 79–85. [Google Scholar] [CrossRef] [Green Version]
- Dołżyk-Szypcio, K. Stress-Dilatancy of Rounded and Angular Rockfill Materials. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Horne, M.R. The Behaviour of an Assembly of Rotund, Rigid, Cohesionless Particles. Part III. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1969, 310, 21–34. [Google Scholar] [CrossRef]
- Jamiołkowski, M.; Lo-Presti, D.C.F.; Manassero, M. Evolution of Relative Density and shear Strength of Sands from CPT and DMT. In Proceedings of the Symposium on Soil Behavior and Soft Ground Construction Honoring Charles C. “Chuck” Ladd, Boston, MA, USA, 5–6 October 2001; ASCE Geotechnical Special Publication No.119. pp. 201–238. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.S. State-Dependent Strength of Sands from the Perspective of United Modeling. J. Geotech. Geoenviron. Eng. 2004, 130, 186–198. [Google Scholar] [CrossRef] [Green Version]
- Hanna, A.M.; Masoud, N.; Youssef, H. Prediction of plane strain angles of shear resistance from triaxial tests results. In Prediction and Performance in Geotechnical Engineering; University of Calgary: Calgary, AB, Canada, 1987; pp. 369–376. [Google Scholar]
- Schanz, T. Zunmodellierung des Mechnischenverhaltens von Reibungsmaterlean; Vermeer, P.A., Ed.; Institute fur Geotechnik, Universitat Stuttgart: Stuttgart, Germany, 1998; Volume 45. [Google Scholar]
- Konrad, J.-M.; Watts, B.D. Undrained shear strength for liquefaction flow failure analysis. Can. Geotech. J. 1995, 32, 783–794. [Google Scholar] [CrossRef]
- Olsen, S.M.; Stark, T.D. Use of laboratory data to confirm yield and liquefied strength ratio concepts. Can. Geotech. J. 2003, 40, 1164–1184. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Sumelka, W.; Gao, Y. Advantages and limitations of an α-plasticity model for sand. Acta Geotech. 2020, 15, 1423–1437. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.G.; Hachey, J. The critical states of sands. Géotechnique 1991, 41, 365–381. [Google Scholar] [CrossRef]
- Riemer, M.F.; Seed, R.B.; Nicholson, P.G.; Jong, H.L. Steady State Testing of Loose Sands: Limiting Minimum Density. J. Geotech. Eng. 1990, 116, 332–337. [Google Scholar] [CrossRef]
- Sasitharan, S.; Robertson, P.K.; Sego, D.C.; Morgenstern, N.R. State-boundary surface for very loose sand and its practical implications. Can. Geotech. J. 1994, 31, 321–334. [Google Scholar] [CrossRef]
- Riemer, M.F.; Seed, R.B. Factors Affecting Apparent Position of Steady-State Line. J. Geotech. Geoenviron. Eng. 1997, 123, 281–288. [Google Scholar] [CrossRef]
- Ishihara, K. Liquefaction and flow failure during earthquakes. Géotechnique 1993, 43, 351–415. [Google Scholar] [CrossRef]
- Chu, J.; Lo, S.C.R. On the Measurement of Critical State Parameters of Dense Granular Soils. Geotech. Test. J. 1993, 16, 27–35. [Google Scholar] [CrossRef]
- Prearo, C. Determination of Cyclic Resistance of Clean Sands from Cone Penetration Test Based on State Parameter. Ph.D. Thesis, University of Ferrara, Ferrara, Italy, 2015. [Google Scholar]
- Yu, H.S.; Khong, C.D.; Wang, J.; Zhang, G. Experimental evaluation and extension of a simple critical state model for sand. Granul. Matter 2005, 7, 213–225. [Google Scholar] [CrossRef]
- Ling, H.I.; Yang, S. Unified Sand Model Based on the Critical State and Generalized Plasticity. ASCE J. Eng. Mech. 2006, 132, 1380–1391. [Google Scholar] [CrossRef]
- Wang, J. The Stress-Strain and Strength Characteristics of Portaway Sand. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2005. [Google Scholar]
- Pestana, J.M.; Nikolinakou, M.; Whittle, A.J. Selection of material parameters for sands using MIT-SI model. In Soil Constitutive Models. Evaluation, Selection, and Calibration; Yamamuro, J.A., Kaliakin, Y.N., Eds.; ASCE Geotechnical Special Publication No. 128; ASCE: Reston, Virginia, 2005; pp. 425–439. [Google Scholar]
- Hettler, A.; Vardoulakis, I. Behaviour of dry sand tested in a large triaxial apparatus. Géotechnique 1984, 34, 183–197. [Google Scholar] [CrossRef]
- Wanatowski, D.; Chu, J. Static liquefaction of sand in plane strain. Can. Geotech. J. 2007, 44, 299–313. [Google Scholar] [CrossRef]
- Green, G.E.; Reades, D.W. Boundary condition, anisotropy and sample shape effects on the stress-strain behaviour of sand in triaxial compression and plane strain. Géotechnique 1975, 25, 333–356. [Google Scholar] [CrossRef]
- Barden, L.; Khayatt, A.J. Incremental Strain Rate Ratios and Strength of Sand in the Triaxial Test. Gèotechnique 1966, 16, 338–357. [Google Scholar] [CrossRef]
- Fern, J.; Soga, K.; Sakanoue, T. Modelling the Shear Strength and Dilatancy of Dry Sand in Triaxial Compression Tests. Geomechanics from Micro to Macro; Soga, K., Kumar, K., Biscontin, G., Kuo, M., Eds.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: London, UK, 2015; Volume 2, pp. 673–678. [Google Scholar]
- Tatsuoka, F.; Sakamoto, M.; Kawamura, T.; Fakushima, S. Strength and deformation characteristics of sand in plane strain compression at extremely low pressures. Soils Found. 1986, 26, 65–84. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, T.B.S.; Tatsuoka, F.; Horii, N. Strength and deformation characteristics of sand in torsional simple shear. Soils Found. 1988, 28, 131–148. [Google Scholar] [CrossRef] [Green Version]
- Leussink, H.; Blinde, A.; Abel, P.-G. Versuche über die Sohldruckverteilung unter Starren Gründungskörpern auf Kohäsionslosem Sand; Veröffentlichungen des Instituts für Bodenmechanik und Grundbau der Technischen Hochschule Fridericiana in Karlsruhe: Karlsruhe, Germany, 1966. [Google Scholar]
- Jiang, M.; Zhang, A.; Shen, Z. Granular soils: From DEM simulation to constitutive modeling. Acta Geotech. 2020, 15, 1723–1744. [Google Scholar] [CrossRef]
- Vasko, A.; El Ghoraiby, M.; Manzari, M.T. An Investigation into the Behaviour of Ottawa Sand under Monotonic and Cyclic Shear Tests; Department of Civil and Environmental Engineering, George Washington University: Washington, DC, USA, 2014. [Google Scholar]
- Green, G.E. Strength and deformation of sand measured in an independent stress control cell. In Proceedings, Roscoe Memorial Symposium on Stress-Strain Behaviour of Soil; Cambridge University: Cambridge, UK, 1971; pp. 285–323. [Google Scholar]
- Wan, R.G.; Guo, P.J. A Simple Constitutive Model for Granular Soils: Modified Stress—Dilatancy Approach. Comput. Geotech. 1998, 22, 109–133. [Google Scholar] [CrossRef]
- Hellings, J.E.; Burland, J.B. Strength and deformation characteristics of a silty sand. In Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundations Engineering, Hamburg, Germany, 6–12 September 1997; pp. 303–306. [Google Scholar]
- Reades, D.W.; Green, G.E. Independent stress control and triaxial extension tests on sand. Géotechnique 1976, 26, 551–576. [Google Scholar] [CrossRef]
- Frydman, S.; Telesnick, M.; Nawatha, H.; Schwartz, K. Stress-dilation of undisturbed sand samples in drained and undrained triaxial shear. Soils Found. 2007, 47, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Mortara, G. A new yield and failure criterion for geomaterials. Géotechnique 2008, 58, 125–132. [Google Scholar] [CrossRef]
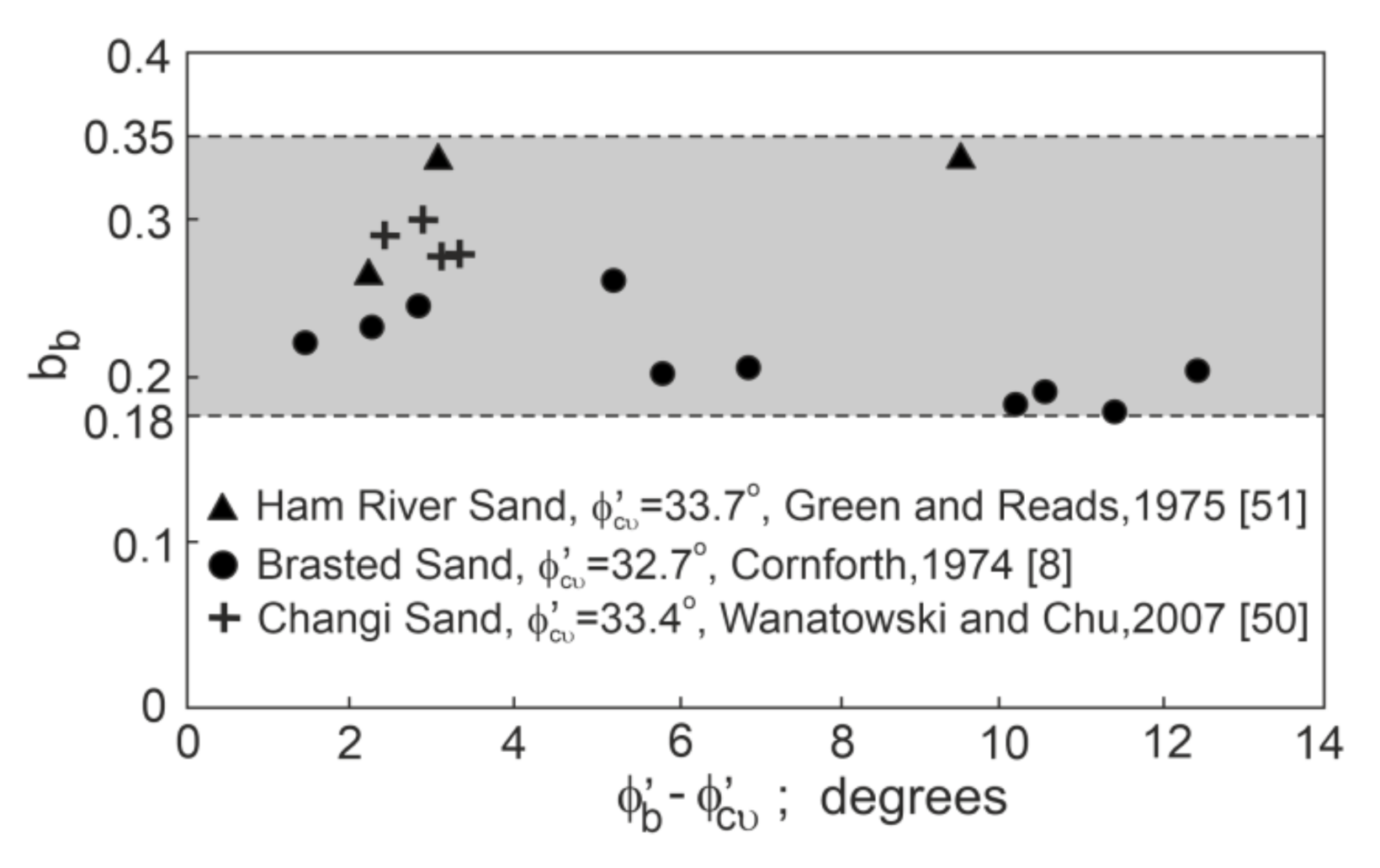
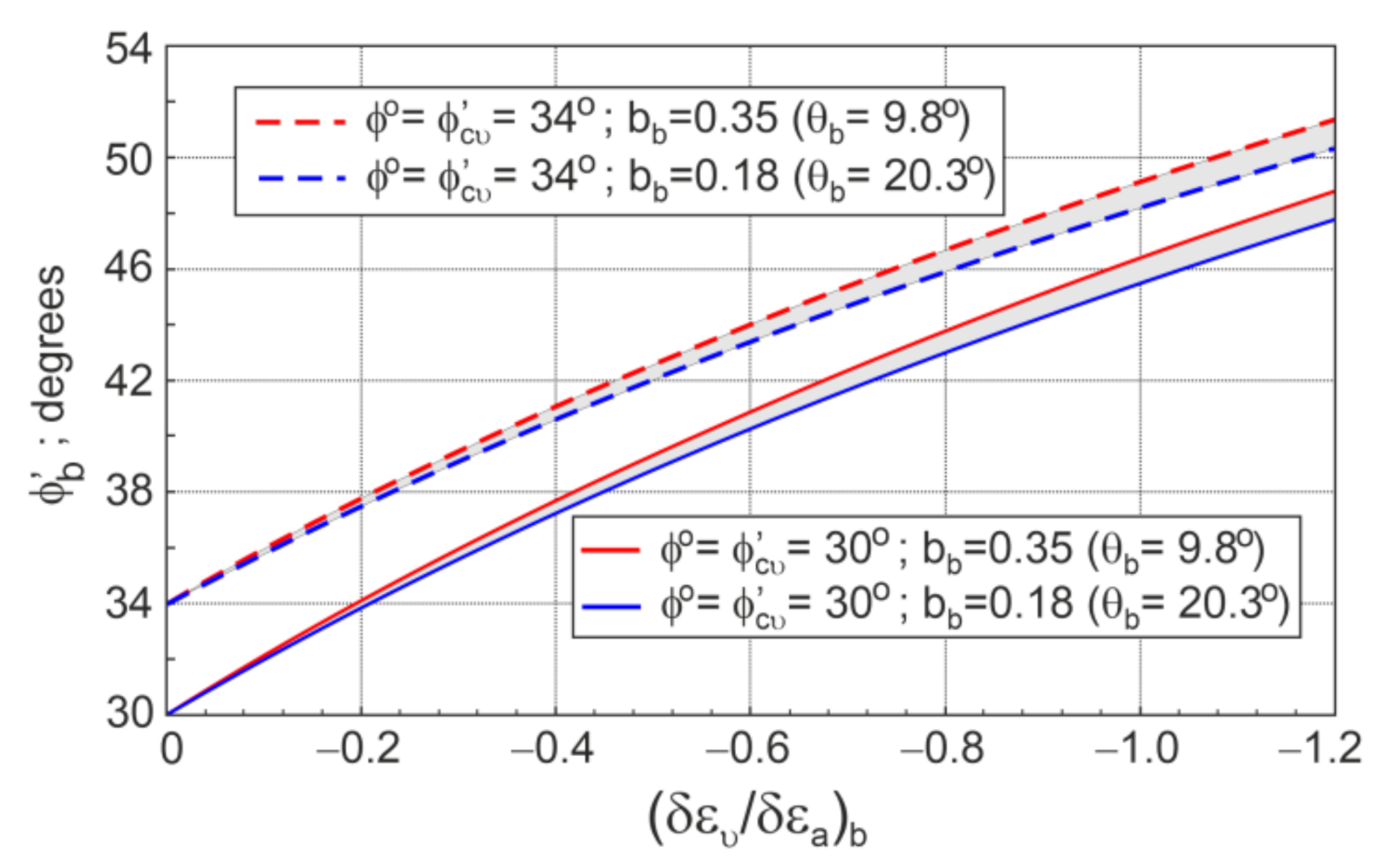

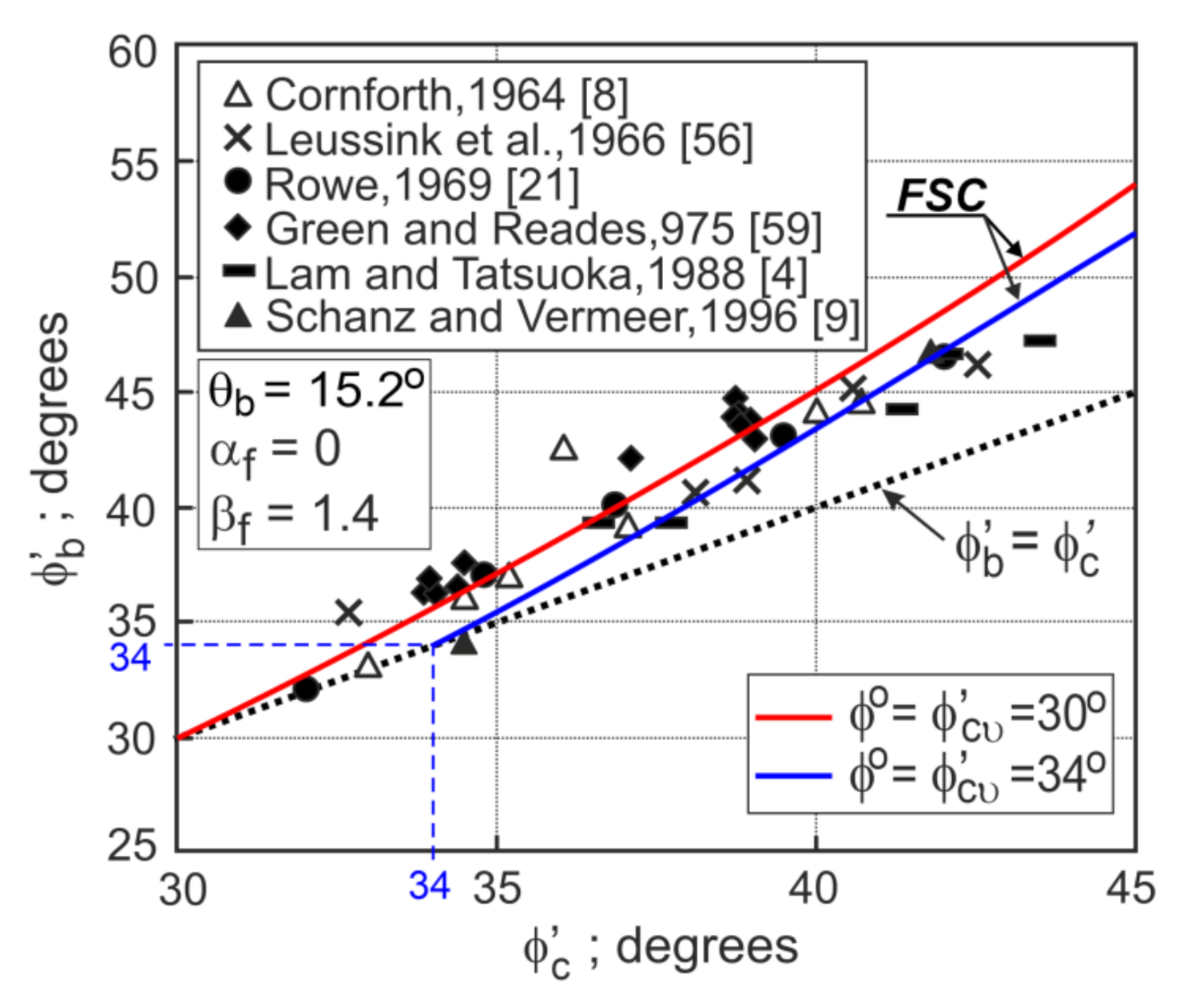


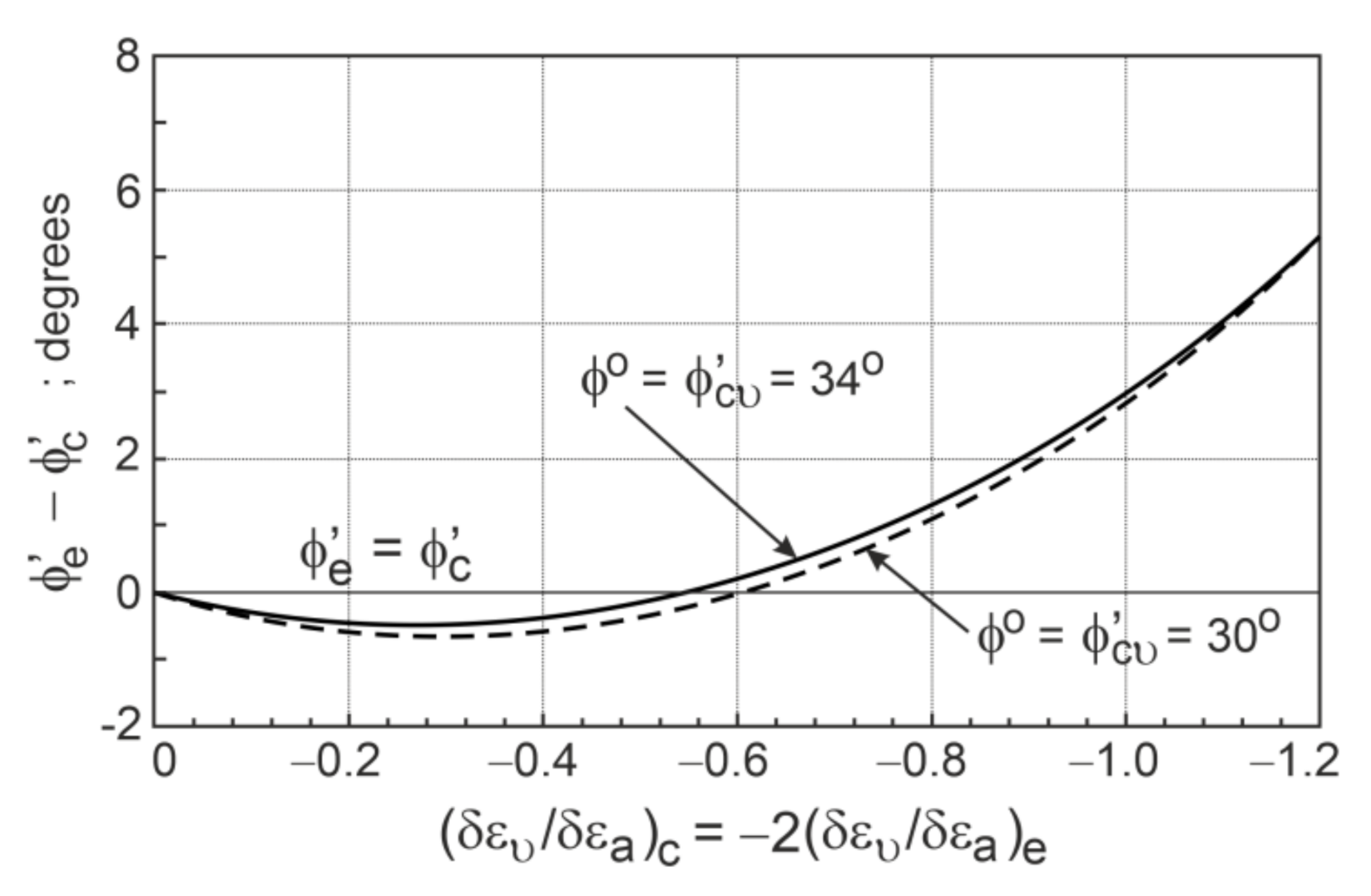



| Sand | d50 | CU | emax | emin | References | |
|---|---|---|---|---|---|---|
| [mm] | [-] | [-] | [-] | [°] | ||
| Erksak 330/07 | 0.33 | 1.60 | 0.753 | 0.527 | 31.0 | Konrad and Watts [35] |
| Hostun RF (0) | 0.32 | 1.80 | 1.000 | 0.655 | 33.5 | Olsen and Stark [36] |
| Hostun RF | 0.35–0.38 | 1.80 | 1.000 | 0.656 | 32.3 | Sun et al. [37] |
| Leighton Buzzard | 0.12 | 1.80 | 1.023 | 0.665 | 30.0 | Been et al. [38] |
| Monterey (0) | 0.38 | 1.60 | 0.860 | 0.530 | 33.0 | Riemer et al. [39] |
| Ottawa C109 | 0.35 | 1.70 | 0.820 | 0.500 | 30.0 | Sasitharan et al. [40] |
| Sacramento River | 0.30 | 1.70 | 0.870 | 0.530 | 33.2 | Riemer and Seed [41] |
| Toyoura | 0.17 | 1.70 | 0.977 | 0.517 | 31.0 | Ishihara [42] |
| Sydney | 0.30 | 1.50 | 0.856 | 0.565 | 31.0 | Chu and Lo [43] |
| Ticino | 0.53 | 1.30 | 0.923 | 0.574 | 34 | Prearo [44] |
| Portaway | 0.40 | 2.05 | 0.790 | 0.460 | 29.8 | Yu et al. [45] |
| Firoozkuh | 0.26 | 1.90 | 0.943 | 0.568 | 30.5 | Sun et al. [37] |
| Fuji River | 0.22 | 2.21 | 0.990 | 0.550 | 36.6 | Sun et al. [37] |
| Nevada | 0.17 | 2.00 | 0.887 | 0.511 | 33.4 | Ling and Yang [46] |
| Hokksund | 0.910 | 0.550 | 32.0 | Wang [47] | ||
| Kogyuk 350/2 | 0.830 | 0.470 | 31.0 | Wang [47] | ||
| Reid Bedford | 0.870 | 0.550 | 32.0 | Wang [47] | ||
| Till | 0.11 | 0.835 | 0.363 | 34.6 | Olsen and Stark [36] | |
| Brasted | 0.28 | 2.14 | 0.792 | 0.475 | 32.7 | Cornforth [8] |
| Berlin | 0.38 | 3.00 | 0.550 | 0.390 | 31.0 | Pestana et al. [48] |
| Karlsruhe | 0.42 | 1.85 | 0.840 | 0.530 | 34.0 | Hettler and Vardoulakis [49] |
| Changi | 0.30 | 2.00 | 0.916 | 0.533 | 33.4 | Wanatowski and Chu [50] |
| Ham River | 0.27 | 1.67 | 0.849 | 0.547 | 33.7 | Green and Reades [51] |
| River Walland | 0.980 | 0.621 | 30.0 | Barden and Khayatt [52] | ||
| Chiba | 2.10 | 0.946 | 0.500 | 33.0 | Fern et al. [53] |
| Values | Deformation Mode | ||
|---|---|---|---|
| Triaxial Compression | Plane Strain | Triaxial Extension | |
| θ | π/6 | −π/6 | |
| θε | π/6 | −π/6 | |
| M° | |||
| A° | |||
| D | |||
| 0 | |||
| 1 | 1.4 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szypcio, Z.; Dołżyk-Szypcio, K.; Mierczyński, J. Dilatant Nature of Sand Shear Strength. Appl. Sci. 2022, 12, 2332. https://doi.org/10.3390/app12052332
Szypcio Z, Dołżyk-Szypcio K, Mierczyński J. Dilatant Nature of Sand Shear Strength. Applied Sciences. 2022; 12(5):2332. https://doi.org/10.3390/app12052332
Chicago/Turabian StyleSzypcio, Zenon, Katarzyna Dołżyk-Szypcio, and Jacek Mierczyński. 2022. "Dilatant Nature of Sand Shear Strength" Applied Sciences 12, no. 5: 2332. https://doi.org/10.3390/app12052332
APA StyleSzypcio, Z., Dołżyk-Szypcio, K., & Mierczyński, J. (2022). Dilatant Nature of Sand Shear Strength. Applied Sciences, 12(5), 2332. https://doi.org/10.3390/app12052332






