Simulation of Static Tyre–Pavement Interaction Using Two FE Models of Different Complexity
Abstract
:1. Introduction
1.1. Objectives
- The establishment of a realistic spatial finite element model of a radial truck tyre based on manufacturer and literature data;
- The development of the spatial finite element simulation of tyre–pavement interactions;
- The calculation of contact areas and stresses using the complex finite element radial tyre model;
- The derivation of a simplified finite element tyre model based on the complex model, for the analysis of dynamic tyre–pavement interactions;
- A comparison between the contact behaviours of the complex and simplified finite element models using an example of a flexible road pavement structure;
- A recommendation for a simplified calculation method of the contact behaviour of finite element tyre models having different content and numbers of elements.
1.2. The Scope of the Analysis
2. Theoretical Background
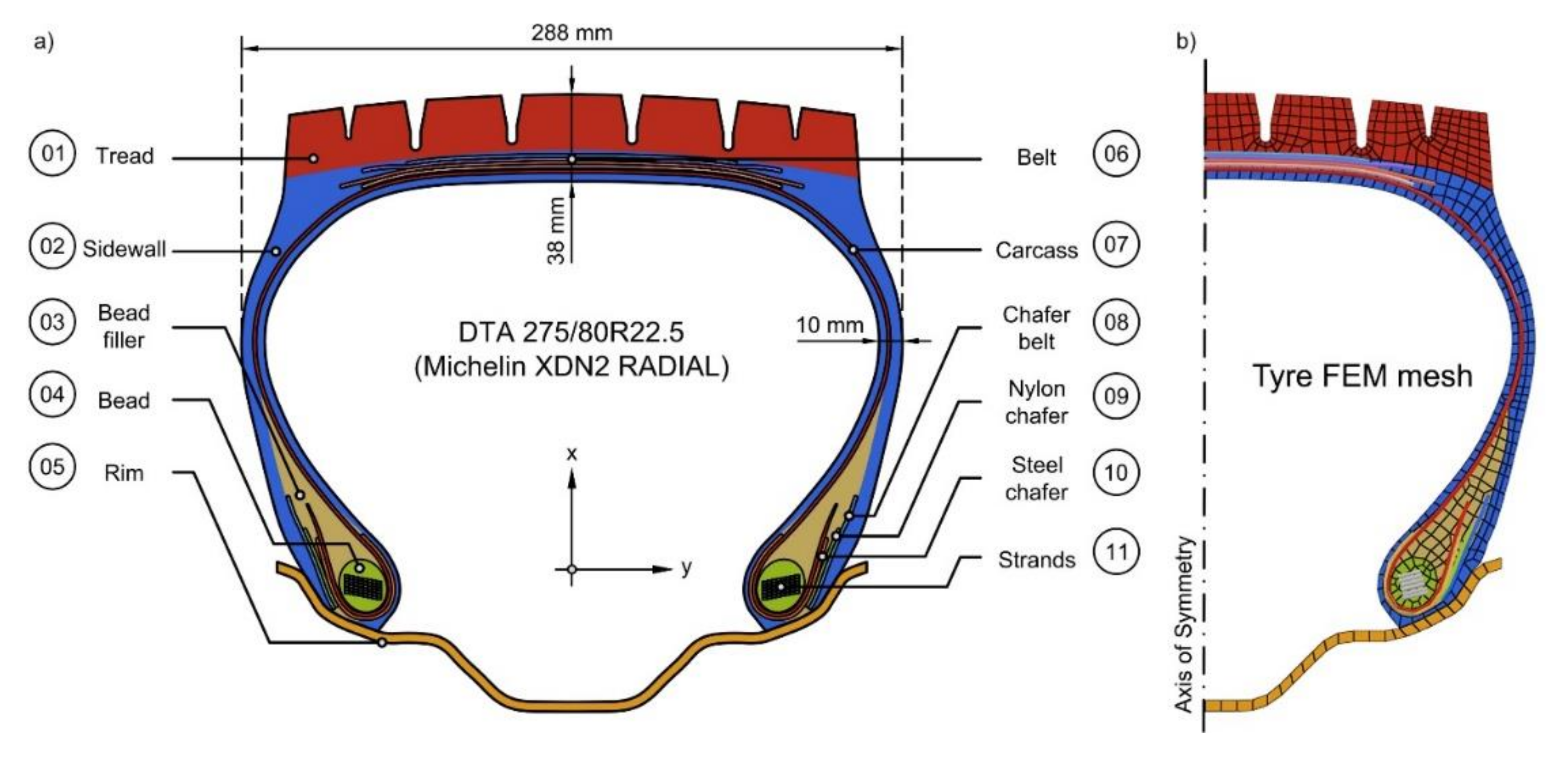
2.1. The Structure of the Rubber Tyre
- The tread is the part of the tyre that is in contact with the pavement; its task is to provide the cohesion, resistance to wear, and movement stability of the vehicle. Characteristically, it is made from synthetic and natural India rubber;
- The belt is aimed at the reinforcement of the tyre, as it absorbs bumps and provides the optimal movement stability and rolling resistance to the vehicle. The belt is made from high-strength rubberized steel fibres; the position of the fibres is at ±10–30° in respect to the centre line, depending on the usage and the load bearing of the radial tyre;
- The carcass provides the truss of the tyre; it keeps the shape of the tyre even in case of high inflation pressure and distributes the loading. It is made from rubberized rayon or polyester textile fibres;
- The sidewall is made from natural rubber; it protects the carcass from sideways forces and transmits the momentum to the tread;
- The filler helps to provide movement stability, steering, and comfort issues; it is made from synthetic rubber;
- The chafer belt amplifies the movement stability and the steering accuracy; its material can be steel or nylon, resulting in different types of chafer belts;
- The steel cord or strands provide stabilized nesting between the tyre and the body of the wheel; it is made from high-strength steel wires embedded in rubber. Depending on its manufacturing technology, the steel cord may include a bead.
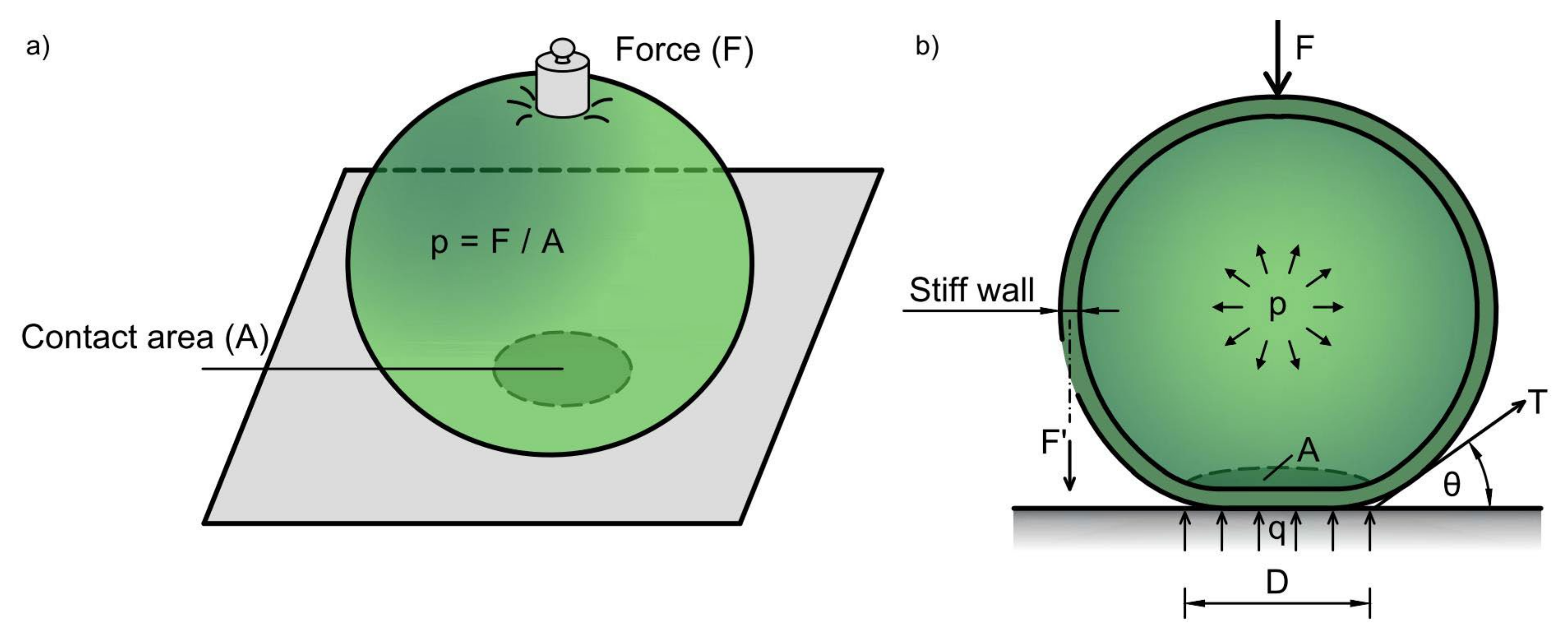
2.2. The Pressure Head of the Tyre
3. Materials and Methods
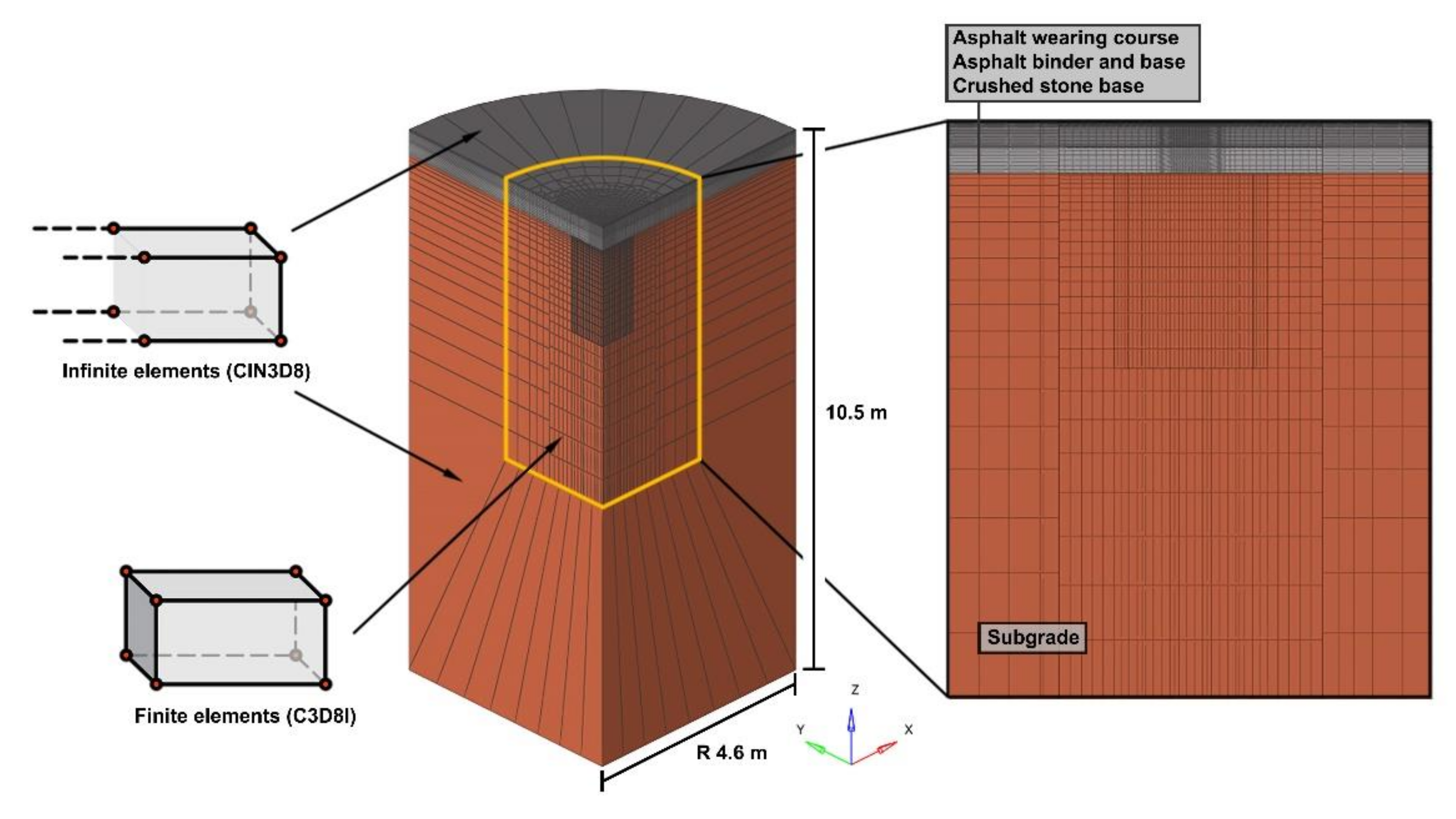
3.1. Finite Element Model of the Road Pavement Structure
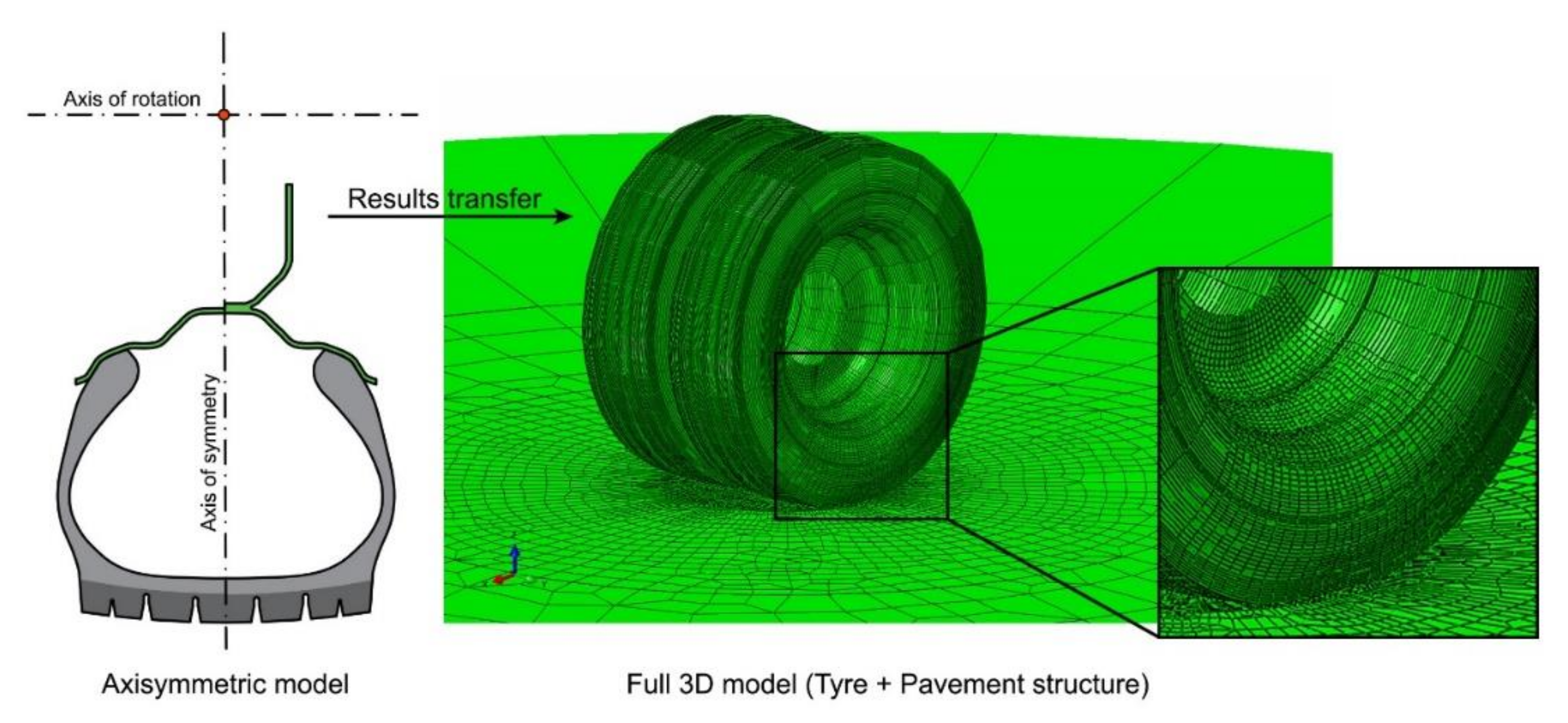
3.2. Complex Finite Element Model of the Rubber Tyre
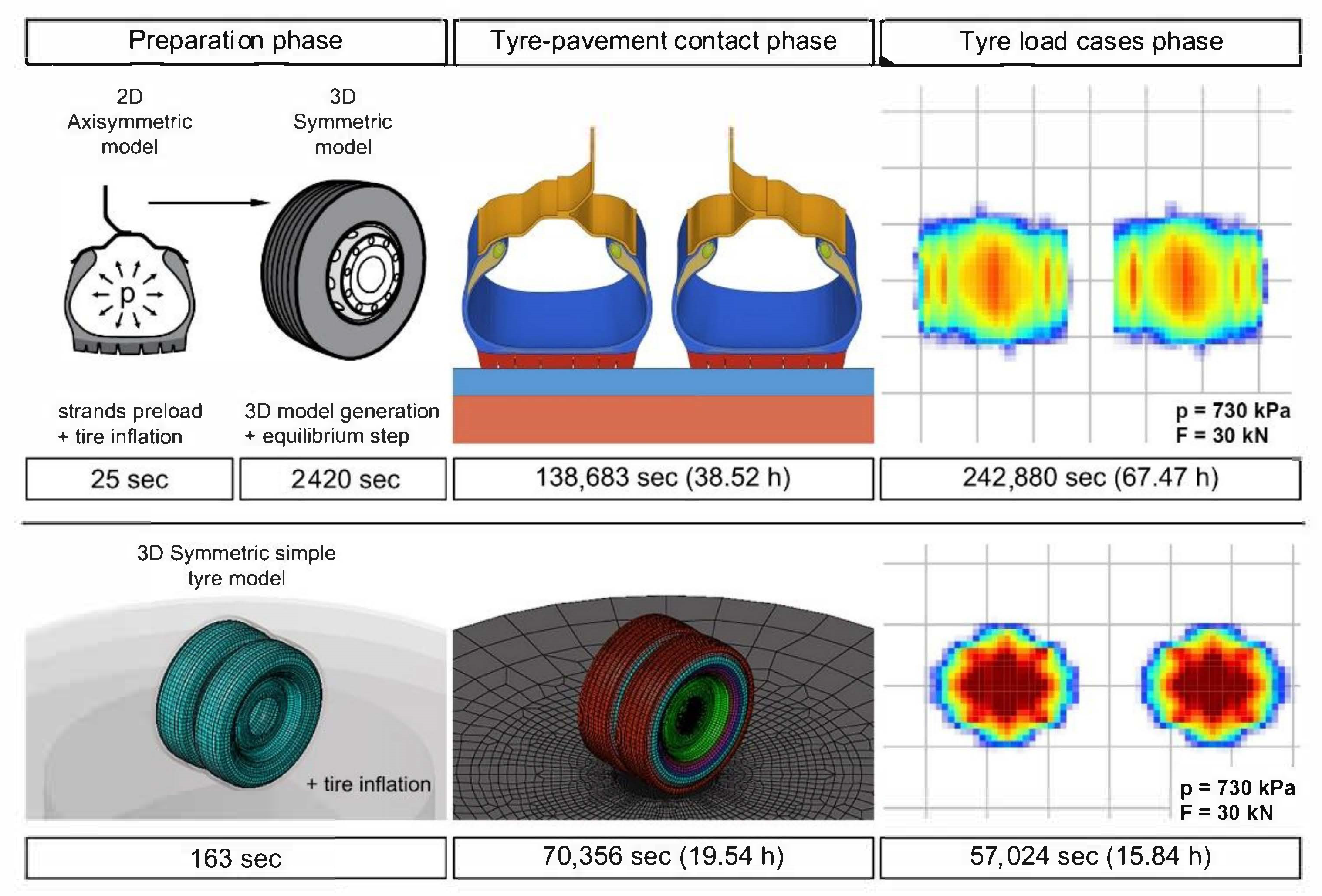
3.2.1. The 2D Axial Symmetric Model
- CAX4 (4-node bilinear continuum element) for linear elastic or elastic–plastic materials;
- CAX4H (4-node bilinear hybrid continuum element) for hyper elastic materials;
- SFMAX1 (2-node linear membrane-like surface element) for rebar.
3.2.2. The 3D Full-Body Model
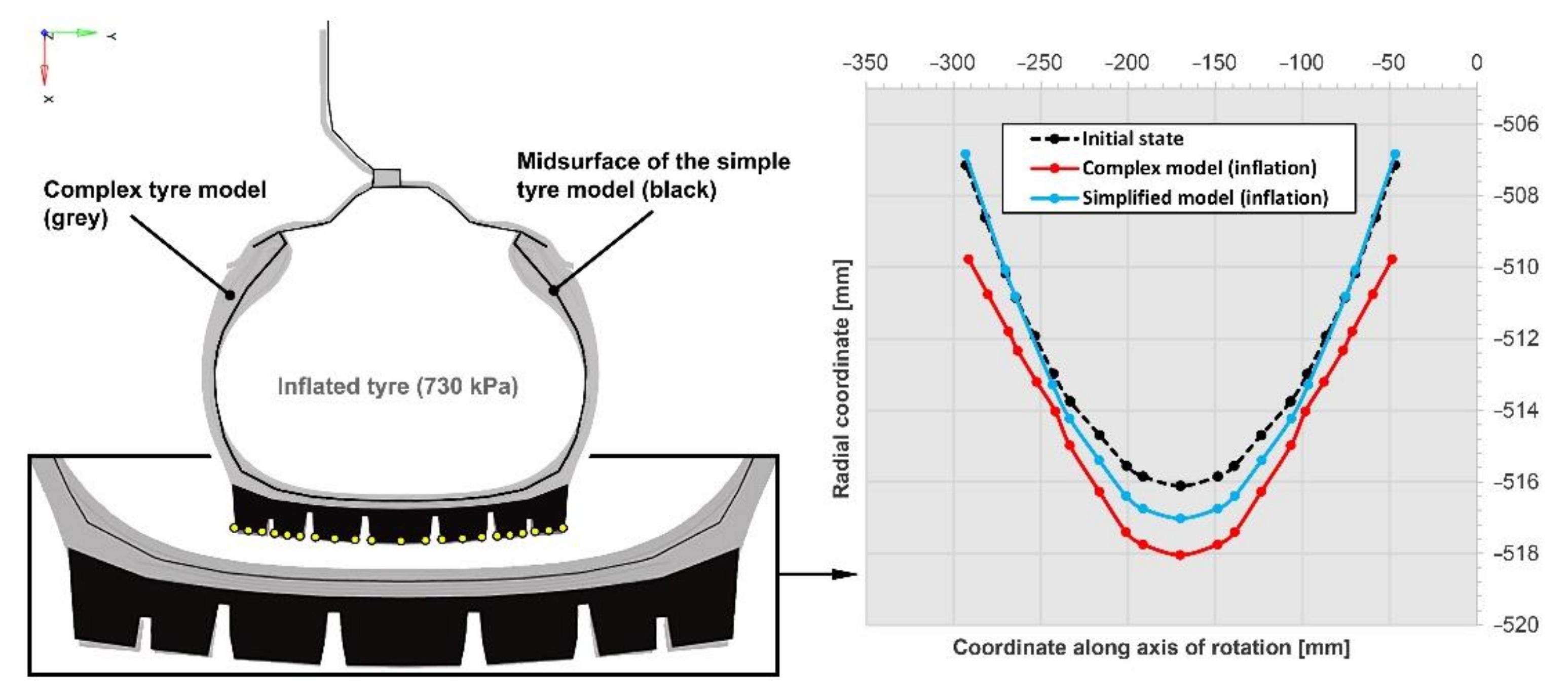
3.3. The Simplified Finite Element Model of the Rubber Tyre
- Tyre stiffness: the load transition is possibly described at the proper accuracy in the model;
- Parametric analysis: the preparation simulations (i.e., inflation) had to run quickly;
- The structure of the FEM model: adjusting tyre parameters independently of the finite element mesh (i.e., thickness of the sidewall, composition of belts, etc.);
- The model had to be suitable for explicit simulations, even as a rotating body, without corrupting the integration time.
- Rubber sidewall: homogeneous, isotropic, hyper elastic rubber layer;
- Rubber filler: homogeneous, isotropic, hyper elastic rubber layer;
- Carcass: simplified, it is a homogeneous, orthotropic thin plate;
- Steel cord: simplified, it is a tight steel ring in the composite layer;
- Steel chafer: simplified, it is a homogeneous, orthotropic thin plate;
- Belt layer: simplified, it is a homogeneous, orthotropic thin plate, where the grainline substantially influences the stiffness of the tread of the tyre.
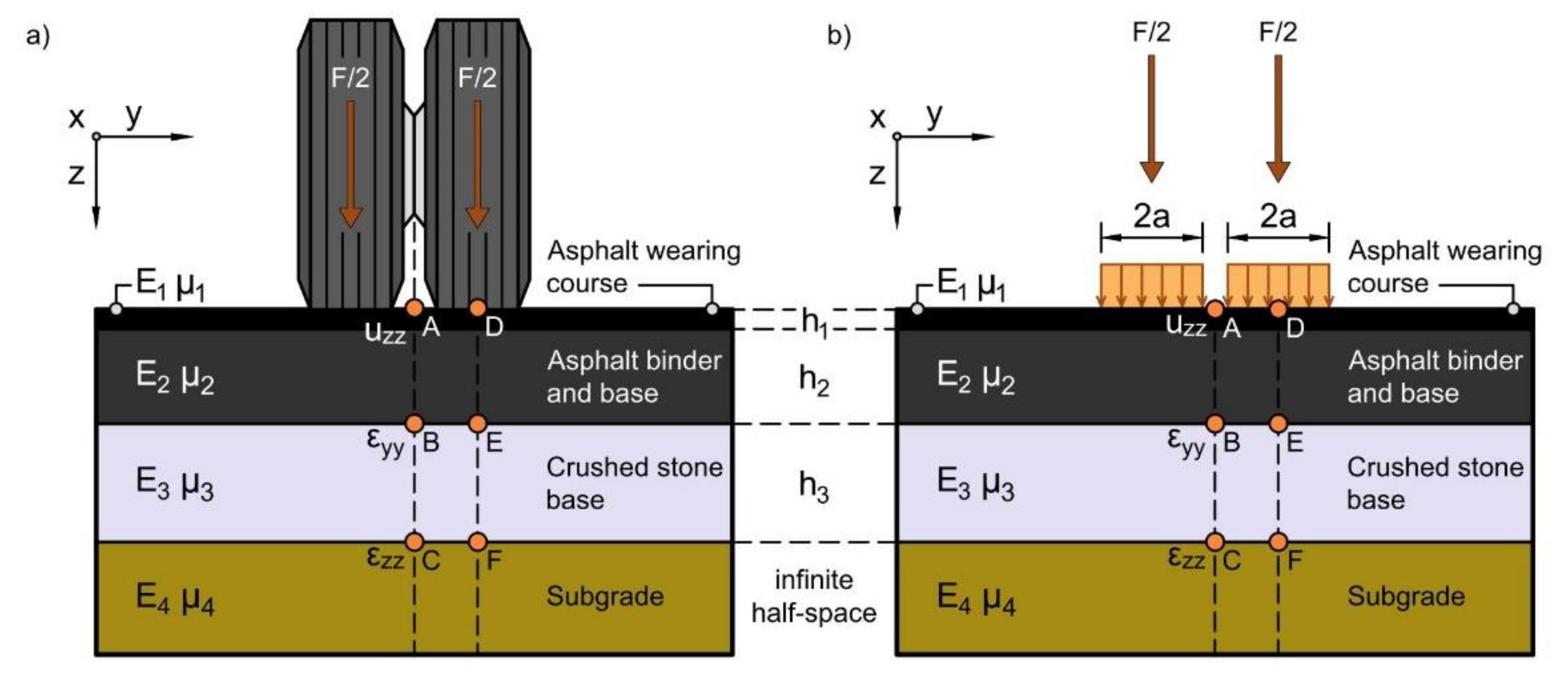
3.4. The Tyre–Pavement Interaction Simulation
- (A), (D) The vertical displacement of the pavement ( deflection);
- (B), (E) The horizontal specific strain at the bottom of the lower asphalt layer;
- (C), (F) The vertical specific compression on the top of the subgrade.
4. Results and Discussion
4.1. The Required Running Time of Finite Element Models
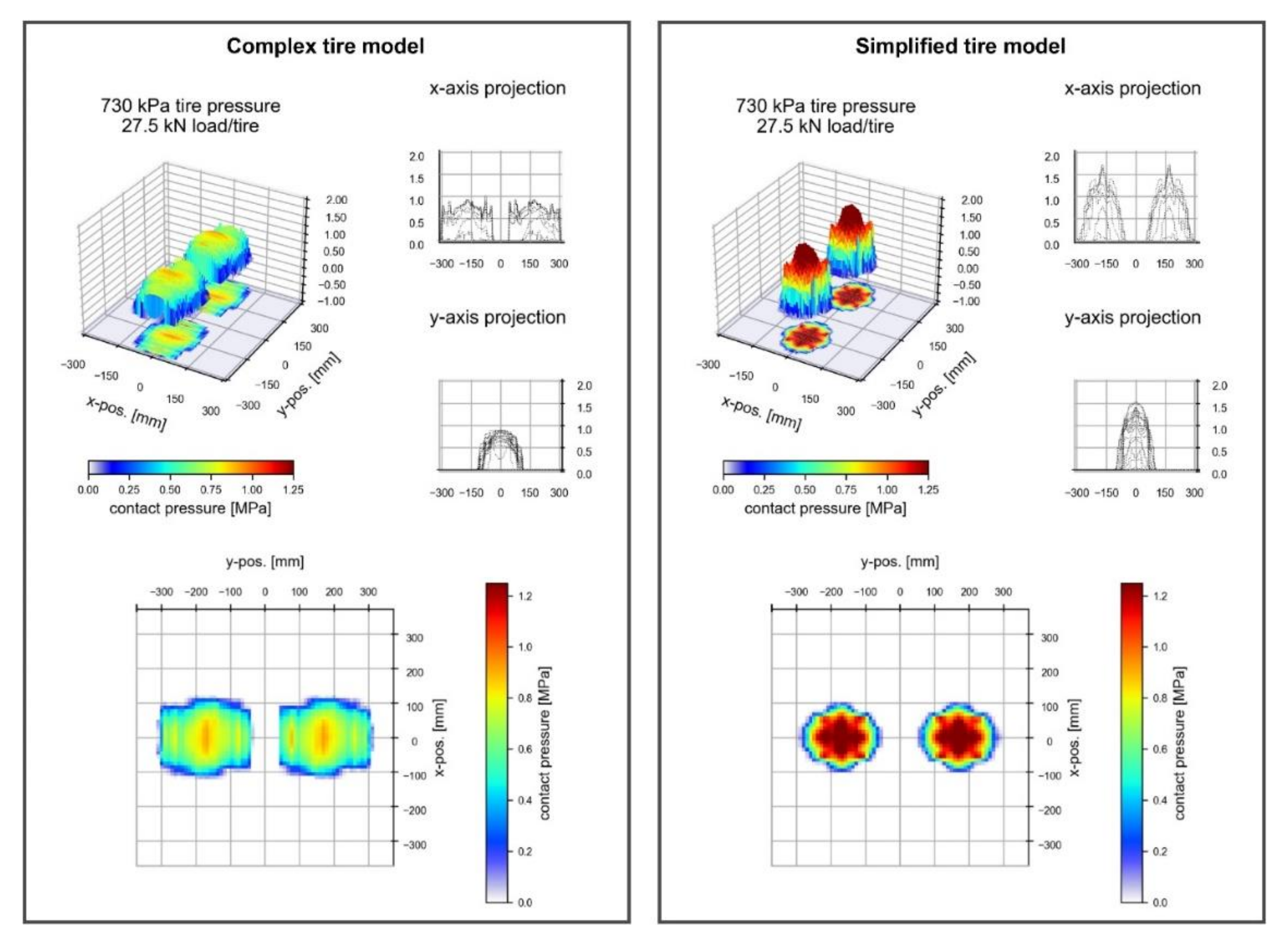
4.2. Comparison of the Behaviour of Finite Element Tyre Models
- 1.
- In the case of the complex tyre model (R2 = 0.973),
- 2.
- In the case of the simplified tyre model (R2 = 0.979),
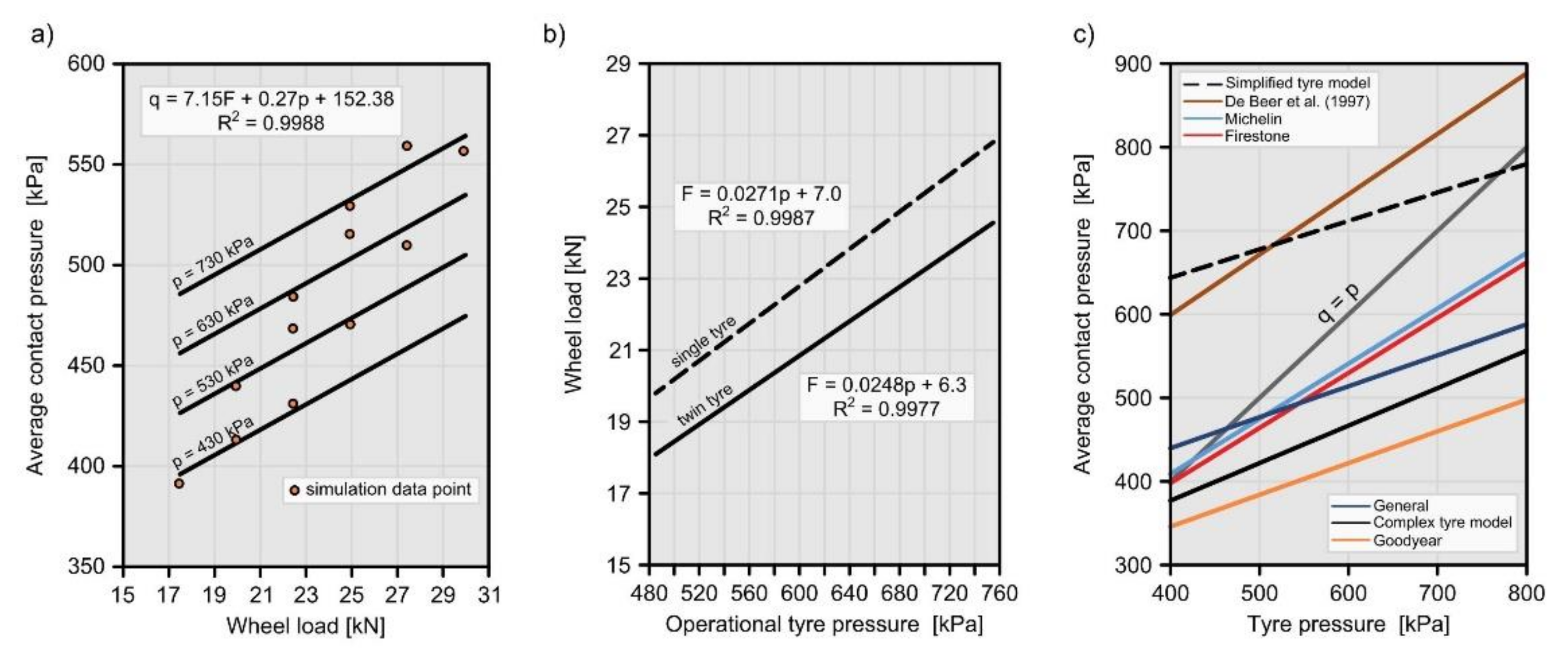
- 1.
- In case of the complex tyre model,
- 2.
- In case of the simplified tyre model,
4.3. Assessment of Tyre Models Considering the Road Pavement Structure
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- McCullough, B.F.; Boedecker, K.J. Use of Linear-Elastic Layered Theory for the Design of CRCP Overlays. Highw. Res. Rec. 1969, 2, 1–13. [Google Scholar]
- De Beer, M. Measurement of Tyre/Pavement Interface Stresses Under Moving Wheel Loads. Int. J. Heavy Veh. Syst. 1996, 3, 97–115. [Google Scholar] [CrossRef]
- Wang, H.; Hasan, O.; Al-Qadi, I.L.; Duarte, C.A. Analysis of Near-Surface Cracking under Critical Loading Conditions Using Uncracked and Cracked Pavement Models. J. Transp. Eng. 2013, 139, 992–1000. [Google Scholar] [CrossRef]
- Wang, G.; Reynaldo, R. Three-Dimensional Finite Element Modeling of Static Tire–Pavement Interaction. Transp. Res. Rec. J. Transp. Res. Board 2010, 2155, 158–169. [Google Scholar] [CrossRef]
- Hernandez, J.A.; Gamez, A.; Shakiba, M.; Al-Qadi, I.L. Numerical Prediction of Three-Dimensional Tire-Pavement Contact Stresses; Technical Report ICT-17-004; Taxas A&M University: College Station, TX, USA, 2017; Available online: http://hdl.handle.net/2142/95142 (accessed on 19 June 2020).
- Hernandez, J.A.; Al-Qadi, I.L. Semicoupled Modeling of Interaction between Deformable Tires and Pavements. J. Transp. Eng. Part A Syst. 2017, 143, 04016015. [Google Scholar] [CrossRef]
- Hernandez, J.A.; Angeli, G.; Maryam, S.; Imad, L. Al-Qadi. Tire–Pavement Interaction Modelling: Hyperelastic Tire and Elastic Pavement. Road Mater. Pavement Des. 2017, 18, 1067–1083. [Google Scholar] [CrossRef]
- Lawton, W.L. Static Load Contact Pressure Patterns under Airplane Tires. Highw. Res. Board Proc. 1957, 36, 233–239. [Google Scholar]
- Yoder, E.J. Principles of Pavement Design; John Wiley and Sons, Inc.: New York, NY, USA, 1959. [Google Scholar]
- Lister, N.W.; Nunn, D.E. Contact Areas of Commercial Vehicle Tyres; Transport and Road Research Laboratory: London, UK, 1968; Available online: https://trl.co.uk/sites/default/files/LR172.pdf (accessed on 23 April 2020).
- Van Vuuren, J.D. Relationship between Tire Inflation Pressure and Mean Tire Contact Pressure. Transp. Res. Rec. 1974, 523, 76–87. [Google Scholar]
- Kennedy, R.H. Experiences with Cylindrical Elements in Tire Modeling. In Proceedings of the ABAQUS Users’ Conference, Munich, Germany, 4–6 June 2003; Volume 247. Available online: http://www.simulia.com/download/solutions/automotive_cust%20references/tires_experience_auc03_hankook.pdf (accessed on 15 November 2019).
- Burmister, D.M. The General Theory of Stresses and Displacements in Layered Systems I. J. Appl. Phys. 1945, 16, 89–94. [Google Scholar] [CrossRef]
- Burmister, D.M. The General Theory of Stresses and Displacements in Layered Soil Systems II. J. Appl. Phys. 1945, 16, 126–127. [Google Scholar] [CrossRef]
- Burmister, D.M. The General Theory of Stresses and Displacements in Layered Soil Systems III. J. Appl. Phys. 1945, 16, 296–302. [Google Scholar] [CrossRef]
- Duncan, J.M.; Monismith, C.L.; Wilson, E.L. Finite Element Analyses of Pavements. Highw. Res. Rec. 1968, 228, 18–33. [Google Scholar]
- Yazdandoost, F.; Saied, T. Finite Element Tyre Model for Antilock Braking System Study. Int. J. Veh. Des. 2016, 72, 248–261. [Google Scholar] [CrossRef]
- Behroozinia, P.; Seyedmeysam, K.; Saied, T.; Reza, M. An Investigation towards Intelligent Tyres Using Finite Element Analysis. Int. J. Pavement Eng. 2020, 21, 311–321. [Google Scholar] [CrossRef]
- Van Blommestein, W.B. Experimentally Determined Material Parameters for Temperature Prediction of an Automobile Tire Using Finite Element Analysis. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2016. [Google Scholar]
- Jeong, K.M. Prediction of Burst Pressure of a Radial Truck Tire Using Finite Element Analysis. World J. Eng. Technol. 2016, 4, 228–237. [Google Scholar] [CrossRef] [Green Version]
- Korunovic, N.; Miroslav, T.; Milos, S. FEA of tyres subjected to static loading. J. Serb. Soc. Comput. Mech. 2007, 1, 87–98. [Google Scholar]
- Wang, H. Analysis of Tire-Pavement Interaction and Pavement Responses Using a Decoupled Modeling Approach. Ph.D. Thesis, College of the University of Illinois, Urbana, IL, USA, 2010. [Google Scholar]
- Zhang, Z.; Hongxun, F.; Xuemeng, L.; Xiaoxia, C.; Di, T. Comparative Analysis of Static and Dynamic Performance of Nonpneumatic Tire with Flexible Spoke Structure. Stroj. Vestn. J. Mech. Eng. 2020, 66, 458–466. [Google Scholar] [CrossRef]
- Nakajima, Y. Advanced Tire Mechanics; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Zhou, H.; Guolin, W.; Yangmin, D.; Jian, Y.; Chen, L.; Jing, F. Effect of Friction Model and Tire Maneuvering on Tire-Pavement Contact Stress. Adv. Mater. Sci. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Shan, Y.; Shugao, Z. Experimental Verification and Finite Element Modeling of Radial Truck Tire Under Static Loading. J. Reinf. Plast. Compos. 2013, 32, 490–498. [Google Scholar] [CrossRef]
- Gent, A.N.; Joseph, D.W. The Pneumatic Tire. DOT HS 810 561. The University of Akron. 2006. Available online: http://works.bepress.com/joseph_walter/7/ (accessed on 1 May 2019).
- De Beer, M.; Fisher, C.; Jooste, F.J. Determination of Pneumatic Tyre/Pavement Interface Contact Stresses Under Moving Loads and Some Effects on Pavements with Thin Asphalt Surfacing Layers. In Proceedings of the Eighth International Conference on Asphalt Pavements, Seattle, WA, USA, 10–14 August 1997; Larsen, H.J.E., Ed.; Road Directorate, Danish Road Institute: Roskilde, Denmark, 1997; Volume 1, pp. 179–227. [Google Scholar]
- Dassault Systèmes. Abaqus 6.14 Online Documentation. 23 April 2014. Available online: http://ivt-abaqusdoc.ivt.ntnu.no:2080/texis/search/?query=wetting&submit.x=0&submit.y=0&group=bk&CDB=v6.14 (accessed on 21 June 2020).
| Tyre Types | Model Parameters | |||
|---|---|---|---|---|
| 07.50–15 Michelin Radial | −0.0029 | 13.0 | 0.520 | 52.0 |
| 08.25–20 × 10 Firestone Transport | 0.0130 | 10.5 | 0.119 | 125.9 |
| 09.00–20 × 10 Firestone | 0.0240 | −0.9 | −0.001 | 259.6 |
| 10.00–20 × 14 Papaleguas Goodyear Brazil | 0.0020 | 6.8 | 0.330 | 110.0 |
| 11.00–20 × 14 General SDT | 0.0080 | 2.3 | 0.040 | 313.0 |
| 11.00–22 × 14 General Jet Cargo | 0.0090 | 2.6 | 0.098 | 211.0 |
| Layer Name | Thickness, h (mm) | Young’s Modulus, E (MPa) | Poisson’s Ratio, µ (-) |
|---|---|---|---|
| Asphalt wearing course | 40 | 4000 | 0.35 |
| Asphalt binder and base | 200 | 5500 | 0.35 |
| Crushed stone base | 250 | 350 | 0.40 |
| Subgrade | infinite | 50 | 0.45 |
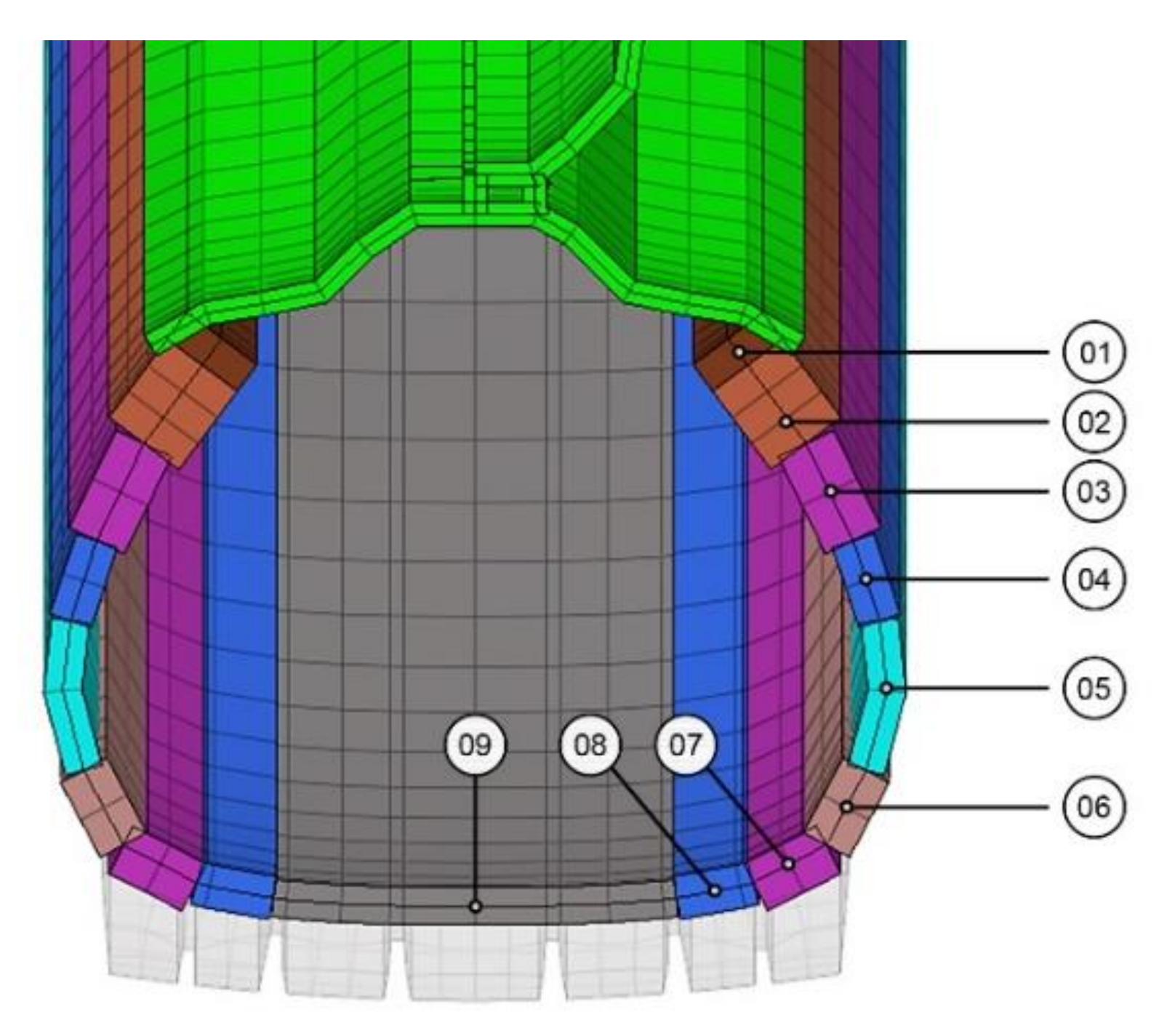
| # | Tyre Region | Material Name | Ply | Angle (°) | Cross-Section | Dimension (mm) | Spacing (mm) |
|---|---|---|---|---|---|---|---|
| 01 | tread | tread rubber | MAIN STRUCTURE | ||||
| 02 | sidewall | sidewall rubber | |||||
| 03 | bead filler | bead rubber | |||||
| 04 | bead | bead rubber | |||||
| 05 | rim | castor steel | |||||
| 06 | belt | belt steel | 1 | 50 | circle | R 0.25 | 1.16 |
| 2 | 78 | circle | R 0.25 | 1.16 | |||
| 3 | 102 | circle | R 0.25 | 1.16 | |||
| 4 | 78 | circle | R 0.25 | 1.16 | |||
| 07 | carcass | carcass steel | 1 | +12 | circle | R 0.40 | 0.80 |
| 2 | −12 | circle | R 0.40 | 0.80 | |||
| 08 | chafer belt | chafer belt steel | 1 | 90 | circle | R 0.36 | 1.19 |
| 09 | nylon chafer | chafer nylon | 1 | 90 | circle | R 0.36 | 1.00 |
| 10 | steel chafer | chafer steel | 1 | 90 | circle | R 0.36 | 1.19 |
| 11 | strands | wire steel | 8 × 6 | 90 | rectangle | 2.0 × 1.3 | 0.00 |
| # | Material Name | Model of Material | Model Parameters | Unit | Literary Source | |
|---|---|---|---|---|---|---|
| 06 | belt steel | Elastic (Hook) | ρ | 7.80 × 10−9 | t/mm3 | [18,19,22] |
| E | 174,700 | N/mm2 | ||||
| µ | 0.3 | - | ||||
| 11 | wire steel | Elastic (Hook) | ρ | 5.90 × 10−9 | t/mm3 | [19] |
| E | 207,000 | N/mm2 | ||||
| µ | 0.3 | - | ||||
| 07 | carcass steel | Elastic (Hook) | ρ | 1.39 × 10−9 | t/mm3 | |
| E | 16,870 | N/mm2 | ||||
| µ | 0.3 | - | ||||
| 08 10 | chafer belt steel | Elastic (Hook) | ρ | 1.50 × 10−9 | t/mm3 | |
| E | 9870 | N/mm2 | ||||
| µ | 0.3 | - | ||||
| 09 | chafer nylon | Elastic (Hook) | ρ | 1.50 × 10−9 | t/mm3 | |
| E | 3970 | N/mm2 | ||||
| µ | 0.3 | - | ||||
| 01 | tread rubber | Hyper elastic (Yeoh) | ρ | 1.10 × 10−9 | t/mm3 | [23] |
| C10 | 6.16 × 10−1 | N/mm2 | ||||
| C20 | −1.91 × 10−1 | N/mm2 | ||||
| C30 | 4.75 × 10−2 | N/mm2 | ||||
| D1 | 8.12 × 10−2 | mm2/N | ||||
| D2 | 8.12 × 10−2 | mm2/N | ||||
| D3 | 8.12 × 10−2 | mm2/N | ||||
| Viscoelastic (Prony) | gi | 0.3 | - | [18] | ||
| ki | 0.0 | - | ||||
| τi | 0.1 | s | ||||
| 02 | sidewall rubber | Hyper elastic (Yeoh) | ρ | 1.12 × 10−9 | t/mm3 | [17,23] |
| C10 | 4.88 × 10−1 | N/mm2 | ||||
| C20 | −1.41 × 10−1 | N/mm2 | ||||
| C30 | 3.86 × 10−2 | N/mm2 | ||||
| D1 | 1.03 × 10−1 | mm2/N | ||||
| D2 | 1.03 × 10−1 | mm2/N | ||||
| D3 | 1.03 × 10−1 | mm2/N | ||||
| Viscoelastic (Prony) | gi | 0.3 | - | [18] | ||
| ki | 0.0 | - | ||||
| τi | 0.1 | s | ||||
| 03 04 | bead rubber | Hyper elastic (Yeoh) | ρ | 1.10 × 10−9 | t/mm3 | [18,23] |
| C10 | 8.76 × 10−1 | N/mm2 | ||||
| C20 | −2.93 × 10−1 | N/mm2 | ||||
| C30 | 7.94 × 10−2 | N/mm2 | ||||
| D1 | 5.71 × 10−2 | mm2/N | ||||
| D2 | 5.71 × 10−2 | mm2/N | ||||
| D3 | 5.71 × 10−2 | mm2/N | ||||
| Viscoelastic (Prony) | gi | 0.3 | - | [18] | ||
| ki | 0.0 | - | ||||
| τi | 0.1 | s | ||||
| 05 | castor steel | Elastic (Hook) | ρ | 7.80 × 10−8 | t/mm3 | [19] |
| E | 207,000 | N/mm2 | ||||
| µ | 0.3 | - | ||||
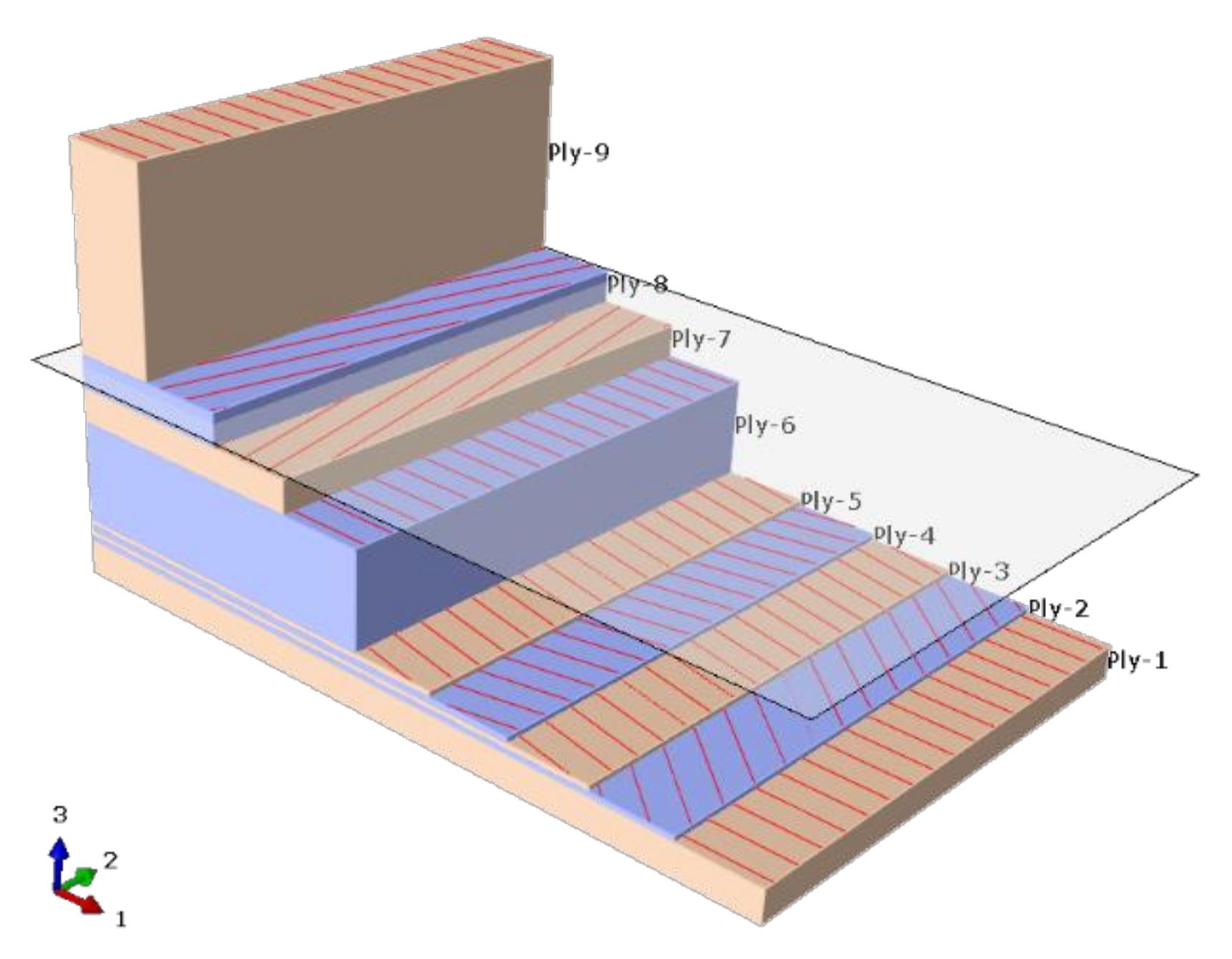
| # | Shell Element Description | Ply | Thickness (mm) | Material Name | Angle (°) |
|---|---|---|---|---|---|
| 1 | SH-340 tyre sidewall with strand | 01 | 2.40 | 02—sidewall rubber | 0 |
| 02 | 0.61 | 07—carcass steel | 102 | ||
| 03 | 0.61 | 07—carcass steel | 78 | ||
| 04 | 8.38 | 03/04—bead rubber | 0 | ||
| 05 | 10.0 | 11—wire steel | 0 | ||
| 06 | 8.38 | 03/04—bead rubber | 0 | ||
| 07 | 0.61 | 07—carcass steel | 102 | ||
| 08 | 0.61 | 07—carcass steel | 78 | ||
| 09 | 2.40 | 02—sidewall rubber | 0 | ||
| 2 | SH-280 tyre sidewall | 01 | 5.00 | 02—sidewall rubber | 0 |
| 02 | 0.43 | 08/10—chafer belt steel | 0 | ||
| 03 | 5.00 | 03/04—bead rubber | 0 | ||
| 04 | 0.43 | 08/10—chafer belt steel | 0 | ||
| 05 | 0.61 | 07—carcass steel | 102 | ||
| 06 | 0.61 | 07—carcass steel | 78 | ||
| 07 | 11.7 | 03/04—bead rubber | 0 | ||
| 08 | 0.61 | 07—carcass steel | 102 | ||
| 09 | 0.61 | 07—carcass steel | 78 | ||
| 10 | 3.00 | 02—sidewall rubber | 0 | ||
| 3 | SH-200 tyre sidewall | 01 | 5.00 | 02—sidewall rubber | 0 |
| 02 | 0.43 | 08/10—chafer belt steel | 0 | ||
| 03 | 8.69 | 03/04—bead rubber | 0 | ||
| 04 | 0.61 | 07—carcass steel | 102 | ||
| 05 | 0.61 | 07—carcass steel | 78 | ||
| 06 | 4.66 | 02—sidewall rubber | 0 | ||
| 4 | SH-140 tyre sidewall | 01 | 8.50 | 02—sidewall rubber | 0 |
| 02 | 0.61 | 07—carcass steel | 102 | ||
| 03 | 0.61 | 07—carcass steel | 78 | ||
| 04 | 4.28 | 02—sidewall rubber | 0 | ||
| 5 | SH-120 tyre sidewall | 01 | 5.90 | 02—sidewall rubber | 0 |
| 02 | 0.61 | 07—carcass steel | 102 | ||
| 03 | 0.61 | 07—carcass steel | 78 | ||
| 04 | 4.88 | 02—sidewall rubber | 0 | ||
| 6 | SH-170 tyre sidewall | 01 | 11.0 | 02—sidewall rubber | 0 |
| 02 | 0.61 | 07—carcass steel | 102 | ||
| 03 | 0.61 | 07—carcass steel | 78 | ||
| 04 | 4.78 | 02—sidewall rubber | 0 | ||
| 7 | SH-170 tyre belt | 01 | 3.00 | 02—sidewall rubber | 0 |
| 02 | 0.25 | 06—belt steel | −12 | ||
| 03 | 0.25 | 06—belt steel | +12 | ||
| 04 | 0.25 | 06—belt steel | −12 | ||
| 05 | 4.80 | 02—sidewall rubber | 0 | ||
| 06 | 0.61 | 07—carcass steel | 102 | ||
| 07 | 0.61 | 07—carcass steel | 78 | ||
| 08 | 7.23 | 02—sidewall rubber | 0 | ||
| 8 | SH-140 tyre belt | 01 | 2.07 | 02—sidewall rubber | 0 |
| 02 | 0.25 | 06—belt steel | −12 | ||
| 03 | 0.25 | 06—belt steel | +12 | ||
| 04 | 0.25 | 06—belt steel | −12 | ||
| 05 | 3.90 | 02—sidewall rubber | 0 | ||
| 06 | 0.61 | 07—carcass steel | 102 | ||
| 07 | 0.61 | 07—carcass steel | 78 | ||
| 08 | 6.06 | 02—sidewall rubber | 0 | ||
| 9 | SH-120 tyre belt | 01 | 0.92 | 02—sidewall rubber | 0 |
| 02 | 0.25 | 06—belt steel | −40 | ||
| 03 | 0.25 | 06—belt steel | −12 | ||
| 04 | 0.25 | 06—belt steel | +12 | ||
| 05 | 0.25 | 06—belt steel | −12 | ||
| 06 | 2.80 | 02—sidewall rubber | 0 | ||
| 07 | 0.61 | 07—carcass steel | 102 | ||
| 08 | 0.61 | 07—carcass steel | 78 | ||
| 09 | 6.06 | 02—sidewall rubber | 0 |
| Tyre Pressure (kPa) | F/2 Load on One Tyre (kN) | ||
|---|---|---|---|
| Operation Load | Overload | Extreme Overload | |
| 430 | 17.5 | 20.0 | 22.5 |
| 530 | 20.0 | 22.5 | 25.0 |
| 630 | 22.5 | 25.0 | 27.5 |
| 730 | 25.0 | 27.5 | 30.0 |
| Element Type | Complex Model (Per Tyre) | Simple Model (Per Tyre) | ||
|---|---|---|---|---|
| Number of Elements | Usage | Number of Elements | Usage | |
| Continuum element | 92,904 | all tyre parts and the body of wheel | 6000 | tread |
| Shell element | 0 | not applied | 2000 | body of wheel |
| Composite shell element | 0 | not applied | 4200 | all tyre parts except the tread |
| Membrane element | 10,500 | strengthening of the tyre, carcass, belts etc. | 0 | not applied |
| Total number of elements | 103,404 | 12,200 | ||
| F (kN) | p (kPa) | Complex Tyre FEM Model | Simple Tyre FEM Model | ||||
|---|---|---|---|---|---|---|---|
| qmax (kPa) | qavg (kPa) | Proportion (-) | qmax (kPa) | qavg (kPa) | Proportion (-) | ||
| 17.5 | 430 | 801 | 391 | 2.0 | 1464 | 717 | 2.0 |
| 20.0 | 430 | 996 | 414 | 2.4 | 1466 | 700 | 2.1 |
| 22.5 | 430 | 1192 | 431 | 2.8 | 1475 | 696 | 2.1 |
| 20.0 | 530 | 788 | 441 | 1.8 | 1527 | 730 | 2.1 |
| 22.5 | 530 | 932 | 469 | 2.0 | 1549 | 720 | 2.2 |
| 25.0 | 530 | 1104 | 471 | 2.3 | 1563 | 729 | 2.1 |
| 22.5 | 630 | 932 | 469 | 2.0 | 1608 | 736 | 2.2 |
| 25.0 | 630 | 918 | 516 | 1.8 | 1637 | 747 | 2.2 |
| 27.5 | 630 | 1031 | 511 | 2.0 | 1651 | 769 | 2.1 |
| 25.0 | 730 | 940 | 531 | 1.8 | 1696 | 759 | 2.2 |
| 27.5 | 730 | 971 | 560 | 1.7 | 1722 | 782 | 2.2 |
| 30.0 | 730 | 1036 | 557 | 1.9 | 1736 | 816 | 2.1 |
| F/2 (kN) | p (kPa) | A | B | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| uzz | εxx | εyy | εzz | ||||||||||
| Complex | Simple | Error | Complex | Simple | Error | Complex | Simple | Error | Complex | Simple | Error | ||
| 17.5 | 430 | −0.190 | −0.192 | 1.1% | 64,231 | 66,684 | 3.8% | 37,338 | 34,519 | −7.5% | −172,790 | −176,405 | 2.1% |
| 20.0 | 430 | −0.217 | −0.220 | 1.4% | 72,651 | 76,111 | 4.8% | 43,006 | 39,733 | −7.6% | −196,978 | −201,465 | 2.3% |
| 22.5 | 430 | −0.244 | −0.247 | 1.2% | 80,737 | 85,434 | 5.8% | 48,678 | 45,019 | −7.5% | −220,977 | −226,480 | 2.5% |
| 20.0 | 530 | −0.217 | −0.220 | 1.4% | 73,055 | 76,108 | 4.2% | 42,195 | 39,607 | −6.1% | −196,690 | −201,511 | 2.5% |
| 22.5 | 530 | −0.243 | −0.247 | 1.6% | 81,511 | 85,446 | 4.8% | 47,808 | 44,861 | −6.2% | −220,820 | −226,534 | 2.6% |
| 25.0 | 530 | −0.270 | −0.274 | 1.5% | 89,684 | 94,690 | 5.6% | 53,424 | 50,143 | −6.1% | −244,752 | −251,511 | 2.8% |
| 22.5 | 630 | −0.242 | −0.247 | 2.1% | 81,718 | 85,441 | 4.6% | 46,998 | 44,708 | −4.9% | −220,251 | −226,569 | 2.9% |
| 25.0 | 630 | −0.269 | −0.274 | 1.9% | 90,180 | 94,711 | 5.0% | 52,563 | 49,978 | −4.9% | −244,314 | −251,577 | 3.0% |
| 27.5 | 630 | −0.296 | −0.302 | 2.0% | 98,429 | 103,912 | 5.6% | 58,142 | 55,279 | −4.9% | −268,243 | −276,510 | 3.1% |
| 25.0 | 730 | −0.268 | −0.274 | 2.2% | 90,178 | 94,745 | 5.1% | 51,714 | 49,824 | −3.7% | −243,319 | −251,630 | 3.4% |
| 27.5 | 730 | −0.294 | −0.302 | 2.7% | 98,639 | 103,953 | 5.4% | 57,240 | 55,073 | −3.8% | −267,326 | −276,584 | 3.5% |
| 30.0 | 730 | −0.321 | −0.329 | 2.5% | 106,925 | 113,132 | 5.8% | 62,776 | 60,406 | −3.8% | −291,213 | −301,504 | 3.5% |
| F/2 (kN) | p (kPa) | D | E | F | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| uzz | εxx | εyy | εzz | ||||||||||
| Complex | Simple | Error | Complex | Simple | Error | Complex | Simple | Error | Complex | Simple | Error | ||
| 17.5 | 430 | −0.194 | −0.207 | 6.7% | 61,187 | 65,135 | 6.5% | 41,607 | 46,355 | 11.4% | −161,948 | −165,293 | 2.1% |
| 20.0 | 430 | −0.220 | −0.235 | 6.8% | 69,016 | 74,197 | 7.5% | 46,945 | 52,595 | 12.0% | −184,614 | −188,767 | 2.2% |
| 22.5 | 430 | −0.246 | −0.262 | 6.5% | 76,520 | 83,121 | 8.6% | 52,174 | 58,761 | 12.6% | −207,093 | −212,192 | 2.5% |
| 20.0 | 530 | −0.221 | −0.235 | 6.3% | 69,718 | 74,255 | 6.5% | 47,700 | 52,757 | 10.6% | −184,361 | −188,814 | 2.4% |
| 22.5 | 530 | −0.247 | −0.263 | 6.5% | 77,594 | 83,200 | 7.2% | 53,071 | 58,952 | 11.1% | −206,668 | −212,249 | 2.7% |
| 25.0 | 530 | −0.273 | −0.291 | 6.6% | 85,196 | 92,029 | 8.0% | 58,334 | 65,095 | 11.6% | −229,390 | −235,638 | 2.7% |
| 22.5 | 630 | −0.248 | −0.263 | 6.0% | 78,085 | 83,267 | 6.6% | 53,689 | 59,120 | 10.1% | −206,455 | −212,292 | 2.8% |
| 25.0 | 630 | −0.274 | −0.291 | 6.2% | 85,979 | 92,132 | 7.2% | 59,081 | 65,309 | 10.5% | −228,999 | −235,709 | 2.9% |
| 27.5 | 630 | −0.299 | −0.319 | 6.7% | 93,665 | 100,905 | 7.7% | 64,389 | 71,393 | 10.9% | −251,421 | −259,062 | 3.0% |
| 25.0 | 730 | −0.274 | −0.292 | 6.6% | 86,249 | 92,211 | 6.9% | 59,538 | 65,488 | 10.0% | −228,086 | −235,765 | 3.4% |
| 27.5 | 730 | −0.300 | −0.319 | 6.3% | 94,152 | 101,012 | 7.3% | 64,948 | 71,637 | 10.3% | −250,578 | −259,138 | 3.4% |
| 30.0 | 730 | −0.326 | −0.347 | 6.4% | 101,884 | 109,750 | 7.7% | 70,286 | 77,690 | 10.5% | −272,961 | −282,481 | 3.5% |
| F/2 (kN) | q (kPa) | A | B | C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| uzz | εxx | εyy | εzz | ||||||||||
| FEM | MLEA | Error | FEM | MLEA | Error | FEM | MLEA | Error | FEM | MLEA | Error | ||
| 17.5 | 385 | −0.190 | −0.293 | 54.5% | 64,231 | 62,750 | −2.3% | 37,338 | 35,800 | −4.1% | −172,790 | −179,150 | 3.7% |
| 20.0 | 408 | −0.217 | −0.335 | 54.5% | 72,651 | 71,230 | −2.0% | 43,006 | 41,280 | −4.0% | −196,978 | −204,390 | 3.8% |
| 22.5 | 430 | −0.244 | −0.377 | 54.6% | 80,737 | 79,570 | −1.4% | 48,678 | 46,840 | −3.8% | −220,977 | −229,540 | 3.9% |
| 20.0 | 415 | −0.217 | −0.335 | 54.5% | 73,055 | 71,620 | −2.0% | 42,195 | 40,990 | −2.9% | −196,690 | −204,670 | 4.1% |
| 22.5 | 438 | −0.243 | −0.377 | 55.2% | 81,511 | 80,200 | −1.6% | 47,808 | 46,390 | −3.0% | −220,820 | −229,990 | 4.2% |
| 25.0 | 460 | −0.270 | −0.419 | 55.2% | 89,684 | 88,270 | −1.6% | 53,424 | 52,140 | −2.4% | −244,752 | −254,950 | 4.2% |
| 22.5 | 445 | −0.242 | −0.377 | 55.9% | 81,718 | 80,420 | −1.6% | 46,998 | 46,230 | −1.6% | −220,251 | −230,150 | 4.5% |
| 25.0 | 468 | −0.269 | −0.419 | 55.8% | 90,180 | 89,030 | −1.3% | 52,563 | 51,610 | −1.8% | −244,314 | −255,490 | 4.6% |
| 27.5 | 491 | −0.296 | −0.461 | 55.7% | 98,429 | 96,950 | −1.5% | 58,142 | 57,460 | −1.2% | −268,243 | −280,330 | 4.5% |
| 25.0 | 475 | −0.268 | −0.419 | 56.4% | 90,178 | 89,250 | −1.0% | 51,714 | 51,450 | −0.5% | −243,319 | −255,640 | 5.1% |
| 27.5 | 498 | −0.294 | −0.461 | 56.8% | 98,639 | 97,820 | −0.8% | 57,240 | 56,850 | −0.7% | −267,326 | −280,950 | 5.1% |
| 30.0 | 521 | −0.321 | −0.503 | 56.7% | 106,925 | 105,780 | −1.1% | 62,776 | 62,680 | −0.2% | −291,213 | −305,830 | 5.0% |
| F/2 (kN) | q (kPa) | D | E | F | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| uzz | εxx | εyy | εzz | ||||||||||
| FEM | MLEA | Error | FEM | MLEA | Error | FEM | MLEA | Error | FEM | MLEA | Error | ||
| 17.5 | 395 | −0.194 | −0.295 | 52.1% | 61,187 | 60,080 | −1.8% | 41,607 | 42,730 | 2.7% | −161,948 | −168,540 | 4.1% |
| 20.0 | 412 | −0.220 | −0.336 | 52.7% | 69,016 | 67,970 | −1.5% | 46,945 | 48,270 | 2.8% | −184,614 | −192,280 | 4.2% |
| 22.5 | 430 | −0.246 | −0.378 | 53.7% | 76,520 | 75,690 | −1.1% | 52,174 | 53,670 | 2.9% | −207,093 | −215,920 | 4.3% |
| 20.0 | 440 | −0.221 | −0.337 | 52.5% | 69,718 | 68,530 | −1.7% | 47,700 | 48,720 | 2.1% | −184,361 | −192,550 | 4.4% |
| 22.5 | 458 | −0.247 | −0.379 | 53.4% | 77,594 | 76,560 | −1.3% | 53,071 | 54,380 | 2.5% | −206,668 | −216,360 | 4.7% |
| 25.0 | 475 | −0.273 | −0.419 | 53.5% | 85,196 | 83,910 | −1.5% | 58,334 | 59,480 | 2.0% | −229,390 | −239,810 | 4.5% |
| 22.5 | 485 | −0.248 | −0.379 | 52.8% | 78,085 | 76,870 | −1.6% | 53,689 | 54,630 | 1.8% | −206,455 | −216,510 | 4.9% |
| 25.0 | 503 | −0.274 | −0.421 | 53.6% | 85,979 | 84,960 | −1.2% | 59,081 | 60,330 | 2.1% | −228,999 | −240,340 | 5.0% |
| 27.5 | 520 | −0.299 | −0.461 | 54.2% | 93,665 | 92,100 | −1.7% | 64,389 | 65,260 | 1.4% | −251,421 | −263,690 | 4.9% |
| 25.0 | 530 | −0.274 | −0.421 | 53.6% | 86,249 | 85,250 | −1.2% | 59,538 | 60,570 | 1.7% | −228,086 | −240,490 | 5.4% |
| 27.5 | 548 | −0.300 | −0.462 | 54.0% | 94,152 | 93,290 | −0.9% | 64,948 | 66,230 | 2.0% | −250,578 | −264,290 | 5.5% |
| 30.0 | 566 | −0.326 | −0.503 | 54.3% | 101,884 | 100,490 | −1.4% | 70,286 | 71,210 | 1.3% | −272,961 | −287,670 | 5.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Király, T.; Primusz, P.; Tóth, C. Simulation of Static Tyre–Pavement Interaction Using Two FE Models of Different Complexity. Appl. Sci. 2022, 12, 2388. https://doi.org/10.3390/app12052388
Király T, Primusz P, Tóth C. Simulation of Static Tyre–Pavement Interaction Using Two FE Models of Different Complexity. Applied Sciences. 2022; 12(5):2388. https://doi.org/10.3390/app12052388
Chicago/Turabian StyleKirály, Tamás, Péter Primusz, and Csaba Tóth. 2022. "Simulation of Static Tyre–Pavement Interaction Using Two FE Models of Different Complexity" Applied Sciences 12, no. 5: 2388. https://doi.org/10.3390/app12052388
APA StyleKirály, T., Primusz, P., & Tóth, C. (2022). Simulation of Static Tyre–Pavement Interaction Using Two FE Models of Different Complexity. Applied Sciences, 12(5), 2388. https://doi.org/10.3390/app12052388






