1. Introduction
As dominators of the earth, human beings have higher intelligence than any other biological species. Humans are skilled in summarizing rules from observed phenomena, forming knowledge, and applying it to understanding new things. Throughout history, the evolution of humans is basically the process by which new methods and techniques are created to alleviate human labor, thus promoting the development of science and technology. As one of the greatest inventions in the 20th century, robotics has made great progress since the late 1950s. The emergence of robots is the inevitable trend of social and economic development, and its rapid growth has been improving the level of social production and the quality of human life.
Although people are eager to have robots in their homes, there is no doubt that the impact of robots on manufacturing is even greater, especially in the last decade when traditional manufacturing has undergone unprecedented changes. Due to the yearning for a better life, many people are unwilling to choose dangerous or boring jobs, which makes different types of human jobs face labor shortages. In this context, industrial robots show extraordinary ability in replacing human labor and improving productivity. However, some tasks that rely heavily on human dexterity or intelligence remain difficult to replace by robots. On one hand, while most industrial robots are adept at repetitive tasks, they are not flexible enough to manipulate forces, especially for some precision or fine machining; on the other hand, most robots today and fully automated production lines are not very good at understanding human intentions or learning sequential strategies from human behavior. Therefore, these automated devices are very sensitive to changes in context. To solve these problems, intelligent learning algorithms and human demonstrations aimed at improving robot autonomy have been studied [
1,
2].
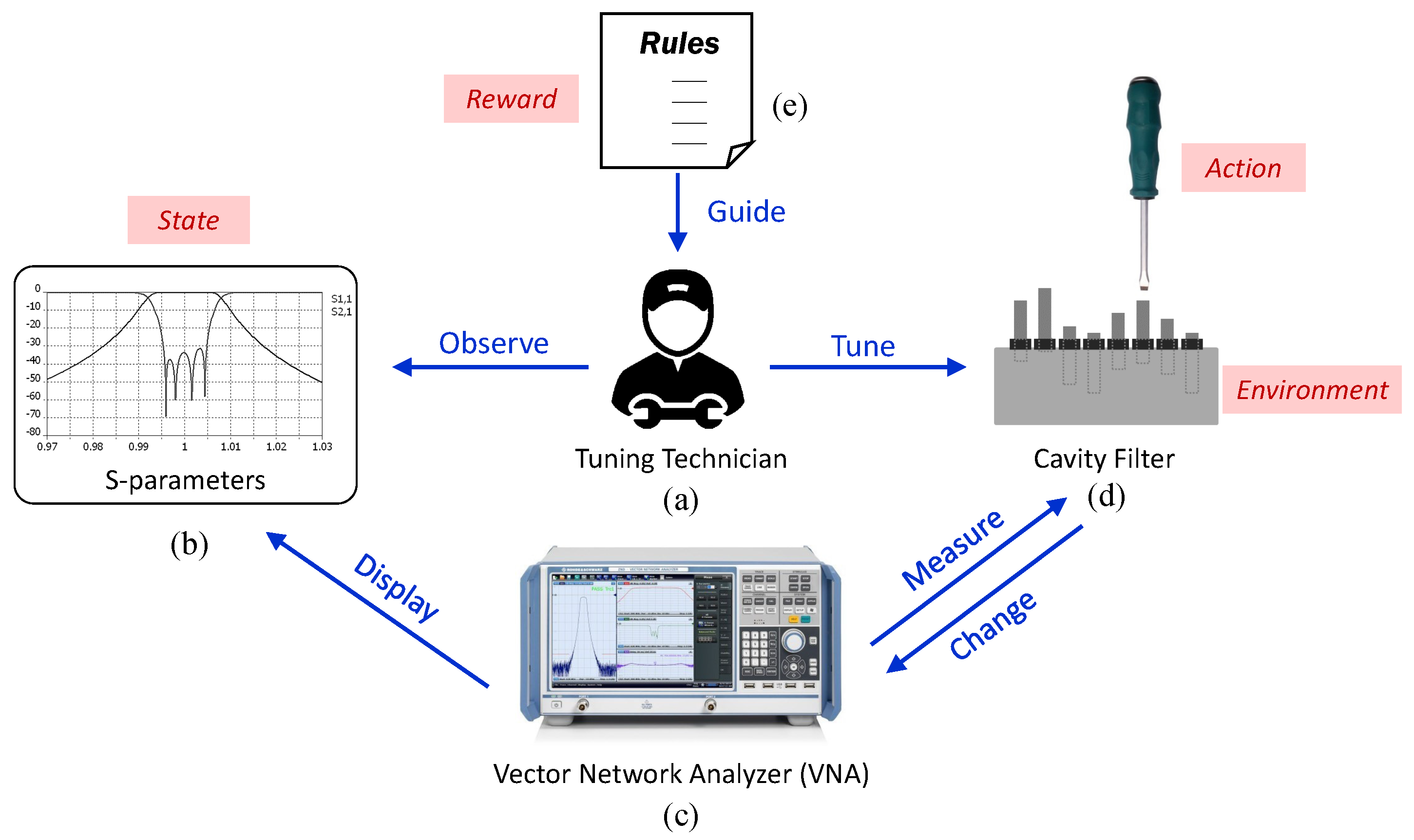
In this work, we mainly consider the second aspect mentioned above. The tuning process of microwave cavity filter is studied in detail. Tuning is the last step of the cavity filter before it leaves the factory. It is usually a boring and complicated work, which is completed manually by experienced tuning technicians. Our goal is to automate tuning.
The cavity filter is a metal device for filtering signals and suppressing noises, which is often used in microwave, satellite, radar, electronic countermeasure (ECM), and various electronic testing devices. A cavity filter is mainly composed of cavities with resonators, inserted tuning screws, locking screw-nuts, and a covering plate; see
Figure 1a. A cavity filter is a product that passes or eliminates microwave signals in specific frequency bands. Due to high working frequencies and inevitable manufacturing errors, unfortunately, almost every cavity filter product needs to be manually adjusted to meet its design specifications. During the tuning process, the measured cavity filter is connected to a Vector Network Analyzer (VNA) (
Figure 1b) and iteratively adjusted by a technician with a screwdriver. Almost every inserted screw will be tuned according to the S–parameter curves shown in the VNA. The curves indicate the current tuning state of the product and give guidance to the tuning technician to perform the next action such that the curves are gradually optimized until reaching the desired targets.
Figure 2 shows the overall manual tuning process.
There are numerous possible difficulties during the task of cavity filter tuning. First, the relations between tuning screws and S–parameters would be complex. Theoretical analysis does not ensure validity since the manufacturing errors are not considered. In fact, each screw has its physical function in adjusting the S–parameter curves, but the actual product differs a lot from the designed pattern. Second, the cavity filter products have the feature of small-batch multiple varieties, which means that the tuning strategy for one filter category is not necessarily valid for another, even though they may have similar structures or tuning elements. Even for the same product type, differences would be obvious between individuals. Therefore, it is futile to simply copy the inserted screw positions of a tuned filter to a detuned one.
The above challenges make experienced technicians very critical. These “experts” are usually trained for several months to master the tuning strategies before they can handle real tuning tasks. An untrained person may get lost in the mazelike tuning task and never reach the target. On the basis of our investigations, experienced tuning technicians differ in two aspects from ordinary people with no experience. The first significant difference is that experienced technicians can accurately identify and evaluate the current situation, i.e., whether a curve’s change is good or bad. This is the foundation of all success. On this basis, they are also expertized in mastering the tuning amount. In other words, they know which screw to tune, and to what extent. However, all of these experiences are usually perceivable but indescribable.
To automate the tuning process, a powerful and stable automated tuning robot is essential. More importantly, a tuning algorithm should be designed that can accurately provide a tuning strategy at each tuning stage to successfully tune the filter as quickly as possible. In previous studies, automatic tuning methods based on time-domain response [
3], model parameter extraction [
4], and data-driven modeling techniques (i.e., Neural Network [
5], Support Vector Regression [
6], fuzzy logic control [
7], etc.) have been investigated; however, these methods either rely heavily on individual product models or require data collection, and have limited generalization capabilities. In this work, we still focus on the tuning algorithm but pay more attention to the autonomy of the algorithm. To easily implement the algorithm, a computer-aided tuning robot system has also been developed, but the details are not the focus of this article.
As a breathtaking achievement in recent years, Reinforcement Learning (RL) has attracted extensive attention worldwide. From the perspective of bionics and behavioral psychology, RL can be seen as a manipulation of the conditioned reflex. Thorndike proposed the Law of Effect, which indicates that the strength of a connection is influenced by the consequences of a response [
8]. Such a biological intelligence model allows animals to learn from the rewards or punishments they receive for trying different behaviors to choose the behavior that the trainer most expects in that situation. Therefore, the agent using RL is able to autonomously discover and select the actions that generate the greatest returns by experimenting with different actions. Intuitively, the manual tuning process is very similar to RL in many ways. To tune the screws of a cavity filter is equivalent to exploring the environment while watching the S–parameters curve from the VNA, which relates closely to obtaining environmental observations. The reward is instantiated in the personal evaluation of the current situation. For these reasons, plenty of studies have exploited RL for automatic tuning [
9]. In this work, we utilize an actor–critic RL method to search for the optimal tuning policy.
Compared with the related work, the contributions of this paper are as follows. First, instead of simply fitting the screw positions to the S–parameters curves, we paid more attention to the process of tuning. In particular, the cavity filter tuning problem was formulated as a continuous RL problem and an effective solution was proposed based on Deep Deterministic Policy Gradient (DDPG). Second, we appropriately designed a reward function inspired by the experienced tuning processes, which stabilizes and accelerates the RL training. The proposed method was tested on a real cavity filter tuning issue and positive results were received. Third, we presented a framework to transfer the learned tuning policy to a new detuned product individual of the same type. With limited steps of exploration on the new product, a data-driven mapping model was built, and the relationship between the new and the old product could be learned. With this framework, the policy learned from RL can be generalized.
The remainder of the article is structured as follows.
Section 2 introduces the tuning method of cavity filter and the basic principles of RL. In
Section 3, our approach to autonomic tuning using continuous reinforcement learning is developed and presented. We first illustrate the framework of the algorithm and then explain the reward shaping through human inspirations. We also consider the generalization issue to make the algorithm more adaptable. A set of simulation experiments are carried out and the results to verify the validity of the framework are given in
Section 4. In
Section 5, some relevant issues are discussed in depth. Finally,
Section 6 concludes the paper and makes a plan for future work.
3. Intelligent Tuning Based on DDPG
3.1. Preliminaries
The observed states from the VNA are S–parameters curves, as shown in
Figure 3. Since the cavity filter is a passive device, all signals passing through it come from external sources. During the test, the cavity filter device under test (DUT) is connected to a VNA through input/output ports. The VNA then sends the signal to the DUT to observe the received signal in the form of scattering parameter, or S–parameter for short. To meet the designed requirements of a cavity filter product, it is necessary to examine some test data, including the Return Loss, the Insertion Loss, the Pass-band Fluctuation, and the Out-of-band Rejection.
is the common notation of S–parameters, indicating the energy measured at port
i injecting to port
j. The return loss of port 1 is represented by
, indicating the energy measured at port 1 after injecting from port 1 and returning to port 1. Similarly, the insertion loss of port 1 is always represented by
, representing the energy measured at port 1 after injecting from port 1 to port 2 and returning to port 1. It is always required that the value of the return loss should be minimized within the passband (always less than or equal to
dB). In other words, the values of
in
Figure 3 must be under the black dashed benchmark line within the specified frequency range. For insertion losses, the value should be maximized within the same passband (always close to 0 dB).
In this work, we only consider the value of return loss, namely, the curve in the passband, as the state of RL, and ignore the other specifications, such as insertion loss. Therefore, the goal of tuning is to adjust the screw to control the curve to the target line. It is important to note that our tuning method can be applied to any filter class of radio frequency (RF) devices, including cavity filters, combiners, duplexers, and multiplexers.
3.2. Formulations
The RL method in this work follows the basic Markov Decision Process (MDP) settings. At each time step t, the agent observes a state from the environment. Then, it takes an action to interact with the environment and the state of the agent is transferred to . At the same time, the reward reflecting the current state and action pairs is obtained from the environment or specified by a human teacher. With the transition set , the agent learns the policy with some optimization process, so that the expected future reward is maximized.
In our previous work, the framework of DQN was applied. A value function
Q is defined based on the Bellman equation to compute the expected future reward. Then, the optimal action to take at each time step is the one that maximizes the
Q values,
where
,
, and
are the state, action, and reward, respectively, at step
t;
is a discounting factor. In DQN, a replay memory
D is used to save transition sequences state, action, reward, new state. At each time step, a minibatch of transitions will be randomly selected from the replay buffer
D for training the Q–network by minimizing the distance between the target Q-network and the current hypothesis model:
where the target is
Instead of using Deep Convolutional Neural Networks to approximate the value function, we extracted a feature set from the original S–parameters as the state. We follow the Experience Replay and the Target Network of DQN to ensure the stability of the algorithm. We also used the Euclidean distance between the S–parameters curves as a reward function. In particular, if the current curve is getting closer to the target, the reward is large, and vice versa. This definition of this reward is somewhat coarse and should be modified in the light of human experience.
In this work, the tuning algorithm is based on another important RL framework—DDPG—in which continuous actions are valid. Experience replay and Target Q-Network are preserved from DQN. DDPG is based on the actor–critic mechanism, where a critic function
and an actor function
are parameterized by two separate neural networks. The actor network is also called the policy network, which updates the policy with policy gradient. The critic network is similar to the value function in Q-learning, which evaluates the action from the actor network by updating the Q-values [
26].
We define the tuning task as an MDP with the following settings. At each time step
t, the agent is in a state
. In the tuning problem, the state
is defined as the S–parameters (
) curve (or some extracted features) drawn from the VNA. The agent performs an action
at each time step
t to transfer state
to a new state
. The action is defined as the tuning amount we can take, i.e., the adjustment of each screw element. Unlike our previous work [
9], screw lengths are continuous values instead of discrete values, which is more accurate and reasonable. Thus, the action at any time step can be represented as a vector of dimension
m, where
m is the number of valid tuning screws. The reward function consists of three parts, which take into account the process of tuning target and human experience.
The main algorithm is concluded in Algorithm 1. For details of the DDPG algorithm, readers can refer to [
26].
3.3. Reward Shaping Inspired by Human Knowledge
After taking the action , a reward will be obtained. The value of the reward is an evaluation of the action taken, and the goal of RL is to learn a policy so that the expected future reward is maximized. In some cases, the reward value can be derived directly from interaction with the environment, such as playing Atari games. In other cases, the reward function should be defined manually, such as the self-driving problem. Other tasks have reward functions that are difficult to define, such as robot manipulations. In these cases, the reward is always learned by demonstration. In this work, we use the experience of human tuning to manually design the reward function to make RL have better performance.
The reward
of each step consists of three parts.
directly describes the cost of each step taken by an action. Any step other than reaching the goal is rewarded with
. If the action results in an eligible S–parameters curve, i.e., reaching the tuning target, the reward will be added by
.
| Algorithm 1 Intelligent Tuning Based on DDPG |
| 1: | Randomly initialize critic network and actor network with weights and . |
| 2: | Initialize the target network and with the same weights as above. |
| 3: | Initialize the replay buffer D. |
| 4: | Randomly initialize inserted screw positions. |
| 5: | for episode = 1,M do |
| 6: | Read S–parameters from the VNA and formulate the initial state . |
| 7: | for step = 1,T do |
| 8: | Select action according to the current policy and exploration noise. |
| 9: | Tune corresponding screws to execute action and compute reward , and observe new S–parameters to formulate new state . |
| |
| 10: | Store the transition in D. |
| 11: | Sample a random minibatch of N transitions from D. |
| 12: | Set . |
| 13: | Update the critic network by minimizing the loss: . |
| 14: | Update the actor network using the sampled policy gradient: . |
| 15: | Update the target networks: |
| | |
| |
| 16: | end for |
| 17: | end for |
To impose a penalty for one or more screws exceeding the length limit, a total reward of
is added. More specifically, if the action causes the screw to exceed its limit, the screw will remain unchanged and the agent will be rewarded with
, where
m is the number of valid screws. The reward
is formulated as
where
is the indicator function with
and
denotes the insertion position of the
i-th tuning screw at the time step
t.
and
denote, respectively, the maximum and minimum insertion position of the
i-th screw.
The third part is the most important reward
, which is formed in the evaluation of transitions from the current state to the next state, inspired by human tuning experience. Take into account the experienced tuning process. Technicians are able to optimize the S–parameters curve because they can evaluate changes to the curve. In other words, they do their best to make the S–parameters curve always move in the right direction. Therefore, the change direction of the S–parameters curve to the new curve can be expressed as a set of vectors. Each
curve is truncated first, leaving only the central core area. The two curves are then discretized into the same number of sampling points. Thus, the vectors connecting two corresponding points of the curves can form a vector field. See
Figure 4 for more details. In
Figure 4a, the vector
represents the moving direction of the point
on the blue curve (current state) to the point
on the green dashed curve (a new state).
Similarly, to represent the changing direction of a curve to a target line, a set of vectors connecting each two corresponding points on the curve and the target line can be applied, as shown in
Figure 4, denoted by
.
Therefore, we can use the sum of each cosine value of the angle
between
and
to calculate the directional difference of two S–parameters curves, i.e.,
where
The intuition to use cosine values is pretty simple. In order to adjust screws to maximally drive the current S–parameters curve to reach the target, we want each point on the curve to move as far as possible toward the goal. The cosine value of two vectors within the range
describes the similarity between the current direction and the target direction. The closer the current vector is to the target, the higher the value. More specifically, the cosine value of angle
in
Figure 4a is larger than 0 because
is less than 90
, representing that
and
almost share the same direction. Conversely, the value of angle
in
Figure 4b will be less than 0 since
is larger than 90
, which indicates that the two vectors have opposite directions. Therefore, the third shaping reward is formulated as
where
in which
denotes the vector connecting the point
j on the
curve before and after tuning at time step
t.
The cosine value only describes the direction of movement of each point on the curve. In addition, the length of each vector represents the extent of the movement. So, we multiply the cosine value by the moving amount of that point in the target direction. Therefore, the human-experience-shaped reward can be improved by
Therefore, the generated shaping reward inspired by human experience naturally shows the overall degree to which the curve changes in the direction of the target. The overall reward function is the sum of these three parts:
where
,
, and
are weights for a trade-off.
3.4. Generalize the Learned Policy
To learn how to tune a filter with RL is only a first and basic step. Since RL training always takes a long time to converge, and every product individual is different, how to adapt the individual differences is a challenging issue. If the trained policy cannot be generalized, RL loses its significance and will have no more advantage than supervised learning. In this work, we present a framework to tackle the generalization problem after RL training. Specifically, our aim is to tune a new detuned cavity filter to its target within as few steps as possible, after RL training on a benchmark product of the same type.
The framework contains two phases: learning and transferring. In the learning phase, we randomly explore the new filter product, collect enough data pairs, and build a data-driven mapping model between the new filter product and the old one. To achieve this, an inverse estimation model needs to be first built, i.e., a mapping from the S–parameters to the screw positions of the old filter product. The inverse estimation model could be built with data examples collected during the RL training process. Once we have a new product individual, we first randomly place the screws and record their corresponding S–parameters curves. Then, the inverse estimation model is used to predict the screw positions on the old filter product (which has already been trained). Finally, the two sets of screw data are used for constructing the data-driven mapping model. The learning phase is concluded in
Figure 5a.
In the transferring phase, the learned data-driven mapping model is used to transfer the trained RL policy to the new product. When connecting the new product to the VNA, S–parameters could be measured. The trained RL policy network
predicts the best action to take. However, since the policy network is based on the old filter product, the predicted action cannot be directly applied. The mapping model learned in the learning phase should be used to transfer screw positions from the old to the new. The action on the new product is executed. The process is shown in
Figure 5b.
It is worth noting that to build the inverse estimation model, data pairs including screw positions and S–parameters curves should be collected. Fortunately, the data could be collected at the same time with RL training. A way to correctly record screw positions is necessary.
5. Discussions
It seems a fuss to use RL, since other methods, such as training supervised learning models [
5,
6,
14,
16,
32] or to study the physical characteristics of the cavity filter [
3,
10,
11,
12], can still achieve the same goal; in most cases, those methods also do not need a large number of iterations. However, these methods always need a pretuned filter model as a benchmark or experienced tuning experts for guidance. In addition, they have weak potential in generalization. As explained in
Section 1, cavity filters have a wide range of types, and they are different in structure and design specifications. Therefore, simply modeling one filter product may fail in adapting to others. In contrast, humans can learn strategies from experience and extract useful information for further use, no matter how the filter type changes. Therefore, it is more reasonable to study the tuning strategies rather than a cavity filter sample.
RL algorithms do not depend on any explicit guidelines or supervision but autonomously learn the tuning strategies from scratch. More importantly, the learned strategies are expected to be generalized to other cases, i.e., to different individuals of the same type or even totally different types. This work is an extension to [
9,
33]. In [
9], DQN is used for the first time to solve the tuning problem but the state and action spaces are both very limited. In [
33], DDPG first shows its effectiveness for tuning. The methods proposed in [
21,
22,
34] also utilize DQN, double DQN, or DDPG, and based on previous studies, these works attempt more filter orders (screw numbers) or more elaborate reward functions, but have little consideration of generalization or transfer problems. In this work, we have considered the issue of transferring the learned knowledge, even though the differences between individuals are man-made, which does not necessarily accord with reality. Therefore, the problem related to generalization or transfer is still demanding work to be addressed in the future. It is also worth noting that some other methods such as Particle Filtering and Particle Swarm Optimization [
35] can also be considered in our future work to focus on the tuning process.
Our current study is somewhat limited by the difficulty of the experiment. Although we have a robotic tuning system, it is not enough efficient, and thus, has not been directly used for executing RL training for safety reasons. Without an effective tuning machine, either a simulation model or manual tuning can be used for the experiment. By comprehensive consideration, we use the robot tuning system for collecting data pairs to build the simulation environment, then train the RL model in simulation.
Another popular way to integrate human experience with RL is to use imitation learning (also called learning from demonstration), which provides a straightforward way for the agent to master flexible policies. Studies in [
36,
37] integrate DQN and DDPG with human demonstrations by pretraining on the demonstrated data. However, this idea is somewhat hard for our task. First, in order to use demonstration data, a tuning expert should be always available, which is not guaranteed. Second, data acquisition is also important. The tuning action is continuous, and the tuning amount directly determines the change amount of the S–parameters. To record the demonstration data, both screw positions and S–parameters should be discretized; it also needs collaboration with tuning technicians. Finally, the recorded data might highly depend on the skills of the tuning technician. Different people perform differently, and even the same person may differ in the process of tuning the same product, which brings additional noise. Due to these reasons, imitation learning is currently not appropriate for this task. Instead of directly using human demonstration, we integrate human intelligence into the design of the reward function, which performs much better than simply learning from human demonstrated data.