Noise-Free Security Assessment of Eviction Set Construction Algorithms with Randomized Caches

Abstract

Cache timing attacks, i.e., a class of remote side-channel attack, have become very popular in recent years. Eviction set construction is a common step for many such attacks, and algorithms for building them are evolving rapidly. On the other hand, countermeasures are also being actively researched and developed. However, most countermeasures have been designed to secure last-level caches and few of them actually protect the entire memory hierarchy. Cache randomization is a well-known mitigation technique against cache attacks that has a low-performance overhead. In this study, we attempted to determine whether address randomization on first-level caches is worth considering from a security perspective. In this paper, we present the implementation of a noise-free cache simulation framework that enables the analysis of the behavior of eviction set construction algorithms. We show that randomization at the first level of caches (L1) brings about improvements in security but is not sufficient to mitigate all known algorithms, such as the recently developed Prime–Prune–Probe technique. Nevertheless, we show that L1 randomization can be combined with a lightweight random eviction technique in higher-level caches to mitigate known conflict-based cache attacks.

1. Introduction

Modern micro-architectures rely on multiple levels of caches to achieve high-performance memory operations. Caches are inherently shared between all processes running on the system, either sequentially (i.e., over time) or concurrently. This sharing opens the door for a large class of attacks, known as cache timing attacks, which exploit any variations in cache access latency. Cache attacks allow a spy process to have a partial view of memory addresses that are being accessed by another process. This ability can be turned into various security exploitations; for example, leaking kernel memory as part of original Spectre [1] and Meltdown [2] attacks and creating key loggers or covert channels [3]. Such attacks have also been successfully employed to retrieve secret keys from various cryptographic algorithms, such as AES [4], RSA [5] and ECDSA [6]. Therefore, preventing cache attacks is a major challenge for modern micro-architectures.

Two approaches that can be used to mitigate cache-based side-channel attacks have been extensively studied: cache partitioning [7,8,9,10,11,12,13,14,15] and cache randomization [15,16,17,18,19,20,21,22]. Cache partitioning provides hardware-level isolation to prevent attackers from interacting with the cache contents of other processes. Cache randomization adds non-determinism to the behavior of the cache to make information extraction more difficult. In contrast to cache partitioning, randomization maximizes the effective use of resources; however, the security level of randomized architecture is more difficult to analyze and quantify.

So far, most randomization countermeasures have been designed for last-level caches [19,20], where data sharing between processes is prominent, but the lower-level caches (e.g., L1 and L2) are still unprotected against cache attacks. This study aimed to determine whether address randomization on first-level caches would be sufficient to mitigate cache attacks, even when higher-level caches are unprotected.

A fundamental tool for carrying out cache attacks is an eviction set: a set of addresses that fall into a specific cache set. When an attacker cannot reliably build an eviction set, many cache attacks are not feasible. Therefore, this study analyzed the behavior of state-of-the-art eviction set construction algorithms with randomized L1 caches. For this, we simulated a noise-free cache hierarchy to avoid any kind of unwanted noise (e.g., buses, MMU or other applications running concurrently). This environment modelled an “ideal” attacker with much stronger capabilities than a real-world attacker.

Our experiments showed that L1 address randomization prevented some, but not all, eviction set construction algorithms. This means that randomization would still be required on higher-level caches in order to mitigate all known algorithms. Nevertheless, we showed that L1 randomization combined with a lightweight randomization approach in the last level would protect against any eviction set construction algorithms; namely, we designed a random eviction scheme to be used in the last-level cache and demonstrated its effectiveness against eviction set construction algorithms.

To summarize, in this paper, we present the following contributions:

• We performed a systematic behavioral study of algorithms for constructing eviction sets in a noise-free environment. Using this approach, we showed that the Prime–Prune–Probe algorithm is not efficient when it uses a large number of addresses to find an eviction set;
• We proposed to dynamically randomize the first-level cache mapping. The experimental results showed that dynamic randomization in the L1 cache effectively mitigates some (but not all) eviction set construction algorithms;
• To protect the last-level cache, we proposed to randomly evict the last-level cache sets. We showed that our solution reduces the success rate of the Prime–Prune–Probe algorithm to below 0.1%.

The rest of this paper is organized as follows. In Section 2, we present the technical background. Then, in Section 3, we introduce our threat model and the hypothesis regarding the attacker’s capabilities. In Section 4, we provide a description of eviction construction algorithms. In Section 5, we present our main security analysis, including the complexity of building an eviction set in a noise-free environment with unprotected caches. We show how we used our simulation framework to analyze the side effects of these algorithms and to evaluate the security of lower-level randomized caches in Section 6. In Section 7, we first consider a random eviction cache as a countermeasure for the last-level cache and we then discuss security parameters used to mitigate the construction of eviction sets through so-called random eviction. Finally, we conclude with some extensions and comments for future research.

2. Background

2.1. Cache Memories

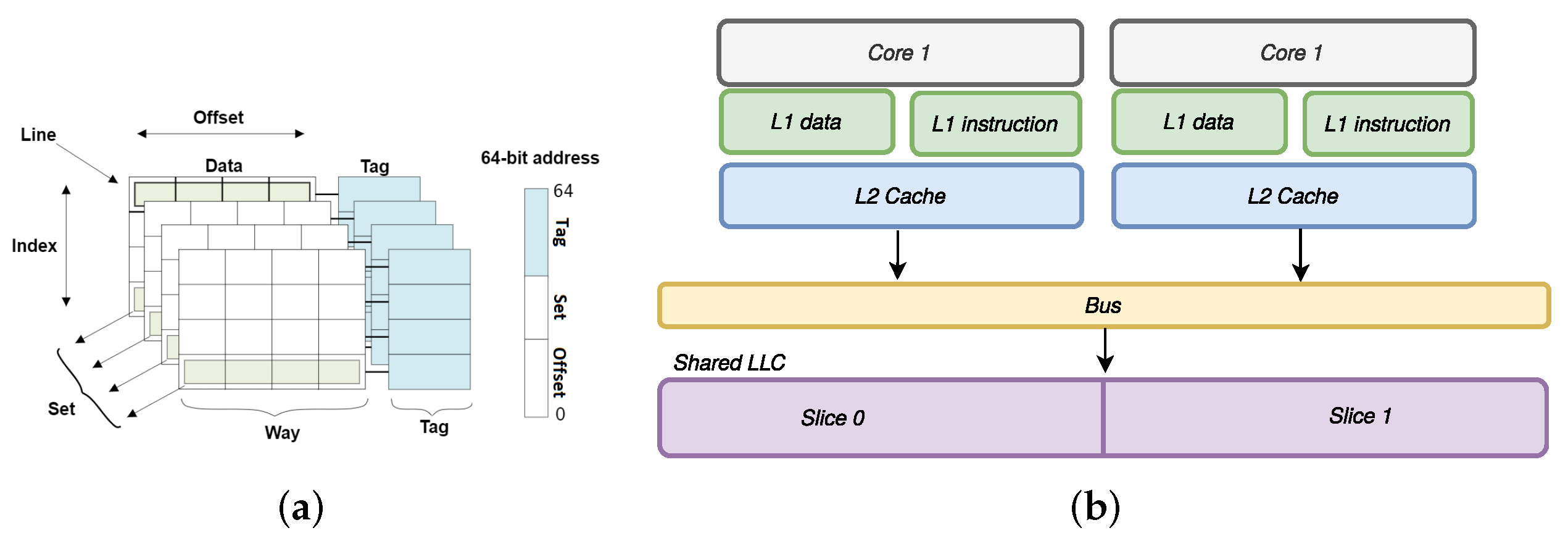
Caches are small memories with very fast access times that are situated between the cores and the main memory. Their purpose is to keep frequently used data and instructions very close to the core to speed up memory access. In this work, we consider set-associative caches. A cache is made of sets, each containing a fixed number of ways (see Figure 1a). We denote the number of sets in the cache as S and the number of ways per set as W. A memory block is the memory representation of a cache line. It can be stored in any of the W ways of a cache set; thus, the cache can store up to $S\times W$ memory blocks. When a set is full and a line has to be deleted, a replacement policy determines which line is to be removed from the set.

Different cache replacement policies exist, such as the least recently used (LRU), pseudo-LRU, first in first out (FIFO), least frequently used (LFU) and pseudo-random replacement policies. In modern micro-architectures, replacement policies are often undocumented. However, the replacement policies of some micro-architectures have been reverse-engineered; for example, Sandy Bridge and Ivy Bridge use a pseudo-LRU replacement policy [23]. Moreover, Ivy Bridge, Skylake and Haswell use adaptive cache replacement policies, which only work as pseudo-LRU policies in some situations [24].

As we have seen so far, a fixed mapping is used to determine whether a memory address is present in the cache. Typically, the input address is decomposed into three parts: a set index, an address tag and a line offset (see Figure 1a). A successful cache access is called a cache hit; in contrast, a failed cache access is called a cache miss. A cache miss results in a longer access time and can be detected with precise timing measurements.

A key feature of the LLCs in some modern processors is that they are divided into different cache slices (see Figure 1b). As well as the set and way indices, a slice index must also be determined in order to place a line into this sort of partitioned cache. Although microprocessor designers do not disclose the mapping that is used between memory blocks and cache slices, it has been reverse-engineered in previous work on Intel architectures [25].

2.2. Multi-Level Cache Organization

Most micro-architectures use multiple levels of caches. The low-level caches are faster and smaller than those at higher levels (Throughout this paper, low-level caches are viewed as closer to the processor, hence, L1 caches are the lowest). The last-level cache is often shared among all cores to improve performance and simplify cache coherency. On the other hand, first-level caches (L1) are usually private. In a Harvard architecture, each core typically has two L1 caches, an instruction cache and a data cache. The memory inclusion policy manages whether a block present at a cache level can also be present in lower cache levels. Policies used can be inclusive, exclusive or non-inclusive.

An inclusive cache hierarchy enforces that the content of each cache is always a subset of the higher-level caches. Suppose a line is evicted from the last-level cache; in that case, inclusion is enforced by back invalidating that line from the lower-level caches. A cache coherence protocol is utilized to ensure that data are correctly updated in all cache levels.

2.3. Cache Side-Channel Attacks

In cache-based side-channel attacks, the attacker exploits secret-dependent memory access patterns to extract private information from a victim process. Such attacks require the attacker and the victim processes to share the same cache at some point. In practice, this can occur with processes that are scheduled on the same core and share a L1 cache [26,27,28] or with processes that are running on different cores and share the LLC [3,6,29,30,31]. Cache sharing implies that cache lines from one process can be evicted by another process. These evictions result in timing variations that help the attacker detect the victim’s memory accesses.

Cache-based side-channel attacks are particularly powerful because they are not limited to attacks on cryptosystems [4,5,6,32,33,34,35]. Recent works [36,37,38,39] have shown how cache-based side-channel attacks can bypass many countermeasures that are based on the address space layout randomization (ASLR) mechanism. Other works have shown that cache-based side-channel attacks are possible at any level and for any type of cache memory. For example, attacks on the instruction cache [26,27,40], translation lookaside buffers (TLBs) [41] and branch prediction buffers [42] have all been successful.

Cache-based side-channel attacks are performed in two steps: a profiling phase and an exploitation phase (see Figure 2). In the profiling phase, the attacker identifies probe addresses, whose access patterns may leak information about the victim access patterns; for example, the probe addresses can be related to cryptographic keys [33] or keyboard input events [3]. In the exploitation phase, the attacker modifies the probe address state in the cache of a known state. Then, it waits for a short period of time to allow the victim to potentially change the state of the probe addresses. Finally, the attacker probes the addresses again to determine the accesses made by the victim process.

These attacks work differently depending on whether the probe addresses are shared (case ➁ on Figure 2) or not (case ➀). The main difference is that when addresses are not shared, the attacker has to construct an eviction set to perform its attack.

2.3.1. Sharing-Based Cache Attacks

Sharing-based attacks rely on unexpected memory sharing between the attacker and the victim. Such sharing is, for example, introduced by the operating system (OS) with shared libraries or memory deduplication [43]. Therefore, the attacker can remove a shared address from any cache level. This can be achieved with a cache maintenance instruction (e.g., clflush instruction in ×86 processors), as shown in the Flush+Reload [6] attack. Another way to remove a shared address from the memory hierarchy is to access a set of addresses mapped to the same cache set, which forces the replacement policy to evict the target address. An example of such an attack is Evict+Reload [3]. In both of these attacks, the attacker reloads the target address. The access latency of the load reveals whether the victim has accessed that address or not. Flush+Flush [29] is another variant of Flush+Reload in which the attacker measures the latency of the clflush instruction.

2.3.2. Conflict-Based Cache Attacks

Unlike sharing-based attacks, conflict-based attacks do not require address sharing. This type of attack has a cache set granularity. The idea is that when the victim’s addresses and the attacker are mapped to the same cache set, they may evict each other from the cache (this phenomenon is called “cache contention”). The attacker can use such evictions to monitor the victim’s access patterns.

In a conflict-based attack, such as Prime+Probe [28,31], the attacker first constructs a set of addresses that are mapped to a particular cache set (called an eviction set). Then, the attacker uses the eviction set to create the target cache set in a known state by overloading the cache set with its data. When the victim accesses the same cache set, one of the attacker’s addresses is replaced. The attacker determines whether the victim accessed its set or not by measuring the access time for each element of the eviction set.

Figure 3 illustrates an example of using the Prime+Probe attack as a conflict-based cache attack on a two way set-associative cache involving three steps: Prime, Wait and Probe. The attacker targets set one by accessing an eviction set of two addresses in the Prime step. Then, the attacker waits to see whether the victim accesses set one or not. When the victim accesses the same cache set, it forces one of the attacker’s addresses to be evicted. Later, in the Probe step, the attacker re-accesses the eviction set and measures the access latency of each address. When the access time for all of the addresses is low (i.e., cache hit), it means that the victim did not access the target set. However, as shown in Figure 3, when one address has a longer access time (i.e., cache miss), the attacker learns that the victim process accessed set one during the Wait phase.

2.4. Countermeasures

Mitigation techniques against cache-based side-channel attacks are divided into partition approaches and randomization approaches.

2.4.1. Partition-Based Countermeasures

Partition-based techniques [7,8,9,11,13,14,44,45] ensure that there is no cache sharing between processes. A straightforward approach is set partitioning, which assigns different cache sets to different processes. This can be achieved at the OS level through page coloring [12,13,46] or dedicated hardware. The cache content can also be partitioned using cache ways, as in CATalyst [10]. This approach requires hardware support, such as Intel’s Cache Allocation Technology (CAT) [47]. Since the number of ways is small, the number of security domains is very limited. As a consequence, the CATalyst design only supports two partitioning domains.

2.4.2. Randomization-Based Countermeasures

Randomization-based countermeasures add non-determinism and noise to the behavior of the cache to make information extraction more difficult for an attacker. Address randomization is a family of randomization techniques that applies a permutation to the address to set mapping. This makes it harder for the adversary to find a set of addresses that always map to the same cache set.

In a static randomization scheme [15,21], the address mapping is fixed, while in a dynamic randomization [19,20], the mapping can change over time. Existing address permutation functions rely on lookup tables [15,21], hashing schemes [19], lightweight permutations [16] or block ciphers [20].

Recent studies have proved that static randomization does not defeat conflict-based cache attacks due to advanced eviction set construction algorithms [48]. For this reason, dynamic randomization [19,20] has been introduced in last-level caches. In the rest of this work, we use the term remapping to refer to a change in the address mapping. The interval in which the mapping is changed determines the time window that is available to an attacker to perform the entire attack. As described in Figure 2, a full attack is made up of the identification of probing addresses, the construction of an eviction set and the attack phase.

Changing the mapping has an overhead; as well as the misses generated, several write backs and data movements in the cache may also be necessary. To minimize the impact on performance, it is important to select the highest possible remapping interval that guarantees security.

3. Problem Statement

3.1. Motivations

Several works have shown that cache attacks are possible in all levels and all types of cache memory. The Prime+Probe [33] attack was initially performed on first-level data caches to attack AES [5,32,33] or instruction caches [40]. The LLC is a more interesting attack target because adversaries and victims do not need to share the same CPU. Improvements to the Prime+Probe [31,49] technique have allowed it to work on LLCs. Kayaalp et al. [50] further relaxed the assumptions of the attacks and achieved a better resolution. Various extensive survey studies have listed the threats at different cache levels [51,52].

Unlike sharing-based cache attacks, conflict-based cache attacks can be applied in any cache level independently [5,31,33,49,50], even when a secure last-level cache exists. Attacking the L1 cache has some advantages because fewer load instructions are required to fill or evict the L1 cache due to its small size. However, since the difference in access time between L1 and L2 caches in modern processors is only a few cycles, performing L1 cache attacks can be complicated due to noise in the timing measurements.

Therefore, to protect a memory hierarchy against conflict-based cache attacks, the different levels of the memory hierarchy should be protected. This raises the question of which countermeasures should be deployed at each cache level. To mitigate conflict-based attacks, it is essential to prevent eviction set construction through the existing single address elimination [31], group testing [48] and Prime–Prune–Probe [53] algorithms. Cache randomization is an effective technique to mitigate against such attacks (see Section 2.4), but the existing solutions have been mainly designed for LLCs. Therefore, an analysis of the effect of low-level cache randomization on existing attacks would help to determine relevant strategies to secure the entire memory hierarchy.

3.2. Threat Model and Attacker Capabilities

In this paper, we assume the existence of a victim and a spy process running on the same machine. They share lower-level caches, and upper-level caches are assumed to be inclusive. The victim process contains secret information that the spy program attempts to recover without having direct access to this information.

We ignore sharing-based cache attacks in this work because the solution to these would be to remove address sharing in the first place (e.g., disable memory deduplication). We focus on conflict-based cache attacks (see Section 2.3.2), where the attacker causes set conflicts to monitor the victim’s access patterns. To study the effectiveness of our defense techniques against conflict-based cache attacks, we assume a scenario that is favorable to the attacker and show that our defenses are effective even under weaker assumptions. To enable a strong attacker model, we assume that there are no sources of interferences (e.g., other processes running concurrently) that could affect the results of the eviction set construction algorithms, which improves the reproducibility of the attacks.

4. Eviction Set Construction Algorithms

This section describes the existing techniques for constructing a set of addresses that are mapped to the same cache set, which is called an eviction set. To perform a conflict-based cache attack, the size of the eviction set needs to be as small as possible. While a larger eviction set has more chances to evict the target access, accessing more addresses is slower and can generate noise.

We now introduce several definitions that are used throughout the rest of this paper:

Definition 1.

Congruent Addresses: Two virtual addresses x and y are said to be congruent when they both fall into the same cache set and the same cache slice;

Definition 2.

Eviction set: A set of virtual addresses E is an eviction set for a target address x when $x\notin E$ and at least $a\ge W$ addresses in E are congruent with x, where W is the number of cache ways.

4.1. Candidate Set

Some eviction set construction algorithms require an initial set of virtual addresses, which is called a candidate set. A candidate set is a set of virtual addresses that has a good chance of falling into the target cache set.

An unprivileged process does not have full control over the cache placement, especially in a large last-level cache. Indeed, as we show in Figure 4, the upper address bits are used to determine the set and the slice that are selected by the operating system through its page allocation mechanism. On Linux, it has been shown that the buddy allocator can be tricked into allocating continuous chunks of memory [54], but page allocation can usually be viewed as a random oracle. Therefore, a candidate set can be built by fixing the controlled bits of the set index to the correct value and selecting many multiples of this address. The use of huge pages (2 MB or 1 GB), either with privileges or through transparent huge pages [55], can increase the number of controlled bits in the address (In general, huge pages can only be requested by privileged processes).

Suppose that the process has no control over virtual addresses (e.g., the address mapping is randomized); in that case, addresses have to be selected randomly. For a candidate set to be used as an eviction set, the collection of n virtual addresses must satisfy Definition 2. Let X be a random variable representing the number of congruent addresses found in a set of n virtual addresses. According to [48], with $p=\frac{1}{S}$ (where S is the number of sets), the probability of having at least a congruent addresses in a candidate set of size n is given by:

$$P(X\ge a)=1-\sum _{i=0}^{a-1}\left(\begin{array}{c}n\\ i\end{array}\right)p^i{(1-p)}^{n-i}$$

(1)

4.2. Eviction Set Construction Algorithms

Algorithms for constructing eviction sets aim to find the congruent addresses in a candidate set and discard all other addresses that do not affect the eviction of the target address x (non-congruent addresses). In this section, we describe the different state-of-the-art eviction set construction algorithms.

4.2.1. Single Address Elimination Algorithm

The single address elimination algorithm (SAE) was introduced by Yarom et al. in [31] to perform Prime+Probe attacks on last-level caches (see Algorithm 1). The algorithm takes a virtual address x and a candidate set C as input. For each element $c\in C$, the algorithm tests whether the candidate set is still an eviction set without c (lines three and four). When the test succeeds, the address c is removed from C (line six). When the test does not succeed, the address c is considered necessary for E to be an eviction set. Then, the address is added to E and the algorithm keeps the iteration, as long as the eviction set E is smaller than the number of ways W (line two). The single address elimination method optimizes an eviction set in $\mathcal{O}\left(n^2\right)$ memory accesses, where n is the candidate set size. This implies that the number of memory accesses grows quadratically with the size of the candidate set.

Algorithm 1: The single address elimination algorithm.

Input: C = candidate set, x = target address Output: E = minimal eviction set 1 $E\leftarrow \left\{\right\}$ 2 while$\left|E\right|<W$do$\phantom{(}$ 3   $c\leftarrow \mathrm{pick}\mathrm{one}\mathrm{address}\mathrm{from}C$ 4   if $E\cup C\backslash \left\{c\right\}$ does not evict x then 5    $\phantom{(}$$E\leftarrow E\cup \left\{c\right\}$ 6    $C\leftarrow C\backslash \left\{c\right\}$ 7 end$\phantom{(}$ 8 returnE

4.2.2. Group Testing Algorithm

The group testing (GT) algorithm [48] is an optimization of the single address elimination method (see Algorithm 2). In the group testing algorithm, the initial candidate set is split into $W+1$ groups (line two). The algorithm iterates over all groups and tests whether E without the group still evicts x (lines three and four). When this is true, the group is removed from E (line five). In the other case, the algorithm tests other groups until it finds one that satisfies this requirement. Then, E is divided into $W+1$ groups again and the same process starts over. This is repeated until there are $W+1$ elements left in E (line one). In this way, an entire group of addresses can be eliminated per iteration instead of just one element, as in the single address elimination algorithm. The group testing method requires $\mathcal{O}\left(W^{2}n\right)$ cache accesses.

Algorithm 2: The group testing algorithm.

Input: E = candidate set, x = target address Output: E = minimal eviction set 1 while$\left|E\right|$ > Wdo$\phantom{(}$ 2   $\{{\mathrm{T}}_0\dots {\mathrm{T}}_{\mathrm{W}+1}\}\leftarrow \mathrm{split}E\mathrm{into}W+1\mathrm{groups}$ 3   for $i\leftarrow 1$ to $W+1$ do 4    $\phantom{(}$if $E\backslash \left\{{\mathrm{T}}_{\mathrm{i}}\right\}$ evict x then 5     $\phantom{(}$$E\leftarrow E\backslash \left\{{\mathrm{T}}_{\mathrm{i}}\right\}$ 6   end 7 end$\phantom{(}$ 8 returnE

4.2.3. Prime–Prune–Probe Algorithm

The Prime–Prune–Probe (PPP) [53] algorithm has shown that faster eviction set construction is possible. As shown in Algorithm 3, the PPP technique begins with the Prime step, where the attacker generates a set of random addresses and accesses them to fill in either a subset or the entire cache, i.e., the candidate set. To eliminate false positives, the attacker accesses the candidate set again in the Prune step and removes any addresses that result in a high access latency. This process is repeated many times to remove self-evicted addresses until all remaining addresses in the Prime set are concurrently cached. Regarding the number of cache accesses, our experiments showed that the pruning process is normally completed in fewer than two rounds. After pruning, the PPP returns a set of $n^{\prime }$ addresses, where $n^{\prime }$ is less than or equal to the initial size n. The pruning step aims to absorb noise so that congruent addresses can be more easily identified in the Probe step. These three steps are repeated until enough congruent addresses are found and added to E.

Algorithm 3: The Prime–Prune–Probe algorithm.

Input: n = candidate set size, x = target address  Output: E = minimal eviction set 1 $E\leftarrow \left\{\right\}$ 2 while True do$\phantom{(}$ 3  $C\leftarrow \mathrm{generate}\mathrm{n}\mathrm{random}\mathrm{addresses}$   /*$\phantom{(}$ Prime step $\phantom{(}$ */ 4   Access $C\cup E$   /*$\phantom{(}$ Prune process $\phantom{(}$ */ 5  while they are no self-eviction in $C\cup E$ do$\phantom{(}$ 6   for each $c\in C$ do$\phantom{(}$ 7     if $\mathit{get}\mathit{latency}\mathit{to}\mathit{access}c>threshold$ then 8       $\phantom{(}$$C\leftarrow C\backslash \left\{c\right\}$ 9   end$\phantom{(}$ 10  end$\phantom{(}$   /*$\phantom{(}$ Probe step $\phantom{(}$ */ 11  for each $c\in C$ do$\phantom{(}$ 12    if $\mathit{latency}\mathit{to}\mathit{access}c>threshold$ then 13      $\phantom{(}$$E\leftarrow E\cup \left\{c\right\}$ 14  end$\phantom{(}$   /*$\phantom{(}$ Test eviction $\phantom{(}$ */ 15  if E evict x then$\phantom{(}$ 16    break 17 end$\phantom{(}$ 18 return E

This algorithm can be used to find eviction sets in LLCs using different replacement policies. The number of cache accesses is estimated as $\mathcal{O}\left(SW\right)$ when the LLC uses an LRU as the replacement policy, i.e., the smallest of the three fast algorithms. However, when using a random replacement policy, the number of cache accesses increases to $\mathcal{O}(W\times n)$. This increase in complexity is due to the candidate set size after the pruning step being much smaller than the cache size $SW$. Using a small set of addresses reduces the chance of finding a congruent address in each PPP iteration.

5. Analysis of Eviction Set Construction Algorithms

In this section, we present the cache simulation framework that we used to study the behavior of the eviction set construction algorithms. We used it to evaluate the complexity of building an eviction set in a noise-free environment with unprotected and randomized caches.

5.1. Evaluation Framework

5.1.1. Simulation Framework Overview

Modern micro-architectures include many optimization features, such as hardware prefetching, TLBs, buses, etc. These optimizations allow programs to run faster and more effectively. However, they introduce noise into the attacker’s observations, making the construction of eviction sets less reliable. In this work, a noise-free cache model was adopted to analyze the complexity of systematically finding eviction sets. This cache framework abstracted the implementation details of the hardware and simulated only the behavior of the memory hierarchy. The cache model was written in Python and had the following features:

• Constant access latency: The latency to access a cache block was the same regardless of its location (set, way or slice);
• Ideal cache hit/miss state: Without latency, a given process could accurately determine the state of a cache block (hit or miss). This eliminated errors due to the access latency measurements on the actual processors. For each memory access, our framework returned the address state (i.e., present or not) in all cache levels of the memory hierarchy and indicated whether it was a miss or a hit;
• Replacement policies: The cache framework supported two replacement policies: the least recently used (LRU) policy and the random policy. The LRU policy maintained a list containing the order in which the cache ways were accessed. When a cache set needed to be filled, the least used cache way was chosen. As its name suggests, the random policy randomly selected a way from the target set;
• No translation lookaside buffer (TLB) noise: Accessing a large candidate set could trigger false positive errors when the TLB entries were mistakenly removed from the TLB [56]. To ignore this effect, we did not model the memory management unit (MMU) or the TLB component;
• No cache prefetching: The hardware prefetchers were used to improve performance by predicting the next memory addresses that would be accessed. However, they introduced noise into the attacker’s observations by accessing unnecessary memory addresses [57]. Thus, the framework did not support model prefetching;
• Address randomization of caches: Address randomization could be enabled at any cache level. The framework used a keyed cryptographic function to distribute the addresses among all cache sets (see Section 6.1). It also supported a configurable remapping interval that changed the address to set mapping after a certain number of memory accesses.

The cache framework also implemented performance counters that could be used to measure the various side effects of the simulated applications. For example, they could provide information about the number of accesses, misses, hits, evictions and more. The performance counters were implemented in each cache level to evaluate and analyze the behavior of the eviction set construction algorithms. The performance counters of each level could be reset or loaded at any time.

5.1.2. Simulation Example

To simulate the behavior of an application in our cache framework, we first built a memory hierarchy by specifying the configuration of each cache level. We needed to specify the addressing used for each cache level, their cache sizes, the size of the cache lines, the number of ways, the replacement policy, etc. To understand how this worked, let us demonstrate the example in Listing 1, which shows the implementation of the single address elimination method to find an eviction set for the target address in the candidate set. At each iteration, the single address elimination function called the test eviction function (line 12) to verify that the candidate set still evicted the target address.

To interact with the cache framework, the single address elimination implementation used memory access instructions, such as the load and the write instructions. Both instructions could be used to determine the cache status (hit or miss) of the accessed address. For example, in line four, the instruction load_state was used to return the cache status of the specified address (hit or miss).

Listing 1.

The implementation of the single address elimination algorithm with our cache simulation framework.

5.2. Behavior Analysis of Eviction Set Construction

5.2.1. Experimental Setup

To investigate how the algorithms constructed their eviction sets, we used our noise-free cache simulator to create a two-level memory hierarchy where the last-level cache was shared. We used a baseline configuration where the target memory hierarchy did not contain any defense techniques (as shown in

Table 1. The baseline configuration.

Parameters	L1 Cache	L2 Cache
Cache size	32 kB	1 MB
Associativity	8 ways	16 ways
Cache line size	64 B	64 B
Inclusion policy	Inclusive	Inclusive
Replacement policy	LRU	LRU

).

We implemented the algorithms described in Section 4 in the form of Python classes. These algorithms used the memory access instructions provided by our framework to simulate their behavior in a noise-free environment. To evaluate the success rate of each eviction set construction algorithm in a given setting, we ran them 1000 times with different candidate sets and recorded the results for later analysis.

More precisely, in each simulation: (1) We reset the performance counters and the content of each cache level; (2) We generated a candidate set with the input size and a target address. For a 32-bit address, the elements of the candidate set and the target addresses were random addresses between 0 and $2^{32}-1$; (3) Then, we ran the eviction set construction algorithm with the generated candidate set; (4) We tested the minimal eviction set returned by the algorithm. The algorithm was considered successful when it could evict the target address from the memory hierarchy; (5) We stored the performance counters and the execution time. At the end of all of the simulations, we computed the success rate. Then, we computed the median for each statistical register after 1000 experiments. The value of 1000 was the highest number of repetitions that allowed the simulations to be performed within a few days on a 48-core machine.

5.2.2. Single Address Elimination Algorithm

Figure 5 shows the success rate and the time required to construct an eviction set from the different sized candidate sets using the single address elimination algorithm. As shown in Figure 5a, the success rate increased when the size of the candidate set contained more than 10,000 addresses.

Due to the quadratic complexity of the algorithm, the simulations took a long time to find an eviction set. As shown in Figure 5b, the execution time could grow up to 160 s per simulation, which resulted in the algorithm needing more than two days to simulate a candidate set with 20,000 addresses.

5.2.3. Group Testing Algorithm

Figure 6 depicts the probability of finding an eviction set as a function of the candidate set size using the group testing algorithm. As shown by the theoretical curve (see Equation (1)), the probability of finding a candidate set with at least W congruent addresses increased with its size. The experiment results show that when the candidate set had at least W addresses, the group testing algorithm could reduce its size to construct a valid eviction set. Furthermore, it can be observed that group testing reduction in a noise-free environment closely matched the theoretical prediction. Vila et al. [48] observed similar trends in a real system.

5.2.4. Prime–Prune–Probe Algorithm

Figure 7 depicts the success rate of the PPP algorithm as a function of the candidate set size. As shown, the PPP algorithm built an eviction set from smaller candidate sets and therefore, was faster than the group testing algorithm. This was due to the use of different candidate sets in each iteration (see Algorithm 3). Intuitively, we expected that by increasing the candidate set size n, the success rate of the algorithm would keep increasing. Our experiments suggested the opposite in the case of PPP, as shown in Figure 7. When the size of the candidate set was greater than $2N$ ($N=SW$ being the number of cache lines), we found that the algorithm failed to find an eviction set despite the presence of sufficient congruent addresses in the candidate set. This effect is not studied in [53].

By analyzing the memory accesses of the Prime–Prune–Probe algorithm, we observed that the Prune filter became more aggressive when the candidate set contained more than W congruent addresses among the n elements. It turns out that it removed all congruent addresses from the candidate set. Consequently, the algorithm could not detect collisions within the victim’s accesses.

Figure 8 illustrates this effect by using a small cache memory with an LRU replacement policy. We used the Prime–Prune–Probe algorithm to construct a minimal eviction set targeting set one. As shown in the first step, the attacker accessed the candidate set containing four congruent addresses. Since the cache was a two-way set-associative cache, the cache memory only contained the last congruent addresses (addresses C and D) in set one after the Prime step. In the Prune step, the attacker accessed the same candidate set again and removed the missing addresses from the candidate set to avoid any noise caused by self-eviction. Since the first two addresses, A and B, were evicted from the cache, the Prune filter found them missing from the cache after accessing them. The other two congruent addresses, C and D, were then evicted from the cache due to accessing addresses A and B. The Prune filter considered them as missing addresses and therefore, removed them from the candidate set. In this case, all congruent addresses were removed from the candidate set, which explains why the Prime–Prune–Probe algorithm failed when the candidate set was large.

6. Randomization in Low-Level Caches

In this section, we analyze the security implications of randomizing low-level caches. This study excluded the single address elimination algorithm because it took too long to run in the relevant parameter range. First, we estimated the remapping interval for the group testing algorithm and the Prime–Prune–Probe algorithm in the baseline configuration (unprotected memory hierarchy). To protect caches against these algorithms using random mapping, the remapping interval had to be chosen carefully. Changing the memory mapping invalidated congruent addresses that had already been collected by these algorithms.

The remapping interval for address randomization was expressed as the number of memory accesses. To ensure security, it had to be less than the minimum number of memory accesses required to create a reliable eviction set. Starting from the baseline configuration, we applied address randomization to L1 caches in the noise-free simulation framework. We then evaluated the success rate of each algorithm under dynamically randomized caches using the precomputed remapping interval.

6.1. Choice of the Addressing Function

In our experiments, we modelled an ideal address randomization. The motivation was to prevent any “shortcut attacks” [53] that could break the randomization function.

Therefore, to perform address randomization, we used a 128-bit AES cipher to perform the address randomization. When a request was made to the cache, the address went through an AES instance and the low bits of the output were selected to determine the set. The 128-bit AES key was private to each cache and to perform a remapping, a new pseudo-random key was generated by the simulator.

We stress that using such a strong randomization function in L1 caches may not be realistic in practice. Any delays introduced into L1 requests would turn into significant slowdowns. The design of a lightweight, secure and optimized hardware address randomization function is a complex topic that is not covered in this paper. As an illustration, the low-latency cipher designed in the CEASER architecture [20,58] is completely unsafe to use [17]. Using an AES-128 function to randomize the cache mapping deferred the problem of designing a safe and lightweight permutation function, but its integration into a hardware cache and the design of a lightweight alternative with similar properties are still open problems.

6.2. Remapping Interval Analysis

This section aims to estimate the remapping interval needed to dynamically randomize an L1 cache. To estimate this interval, we reproduced the experiments performed in Section 5 to estimate the number of accesses required to find a usable eviction set. As described earlier, each experiment was repeated 1000 times to compute the success rate of each algorithm. At the end of each experiment, we obtained an array containing the number of memory accesses for each repetition. After determining the median of all of the experiments for each candidate set size and their success rates, we computed the minimum number of memory accesses required to achieve a success rate of at most $\lambda$, with $\lambda$ varying from 0 to 1.

In Figure 9, we plot the number of memory accesses needed to construct an eviction set as a function of the success rate for the group testing and Prime–Prune–Probe algorithms. For each success rate $\lambda$, we returned the median of the different experiments with success rates of lower than $\lambda$. Then, we computed the minimum number of memory accesses.

Since we did not want the attacker to construct an eviction set using the group testing algorithm, the remapping interval had to be at most 260 K memory accesses to ensure a success rate of less than 1% (see Figure 9a). Regarding the number of memory accesses, we noted that the group testing algorithm required more memory accesses to construct a valid eviction set. In contrast, PPP could create an eviction set with a small candidate set at each iteration, resulting in fewer memory accesses. As shown in Figure 9b, PPP took less time to construct an eviction set than the group testing algorithm. The minimum number of memory accesses was consistent for all experiments. This occurred because the PPP algorithm required a small candidate set for each iteration and found at least one congruent address for each candidate set. However, using a small candidate set in each iteration increased the success rate of the PPP algorithm. Consequently, the remapping interval of the PPP algorithm had to be fewer than 47.6 K memory accesses to guarantee a success rate of less than 1% for constructing a reliable eviction set.

6.3. Randomization of L1 Cache

Previously, we showed that the group testing and Prime–Prune–Probe algorithms required 260 K and 47.6 K memory accesses, respectively, to construct an eviction set with a success rate of $\lambda \ge 1\%$ in the unprotected memory hierarchy.

As shown in Figure 10a, the group testing algorithm with the baseline configuration was successful in finding an eviction set when the candidate set size contained more than 30 K addresses with a success rate of 100%. When using a dynamically randomized L1 cache with a remapping frequency of 260 K memory accesses, the results show that the group testing algorithm failed to find a useful eviction set. Indeed, we can observe a consistent success rate of less than $1\%$ in Figure 10. This was because a single candidate set was used throughout the overall construction process. The randomization in the L1 cache interfered with the operation of this algorithm and distorted its results.

On the other hand, randomization in the L1 cache did not affect its success rate of the Prime–Prune–Probe algorithm (see Figure 11a), which generated a new candidate set at each iteration, even when the remapping changed every 30 k memory accesses.

Note that the primary purpose of these algorithms was to find at least W congruent addresses. To verify this assumption for the resulting eviction sets in Figure 10a and Figure 11a, we extracted the resulting eviction set and the number of congruent addresses it contained for each experiment. Figure 10b and Figure 11b show the resulting number of congruent addresses for the group testing algorithm and the Prime–Prune–Probe algorithm, respectively. When the group-testing algorithm was used, we can see in Figure 10b that the resulting eviction set had fewer congruent addresses than the number of ways (in our case, we targeted a cache with 16 ways), even for a large candidate set that should have contained more congruent addresses. This lack of congruent addresses in the eviction set resulted in the target address not being evicted, which confirmed our results in Figure 10a. For the Prime–Prune–Probe algorithm (see Figure 11b), we observed that for a candidate set of between 10 K and 26 K, the algorithm could find sufficient congruent addresses to form a valid eviction set. We also noted that the inability of this algorithm to find an eviction set when the candidate set size was greater than 32 K was due to the small number of congruent addresses in the resulting eviction set.

7. Random Eviction Last-Level Cache

7.1. Overview

As described in Section 6, the Prime–Prune–Probe could bypass randomized lower-level caches by observing the last-level cache eviction patterns. This algorithm used a Prune filter to remove all addresses that were subject to self-eviction. At the end of the Prune filter, the candidate set should not have contained any addresses that collided with each other. In this way, a purely deterministic decision could be made about which cache set was accessed in the Probe phase. This algorithm could then determine eviction sets in the shortest possible time by bypassing randomization, even when the mapping changed more frequently. Thus, it seemed natural to add random evictions in the last-level cache to disturb the Prune filter’s operation. This should have made it more difficult (ideally impossible) for an attacker to construct an eviction set.

The concept of adding non-deterministic eviction is well known [59,60]. The idea is to evict one or more lines randomly from the cache at a given interval of time. We can use the Prime+Probe attack as an example to understand the intuition behind it. During the Probe step, the attacker accesses the eviction set and measures the memory access latency. In this way, the attacker can determine which cache sets the victim has accessed. However, when the cache eviction is not deterministic, the attacker cannot know whether the cache line was evicted randomly by the random eviction policy or by the victim’s accesses. This can make the attacker’s observations noisy and thus, mitigate against conflict-based cache attacks.

We added a random eviction mechanism to the last-level cache model of our simulation framework. It supported two security parameters: the eviction frequency f and the number of evicted lines n. Every f memory accesses, n cache lines were randomly generated. For example, for a cache with the random eviction strategy parameters $(f,n)=(5,1)$, a random cache line would be evicted every five memory accesses. Intuitively, the lower the eviction frequency, the more robust the cache. Depending on the two values of f and n, the performance counters were used to count the number of memory accesses. Every f accesses, a pseudo-random number generator generated a random cache set and a cache way for each line among the n. After the requests were sent to the cache, when the line was found in the cache and modified, it was written back to the upper-level caches or to the main memory to ensure memory coherence. Otherwise, it was sufficient to invalidate the cache line by setting the validity bit to 0.

7.2. Results and Discussion

To evaluate the resilience of the random eviction strategy against the Prime–Prune–Probe algorithm, we evaluated the success rate of this algorithm as a function of the two parameters f and n. For this purpose, we modelled a two-level cache memory hierarchy. The size, associativity number and replacement policy of each cache level were the same as in the previous analysis (see Section 5). To provide security against the group testing algorithm, we used a L1 cache with a dynamically random addressing policy and a remapping frequency of 260 K memory accesses. For the last cache level, we enabled the random eviction policy.

To evaluate the success rate for each parameter of the random eviction strategy, we ran the Prime–Prune–Probe algorithm 100 times. According to the analysis results in Section 6, the size of the candidate set was fixed at 20 K. Thus, the Prime–Prune–Probe algorithm had a probability of 100% of being successful. Figure 12 shows the success rate of this algorithm for different eviction frequencies and different numbers of lines to be evicted. As shown in Figure 12, the success rate was about 0% when the frequency of eviction was low. When the eviction frequency increased, the success rate started to increase. However, a small eviction frequency increased the miss rate, which drastically degraded the performance. Therefore, the eviction frequency and the number of evicted lines should be carefully chosen so as not to compromise security and performance. For example, suppose we evict 16 cache lines per 20 K memory accesses; in that case, the success rate of the Prime–Prune–Probe algorithm would be reduced from 100% to 4%.

The reason for the decrease in the success rate when using the Prime–Prune–Probe algorithm was that the pruning filter became more aggressive. During the pruning phase, the attacker re-accessed the candidate set in multiple iterations (three iterations at most for a cache with no countermeasures [53]) to eliminate the addresses that evicted others. In this way, the attacker could determine which cache sets were accessed by the victim. However, when the random eviction strategy was enabled, the pruning filter ran many times due to the unexpected evictions that were not caused by cache collisions. In this case, the pruning filter became aggressive and removed congruent addresses from the candidate set. Even when the attacker succeeded in constructing eviction sets and observing that the cache line had been evicted, it could not know whether the line was randomly evicted by the random eviction policy or by the victim’s accesses. This prevented the attacker from creating minimal eviction sets.

8. Related Work

Our work was concerned with analyzing and developing an efficient solution to mitigate against conflict-based cache attacks. There are some research studies that have addressed this problem. In this section, we only focus on the most relevant and closely related designs, which all propose hardware changes in the cache architecture.

Wang and Lee [15] proposed an RP cache to randomize cache mapping by using an indirection table. This table stores the correspondence of the cache sets. The address set is first used to index the indirection table for each cache access. Then, the returned cache set is used to access the cache memory. Such a design is linearly scaleable in terms of cache sets and the number of concurrent applications. Therefore, it is not suitable for larger caches. Moreover, the effectiveness of table-based randomization schemes depends on the OS to assign different hardware process identifiers and classify applications into protected and unprotected applications.

ScrambleCache [16] was proposed to dynamically randomize L1 caches using a lightweight permutation function that depends on a pseudo-random key. The ScrambleCache frequently changes the cache mapping to prevent prime+probe attacks. The authors use a history table to store the previously used pseudo-random keys and reduce the performance overhead caused by the mapping change. The authors show that, for a remapping frequency of 8192 memory accesses, the performance overhead is about 4% in the worst case scenario.

CEASER [20] was proposed to secure the last-level cache with a keyed indexing encryption function. It also requires dynamic remapping to its encryption function to change the mapping and limit the time interval in which an attacker can construct a minimal eviction set. It has been shown that CEASER can defend against attacks that use a eviction set construction algorithm with a complexity of $\mathcal{O}\left(n^2\right)$ when the remapping rate is 1% (on average, one line remapped per 100 accesses). However, for eviction set construction algorithms with a complexity of $\mathcal{O}\left(n\right)$ [58] (e.g., the group testing algorithm), the remapping rate must increase to 35–100%, which results in high-performance overheads. To mitigate against these algorithms, the same authors proposed CEASER-S [58], which uses a skewed-associative cache. In CEASER-S, the cache ways are divided into multiple partitions and each uses a different encryption key. Thus, a cache line for each partition is assigned to a different cache set, making the construction of the minimal eviction set more complicated.

ScatterCache [19] was also proposed to achieve randomization mapping using a key-dependent cryptographic function. Moreover, its mapping function depends on the security domain, where the indexing of the cache set is different and random for each domain. Therefore, a new key may be required at certain intervals to prevent the attacker from creating and using an eviction set to collide with the victim’s access. However, ScatterCache, which claims to tolerate years of attacks, has been broken by more advanced eviction set construction algorithms [61]. Mirage [62] attempts to overcome the weaknesses of ScatterCache by preventing faster eviction set construction algorithms. Mirage is a fully associative cache that uses pointer-based indirection to associate tags with data blocks and vice versa (inspired by V-way Cache [63]). The eviction candidates are randomly selected from all of the lines in the cache that are to be protected against set conflicts.

PhantomCache [64] relies on address randomization by using an efficient hardware hash function and XOR operations to map an incoming cache block to one of eight randomly selected cache sets, increasing the associativity to $8\times W$. Unfortunately, this requires accessing $8\times W$ memory locations for each cache access to check whether an address is stored in the cache, resulting in a high-power overhead of 67%. The authors show that PhantomCache can safely defeat the group testing algorithm; however, its effectiveness over the Prime–Prune–Probe algorithm needs further investigation.

Randomization-based defenses, such as CEASER/-S [20,58] and ScatterCache [19], claim to thwart conflict-based cache attacks. ScatterCache [19] even argues that dynamic remapping is unnecessary due to the complexity of using a skew-associative cache. Song et al. [18] identified the flawed hypothesis in the implementations of ScatterCache and CEASER-S [58]. By exploiting these flaws, the authors succeeded in constructing eviction sets. Both caches are also vulnerable to cryptanalysis, which can be used to construct eviction sets. For example, Bodduna et al. [17] identified invariant bits in the encrypted address that was computed in CEASER/-S [58]. The authors show that these bits can be managed to construct a valid eviction set, even when the mapping changes.

Bao and Srivastava [65] exploited the lower latency of 3D integration technology to implement the random eviction strategy to mitigate against cache-based side-channel attacks. The authors show that such a technique provides inherent security benefits within a 3D cache integration. They investigated a random eviction component that evicts one cache line every five cycles. On average, their experimental results show that such techniques reduce the performance overheads from 10.73% (in a 2D configuration) to around 0.24% (in a 3D integration). The performance overhead is more negligible in 3D integration since the penalty for a cache miss is smaller.

9. Conclusions

This work provides an experimental security analysis of randomly mapped low-level caches using a noise-free cache simulator. Our study tried to determine a suitable remapping interval. We show that, when the mapping changes every 260 K accesses, the success rate of finding an eviction set using the group testing algorithm is less than 1%, leading to improved security against conflict-based cache timing attacks. However, randomizing the lower cache levels does not protect against the Prime–Prune–Probe algorithm. To mitigate against this algorithm, we proposed the use of a random eviction policy in the last cache level, which disrupts the attacker’s observations and undermines the Prune filter. This solution is efficient against the Prime–Prune–Probe algorithm.