Characterization of a Continuous Muon Source for the Non-Destructive and Depth-Selective Elemental Composition Analysis by Muon Induced X- and Gamma-rays
Abstract
1. Introduction
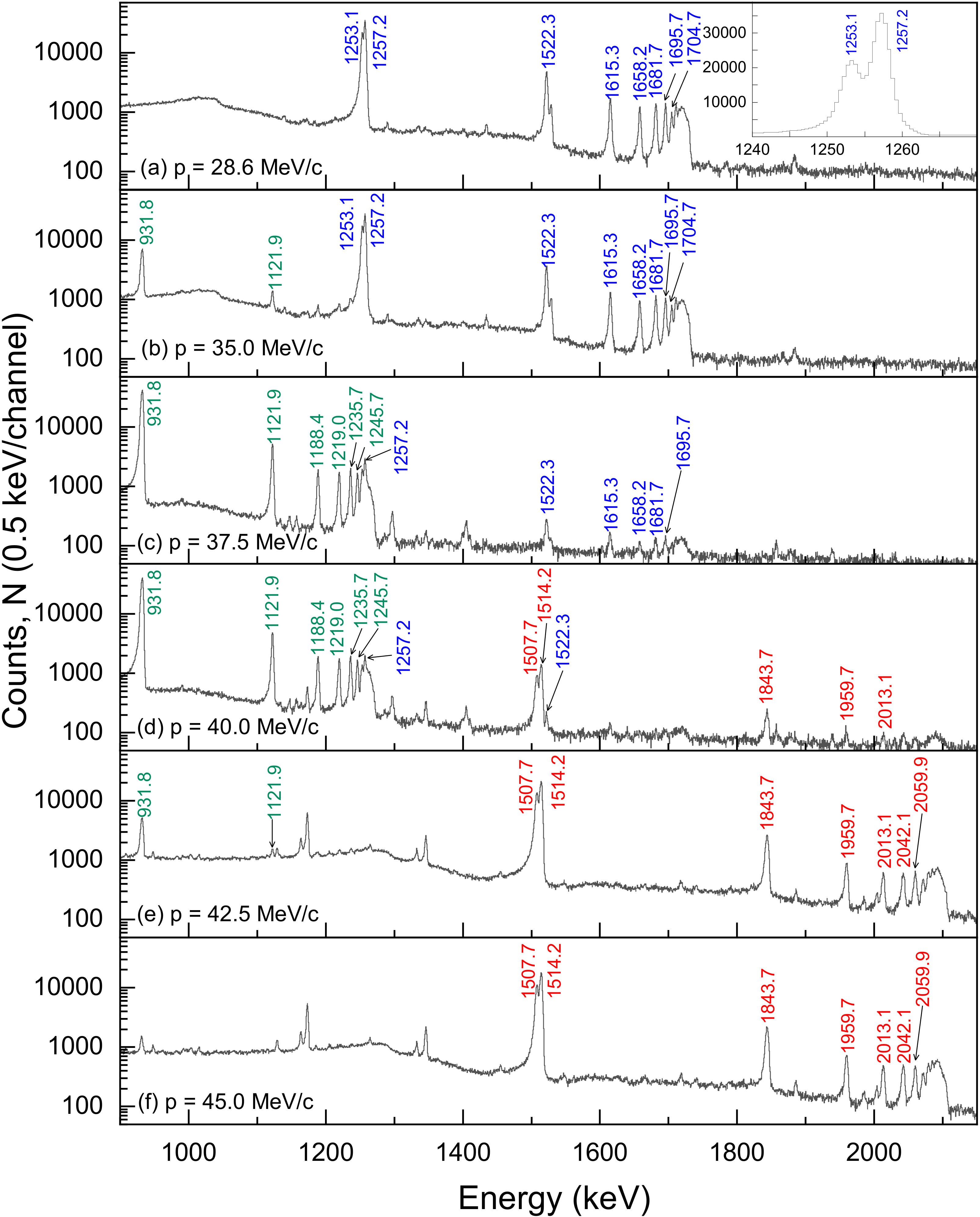
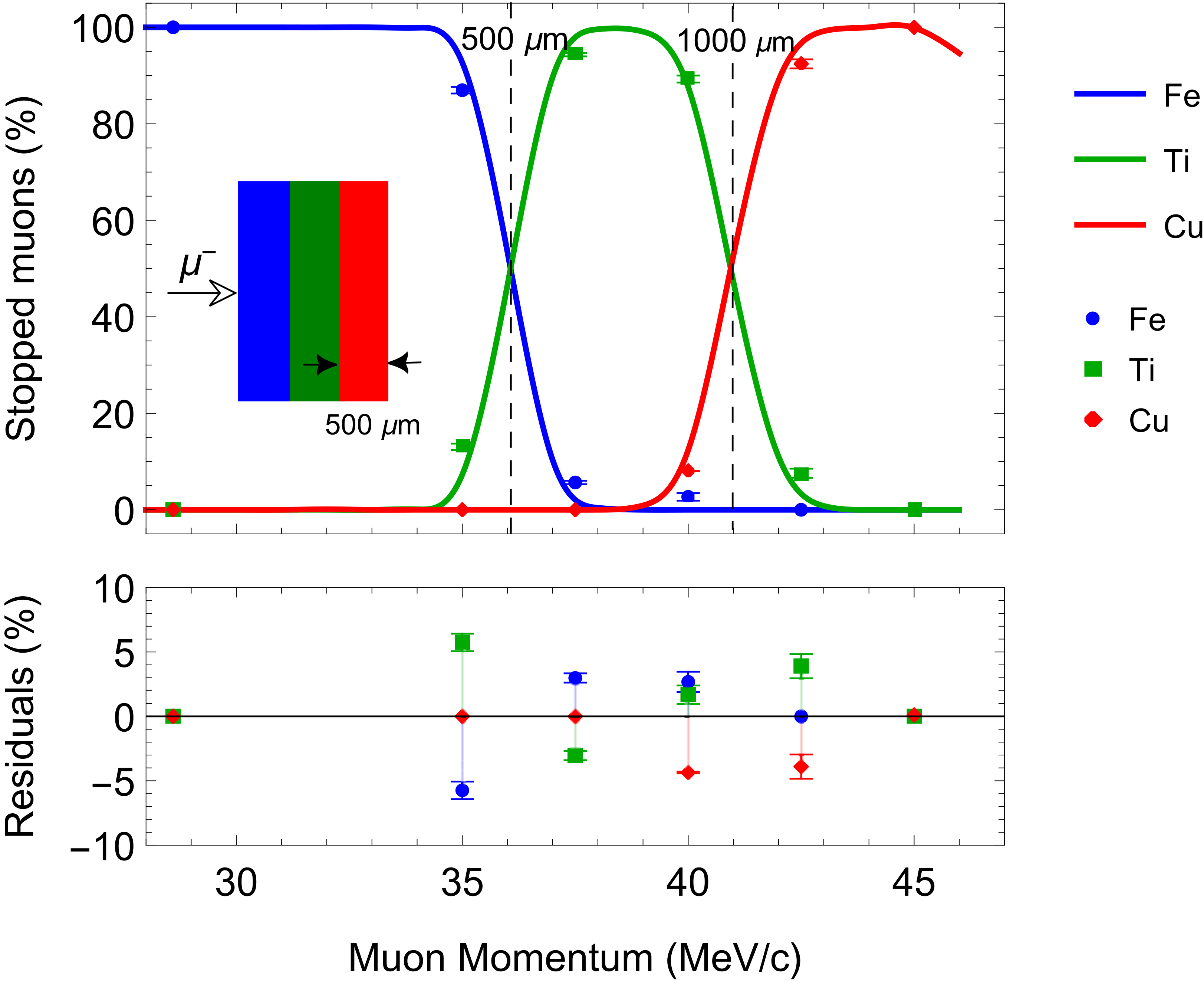
2. The MIXE Technique
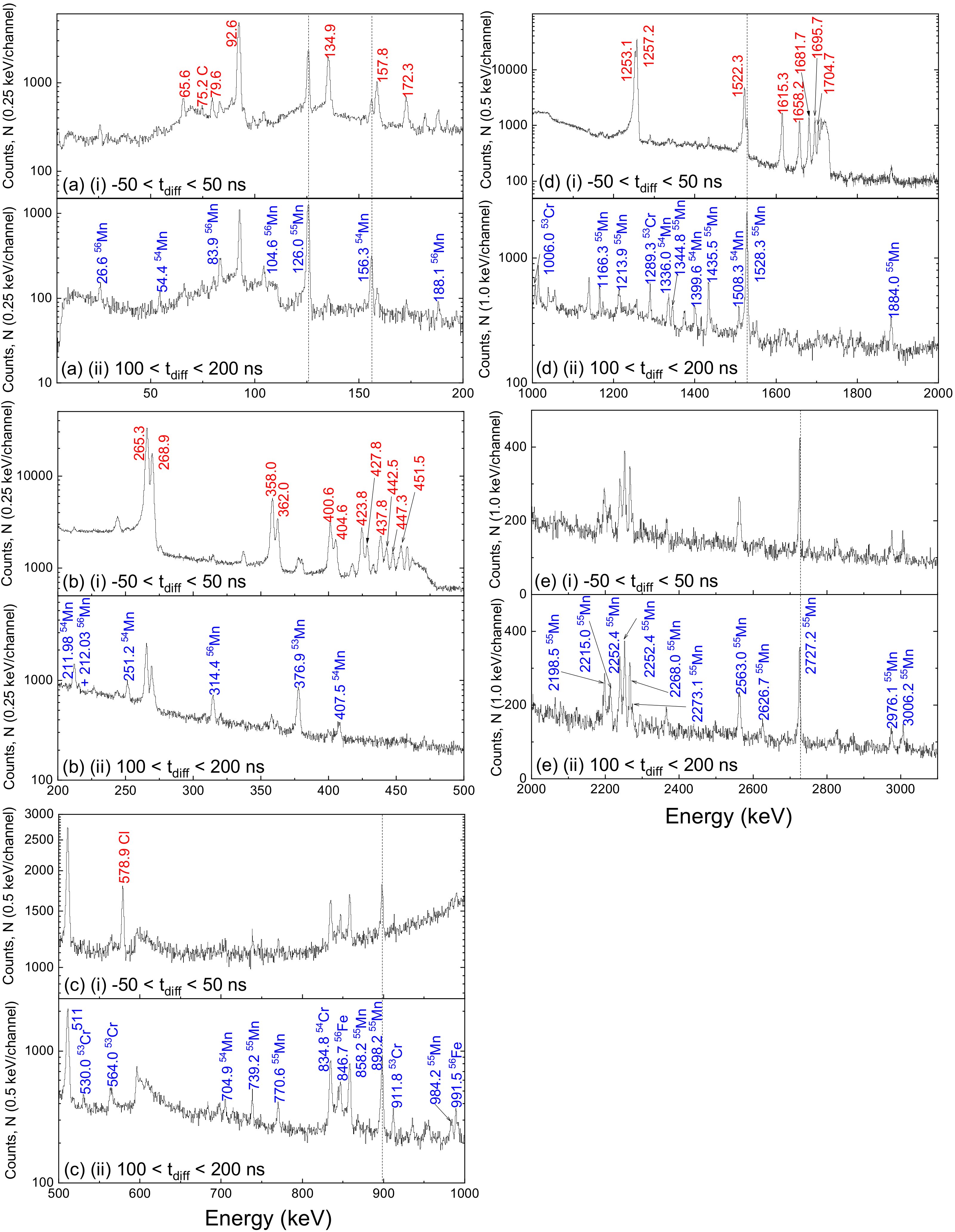
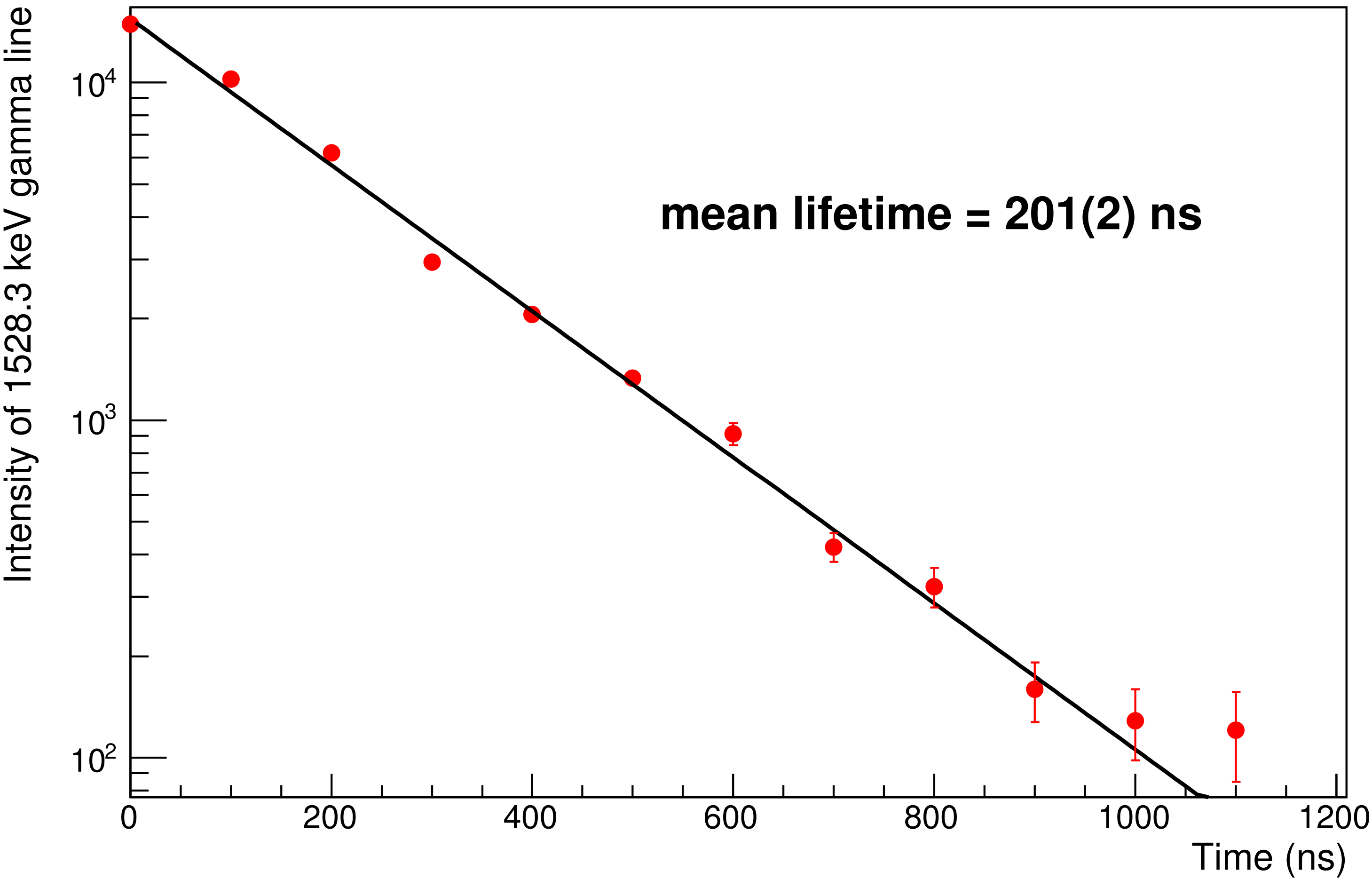
3. Experimental Details and Results
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lannon, J.M., Jr.; Stinespring, C.D. Auger Electron Spectroscopy in Analysis of Surfaces. In Encyclopedia of Analytical Chemistry; American Cancer Society: Carthage, MO, USA, 2006; p. 1. [Google Scholar] [CrossRef]
- Newbury, D.E.; Ritchie, N.W.M. Is Scanning Electron Microscopy/Energy Dispersive X-ray Spectrometry (SEM/EDS) Quantitative? Scanning 2013, 35, 141–168. [Google Scholar] [CrossRef]
- Colton, R.J. Molecular Secondary Ion Mass Spectrometry. J. Vac. Sci. Technol. 1981, 18, 737. [Google Scholar] [CrossRef]
- Barnes, R.M. Inductively coupled plasma atomic emission spectroscopy: A review: In the less than 10 years since the commercial introduction of inductively coupled plasma (ICP) instruments, ICP atomic emission spectroscopy (AES) has developed into one of the most used new analytical tools of the decade. TrAC Trends Anal. Chem. 1981, 1, 51–55. [Google Scholar] [CrossRef]
- Pröfrock, D.; Prange, A. Inductively Coupled PlasmaMass Spectrometry (ICP-MS) for Quantitative Analysis in Environmental and Life Sciences: A Review of Challenges, Solutions, and Trends. Appl. Spectrosc. 2012, 66, 843–868. [Google Scholar] [CrossRef] [PubMed]
- Aziz, M.; Ismail, A. Chapter 5—X-ray Photoelectron Spectroscopy (XPS). In Membrane Characterization; Hilal, N., Ismail, A.F., Matsuura, T., Oatley-Radcliffe, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 81–93. [Google Scholar] [CrossRef]
- Potts, P.J.; Webb, P.C. X-ray fluorescence spectrometry. J. Geochem. Explor. 1992, 44, 251–296. [Google Scholar] [CrossRef]
- Henley, E.; Kassouny, M.; Nelson, J. Proton-induced X-ray emission analysis of single human hair roots. Science 1977, 197, 277–278. [Google Scholar] [CrossRef]
- Herman, M.H. Applications of Rutherford backscattering spectrometry to refractory metal silicide characterization. J. Vac. Sci. Technol. B Microelectron. Process. Phenom. 1984, 2, 748–755. [Google Scholar] [CrossRef]
- Amsel, G.; Lanford, W.A. Nuclear Reaction Techniques in Materials Analysis. Annu. Rev. Nucl. Part. Sci. 1984, 34, 435–460. [Google Scholar] [CrossRef]
- Im, H.J.; Song, K. Applications of Prompt Gamma ray Neutron Activation Analysis: Detection of Illicit Materials. Appl. Spectrosc. Rev. 2009, 44, 317–334. [Google Scholar] [CrossRef]
- Druyan, R.; Mitchell, T.G.; King, E.R.; Spencer, R.P. Neutron Activation Analysis. Radiology 1958, 71, 856–859. [Google Scholar] [CrossRef]
- Trunk, M.; Wetjen, M.; Werner, L.; Gernhäuser, R.; Märkisch, B.; Révay, Z.; Gasteiger, H.; Gilles, R. Materials science applications of Neutron Depth Profiling at the PGAA facility of Heinz Maier-Leibnitz Zentrum. Mater. Charact. 2018, 146, 127–134. [Google Scholar] [CrossRef]
- Reidy, J.J.; Hutson, R.L.; Daniel, H.; Springer, K. Use of muonic X-rays for nondestructive analysis of bulk samples for low Z constituents. Anal. Chem. 1978, 50, 40–44. [Google Scholar] [CrossRef]
- Papa, A. Search for the Lepton Flavour Violation in μ+⟶e+γ. The Calibration Methods for the MEG Experiment. Ph.D. Thesis, Univeristy of Pisa, Edizioni ETS, Pisa, Italy, 2009. [Google Scholar]
- Ninomiya, K. Non-destructive, position-selective, and multi-elemental analysis method involving negative muons. J. Nucl. Radiochem. Sci. 2019, 19, 8–13. [Google Scholar] [CrossRef]
- Ninomiya, K.; Kajino, M.; Inagaki, M.; Terada, K.; Sato, A.; Tomono, D.; Kawashima, Y.; Shinohara, A. Per atom muon capture ratios and effects of molecular structure on muon capture by γ-Fe2O3 and Fe3O4. J. Radioanal. Nucl. Chem. 2020, 324, 403–408. [Google Scholar] [CrossRef]
- Clemenza, M.; Bonesini, M.; Carpinelli, M.; Cremonesi, O.; Fiorini, E.; Gorini, G.; Hillier, A.; Ishida, K.; Menegolli, A.; Mocchiutti, E.; et al. Muonic atom X-ray spectroscopy for non-destructive analysis of archeological samples. J. Radioanal. Nucl. Chem. 2019, 322, 1357–1363. [Google Scholar] [CrossRef]
- Köhler, E.; Bergmann, R.; Daniel, H.; Ehrhart, P.; Hartmann, F. Application of muonic X-ray techniques to the elemental analysis of archeological objects. Nucl. Instrum. Methods Phys. Res. 1981, 187, 563–568. [Google Scholar] [CrossRef]
- Hutson, R.L.; Reidy, J.J.; Springer, K.; Daniel, H.; Knowles, H.B. Tissue Chemical Analysis with Muonic X rays. Radiology 1976, 120, 193–198. [Google Scholar] [CrossRef]
- Taylor, M.C.; Coulson, L.; Phillips, G.C. Observation of Muonic X-rays from Bone. Radiat. Res. 1973, 54, 335–342. [Google Scholar] [CrossRef]
- Terada, K.; Ninomiya, K.; Osawa, T.; Tachibana, S.; Miyake, Y.; Kubo, M.K.; Kawamura, N.; Higemoto, W.; Tsuchiyama, A.; Ebihara, M.; et al. A new X-ray fluorescence spectroscopy for extraterrestrial materials using a muon beam. Sci. Rep. 2014, 4, 5072. [Google Scholar] [CrossRef]
- Ninomiya, K.; Kubo, M.K.; Strasser, P.; Nagatomo, T.; Kobayashi, Y.; Ishida, K.; Higemoto, W.; Kawamura, N.; Shimomura, K.; Miyake, Y.; et al. Elemental Analysis of Bronze Artifacts by Muonic X-ray Spectroscopy. JPS Conf. Proc. 2015, 8, 033005. [Google Scholar] [CrossRef]
- Terada, K.; Sato, A.; Ninomiya, K.; Kawashima, Y.; Shimomura, K.; Yoshida, G.; Kawai, Y.; Osawa, T.; Tachibana, S. Non-destructive elemental analysis of a carbonaceous chondrite with direct current Muon beam at MuSIC. Sci. Rep. 2017, 7, 15478. [Google Scholar] [CrossRef] [PubMed]
- Ninomiya, K.; Kitanaka, M.; Shinohara, A.; Tampo, M.; Miyake, Y.; Sakai, Y.; Kubo, M.K. Muonic X-ray measurements on mixtures of CaO/MgO and Fe3O4/MnO. J. Radioanal. Nucl. Chem. 2018, 316, 1107–1111. [Google Scholar] [CrossRef]
- Umegaki, I.; Higuchi, Y.; Nozaki, H.; Ninomiya, K.; Kubo, M.K.; Tampo, M.; Hamada, K.; Doiuchi, S.; Strasser, P.; Kawamura, N.; et al. Detection of Li in Li-ion Battery Electrode Materials by Muonic X-ray. JPS Conf. Proc. 2018, 21, 011041. [Google Scholar] [CrossRef][Green Version]
- Ninomiya, K.; Kudo, T.; Strasser, P.; Terada, K.; Kawai, Y.; Tampo, M.; Miyake, Y.; Shinohara, A.; Kubo, K.M. Development of non-destructive isotopic analysis methods using muon beams and their application to the analysis of lead. J. Radioanal. Nucl. Chem. 2019, 320, 801–805. [Google Scholar] [CrossRef]
- Umegaki, I.; Higuchi, Y.; Kondo, Y.; Ninomiya, K.; Takeshita, S.; Tampo, M.; Nakano, H.; Oka, H.; Sugiyama, J.; Kubo, M.K.; et al. Nondestructive High-Sensitivity Detections of Metallic Lithium Deposited on a Battery Anode Using Muonic X-rays. Anal. Chem. 2020, 92, 8194–8200. [Google Scholar] [CrossRef]
- Hillier, A.; Paul, D.; Ishida, K. Probing beneath the surface without a scratch—Bulk non-destructive elemental analysis using negative muons. Microchem. J. 2016, 125, 203–207. [Google Scholar] [CrossRef]
- Brown, K.L.; Stockdale, C.P.J.; Luo, H.; Zhao, X.; Li, J.F.; Viehland, D.; Xu, G.; Gehring, P.M.; Ishida, K.; Hillier, A.D.; et al. Depth dependant element analysis of PbMg1/3Nb2/3O3 using muonic X-rays. J. Phys. Condens. Matter 2018, 30, 125703. [Google Scholar] [CrossRef]
- Clemenza, M.; Baldazzi, G.; Ballerini, G.; Bonesini, M.; Carpinelli, M.; Cremonesi, O.; Di Stefano, E.; Fiorini, E.; Gorini, G.; Hillier, A.; et al. CHNET-TANDEM experiment: Use of negative muons at RIKEN-RAL Port4 for elemental characterization of “Nuragic votive ship” samples. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 936, 27–28. [Google Scholar] [CrossRef]
- Hampshire, B.V.; Butcher, K.; Ishida, K.; Green, G.; Paul, D.M.; Hillier, A.D. Using Negative Muons as a Probe for Depth Profiling Silver Roman Coinage. Heritage 2019, 2, 28. [Google Scholar] [CrossRef]
- Aramini, M.; Milanese, C.; Hillier, A.D.; Girella, A.; Horstmann, C.; Klassen, T.; Ishida, K.; Dornheim, M.; Pistidda, C. Using the Emission of Muonic X-rays as a Spectroscopic Tool for the Investigation of the Local Chemistry of Elements. Nanomaterials 2020, 10, 1260. [Google Scholar] [CrossRef]
- Green, G.A.; Ishida, K.; Hampshire, B.V.; Butcher, K.; Pollard, A.; Hillier, A.D. Understanding Roman Gold Coinage Inside Out. J. Archaeol. Sci. 2021, 134, 105470. [Google Scholar] [CrossRef]
- Blundell, S.J.; De Renzi, R.; Lancaster, T.; Pratt, F.L. (Eds.) Muon Spectroscopy—An Introduction; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Sugiyama, J.; Umegaki, I.; Nozaki, H.; Higemoto, W.; Hamada, K.; Takeshita, S.; Koda, A.; Shimomura, K.; Ninomiya, K.; Kubo, M.K. Nuclear Magnetic Field in Solids Detected with Negative-Muon Spin Rotation and Relaxation. Phys. Rev. Lett. 2018, 121, 087202. [Google Scholar] [CrossRef] [PubMed]
- Nagamine, K. Introductory Muon Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Measday, D. The nuclear physics of muon capture. Phys. Rep. 2001, 354, 243–409. [Google Scholar] [CrossRef]
- Anderson, H.L.; Hargrove, C.K.; Hincks, E.P.; McAndrew, J.D.; McKee, R.J.; Barton, R.D.; Kessler, D. Precise Measurement of the Muonic X rays in the Lead Isotopes. Phys. Rev. 1969, 187, 1565–1596. [Google Scholar] [CrossRef]
- Knecht, A.; Skawran, A.; Vogiatzi, S.M. Study of nuclear properties with muonic atoms. Eur. Phys. J. Plus 2020, 135, 777. [Google Scholar] [CrossRef]
- Krauth, J.J.; Schuhmann, K.; Ahmed, M.A.; Amaro, F.D.; Amaro, P.; Biraben, F.; Chen, T.L.; Covita, D.S.; Dax, A.J.; Diepold, M.; et al. Measuring the α-particle charge radius with muonic helium-4 ions. Nature 2021, 589, 527–531. [Google Scholar] [CrossRef]
- Groom, D.E.; Mokhov, N.V.; Striganov, S.I. Muon stopping power and range tables 10 MeV–100 TeV. At. Data Nucl. Data Tables 2001, 78, 183–356. [Google Scholar] [CrossRef]
- Moseley, H.G.J. XCIII. The high-frequency spectra of the elements. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1913, 26, 1024–1034. [Google Scholar] [CrossRef]
- Borie, E.; Rinker, G.A. The energy levels of muonic atoms. Rev. Mod. Phys. 1982, 54, 67–118. [Google Scholar] [CrossRef]
- Suzuki, T.; Measday, D.F.; Roalsvig, J.P. Total nuclear capture rates for negative muons. Phys. Rev. C 1987, 35, 2212–2224. [Google Scholar] [CrossRef]
- Hillier, A.D.; Blundell, S.J.; McKenzie, I.; Umegaki, I.; Shu, L.; Wright, J.A.; Prokscha, T.; Bert, F.; Shimomura, K.; Berlie, A.; et al. Muon spin spectroscopy. Nat. Rev. Methods Prim. 2022, 2, 4. [Google Scholar] [CrossRef]
- Hartmann, F.J.; von Egidy, T.; Bergmann, R.; Kleber, M.; Pfeiffer, H.J.; Springer, K.; Daniel, H. Measurement of the Muonic X-ray Cascade in Metallic Iron. Phys. Rev. Lett. 1976, 37, 331–334. [Google Scholar] [CrossRef]
- Daniel, H.; Denk, W.; Hartmann, F.J.; Wilhelm, W.; von Egidy, T. Empirical Intensity Correlations in Muonic X-ray Spectra of Oxides. Phys. Rev. Lett. 1978, 41, 853–855. [Google Scholar] [CrossRef]
- Von Egidy, T.; Denk, W.; Bergmann, R.; Daniel, H.; Hartmann, F.J.; Reidy, J.J.; Wilhelm, W. Muonic Coulomb capture ratios and X-ray cascades in oxides. Phys. Rev. A 1981, 23, 427–440. [Google Scholar] [CrossRef]
- Grillenberger, J.; Baumgarten, C.; Seidel, M. The High Intensity Proton Accelerator Facility. SciPost Phys. Proc. 2021, 5, 002. [Google Scholar] [CrossRef]
- πE1 Beam Line. Available online: https://www.psi.ch/en/sbl/pie1-beamline (accessed on 30 November 2021).
- Skawran, A.A. Development of a New Method to Perform Muonic Atom Spectroscopy with Microgram Targets. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2021. [Google Scholar]
- Wauters, F.; Knecht, A.; on behalf of the muX collaboration. The muX project. SciPost Phys. Proc. 2021, 5, 022. [Google Scholar] [CrossRef]
- Warr, N.; Van de Walle, J.; Albers, M.; Ames, F.; Bastin, B.; Bauer, C.; Bildstein, V.; Blazhev, A.; Bönig, S.; Bree, N.; et al. The Miniball spectrometer. Eur. Phys. J. A 2013, 49, 40. [Google Scholar] [CrossRef]
- IN2P3/STFC French/UK Ge Pool. Available online: https://gepool.in2p3.fr (accessed on 30 November 2021).
- Morháč, M.; Kliman, J.; Matoušek, V.; Veselský, M.; Turzo, I. Background elimination methods for multidimensional coincidence γ-ray spectra. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 401, 113–132. [Google Scholar] [CrossRef]
- Sato, T.; Iwamoto, Y.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Ichiro Abe, S.; Kai, T.; Tsai, P.E.; Matsuda, N.; Iwase, H.; et al. Features of Particle and Heavy Ion Transport code System (PHITS) version 3.02. J. Nucl. Sci. Technol. 2018, 55, 684–690. [Google Scholar] [CrossRef]
- Iwamoto, Y.; Sato, T.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Ichiro Abe, S.; Kai, T.; Matsuda, N.; Hosoyamada, R.; Niita, K. Benchmark study of the recent version of the PHITS code. J. Nucl. Sci. Technol. 2017, 54, 617–635. [Google Scholar] [CrossRef]
- μ X-rays Catalogue. Available online: http://muxrays.jinr.ru/ (accessed on 30 November 2021).
- Measday, D.F.; Stocki, T.J. γ rays from muon capture in natural Ca, Fe, and Ni. Phys. Rev. C 2006, 73, 045501. [Google Scholar] [CrossRef]
- Evans, H. Gamma-rays following muon capture. Nucl. Phys. A 1973, 207, 379–400. [Google Scholar] [CrossRef]
- Zinatulina, D.; Briançon, C.; Brudanin, V.; Egorov, V.; Perevoshchikov, L.; Shirchenko, M.; Yutlandov, I.; Petitjean, C. Electronic catalogue of muonic X-rays. EPJ Web Conf. 2018, 177, 03006. [Google Scholar] [CrossRef]
- National Nuclear Data Center. Available online: https://www.nndc.bnl.gov/ (accessed on 30 November 2021).
- Sens, J.C. Capture of Negative Muons by Nuclei. Phys. Rev. 1959, 113, 679–687. [Google Scholar] [CrossRef]
- Blair, I.M.; Muirhead, H.; Woodhead, T. A Measurement of the Capture Rate of Negative Muons in Various Elements. Proc. Phys. Soc. 1962, 80, 945–946. [Google Scholar] [CrossRef]
- Eckhause, M.; Siegel, R.; Welsh, R.; Filippas, T. Muon capture rates in complex nuclei. Nucl. Phys. 1966, 81, 575–584. [Google Scholar] [CrossRef]
- Amato, A. MIXE 2018 Fe/Ti/Cu Sandwich Sample Raw Data. Available online: https://doi.org/10.16907/24ee1f7e-f047-4973-95bf-656943d63774 (accessed on 30 November 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswas, S.; Gerchow, L.; Luetkens, H.; Prokscha, T.; Antognini, A.; Berger, N.; Cocolios, T.E.; Dressler, R.; Indelicato, P.; Jungmann, K.; et al. Characterization of a Continuous Muon Source for the Non-Destructive and Depth-Selective Elemental Composition Analysis by Muon Induced X- and Gamma-rays. Appl. Sci. 2022, 12, 2541. https://doi.org/10.3390/app12052541
Biswas S, Gerchow L, Luetkens H, Prokscha T, Antognini A, Berger N, Cocolios TE, Dressler R, Indelicato P, Jungmann K, et al. Characterization of a Continuous Muon Source for the Non-Destructive and Depth-Selective Elemental Composition Analysis by Muon Induced X- and Gamma-rays. Applied Sciences. 2022; 12(5):2541. https://doi.org/10.3390/app12052541
Chicago/Turabian StyleBiswas, Sayani, Lars Gerchow, Hubertus Luetkens, Thomas Prokscha, Aldo Antognini, Niklaus Berger, Thomas Elias Cocolios, Rugard Dressler, Paul Indelicato, Klaus Jungmann, and et al. 2022. "Characterization of a Continuous Muon Source for the Non-Destructive and Depth-Selective Elemental Composition Analysis by Muon Induced X- and Gamma-rays" Applied Sciences 12, no. 5: 2541. https://doi.org/10.3390/app12052541
APA StyleBiswas, S., Gerchow, L., Luetkens, H., Prokscha, T., Antognini, A., Berger, N., Cocolios, T. E., Dressler, R., Indelicato, P., Jungmann, K., Kirch, K., Knecht, A., Papa, A., Pohl, R., Pospelov, M., Rapisarda, E., Reiter, P., Ritjoho, N., Roccia, S., ... Amato, A. (2022). Characterization of a Continuous Muon Source for the Non-Destructive and Depth-Selective Elemental Composition Analysis by Muon Induced X- and Gamma-rays. Applied Sciences, 12(5), 2541. https://doi.org/10.3390/app12052541






