Aerodynamic Behavior and Impact on Driving Safety of Spalling Blocks Comprising High-Speed-Railway Tunnel Lining
Abstract
:1. Introduction
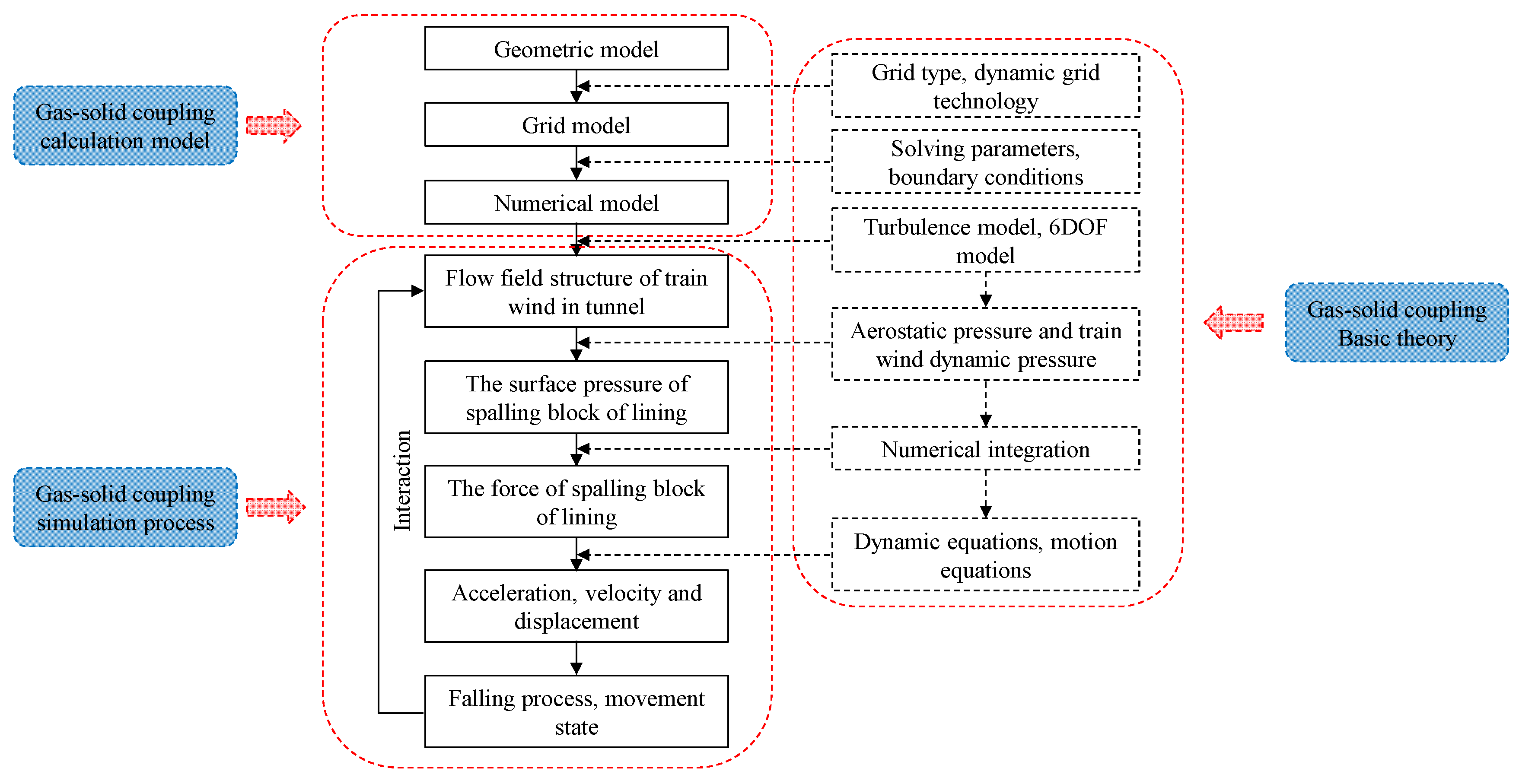
2. Gas–Solid-Coupling Model of Spalling Blocks–Train–Tunnel–Air
2.1. Overview of Aerodynamic Coupling Model
2.2. Basic Theory of Gas–Solid Coupling
- (1)
- Turbulence model
- (2)
- Gas–solid-coupling interaction
2.3. Gas–Solid-Coupling Calculation Model
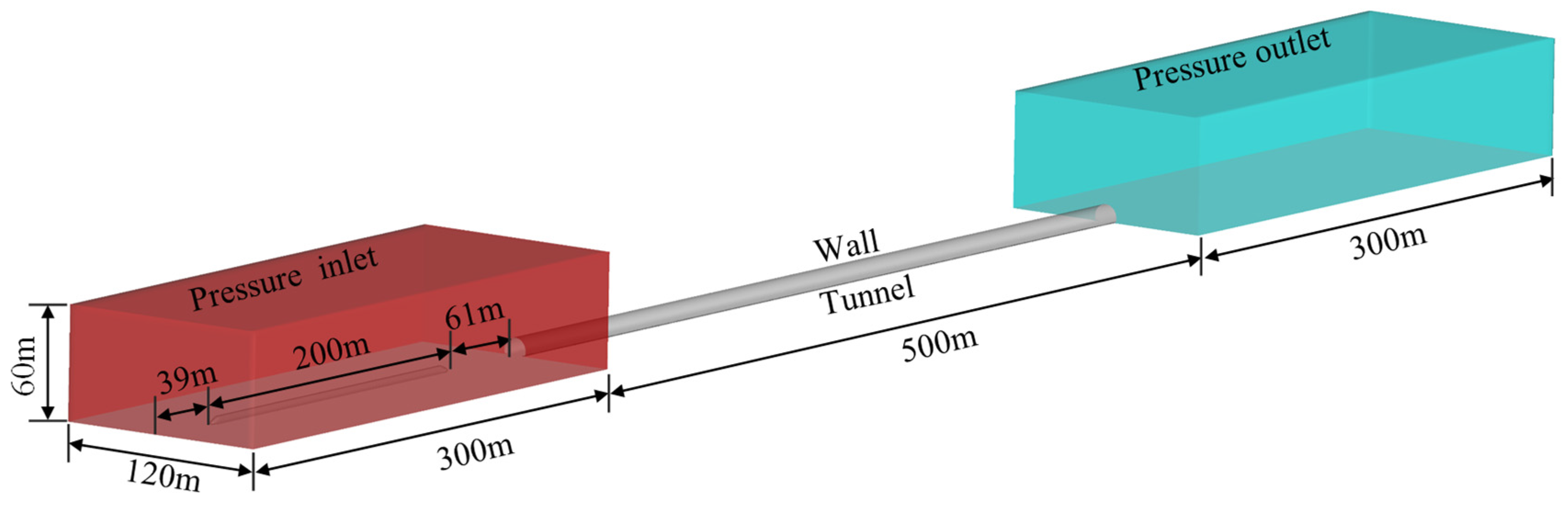
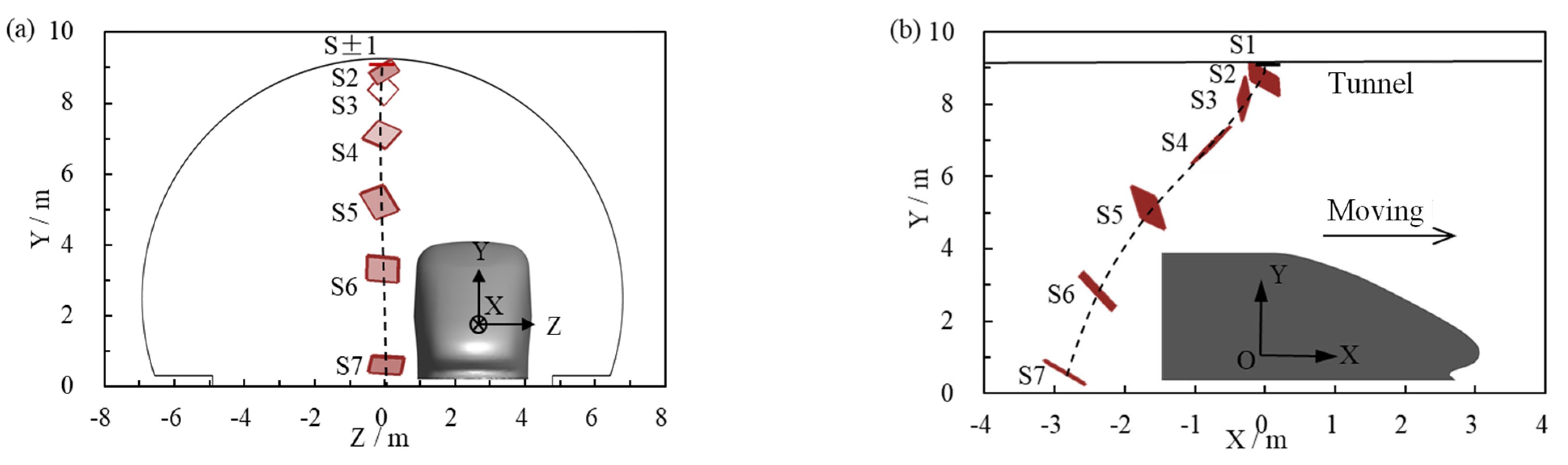
2.3.1. Geometric Model
2.3.2. Grid Model
2.3.3. Boundary Conditions and Solution Settings
2.3.4. Calculation Conditions
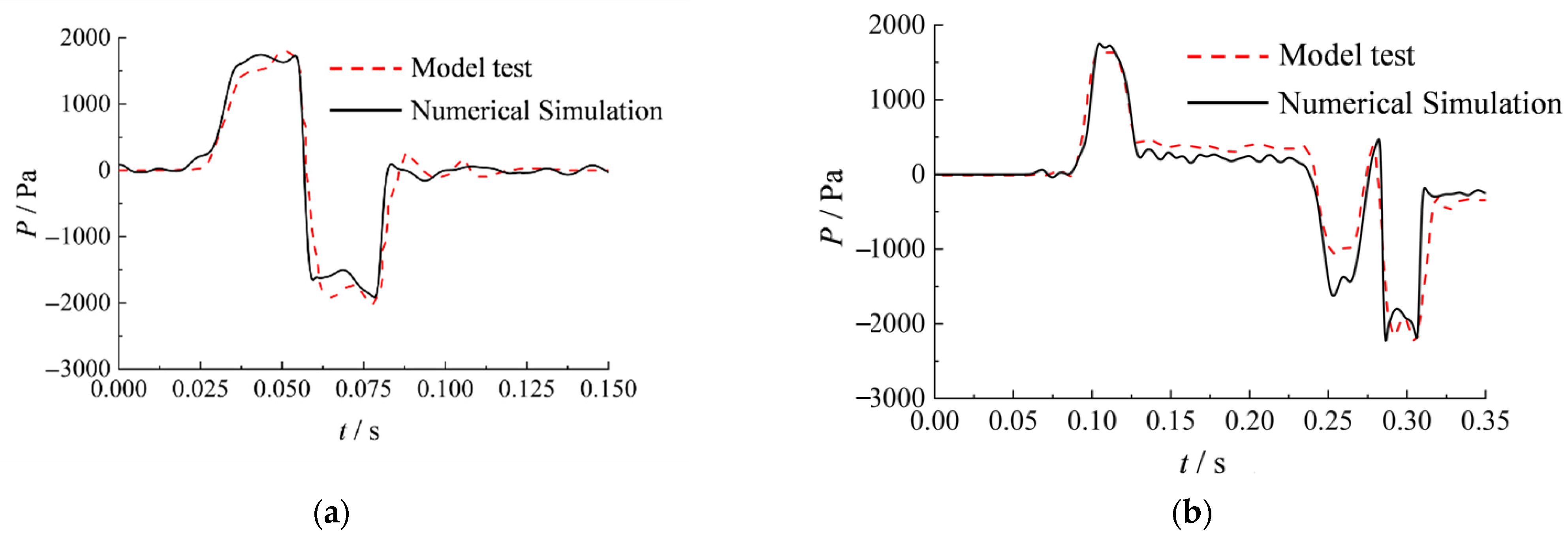
2.4. Model Reliability Verification
2.4.1. Checking of Grid Independence
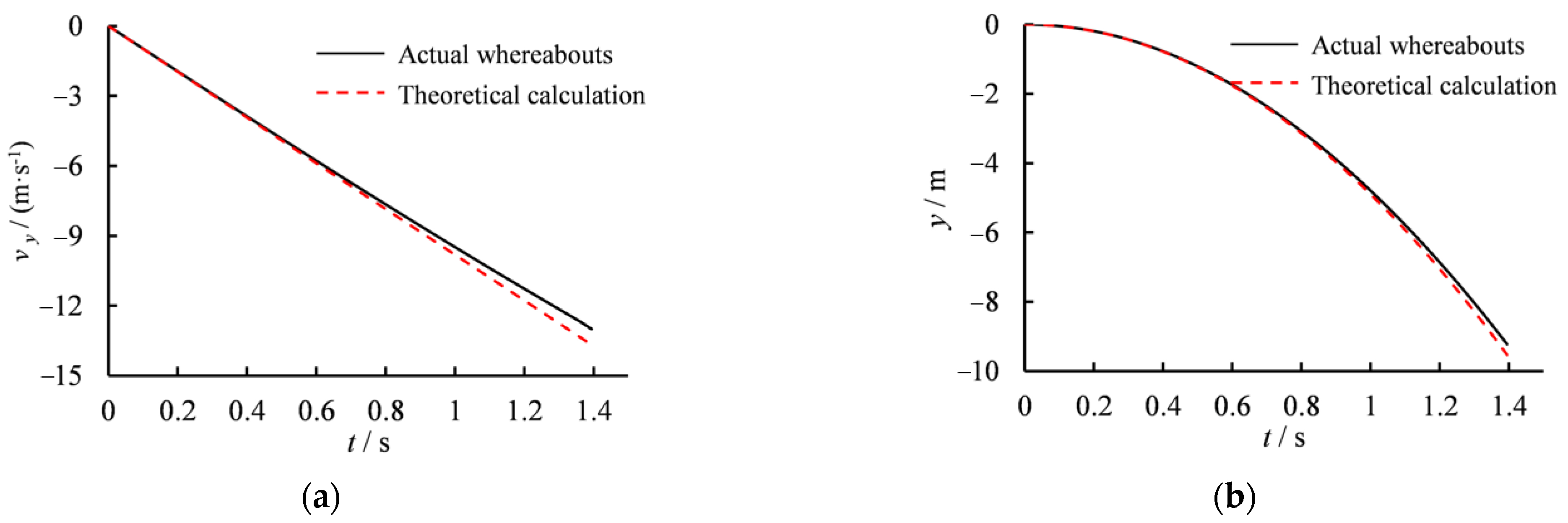
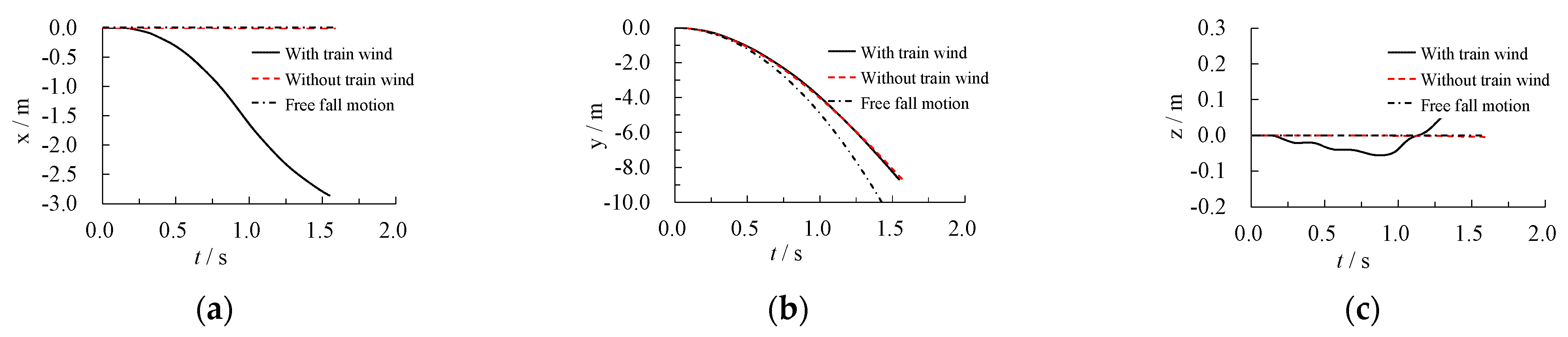
2.4.2. Verification of the Free-Fall Model
2.4.3. Turbulence Model Verification
3. Aerodynamic Evolution Mechanism of a Spalling Block under Train Wind Environment
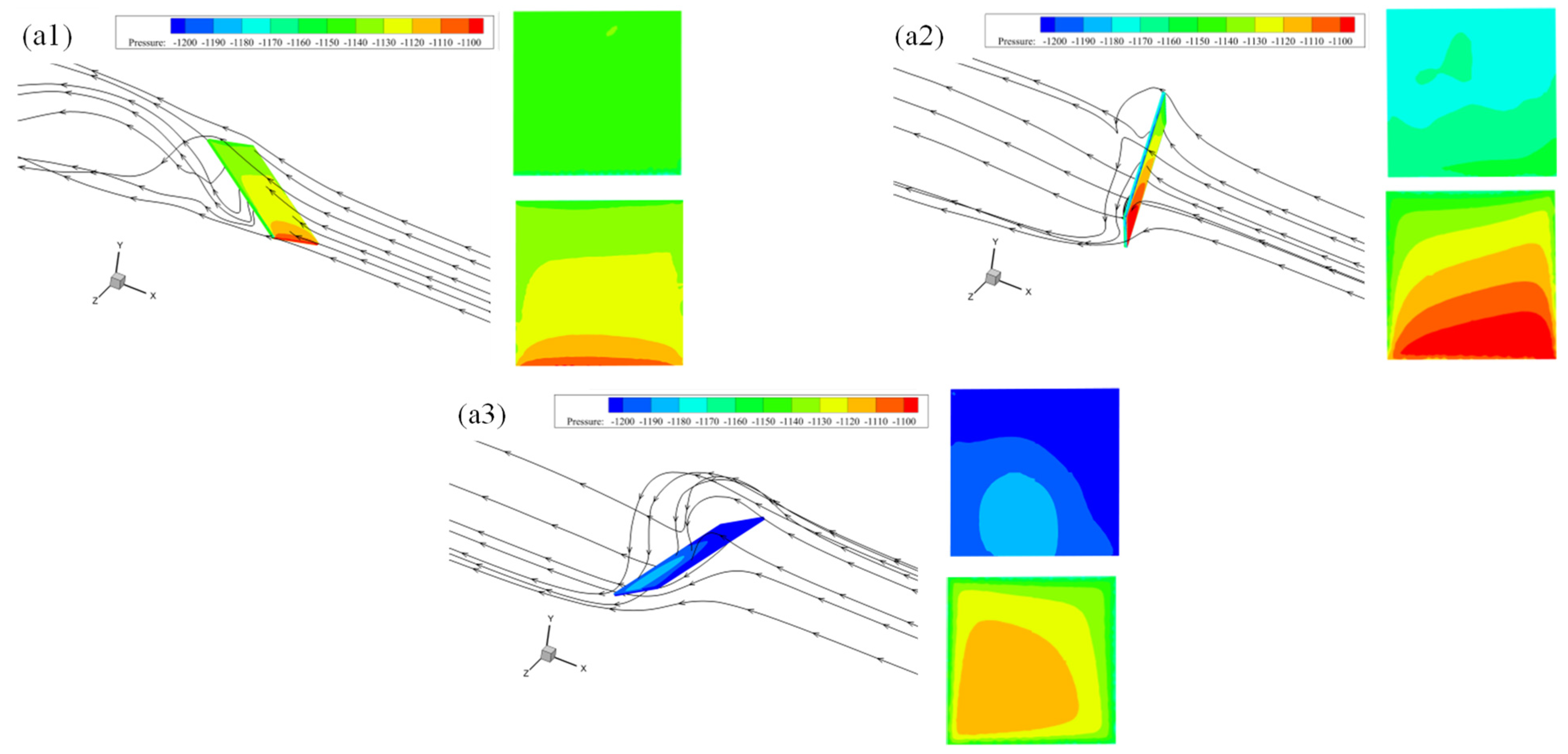
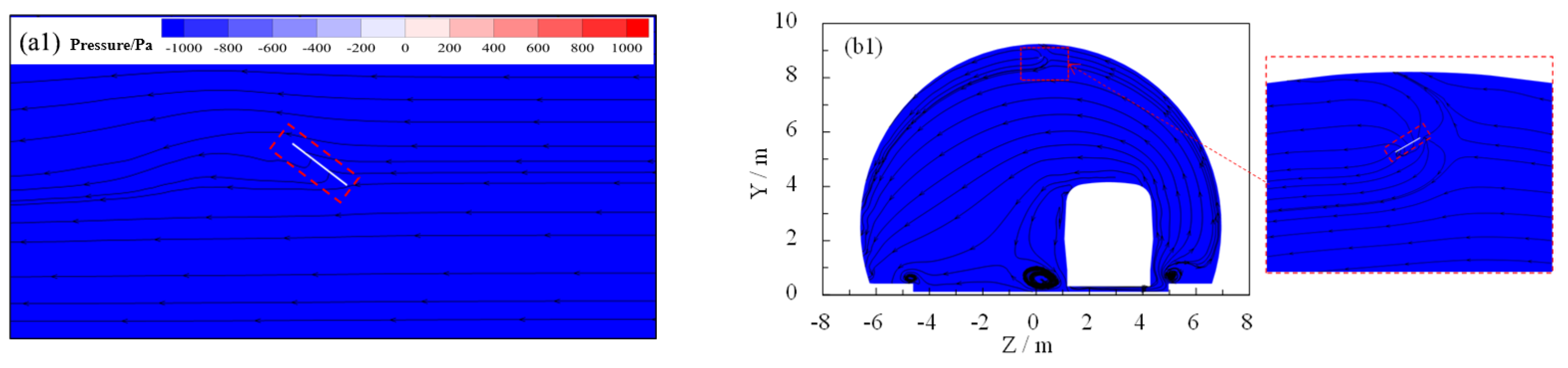
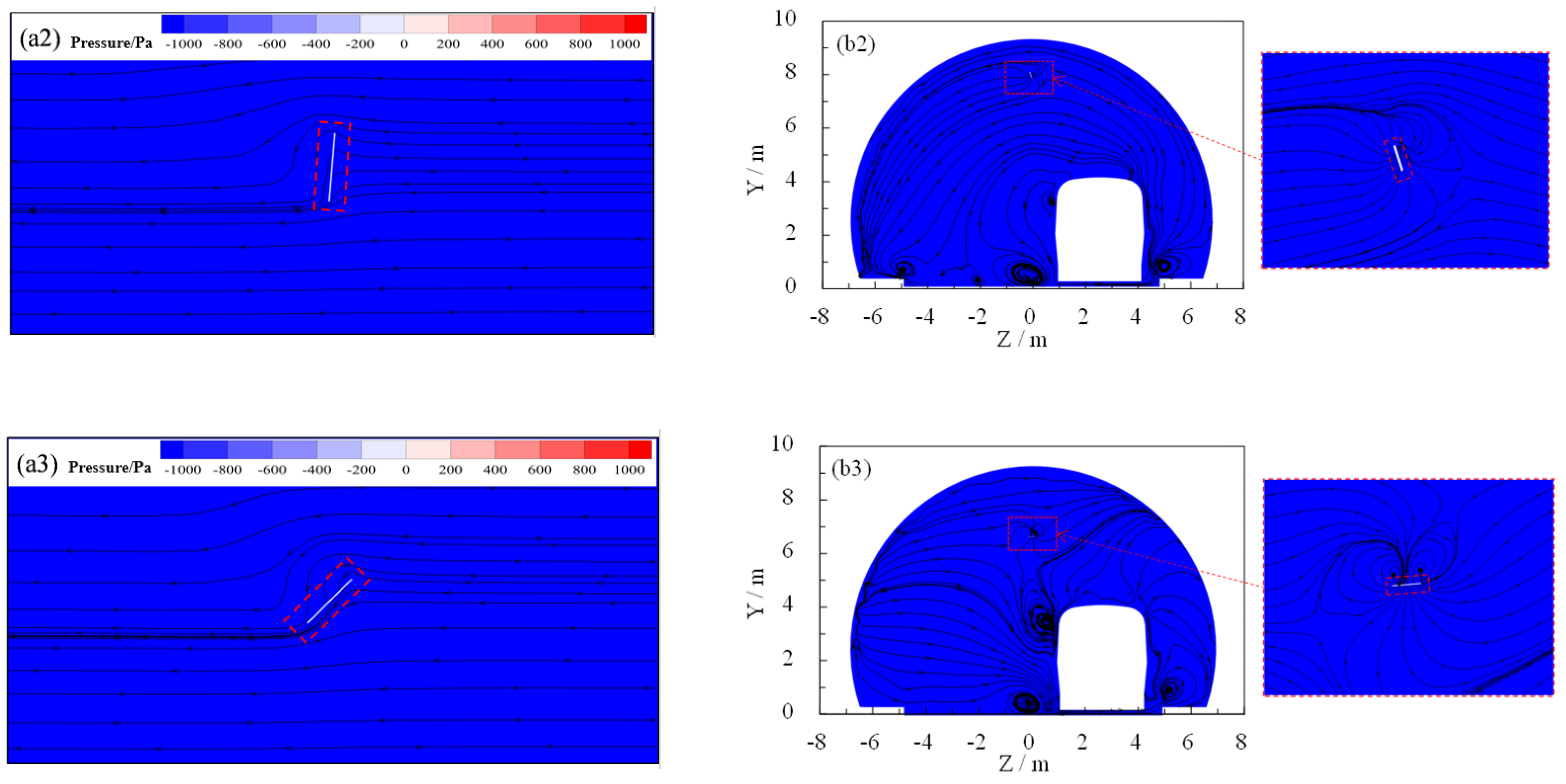
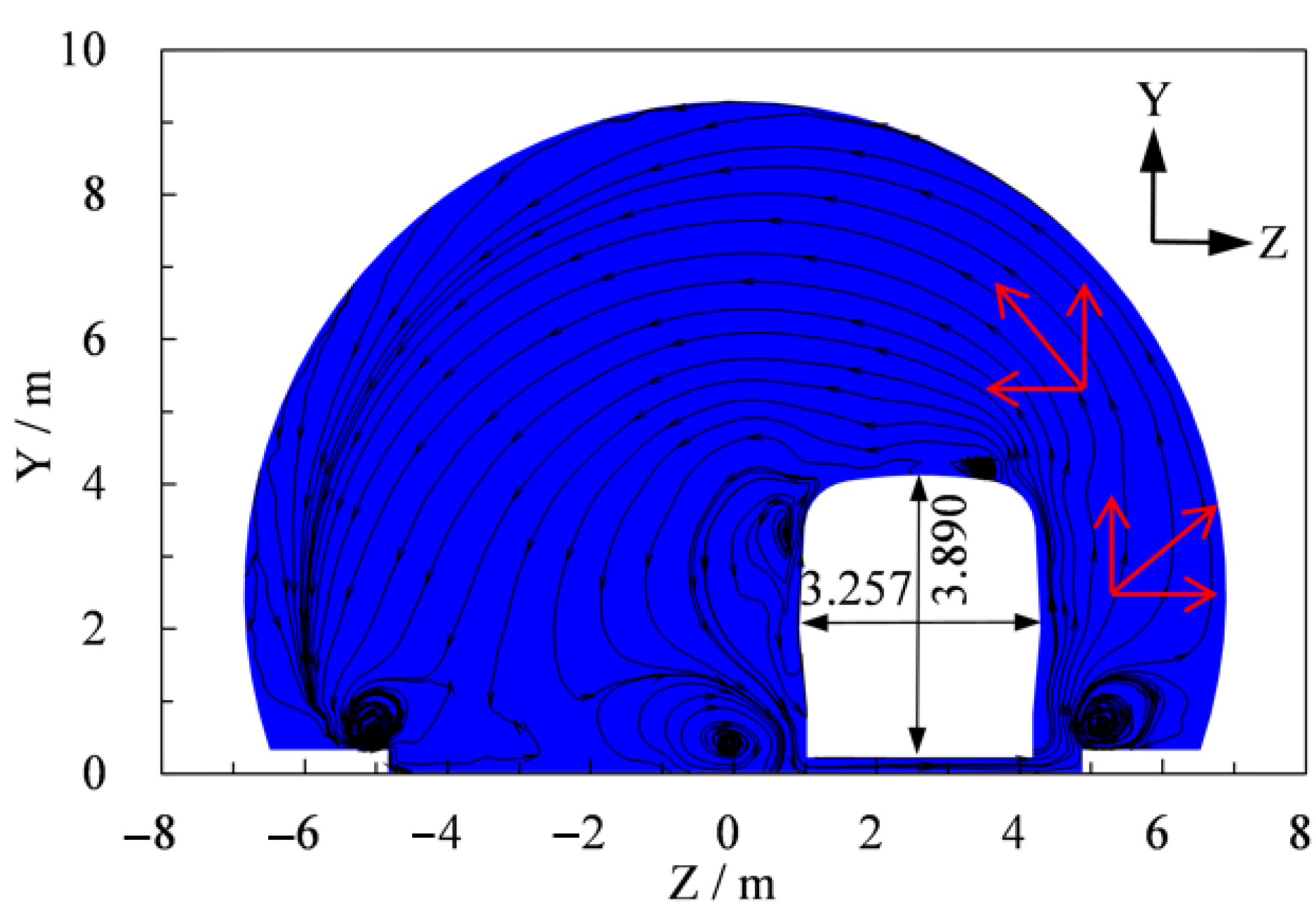
3.1. Aerodynamic Behavior
3.2. Aerodynamic Evolution Mechanism
- (1)
- In the falling process of the flaky spalling block, the train wind pressure played a considerably greater role than the aerodynamic static pressure in the tunnel. The uneven train wind pressure on the relative surface of the spalling block promoted the translation and rotation of the lining block.
- (2)
- The falling process of the flaky spalling block was affected by the coupling effect of the block (geometric size and heavy weight) and transient train wind. The train wind acted directly on the block and gradually pushed the movement of the block, resulting in circumfluence, vortex, and other phenomena that further changed its motion state. The changed motion state of the spalling block affected the driving effect of the train wind on the lining block, surrounding flow, and vortex structure.
- (3)
- The main movement direction of the spalling block was opposite the direction of train movement due to the influence of the wind field structure associated with the train. For the body surrounding the flow field structure from the front to the rear, the longitudinal flow velocity (the direction of train movement) was larger than the other velocity. The flow field directly drove the falling-backward movement of the spalling block along the flow field structure. In addition, the block and streamline were characterized by different time-dependent angles and intensities of flow; hence, an uneven force was exerted on the spalling block’s surface. Therefore, a moment that induced rotation around the horizontal axis (z-axis, perpendicular to the train) was generated, and the block rotated around this axis. The lateral flow velocity was relatively small and had a weak promoting effect on the lateral horizontal movement of the block. The significant vortex phenomenon around the block reduced the unevenness of the force associated with the block, and the rotation around the longitudinal axis was negligible. The vertical velocity was smaller than the lateral flow velocity and had no significant effect on the falling motion of the falling lining block; the spalling block was affected more by air resistance.
4. Traffic Safety Partition for Spalling Block
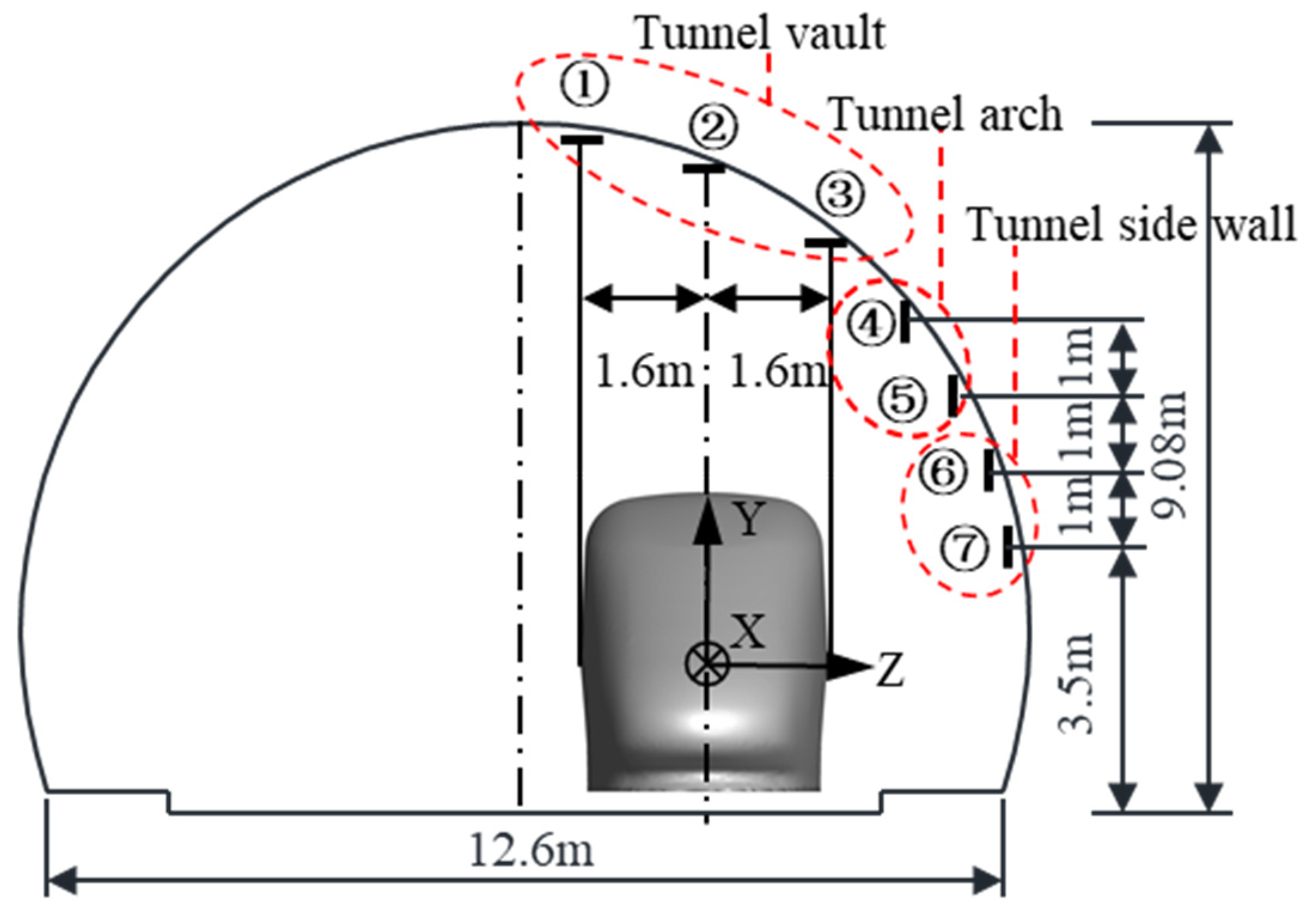
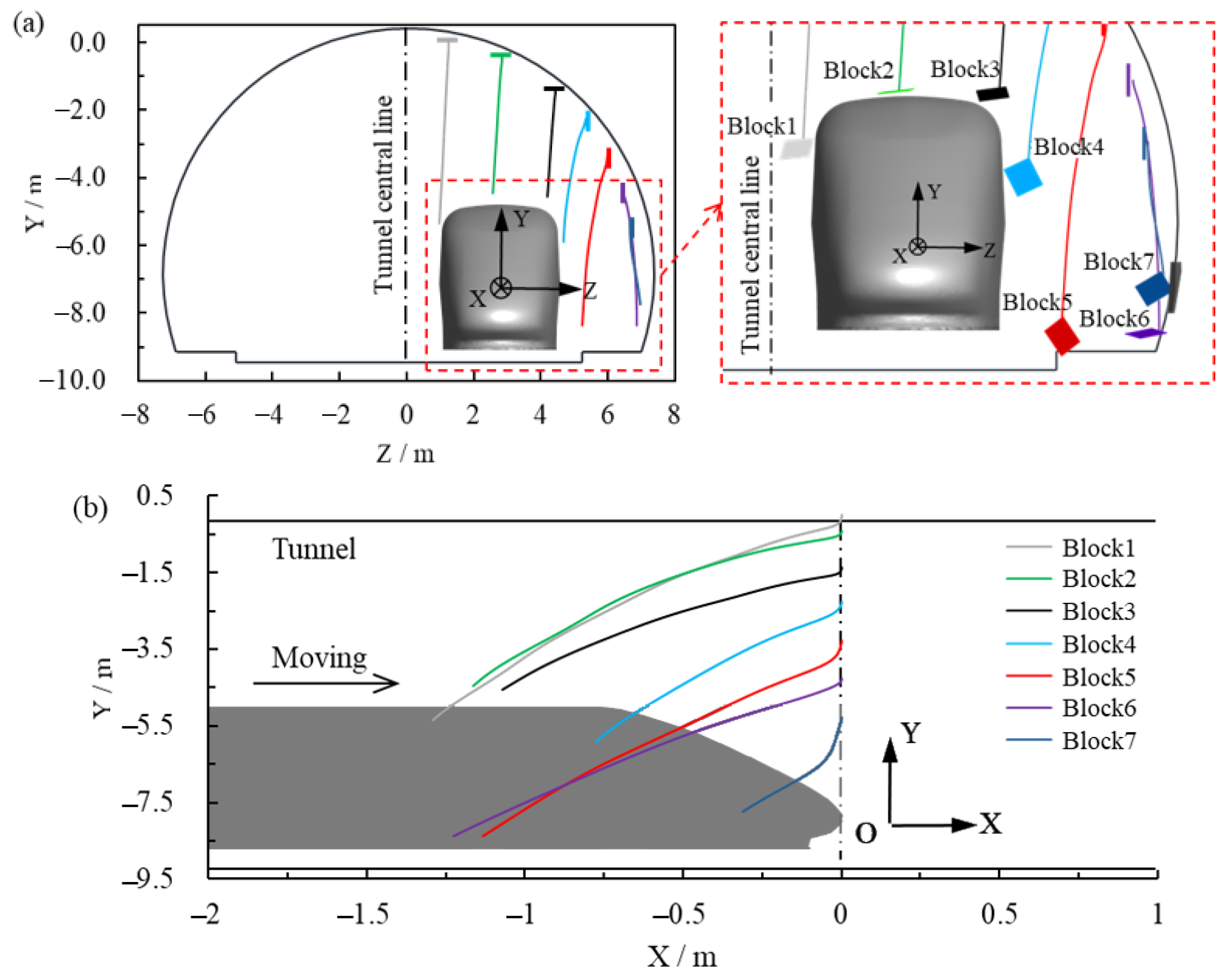
4.1. Trajectories of Spalling Blocks at Different Positions
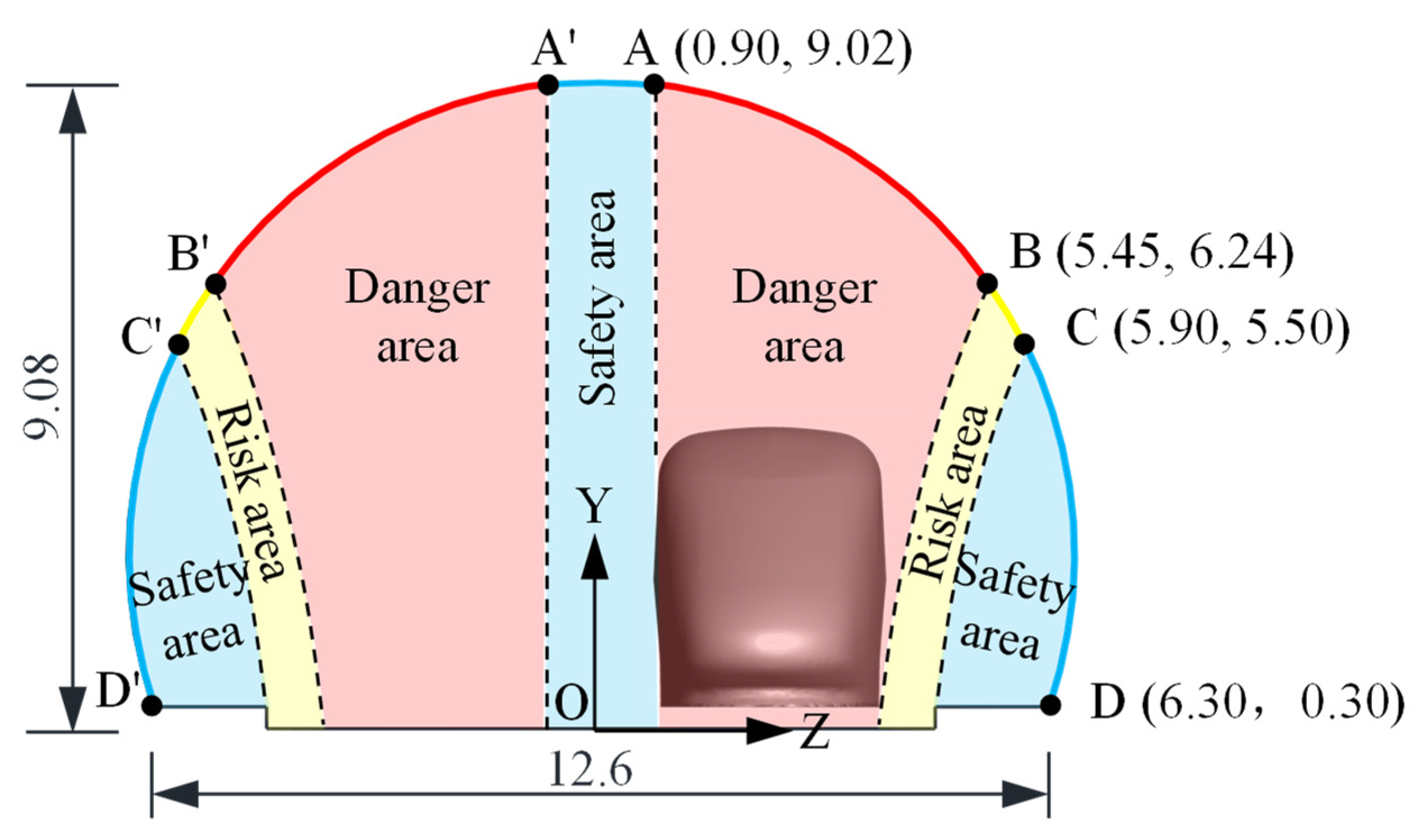
4.2. Driving Safety Partitions of Flaky Block
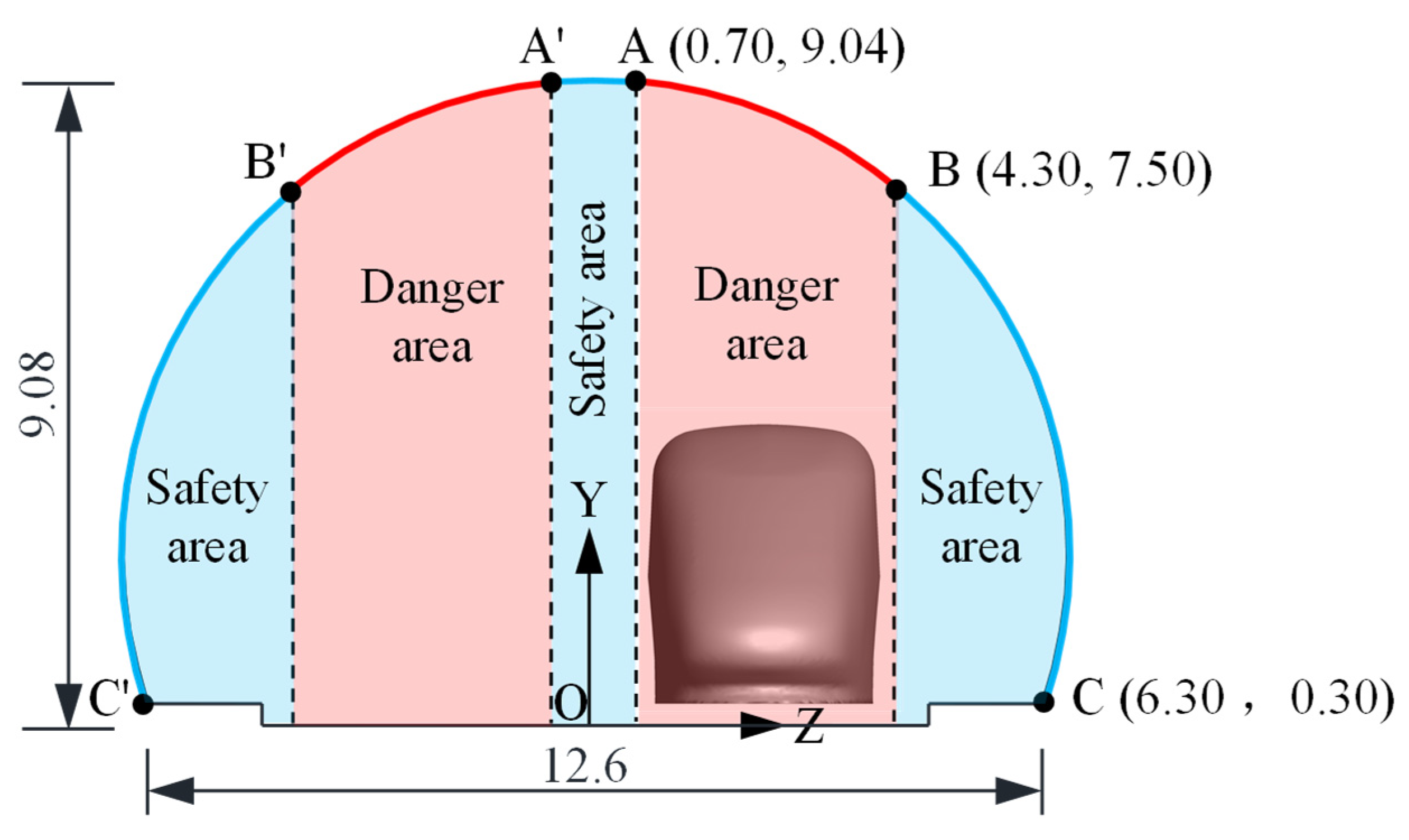
4.3. Driving Safety Partitions of Blocky Block
4.4. Differences between Flaky and Blocky Blocks on Driving Safety
5. Conclusions and Outlook
- (1)
- A three-dimensional gas–solid-coupling calculation model of spalling blocks, a train, a tunnel, and air was established on the basis of the basic theory of gas–solid interaction and the numerical simulation software, FLUENT. The transient coupling between a spalling block of a tunnel lining and turbulent train wind, as well as the numerical simulation of the entire falling process, were realized. The simulation results were consistent with the test results.
- (2)
- The aerodynamic evolution mechanism governing the falling motion of a flaky spalling block associated with a high-speed-railway tunnel lining operated as follows: The falling process of the block was affected by the transient coupling of its characteristics and the transient train wind. The train wind acted directly on the block, leading to horizontal movement of the block and consequent phenomena such as circumfluence and vortex that further changed the motion state of the block. Due to its changed motion state, the spalling block affected the flow field structure.
- (3)
- The impact of train wind was more significant for a flaky spalling block than for a blocky spalling block. The spalling blocks that peeled off the tunnel vault risked colliding directly with the train and had a considerable effect on driving safety. The falling lining blocks that peeled off the tunnel’s arched waist were attracted to the train wind and risked colliding with the side of the vehicle body or becoming involved with the wheel and rail, thereby affecting driving safety. The falling lining blocks that peeled off the tunnel side wall were repelled by the wind of the train and moved away from the vehicle body; hence, they had no effect on driving safety.
- (4)
- The impact partitions of the flaky blocks on driving safety were divided into three areas along the circular direction of the tunnel lining: dangerous zone, risk zone, and safety zone. The dangerous areas of flaky and blocky blocks were 5.5 and 7.5 m above the ground in the vault area, respectively, indicating that flaky blocks are more dangerous. Thus, during the operation of a tunnel, attention should be paid to the maintenance of the weak area above 5.5 m above the ground to ensure driving safety.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- China Railway Corporation. Bulletin of China Railway Corporation on Handling Quality Problems of Guizhou Section of Shanghai-Kunming High-Speed Railway (Railway Construction Letter [2017] No. 839). 21 July 2017. Available online: https://wenku.baidu.com/view/3ac95bc703d276a20029bd64783e0912a3167c11.html (accessed on 11 February 2022). (In Chinese).
- Dong, S.; Li, Y.Z. Treatment of post-construction settlement of open tunnel of high-speed railway tunnel. Archit. Eng. Technol. Des. 2016, 18, 1227. [Google Scholar]
- Wang, L.C.; Xiao, X.W.; Lin, H. Analysis on causes for and renovation of floor structure of a high-speed railway tunnel located in slightly-dipping interbedded rock mass. Tunn. Constr. 2014, 34, 823–836. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. On the Railway Construction Maintenance Management Standard Verification Results. 25 November 2014. Available online: https://www.mlit.go.jp/report/press/tetsudo07_hh_000078.html (accessed on 11 February 2022). (In Japanese)
- The In-Depth Analysis Report of High Speed Railway Tunnel Construction Joint Block Falling Accident. 12 January 2012. Available online: https://www.docin.com/p-2038643566.html (accessed on 11 February 2022). (In Chinese).
- Simanjuntak, T.; Marence, M.; Mynett, A.E.; Schleiss, A.J. Mechanical–hydraulic interaction in the cracking process of pressure tunnel linings. Int. J. Hydropower Dams 2013, 20, 112–119. [Google Scholar]
- Amorim, D.; Proenca, S.; Flrez, L.J. Simplified modeling of cracking in concrete: Application in tunnel linings. Eng. Struct. 2014, 70, 23–35. [Google Scholar] [CrossRef]
- Fernandez, G. Behavior of pressure tunnels and guidelines for liner design. J. Geotech. Eng. 1994, 120, 1768–1791. [Google Scholar] [CrossRef] [Green Version]
- Schleiss, A.J. Design of concrete linings of pressure tunnels and shafts for external water pressure. In Proceedings Tunnelling Asia; CRC Press: Boca Raton, FL, USA, 2020; pp. 147–156. [Google Scholar]
- Schleiss, A. Design of reinforced concrete linings of pressure tunnels and shafts. Hydropower Dams 1997, 4, 88–94. [Google Scholar]
- Schleiss, A. Design criteria applied for the lower pressure tunnel of the North Fork Stanislaus river hydroelectric project in California. Rock Mech. Rock Eng. 1998, 21, 161–181. [Google Scholar] [CrossRef]
- Asakura, T.; Kojima, Y. Tunnel maintenance in Japan. Tunn. Underg-Round Space Technol. 2003, 18, 161–169. [Google Scholar] [CrossRef]
- Gálvez, J.C.; Červenka, J.; Cendón, D.A.; Saouma, V. Discrete crack approach to normal/shear cracking of concrete. Cem. Concr. Res. 2002, 32, 1567–1585. [Google Scholar] [CrossRef]
- Standing, J.R.; Lau, C. Small-scale model for investigating tunnel lining deform-ations. Tunn. Undergr. Space Technol. 2017, 68, 130–141. [Google Scholar] [CrossRef]
- Suzuki, M.; Fujimoto, H.; Sakuma, Y. Measures to reduce aerodynamic force acting on high-speed train in tunnel. Proc. Transp. Logist. Conf. 2002, 11, 277–278. [Google Scholar] [CrossRef]
- Liu, T.H.; Tian, H.Q.; Jin, X.S. Experimental study of full scale train on aerodynamics in tunnel. Acta Aerodyn. Sin. 2008, 26, 42–46. (In Chinese) [Google Scholar]
- Zhang, L.; Yang, M.Z.; Zhang, H.; Jin, Q. Influence of Tunnel Portals on Tunnel Aerodynamic Effects in Operation of High-speed Railways. J. China Railw. Soc. 2013, 35, 92–97. (In Chinese) [Google Scholar]
- Wang, R.L. Numerical Study on Aerodynamic Effect of High Speed Train Entering Tunnel. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2015. (In Chinese). [Google Scholar]
- Deng, E.; Yang, W.C.; Lei, M.F.; Zhu, Z.; Zhang, P. Aerodynamic loads and traffic safety of high-speed trains when passing through two windproof facilities under crosswind: A comparative study. Eng. Struct. 2019, 188, 320–339. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.C.; Lei, M.F.; Zhu, Z.H.; Zhang, P.P. Transient aerodynamic performance of high-speed trains when passing through two windproof facilities under crosswinds: A comparative study. Eng. Struct. 2019, 188, 729–744. [Google Scholar] [CrossRef]
- Yang, W.C.; Deng, E.; Lei, M.F.; Zhang, P.P.; Yin, R.S. Flow structure and aerodynamic behavior evolution during train entering tunnel with entrance in crosswind. J. Wind. Eng. Ind. Aerodyn. 2018, 175, 229–243. [Google Scholar] [CrossRef]
- Hsiao, L.F. An EOF analysis and modeling study of the multi-typhoons movement over the west northern Pacific and the South China Sea. In Proceedings of the 24th Conference on Hurricanes and Tropical Meteorology, Fort Lauderdale, FL, USA, 29 May–2 June 2000; pp. 466–467. [Google Scholar]
- Li, L.B. Analysis of Train-Track- Bridge Coupling Vibration of Cable-Stayed Bridge. Master’s Thesis, Central South University, Changsha, China, 2015. [Google Scholar]
- Deng, E.; Yang, W.C.; He, X.H.; Ye, Y.C.; Wang, A. Transient aerodynamic performance of high-speed trains when passing through an infrastructure consisting of tunnel–bridge–tunnel under crosswind. Tunn. Undergr. Space Technol. 2020, 102, 103440. [Google Scholar] [CrossRef]
- Yang, W.C.; Deng, E.; Zhu, Z.H.; Lei, M.F.; Shi, C.H.; He, H. Sudden variation effect of aerodynamic loads and safety analysis of running trains when entering tunnel under crosswind. Appl. Sci. 2020, 10, 1445. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.H.; Yang, W.C.; Peng, L.M.; Wang, Z.W.; Lei, M.F. Analysis of catenary’ s safety under train wind action in high-speed railway tunnel. J. Cent. South Univ. Sci. Technol. 2012, 43, 3652–3658. (In Chinese) [Google Scholar]
- Yang, Y.; Cui, J. Analysis into the Characteristic Damaged Marks Resulted from Aerodynamic Impact in High-speed-railway Tunnel. Forensic Sci. Technol. 2020, 45, 215–217. (In Chinese) [Google Scholar]
- Ansys Fluent. Fluid Simulation Software. (Version 19.0). Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 11 February 2022).
- Niu, J.Q.; Zhou, D.; Wang, Y. Numerical comparison of aerodynamic performance of stationary and moving trains with or without windbreak wall under crosswind. J. Wind. Eng. Ind. Aerodyn. 2018, 182, 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.J.; Tian, H.Q.; Gao, G.J.; Sheridan, J. Impact of ground and wheel boundary conditions on numerical simulation of the high-speed train aerodynamic performance. Fluid Struct. 2016, 61, 249–261. [Google Scholar] [CrossRef]
- Morden, J.A.; Hemida, H.; Baker, C.J. Comparison of RANS and detached eddy simulation results to wind-tunnel data for the surface pressures upon a class 43 highspeed train. Fluid Eng. 2015, 137, 041108. [Google Scholar] [CrossRef]
- Muld, T.W.; Efraimsson, G.; Henningson, D.S. Wake characteristics of high-speed trains with different lengths. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2013, 228, 333–342. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two equation k-ω turbulence models for aerodynamic flow. In Proceedings of the 24th Fluid Dynamics Conference, Orlando, FL, USA, 6–9 June 1993. [Google Scholar]
- Paz, C.; Suarez, E.; Gil, C. Numerical methodology for evaluating the effect of sleepers in the underbody flow of a high-speed train. J. Wind. Eng. Ind. Aerodyn. 2017, 167, 140–147. [Google Scholar] [CrossRef]
- Muñoz-Paniagua, J.; García, J.; Crespo, A. Genetically aerodynamic optimization of the nose shape of a high-speed train entering a tunnel. J. Wind. Eng. Ind. Aerodyn. 2014, 130, 48–61. [Google Scholar] [CrossRef] [Green Version]
- Niu, J.Q.; Zhou, D.; Liang, X.F.; Liu, T.H.; Liu, S. Numerical study on the aerodynamic pressure of a metro train running between two adjacent platforms. Tunn. Undergr. Space Technol. 2017, 65, 187–199. [Google Scholar] [CrossRef]
- Wang, A. Study on Aerodynamic Behavior and Driving Safety of Lining Fall-Block in High-Speed Railway Tunnel. Master’s Thesis, Central South University, Changsha, China, 2009. (In Chinese). [Google Scholar]





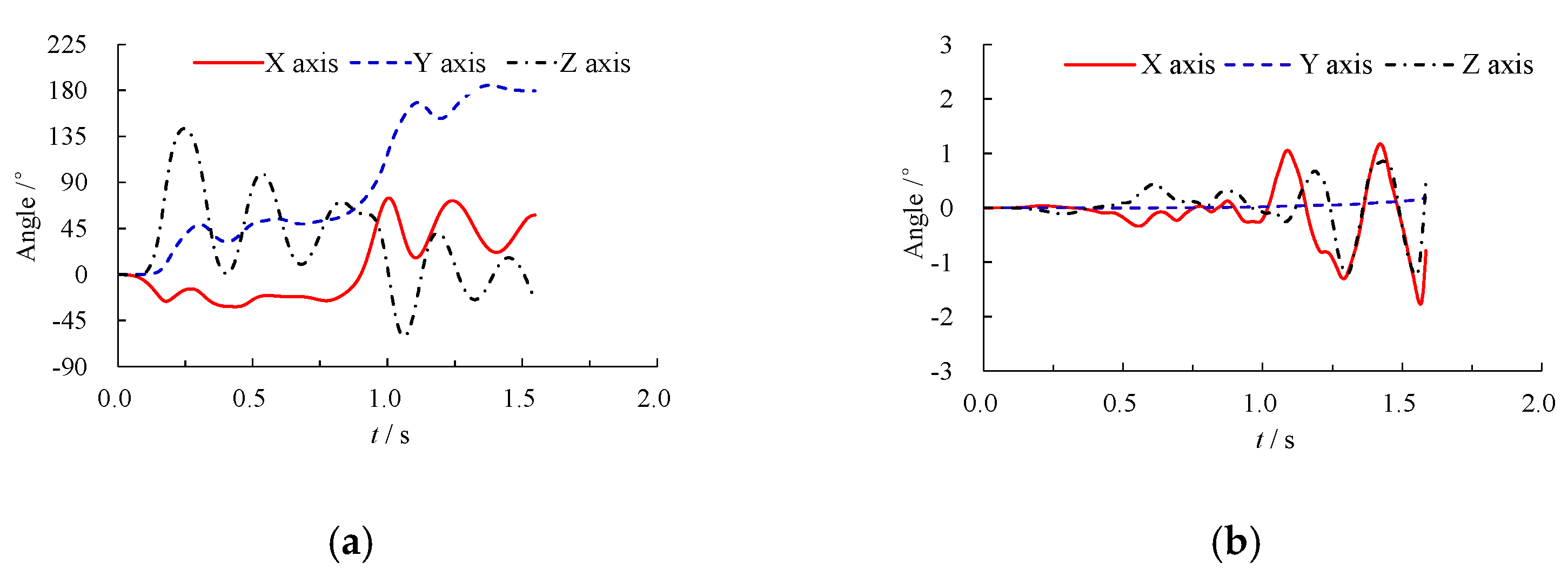
| Peak Pressure Fluctuation | Monitoring Point 1 | Monitoring Point 2 | ||||
|---|---|---|---|---|---|---|
| Model Test /Pa | Numerical Simulation /Pa | Relative Error /% | Model Test /Pa | Numerical Simulation /Pa | Relative Error /% | |
| Maximum | 1809 | 1744 | 3.6 | 1631 | 1753 | 7.4 |
| Minimum | −2011 | −1914 | 4.9 | −2251 | −2225 | 1.2 |
| Spalling Block | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| Displacement/m | x | −0.86 | −0.97 | −1.03 | −0.68 | −0.70 | −0.94 | −0.31 |
| z | −0.15 | −0.21 | −0.23 | −0.64 | −0.60 | 0.41 | 0.30 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.-H.; Wang, A.; Sun, X.-H.; Yang, W.-C. Aerodynamic Behavior and Impact on Driving Safety of Spalling Blocks Comprising High-Speed-Railway Tunnel Lining. Appl. Sci. 2022, 12, 2593. https://doi.org/10.3390/app12052593
Shi C-H, Wang A, Sun X-H, Yang W-C. Aerodynamic Behavior and Impact on Driving Safety of Spalling Blocks Comprising High-Speed-Railway Tunnel Lining. Applied Sciences. 2022; 12(5):2593. https://doi.org/10.3390/app12052593
Chicago/Turabian StyleShi, Cheng-Hua, Ang Wang, Xiao-He Sun, and Wei-Chao Yang. 2022. "Aerodynamic Behavior and Impact on Driving Safety of Spalling Blocks Comprising High-Speed-Railway Tunnel Lining" Applied Sciences 12, no. 5: 2593. https://doi.org/10.3390/app12052593
APA StyleShi, C.-H., Wang, A., Sun, X.-H., & Yang, W.-C. (2022). Aerodynamic Behavior and Impact on Driving Safety of Spalling Blocks Comprising High-Speed-Railway Tunnel Lining. Applied Sciences, 12(5), 2593. https://doi.org/10.3390/app12052593






