Next Article in Journal
Technical Analysis of the Masonry of the Bargello’ Palace, Florence (Italy)
Next Article in Special Issue
Evaluation of Neuromuscular Fatigue According to Injury History in a Repeat Sprint Ability Test, Countermovement Jump, and Hamstring Test in Elite Female Soccer Players
Previous Article in Journal
One-Step Fabrication of Nickel-Electrochemically Reduced Graphene Oxide Nanocomposites Modified Electrodes and Application to the Detection of Sunset Yellow in Drinks
Previous Article in Special Issue
No Association between Jump Parameters and Tissue Stiffness in the Quadriceps and Triceps Surae Muscles in Recreationally Active Young Adult Males
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 12
Issue 5
10.3390/app12052616
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Identification of Sex Differences within Lunge Decelerations via Lower Extremity Support Moments; Implications for ACL Injury Disparity, Prevention, and Rehabilitation

by
Jeffery T. Podraza
1,* and
Scott C. White
2
1
Department of Physical Therapy, D’Youville University, Buffalo, NY 14201, USA
2
Department of Exercise and Nutrition Sciences, University at Buffalo, Buffalo, NY 14214, USA
*
Author to whom correspondence should be addressed.
Appl. Sci. 2022, 12(5), 2616; https://doi.org/10.3390/app12052616
Submission received: 2 February 2022 / Revised: 25 February 2022 / Accepted: 1 March 2022 / Published: 3 March 2022
(This article belongs to the Special Issue Applied Biomechanics: Sport Performance and Injury Prevention II)
Browse Figures
Versions Notes

Abstract

:

Featured Application

The utilization of the limb support moment allows for a concise assessment of the support needed within the lower extremity (hip, knee, ankle) to avoid collapse during impact decelerations. Insufficient support contributions may be identified at a particular joint corresponding to a particular phase of motion. Identification of these support deficiencies within individuals and or groups may yield preventative and or rehabilitative strategies in relation to specific injury mechanisms.

Abstract

Loading characteristics and lower extremity injury mechanisms, such as the non-contact mechanism of cruciate ligament injury, differ between sexes. The Limb Support Moment (LSM) quantifies hip, knee, and ankle moment contribution to the net moment required to prevent limb collapse during deceleration tasks. In total, 10 males and 10 females performed single limb deceleration landings within three knee flexion ranges: 0–25°, 25–50°, and 50–75°. Lower extremity joint moments and LSMs were calculated for all planes at initial contact (IC) through 50 ms. A two-way multivariate ANOVA compared LSMs and joint moments between sexes for all planes. Female LSMs were significantly greater at IC in the sagittal and transverse planes due to the generation of hip and ankle extensor moments and larger hip, knee, and ankle internal rotation moments. Males demonstrated significantly greater LSMs in the frontal plane due to the generation of hip abductor moments. Results suggest that females have a more rigid lower limb than males at landing, with less shock absorption capacity and greater potential for frontal plane collapse due to an unsupportive hip adductor moment. Quantifying the contribution of joint moments to limb support via LSMs suggests that there are landing characteristic sex differences, which may provide insight into injury disparity while guiding injury prevention/rehabilitation methodology.

1. Introduction

Lower extremity loading characteristics differ between males and females [1,2,3]. Loading differences have been linked to sex disparity in injuries such as the non-contact mechanism of anterior cruciate ligament (ACL) rupture [3,4]. Females have a 2–6 times greater rate of ACL injury versus males [4]. Multiple theories, regarding these sex disparities, have been proposed related to intrinsic factors, including hormonal effects and anatomical differences, along with extrinsic factors related to neuromuscular control [3,4,5,6,7,8,9,10,11] Little, if anything, can be done to alter intrinsic factors related to injury; therefore, emphasis has been placed on assessment and modification of extrinsic factors, specifically loading characteristics, including lower extremity kinematics, joint moments, and neuromuscular variables, including antagonist–agonist muscle relationships, timing of muscle activation, and proprioception [10,12,13,14]. Sex differences in loading characteristics are considered the product of biomechanical and neuromuscular control differences and their effects on multiple planes and on multiple joints [5,8,15,16,17,18,19,20,21,22,23].
Standardized in-vivo analysis tasks, such as landing from a jump [2,10,24,25,26,27], cutting maneuvers [4,28], or higher shear force tasks [29], have been used to investigate sex differences within lower extremity biomechanical factors linked to injuries such as ACL rupture. These tasks inherently assess a single plane and/or joint. Sagittal plane analyses of this nature have shown that females utilize their hip extensors less than males [4,15], utilize less knee flexion during landings [1,29,30,31,32,33], and demonstrate no significant difference versus males in ankle loading [26,34]. Frontal plane analyses reveal that females generate greater hip adductor moments [24,35], generate greater knee abductor moments, which may stem from the larger hip adductor moments [24,28], and demonstrate greater frontal plane ankle eversion, which may elicit valgus knee stress and proximal tibial anterior translation [4,28]. Transverse plane assessments are more limited, revealing that females generate greater hip internal rotation displacement during drop landings [27] and that knee and ankle rotation moments may play a role in injury for both sexes [36]. These findings suggest that there are sex differences in hip and ankle joint mechanics, which are related to the knee; however, these single plane–single joint results do not provide a means of determining the interactive relationship that each joint has on the entire limb. The Limb Support Moment (LSM) provides a means of quantifying this interactive relationship while identifying loading characteristic sex differences, which may potentially help to identify sources of sex disparity in injuries.
The use of the Limb Support Moment (LSM) to represent the lower extremity as a three-component structure yields a model for making sex comparisons within a task not limited to a single plane or joint [37]. The LSM quantifies the contribution of hip, knee, and ankle moments as supportive or unsupportive to the net support moment, preventing limb collapse during rapid deceleration [37,38]. The net LSM indicates whether the assessed limb is in a state of support or collapse, as defined by the polarity of the sum of the joint moments within a single plane, as defined in a right-hand orthogonal system [37]. The role played by each joint may vary depending on the positioning of the joint, which may also vary between sexes [37]. The LSM has been shown to be useful in assessing tri-planar lower extremity joint moment contributions to overall knee stability during a lunge deceleration with varying knee flexion angles [37]. The contribution of individual joint moments to preventing limb collapse was shown to vary with the degree of knee flexion and the time frame of initial contact through 50 ms [37]. Hip joint moments were noted as playing a particularly important role in balancing potentially damaging knee moments across all planes and conditions [37].
The current literature regarding sex differences in loading characteristics focuses on single plane and or joint assessments without consideration of the interactive effect of all joints in the lower limb. The LSM analysis provides a single quantitative value of support based on the interaction of the hip, knee, and ankle moments. The LSM has not been extended to sex comparisons within a dynamic lunge movement model. To our knowledge, this investigation is the first to utilize the LSM analysis to identify sex differences for a lunge deceleration task. It was hypothesized that females would demonstrate smaller frontal plane net LSMs with a larger hip adductor moment vs. males but there would be no difference between males and female sagittal plane LSMs despite females generating larger sagittal plane knee extensor moments and that there would be no sex differences in transverse plane LSMs. Identification of sex differences in movement control strategies via the LSM may provide insight to injury disparity and potentially guide and or justify existing injury prevention and rehabilitation methodology.

2. Materials and Methods

2.1. Participants

Twenty healthy, college-age subjects participated in the study: 10 males (age: 22.6 ± 2.1 years, mass: 78.51 ± 11.1 kg, height: 1.78 ± 0.04 m) and 10 females (age: 23.1 ± 3.3 years, mass: 59.45 ± 9.28 kg, height 1.66 ± 0.06 m). The protocol was approved by a University Institutional Review Board. Written informed consent was obtained from each subject. Participants had no history of lower extremity surgery or current lower extremity injury based on a medical screening questionnaire. Subjects were healthy and physically active, with varying athletic backgrounds from their adolescence and high school years. None were collegiate athletes or professional athletes. Data collection, processing, and analysis was performed by a tenured professor of Biomechanics and a senior Biomechanics doctoral student who was also a physical therapist.

2.2. Protocol

Data was collected in an air-conditioned enclosed lab space, maintained at a temperature of approximately 68 degrees (F). Subjects performed a standardized landing task (lunge deceleration), simulating vertical impact forces in combination with rapid deceleration shear forces requiring joint moment responses to prevent limb collapse within varying knee flexion angles [37]. This maneuver with the varying knee flexion angles has proven useful in closely representing real-world landing scenarios [37]. Subjects approached a bench step from an established distance (~4 m), stepped onto the bench (height: 10.5 cm), then dropped forward and down for a single limb, landing near the center of a force plate (~30 cm forward). The cadence of the entire task was matched to an audible metronome set at 100 beats per minute. Subjects chose the limb to be analyzed and practiced the task of landing into each knee flexion range, 0–25°, 25–50°, and 50–75°, until they were subjectively comfortable with the maneuver. Subjects were allowed to choose the assessed limb as the maneuver required substantial motor control. Therefore, subjective comfort performing the maneuver was required. Subjects were required to attain and halt further motion within the respective range of knee flexion required for the respective trial. Subjects performed a minimum of five trials for each condition in a randomized manner. Trials were viewed in real time and repeated if subjects failed to land within the required ranges of knee flexion. Additionally, preliminary data was screened so only those trials attaining the correct knee flexion ranges were analyzed.

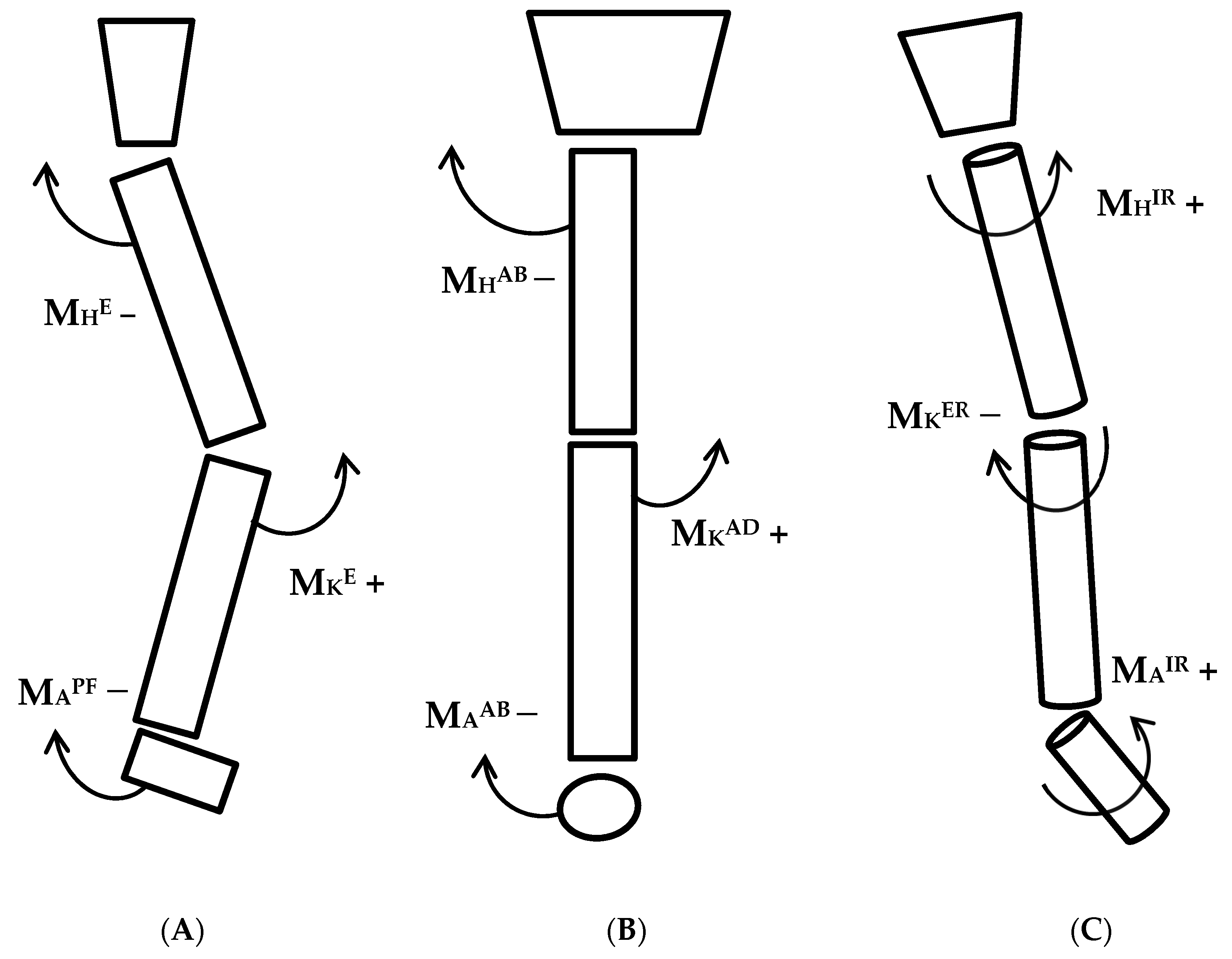
2.3. Motion Capture and Data Analysis

Twenty-five retro-reflective markers were positioned on the lower extremities [2], along with a markered rigid pelvic shell [37]. Pelvic and lower extremity segments were tracked at 120 Hz and reconstructed three-dimensionally using an eight-camera motion capture system (Vicon Nexus 1.8, Oxford metrics; Yarnton, UK), synchronized with ground reaction forces (GRF) obtained from an indwelling force plate (Kistler Instrument Corp. Amherst, NY, USA), sampled at 1080 Hz. Standing calibration determined joint centers of rotation, defined respective segmental coordinate axes, and established neutral alignment for reference of kinematic measures. Hip, knee, and ankle joint centers were established via Visual 3D (V3D) software version 5.10-2 (C-Motion, Inc. Germantown, MD, USA). A CODA pelvis model and regression equation format [39,40] were utilized for the hip joint center, while knee and ankle joint centers were based on distal joint segment position. Data post-processing was performed in V3D. Inverse dynamics were utilized to calculate internal joint moments relative to anatomical segment axes without filtering marker coordinates or GRFs. Moment filtering was performed with a critically damped, dual pass, low pass filter, utilizing different cut-off frequencies calculated for each subject [41]. This filtering method avoids moment artifacts, which occur when coordinates and forces are filtered with different cut-offs [42,43,44]. Frontal and transverse plane LSM algorithms were defined by Podraza et al., while the sagittal plane LSM formula was first presented by Winter [37,38]. Support moments were calculated by summing ankle (MA), knee (MK), and hip (MH) joint moments in each plane (Figure 1), assuming that each moment was a single joint actuator. The moment polarity at the proximal aspect of the distal joint segment was the basis of the LSM formulas, with counterclockwise moments being positive as defined in a right-hand, orthogonal axes system. Sagittal and frontal plane LSMs were based on the same algorithm, LSM = MK + (−MA) + (−MH). A positive sagittal plane LSM (MKE, MAPF, MHE, where E is the extensor and PF is the plantarflexor) represents a net extensor pattern preventing flexion collapse; a positive frontal plane LSM (MKAD, MAAB, MHAB, where AD is the adductor and AB is the abductor) represents a net abductor pattern preventing medial collapse. Net transverse internal tibial rotation relative to the femur is thought to elicit ACL strain, while external tibial rotation reduces strain in the ACL [45]. Therefore, a positive transverse plane LSM, derived from the formula LSM = MH + MA + (−MK), would represent a support pattern that prevents tibial internal rotation relative to the femur (MHIR, MAIR, MKER, where IR is the internal rotator and ER is the external rotator). Joint moment curves, for each joint, plane, and trial, were expressed as a ratio normalized to subject LSM for presentation (Figure 2, Figure 3 and Figure 4). A positive joint moment ratio was indicative of contributing to the overall LSM, while a negative ratio detracted from the LSM, as defined by the equations. Five trials for each joint moment in each plane and their support moments were averaged for each subject after normalizing to subject mass. Dependent measures were then averaged across all subjects, creating a group average for sex comparisons across landing conditions at IC and 50 ms after IC. IC was defined as the first data sample (8.3 ms) when the vertical ground reaction force was positive and closest to 20 N. The moment values for the 50 ms after IC represent the average of data points over that epoch. This time frame was chosen because ACL injuries are thought to occur from initial contact through 50 ms [25,46].

2.4. Statistical Analysis

Support moments and individual joint moments in each plane, across landing conditions, were compared between males and females by separate repeated measures; two-way ANOVAs with post hoc pairwise comparisons via SPSS. Significance was determined a priori at p ≤ 0.05 for all comparisons. The collected data met all assumptions required for conducting an ANOVA analysis.

3. Results

3.1. Sagittal Plane

Female sagittal plane LSMs were significantly greater than male LSMs, with a net supportive extensor LSM at IC within the 0–25° and 25–50° conditions (Figure 2, Table 1). Males produced significantly greater sagittal plane net hip flexor and knee extensor moments at IC within the 0–25° and 25–50° conditions (Figure 2, Table 2. Supportive net ankle plantarflexion moments were generated by females in the 0–25° and 25–50° conditions, while males generated dorsiflexion flexor moments at IC (Figure 2; Table 2). During the 50 ms epoch following IC, both sexes demonstrated supportive extensor LSMs (Figure 2, Table 3), with males generating greater hip extensor moments (Table 4). Female ankle plantarflexion moments at 50 ms were significantly greater than male moments in the 25–50° condition (Table 4).

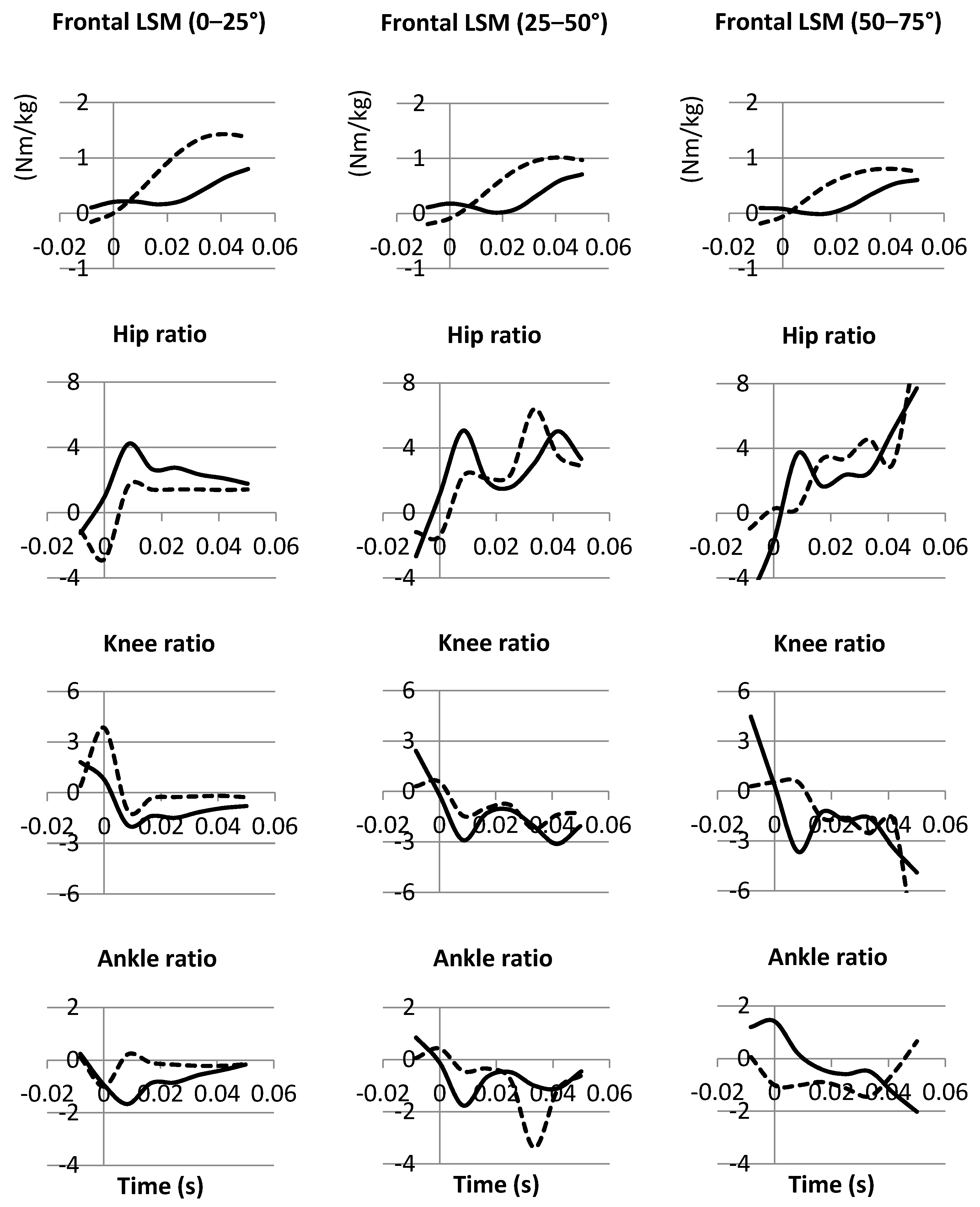
3.2. Frontal Plane

Male frontal plane LSMs were significantly greater than female LSMs at IC within the 0–25° and 25–50° conditions (Figure 3; Table 1). Females generated significantly greater hip adductor moments at IC in the 0–25° and 25–50° conditions (Figure 3, Table 2). No significant knee or ankle moment differences were noted at IC; however, both sexes utilized supportive knee adductor moments at IC, 0–25° (Figure 3, Table 2). Female LSMs were significantly more supportive at 50 ms in the 0–25° condition (Figure 3; Table 3). Males produced significantly greater hip abductor moments in the 50 ms after IC in the 0–25° condition (Table 4). Beyond IC, both sexes utilized knee abductor and ankle adductor moments with no significant differences noted (Table 4).

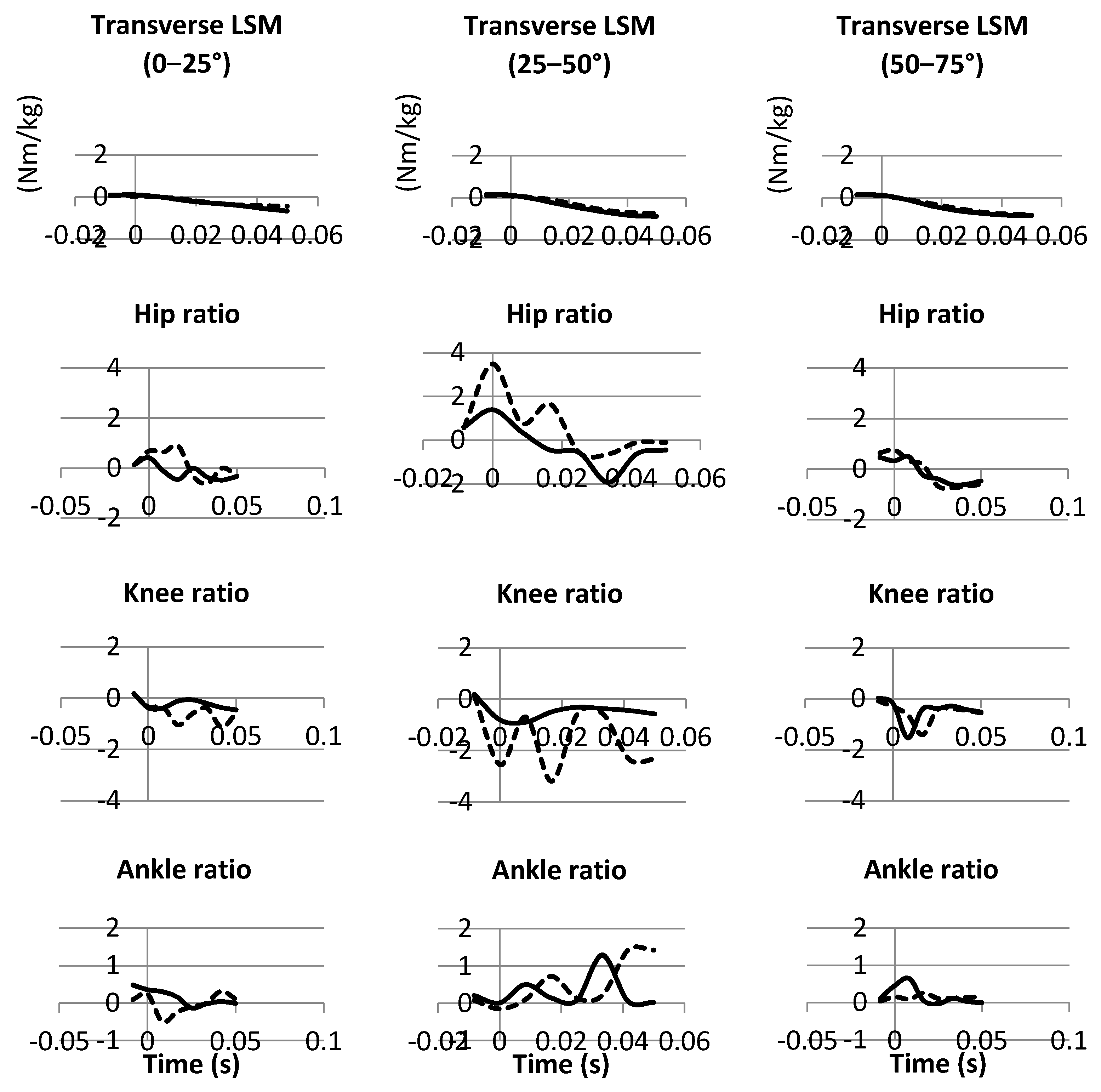
3.3. Transverse Plane

Supportive transverse plane LSMs were generated by both sexes, with females being significantly more supportive than males at IC in the 0–25° condition (Table 1). Both sexes produced internal rotation hip moments and knee moments at IC (Figure 4; Table 2). Internal rotation moments at the ankle were noted for both sexes at IC, 0–25° (Figure 4; Table 2). Beyond IC, all transverse LSM values were unsupportive (Figure 4; Table 3). Hip rotation moments shifted to external rotation, while internal rotation knee moments persisted for both sexes beyond IC (Table 4). Female ankle moments were near zero, up to 50 ms, and significantly less than males at 25–50° (Figure 4; Table 4). Contributions to overall support in the transverse plane by the ankle moments were inconsequential for males and females, relative to those generated at the hip (Figure 4).

4. Discussion

The present study compares three dimensional LSMs and the relative contribution of hip, knee, and ankle joint moments to the prevention of limb collapse between males and females. The LSM model allows for a unique sex comparison with the lower extremity represented as a dynamic three component structure. Significant sex differences were noted as females performed the landing task differently than males. Sex differences were most evident at IC in all planes in the most extended 0–25° condition; no significant differences were noted in the most flexed landing of 50–75°. The differences may therefore be relevant to injuries that occur near full knee extension, such as the non-contact mechanism of ACL injury [1,4,28,34]. Female LSMs preventing frontal plane collapse were significantly less supportive than male LSMs at IC. These findings are consistent with the link between higher incidence of female ACL injury and frontal plane hip and knee moments [3,28]. In the sagittal plane, females landed with net extensor LSMs at IC, while males utilized flexor LSMs (which subsequently shifted to extensor by 50 ms to generate support), suggesting that females have a more rigid lower limb than males at the point of IC. Transverse plane LSMs supported against internal rotation of the tibia relative to the femur (as defined in the present study), for both sexes at IC. LSM differences suggest that overall female joint moment synergies are different from males at IC for the same deceleration task.
The 0–25° condition of this study correlates to the near full knee extension positioning defined within the non-contact valgus collapse ACL injury mechanism [2,3,10]. The valgus collapse mechanism is thought to occur, due in part to frontal plane hip adductor moments, instigating increased knee valgus angles and/or knee abductor moments [2,3,10,28]. Hip abductor moments are thought to mitigate the non-contact mechanism as they yield femoral abduction, which serves to limit medial knee joint opening [3,24,28]. Proving our hypothesis, males exhibited greater LSM resistance to frontal plane medial collapse at IC through the generation of supportive hip abductor, knee adductor, and ankle abductor moments, while females produced only supportive knee and ankle moments (Figure 3, Table 1 and Table 2). Females produced unsupportive hip adductor moments (Table 2). These findings indicate that females landed with less frontal plane limb support due to the hip contributing unsupportive hip adductor moments at IC. This sex difference may predispose females to increased valgus knee loading compared to males, regardless of support contributed at the knee and ankle. Furthermore, this pattern is in keeping with previously defined patterns of increased female hip adductor utilization at landing [3,28]. It should be noted that the diminished support against frontal plane collapse in females was limited to IC, by 50 ms female frontal plane LSMs were significantly greater than males (Table 2). Therefore, the timing of utilized hip moments would seem to be a critical factor in the potential injury process.
Sagittal plane injury theories are founded on the quadriceps overload premise, implying that damage to structures, such as the ACL, occurs due to excessive knee extensor moments [45,47,48]. In the present study, knee extensor moments increased as knee flexion increased at landing (Table 2 and Table 4). If viewed from the perspective of quadriceps overload, this finding implies a greater risk of injury with deeper knee flexion, which is contrary to non-contact ACL injury mechanisms, which are noted to occur with the knee near full extension [2,3,10]. The sagittal plane results identify sex differences that do not support the quadriceps overload theory but rather an injury mechanism of multiple joint and plane involvement.
The impact of sagittal plane hip and ankle moments on sagittal plane models of injury has received minimal consideration. Contrary to our hypothesis, females generated a sagittal plane net extensor LSM, while males produced a net flexor LSM (Table 1), suggesting that females landed differently than males. Both sexes produced hip flexor moments at IC (Table 2); however, male hip flexor moments were significantly larger than females, resulting in a net flexor LSM pattern at IC (Figure 2, Table 2) that would be considered unsupportive. The ankle provides support against sagittal plane collapse through an extensor (plantarflexor) moment. Females produced an ankle plantarflexor moment, while males produced a flexor (dorsiflexor) moment at IC (Table 2). Lastly, male sagittal plane knee moments were significantly greater at IC (Table 2). This finding was contrary to our hypothesis; however, in combination with the hip and ankle moments, a noticeable sex difference became apparent. Males seemingly produced less support against sagittal plane flexion collapse at IC (smaller LSMs vs. females) due to hip flexor and ankle dorsiflexor moments, despite a larger knee extensor moment. Males may possibly utilize the hip and ankle flexor moments to land with less rigidity at IC. Male LSMs subsequently became supportive (extensor) by 50 ms, so the hip-ankle flexor pattern was, in fact, short-lived and may be a sex-based landing characteristic, similar to what was noted in the frontal plane, with equally short-lived female hip adductor moments.
Support against transverse plane internal rotation of the tibia relative to the femur was present for both sexes at IC, with female values being significantly greater in the 0–25° condition, which disproved our hypothesis. (Figure 4, Table 1). Both sexes produced hip internal rotation moments in all conditions, which would prevent external rotation of the femur on a fixed tibia (Table 2). Neither sex generated an external rotation knee moment (Table 2); therefore, there was no support from the knee that could limit internal tibial rotation relative to the femur. Overall, the knee moments failed to provide support against the transverse plane motion that is linked to injury [45]. Both sexes generated small net internal rotation ankle moments at IC (Table 2). Despite being small in magnitude, these internal rotation moments in combination with the internal rotation hip moments aide in protection of the knee. Overall, the results suggest that support against transverse plane collapse was most prominent at IC, with internal rotation hip moments providing the greatest contribution to support.
The consensus regarding the investigation of mechanisms of injury, such as in non-contact ACL injury, is that all lower extremity joints and planes of motion must be considered in the analysis [49]. Movement model analyses have been limited to single planes or single joints [2,10,35,43,48,50,51,52]. The LSM model [37,38] provides a means of quantifying lower extremity support in each plane with contributions from the hip knee and ankle joints; however, the analysis is not without limitations. Measurement errors consist of those inherent to inverse dynamic calculation [7,53,54,55,56]. Furthermore, as with other investigations that utilize a deceleration movement model, the magnitude of the loads does not recreate those associated with actual ACL injuries [2,10,29,37,43,44,57]. A more rapid deceleration and/or fall from a greater height may result in greater moments, which could influence the kinematic and kinetic response [57,58,59]. However, the present data is within the range of what has been reported in publications utilizing similar movement models [44,57]. Given the relatively small sample size of 20 healthy subjects, care must be taken with broad generalization of the results. However, our findings provide encouragement to conduct broader assessments of healthy and clinical subjects to generate clinical correlations.

5. Conclusions

To our knowledge, there have been no multi-plane, multi-joint investigations with sex comparison using a movement model that quantifies the lower extremity in the context of limb support moments. The results suggest there are sex differences in deceleration landing tasks that may provide insight to injury mechanism sex disparity. The most significant sex differences existed at IC in the 0–25° landing position. Females appear to have a greater potential for frontal plane collapse due to utilizing unsupportive net hip adductor moments at IC. The sagittal plane sex differences imply a male-specific multi-joint synergistic support relationship between the hip, knee, and ankle, occurring at IC. Males utilized flexor moments at the hip and ankle around a significantly larger knee extensor moment, which may allow males to land with less rigidity in the lower extremity. Lastly, both sexes demonstrated support against transverse plane collapse, with females being more supportive than males.
Overall, these results indicate the presence of sex differences, which may provide insight into causation of injury and in turn provide a basis for injury prevention and rehabilitation strategies. Such strategies should serve to counter the noted deviations. Specifically, ACL injury prevention methods and rehabilitation in females may emphasize techniques that counter hip adductor moments at initial contact and incorporate hip flexor and ankle dorsiflexor moments at landing [12,25,60]. Females who train to utilize hip flexor and ankle dorsiflexor moments may avoid initiation of ACL injury mechanisms, such as valgus collapse, which includes sagittal plane knee extension, frontal plane valgus loading, and frontal plane hip adduction [4].

Author Contributions

J.T.P. and S.C.W. participated fully in the conceptualization, research design, methodology, data acquisition, analysis, interpretation, and the initial creation of the manuscript. Due to the passing of S.C.W., final manuscript preparation was completed solely by J.T.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by The University of Buffalo Mark Diamond Research Fund (SP-12-12).

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board (or Ethics Committee) of The University of Buffalo, Sate University of New York (434994-1, 17 April 2013).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Not applicable.

Acknowledgments

I would like to acknowledge my co-author, mentor, and friend, Scott White. Scott was my principal advisor for both my Master’s and Doctoral degrees. We completed the initial version of this manuscript just prior to his sudden passing. It was an honor and pleasure to work with and learn from such an outstanding teacher, researcher, and mentor. This manuscript is dedicated to Scott.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Boden, B.P.; Dean, G.S.; Feagin, J.A.; Garrett, W.E. Mechanisms of Anterior Cruciate Ligament Injury. Orthopedics 2000, 23, 573–578. [Google Scholar] [CrossRef] [PubMed]
  2. Hewett, T.E.; Myer, G.D.; Ford, K.R.; Heidt, R.S.; Colosimo, A.J.; McLean, S.G.; van den Bogert, A.J.; Paterno, M.V.; Succop, P. Biomechanical Measures of Neuromuscular Control and Valgus Loading of the Knee Predict Anterior Cruciate Ligament Injury Risk in Female Athletes: A Prospective Study. Am. J. Sports Med. 2005, 33, 492–501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Powers, C.M. The Influence of Abnormal Hip Mechanics on Knee Injury: A Biomechanical Perspective. J. Orthop. Sports Phys. Ther. 2010, 40, 42–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Hewett, T.E.; Myer, G.D.; Ford, K.R. Anterior Cruciate Ligament Injuries in Female Athletes: Part 1, Mechanisms and Risk Factors. Am. J. Sports Med. 2006, 34, 299–311. [Google Scholar] [CrossRef]
  5. Speer, K.P.; Spritzer, C.E.; Bassett, F.H.; Feagin, J.A.; Garrett, W.E. Osseous Injury Associated with Acute Tears of the Anterior Cruciate Ligament. Am. J. Sports Med. 1992, 20, 382–389. [Google Scholar] [CrossRef] [PubMed]
  6. Abt, J.P.; Sell, T.C.; Laudner, K.G.; McCrory, J.L.; Loucks, T.L.; Berga, S.L.; Lephart, S.M. Neuromuscular and Biomechanical Characteristics Do Not Vary across the Menstrual Cycle. Knee Surg. Sports Traumatol. Arthrosc. 2007, 15, 901–907. [Google Scholar] [CrossRef] [PubMed]
  7. Beaulieu, M.L.; McLean, S.G. Sex-Dimorphic Landing Mechanics and Their Role within the Noncontact ACL Injury Mechanism: Evidence, Limitations and Directions. Sports Med. Arthrosc. Rehabil. Ther. Technol. 2012, 4, 10. [Google Scholar] [CrossRef] [Green Version]
  8. Chaudhari, A.M.W.; Lindenfeld, T.N.; Andriacchi, T.P.; Hewett, T.E.; Riccobene, J.; Myer, G.D.; Noyes, F.R. Knee and Hip Loading Patterns at Different Phases in the Menstrual Cycle: Implications for the Gender Difference in Anterior Cruciate Ligament Injury Rates. Am. J. Sports Med. 2007, 35, 793–800. [Google Scholar] [CrossRef] [PubMed]
  9. Feucht, M.J.; Mauro, C.S.; Brucker, P.U.; Imhoff, A.B.; Hinterwimmer, S. The Role of the Tibial Slope in Sustaining and Treating Anterior Cruciate Ligament Injuries. Knee Surg. Sports Traumatol. Arthrosc. 2013, 21, 134–145. [Google Scholar] [CrossRef] [PubMed]
  10. Hewett, T.E.; Stroupe, A.L.; Nance, T.A.; Noyes, F.R. Plyometric Training in Female Athletes. Decreased Impact Forces and Increased Hamstring Torques. Am. J. Sports Med. 1996, 24, 765–773. [Google Scholar] [CrossRef]
  11. Sturnick, D.R.; Vacek, P.M.; DeSarno, M.J.; Gardner-Morse, M.G.; Tourville, T.W.; Slauterbeck, J.R.; Johnson, R.J.; Shultz, S.J.; Beynnon, B.D. Combined Anatomic Factors Predicting Risk of Anterior Cruciate Ligament Injury for Males and Females. Am. J. Sports Med. 2015, 43, 839–847. [Google Scholar] [CrossRef] [PubMed]
  12. Silvers, H.J.; Mandelbaum, B.R. Prevention of Anterior Cruciate Ligament Injury in the Female Athlete. Br. J. Sports Med. 2007, 41 (Suppl. S1), i52–i59. [Google Scholar] [CrossRef] [PubMed]
  13. Stearns, K.M.; Powers, C.M. Improvements in Hip Muscle Performance Result in Increased Use of the Hip Extensors and Abductors during a Landing Task. Am. J. Sports Med. 2014, 42, 602–609. [Google Scholar] [CrossRef] [PubMed]
  14. Tsuda, E.; Okamura, Y.; Otsuka, H.; Komatsu, T.; Tokuya, S. Direct Evidence of the Anterior Cruciate Ligament-Hamstring Reflex Arc in Humans. Am. J. Sports Med. 2001, 29, 83–87. [Google Scholar] [CrossRef] [PubMed]
  15. Decker, M.J.; Torry, M.R.; Wyland, D.J.; Sterett, W.I.; Richard Steadman, J. Gender Differences in Lower Extremity Kinematics, Kinetics and Energy Absorption during Landing. Clin. Biomech. 2003, 18, 662–669. [Google Scholar] [CrossRef]
  16. Fleming, B.C.; Renstrom, P.A.; Ohlen, G.; Johnson, R.J.; Peura, G.D.; Beynnon, B.D.; Badger, G.J. The Gastrocnemius Muscle Is an Antagonist of the Anterior Cruciate Ligament. J. Orthop. Res. 2001, 19, 1178–1184. [Google Scholar] [CrossRef]
  17. Hashemi, J.; Breighner, R.; Chandrashekar, N.; Hardy, D.M.; Chaudhari, A.M.; Shultz, S.J.; Slauterbeck, J.R.; Beynnon, B.D. Hip Extension, Knee Flexion Paradox: A New Mechanism for Non-Contact ACL Injury. J. Biomech. 2011, 44, 577–585. [Google Scholar] [CrossRef] [PubMed]
  18. Herzog, W.; Read, L.J. Lines of Action and Moment Arms of the Major Force-Carrying Structures Crossing the Human Knee Joint. J. Anat. 1993, 182 Pt 2, 213–230. [Google Scholar] [PubMed]
  19. Kanamori, A.; Zeminski, J.; Rudy, T.W.; Li, G.; Fu, F.H.; Woo, S.L.-Y. The Effect of Axial Tibial Torque on the Function of the Anterior Cruciate Ligament: A Biomechanical Study of a Simulated Pivot Shift Test. Arthroscopy 2002, 18, 394–398. [Google Scholar] [CrossRef] [PubMed]
  20. Gabriel, M.T.; Wong, E.K.; Woo, S.L.; Yagi, M.; Debski, R.E. Distribution of in situ forces in the anterior cruciate ligament in response to rotatory loads. J. Orthop. Res. 2004, 22, 85–89. [Google Scholar] [CrossRef]
  21. Myer, G.D.; Ford, K.R.; Brent, J.L.; Hewett, T.E. Differential Neuromuscular Training Effects on ACL Injury Risk Factors in”high-Risk” versus “Low-Risk” Athletes. BMC Musculoskelet. Disord. 2007, 8, 39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Quatman, C.; Hewett, T. The Anterior Cruciate Ligament Injury Controversy: Is “Valgus Collapse” a Sex-Specific Mechanism? Br. J. Sports Med. 2009, 43, 328–335. [Google Scholar] [CrossRef] [PubMed]
  23. Shimokochi, Y.; Shultz, S.J. Mechanisms of Noncontact Anterior Cruciate Ligament Injury. J. Athl. Train. 2008, 43, 396–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Ford, K.R.; Myer, G.D.; Hewett, T.E. Valgus Knee Motion during Landing in High School Female and Male Basketball Players. Med. Sci. Sports Exerc. 2003, 35, 1745–1750. [Google Scholar] [CrossRef] [Green Version]
  25. Hewett, T.E.; Lindenfeld, T.N.; Riccobene, J.V.; Noyes, F.R. The Effect of Neuromuscular Training on the Incidence of Knee Injury in Female Athletes. A Prospective Study. Am. J. Sports Med. 1999, 27, 699–706. [Google Scholar] [CrossRef]
  26. Kernozek, T.W.; Torry, M.R.; Van Hoof, H.; Cowley, H.; Tanner, S. Gender Differences in Frontal and Sagittal Plane Biomechanics during Drop Landings. Med. Sci. Sports Exerc. 2005, 37, 1003–1012; discussion 1013. [Google Scholar]
  27. Lephart, S.M.; Ferris, C.M.; Riemann, B.L.; Myers, J.B.; Fu, F.H. Gender Differences in Strength and Lower Extremity Kinematics during Landing. Clin. Orthop. Relat. Res. 2002, 162–169. [Google Scholar] [CrossRef]
  28. Ford, K.R.; Myer, G.D.; Toms, H.E.; Hewett, T.E. Gender Differences in the Kinematics of Unanticipated Cutting in Young Athletes. Med. Sci. Sports Exerc. 2005, 37, 124–129. [Google Scholar] [CrossRef] [Green Version]
  29. Steele, J.R.; Brown, J.M. Effects of Chronic Anterior Cruciate Ligament Deficiency on Muscle Activation Patterns during an Abrupt Deceleration Task. Clin. Biomech. 1999, 14, 247–257. [Google Scholar] [CrossRef]
  30. Chappell, J.D.; Creighton, R.A.; Giuliani, C.; Yu, B.; Garrett, W.E. Kinematics and Electromyography of Landing Preparation in Vertical Stop-Jump: Risks for Noncontact Anterior Cruciate Ligament Injury. Am. J. Sports Med. 2007, 35, 235–241. [Google Scholar] [CrossRef]
  31. Chappell, J.D.; Yu, B.; Kirkendall, D.T.; Garrett, W.E. A Comparison of Knee Kinetics between Male and Female Recreational Athletes in Stop-Jump Tasks. Am. J. Sports Med. 2002, 30, 261–267. [Google Scholar] [CrossRef] [PubMed]
  32. Fagenbaum, R.; Darling, W.G. Jump Landing Strategies in Male and Female College Athletes and the Implications of Such Strategies for Anterior Cruciate Ligament Injury. Am. J. Sports Med. 2003, 31, 233–240. [Google Scholar] [CrossRef] [Green Version]
  33. Malinzak, R.A.; Colby, S.M.; Kirkendall, D.T.; Yu, B.; Garrett, W.E. A Comparison of Knee Joint Motion Patterns between Men and Women in Selected Athletic Tasks. Clin. Biomech. 2001, 16, 438–445. [Google Scholar] [CrossRef]
  34. Griffin, L.Y.; Agel, J.; Albohm, M.J.; Arendt, E.A.; Dick, R.W.; Garrett, W.E.; Garrick, J.G.; Hewett, T.E.; Huston, L.; Ireland, M.L.; et al. Noncontact Anterior Cruciate Ligament Injuries: Risk Factors and Prevention Strategies. J. Am. Acad. Orthop. Surg. 2000, 8, 141–150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. McLean, S.G.; Huang, X.; Su, A.; Van Den Bogert, A.J. Sagittal Plane Biomechanics Cannot Injure the ACL during Sidestep Cutting. Clin. Biomech. 2004, 19, 828–838. [Google Scholar] [CrossRef] [Green Version]
  36. Besier, T.F.; Lloyd, D.G.; Ackland, T.R.; Cochrane, J.L. Anticipatory Effects on Knee Joint Loading during Running and Cutting Maneuvers. Med. Sci. Sports Exerc. 2001, 33, 1176–1181. [Google Scholar] [CrossRef] [PubMed]
  37. Podraza, J.T.; White, S.C.; Ramsey, D.K. Multi-Plane, Multi-Joint Lower Extremity Support Moments during a Rapid Deceleration Task: Implications for Knee Loading. Hum. Mov. Sci. 2018, 58, 155–164. [Google Scholar] [CrossRef] [PubMed]
  38. Winter, D.A. Overall Principle of Lower Limb Support during Stance Phase of Gait. J. Biomech. 1980, 13, 923–927. [Google Scholar] [CrossRef]
  39. Bell, A.L.; Pedersen, D.R.; Brand, R.A. A Comparison of the Accuracy of Several Hip Center Location Prediction Methods. J. Biomech. 1990, 23, 617–621. [Google Scholar] [CrossRef]
  40. Bell, A.L.; Brand, R.A.; Pedersen, D.R. Prediction of Hip Joint Centre Location from External Landmarks. Hum. Mov. Sci. 1989, 8, 3–16. [Google Scholar] [CrossRef]
  41. Yu, B.; Gabriel, D.; Noble, L.; An, K. Estimate of the Optimum Cutoff Frequency for the Butterworth Low-Pass Digital Filter. J. App. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
  42. Bisseling, R.W.; Hof, A.L. Handling of Impact Forces in Inverse Dynamics. J. Biomech. 2006, 39, 2438–2444. [Google Scholar] [CrossRef]
  43. Podraza, J.T.; White, S.C. Effect of Knee Flexion Angle on Ground Reaction Forces, Knee Moments and Muscle Co-Contraction during an Impact-like Deceleration Landing: Implications for the Non-Contact Mechanism of ACL Injury. Knee 2010, 17, 291–295. [Google Scholar] [CrossRef]
  44. Kristianslund, E.; Krosshaug, T.; van den Bogert, A.J. Effect of Low Pass Filtering on Joint Moments from Inverse Dynamics: Implications for Injury Prevention. J. Biomech. 2012, 45, 666–671. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  45. Markolf, K.L.; Burchfield, D.M.; Shapiro, M.M.; Shepard, M.F.; Finerman, G.A.; Slauterbeck, J.L. Combined Knee Loading States That Generate High Anterior Cruciate Ligament Forces. J. Orthop. Res. 1995, 13, 930–935. [Google Scholar] [CrossRef] [PubMed]
  46. Kernozek, T.W.; Ragan, R.J. Estimation of Anterior Cruciate Ligament Tension from Inverse Dynamics Data and Electromyography in Females during Drop Landing. Clin. Biomech. 2008, 23, 1279–1286. [Google Scholar] [CrossRef] [PubMed]
  47. Beynnon, B.D.; Fleming, B.C.; Johnson, R.J.; Nichols, C.E.; Renström, P.A.; Pope, M.H. Anterior Cruciate Ligament Strain Behavior during Rehabilitation Exercises in Vivo. Am. J. Sports Med. 1995, 23, 24–34. [Google Scholar] [CrossRef] [PubMed]
  48. Draganich, L.F.; Vahey, J.W. An in Vitro Study of Anterior Cruciate Ligament Strain Induced by Quadriceps and Hamstrings Forces. J. Orthop. Res. 1990, 8, 57–63. [Google Scholar] [CrossRef] [PubMed]
  49. Hashemi, J.; Breighner, R.; Chandrashekar, N.; Slauterbeck, J.R.; Beynnon, B.D. Letter to the Editor: A Framework for Assessing the Viability of Proposed Anterior Cruciate Ligament Injury Mechanisms. Am. J. Sports Med. 2010, 38, NP3-7. [Google Scholar] [CrossRef] [PubMed]
  50. Howell, S.M. Anterior Tibial Translation during a Maximum Quadriceps Contraction: Is It Clinically Significant? Am. J. Sports Med. 1990, 18, 573–578. [Google Scholar] [CrossRef] [PubMed]
  51. Kvist, J.; Gillquist, J. Sagittal Plane Knee Translation and Electromyographic Activity during Closed and Open Kinetic Chain Exercises in Anterior Cruciate Ligament-Deficient Patients and Control Subjects. Am. J. Sports Med. 2001, 29, 72–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  52. Yu, B.; Garrett, W.E. Mechanisms of Non-Contact ACL Injuries. Br. J. Sports Med. 2007, 41 (Suppl. S1), i47–i51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Cappozzo, A.; Catani, F.; Leardini, A.; Benedetti, M.G.; Croce, U.D. Position and Orientation in Space of Bones during Movement: Experimental Artefacts. Clin. Biomech. 1996, 11, 90–100. [Google Scholar] [CrossRef]
  54. Holden, N.P.; Stanhope, S.J. The Effect of Variation in Knee Center Location Estimates on Net Knee Joint Moments. Gait Posture 1998, 7, 1–6. [Google Scholar] [CrossRef]
  55. Holden, J.; Orsini, J.; Siegel, K.; Kepple, T.; Gerber, L.; Stanhope, S. Surface Movement Errors in Shank Kinematics and Knee Kinetics during Gait. Gait Posture 1997, 5, 217–227. [Google Scholar] [CrossRef]
  56. Winter, D.A. Biomechanics and Motor Control of Human Movement, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
  57. Bates, N.A.; Ford, K.R.; Myer, G.D.; Hewett, T.E. Kinetic and Kinematic Differences between First and Second Landings of a Drop Vertical Jump Task: Implications for Injury Risk Assessments. Clin. Biomech. 2013, 28, 459–466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. Dickin, D.C.; Johann, E.; Wang, H.; Popp, J.K. Combined Effects of Drop Height and Fatigue on Landing Mechanics in Active Females. J. Appl. Biomech. 2015, 31, 237–243. [Google Scholar] [CrossRef] [PubMed]
  59. Vanrenterghem, J.; Venables, E.; Pataky, T.; Robinson, M.A. The Effect of Running Speed on Knee Mechanical Loading in Females during Side Cutting. J. Biomech. 2012, 45, 2444–2449. [Google Scholar] [CrossRef] [PubMed]
  60. Chappell, J.D.; Limpisvasti, O. Effect of a Neuromuscular Training Program on the Kinetics and Kinematics of Jumping Tasks. Am. J. Sports Med. 2008, 36, 1081–1086. [Google Scholar] [CrossRef] [PubMed]
Applsci 12 02616 g001 550
Figure 1. Left to right; sagittal (A), frontal (B), and transverse (C) plane representation of the hip, knee, and ankle joint moments during limb support. Counterclockwise moments (+) and clockwise moments (−). Sagittal plane ankle plantarflexor (MAPF), knee extensor (MKE), and hip extensor (MHE) moments contribute to an extensor support moment. Frontal plane ankle abductor (MAAB), knee adductor (MKAD), and hip abductor (MHAB) moments resist medial knee opening. Transverse plane ankle internal rotator (MAIR), knee external rotator (MKER), and hip internal rotator (MHIR) moments resist internal rotation of the tibia.
Figure 1. Left to right; sagittal (A), frontal (B), and transverse (C) plane representation of the hip, knee, and ankle joint moments during limb support. Counterclockwise moments (+) and clockwise moments (−). Sagittal plane ankle plantarflexor (MAPF), knee extensor (MKE), and hip extensor (MHE) moments contribute to an extensor support moment. Frontal plane ankle abductor (MAAB), knee adductor (MKAD), and hip abductor (MHAB) moments resist medial knee opening. Transverse plane ankle internal rotator (MAIR), knee external rotator (MKER), and hip internal rotator (MHIR) moments resist internal rotation of the tibia.
Applsci 12 02616 g001
Applsci 12 02616 g002 550
Figure 2. Sagittal plane limb support moment sex comparisons with contribution ratios for each landing condition. Male: solid line; female: dashed line. LSM at top: Sagittal LSM = MK − MH − MA. Moment ratios at each joint are expressed, relative to the LSM, as contributing (+) or not contributing (−) to limb support. Initial contact is 0 s.
Figure 2. Sagittal plane limb support moment sex comparisons with contribution ratios for each landing condition. Male: solid line; female: dashed line. LSM at top: Sagittal LSM = MK − MH − MA. Moment ratios at each joint are expressed, relative to the LSM, as contributing (+) or not contributing (−) to limb support. Initial contact is 0 s.
Applsci 12 02616 g002
Applsci 12 02616 g003 550
Figure 3. Frontal plane limb support moment sex comparisons with contribution ratios for each landing condition. Male: solid line; female: dashed line. LSM at top: Frontal LSM = MK − MA − MH. Moment ratios at each joint are expressed, relative to the LSM, as contributing (+) or not contributing (−) to limb support. Initial contact is 0 s.
Figure 3. Frontal plane limb support moment sex comparisons with contribution ratios for each landing condition. Male: solid line; female: dashed line. LSM at top: Frontal LSM = MK − MA − MH. Moment ratios at each joint are expressed, relative to the LSM, as contributing (+) or not contributing (−) to limb support. Initial contact is 0 s.
Applsci 12 02616 g003
Applsci 12 02616 g004 550
Figure 4. Transverse plane limb support moment sex comparisons with contribution ratios for each landing condition, male solid line female dashed line. LSM at top: Transverse LSM = MH + MA − MK. Moment ratios at each joint are expressed relative to the LSM as contributing (+) or not contributing (−) to limb support. Initial contact is 0 s.
Figure 4. Transverse plane limb support moment sex comparisons with contribution ratios for each landing condition, male solid line female dashed line. LSM at top: Transverse LSM = MH + MA − MK. Moment ratios at each joint are expressed relative to the LSM as contributing (+) or not contributing (−) to limb support. Initial contact is 0 s.
Applsci 12 02616 g004
Table
Table 1. Limb support moments (sex comparison) initial contact.
Table 1. Limb support moments (sex comparison) initial contact.
ConditionSexPlane
SagittalFrontalTransverse
0–25Female0.30 ± 0.32 (0.102–0.498) *0.01 ± 0.23 (−0.133–0.153)0.45 ± 0.32 (0.252–0.648) *
Male−0.25 ± 0.54 (−0.584–0.084)0.71 ± 0.44 (0.437–0.983) ^0.10 ± 0.15 (0.007–0.193)
25–50Female0.28 ± 0.29 (0.073–0.488) *−0.09 ± 0.22 (−0.247–0.067)0.08 ± 0.12 (−0.006–0.166)
Male−0.36 ± 0.58 (−0.775–0.055)0.18 ± 0.19 (0.044–0.316) ^^0.12 ± 0.17 (−0.002–0.242)
50–75Female0.22 ± 0.44 (−0.095–0.535)−0.06 ± 0.22 (−0.217–0.097)0.01 ± 0.13 (−0.083–0.103)
Male −0.05 ± 0.64 (−0.508–0.408) 0.08 ± 0.23 (−0.085–0.245)0.12 ± 0.20 (−0.023–0.263)
All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Female > Male (p = 0.01) * Male > Female (p = 0.00) ^, (p = 0.01) ^^.
Table
Table 2. Joint moments (sex comparison) initial contact.
Table 2. Joint moments (sex comparison) initial contact.
Hip
ConditionSexPlane
SagittalFrontalTransverse
0–25Female0.02 ± 0.21 (−0.130–0.170)0.08 ± 0.27 (−0.113–0.273) *0.05 ± 0.10 (−0.022–0.122)
Male0.54 ± 0.50 (0.182–0.898) ^−0.18 ± 0.24 (−0.3517–−0.0083)0.11 ± 0.15 (0.003–0.217)
25–50Female0.03 ± 0.28 (−0.170–0.230)0.11 ± 0.24 (−0.062–0.282) **0.09 ± 0.11 (0.011–0.169)
Male0.71 ± 0.40 (0.424–0.996) ^^−0.17 ± 0.25 (−0.349–0.009)0.11 ± 0.15 (0.003–0.217)
50–75Female0.21 ± 0.33 (−0.026–0.446)0.03 ± 0.21 (−0.120–0.180)0.11 ± 0.12 (0.024–0.196)
Male0.40 ± 0.51 (0.035–0.765)−0.06 ± 0.28 (−0.260–0.140)0.12 ± 0.16 (0.006–0.235)
Knee
ConditionSexPlane
SagittalFrontalTransverse
0–25Female0.17 ± 0.16 (0.056–0.285)0.06 ± 0.08 (0.003–0.117)0.02 ± 0.02 (0.006–0.034)
Male0.34 ± 0.17 (0.218–0.462) *0.02 ± 0.08 (−0.037–0.077)0.02 ± 0.03 (−0.002–0.042)
25–50Female0.17 ± 0.19 (0.034–0.306)0.01 ± 0.07 (−0.040–0.060)0.02 ± 0.02 (0.006–0.034)
Male0.43 ± 0.16 (0.316–0.545) **−0.01 ± 0.13 (−0.103–0.083)0.02 ± 0.03 (−0.002–0.042)
50–75Female0.34 ± 0.22 (0.183–0.497)−0.01 ± 0.08 (−0.067–0.047)0.04 ± 0.03 (0.019–0.062)
Male0.43 ± 0.20 (0.287–0.573)0.00 ± 0.14 (−0.1–0.1)0.03 ± 0.06 (−0.013–0.073)
Ankle
ConditionSexPlane
SagittalFrontalTransverse
0–25Female−0.16 ± 0.27 (−0.353–0.033)−0.03 ± 0.08 (−0.087–0.027)0.01 ± 0.02 (−0.004–0.024)
Male0.04 ± 0.19 (−0.096–0.176)−0.03 ± 0.11 (−0.109–0.049)0.02 ± 0.02 (0.006–0.034)
25–50Female−0.14 ± 0.15 (−0.247–−0.033)−0.01 ± 0.07 (−0.060–0.040)0.01 ± 0.02 (−0.004–0.024)
Male0.08 ± 0.14 (−0.020–0.180) *−0.01 ± 0.09 (−0.074–0.054)0.03 ± 0.02 (0.016–0.044) **
50–75Female−0.09 ± 0.24 (−0.262–0.082)0.02 ± 0.11 (−0.059–0.099)0.02 ± 0.02 (0.006–0.034)
Male0.09 ± 0.25 (−0.089–0.269)−0.01 ± 0.07 (−0.060–0.040)0.02 ± 0.03 (−0.002–0.041)
Hip: All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Female > Male (p = 0.03) *, (p = 0.02) **. Male > Female (p = 0.01) ^, (p = 0.00) ^^. Knee: All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Male > Female (p = 0.03) *, (p = 0.01) **. Ankle: All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Male > Female (p = 0.03) *, (p = 0.02) **.
Table
Table 3. Limb support moments (sex comparison) 50 ms.
Table 3. Limb support moments (sex comparison) 50 ms.
ConditionSexPlane
SagittalFrontalTransverse
0–25Female1.93 ± 0.95 (1.25–2.61)1.07 ± 0.51 (0.705–1.44) *−0.27 ± 0.19 (−0.406–−0.134)
Male2.07 ± 1.28 (1.15–2.99)0.41 ± 0.49 (0.059–0.761)−0.35 ± 0.39 (−0.629–−0.071)
25–50Female2.54 ± 0.64 (2.08–2.99)0.74 ± 0.51 (0.375–1.10)−0.43 ± 0.25 (−0.609–−0.251)
Male2.95 ± 0.65 (2.49–3.42)0.31 ± 0.50 (−0.048–0.668)−0.55 ± 0.31 (−0.772–−0.328)
50–75Female2.69 ± 0.69 (2.19–3.18)0.63 ± 0.54 (0.243–1.02)−0.51 ± 0.24 (−0.682–−0.338)
Male2.92 ± 0.62 (2.48–3.36)0.27 ± 0.50 (−0.088–0.628)−0.58 ± 0.31 (−0.802–−0.358)
All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Female > Male (p = 0.01) *.
Table
Table 4. Joint moments (sex comparison) 50 ms.
Table 4. Joint moments (sex comparison) 50 ms.
Hip
ConditionSexPlane
SagittalFrontalTransverse
0–25Female0.27 ± 0.62 (−0.174–0.714)−1.34 ± 0.38 (−1.61–−1.07)−0.14 ± 0.15 (−0.247–−0.033)
Male−0.31 ± 0.70 (−0.811–0.191)−0.91 ± 0.45 (−1.23–−0.588) ^−0.22 ± 0.31 (−0.442–0.002)
25–50Female−0.14 ± 0.49 (−0.491–0.211) *−1.19 ± 0.30 (−2.12–−1.70)−0.27 ± 0.17 (−0.392–−0.148)
Male−0.92 ±0.57 (−1.33–−0.512)−0.92 ± 0.57 (−1.33–−0.512)−0.35 ± 0.23 (−0.515–−0.186)
50–75Female−0.37 ± 0.52 (−0.742–0.002) **−1.15 ± 0.25 (−1.33–−0.971)−0.32 ±0.16 (−0.435–−0.206)
Male−1.02 ± 0.68 (−1.51–−0.534)−0.76 ± 0.58 (−1.17–−0.3451)−0.36 ± 0.27(−0.553–−0.167)
Knee
ConditionSexPlane
SagittalFrontalTransverse
0–25Female1.43 ± 0.55 (1.04–1.82)−0.17 ± 0.23 (−0.334–−0.006)0.13 ± 0.11 (0.051–0.209)
Male1.57 ± 0.55 (1.18–1.96)−0.38 ± 0.27 (−0.573–−0.187)0.13 ± 0.11 (0.051–0.209)
25–50Female1.68 ± 0.56 (1.28–2.08)−0.33 ± 0.33 (−0.566–−0.094)0.20 ± 0.10 (0.128–0.272)
Male1.84 ± 0.42 (1.54–2.14)−0.49 ± 0.34 (−0.733–−0.246)0.24 ± 0.13 (0.147–0.333)
50–75Female1.80 ± 0.53 (1.42–2.18)−0.40 ± 0.29 (−0.607–−0.193)0.24 ± 0.10 (0.169–0.312)
Male1.73 ± 0.52 (1.36–2.10)−0.41 ± 0.34 (−0.653–−0.167)0.25 ± 0.15 (0.143–0.357)
Ankle
ConditionSexPlane
SagittalFrontalTransverse
0–25Female−0.77 ± 0.74 (−1.30–−0.241)0.11 ± 0.25 (−0.069–0.289)0.00 ± 0.04 (−0.03−0.03)
Male−0.19 ± 0.51 (−0.555–0.175)0.12 ± 0.23 (−0.045–0.285)0.00 ± 0.07 (−0.05−0.05)
25–50Female−0.73 ± 0.44 (−1.04–−0.415)0.12 ± 0.21 (−0.030–0.270)0.03 ± 0.04 (0.001−0.059)
Male−0.18 ± 0.35 (−0.430–0.070) *0.12 ± 0.21 (−0.030–0.270)0.03 ± 0.07 (−0.020−0.080)
50–75Female−0.52 ± 0.59 (−0.942–−0.098)0.11 ± 0.26 (−0.076–0.296)0.05 ± 0.04 (0.021–0.079)
Male−0.17 ± 0.51 (−0.534–0.195)0.08 ± 0.15 (−0.027–0.187)0.02 ± 0.07 (−0.030–0.070)
Hip: All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Female > Male (p = 0.04) *, (p = 0.03) **. Male > Female (p = 0.03) ^. Knee: All values are means in Nm/kg ± SD (95% CI). No significant differences. Ankle: All values are means in Nm/kg ± SD (95% CI). Significant differences in bold: Male > Female (p = 0.01) *.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Podraza, J.T.; White, S.C. Identification of Sex Differences within Lunge Decelerations via Lower Extremity Support Moments; Implications for ACL Injury Disparity, Prevention, and Rehabilitation. Appl. Sci. 2022, 12, 2616. https://doi.org/10.3390/app12052616

AMA Style

Podraza JT, White SC. Identification of Sex Differences within Lunge Decelerations via Lower Extremity Support Moments; Implications for ACL Injury Disparity, Prevention, and Rehabilitation. Applied Sciences. 2022; 12(5):2616. https://doi.org/10.3390/app12052616

Chicago/Turabian Style

Podraza, Jeffery T., and Scott C. White. 2022. "Identification of Sex Differences within Lunge Decelerations via Lower Extremity Support Moments; Implications for ACL Injury Disparity, Prevention, and Rehabilitation" Applied Sciences 12, no. 5: 2616. https://doi.org/10.3390/app12052616

APA Style

Podraza, J. T., & White, S. C. (2022). Identification of Sex Differences within Lunge Decelerations via Lower Extremity Support Moments; Implications for ACL Injury Disparity, Prevention, and Rehabilitation. Applied Sciences, 12(5), 2616. https://doi.org/10.3390/app12052616

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop