Finite Element Analysis of the Epiretinal Membrane Contraction

Abstract

The epiretinal membrane is a thin sheet of fibrous tissue that can form over the macular area of the retina, and may result in the loss of visual acuity or metamorphopsia, due to superficial retinal folds. A vitrectomy surgery, the current treatment procedure for this pathology, is only performed after symptoms are present. However, sometimes the patients do not present any vision improvements after the surgery. The use of computational methods for a patient-specific biomechanical analysis can contribute to better understanding the mechanisms behind the success or failure of a vitrectomy. Using medical data from two patients who underwent a vitrectomy, one with substantial improvements and another with no improvements, an analysis of the retinal displacement due to the contraction of the epiretinal membrane was performed. Our results suggest a causal effect between the magnitude of the retinal displacements caused by the epiretinal membrane contraction and the outcome of the vitrectomy procedure.

1. Introduction

The development of an Epiretinal Membrane (ERM) is a relatively common disorder of the vitreomacular interface that can cause visual impairment [1]. The ERM is a pathologic fibrocellular membrane that lies immediately superjacent to the inner surface of the retina, the Internal Limiting Membrane (ILM), and varies in thickness from a single layer of collagen with interspersed cells to a thicker, multilayered fibrocellular proliferation, which often results in coarse folds on the retinal surface [2].

This pathology can be classified into two types: idiopathic and secondary ERM. An ERM may develop without any antecedent ocular conditions or surgical procedures, termed idiopathic or primary ERM. Oppositely, secondary ERM is associated with a variety of ocular diseases, such as ocular inflammatory diseases, retinal vascular disease, retinal detachments, trauma, or surgery [1,3]. The prevalence of this disease ranges from 4.0 to 6.2% and increases with age [1] with peak prevalence being observed in those between 70 and 79 years (11.6∼35.7%) [2].

In the earlier stages, ERMs do not cause visual symptoms. However, as it progresses, it can contract and create superficial retinal folds leading to distortion of the retinal anatomy that can result in visual symptoms such as loss of visual acuity and metamorphopsia [2,3].

Current imaging techniques, such as Spectral-Domain Optical Coherence Tomography (SD-OCT) with three-dimensional reconstruction can allow evaluation of the macula in cross-section and three-dimensionally [4,5]. SD-OCT is a harmless, noninvasive medical imaging technique used to produce high-resolution cross-sectional images of biological tissues [5,6]. Another relevant feature of SD-OCT is that due to its scanning speed, cross-sectional nature and image quality, it can be used for 3D reconstruction of the retina and ERM, enabling detailed analysis [7].

Currently, the treatment options for ERM are limited, consisting of either observation or surgical intervention. Surgical intervention corresponds to pars plana vitrectomy with ERM removal with or without ILM removal [4,8]. At this stage, it is not possible to know in advance, in the pre-operative stage, which patients will benefit visually from the surgery. We hypothesize a link between the displacements of the retinal surface and the capacity of recovering visual acuity from the surgery. To test the hypothesis, it is necessary to pre-operatively quantify the displacements that the ERM can cause on the retina. Numerical simulation can be a powerful tool for a variety of purposes, and it will be used in this study as a way to compute displacements on the retinal surface, by simulating the EMR contraction.

Although numerical simulation studies can be found on the literature related to the eye, ranging from the study of the eye temperature to the study of specific eye components [9,10,11,12,13,14,15], to the authors’ knowledge no study exists concerning the numerical simulations of the ERM contraction. In the existing literature related to numerical studies of the eye [16,17,18,19,20,21], the most used method in these types of works is the Finite Element Method (FEM), being the method chosen in the present study.

No consensus exists on the most adequate type of materials to simulate the behaviour of the retina membrane, with several sources using different material models. However, a correct understanding of previous studies found in the literature allows the selection of two preferential constitutive models, the hyperelastic and linear elastic constitutive models [12,20,22,23]. Considering the work performed by both Chagnon et al. [24], where the author concluded that most biological tissues can be described by hyperelastic materials, and by Qian et al. [21], where it is reported that the results obtained with hyperelastic models to simulate the retina behaviour are similar to the experimental results, it becomes reasonable to take these constitutive models as the baseline for the following work.

2. Materials and Methods

2.1. Hyperelastic Constitutive Model for the Retina

For the numerical simulation of the retina, the Mooney-Rivlin model [25,26] was implemented using a user subroutine UMAT for ABAQUS [20,21]. Equation (1) represents the strain energy density function for the Mooney-Rivlin constitutive model.

$${\mathrm{\Psi }}_{\mathrm{MR}}={\mathrm{\Psi }}_{\mathrm{MRiso}}({\overline{I}}_1,{\overline{I}}_2)+{\mathrm{\Psi }}_{\mathrm{vol}}\left(J\right)$$

(1)

The isochoric component ${\mathrm{\Psi }}_{\mathrm{MRiso}}$, representing the isotropic matrix behaviour is given by:

$${\mathrm{\Psi }}_{\mathrm{MRiso}}=C_{10}\left({\overline{I}}_1-3\right)+C_{01}\left({\overline{I}}_2-3\right).$$

(2)

The strain energy associated with the volume change is given by:

$${\mathrm{\Psi }}_{\mathrm{vol}}=\frac{1}{D_1}{(J-1)}^2.$$

(3)

In these equations $C_{01}$, $C_{10}$ and $D_1$ are material parameters obtained from stress/strain experimental measurements from real mechanical tests, J represents the Jacobian of the deformation and ${\overline{I}}_1$ and ${\overline{I}}_2$ represent the strain invariants [27,28]:

$${\overline{I}}_1=tr\left(\overline{\mathbf{C}}\right)=J^{-2/3}tr\left(\mathbf{C}\right)$$

(4)

$${\overline{I}}_2=\frac{1}{2}\left({\overline{I}}_1^2-\overline{\mathbf{C}}:\overline{\mathbf{C}}\right)=\frac{1}{2}{J}^{-4/3}\left({I_1}^2-\mathbf{C}:\mathbf{C}\right)$$

(5)

where $\overline{\mathbf{C}}$ is the modified left Cauchy Green deformation tensor:

$$\overline{\mathbf{C}}={\overline{\mathbf{F}}}^T\overline{\mathbf{F}}$$

(6)

and $\overline{\mathbf{F}}$ is the modified deformation gradient:

$$\overline{\mathbf{F}}=J^{-1/3}\mathbf{F}.$$

(7)

2.2. Anisotropic Hyperelastic Constitutive Model for the ERM

In order to simulate the ERM contraction, a fibrocellular tissue, the transversely isotropic constitutive model proposed by Martins et al. [29] for the simulation of skeletal muscles contraction, was considered. The original model was implemented and modified so that it takes into account two families of fibres embedded into the isotropic matrix. The soft ERM will act as an orthotropic material if the fibres form an angle of 90° between them. In any other case, if the angle is different, the ERM membrane will present an anisotropic behaviour [27,28].

For the modified version of the Martins, J.A.C. et al. [29], the stored strain energy function is defined by:

$${\mathrm{\Psi }}_{\mathrm{JACf}}={\mathrm{\Psi }}_{\mathrm{JACmat}}+\sum _{i=1}^2{\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}+{\mathrm{\Psi }}_{\mathrm{vol}}$$

(8)

where ${\mathrm{\Psi }}_{\mathrm{JACmat}}$ is the isotropic contribution of the matrix:

$${\mathrm{\Psi }}_{\mathrm{JACmat}}=c\left\{exp\left[b\left({\overline{I}}_1-3\right)\right]\right\}.$$

(9)

The contribution of each family of fibres ${\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}$ can be divided into a passive elastic part, ${\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}^{PE}$ and an active part, ${\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}^{SE}$, responsible for the muscles contraction:

$${\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}={\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}^{PE}+{\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}^{SE}$$

(10)

where

$${\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}^{PE}=A\left\{exp\left[a{\left({\overline{\lambda }}_f-1\right)}^2\right]-1\right\}$$

(11)

is the passive elastic part and

$${\mathrm{\Psi }}_{{\mathrm{fib}}_{\mathrm{i}}}^{SE}=T_0^m{\int }_1^{{\overline{\lambda }}_f}{f}_{SE}d{\overline{\lambda }}_f$$

(12)

is the active part.

For the volumetric strain energy, associated with the volume change ${\mathrm{\Psi }}_{\mathrm{vol}}$, the same equation given by Equation (3) is used.

In these equations c, b, A and a are material constants, ${\overline{\lambda }}_f$ is the stretch ratio of the ERM fibres, $T_0^m$ is the maximum tension produced by the fibres at resting length and $f_{SE}$ is given by Equation (13) [29]:

$$f_{SE}=\delta \left\{\begin{array}{cc}1-4{({\overline{\lambda }}_f-1)}^2\hfill & \mathrm{for} 0.5<{\overline{\lambda }}_f<1.5\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

where $\delta \in [0,1]$ is the activation variable [27].

2.3. Parameters Calibration

For the Mooney-Rivlin constitutive model, used for the retina, the values obtained by Rusovici et al. [20], in a study on the inclusion of a stent inside the eye, were used on this work. The values considered for the Mooney-Rivlin constitutive model are $C_{10}=11.765$ kPa, $C_{01}=27$ kPa and $D_1=1\times {10}^{-3}$${\mathrm{kPa}}^{-1}$.

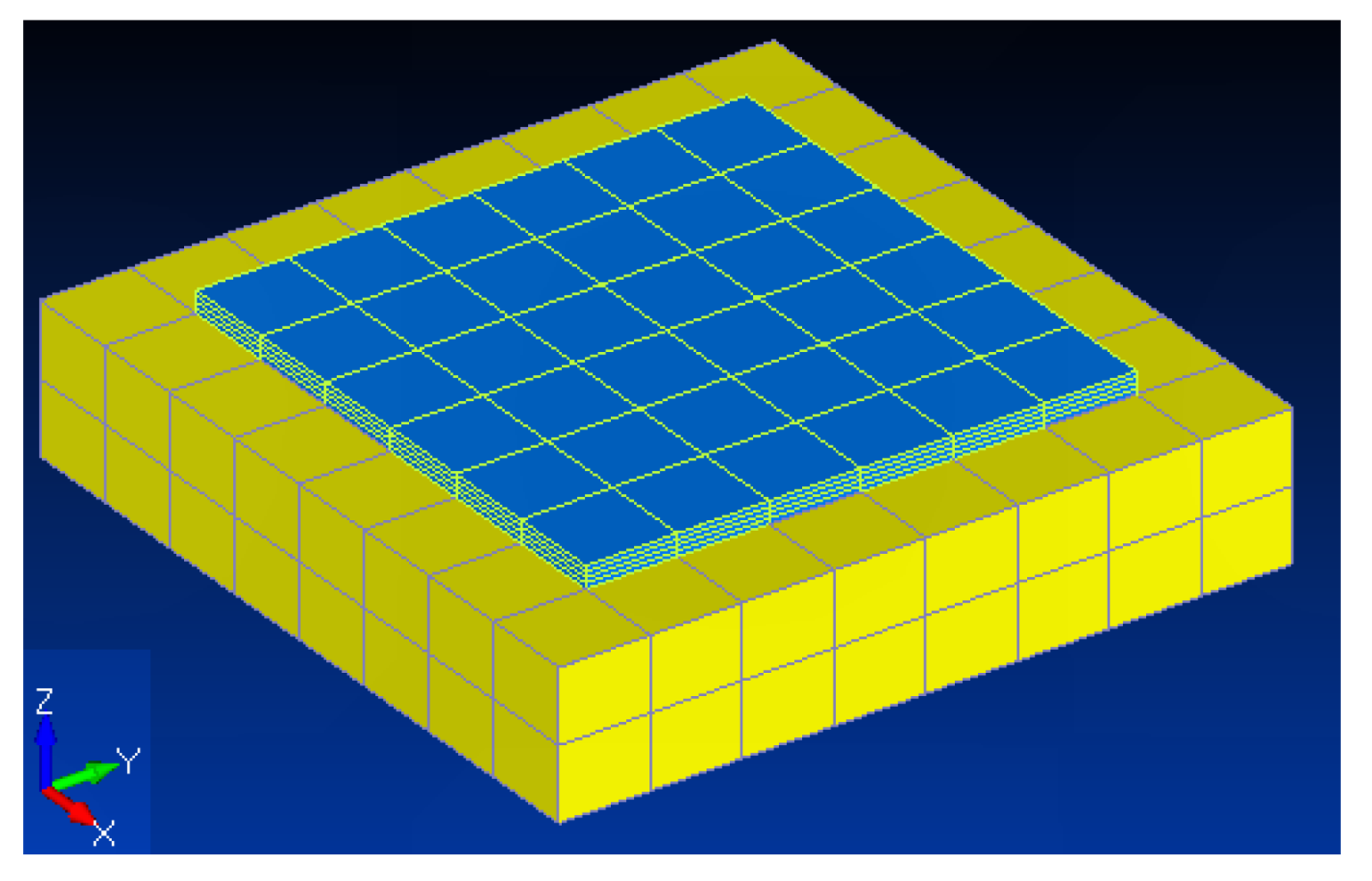
In order to obtain the material parameters for the ERM, a simple calibration model was developed, Figure 1. The calibration model was defined as a simplified representation of the retina and ERM (Figure 1). The dimensions for the ERM were based on the case of formation over the macula, leading to a higher loss of visual acuity. As such, taking into consideration the normal diameter of the macula, the ERM was created with a length and width of 1.5 mm. The thickness of the membrane, 0.05 mm, was extracted from an SD-OCT scan image. Regarding the retina, a thickness of 0.4 mm, supported in the literature [30], was used, while its transversal dimensions of 2.0 mm were defined to be bigger than the ERM dimensions. Although the retina is composed of seven layers, in the present work, only one layer with homogeneous properties was considered [20], in order to reduce the model complexity. The boundary conditions were assigned to prevent movement in the inferior face. Several model properties and the number of elements along the retina thickness were tested through a trial and error process.

For the calibration process, the results from Arimura et al. [31] were used. In his work, Arimura et al studied the retinal vessels contraction during an epiretinal membrane evaluation, conducted in 29 eyes with epiretinal membranes during 3 years. The allowed obtaining a maximum horizontal displacement of 0.22 mm and a maximum vertical displacement of 0.14 mm. These values were used in the calibration process, for obtaining the material properties that best represent the ERM membrane behaviour.

The calibrated results for the ERM constitutive model parameters, with two fibre families, are shown in

Table 1. Constitutive parameters for the J. Martins constitutive model [29], used on the ERM.

c [kPa]	b	A [kPa]	a	${\mathbf{T}}_{\mathbf{o}}^{\mathbf{m}}$ [kPa]	1st FF	2nd FF	${\mathbf{D}}_1$ $[{\mathbf{kPa}}^{-1}$]
152.25	0.206	$0.86$	12.43	600	0	50	$1.0\times {10}^{-3}$

.

2.4. Case Studies

To test the developed models in real case scenarios, two different patients, with two different outcomes, were selected from the S. Joao Hospital. The first patient showed improvement of visual acuity post-procedure, while the second patient showed no improvements. The characteristics of each patient are represented in

Table 2. Patients characteristics.

	Recovered Patient	Non-Recovered Patient
Gender	Male	Female
Other Eye	Healthy	With Membrane
Time between exams [months]	2	13

.

The present research was approved by the Ethics and Health Committee of Centro Hospitalar São João, Porto, with CES 81/18 approval code.

In order to experimentally obtain the displacements caused by the ERM contraction, the pre and post-operative Scanning Laser Ophthalmoscopy (SLO) images for each patient were overlapped. By comparing the differences in the position of the blood vessels it is possible to obtain the displacement field suffered by the retina, directly caused by the presence of the membrane. The pre and post operative SLO and OCT images are shown in Figure 2, with the overlaid images and computed displacements, represented by arrows, shown in Figure 3.

Table 3. Maximum retinal displacements for the recovered and non-recovered patient.

	Horizontal Disp. [mm]	Vertical Disp. [mm]
Recovered Patient	0.4265	0.2890
Non-recovered Patient	0.3497	0.2491

represents the maximum obtained displacements in each orthogonal direction, which are relevant for determining the degree of metamorphopsia [31].

2.5. Image Acquisition and 3D Model Reconstruction

The characteristics of the SD-OCT images allows them to be used for a 3D reconstruction based on multiple slice images - as shown in Figure 2, represented by the green lines. Since the objective of the numerical simulations is the analysis of the effects of an ERM contraction, starting from a healthy state, the 3D model was built, based on the healthy eye of Patient 1, as shown in Figure 4.

The images of interest were initially imported to MIMICS^®, where a manual segmentation was performed on all sequential images, resulting in a 3D reconstruction. The initial model was then imported into 3-matic^® to be improved, evolving into a more coherent mesh. Ultimately, the improved mesh was imported to FEMAP^® to generate an interior mesh, necessary for the numerical simulations. The retina finite element model obtained from the OCT images reconstruction is shown in Figure 5 and consists of 17,793 linear tetrahedral elements and 4616 nodes.

In relation to the 3D modelling of the ERM, there was no available information regarding its initial configuration, since the available OCT images show the ERM on its final, contracted configuration. To overcome this limitation, the initial form of the ERM of both patients was estimated based on the final form and the displacements shown in Figure 3. The model for the ERM was obtained by extruding the projected shape of the enlarged ERM, using linear wedge elements. The thickness of the ERM, was computed in order to maintain the ERM volume constant, after the contraction, since it was possible to obtain the final thickness of the ERM using the OCT scans. From the OCT scans a thickness of 0.14 mm for Patient 1 and 0.07 mm for Patient 2 were measured. An initial thickness of 0.1 mm for Patient 1 and 0.04 mm for Patient 2 were considered for the ERM.

The final models for both the retina and the ERM were combined in ABAQUS to run the finite elements simulations, as can be seen in Figure 6. For the number of elements along the thickness of the membrane, after several tests conducted, only one element was used along the thickness, for the final model, since it allowed to produce the best results. The final mesh for the ERM, shown in Figure 6 consisted of 130 elements and 90 nodes, for Patient 1 and 657 elements and 480 nodes, for Patient 2.

The models only differ between patients in the shape and thickness of the ERM, since the same 3D reconstruction of the retina was used in both cases. Boundary conditions were set to simulate the contraction of the retina, similar to the calibration model. As such, the inferior face of the retina was fixed, inhibiting any displacements and the activation level $\delta$ of the contractile fibres was ramped up to 1.0.

3. Results

Simulations using the constitutive models with the optimized material properties, obtained in the calibration process were run and for each patient, the maximum displacements suffered by the retina and the membrane final thickness were measured. The numerical results were compared with the displacements measured for both patients and the already known thickness, allowing to obtain the relative errors.

For the selected material model, simulation results concerning the displacements are shown in Figure 7, Figure 8 and Figure 9 for both patients. By the analysis of these Figures and

Table 4. Results for the retina displacements and membrane thickness.

Patient	Horizontal Displacement [mm]	Error [%]	Vertical Displacement [mm]	Error [%]	Final Thickness [mm]	Error [%]
Recovered	0.4151	2.668	0.26481	8.383	0.1439	2.798
Non-Recovered	0.3506	0.271	0.2603	4.527	0.0723	3.347

, it is possible to conclude that the retina of the Recovered Patient suffered a higher contraction than the retina of the non-recovered Patient.

The simulation results for both cases are presented in Table 4. For the patient that showed signs of recovery the minimum errors for both the horizontal and vertical displacements were 2.668% and 8.383% respectively and the membrane final thickness error was 2.798%.

On other hand, for the patient that did not show condition improvement, the minimum errors for horizontal and vertical displacements were 0.271% and 4.527%, respectively and the membrane final thickness error was 3.347%.

This allows to conclude that for both patients the models used, namely the Martins constitutive model and the Mooney-Rivlin constitutive model, were able to correctly simulate the contraction of the ERM and the deformations that this contraction causes on the retina.

The difference between the retina contraction of the patients may indicate a connection between the recovery of one of the patients after the surgery and the non-recovery of the other patient. In fact, for the non-recovered Patient, the low contraction of the membrane and retina, resulted in smaller displacements and in a lower difference between the initial and the final membrane thickness. For this patient, this means that if the membrane is removed, the displacements suffered by the retina will also be small, which results in minor changes to the retina configuration and reduced recovery of visual acuity.

On the other side, for the recovered Patient, since the displacements induced in the retina, by the ERM contraction, are high, the retina will show large displacements if the ERM is removed. When the membrane is removed, the displacements suffered by the retina, to return to its initial configuration are much higher, which will lead to an improvement of the visual acuity.

4. Discussion

In a more complex and developed world the alliance between mechanical engineering and medicine, especially the use of numerical simulations to solve medical problems, is increasingly important. The human eye saw some developments with this collaboration, with an increasing number of studies made about the use of approaches typical of mechanical engineering on it and its pathologies. One of these pathologies is the ERM, which is treated resorting to a surgery called vitrectomy, in the most critical cases. This surgery does not always have the desired results, since some patients do not present any improvements in their symptoms. A study of this pathology and related aspects is an area with great impact on the life quality of the patients as well as in the understanding of the conditions where the surgery is the indicated step.

5. Conclusions

For that, we constructed a model that allow us to simulate the membrane contraction and measure the displacements that this pathology causes in the patient’s retina. This model was then applied to two different cases: one where the patient recovered his visual acuity and another one where, even after surgery, his visual acuity was not recovered. From these two cases, it was possible to conclude that the displacements for the patient that recovers the vision acuity are much higher than for the other patient. One possible explanation is related to the accommodation of the retina in the second patient.

The present methodology was only tested for two extreme scenarios, a fully recovered patient and a non recovered patient. In order to further test the present methodology, it would be important to apply it to more patients, including patients who had different degrees of recovery.