Discriminative Frequencies and Temporal EEG Segmentation in the Motor Imagery Classification Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset and Subjects
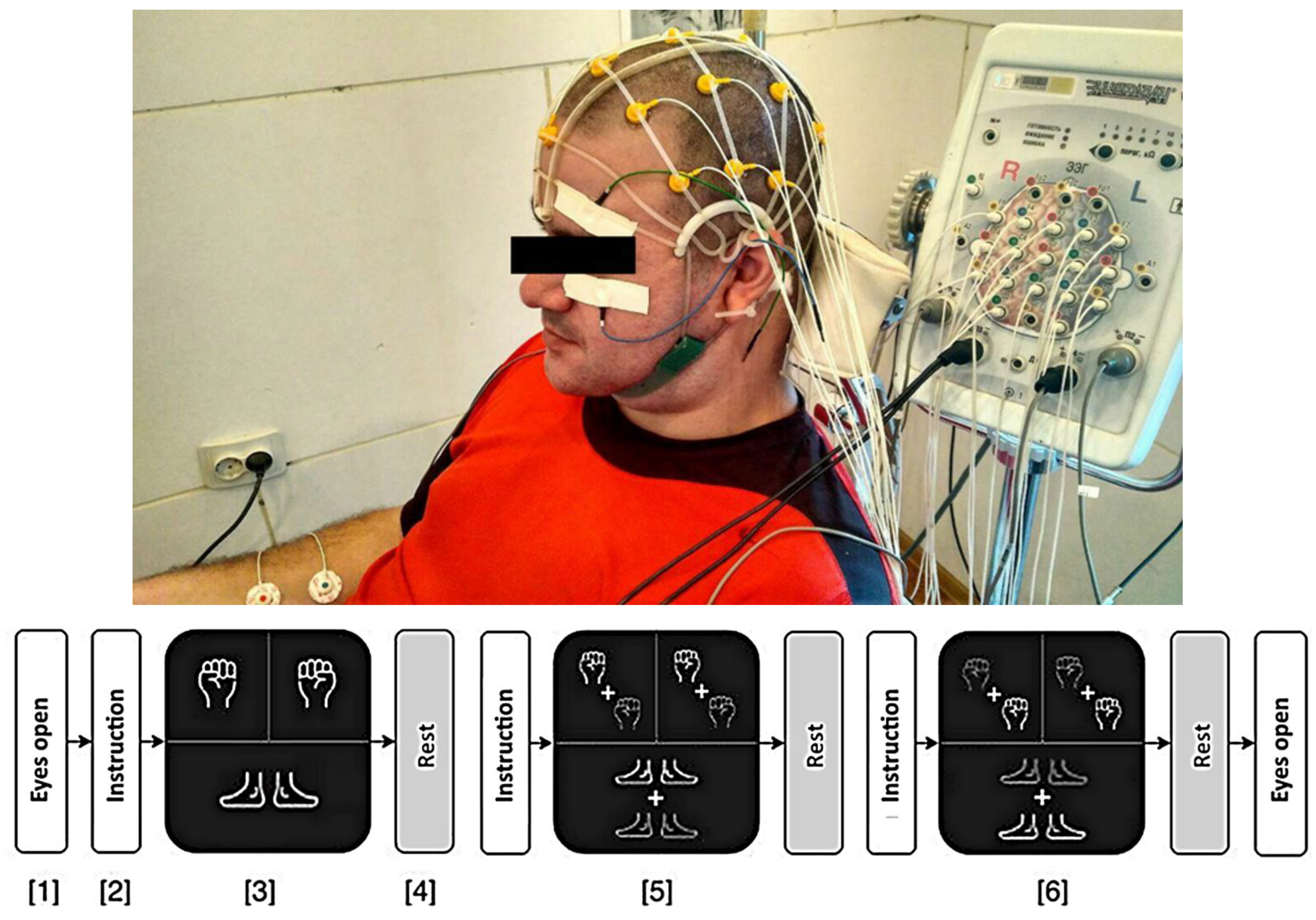
2.2. Experimental Design
2.3. Linear Transformations
- For each class of movement, a separate model of a 1-component LDA model (transformer) was trained: the training sample included all the examples of the given class and as many resting state signal examples.
- On the completion of the transformation, 153 values of features collapsed into one, a linear combination, while for each class, there was a specific set of coefficients.
- After tuning all class-specific transformers, the final feature vector was three-dimensional (one feature for each class).
- A two second long epoch of a single MI and a single randomly chosen two second long epoch of background signal are independently split into windows of lengths of 750 ms with 100 ms shift; this results in 13 windows of the MI and 13 windows of the background signal.
- Features are computed for each of 26 examples considering the results of previous searches for informatory frequencies for the current subject.
- The sample of the current MI is formed as follows:
- Each MI example feature vector is the result of stacking differences between fixed background window features and all the MI windows features (thus, on a smaller scale, the resulting feature vector periodically represents a feature number for each window, and, on larger scale, it represents window number, i.e., time);
- Each background example feature vector is the result of stacking differences between a fixed background window’s features and all the background windows’ features.
- The resulting two-class sample is of shape 26 * (13 * n features).
- An LDA model is trained on the sample obtained.
- The trained LDA model is applied to the windowed example feature representation of the whole MI example calculated as the result of stacking differences between the averaged background windows feature vector and all the MI window features.
- The transformed representation of the whole MI is added to the final sample.
- Steps 1–6 are repeated for each MI.
- Logistic regression is applied to classify the resulting three-class transformed sample.
2.4. Classification
2.5. Frequency Spectrum Features
2.6. Frequency Filtering
2.7. Receiver Operating Characteristic Curves
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frolov, A.A.; Bobrov, P.D. Brain–Computer Interfaces: Neurophysiological Bases and Clinical Applications. Neurosci. Behav. Physiol. 2018, 48, 1033–1040. [Google Scholar] [CrossRef]
- Mane, R.; Chouhan, T.; Guan, C. BCI for stroke rehabilitation: Motor and beyond. J. Neural Eng. 2020, 17, 041001. [Google Scholar] [CrossRef] [PubMed]
- Lazurenko, D.; Kiroy, V.N.; Shepelev, I.E.; Podladchikova, L.N. Motor Imagery-based Brain-Computer Interface: Neural Network Approach. Opt. Mem. Neural Netw. 2019, 28, 109–117. [Google Scholar] [CrossRef]
- Khan, M.A.; Das, R.; Iversen, H.K.; Puthusserypady, S. Review on motor imagery based BCI systems for upper limb post-stroke neurorehabilitation: From designing to application. Comput. Biol. Med. 2020, 123, 103843. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G. S5: Movement-related desynchronization and resting state sensorimotor networks. Clin. Neurophysiol. 2014, 125, S2. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C. Future prospects of ERD/ERS in the context of brain–computer interface (BCI) developments. Prog. Brain Res. 2006, 159, 433–437. [Google Scholar] [CrossRef]
- Yao, L.; Sheng, X.; Zhang, D.; Jiang, N.; Farina, D.; Zhu, X. A BCI System Based on Somatosensory Attentional Orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Neuper, C.; Scherer, R.; Wriessnegger, S.; Pfurtscheller, G. Motor imagery and action observation: Modulation of sensorimotor brain rhythms during mental control of a brain—computer interface. Clin. Neurophysiol. 2009, 120, 239–247. [Google Scholar] [CrossRef]
- Friedrich, E.V.; McFarland, D.J.; Neuper, C.; Vaughan, T.M.; Brunner, P.; Wolpaw, J.R. A scanning protocol for a sensorimotor rhythm-based brain–computer interface. Biol. Psychol. 2009, 80, 169–175. [Google Scholar] [CrossRef] [Green Version]
- McFarland, D.J.; Krusienski, D.J.; Sarnacki, W.A.; Wolpaw, J.R. Emulation of computer mouse control with a noninvasive brain–computer interface. J. Neural Eng. 2008, 5, 101–110. [Google Scholar] [CrossRef]
- Markazi, S.A.; Qazi, S.; Stergioulas, L.S.; Ramchurn, A.; Bunce, D. Wavelet Filtering of the P300 Component in Event-Related Potentials. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; Volume 1, pp. 1719–1722. [Google Scholar] [CrossRef]
- Kiroi, V.N.; Vladimirskii, B.M.; Aslanyan, E.V.; Bakhtin, O.M.; Minyaeva, N.R. Electrographic Correlates of Actual and Imagined Movements: Spectral Analysis. Neurosci. Behav. Physiol. 2012, 42, 21–27. [Google Scholar] [CrossRef]
- McFarland, D.J.; McCane, L.M.; David, S.; Wolpaw, J. Spatial filter selection for EEG-based communication. Electroencephalogr. Clin. Neurophysiol. 1997, 103, 386–394. [Google Scholar] [CrossRef]
- Garrett, D.; Peterson, D.; Anderson, C.; Thaut, M. Comparison of linear, nonlinear, and feature selection methods for EEG signal classification. IEEE Trans. Neural Syst. Rehabilit. Eng. 2003, 11, 141–144. [Google Scholar] [CrossRef]
- Peterson, D.A.; Knight, J.N.; Kirby, M.J.; Anderson, C.W.; Thaut, M.H. Feature Selection and Blind Source Separation in an EEG-Based Brain-Computer Interface. EURASIP J. Adv. Signal Process. 2005, 2005, 218613. [Google Scholar] [CrossRef] [Green Version]
- Attallah, O.; Abougharbia, J.; Tamazin, M.; Nasser, A.A. A BCI System Based on Motor Imagery for Assisting People with Motor Deficiencies in the Limbs. Brain Sci. 2020, 10, 864. [Google Scholar] [CrossRef]
- Allison, B.Z.; Cho, W.; Ortner, R.; Heilinger, A.; Edlinger, G.; Guger, C. Validation of a Brain-Computer Interface (BCI) System Designed for Patients with Disorders of Consciousness (DOC): Regular and Sham Testing with Healthy Participants. In Lecture Notes in Computer Science—Leibniz Center for Informatics; Springer: Cham, Germany, 2017; pp. 253–265. [Google Scholar] [CrossRef]
- Jiang, L.; Stocco, A.; Losey, D.M.; Abernethy, J.A.; Prat, C.S.; Rao, R.P.N. BrainNet: A Multi-Person Brain-to-Brain Interface for Direct Collaboration Between Brains. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Kruse, A.; Suica, Z.; Taeymans, J.; Schuster-Amft, C. Effect of brain-computer interface training based on non-invasive electroencephalography using motor imagery on functional recovery after stroke—A systematic review and meta-analysis. BMC Neurol. 2020, 20, 1–14. [Google Scholar] [CrossRef]
- Wu, S.-L.; Wu, C.-W.; Pal, N.R.; Chen, C.-Y.; Chen, S.-A.; Lin, C.-T. Common spatial pattern and linear discriminant analysis for motor imagery classification. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind, and Brain (CCMB), Singapore, 16–19 April 2013; pp. 146–151. [Google Scholar] [CrossRef]
- Birbaumer, N.; Kübler, A.; Ghanayim, N.; Hinterberger, T.; Perelmouter, J.; Kaiser, J.; Iversen, I.; Kotchoubey, B.; Neumann, N.; Flor, H. The thought translation device (TTD) for completely paralyzed patients. IEEE Trans. Rehabilit. Eng. 2000, 8, 190–193. [Google Scholar] [CrossRef] [Green Version]
- Kiroy, V.N.; Lazurenko, D.; Shepelev, I.E.; Minyaeva, N.R.; Aslanyan, E.V.; Bakhtin, O.M.; Shaposhnikov, D.; Vladimirskiy, B.M. Changes in EEG spectral characteristics in the course of neurofeedback training. Hum. Physiol. 2015, 41, 269–279. [Google Scholar] [CrossRef]
- Shepelev, I.E.; Lazurenko, D.; Kiroy, V.N.; Aslanyan, E.V.; Bakhtin, O.M.; Minyaeva, N.R. A Novel Neural Network Approach to Creating a Brain–Computer Interface Based on the EEG Patterns of Voluntary Muscle Movements. Neurosci. Behav. Physiol. 2018, 48, 1145–1157. [Google Scholar] [CrossRef]
- Selim, S.; Tantawi, M.M.; Shedeed, H.A.; Badr, A. A csp\am-ba-svm approach for motor imagery bci system. IEEE Access 2018, 6, 49192–49208. [Google Scholar] [CrossRef]
- Tang, Z.; Li, C.; Sun, S. Single-trial EEG classification of motor imagery using deep convolutional neural networks. Optik 2017, 130, 11–18. [Google Scholar] [CrossRef]
- Aggarwal, S.; Chugh, N. Signal processing techniques for motor imagery brain computer interface: A review. Array 2019, 1–2, 100003. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, W.; Lin, C.L.; Pei, Z.; Chen, J.; Chen, Z. Boosting-LDA algriothm with multi-domain feature fusion for mo-tor imagery EEG decoding. Biomed. Signal Processing Control 2021, 70, 102983. [Google Scholar] [CrossRef]
- Tyagi, A.; Nehra, V. Classification of motor imagery EEG signals using SVM, k-NN and ANN. CSI Trans. ICT 2016, 4, 135–139. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Yusoff, M.Z.; Malik, A.S.; Bahloul, M.R.; Adam, D.M.; Adam, I.K. Comparison of EEG signal decomposition methods in classification of motor-imagery BCI. Multimedia Tools Appl. 2018, 77, 21305–21327. [Google Scholar] [CrossRef]
- Shankar, A.; Muttan, S.; Vaithiyanathan, D. Signal Processing and Classification for Electroencephalography Based Motor Imagery Brain Computer Interface. J. Med. Imaging Health Inform. 2021, 11, 2918–2927. [Google Scholar] [CrossRef]
- Ma, T.; Wang, S.; Xia, Y.; Zhu, X.; Evans, J.; Sun, Y.; He, S. CNN-based classification of fNIRS signals in motor imagery BCI system. J. Neural Eng. 2021, 18, 056019. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, F.; Solé-Casals, J.; Dinares-Ferran, J.; Cichocki, A.; Yang, Z.; Sun, Z. A Novel Deep Learning Approach With Data Augmentation to Classify Motor Imagery Signals. IEEE Access Digit. Object Identifier 2019, 15945. [Google Scholar] [CrossRef]
- Hou, Y.; Zhou, L.; Jia, S.; Lun, X. A novel approach of decoding EEG four-class motor imagery tasks via scout ESI and CNN. J. Neural Eng. 2019, 17, 016048. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, E. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Welch, P.D. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Feng, Z.; Lu, N.; Luo, J. Toward optimal feature and time segment selection by divergence method for EEG signals classification. Comput. Biol. Med. 2018, 97, 161–170. [Google Scholar] [CrossRef]
- Hjorth, B. EEG analysis based on time domain properties. Electroencephalogr. Clin. Neurophysiol. 1970, 29, 306–310. [Google Scholar] [CrossRef]
- Jusas, V.; Samuvel, S.G. Classification of Motor Imagery Using Combination of Feature Extraction and Reduction Methods for Brain-Computer Interface. Inf. Technol. Control 2019, 48, 225–234. [Google Scholar] [CrossRef] [Green Version]
- Craik, A.; He, Y.; Contreras-Vidal, J.L. Deep learning for electroencephalogram (EEG) classification tasks: A review. J. Neural Eng. 2019, 16, 031001. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, X.; Yang, Y.; Mu, C.; Cai, Q.; Dang, W.; Zuo, S. EEG-Based Spatio–Temporal Convolutional Neural Network for Driver Fatigue Evaluation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2755–2763. [Google Scholar] [CrossRef]
- Xu, G.; Shen, X.; Chen, S.; Zong, Y.; Zhang, C.; Yue, H.; Liu, M.; Chena, F.; Che, W. A Deep Transfer Convolutional Neural Network Framework for EEG Signal Classification. IEEE Access 2019, 7, 112767–112776. [Google Scholar] [CrossRef]
- Chaudhary, S.; Taran, S.; Bajaj, V.; Sengur, A. Convolutional Neural Network Based Approach Towards Motor Imagery Tasks EEG Signals Classification. IEEE Sens. J. 2019, 19, 4494–4500. [Google Scholar] [CrossRef]
- Dai, G.; Zhou, J.; Huang, J.; Wang, N. HS-CNN: A CNN with hybrid convolution scale for EEG motor imagery classification. J. Neural Eng. 2019, 17, 016025. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Zhang, L.; Bais, A. Dynamical system based compact deep hybrid network for classification of Parkinson disease related EEG signals. Neural Netw. 2020, 130, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Bhatti, M.H.; Khan, U.G.; Iqbal, R. Multiclass EEG motor-imagery classification with sub-band common spatial patterns. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 174. [Google Scholar] [CrossRef] [Green Version]
- Jochumsen, M.; Knoche, H.; Kjaer, T.W.; Dinesen, B.; Kidmose, P. EEG Headset Evaluation for Detection of Single-Trial Movement Intention for Brain-Computer Interfaces. Sensors 2020, 20, 2804. [Google Scholar] [CrossRef] [PubMed]
- Nam, C.S.; Jeon, Y.; Kim, Y.-J.; Lee, I.; Park, K. Movement imagery-related lateralization of event-related (de)synchronization (ERD/ERS): Motor-imagery duration effects. Clin. Neurophysiol. 2011, 122, 567–577. [Google Scholar] [CrossRef]
- Kaiser, V.; Bauernfeind, G.; Kreilinger, A.; Kaufmann, T.; Kübler, A.; Neuper, C.; Müller-Putz, G. Cortical effects of user training in a motor imagery based brain–computer interface measured by fNIRS and EEG. NeuroImage 2014, 85, 432–444. [Google Scholar] [CrossRef]
- McFarland, D.J.; Sarnacki, W.A.; Wolpaw, J. Effects of training pre-movement sensorimotor rhythms on behavioral performance. J. Neural Eng. 2015, 12, 066021. [Google Scholar] [CrossRef]
- Lorey, B.; Naumann, T.; Pilgramm, S.; Petermann, C.; Bischoff, M.; Zentgraf, K.; Stark, R.; Vaitl, D.; Munzert, J. How equivalent are the action execution, imagery, and observation of intransitive movements? Revisiting the concept of somatotopy during action simulation. Brain Cogn. 2013, 81, 139–150. [Google Scholar] [CrossRef]
- Velu, P.D.; De Sa, V.R. Single-trial classification of gait and point movement preparation from human EEG. Front. Neurosci. 2013, 7, 84. [Google Scholar] [CrossRef] [Green Version]
- de Peralta Menendez, R.G.; Andino, S.G.; Ferrez, P.W.; Millán, J.D.R. 16 Noninvasive Estimates of Local Field Potentials for Brain-Computer Interfaces. In Toward Brain-Computer Interfacing; MIT Press: Cambridge, UK, 2007; ISBN 9780262042444. [Google Scholar]
- O’Shea, H.; Moran, A. To go or not to go? Pupillometry elucidates inhibitory mechanisms in motor imagery. J. Cogn. Psychol. 2018, 30, 466–483. [Google Scholar] [CrossRef]
- Delisle-Rodriguez, D.; Cardoso, V.; Gurve, D.; Loterio, F.; Romero-Laiseca, M.A.; Krishnan, S.; Bastos-Filho, T. System based on subject-specific bands to recognize pedaling motor imagery: Towards a BCI for lower-limb rehabilitation. J. Neural Eng. 2019, 16, 056005. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, S.L.; De Peralta, R.G.; Thut, G.; Millán, J.D.R.; Morier, P.; Landis, T. Very high frequency oscillations (VHFO) as a predictor of movement intentions. NeuroImage 2006, 32, 170–179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lazurenko, D.M.; Kiroy, V.N.; Aslanyan, E.V.; Shepelev, I.E.; Bakhtin, O.M.; Minyaeva, N.R. Electrographic Properties of Movement-Related Potentials. Neurosci. Behav. Physiol. 2018, 48, 1078–1087. [Google Scholar] [CrossRef]
- Smith, M.M.; Weaver, K.E.; Grabowski, T.J.; Rao, R.P.N.; Edarvas, F. Non-invasive detection of high gamma band activity during motor imagery. Front. Hum. Neurosci. 2014, 8, 817. [Google Scholar] [CrossRef] [PubMed]
- Mashat, M.E.M.; Lin, C.-T.; Zhang, D. Effects of Task Complexity on Motor Imagery-Based Brain–Computer Interface. IEEE Trans. Neural Syst. Rehabilit. Eng. 2019, 27, 2178–2185. [Google Scholar] [CrossRef]
- Kiroy, V.; Bakhtin, O.; Krivko, E.; Lazurenko, D.; Aslanyan, E.; Shaposhnikov, D.; Shcherban, I. Spoken and Inner Speech-related EEG Connectivity in Different Spatial Direction. Biomed. Signal Process. Control 2021, 71, 103224. [Google Scholar] [CrossRef]
- Thomas, K.P.; Guan, C.; Lau, C.T.; Vinod, A.P.; Ang, K.K. Adaptive tracking of discriminative frequency components in electroencephalograms for a robust brain–computer interface. J. Neural Eng. 2011, 8, 036007. [Google Scholar] [CrossRef]
- Yang, B.H.; Wu, T.; Wang, Q.; Han, Z.J. Motor Imagery EEG Recognition Based on WPD-CSP and KF-SVM in Brain Computer Interfaces. Appl. Mech. Mater. 2014, 556–562, 2829–2833. [Google Scholar] [CrossRef]
- Freudenburg, Z.V.; Branco, M.; Leinders, S.; Van Der Vijgh, B.H.; Pels, E.G.M.; Denison, T.; Berg, L.H.V.D.; Miller, K.J.; Aarnoutse, E.J.; Ramsey, N.F.; et al. Sensorimotor ECoG Signal Features for BCI Control: A Comparison between People with Locked-In Syndrome and Able-Bodied Controls. Front. Neurosci. 2019, 13, 1058. [Google Scholar] [CrossRef]
- Belkacem, A.N.; Jamil, N.; Palmer, J.A.; Ouhbi, S.; Chen, C. Brain Computer Interfaces for Improving the Quality of Life of Older Adults and Elderly Patients. Front. Neurosci. 2020, 14, 692. [Google Scholar] [CrossRef]







| Approach | Feature | Classification Accuracy |
|---|---|---|
| CSP + LR | CSP patterns | 51.1 ± 10.8% |
| Search for informative frequencies | PSD | 65.4 ± 9.1% |
| Hjorth parameters | 53.9 ± 11.4% | |
| Correlation coefficients | 53.7 ± 8.2% |
| Window Length | 500 ms | 750 ms | 1000 ms | 2000 ms | |
|---|---|---|---|---|---|
| Feature | |||||
| PSD | 59.8 ± 9.6% | 57.9 ± 8.4% | 54.3 ± 8.3% | 64.8 ± 7.6% | |
| Hjorth parameters | 67.9 ± 4.7% | 68.6 ± 3.1% | 68.9 ± 3.9% | 54.0 ± 12.6% | |
| Correlation coefficients | 68.8 ± 3.1% | 71.6 ± 3.9% | 68.5 ± 4.3% | 53.9 ± 8.3% | |
| Window Length | 500 ms | 750 ms | 1000 ms | 2000 ms | |
|---|---|---|---|---|---|
| Feature | |||||
| PSD | 38.55% | 35.29% | 34.64% | 64.7% | |
| Hjorth parameters | 66.08% | 67.77% | 68.01% | 35.48% | |
| Correlation coefficients | 68.07% | 68.01% | 67.65% | 35.72% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazurenko, D.; Shepelev, I.; Shaposhnikov, D.; Saevskiy, A.; Kiroy, V. Discriminative Frequencies and Temporal EEG Segmentation in the Motor Imagery Classification Approach. Appl. Sci. 2022, 12, 2736. https://doi.org/10.3390/app12052736
Lazurenko D, Shepelev I, Shaposhnikov D, Saevskiy A, Kiroy V. Discriminative Frequencies and Temporal EEG Segmentation in the Motor Imagery Classification Approach. Applied Sciences. 2022; 12(5):2736. https://doi.org/10.3390/app12052736
Chicago/Turabian StyleLazurenko, Dmitry, Igor Shepelev, Dmitry Shaposhnikov, Anton Saevskiy, and Valery Kiroy. 2022. "Discriminative Frequencies and Temporal EEG Segmentation in the Motor Imagery Classification Approach" Applied Sciences 12, no. 5: 2736. https://doi.org/10.3390/app12052736
APA StyleLazurenko, D., Shepelev, I., Shaposhnikov, D., Saevskiy, A., & Kiroy, V. (2022). Discriminative Frequencies and Temporal EEG Segmentation in the Motor Imagery Classification Approach. Applied Sciences, 12(5), 2736. https://doi.org/10.3390/app12052736






