1. Introduction
Metallic additive manufacturing (MAM) is a family of technological processes where metallic components are manufactured by the successive deposition of cross-sections (or layers) of the final part until it is built [
1]. This classification encompasses a considerable variety of processes, varying in complexity, productivity and cost; the present study focuses on direct energy deposition (DED), a process where the feedstock, which may be powdered (DED) or a wire (wDED) metallic compound, is melted by a heat source as it is being inserted into the melting pool [
2].
The heat-source is usually a solid-state laser or a fibre laser [
3], although an electron beam may be employed. In order to prevent corrosion phenomena, a localised inert atmosphere is created by the coaxial ejection of an inert gas—typically argon.
DED technologies may be compared to selective laser melting (SLM), another well-established MAM process, which produces parts through the successive melting of evenly spread metallic powder layers: at each cross-section, a thin coat (usually around 30
is spread by a powder roller or rake) before the heat source melts the powder as it is diverted through a system of mirrors to follow the cross-section of the built part. While DED features increased productivity at the cost of decreased part accuracy and surface finishing [
4], often being named a near-net shape process [
5], SLM is capable of producing more complex geometries, as it not only has better dimensional fidelity but also is capable of producing support structures [
6].
Due to the aforementioned characteristics, SLM is capable of producing structural components with geometries of extreme complexity, such as implicit surfaces or internal porosities demanded by the aerospace [
7] and biomedical [
8] industries. However, due to the absence of a powder bed, DED is capable of depositing in existing surfaces with complex shapes, granting it the flexibility required for repairing applications [
9] and surface cladding [
10].
DED processes feature a considerable amount of processing variables, including the laser power, powder feeding rate, laser scanning speed, carrier gas flow rate, shielding gas flow rate, nozzle angle and nozzle-to-substrate distance, among others [
2]. Furthermore, complex parameters may be analysed: researchers [
11] have indicated a total of fourteen relevant dimensionless numbers that may be obtained to ascertain the deposition quality, efficiency and productivity; additional, non-dimensionless variables may be computed from the process parameters [
2], translating them into concepts with physical significance that aids the development of optimised process parameter windows. The current work mentions the energy density
E,
in which
P is the laser power,
is the scanning speed and
is the laser spot size. The successful production of components through this technology thus revolves around the optimisation of the aforementioned variables for each material–substrate combination and its subsequent analysis, a process common for both DED and SLM technologies that is often expensive and time-consuming as it is based on trial-and-error depositions [
2].
DED has already been used in depositing nickel-based super alloys, such as Inconel 625 [
12,
13] and Inconel 718 [
14], 316L stainless steel [
15], tool steels, such as AISI H13 [
16], as well as in developing functionally graded materials (FGMs), which are components whose chemical and/or conditions show a spacial variation across the component [
17]; SLM, on the other hand, has also been used to successfully deposit precipitation-hardened steel, such as 17-4PH [
18], Ti6Al4V [
19], 316L stainless steel [
20], nickel super alloys [
21] and aluminium alloys [
22], among others.
A frequently used alloy within the context of MAM is Maraging steel, a ferrous alloy whose name is derived from the junction of the terms martensite and ageing as it obtains its mechanical strength from the precipitation hardening phenomenon resulting from ageing heat treatments [
23]. Maraging alloys have very low levels of C as it contributes to the formation of fragile carbides, such as TiC [
24]. Furthermore, it contains appreciable quantities of Ti, Al and Co and large quantities (between 18 and 25 weight %) of Ni, with the latter leading to a soft but heavily dislocated martensite [
25] upon quenching.
These alloys find application in the automotive, aerospace, military and tool die industries [
26]. One of the advantages of this alloy, apart from its exceptional combination of high strength and toughness, is its printability: a recent research work [
27] conducted 16 single tracks in which the energy density (expressed in Equation (
1)) oscillated from
and
, returning beads with dilution proportions between
and
, values generally considered too excessive [
12]; Additionally, researchers [
28] developed processing maps for 18Ni300, concluding that laser powers larger than 1200
with a laser spot size of
resulted in porosities below
, although speeds below 9
for the same power setting lead to dilution proportions (given by Equation (
2)) below
.
Recent work [
29], in which 18Ni300 tensile specimens were obtained from nine different parameter combinations, concluded that energy density values over 180
lead to components with near
density, with the laser power being considered the most influential parameter on tensile property. Investigations into the influence of the powder feeding rate in depositing precipitation hardened steel on 304L stainless steel substrates were also conducted [
30], where the dilution proportion was larger for increased feeding rates.
DED-related processes have different levels of in-situ control: recent research monitored the melting pool geometry during wire arc additive manufacturing to control for the bead’s geometry and symmetry [
31]; additional research was conducted on the use of a structured light system in the development of a real-time monitoring tool to aid the repair of an engine component [
32]. Moreover, research towards establishing process maps that guide the deposition process towards avoiding lack-of-fusion and keyhole porosities has been conducted [
33].
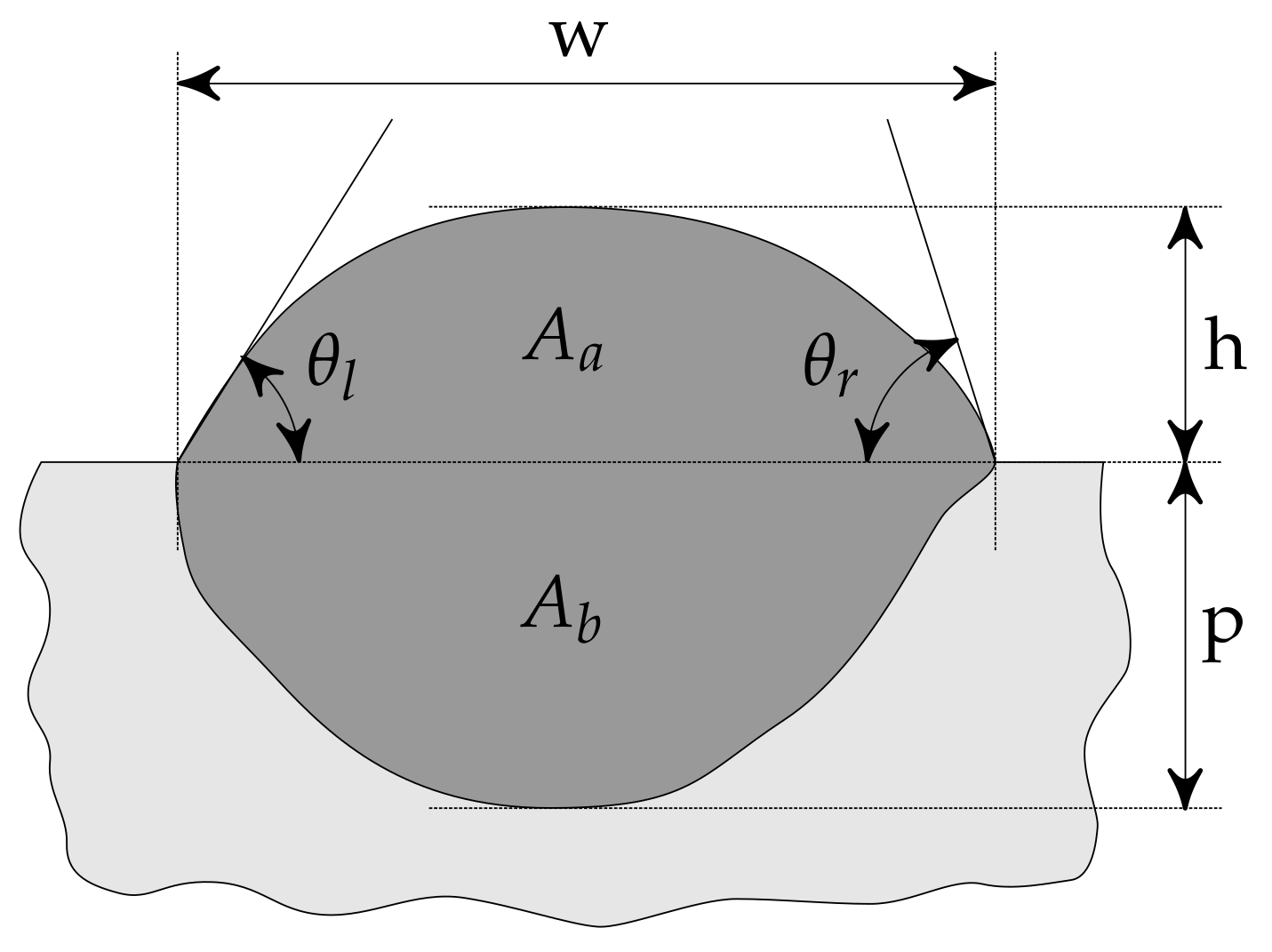
However, the aforementioned research mainly focuses on in-situ measurements and control over process variables, rather than output analysis, which is the case of this research work: the workflow associated with the parameter optimisation for different materials is similar, where different combinations of inputs are used in depositing single track line beads, which are subsequently cross-sectionally cut and analysed through optical microscopy (OM). In addition to probing for defects inherent to this technology, such as entrapped gas, lack-of-fusion pores and cracking [
2], several macroscopic parameters were obtained, such as the track width
w, height
h, penetration
p, wettability angles
and
and dilution proportion
; the latter is computed as:
where
and
are the areas above and below the substrate line, respectively. A schematic representation of these outputs is shown in
Figure 1.
The computation of the aforementioned bead properties is usually done manually through image processing software, such as ImageJ; the novelty of this work thus arises in the development of an algorithm, using the scikit-image [
34] package for Python, to obtain properties in a reliable and automated way. The OM images used as samples for developing and testing the developed algorithm were self-obtained, pertaining to the deposition optimisation of 18Ni300 Maraging steel on H13 tool steel substrates. It is important to mention that despite the images used in the benchmark of this code being comprised of 18Ni300 deposited on H13, this code should work regardless of the material as it is based on image segmentation and not in metallurgical expectations.
4. Discussion
As stated in
Section 2, the initial depositions followed a Taguchi L9 array between the scanning speed, feeding rate and laser power of the line beads; the parameters shown in
Table 2 highlight four of the initial nine depositions, with their numbers being 1, 2, 6, 7 and 10, which were deemed the most interesting to further in additional DOEs: Track 1 displayed very large dilution values, attributed to its low relative scanning speed and low feeding rate. Track 2 also shows dilutions above the established limit of
, despite the larger scanning speed, attributing the dilution to the low feeding rate.
Track 6 improved the dilution proportion by decreasing it to , although the wettability angles were too large and disparate. Tracks 7 and 10 also proved unsatisfactory, with wettability angles that were overly large. The following DOE oscillated process parameters around Track 1, by creating another L9 Taguchi array with laser power values of 1250 , 1400 and 1550 , scanning speeds of 3 , 6 and 9 and feeding rates of 5 , 9 and 12 .
These depositions, of which Tracks 12 and 16 were analysed, yielded beads whose dilution proportion was too low and wettability angles too large, as easily perceptible through
Figure 11, which shows the resulting outputs according to different parameters. The following depositions followed an orthogonal design and increased the scanning speeds while reducing the feeding rates: the ratio between scanning speed feeding rate was restricted to an interval between
and
.
Track 32 showed wettability angles that were too large, z possessed too large a dilution proportion, and finally Track 35 displayed acceptable values throughout. Further parameter variation ensued, with shielding gas flow rate, carrier gas flow rate, nozzle-to-substrate distance iterations resulted in beads with similar heights but considerably different dilution proportion and wettability angles; an increase in the disparity between the left and right angles in Track 56 could be attributed to the turbulence in the melting pool induced by the increase in shielding gas; Tracks 38 and 41 display large wettability angles, leading to the conclusion that very slow speeds (≤3 ) may increase the skewness of the produced bead.
Recent research [
40] delved into the influence of the shielding gas flow rate on the porosity and quality of DED-produced 316L, concluding that the oxygen content present in the melt pool alters its surface tension, consequently affecting the melting pattern.
The feeding rate proved to have a significant impact on the dilution proportion, a conclusion also found in the literature, although the observed phenomena was contrary to the one reported by another research work [
30], in which an increase in feeding rate led to larger dilution proportions. However, considering that the increase in powder delivered to the melt pool requires more heat energy to melt, it is expected for the available energy to be less capable of melting the substrate.
This conclusion is supported by similar research [
41] that found the dilution proportion increases inversely when compared to the powder delivery per unit length. Additional research showed the possible instability due to excess power feed rate, which leads to poor overlapping [
42]; track 7 and 10 highlight this problem, as their wettability angles are both greater than
.
The optimised process parameters resulted in a ratio between the laser power and laser spot size of
720
and a specific energy of
; other research [
29] deposited 18Ni300 tensile specimens using an orthogonal DOE between the laser power, scanning speed and feeding rate; the specimen produced with a specific energy of
achieved the highest ultimate tensile strength. Additional research [
28] optimised process parameters for 18Ni300 processing, obtaining specific energy of
in the optimised parameters for dilution proportion. A comparison between process variables the present work and the aforementioned research is visualised in
Figure 13.
Regarding the developed algorithm and its output results, the width values proved to be the computed variable displaying the smallest error percentage, with the average error being . This constitutes a satisfying error for the computed width, with no particular outlier or track whose error is significant or would otherwise highlight a shortcoming in the algorithm. Regarding the height, track 2 shows a error, attributable to a small chip developed during the cutting procedure of the sample that remained attached to the deposited part; this increase in height was not considered when manually measuring the height but was taken into account by the algorithm.
The penetration limit displayed two very evident outliers—track 32 and track 35—with both cases underestimating the values. In the former, the substrate line is significantly asymmetric—shown in
Figure 12c, with the right and left sides of the track being misaligned by circa 50
; as the computed substrate line sits near the substrate side, which is located nearer to the penetration limit, its value is underestimated when compared to the manually determined one. This measurement could be improved by considering the differential between the substrate height to the left and to the right hand sides of the bead.
Alternatively, track 35—
Figure 12d—miscalculated the penetration limit; the dilution zone of this track is asymmetric and presents a bulge to the left side of the dilution zone, which the algorithm failed to include, thus underestimating the penetration limit and the area below the substrate. This could be avoided by additional criteria in detecting the penetration limit in addition to the maximum of the derivative of the filtered sum of pixel values by row, similarly to the additional criteria used when detecting the substrate.
The wettability angles displayed errors of and for the left and right angles, respectively. Interestingly, it proved common for analysis to return angles with significant error disparity, such as tracks 12, 16, 33, 41 and 50; a potential explanation is the fact that both angles are measured considering the substrate line, instead of taking into account a possible height difference between the left and right hand side of the beads. The area below the substrate should also be improved, with tracks 7, 10, 32 and 50 displaying errors above ; in these cases, the area is considerably overestimated due to poor mapping of the sum of pixel values by column into the melting pool dimensions, stretching the area to the horizontal limits of the line bead, instead of the horizontal limits of the diluted zone.
In short, the current function works under the assumption that the area under the substrate’s width and the line bead’s widths are the same, a consideration that should be avoided in future adaptations. The larger error in the computation of the area below the substrate is ultimately due to the lesser contrast between the substrate and the diluted zone in the bead, when compared to the contrast between the background of the image and the line itself, for example.