2D/3D Multimode Medical Image Registration Based on Normalized Cross-Correlation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Methods
2.2.1. Normalized Cross-Correlation Based on Sobel Operator
2.2.2. Normalized Cross-Correlation Based on LOG Operator
2.2.3. Multiresolution Strategy
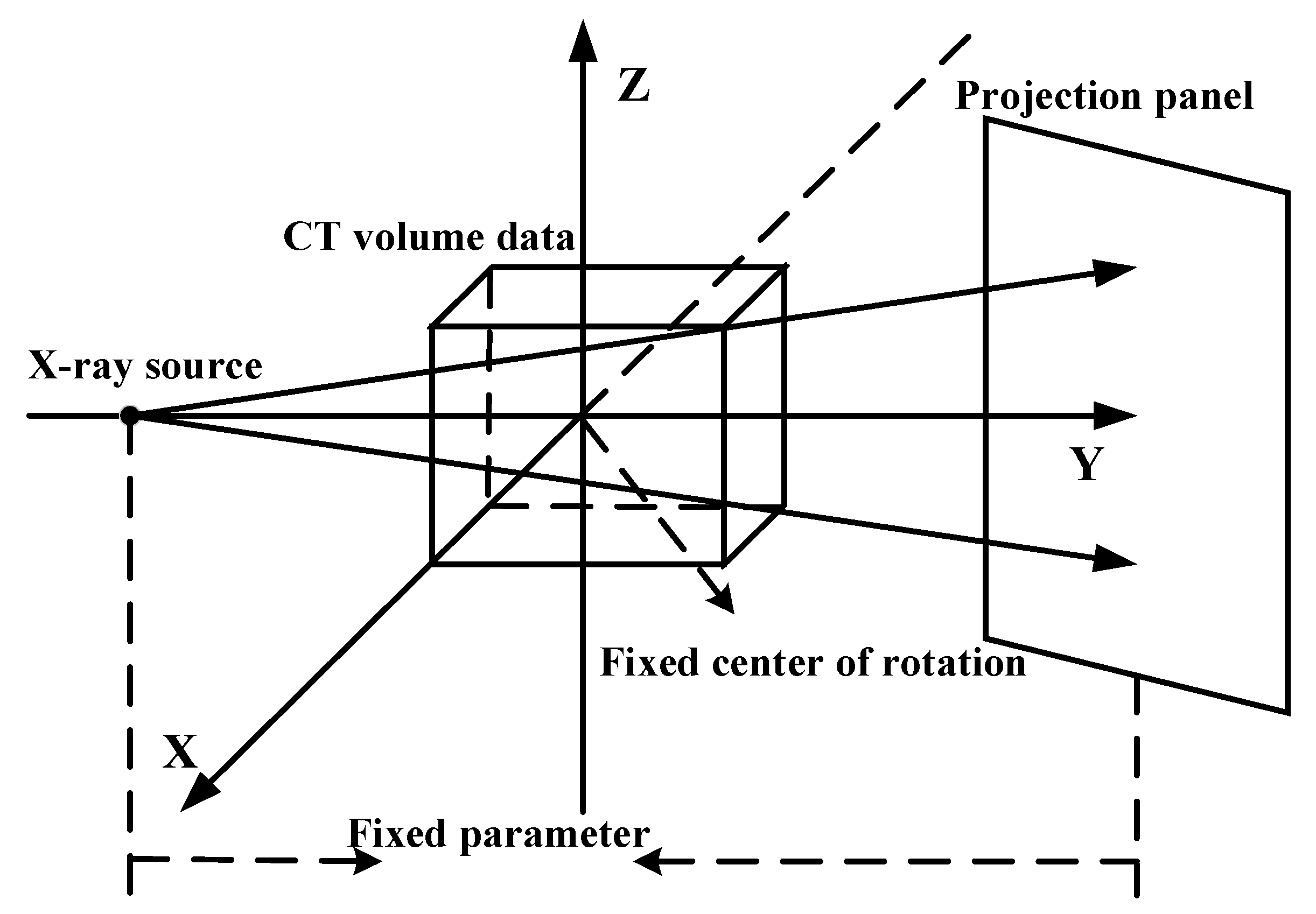
3. Experiments and Results
3.1. Experiment Process
3.2. Experimental Evaluation Criteria
3.3. Multiresolution Registration Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alam, F.; Rahman, S.U.; Ullah, S.; Gulati, K. Medical image registration in image guided surgery: Issues, challenges and research opportunities. Biocybern. Biomed. Eng. 2018, 38, 71–89. [Google Scholar] [CrossRef]
- Chen, X.; Yin, L.; Fan, Y.; Song, L.; Ji, T.; Liu, Y.; Tian, J.; Zheng, W. Temporal evolution characteristics of PM 2.5 concentration based on continuous wavelet transform. Sci. Total Environ. 2020, 699, 134244. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Yin, L.; Chen, X.; Liu, S.; Yang, B.; Zheng, W. Semantic representation for visual reasoning. MATEC Web Conf. 2019, 277, 02006. [Google Scholar] [CrossRef]
- Otake, Y.; Armand, M.; Armiger, R.S.; Kutzer, M.D.; Basafa, E.; Kazanzides, P.; Taylor, R.H. Intraoperative image-based multiview 2D/3D registration for image-guided orthopaedic surgery: Incorporation of fiducial-based C-arm tracking and GPU-acceleration. IEEE Trans. Med. Imaging 2011, 31, 948–962. [Google Scholar] [CrossRef] [Green Version]
- Steininger, P.; Neuner, M.; Fritscher, K.; Sedlmayer, F.; Deutschmann, H. A Novel Class of Machine-Learning-Driven Real-Time 2D/3D Tracking Methods: Texture Model Registration (TMR). In Proceedings of the Medical Imaging 2011: Visualization, Image-Guided Procedures, and Modeling. International Society for Optics and Photonics, Lake Buena Vista, FL, USA, 12–17 February 2011; p. 79640G. [Google Scholar]
- Cleary, K.; Peters, T.M. Image-guided interventions: Technology review and clinical applications. Annu. Rev. Biomed. Eng. 2010, 12, 119–142. [Google Scholar] [CrossRef]
- Fu, D.; Kuduvalli, G. A fast, accurate, and automatic 2D–3D image registration for image-guided cranial radiosurgery. Med. Phys. 2008, 35, 2180–2194. [Google Scholar] [CrossRef]
- Markelj, P.; Tomaževič, D.; Pernuš, F.; Likar, B. Optimizing bone extraction in MR images for 3D/2D gradient based registration of MR and X-ray images. In Proceedings of the Medical Imaging 2007: Image Processing. International Society for Optics and Photonics, San Diego, CA, USA, 17–22 February 2007; p. 651224. [Google Scholar]
- Ding, Y.; Tian, X.; Yin, L.; Chen, X.; Liu, S.; Yang, B.; Zheng, W. Multi-scale Relation Network for Few-Shot Learning Based on Meta-learning. In International Conference on Computer Vision Systems; Springer: Cham, Switzerland, 2019; pp. 343–352. [Google Scholar]
- Liu, S.; Gao, Y.; Zheng, W.; Li, X. Performance of two neural network models in bathymetry. Remote Sens. Lett. 2015, 6, 321–330. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, W.; Mou, Y.; Li, Y.; Yin, L. Microscopic 3D reconstruction based on point cloud data generated using defocused images. Meas. Control 2021, 54, 1309–1318. [Google Scholar] [CrossRef]
- Xu, C.; Yang, B.; Guo, F.; Zheng, W.; Poignet, P. Sparse-view CBCT reconstruction via weighted Schatten p-norm minimization. Opt. Express 2020, 28, 35469–35482. [Google Scholar] [CrossRef]
- Yang, B.; Liu, C.; Zheng, W.; Liu, S.; Huang, K. Reconstructing a 3D heart surface with stereo-endoscope by learning eigen-shapes. Biomed. Opt. Express 2018, 9, 6222–6236. [Google Scholar] [CrossRef] [Green Version]
- Aouadi, S.; Sarry, L. Accurate and precise 2D–3D registration based on X-ray intensity. Comput. Vis. Image Underst. 2008, 110, 134–151. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, S.; Deng, Y.; Zhang, Y.; Yin, L.; Zheng, W. Construction of force haptic reappearance system based on Geomagic Touch haptic device. Comput. Methods Programs Biomed. 2020, 190, 105344. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Liu, S.; Deng, Y.; Zhang, Y.; Yin, L.; Zheng, W. An improved method for soft tissue modeling. Biomed. Signal Process. Control 2021, 65, 102367. [Google Scholar] [CrossRef]
- Yang, B.; Liu, C.; Huang, K.; Zheng, W. A triangular radial cubic spline deformation model for efficient 3D beating heart tracking. Signal Image Video Process. 2017, 11, 1329–1336. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Liu, C.; Zheng, W.; Liu, S. Motion prediction via online instantaneous frequency estimation for vision-based beating heart tracking. Inf. Fusion 2017, 35, 58–67. [Google Scholar] [CrossRef]
- Yang, B.; Liu, C.; Zheng, W. PCA-based 3D pose modeling for beating heart tracking. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; pp. 586–590. [Google Scholar] [CrossRef]
- Zheng, W.; Li, X.; Yin, L.; Wang, Y. The retrieved urban LST in Beijing based on TM, HJ-1B and MODIS. Arab. J. Sci. Eng. 2016, 41, 2325–2332. [Google Scholar] [CrossRef]
- Yang, B.; Cao, T.; Zheng, W. Beating heart motion prediction using iterative optimal sine filtering. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, W.; Shen, Z. A New Algorithm for Distributed Control Problem with Shortest-Distance Constraints. Math. Probl. Eng. 2016, 2016, 1604824. [Google Scholar] [CrossRef]
- Goitein, M.; Abrams, M.; Rowell, D.; Pollari, H.; Wiles, J. Multi-dimensional treatment planning: II. Beam’s eye-view, back projection, and projection through CT sections. Int. J. Radiat. Oncol. Biol. Phys. 1983, 9, 789–797. [Google Scholar] [CrossRef]
- Mu, Z. A fast DRR generation scheme for 3D-2D image registration based on the block projection method. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 169–177. [Google Scholar]
- Ghafurian, S.; Hacihaliloglu, I.; Metaxas, D.N.; Tan, V.; Li, K. A computationally efficient 3D/2D registration method based on image gradient direction probability density function. Neurocomputing 2017, 229, 100–108. [Google Scholar] [CrossRef]
- Pan, H.; Zhou, C.; Zhu, Q.; Zheng, D. A fast registration from 3D CT images to 2D X-ray images. In Proceedings of the 2018 IEEE 3rd International Conference on Big Data Analysis (ICBDA), Shanghai, China, 9–12 March 2018; pp. 351–355. [Google Scholar]
- Zheng, G.; Zhang, X.; Jonić, S.; Thévenaz, P.; Unser, M.; Nolte, L.-P. Point similarity measures based on MRF modeling of difference images for spline-based 2D-3D rigid registration of X-ray fluoroscopy to CT images. In International Workshop on Biomedical Image Registration; Springer: Cham, Switzerland, 2006; pp. 186–194. [Google Scholar]
- Zheng, J.; Miao, S.; Liao, R. Learning CNNS with pairwise domain adaption for real-time 6dof ultrasound transducer detection and tracking from X-ray images. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2017; pp. 646–654. [Google Scholar]
- Dorgham, O.M.; Laycock, S.D.; Fisher, M.H. GPU accelerated generation of digitally reconstructed radiographs for 2-D/3-D image registration. IEEE Trans. Biomed. Eng. 2012, 59, 2594–2603. [Google Scholar] [CrossRef]
- Zheng, J.; Miao, S.; Wang, Z.J.; Liao, R. Pairwise domain adaptation module for CNN-based 2-D/3-D registration. J. Med. Imaging 2018, 5, 021204. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Miao, S.; de Tournemire, P.; Grbic, S.; Kamen, A.; Mansi, T.; Comaniciu, D. An artificial agent for robust image registration. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Miao, S.; Piat, S.; Fischer, P.; Tuysuzoglu, A.; Mewes, P.; Mansi, T.; Liao, R. Dilated fcn for multi-agent 2D/3D medical image registration. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Miao, S.; Wang, Z.J.; Liao, R. A CNN regression approach for real-time 2D/3D registration. IEEE Trans. Med. Imaging 2016, 35, 1352–1363. [Google Scholar] [CrossRef] [PubMed]
- Toth, D.; Miao, S.; Kurzendorfer, T.; Rinaldi, C.A.; Liao, R.; Mansi, T.; Rhode, K.; Mountney, P. 3D/2D model-to-image registration by imitation learning for cardiac procedures. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1141–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valenti, M.; Ferrigno, G.; Martina, D.; Yu, W.; Zheng, G.; Shandiz, M.A.; Anglin, C.; De Momi, E. Gaussian mixture models based 2D–3D registration of bone shapes for orthopedic surgery planning. Med. Biol. Eng. Comput. 2016, 54, 1727–1740. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Q.; Yu, W. An improved Normalized Cross Correlation algorithm for SAR image registration. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2086–2089. [Google Scholar]
- Heo, Y.S.; Lee, K.M.; Lee, S.U. Robust Stereo Matching Using Adaptive Normalized Cross-Correlation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 807–822. [Google Scholar] [CrossRef] [Green Version]
- Johnson, H.; McCormick, M.; Ibanez, L. The ITK Software Guide Book 2: Design and Functionality—Volume 2; Kitware. Inc.: Clifton Park, NY, USA, 2015. [Google Scholar]
- Kaso A Computation of the normalized cross-correlation by fast Fourier transform. PLoS ONE 2018, 13, e0203434. [CrossRef]
- Zhang, Z.; Wang, L.; Zheng, W.; Yin, L.; Hu, R.; Yang, B. Endoscope image mosaic based on pyramid ORB. Biomed. Signal Process. Control 2022, 71, 103261. [Google Scholar] [CrossRef]
- Eresen, A.; Birch, S.M.; Alic, L.; Griffin, J.F.; Kornegay, J.N.; Ji, J.X. New similarity metric for registration of MRI to histology: Golden retriever muscular dystrophy imaging. IEEE Trans. Biomed. Eng. 2018, 66, 1222–1230. [Google Scholar] [CrossRef]
- Guo, F.; Yang, B.; Zheng, W.; Liu, S. Power Frequency Estimation Using Sine Filtering of Optimal Initial Phase. Measurement 2021, 186, 110165. [Google Scholar] [CrossRef]
- Liu, S.; Wei, X.; Zheng, W.; Yang, B. A Four-channel Time Domain Passivity Approach for Bilateral Teleoperator. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 318–322. [Google Scholar] [CrossRef]
- Lai, W.; Huang, J.; Ahuja, N.; Yang, M. Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2599–2613. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Tian, J.; Liu, Y.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive Neural Network Control of Time Delay Teleoperation System Based on Model Approximation. Sensors 2021, 21, 7443. [Google Scholar] [CrossRef] [PubMed]
- Nasihatkon, B.; Kahl, F. Multiresolution Search of the Rigid Motion Space for Intensity-Based Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 179–191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, Z.; Han, J.; Liang, W.; Tan, J.; Guan, Y. Robust and fast initialization for intensity-based 2D/3D registration. Adv. Mech. Eng. 2014, 6, 989254. [Google Scholar] [CrossRef]
- Jacobs, F.; Sundermann, E.; De Sutter, B.; Christiaens, M.; Lemahieu, I. A fast algorithm to calculate the exact radiological path through a pixel or voxel space. J. Comput. Inf. Technol. 1998, 6, 89–94. [Google Scholar]
- Siddon, R.L. Fast calculation of the exact radiological path for a three-dimensional CT array. Med. Phys. 1985, 12, 252–255. [Google Scholar] [CrossRef]
- Hurvitz, A.; Joskowicz, L. Registration of a CT-like atlas to fluoroscopic X-ray images using intensity correspondences. Int. J. Comput. Assist. Radiol. Surg. 2008, 3, 493–504. [Google Scholar] [CrossRef]
- Pei-fenga, J.; Anb, Q.; Wei-donga, Z.; Juna, O.; Mei-chaoa, Z.; Ji-honga, F.; Shi-zhena, Z.; Jian-yia, L. 2D/3D registration system based on single X-ray image and CT data. J. Med. Biomech. 2010, 67, 101815. [Google Scholar]
- Zhang, Z.; Liu, Y.; Tian, J.; Liu, S.; Yang, B.; Xiang, L.; Yin, L.; Zheng, W. Study on Reconstruction and Feature Tracking of Silicone Heart 3D Surface. Sensors 2021, 21, 7570. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, W.; Liu, X.; Mou, Y.; Yin, L.; Yang, B. Research and improvement of feature detection algorithm based on FAST. Rend. Lincei. Sci. Fis. Nat. 2021, 32, 775–789. [Google Scholar] [CrossRef]
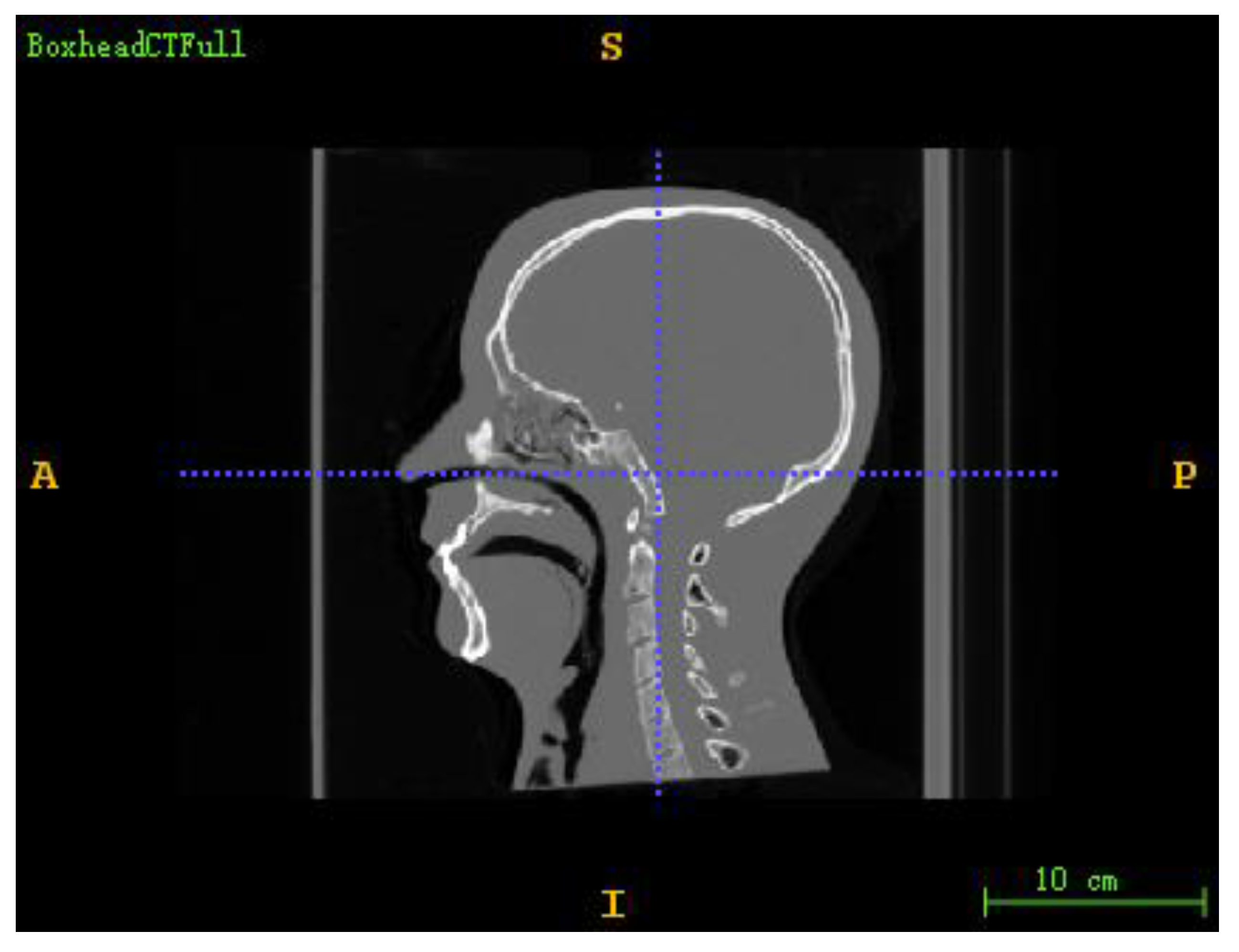








| Data | Size | Spacing (mm) | Pixel Range |
|---|---|---|---|
| CT image | 200 × 200 × 142 | 2 × 2 × 2 | −1024~2976 |
| Analog X-ray image (DRR) | 256 × 256 | 1 × 1 | 0~255 |
| Rotation (°) | Translation (mm) | ||
|---|---|---|---|
| NCCS | MAE | 0.4955 | 0.9883 |
| MTRE | 1.94117 mm | ||
| time | 6012.6 s | ||
| NCCL | MAE | 0.3189 | 0.7750 |
| MTRE | 1.4759 mm | ||
| time | 5765.6 s | ||
| NCC | MAE | 1.2083 | 1.4079 |
| MTRE | 3.19295 mm | ||
| time | 5129 s | ||
| (α, β, θ, tx, ty, tz) | ||
|---|---|---|
| Truth point | (10,10,10,40,40,40) | (40,40,40,10,10,10) |
| Initial value point | (0,0,0,0,0,0) | (0,0,0,0,0,0) |
| NCCS | (10.325, 9.00845, 10.0975 39.6466, 36.2063, 40.0849) | (39.6403, 40.2076, 39.8805, 10.0196, 11.3873, 9.70042) |
| NCCL | (17.3676, 17.3365, 16.7622 46.5633, 47.9499, 40.5774) | (50.6946, 34.7924, 10.1197, 56.3769, 74.0497, 8.35779) |
| NCC | (16.1266, 7.13819, 16.4462 41.8934, 47.7294, 40.4012) | (49.3488, −8.45826, 0.334837, −3.30738, 139.747, 5.38556) |
| Rotation (°) | Translation (mm) | ||
|---|---|---|---|
| NCCS | MAE | 0.5254 | 0.6491 |
| time | 2477.6 s | ||
| NCCL | MAE | 0.4712 | 0.6250 |
| time | 1202.2 s | ||
| NCC | MAE | 1.0858 | 1.0259 |
| time | 1291.6 s | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yang, B.; Wang, Y.; Tian, J.; Yin, L.; Zheng, W. 2D/3D Multimode Medical Image Registration Based on Normalized Cross-Correlation. Appl. Sci. 2022, 12, 2828. https://doi.org/10.3390/app12062828
Liu S, Yang B, Wang Y, Tian J, Yin L, Zheng W. 2D/3D Multimode Medical Image Registration Based on Normalized Cross-Correlation. Applied Sciences. 2022; 12(6):2828. https://doi.org/10.3390/app12062828
Chicago/Turabian StyleLiu, Shan, Bo Yang, Yang Wang, Jiawei Tian, Lirong Yin, and Wenfeng Zheng. 2022. "2D/3D Multimode Medical Image Registration Based on Normalized Cross-Correlation" Applied Sciences 12, no. 6: 2828. https://doi.org/10.3390/app12062828
APA StyleLiu, S., Yang, B., Wang, Y., Tian, J., Yin, L., & Zheng, W. (2022). 2D/3D Multimode Medical Image Registration Based on Normalized Cross-Correlation. Applied Sciences, 12(6), 2828. https://doi.org/10.3390/app12062828








