A Compensation Strategy Using an H∞ Control Law for a Multi-Time-Delay Control System
Abstract
:1. Introduction
2. Establishment of the Multi-Time-Delay Control System
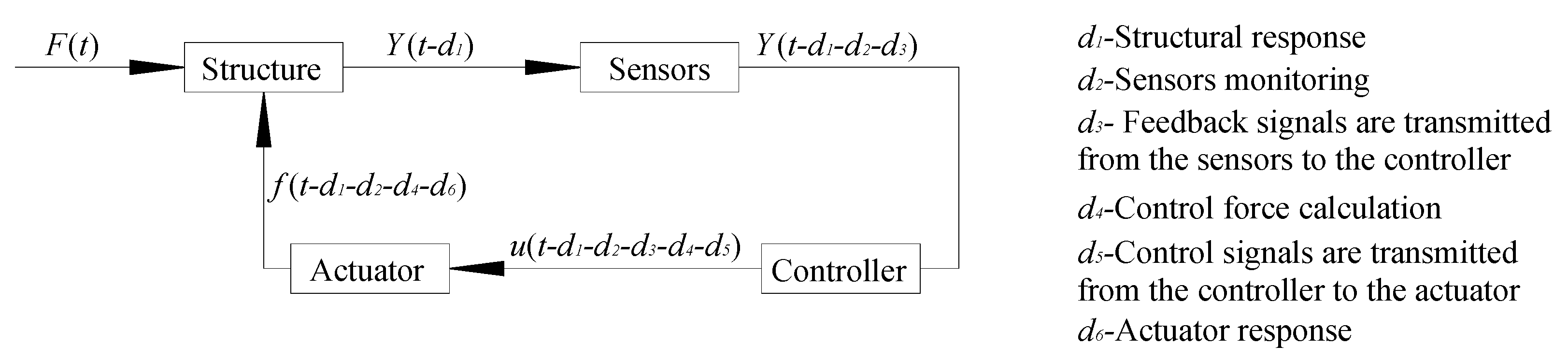
2.1. Time-Delay Sources
2.2. Impact Analysis of Multi-Time Delays
3. A Compensation Strategy Using an H∞ Control Law
3.1. Design Principle
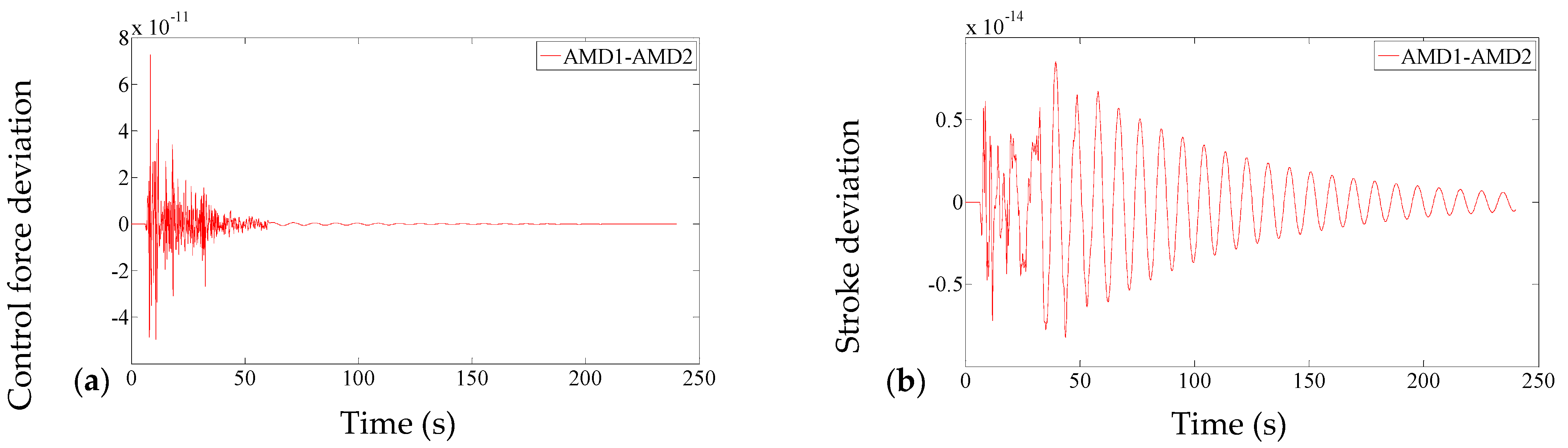
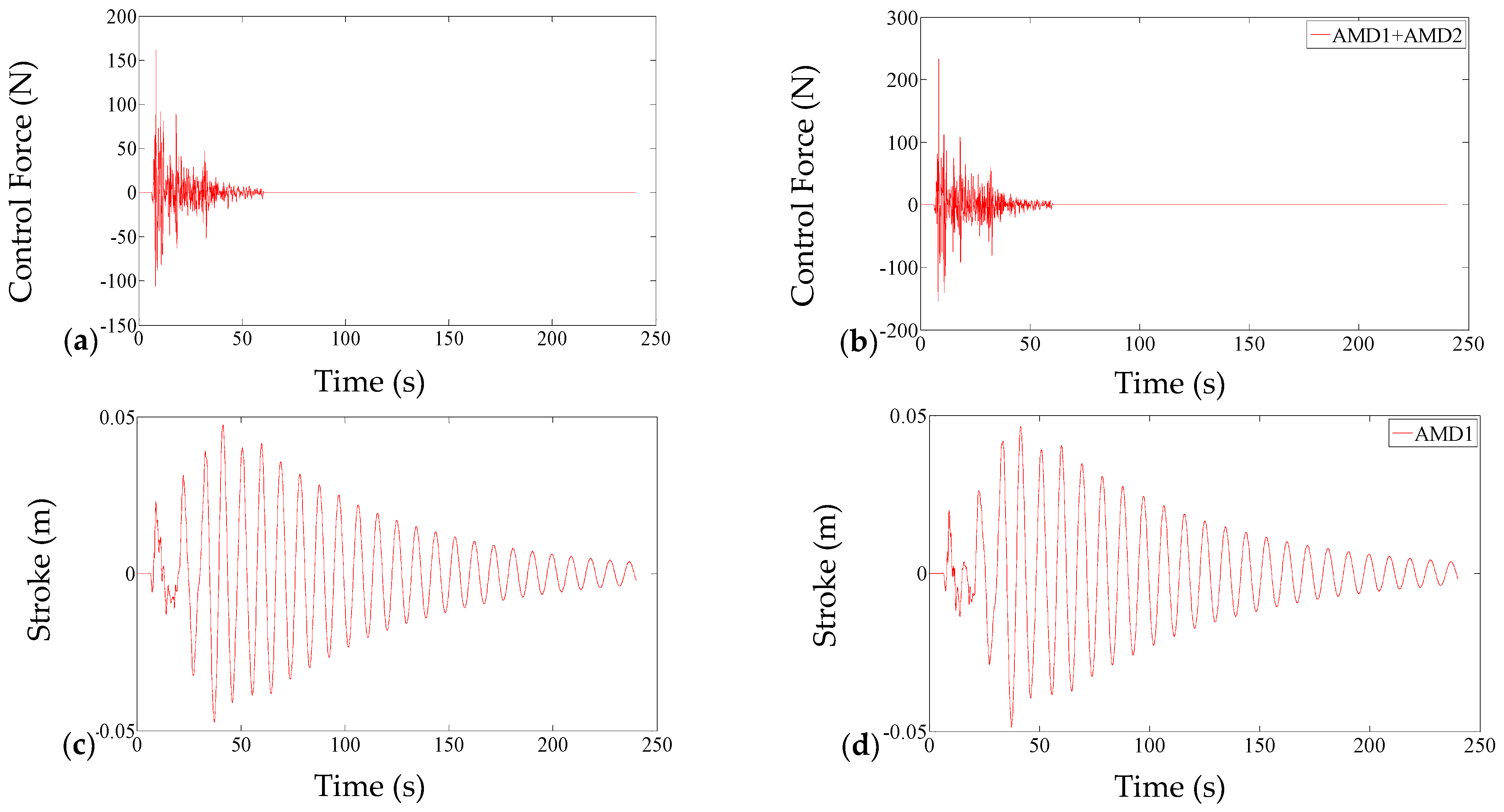
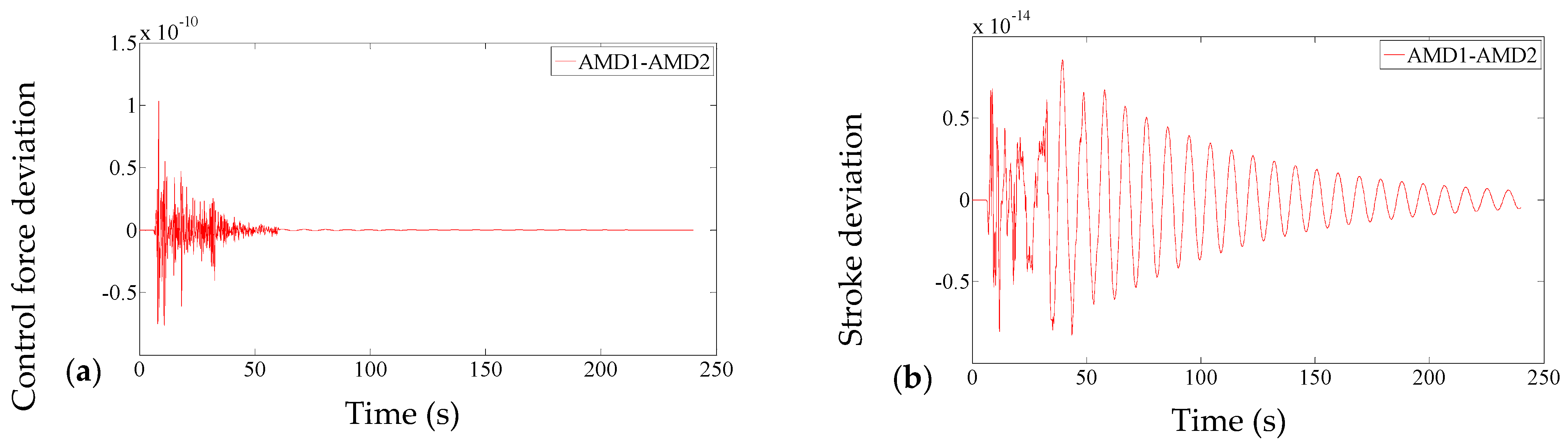
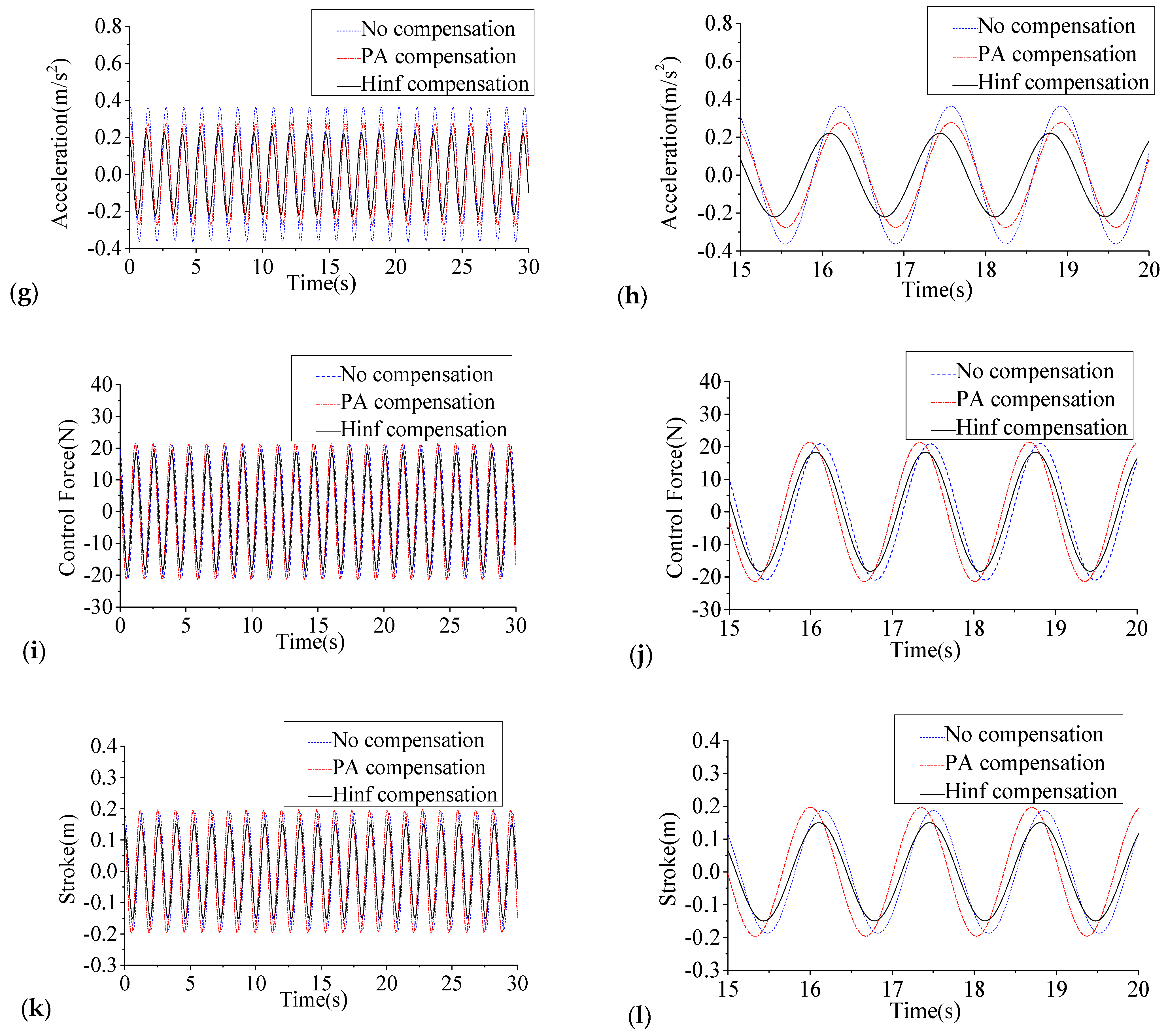
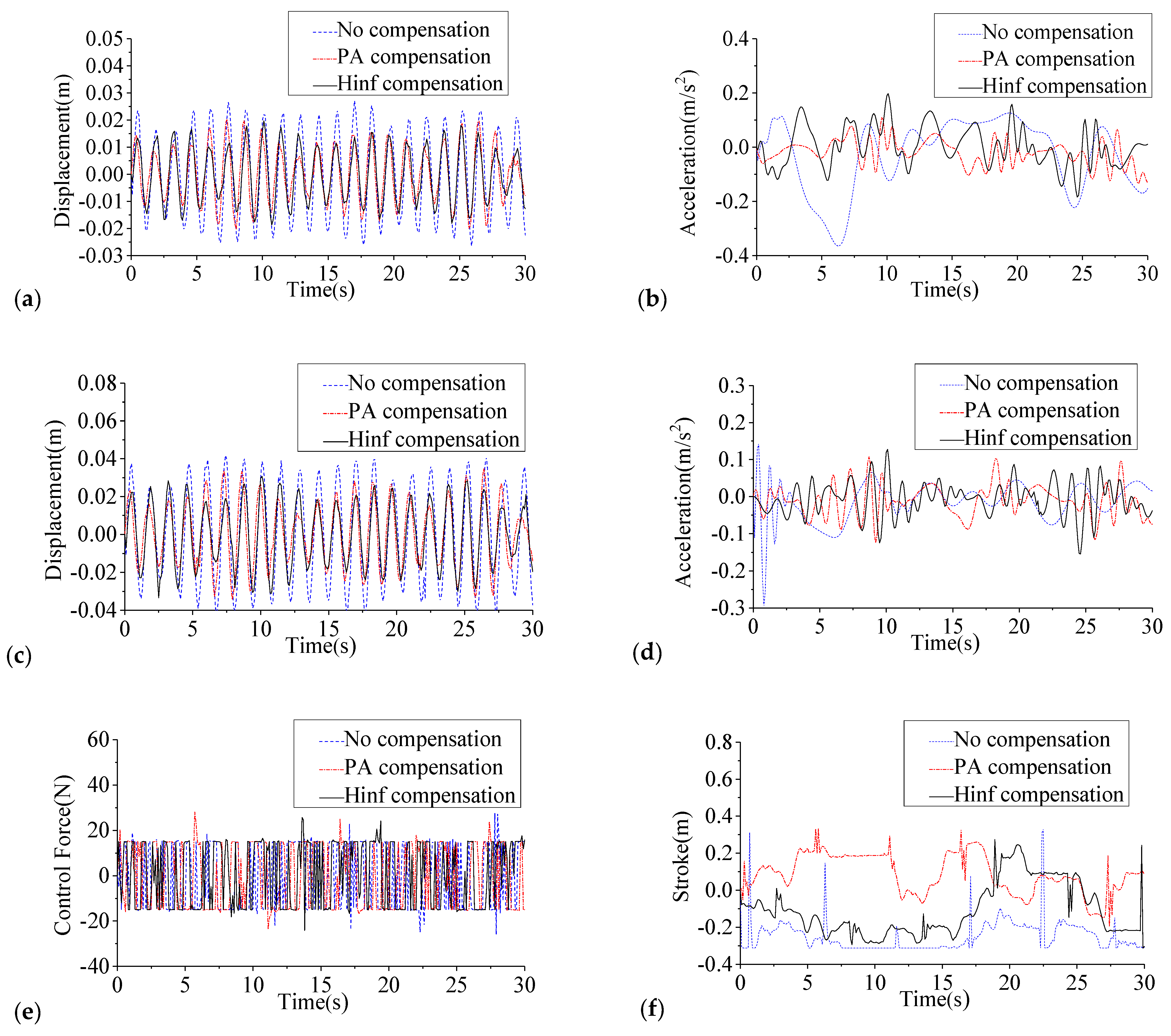
3.2. Numerical and Experimental Verification
4. Conclusions
5. Future Investigations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cao, L.; Li, C.; Chen, X. Performance of multiple tuned mass dampers-inerters for structures under harmonic ground acceleration. Smart Struct. Syst. Int. J. Smart Struct. Syst 2020, 26, 49–61. [Google Scholar]
- Jiang, J.; Zhang, P.; Patil, D.; Li, H.; Song, G. Experimental studies on the effectiveness and robustness of a pounding tuned mass damper for vibration suppression of a submerged cylindrical pipe. Struct Control Health Monit 2017, 26, e2319. [Google Scholar] [CrossRef]
- Zhang, P.; Song, G.; Li, H.N.; Lin, Y.X. Seismic Control of Power Transmission Tower Using Pounding TMD. J. Eng. Mech. 2013, 139, 1395–1406. [Google Scholar] [CrossRef]
- Chen, J.; Lu, G.; Li, Y.; Wang, T.; Wang, W.; Song, G. Experimental Study on Robustness of an Eddy Current-Tuned Mass Damper. Appl. Sci. 2017, 7, 895. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, C. Performance of tuned tandem mass dampers for structures under the ground acceleration. Struct. Control Health Monit. 2016, 24, e1974. [Google Scholar] [CrossRef]
- Zhang, C.; Ou, J. Modeling and dynamical performance of the electromagnetic mass driver system for structural vibration control. Eng. Struct. 2015, 82, 93–103. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, C.; Li, H.; Ou, J. Real-time hybrid simulation approach for performance validation of structural active control systems: A linear motor actuator based active mass driver case study. Struct. Control Health Monit. 2013, 21, 574–589. [Google Scholar] [CrossRef]
- Chen, C.-J.; Li, Z.-H.; Teng, J.; Wu, Q.-G.; Lin, B.-C. A variable gain state-feedback technique for an AMD control system with stroke limit and its appli-cation to a high-rise building. Struct Design Tall Spec Build. 2020, 30, 1816. [Google Scholar]
- Zhang, C.; Wang, H. Robustness of the Active Rotary Inertia Driver System for Structural Swing Vibration Control Subjected to Multi-Type Hazard Excitations. Appl. Sci. 2019, 9, 4391. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Li, J.; Qu, Y. An optimum design methodology of active tuned mass damper for asymmetric structures. Mech. Syst. Signal Process. 2010, 24, 746–765. [Google Scholar] [CrossRef]
- Li, C.; Qu, W. Evaluation of elastically linked dashpot based active multiple tuned mass dampers for structures under ground acceleration. Eng. Struct. 2004, 26, 2149–2160. [Google Scholar] [CrossRef]
- Lu, X.; Li, P.; Guo, X.; Shi, W.; Liu, J. Vibration control using ATMD and site measurements on the Shanghai World Financial Center Tower. Struct. Des. Tall Spéc. Build. 2012, 23, 105–123. [Google Scholar] [CrossRef]
- Fu, W.; Zhang, C.; Li, M.; Duan, C. Experimental Investigation on Semi-Active Control of Base Isolation System Using Magnetorheological Dampers for Concrete Frame Structure. Appl. Sci. 2019, 9, 3866. [Google Scholar] [CrossRef] [Green Version]
- Qu, C.; Huo, L.; Li, H.; Wang, Y. A double homotopy approach for decentralized H-infinity control of civil structures. Struct. Control Health Monit 2014, 21, 269–281. [Google Scholar] [CrossRef]
- Huo, L.; Qu, C.; Li, H. Robust control of civil structures with parametric uncertainties through D-K iteration. Struct. Des. Tall Spéc. Build. 2015, 25, 158–176. [Google Scholar] [CrossRef]
- Pu, Z.; Rao, R. Delay-dependent LMI-based robust stability criterion for discrete and distributed time-delays Markovian jumping reaction–diffusion CGNNs under Neumann boundary value. Neurocomputing 2016, 171, 1367–1374. [Google Scholar] [CrossRef]
- Mobayen, S. An LMI-based robust tracker for uncertain linear systems with multiple time-varying delays using optimal composite nonlinear feedback technique. Nonlinear Dyn 2015, 80, 917–927. [Google Scholar] [CrossRef]
- Teng, J.; Xing, H.; Lu, W.; Li, Z.; Chen, C. Influence analysis of time delay to active mass damper control system using pole assignment method. Mech. Syst. Signal Process. 2016, 80, 99–116. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Lv, C.; Gou, J.; Yuan, Y. Time-varying delays compensation algorithm for powertrain active damping of an electrified vehicle equipped with an axle motor during regenerative braking. Mech. Syst. Signal Process. 2017, 87, 45–63. [Google Scholar] [CrossRef]
- Obuz, S.; Klotz, J.R.; Kamalapurkar, R.; Dixon, W. Unknown time-varying input delay compensation for uncertain nonlinear systems. Automatica 2017, 76, 222–229. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Choi, S.G. Stability analysis of discrete-time switched systems with time-varying delays via a new summation inequality. Nonlinear Anal. Hybrid Syst. 2017, 23, 76–90. [Google Scholar] [CrossRef]
- Chen, C.; Li, Z.; Teng, J.; Wang, Y. Influence Analysis of a Higher-Order CSI Effect on AMD Systems and Its Time-Varying Delay Compensation Using a Guaranteed Cost Control Algorithm. Appl. Sci. 2017, 7, 313. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.H.; Chen, C.J.; Teng, J.; Hu, W.H.; Xing, H.B.; Wang, Y. A Reduced-Order Controller Considering High-Order Modal Information of High-Rise Buildings for AMD Control System with Time-Delay. Shock Vib. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Stewart, G.M.; Lackner, M.A. The effect of actuator dynamics on active structural control of offshore wind turbines. Eng. Struct. 2011, 33, 1807–1816. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Li, Y.; Li, H. Stability and bifurcation for a coupled nonlinear relative rotation system with multi-time delay feedbacks. Nonlinear Dyn. 2014, 77, 923–934. [Google Scholar] [CrossRef]
- Marinescu, B.; Bourles, H. Robust state-predictive control with separation property: A reduced-state design for control systems with non-equal time delays. Automatica 2000, 36, 555–562. [Google Scholar] [CrossRef]
- Chen, C.W. A criterion of robustness intelligent nonlinear control for multiple time-delay systems based on fuzzy Lyapunov methods. Nonlinear Dyn. 2013, 76, 23–31. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, M.J.; Kwon, O.M.; Lee, S.M.; Cha, E.J. Stability and robust H-infinity control for time-delayed systems with parameter uncertainties and stochastic disturbances. J. Electr. Eng. Technol. 2016, 11, 200–214. [Google Scholar] [CrossRef]
- Sang, H.; Nie, H. H-infinity switching synchronization for multiple time-delay chaotic systems subject to controller failure and its application to aperiodically intermittent control. Nonlinear Dyn. 2018, 92, 869–883. [Google Scholar] [CrossRef]
- Pérez, A.T. Measuring the speed of electromagnetic waves using the cross correlation function of broadband noise at the ends of a transmission line. Am. J. Phys. 2011, 79, 1042–1045. [Google Scholar] [CrossRef]
- Chen, C.-J.; Li, Z.-H.; Teng, J.; Hu, W.-H.; Wang, Y. An Observer-Based Controller with a LMI-Based Filter against Wind-Induced Motion for High-Rise Buildings. Shock Vib. 2017, 2017, 1427270. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Chen, C.; Teng, J. A multi-time-delay compensation controller using a Takagi–Sugeno fuzzy neural network method for high-rise buildings with an active mass damper/driver system. Struct. Des. Tall Spéc. Build. 2019, 28, e1631. [Google Scholar] [CrossRef]
- Sastry, S. Lyapunov Stability Theory in Nonlinear Systems: Analysis, Stability, and Control, 1st ed.; Springer: New York, NY, USA, 1999; pp. 137–162. [Google Scholar]
- Briat, C.; Sename, O.; Lafay, J.F. H-infinity delay-scheduled control of linear systems with time-varying delays. IEEE Trans. Autom. Control 2009, 54, 2255–2260. [Google Scholar] [CrossRef]
- Ahmadi, A.; Aldeen, M. An LMI approach to the design of robust delay-dependent overlapping load frequency control of uncertain power systems. Int. J. Elec. Power 2016, 81, 48–63. [Google Scholar] [CrossRef]
- Zhang, F. The Schur Complement and Its Applications, 1st ed.; Springer: New York, NY, USA, 2005; pp. 137–162. [Google Scholar]
- Yu, L. Robust Control-Linear Matrix Inequalities Approach, 1st ed.; Tsinghua University Press: Beijing, China, 2002; pp. 41–67. [Google Scholar]


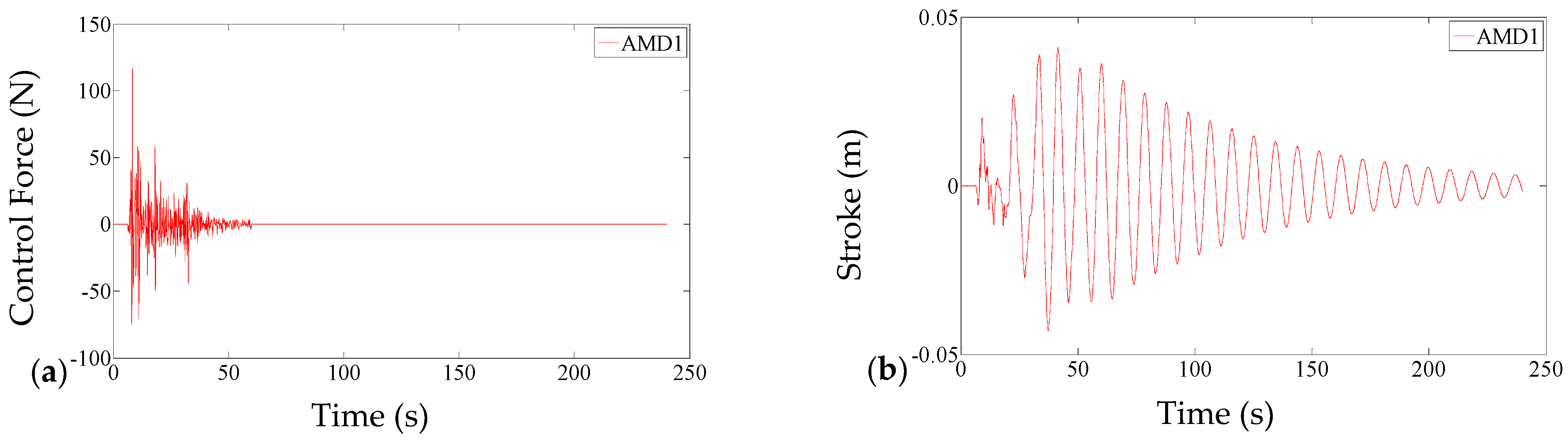
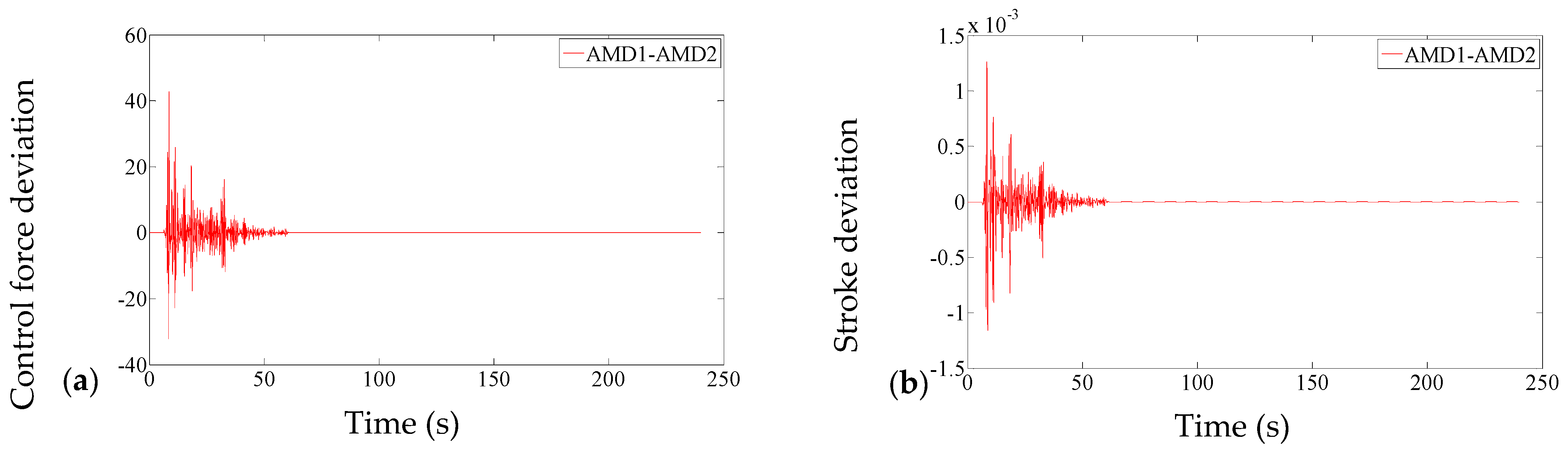


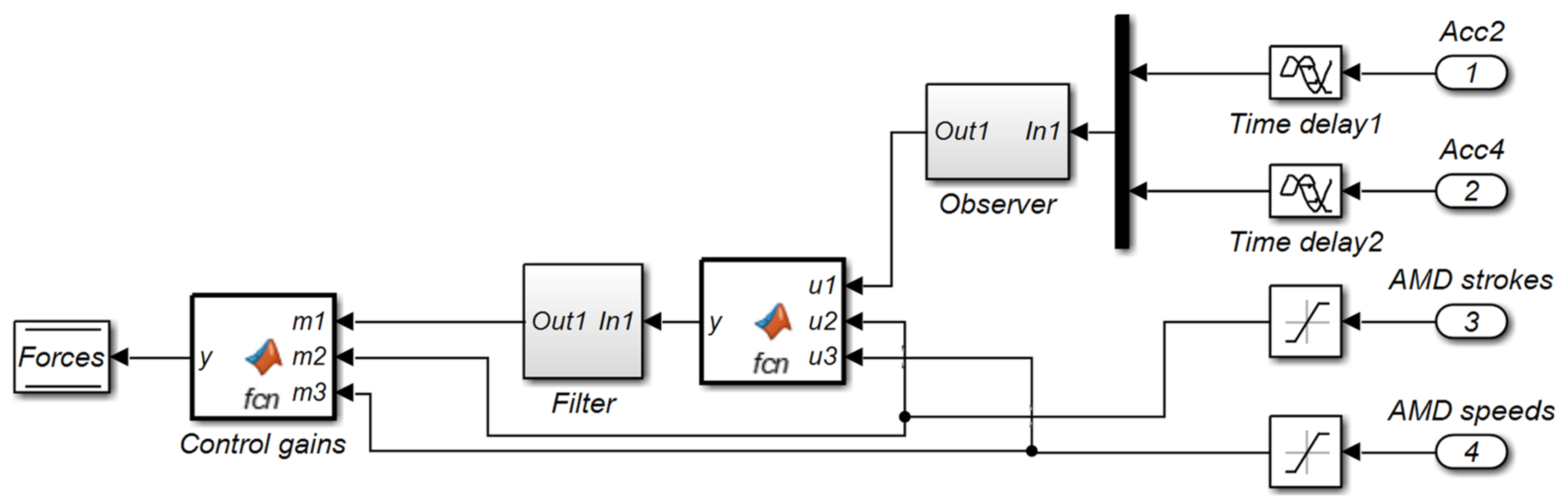
| Index | System1 | System2 |
|---|---|---|
| The weight of the auxiliary mass (kg) | 20 × 1 | 10 × 2 |
| The effective stroke (m) | 0.4 | 0.4 |
| The maximum driving force (N) | ±1000 × 1 | ±500 × 2 |
| Index | No Time Delays | With Equal Time Delays | With Unequal Time Delays | |||
|---|---|---|---|---|---|---|
| System1 | System2 | System1 | System2 | System1 | System2 | |
| 2nd floor | 36.21 | 36.08 | −11.19 | −17.29 | — | −15.97 |
| 3rd floor | 38.51 | 38.37 | −8.70 | −13.88 | — | −12.94 |
| 4th floor | 39.95 | 39.79 | −7.27 | −11.56 | — | −9.15 |
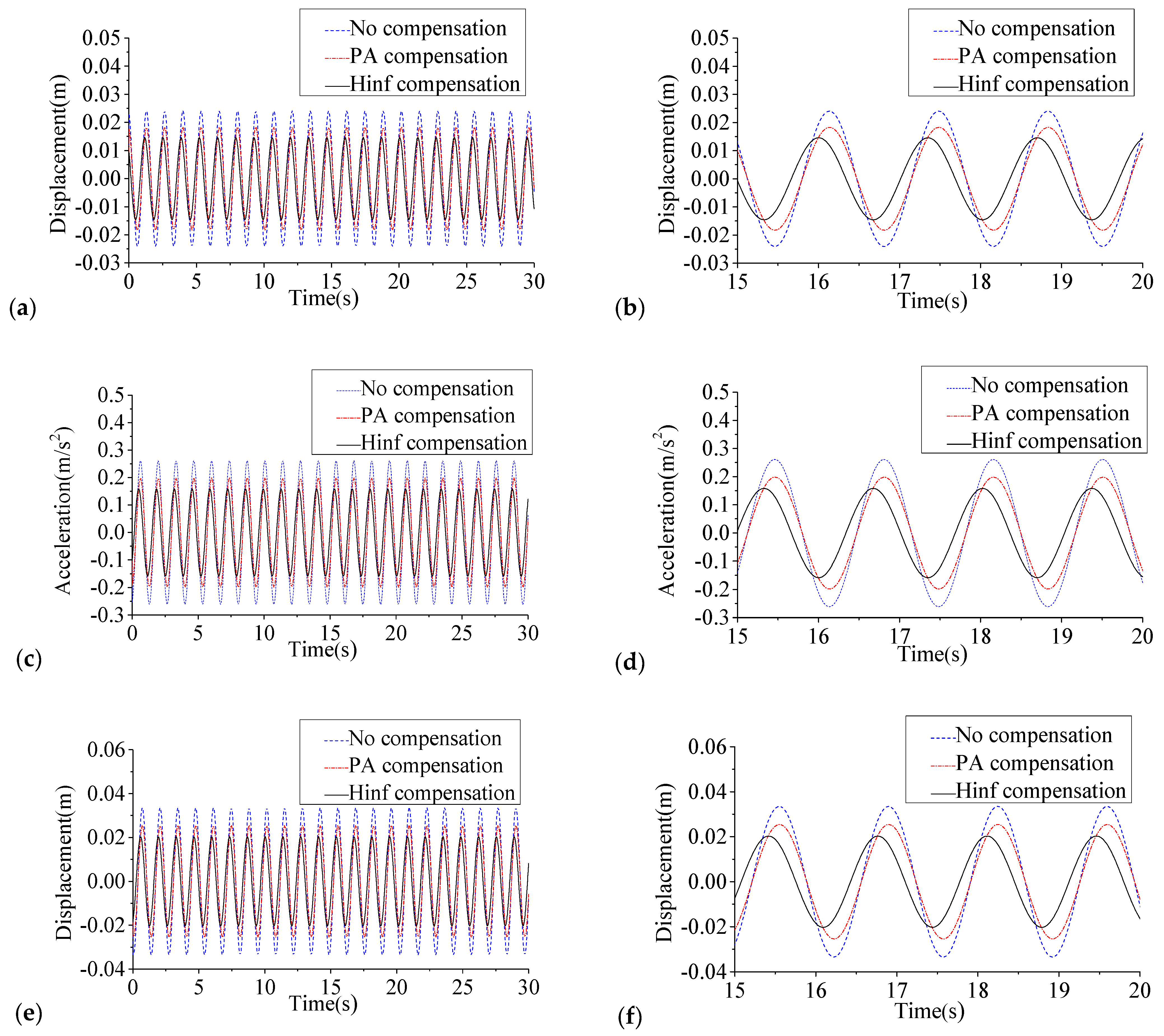
| Index | No Control | No Compensation | PA Compensation | H∞ Compensation | ||||
|---|---|---|---|---|---|---|---|---|
| Responses | Effect (%) | Responses | Effect (%) | Responses | Effect (%) | |||
| Displacement (cm) | 2nd floor | 1.54 | 1.70 | −10.22 | 1.29 | 16.24 | 1.03 | 33.26 |
| 4th floor | 2.15 | 2.37 | −10.25 | 1.80 | 16.21 | 1.43 | 33.23 | |
| Acceleration (cm/s2) | 2nd floor | 16.76 | 18.48 | −10.23 | 14.04 | 16.23 | 11.19 | 33.25 |
| 4th floor | 23.33 | 25.72 | −10.25 | 19.54 | 16.23 | 15.58 | 33.24 | |
| Control force (N) | — | 14.80 | — | 15.13 | — | 12.96 | — | |
| Stroke (cm) | — | 13.23 | — | 13.91 | — | 10.60 | — | |
| Index | No Control | No Compensation | PA Compensation | H∞ Compensation | ||||
|---|---|---|---|---|---|---|---|---|
| Responses | Effect (%) | Responses | Effect (%) | Responses | Effect (%) | |||
| Displacement (cm) | 2nd floor | 1.58 | 1.62 | −2.53 | 1.11 | 29.75 | 1.01 | 36.08 |
| 4th floor | 2.67 | 2.62 | 1.87 | 1.86 | 30.34 | 1.69 | 36.70 | |
| Acceleration (cm/s2) | 2nd floor | 14.95 | 16.81 | −12.44 | 5.86 | 60.80 | 6.09 | 59.26 |
| 4th floor | 11.74 | 16.03 | −36.54 | 4.29 | 63.46 | 3.84 | 67.29 | |
| Control force (N) | — | 14.90 | — | 14.19 | — | 14.12 | — | |
| Stroke (cm) | — | 17.55 | — | 15.13 | — | 11.82 | — | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Teng, J.; Li, Z.; Lin, B. A Compensation Strategy Using an H∞ Control Law for a Multi-Time-Delay Control System. Appl. Sci. 2022, 12, 2860. https://doi.org/10.3390/app12062860
Chen C, Teng J, Li Z, Lin B. A Compensation Strategy Using an H∞ Control Law for a Multi-Time-Delay Control System. Applied Sciences. 2022; 12(6):2860. https://doi.org/10.3390/app12062860
Chicago/Turabian StyleChen, Chaojun, Jun Teng, Zuohua Li, and Beichun Lin. 2022. "A Compensation Strategy Using an H∞ Control Law for a Multi-Time-Delay Control System" Applied Sciences 12, no. 6: 2860. https://doi.org/10.3390/app12062860
APA StyleChen, C., Teng, J., Li, Z., & Lin, B. (2022). A Compensation Strategy Using an H∞ Control Law for a Multi-Time-Delay Control System. Applied Sciences, 12(6), 2860. https://doi.org/10.3390/app12062860






