Numerical Assessment and Repair Method of Runway Pavement Damage Due to CBU Penetration and Blast Loading
Abstract
:1. Introduction
2. The Depth of CBU Penetration
2.1. Calculation of Penetration Depth
- x = Penetration depth;
- N = Nose shape factor;
- W = Projectile weight;
- d = Projectile diameter;
- = Compressive strength of concrete;
- = Velocity of projectile.
| Projectile weight (W) | 32 kg | Effective sectional area of projectile (A) | 7.854 × 10−3 m2 |
| Projectile diameter (d) | 0.1 m | Gravitational acceleration (g) | 9.8 m/s |
| Shape coefficient (D) | 0.3 | Density of air (ρ) | 1.2 kg/m3 |
| Velocity of projectile (v) | 470 m/s | Compressive strength of concrete () | 35 MPa |
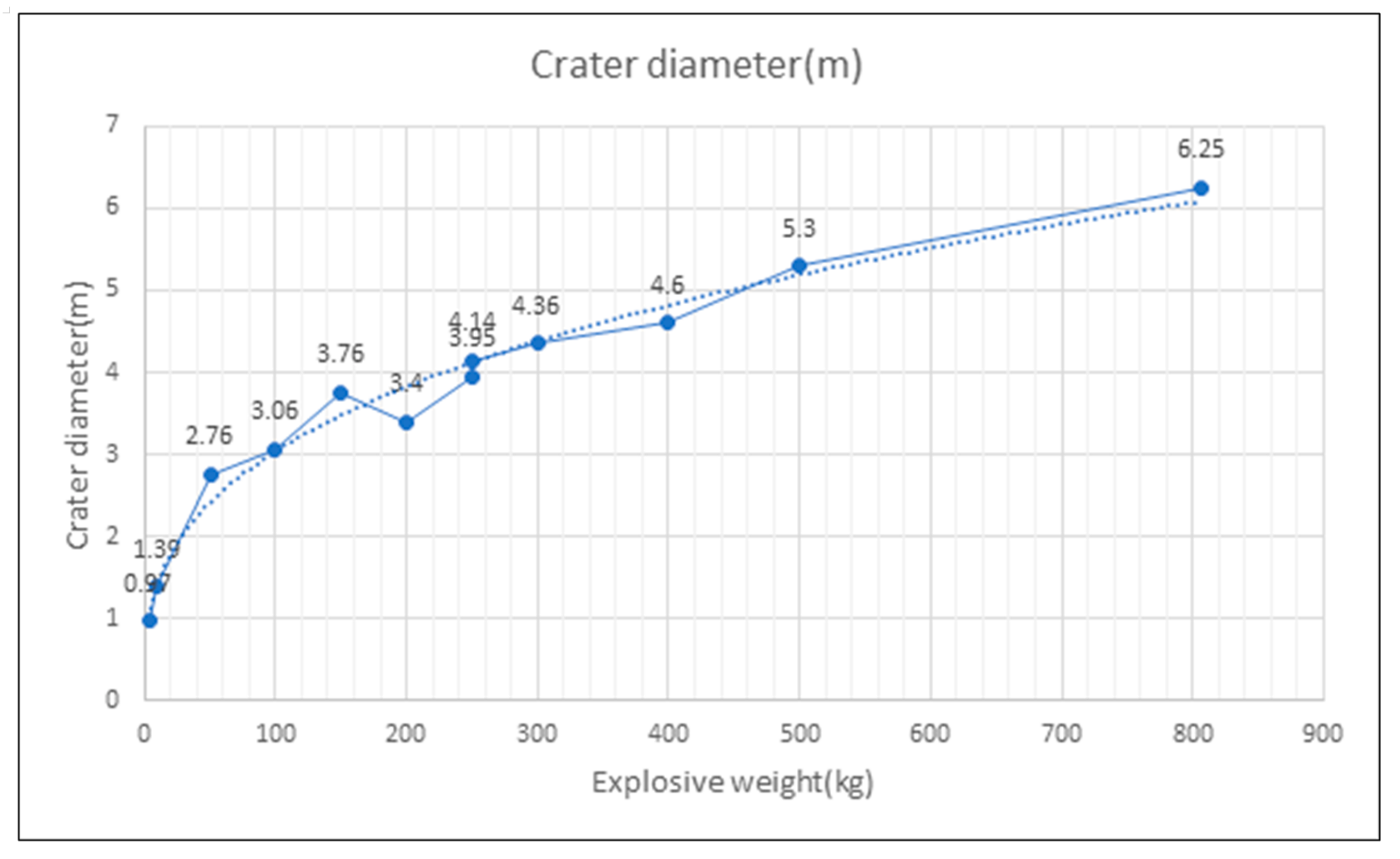
2.2. Field Trial Blast Test Result
2.3. Verification of Field Test Results
- C = Weight of Explosive (kg);
- K = Specific Charge Weight (kg/m3);
- r = Radius of Crater.
3. Numerical Simulation (LS-DYNA M&S)
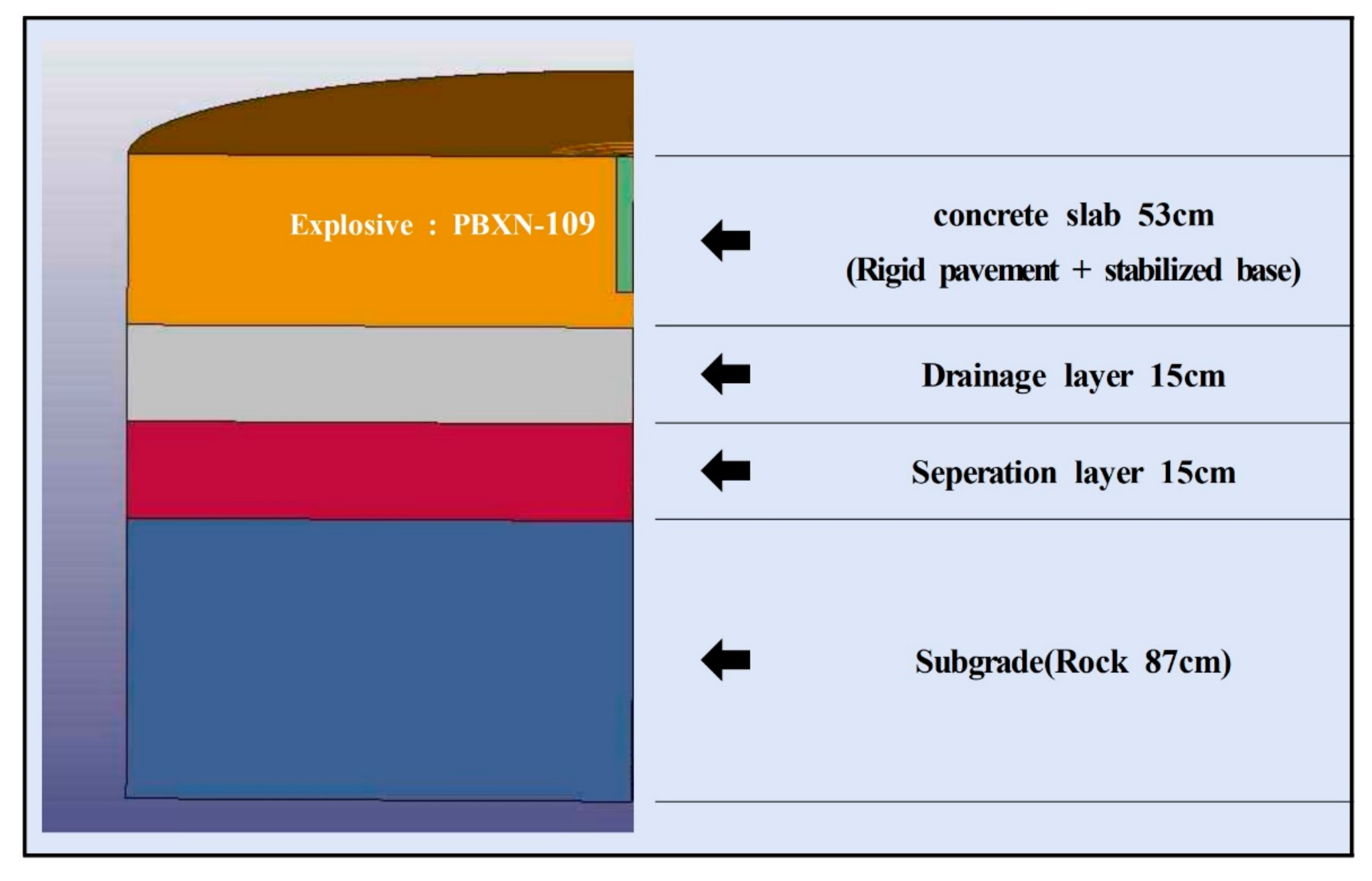
3.1. Construction of Simulated Runway Pavement
3.2. RHT Concrete Model and Material
- p = Pressure;
- A1, A2, A3, B0, B1, T1, T2 = Constant;
- e = Internal energy.
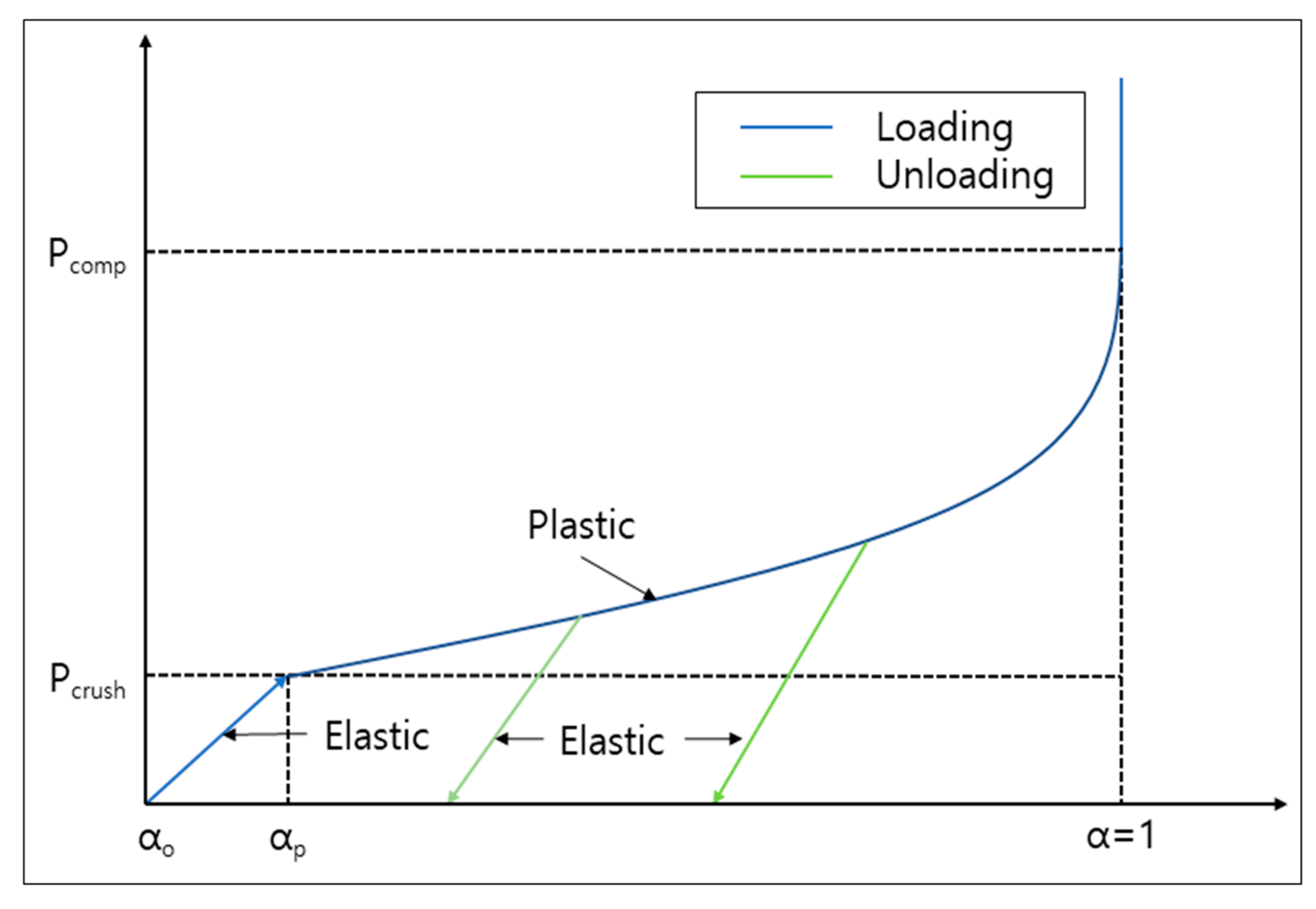
- = Porosity ratio;
- = compaction pressure;
- = Pore crush pressure (Initial compaction pressure);
- = Solid compaction pressure.
- = the material’s uniaxial compressive strength;
- = the material’s tensile strength;
- and = pressure and spall strength, respectively;
- = strain rate;
- n = porosity exponent;
- = function of the DIF (Dynamic Increase Factor).
- = function of Lode angle;
- Q = Portion of the equivalent strength;
- B = Reflects a brittle-to-ductile transition;
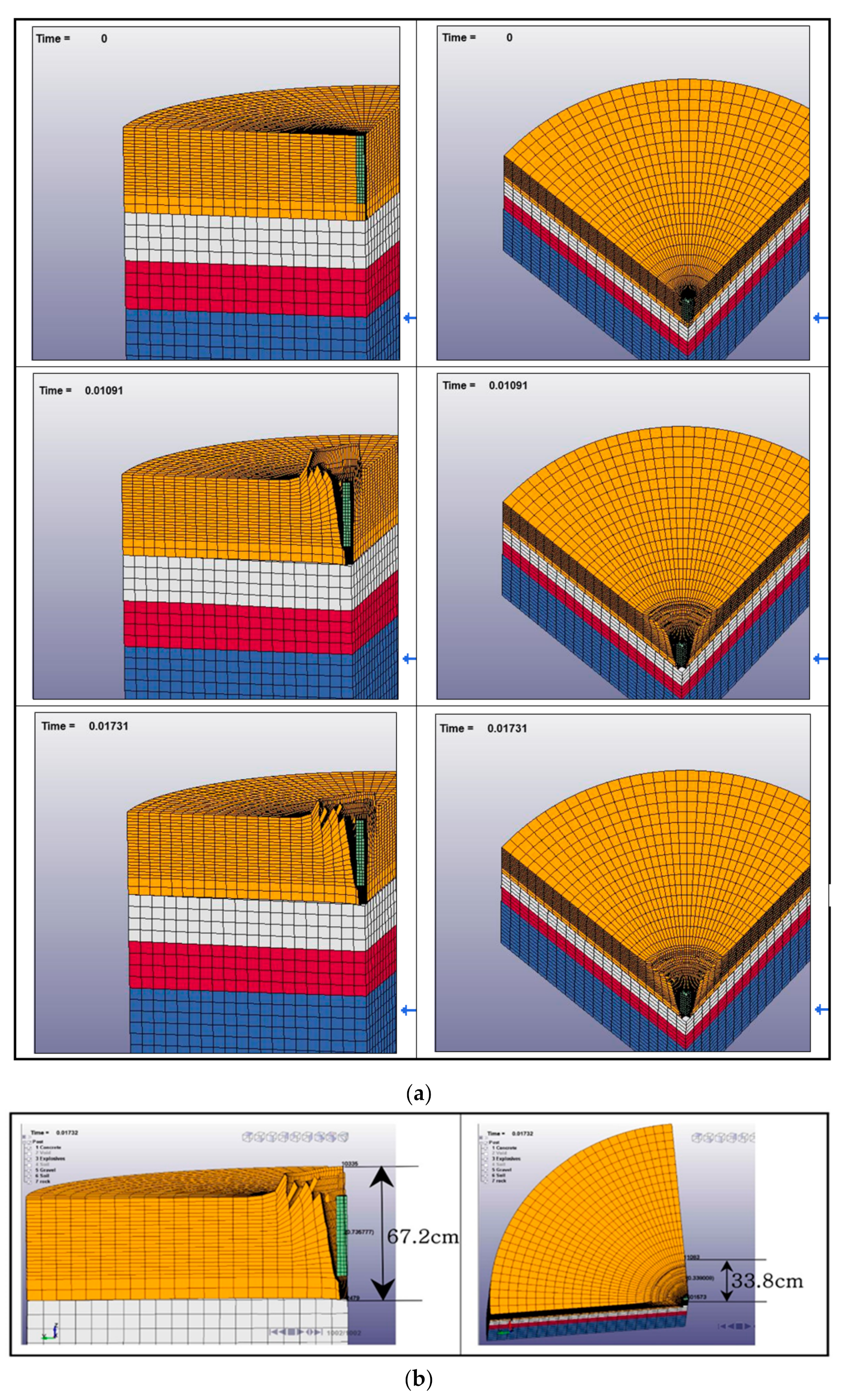
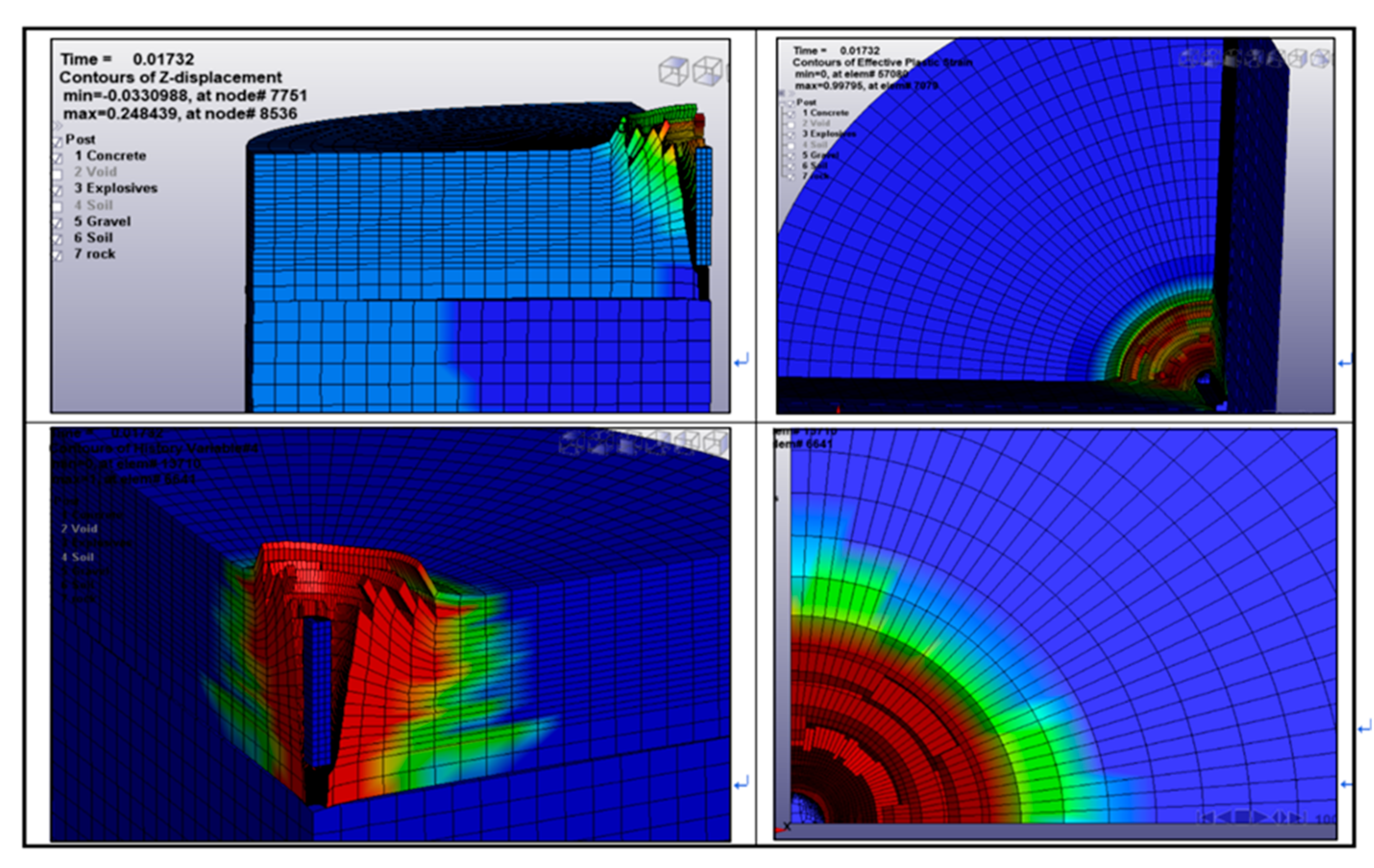
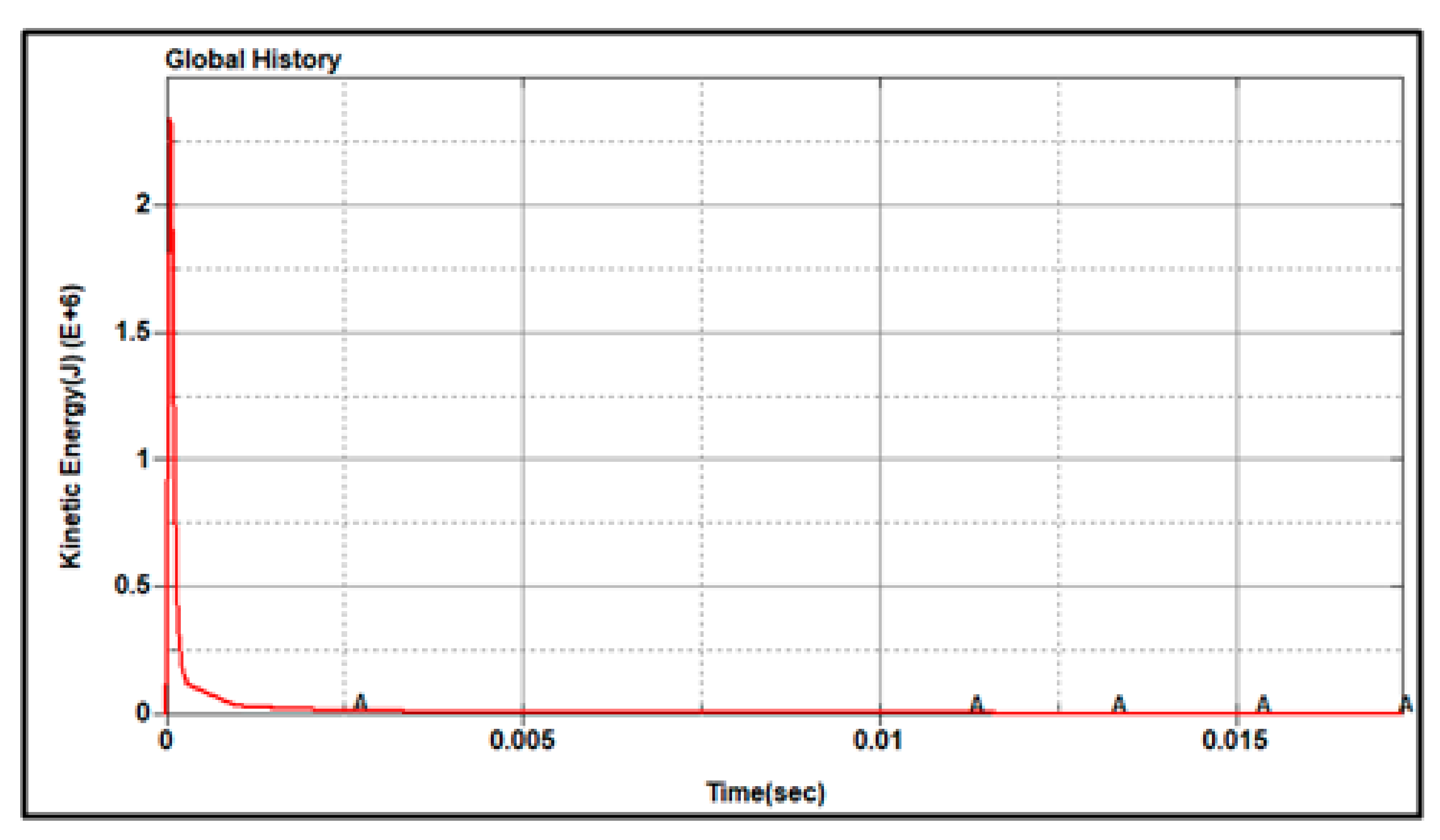
3.3. Results and Analysis of Modeling
3.4. Comparison and Discussion with Regard to the Results of Numerical Simulation
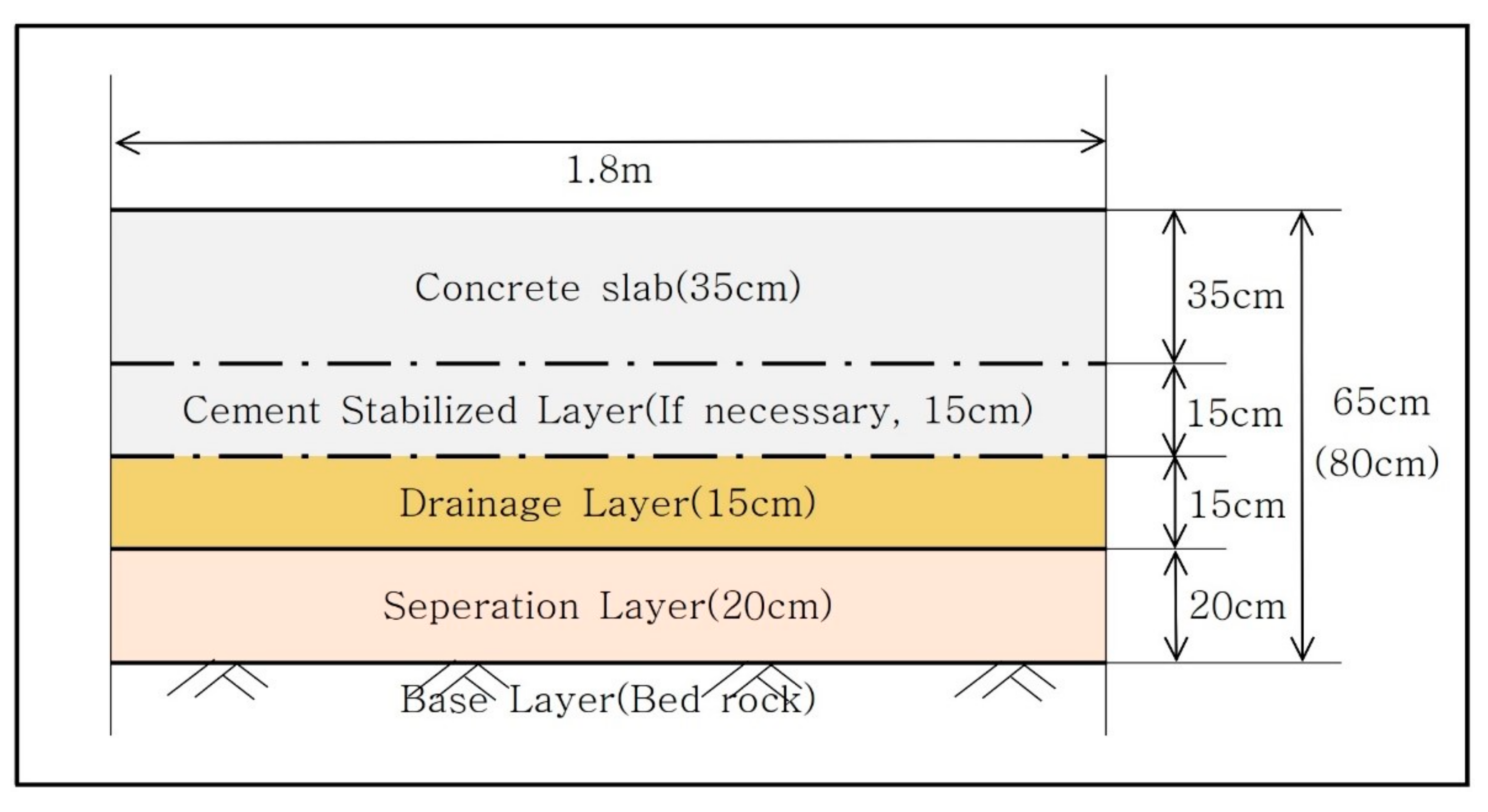
4. Proposal of Crater Repair Method
4.1. Application of the Damage Repair Section
4.2. Proposal of Rapid Damage Repair Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kenneth, C.; Ove, D.; Jenzen-Jones, N.R.; Marc, G. Explosive Weapons in Populated Areas: Technical Considerations Relevant to Their Use and Effects; Armament Research Services (ARES): Canberra, Australia, 2016; Available online: https://reliefweb.int/sites/reliefweb.int/files/resources/aresweb-generic.pdf (accessed on 22 December 2021).
- Wu, J.; Chew, S.H. Field performance and numerical modeling of multi-layer pavement system subject to blast load. Sci. Constr. Mater. 2014, 52, 177–188. [Google Scholar] [CrossRef]
- Mo, L.; Victor, C. High-Early-Strength Engineered Cementitious Composites for Fast, Durable Concrete Repair—Material Properties. ACI Mater. J. 2011, 108, 3–12. [Google Scholar]
- Air Force Tactics, Techniques, and Procedures. Airfield Damage Assessment after Major Attack. Air Force Tactics, Techniques, and Procedures; ATTP 3-32.11; Department of the Air Force: Virginia Beach, VA, USA, 2016.
- Kim, S.H.; Tomas, H.; Kang, K. Development of Energy-Based Impact Formula-Part I: Penetration Depth. Appl. Sci. 2020, 10, 4964. [Google Scholar] [CrossRef]
- UFC. Design and Analysis of Hardened Structures to Conventional Weapons Effects; UFC 3-340-01; USA Department of Defense: Washington, DC, USA, 2002.
- Rama, C.M.A.; Palani, G.S.; Nagesh, R.I. Evaluation of Concrete Penetration Depth under Impact Loading Employing Empirical Formula. SDHM 2008, 4, 221–229. [Google Scholar]
- Frew, D.J.; Hanchak, S.J.; Green, M.L.; Forrestals, M.J. Penetration of concrete targets with ogive nose steel rods. Int. J. Impact Eng. 1998, 21, 489–497. [Google Scholar] [CrossRef]
- Bulson, P.S. Explosive Loading of Engineering Structures; Taylor & Francis e-Library: London, UK, 1997. [Google Scholar]
- Kingery, C.N.; Bulmash, G. Technical Report ARBRL-TR-02555: Air Blast Parameters from TNT Spherical Air Burst and Hemispherical Burst; AD-B082 713; U.S. Army Ballistic Research Laboratory, Aberdeen Proving Ground: Adelphi, MD, USA, 1984. [Google Scholar]
- Hwang, I.J.; Kim, S.K. Field Performance and Rapid Repair Method of an Airfield Pavement under the Blast Load of Cluster Bomb Unit, WMCAUS 2021. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1203, 032070. [Google Scholar] [CrossRef]
- Advisory Circular of US. Pavement Design and Evaluation; AFPAM, AC 150/5320-6F; Advisory Circular of U.S. Department of Transportation Federal Aviation: Washington, DC, USA, 2016.
- Karlos, V.; Solomos, G. Calculation of Blast Loads for Application to Structural Components; JRC Technical Reports; Publications Office of the European Union: Luxembourg, 2013; p. 8. [Google Scholar]
- US. Department of Energy, Amarillo Energy Office. A Manual for the Predictions of Blast and Fragment Loadings on Structures; DOE/TIC-11268; US. Department of Energy, Amarillo Energy Office: Amarillo, TX, USA, 1981; pp. 79–101.
- Brode, H.L. Numerical solution of spherical blast waves. J. Appl. Phys. 1955, 26, 766–775. [Google Scholar] [CrossRef]
- Mills, C.A. The design of concrete structures to resist explosions and weapon effects. In Proceedings of the 1st International Conference on Concrete for Hazard Protections, Edinburgh, UK, 27–30 September 1987. [Google Scholar]
- Malvar, L.J.; Crawford, J.E.; Wesevich, J.W.; Simons, D. A plasticity concrete material model for DYNA3D. Int. J. Impact Eng. 1997, 19, 847–873. [Google Scholar] [CrossRef]
- Alia, A.; Souli, M. High explosive simulation using multi-material formulations. Appl. Therm. Eng. 2006, 26, 1032–1042. [Google Scholar] [CrossRef]
- Christian, H.; Jürgen, S. Comparison of the RHT Concrete Material Model in LS-DYNA and ANSYS AUTODYN. In Proceedings of the 11th European LS-DYNA Conference 2017, Salzburg, Austria, 9–11 May 2017. [Google Scholar]
- Park, D. Numerical Models for Simulating the Dynamic Behavior of Concrete Subjected to High Velocity Impact. J. Korean Soc. Miner. Energy Resour. Eng. 2017, 54, 429–436. [Google Scholar] [CrossRef]
- Herrmann, W. Constitutive Equation for the Dynamic Compaction of Ductile Porous Materials. J. Appl. Phys. 1969, 40, 2490–2499. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R.; Gooch, W.A. Modeling the 14.5 mm BS41 projectile for ballistic impact computations. WIT Trans. Model. Simul. 2005, 40, 61–75. [Google Scholar]
- Thomas, B.; Riedel, W. The Rht Concrete Model in Ls-Dyna. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 24 May 2011. [Google Scholar]
- Ryu, Y.-S.; Cho, H.-M.; Kim, S.-H. Collision Behavior Evaluatio of Flexible Concrete Mattress Depending on Material Models. J. Ocean. Eng. Technol. 2015, 29, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Riedel, W.; Kawai, N.; Kondo, K.-I. Numerical assessment for impact strength measurements in concrete materials. Int. J. Impact Eng. 2009, 36, 283–293. [Google Scholar] [CrossRef] [Green Version]
- Robert, H. IHS Jane’s Weapons: Air Launched 2014–2015; FSC: Llanidloes, UK, 2014. [Google Scholar]

| Sort | Result of Field Test | Sort | Repair Range |
|---|---|---|---|
| Diameter | 30 cm | Cutting and Removal Area | 1.8 m × 1.8 m |
| Depth | 78 cm | Repaired Depth | 84 cm |
| Damage layer | Separation layer (Sand layer) | Repaired layer | Separation layer (Sand layer) |
| Upheaval | 0~0.7 cm | ||
| Fracture zone | 155.8 cm |
| Material | K (kg/m3) |
|---|---|
| Masonry | 1.2–2.0 |
| Plane Concrete (29 MPa) | 2.5–3.0 |
| Reinforced Concrete (without cutting reinforcement) | 8.4 |
| Reinforced Concrete (with partial cutting of reinforcement) | 33.6 |
| Parameters | Symbol | Units | Value |
|---|---|---|---|
| Young’s modulus | E | GPa | 27 |
| Compressive strength | fc | MPa | 3.5 |
| Shear modulus | GPa | 16.7 | |
| Density | ρ | kg/m3 | 2314 |
| Material | Density | Elastic Shear Modulus | Eroding Plastic Strain | B0 |
|---|---|---|---|---|
| Concrete | 2314 kg/m3 | 16.70 GPa | 0.5 | 1.22 |
| B1 | T1 | A | N | Compressive strength |
| 1.22 | 35.27 GPa | 1.6 | 0.61 | 35 MPa |
| Relative shear strength | Relative tensile strength | Q0 | B | T2 |
| 0.18 | 0.1 | 0.6805 | 0.01 | 0.0 |
| Reference compressive strain rate | Reference tensile strain rate | Break compressive strain rate | Break tensile strain rate | Compressive strain rate dependence exponent |
| 3.0 × 10−8 | 3.0 × 10−9 | 3.0 × 10−22 | 3.0 × 10−22 | 0.032 |
| Tensile strain rate dependence exponent | Pressure influence on plastic flow in tension | Compressive yield surface parameter | Tensile yield surface parameter | Shear modulus reduction factor |
| 0.036 | 0.001 | 0.53 | 0.7 | 0.5 |
| D1 | D2 | Minimum damaged residual strain | Af | Nf |
| 0.04 | 1.0 | 0.01 | 1.6 | 0.61 |
| Gruneisen Gamma | A1 | A2 | A3 | Crush pressure |
| 0.0 | 35.27 GPa | 39.58 GPa | 9.04 GPa | 23.30 GPa |
| Compaction pressure | Porosity exponent | Initial porosity | ||
| 6.0 GPa | 3.0 | 1.1884 |
| Sort | Field Test | M&S |
|---|---|---|
| Crater Diameter | 30 cm | 67.6 cm |
| Crater Depth | 78 cm | 55.2 cm |
| Damage layer | Separation Layer | Drainage Layer |
| Upheaval | 0~0.7 cm | 12 cm |
| Repair Method | Advantages and Disadvantages | Applicability |
|---|---|---|
| High-Early-Strength Concrete |
| ○ |
| Precast Concrete (PCC) |
| △ |
| FOD Cover Mat |
| × |
| Asphalt Concrete |
| × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Kim, S.; Hwang, I. Numerical Assessment and Repair Method of Runway Pavement Damage Due to CBU Penetration and Blast Loading. Appl. Sci. 2022, 12, 2888. https://doi.org/10.3390/app12062888
Han J, Kim S, Hwang I. Numerical Assessment and Repair Method of Runway Pavement Damage Due to CBU Penetration and Blast Loading. Applied Sciences. 2022; 12(6):2888. https://doi.org/10.3390/app12062888
Chicago/Turabian StyleHan, Jaeduk, Sungil Kim, and Injae Hwang. 2022. "Numerical Assessment and Repair Method of Runway Pavement Damage Due to CBU Penetration and Blast Loading" Applied Sciences 12, no. 6: 2888. https://doi.org/10.3390/app12062888
APA StyleHan, J., Kim, S., & Hwang, I. (2022). Numerical Assessment and Repair Method of Runway Pavement Damage Due to CBU Penetration and Blast Loading. Applied Sciences, 12(6), 2888. https://doi.org/10.3390/app12062888





