Investigation of Grain, Grain Boundary, and Interface Contributions on the Impedance of Ca2FeO5
Abstract
:1. Introduction
2. Experimental Set-Up
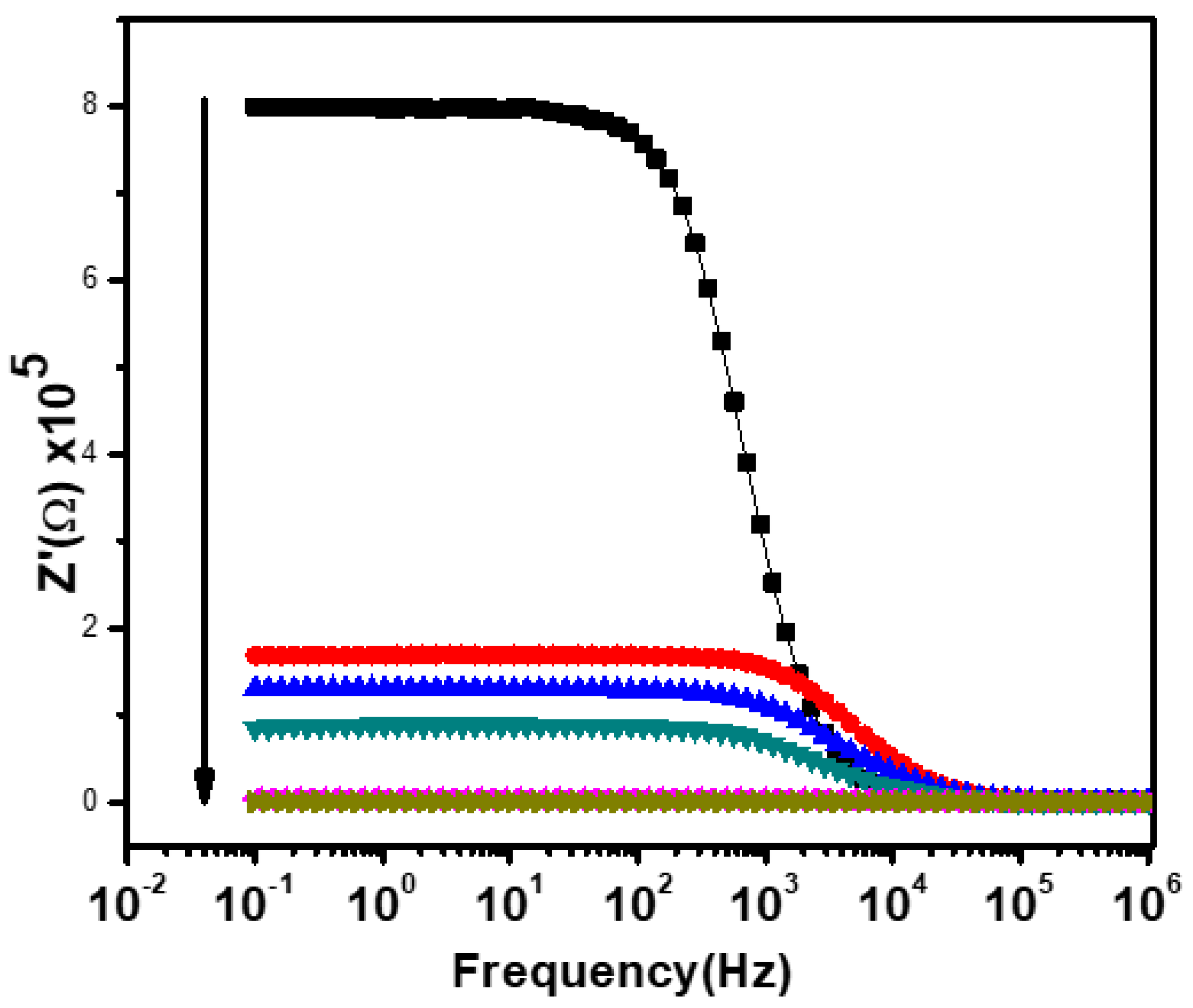
3. Results and Discussion
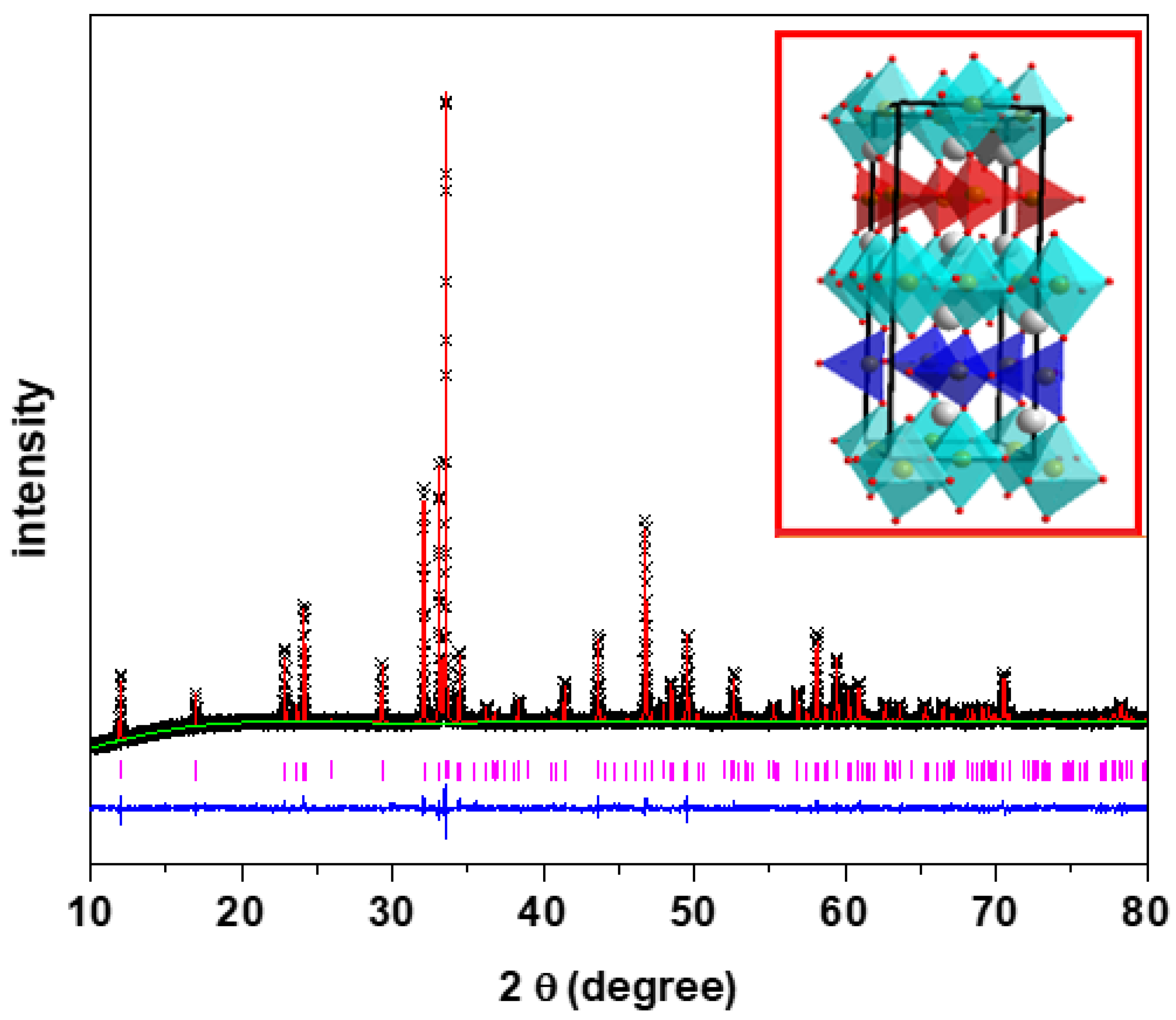
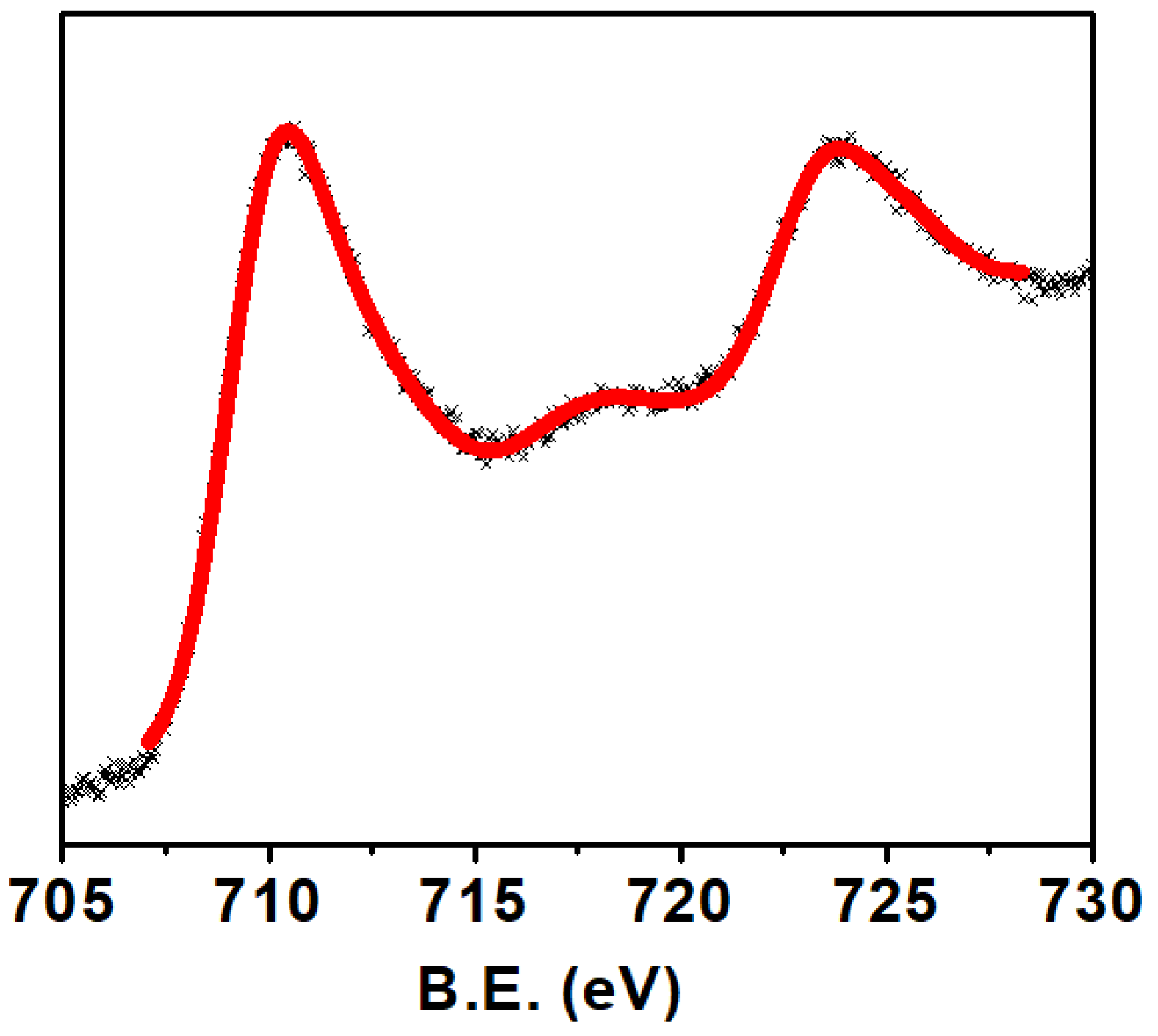
3.1. Material Synthesis and Characterization
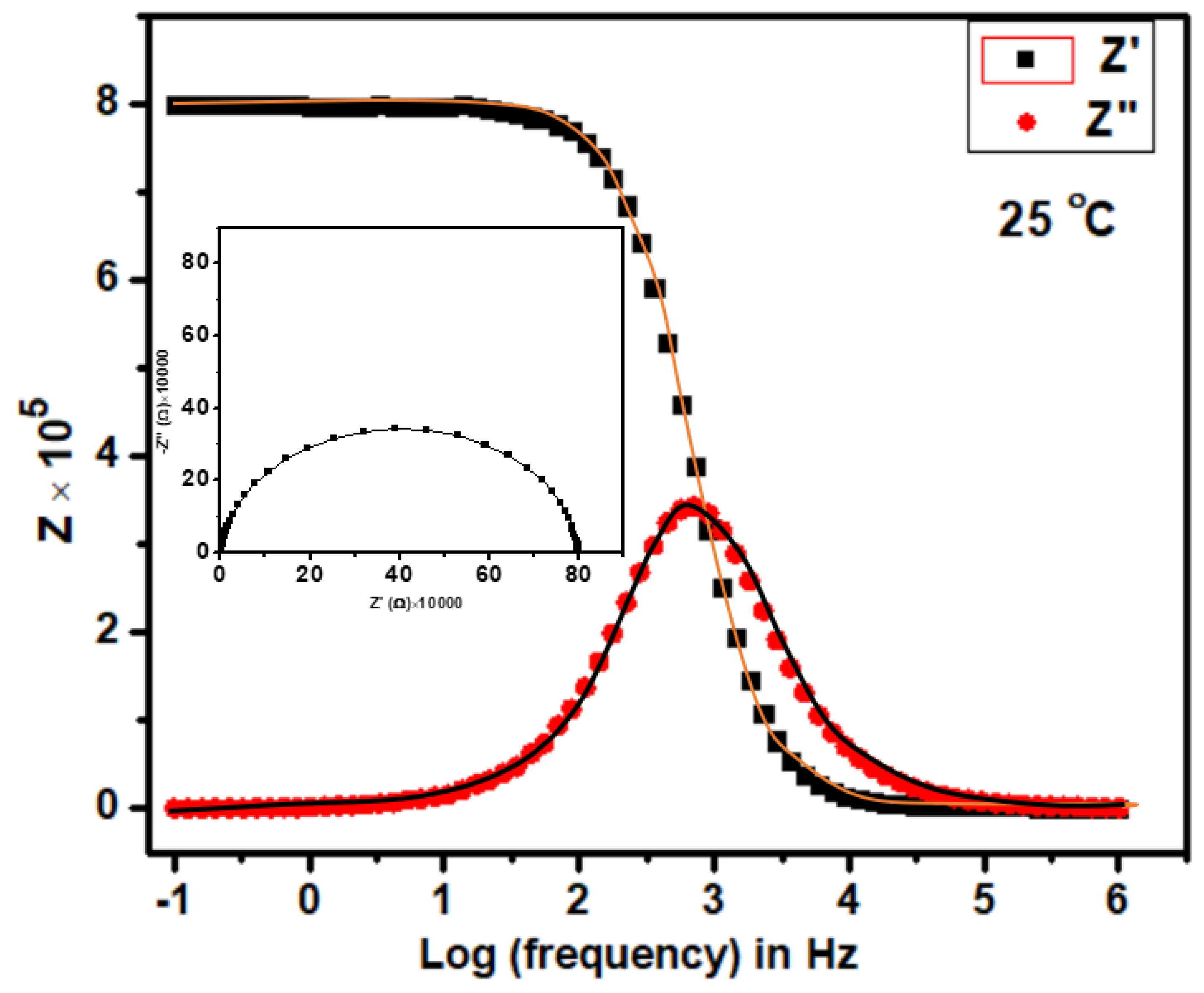
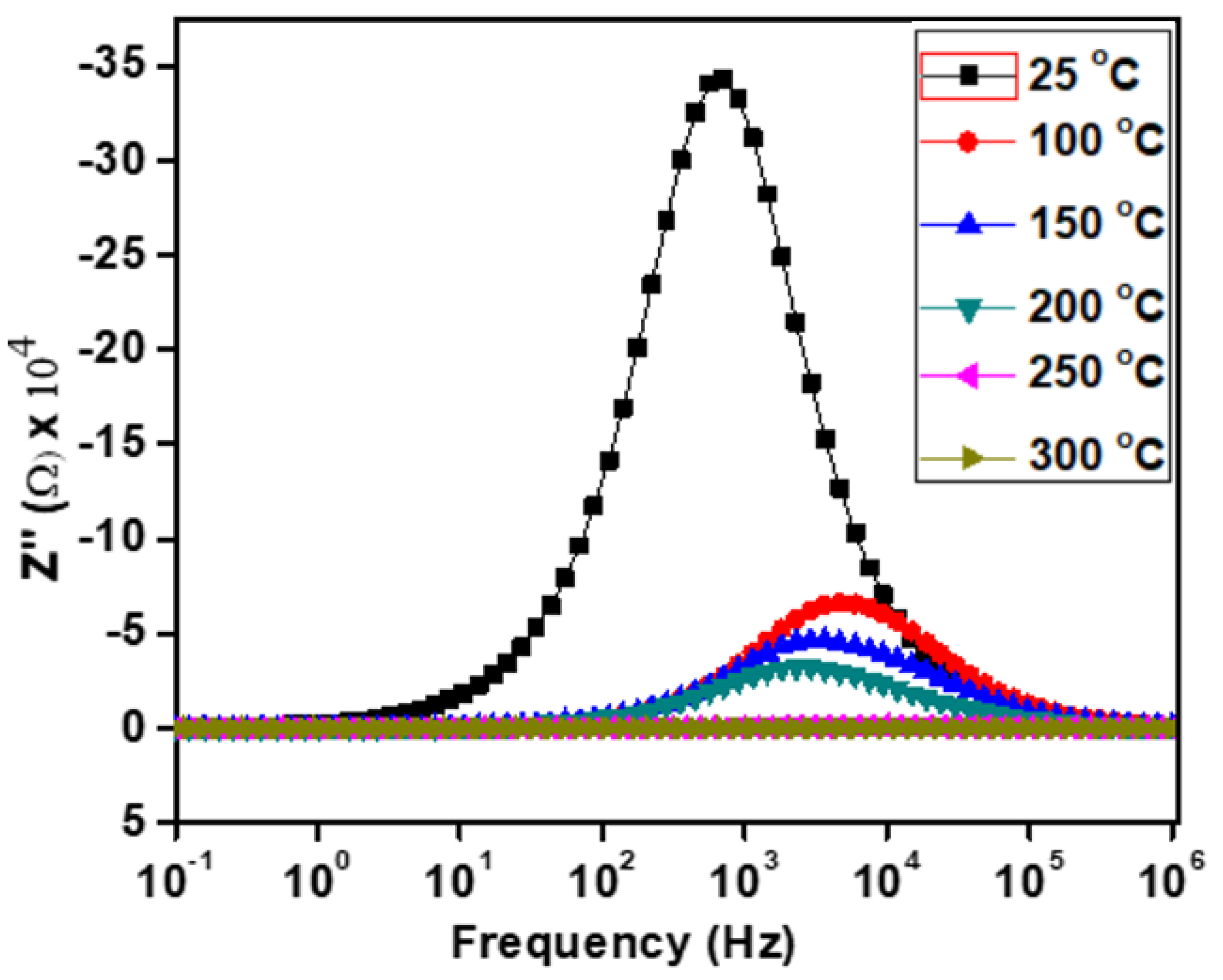
3.2. Electrical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Sun, L.; Zeng, X.; Zhao, H.; Huo, L.; Grenier, J.-C.; Bassat, J.-M.; Mauvy, F. Evaluation of a brownmillerite oxide as cathode for solid oxide fuel cells. J. Power Sources 2013, 238, 11–16. [Google Scholar] [CrossRef]
- Kharton, V.; Marozau, I.; Vyshatko, N.; Shaula, A.; Viskup, A.; Naumovich, E.; Marques, F. Oxygen ionic conduction in brownmillerite CaAl0.5Fe0.5O2.5+δ. Mater. Res. Bull. 2003, 38, 773–782. [Google Scholar] [CrossRef] [Green Version]
- Hona, R.K.; Ramezanipour, F. Remarkable Oxygen-Evolution Activity of a Perovskite Oxide from the Ca2−xSrxFe2O6−δ Series. Angew. Chem. 2019, 58, 2060–2063. [Google Scholar] [CrossRef] [PubMed]
- Hona, R.K.; Karki, S.B.; Ramezanipour, F. Oxide Electrocatalysts Based on Earth-Abundant Metals for Both Hydrogen- and Oxygen-Evolution Reactions. ACS Sustain. Chem. Eng. 2020, 8, 11549–11557. [Google Scholar] [CrossRef]
- Stahl, Q.E.; Redhammer, G.J.; Tippelt, G.; Reyer, A. Structural and spectroscopic characterization of the brownmillerite-type Ca2Fe2−xGaxO5 solid solution series. Phys. Chem. Miner. 2019, 46, 271–298. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, M.; Rammeh, N.; Kabadou, A.; Dhahri, E.; van der Lee, A. Effect of the partial substitution of Fe on the magnetic properties of new brownmillerite oxides LaSrMn2−xFexO5 (0 ≤ x ≤ 0.5). J. Magn. Magn. Mater. 2014, 361, 44–49. [Google Scholar] [CrossRef]
- Cascos, V.; Martínez-Coronado, R.; Alonso, J.A.; Fernández-Díaz, M. Structural and electrical characterization of the Co-doped Ca2Fe2O5 brownmillerite: Evaluation as SOFC -cathode materials. Int. J. Hydrog. Energy 2015, 40, 5456–5468. [Google Scholar] [CrossRef]
- Xue, B.-J.; Luo, J.; Zhang, F.; Fang, Z. Biodiesel production from soybean and Jatropha oils by magnetic CaFe2O4–Ca2Fe2O5-based catalyst. Energy 2014, 68, 584–591. [Google Scholar] [CrossRef]
- Sundriyal, S.K.; Sharma, Y. Controlled generation and tuning the oxygen defects in nanofibers of Ca2Fe2O5 toward high and stable Li-ion battery anode. Appl. Surf. Sci. 2021, 560, 150055. [Google Scholar] [CrossRef]
- Zhang, G.B.; Smyth, D.M. Defects and transport of the brownmillerite oxides with high oxygen ion conductivity—Ba2In2O5. Solid State Ion. 1995, 82, 161–172. [Google Scholar] [CrossRef]
- Shaula, A.; Pivak, Y.; Waerenborgh, J.C.; Gaczynski, P.; Yaremchenko, A.; Kharton, V. Ionic conductivity of brownmillerite-type calcium ferrite under oxidizing conditions. Solid State Ion. 2006, 177, 2923–2930. [Google Scholar] [CrossRef]
- Lima, C.G.M.; Araújo, A.J.M.; Silva, R.M.; Raimundo, R.A.; Grilo, J.P.F.; Constantinescu, G.; Kovalevsky, A.V.; Macedo, D.A. Electrical assessment of brownmillerite-type calcium ferrite materials obtained by proteic sol-gel route and by solid-state reaction using mollusk shells. J. Solid State Chem. 2021, 299, 122172. [Google Scholar] [CrossRef]
- Chérif, S.F.; Zid, M.F.; Driss, A. Conductivity study by complex impedance spectroscopy of Na3Nb4As3O19. Arab. J. Chem. 2019, 12, 3309–3315. [Google Scholar] [CrossRef] [Green Version]
- Barik, S.K.; Choudhary, R.; Singh, A. Ac Impedance Spectroscopy and Conductivity Studies of Ba0.8Sr0.2TiO3 Ceramics . Adv. Mater. Lett. 2011, 2, 419–424. [Google Scholar] [CrossRef]
- Vavilapalli, D.S.; Peri, R.G.; Banik, S.; Muthuraaman, B.; Rao, M.R.; Singh, S. Electrochemical properties of brownmillerite structured KBiFe2O5. Appl. Surf. Sci. Adv. 2021, 6, 100162. [Google Scholar] [CrossRef]
- Chandrakanta, K.; Jena, R.; Pal, P.; Abdullah, F.; Kaushik, S.; Singh, A. Enhanced magnetic and magnetodielectric properties of Co-doped brownmillerite KBiFe2O5 at room temperature. J. Alloy. Compd. 2021, 886, 161294. [Google Scholar] [CrossRef]
- Colville, A.A. The crystal structure of Ca2Fe2O6 and its relation to the nuclear electric field gradient at the iron sites. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1970, 26, 1469–1473. [Google Scholar] [CrossRef]
- Grant, R.W. Nuclear Electric Field Gradient at the Iron Sites in Ca2Fe2O5 and Ca2FeAlO5. J. Chem. Phys. 1969, 51, 1156. [Google Scholar] [CrossRef]
- Shaula, A.L.; Kolotygin, V.A.; Naumovich, E.N.; Pivak, Y.V.; Kharton, V.V. Oxygen Ionic Transport in Brownmillerite-Type Ca2Fe2O5-δ and Calcium Ferrite-Based Composite Membranes. Solid State Phenom. 2013, 200, 286–292. [Google Scholar] [CrossRef]
- Asenath-Smith, E.; Lokuhewa, I.N.; Misture, S.T.; Edwards, D.D. p-Type thermoelectric properties of the oxygen-deficient perovskite Ca2Fe2O5 in the brownmillerite structure. J. Solid State Chem. 2010, 183, 1670–1677. [Google Scholar] [CrossRef]
- Dhankhar, S.; Bhalerao, G.; Ganesamoorthy, S.; Baskar, K.; Singh, S. Growth and comparison of single crystals and polycrystalline brownmillerite Ca2Fe2O5. J. Cryst. Growth 2017, 468, 311–315. [Google Scholar] [CrossRef]
- Chan, M.S.; Liu, W.; Ismail, M.; Yang, Y.; Scott, S.A.; Dennis, J.S. Improving hydrogen yields, and hydrogen:steam ratio in the chemical looping production of hydrogen using Ca2Fe2O5. Chem. Eng. J. 2016, 296, 406–411. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.; Gaur, N.K.; Ghosh, P. First principles investigations of structure, stability and electronic properties of polar Ca2Fe2O5 (0 1 0) surfaces. Appl. Surf. Sci. 2020, 527, 146703. [Google Scholar] [CrossRef]
- Bo, X.; Wang, D.; Wan, X. Calculated magnetic exchange interactions in brownmillerite Ca2Fe2O5. Phys. Lett. A 2021, 394, 127202. [Google Scholar] [CrossRef]
- Rosten, R.; Koski, M.; Koppana, E. A Guide to the Calculation of Theoretical Densities of Crystal Structures for Solid Oxide Fuel Cells. J. Undergrad. Mater. Res. 2006, 2, 38–41. [Google Scholar] [CrossRef] [Green Version]
- Ruttanapun, C.; Maensiri, S. Effects of spin entropy and lattice strain from mixed-trivalent Fe3+/Cr3+ on the electronic, thermoelectric and optical properties of delafossite CuFe1−xCrxO2 (x = 0.25, 0.5, 0.75). J. Phys. D Appl. Phys. 2015, 48, 495103. [Google Scholar] [CrossRef]
- Morales, J.; Saánchez, L.; Martiín, F.; Berry, F.; Ren, X.; Jiménez, F.D.P.M. Synthesis and Characterization of Nanometric Iron and Iron-Titanium Oxides by Mechanical Milling. J. Electrochem. Soc. 2005, 152, A1748. [Google Scholar] [CrossRef] [Green Version]
- Choi, W.; Shin, H.-C.; Kim, J.M.; Choi, J.-Y.; Yoon, W.-S. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-ion Batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Shimakawa, K. Electrical Transport Properties of Glass. In Springer Handbook of Glass; Springer: Berlin/Heidelberg, Germany, 2019; p. 343. [Google Scholar]
- Batool, S.S.; Imran, Z.; Rasool, K.; Ambreen, J.; Hassan, S.; Arif, S.; Ahmad, M.; Rafiq, M.A. Study of electric conduction mechanisms in bismuth silicate nanofibers. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Liu, F.; Brinkman, K.; Reifsnider, K.L.; Virkar, A.V. A study of gadolinia-doped ceria electrolyte by electrochemical impedance spectroscopy. J. Power Sources 2014, 247, 947–960. [Google Scholar] [CrossRef]
- Nasri, S.; Ben Hafsia, A.L.; Tabellout, M.; Megdiche, M. Complex impedance, dielectric properties and electrical conduction mechanism of La0.5Ba0.5FeO3−δ perovskite oxides. RSC Adv. 2016, 6, 76659–76665. [Google Scholar] [CrossRef]
- Neyret, M.; Lenoir, M.; Grandjean, A.; Massoni, N.; Penelon, B.; Malki, M. Ionic transport of alkali in borosilicate glass. Role of alkali nature on glass structure and on ionic conductivity at the glassy state. J. Non-Cryst. Solids 2015, 410, 74–81. [Google Scholar] [CrossRef]
- Mohan, U.; Gogoi, P.; Baruah, S. Impedance Spectroscopy Study of the AC Conductivity and Dielectric properties of 3, 5-Dimethylpyridine-Iodine Charge Transfer Complex. Orient. J. Chem. 2016, 32, 1003–1014. [Google Scholar] [CrossRef] [Green Version]
- Omari, L.H.; Moubah, R.; Boutahar, A.; Hajji, L.; El Ouatib, R. Analysis of electrical properties using complex impedance spectroscopy in solid solutions (PbTiO3)0.97-(LaFeO3)0.03 prepared by sol-gel technique. J. Electroceramics 2020, 44, 23–31. [Google Scholar] [CrossRef]
- Casallas-Caicedo, F.M.; Vera-López, E.; Roa-Rojas, J. Impedance spectroscopy study of electrical response and correlation with structural properties in the La2SrFe2CoO9 triple complex perovskite. Phys. B Condens. Matter 2021, 607, 412865. [Google Scholar] [CrossRef]
- Mahato, D.K.; Dutta, A.; Sinha, T.P. Impedance spectroscopy analysis of double perovskite Ho2NiTiO6. J. Mater. Sci. 2010, 45, 6757–6762. [Google Scholar] [CrossRef]
- Benali, A.; Souissi, A.; Bejar, M.; Dhahri, E.; Graça, M.F.P.; Valente, M.A. Dielectric properties and alternating current conductivity of sol–gel made La0.8Ca0.2FeO3 compound. Chem. Phys. Lett. 2015, 637, 7–12. [Google Scholar] [CrossRef]



| Elements | X | y | z | Occupancy | Uiso |
|---|---|---|---|---|---|
| Ca | 0.4820 | 0.1081 | 0.0226 | 1.0000 | 0.006 (5) |
| Fe1 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.001 (5) |
| Fe2 | −0.0512 | 0.2500 | 0.0680 | 1.0000 | 0.003 (8) |
| O1 | 0.2838 | −0.0141 | 0.2345 | 1.0000 | 0.019 (9) |
| O2 | 0.0315 | 0.1394 | 0.0811 | 1.0000 | 0.009 (4) |
| O3 | 0.5878 | 0.2500 | 0.1248 | 1.0000 | 0.007 (9) |
| T (°C) | Rg (Ω) | Rgb (Ω) | Rel (Ω) |
|---|---|---|---|
| 25 | 2364 | 605,910 | 190,730 |
| 100 | 217,070 | 2443 | 568,380 |
| 200 | 13,771 | 203 | 73,776 |
| 300 | 14.22 | 13.26 | 4.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hona, R.K.; Dhaliwal, G.S.; Thapa, R. Investigation of Grain, Grain Boundary, and Interface Contributions on the Impedance of Ca2FeO5. Appl. Sci. 2022, 12, 2930. https://doi.org/10.3390/app12062930
Hona RK, Dhaliwal GS, Thapa R. Investigation of Grain, Grain Boundary, and Interface Contributions on the Impedance of Ca2FeO5. Applied Sciences. 2022; 12(6):2930. https://doi.org/10.3390/app12062930
Chicago/Turabian StyleHona, Ram Krishna, Gurjot S. Dhaliwal, and Rajesh Thapa. 2022. "Investigation of Grain, Grain Boundary, and Interface Contributions on the Impedance of Ca2FeO5" Applied Sciences 12, no. 6: 2930. https://doi.org/10.3390/app12062930






