Spatial Location of Sugarcane Node for Binocular Vision-Based Harvesting Robots Based on Improved YOLOv4
Abstract
:1. Introduction
2. Prior Work
2.1. Binocular Stereo Vision Location Theory
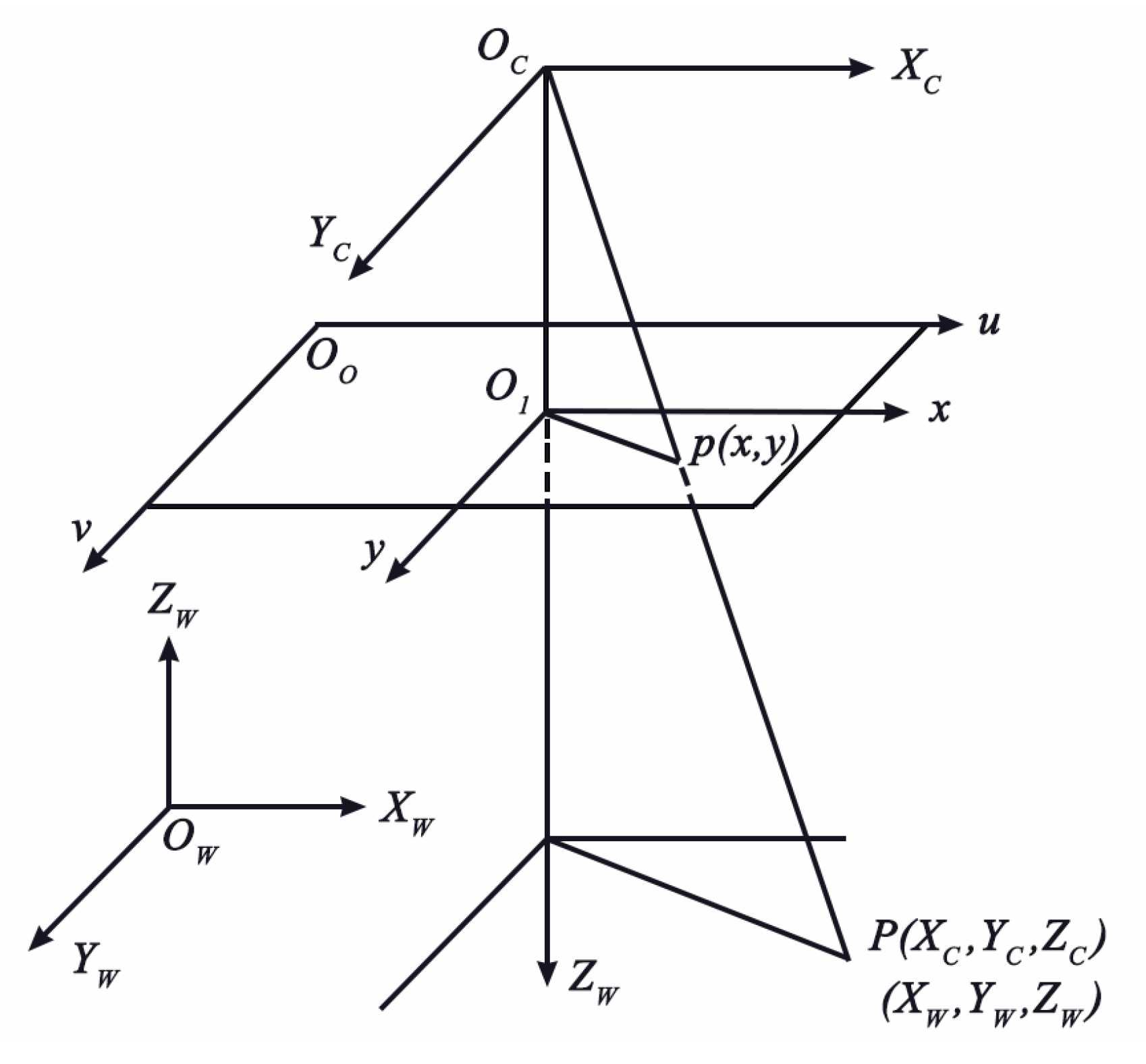
2.1.1. Camera Imaging Model
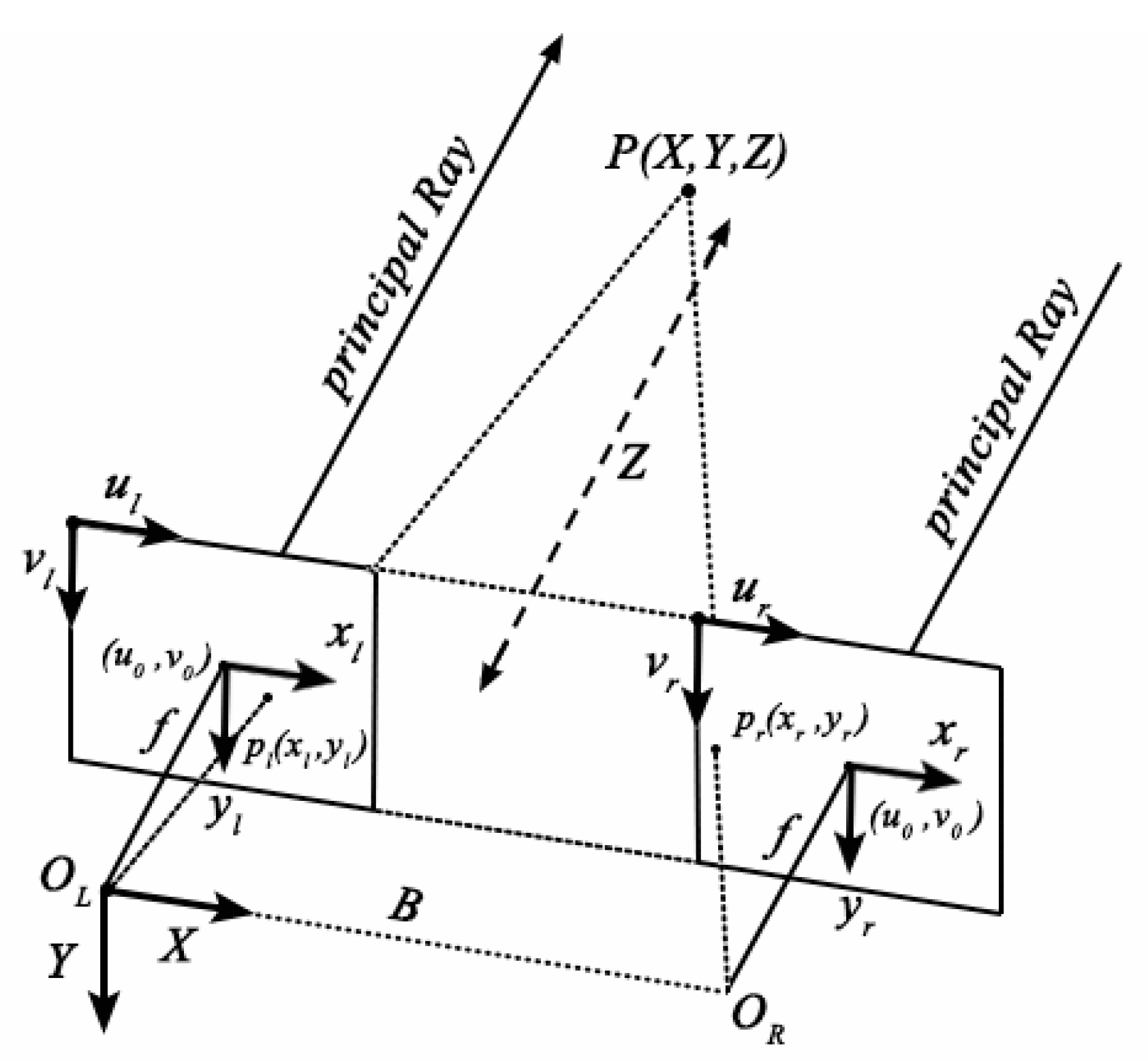
2.1.2. Binocular Stereo Vision System Imaging Model
2.2. Calibration and Rectification of Binocular Camera
2.2.1. Calibration of Binocular Camera
2.2.2. Stereo Rectification of Binocular Camera
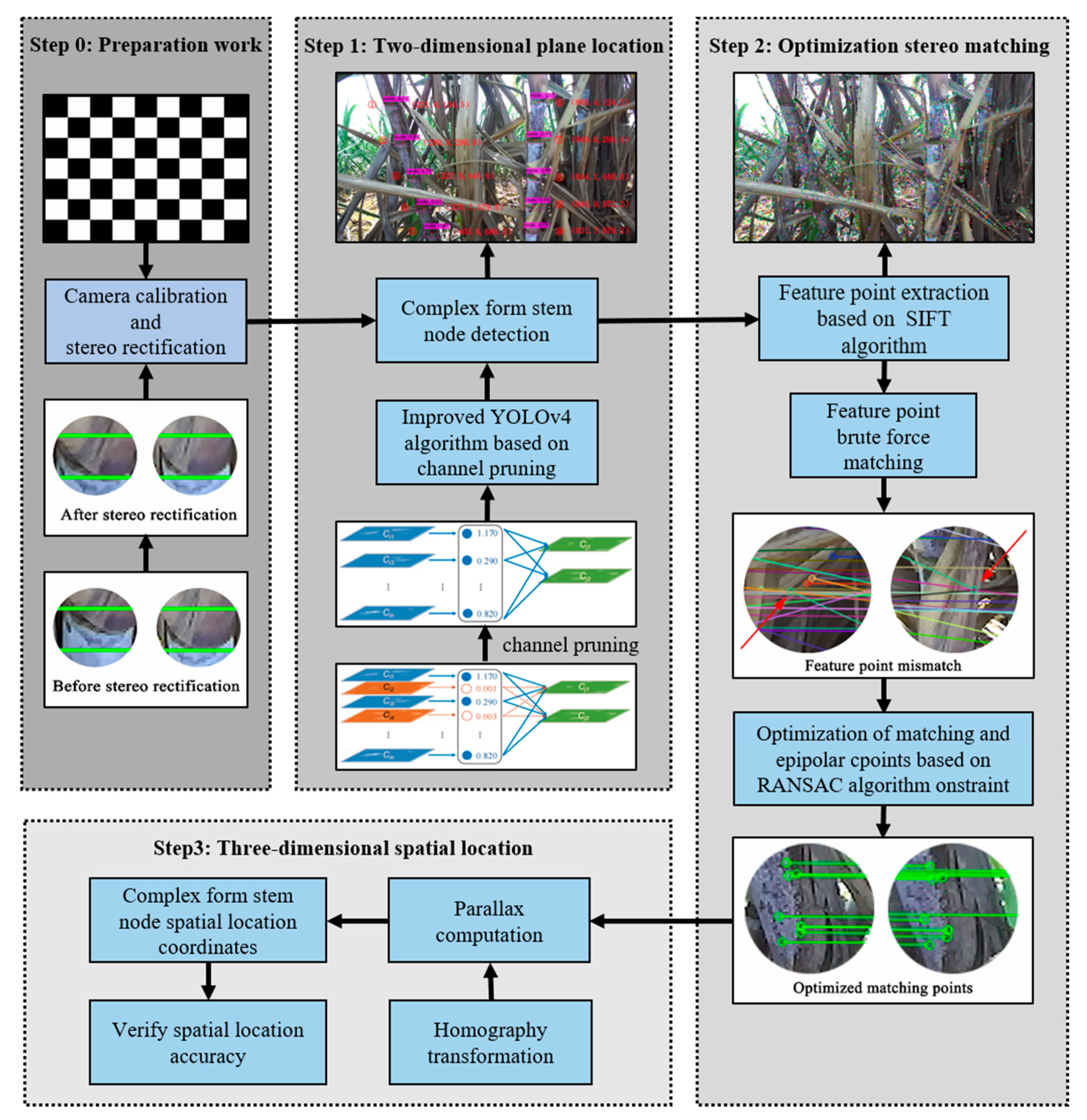
3. Methodology
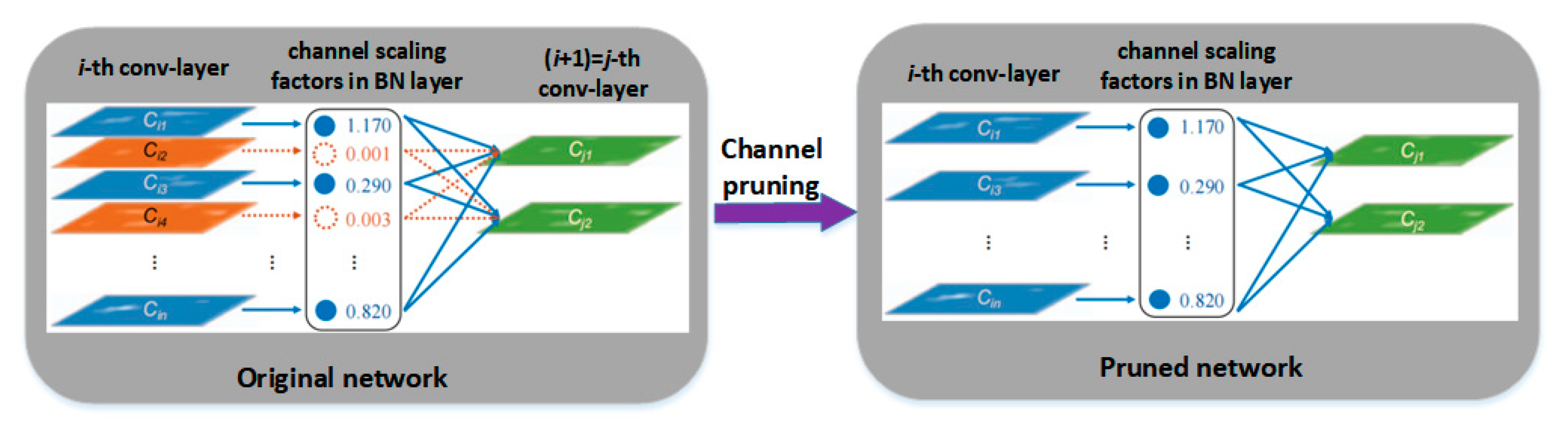
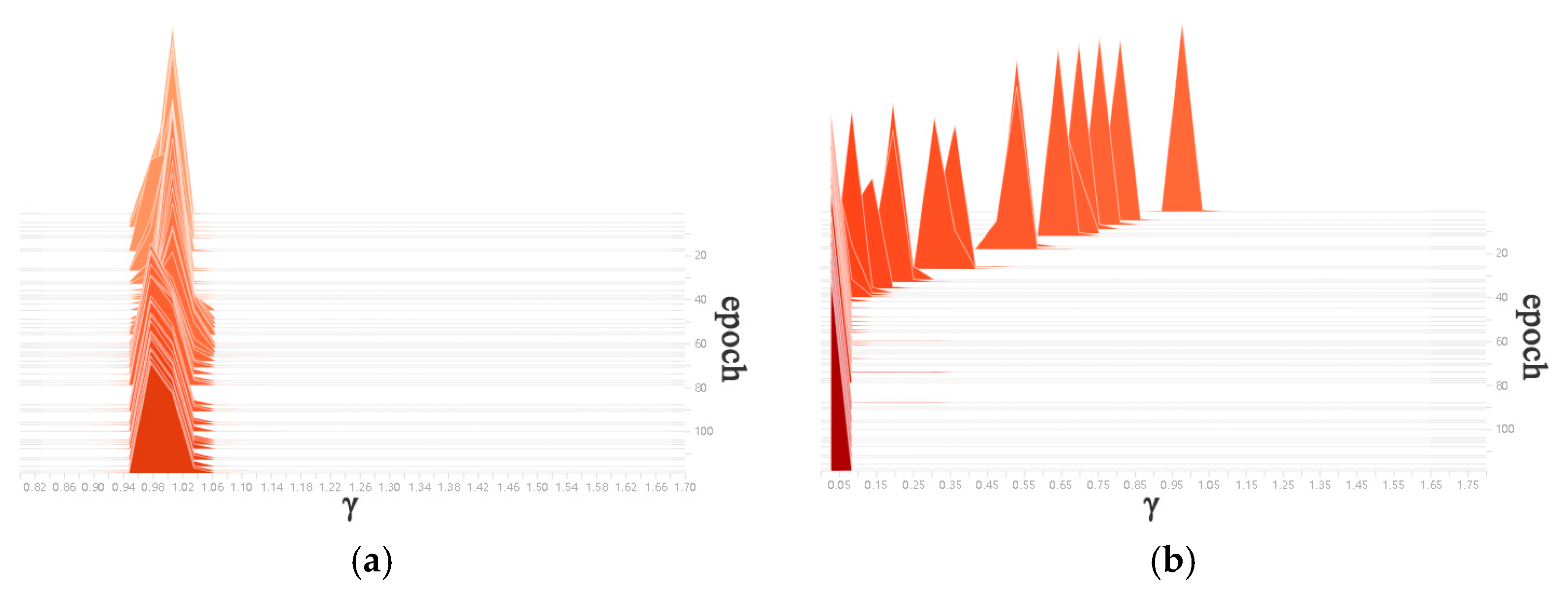
3.1. YOLOv4 Model Improved by Channel Pruning Technology
- (1)
- Normal training. A convergent and accurate YOLOv4 sugarcane node identification model is trained normally.
- (2)
- Sparse training. The L1 regularisation training is carried out on the BN layer of the normal training model, so that the γ coefficient of the BN layer is as close to 0 as possible, and the sparse weights are redistributed to other effective layers of the network.
- (3)
- Pruning. The channels in the BN layer with the γ coefficients approaching zero are picked out, and the channels are pruned according to the set pruning ratio to generate a simplified model that occupies less memory space.
- (4)
- Fine-tuning of the pruned model. All the BN layers are pruned at one time and then re-trained to fine-tune to overcome the decline of model accuracy after channel pruning.
3.2. Identification of Sugarcane Nodes Based on Improved YOLOv4
3.3. Spatial Location of Sugarcane Nodes Based on Binocular Vision
3.3.1. Stereo Matching Based on SIFT Feature Points
3.3.2. Solution of Homography Matrix H
3.3.3. Spatial Location of Sugarcane Nodes
- (1)
- The binocular camera was fixed on the bracket guide rail with a scale, and the position of the guide rail where the camera was currently located was recorded. Subsequently, the sugarcane images in the field were collected and the spatial location experiment was carried out according to the method mentioned above. After sampling three times, the average XYZ coordinates of each node were recorded as the coordinates before moving. At the same time, the time spent in each location experiment was recorded.
- (2)
- The position of the binocular camera in the X and Y directions was kept unchanged, the camera was moved on the guide rail in the Z direction by D = 100 mm, the spatial location experiment was conducted again, and the average xyz coordinates of each node were recorded as the moved coordinates. In addition, the time required for each location experiment was recorded again.
- (3)
- The Z coordinate was subtracted before and after moving to get the average distance difference of two positions, and finally D was subtracted from the difference to get the location error in the Z coordinate.
4. Results and Discussion
4.1. Target Detection Results of YOLOv4 Improved by Channel Pruning Technology
4.2. Comparison between Improved YOLOv4 and Other Target Detection Algorithms
4.3. Analysis of Spatial Location Accuracy of Sugarcane Nodes
4.4. Real-Time Performance of the Proposed Method
4.5. Location Methods Comparison and Discussion
5. Conclusions
- (1)
- The deep learning algorithm of YOLOv4 was improved by the Channel Pruning Technology in network slimming, so as to ensure the high recognition accuracy of the deep learning algorithm and to facilitate transplantation to embedded chips. The experimental results showed that the Params, FLOPs and model size were all reduced by about 89.1%, while the average precision (AP) decreased by only 0.1% (from 94.5% to 94.4%). To be specific, the Params decreased from 63,937,686 to 6,973,211, the FLOPs decreased from 29.88 G to 3.26 G, and the model size decreased from 244 M to 26.7 M, which greatly reduced the computational demand.
- (2)
- Compared with other deep learning algorithms, the improved YOLOv4 algorithm also has great advantages. Specifically, the improved algorithm was 1.3% and 0.3% higher than SSD and YOLOv3 in average precision (AP). In terms of parameters, FLOPs and model size, the improved YOLOv4 algorithm was only about 1/3 of SSD and 1/10 of YOLOv3. The above data sufficiently demonstrated the superiority of the improved YOLOv4 algorithm model.
- (3)
- The SIFT algorithm, with its strong anti-light interference ability, was used to extract feature points from complex form sugarcane pictures. Furthermore, the SIFT feature points were optimised by the RANSAC algorithm and epipolar constraint, which effectively reduced the mismatching problem caused by the similarity between stem nodes and sugarcane leaves.
- (4)
- The optimised matching point pairs were used to solve the homography transformation matrix, so as to obtain the three-dimensional spatial coordinates of the complex form stem nodes and verify their spatial location accuracy. The experimental results showed that the maximum error of the Z coordinate in the spatial location of complex form stem nodes was 2.86 mm, the minimum error was 1.13 mm, and the average error was 1.88 mm, which totally meet the demand of sugarcane harvesting robots in the next stage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silwal, A.; Davidson, J.R.; Karkee, M.; Mo, C.; Zhang, Q.; Lewis, K. Design, integration, and field evaluation of a robotic apple harvester. J. Field Robot. 2017, 34, 1140–1159. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, W.; Wang, C.; Gong, L.; Zhao, C.; Liu, C.; Huang, D. Computer vision recognition of stem and calyx in apples using near-infrared linear-array structured light and 3D reconstruction. Biosyst. Eng. 2015, 139, 25–34. [Google Scholar] [CrossRef]
- Williams, H.A.; Jones, M.H.; Nejati, M.; Seabright, M.J.; Bell, J.; Penhall, N.D.; Barnett, J.J.; Duke, M.D.; Scarfe, A.J.; Ahn, H.S. Robotic kiwifruit harvesting using machine vision, convolutional neural networks, and robotic arms. Biosyst. Eng. 2019, 181, 140–156. [Google Scholar] [CrossRef]
- Ling, X.; Zhao, Y.; Gong, L.; Liu, C.; Wang, T. Dual-arm cooperation and implementing for robotic harvesting tomato using binocular vision. Robot. Auton. Syst. 2019, 114, 134–143. [Google Scholar] [CrossRef]
- Li, J.; Tang, Y.; Zou, X.; Lin, G.; Wang, H. Detection of fruit-bearing branches and localization of litchi clusters for vision-based harvesting robots. IEEE Access 2020, 8, 117746–117758. [Google Scholar] [CrossRef]
- Meng, Y.; Ye, C.; Yu, S.; Qin, J.; Zhang, J.; Shen, D. Sugarcane node recognition technology based on wavelet analysis. Comput. Electron. Agric. 2019, 158, 68–78. [Google Scholar] [CrossRef]
- Chen, J.; Wu, J.; Qiang, H.; Zhou, B.; Xu, G.; Wang, Z. Sugarcane nodes identification algorithm based on sum of local pixel of minimum points of vertical projection function. Comput. Electron. Agric. 2021, 182, 105994. [Google Scholar] [CrossRef]
- Lu, S.; Wen, Y.; Ge, W.; Peng, H. Recognition and features extraction of sugarcane nodes based on machine vision. Trans. Chin. Soc. Agric. Mach. 2010, 41, 190–194. [Google Scholar]
- Chen, W.; Ju, C.; Li, Y.; Hu, S.; Qiao, X. Sugarcane stem node recognition in field by deep learning combining data expansion. Appl. Sci. 2021, 11, 8663. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.; Liao, H.M. YOLOv4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Suo, R.; Gao, F.; Zhou, Z.; Fu, L.; Song, Z.; Dhupia, J.; Li, R.; Cui, Y. Improved multi-classes kiwifruit detection in orchard to avoid collisions during robotic picking. Comput. Electron. Agric. 2021, 182, 106052. [Google Scholar] [CrossRef]
- Liu, G.; Nouaze, J.C.; Touko Mbouembe, P.L.; Kim, J.H. YOLO-tomato: A robust algorithm for tomato detection based on YOLOv3. Sensors 2020, 20, 2145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.; Wang, B.; Zhang, R.; Zhou, H.; Wang, R. Analysis on location accuracy for the binocular stereo vision system. IEEE Photonics J. 2017, 10, 7800316. [Google Scholar] [CrossRef]
- Bouguet, J. Camera Calibration Toolbox for Matlab. 2004. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/index.html (accessed on 19 January 2022).
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning efficient convolutional networks through network slimming. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Wang, Z.; Zheng, Z. A region based stereo matching algorithm using cooperative optimization. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Zhao, H.; Wang, Z.; Jiang, H.; Xu, Y.; Dong, C. Calibration for stereo vision system based on phase matching and bundle adjustment algorithm. Opt. Laser. Eng. 2015, 68, 203–213. [Google Scholar] [CrossRef]
- Birinci, M.; Diaz-De-Maria, F.; Abdollahian, G.; Delp, E.J.; Gabbouj, M. Neighborhood matching for object recognition algorithms based on local image features. In Proceedings of the 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Barath, D.; Kukelova, Z. Homography from two orientation-and scale-covariant features. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Peng, H.; Huang, B.; Shao, Y.; Li, Z.; Zhang, C.; Chen, Y.; Xiong, J. General improved SSD model for picking object recognition of multiple fruits in natural environment. Trans. Chin. Soc. Agric. Eng. 2018, 34, 155–162. [Google Scholar]
- Jing, L.; Wang, R.; Liu, H.; Shen, Y. Orchard pedestrian detection and location based on binocular camera and improved YOLOv3 algorithm. Trans. Chin. Soc. Agric. Eng. Mach. 2020, 51, 34–39. [Google Scholar]
- Yuan, W.; Choi, D. UAV-based heating requirement determination for frost management in apple orchard. Remote Sens. 2021, 13, 273. [Google Scholar] [CrossRef]
- Xiong, J.; He, Z.; Lin, R.; Liu, Z.; Bu, R.; Yang, Z.; Peng, H.; Zou, X. Visual positioning technology of picking robots for dynamic litchi clusters with disturbance. Comput. Electron. Agric. 2018, 151, 226–237. [Google Scholar] [CrossRef]
- Hsieh, K.; Huang, B.; Hsiao, K.; Tuan, Y.; Shih, F.; Hsieh, L.; Chen, S.; Yang, I. Fruit maturity and location identification of beef tomato using R-CNN and binocular imaging technology. J. Food Meas. Charact. 2021, 15, 5170–5180. [Google Scholar] [CrossRef]
- Luo, L.; Tang, Y.; Zou, X.; Ye, M.; Feng, W.; Li, G. Vision-based extraction of spatial information in grape clusters for harvesting robots. Biosyst. Eng. 2016, 151, 90–104. [Google Scholar] [CrossRef]
- Wang, C.; Luo, T.; Zhao, L.; Tang, Y.; Zou, X. Window zooming–based localization algorithm of fruit and vegetable for harvesting robot. IEEE Access 2019, 7, 103639–103649. [Google Scholar] [CrossRef]








| Time | Fully Wrapped | Half Wrapped | Not Wrapped | 45 Degrees | 90 Degrees | 135 Degrees | 30 cm Distance | 40 cm Distance | Total |
|---|---|---|---|---|---|---|---|---|---|
| 08:00 a.m. | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 400 |
| 13:00 p.m. | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 800 |
| 18:00 p.m. | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 400 |
| Stage | Parameter Name | Parameter Value |
|---|---|---|
| Sparse training | Training batch size | 8 |
| Learning rate | 0.002 | |
| Epoch | 120 | |
| Sparseness rate | 0.001 | |
| Channel pruning | Pruning rate | 0.6 |
| Fine-tune model | Epoch | 120 |
| Training batch size | 8 |
| Algorithm | AP (%) | Params | FLOPs | Model Size | Speed (s) |
|---|---|---|---|---|---|
| SSD [22] | 93.1 | 23,612,246 | 30.44 G | 90.5 M | 0.023 |
| YOLOv3 [23] | 94.1 | 61,523,734 | 32.76 G | 235 M | 0.042 |
| YOLOv4 [24] | 94.5 | 63,937,686 | 29.88 G | 244 M | 0.035 |
| Pruned YOLOv4 | 94.4 | 6,973,211 | 3.26 G | 26.7 M | 0.032 |
| Node Number | Coordinate before Move (mm) | Coordinate after Move (mm) | Z-Coordinate D-Value (mm) | Actual D-Value (mm) | Z-Coordinate Error (mm) |
|---|---|---|---|---|---|
| 1 | (−237.98, 131.46, 370.52) | (−236.26, 133.02, 468.25) | 97.73 | 100 | −2.27 |
| 2 | (−209.58, 35.62, 382.81) | (−208.17, 36.94, 481.17) | 98.36 | 100 | −1.64 |
| 3 | (−181.95, −50.02, 403.56) | (−179.97, −48.98, 502.43) | 98.87 | 100 | −1.13 |
| 4 | (−157.01, −128.03, 422.13) | (−155.64, −126.08, 520.72) | 98.59 | 100 | −1.41 |
| 5 | (−137.82, −190.23, 438.76) | (−136.56, −189.20, 536.67) | 97.91 | 100 | −2.09 |
| 6 | (131.41, 137.18, 273.34) | (133.42, 138.83, 371.46) | 98.12 | 100 | −1.88 |
| 7 | (122.20, 42.91, 288.73) | (123.62, 44.29, 386.64) | 97.91 | 100 | −2.09 |
| 8 | (118.98, −50.49, 302.48) | (119.48, −49.21, 401.29) | 98.81 | 100 | −1.19 |
| 9 | (119.52, −123.13, 320.42) | (120.98, −121.68, 418.16) | 97.74 | 100 | −2.26 |
| 10 | (111.76, −186.15, 328.24) | (113.04, −184.36, 425.38) | 97.14 | 100 | −2.86 |
| Number | Identification Time (ms) | Other Time (ms) | Total Time (ms) |
|---|---|---|---|
| Before move—1 | 32 | 1533 | 1565 |
| Before move—2 | 33 | 1537 | 1570 |
| Before move—3 | 30 | 1539 | 1569 |
| After move—1 | 32 | 1538 | 1570 |
| After move—2 | 31 | 1540 | 1571 |
| After move—3 | 34 | 1535 | 1569 |
| Average time | 32 | 1537 | 1569 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Wu, C.; Li, Y.; Hu, S.; Gong, H. Spatial Location of Sugarcane Node for Binocular Vision-Based Harvesting Robots Based on Improved YOLOv4. Appl. Sci. 2022, 12, 3088. https://doi.org/10.3390/app12063088
Zhu C, Wu C, Li Y, Hu S, Gong H. Spatial Location of Sugarcane Node for Binocular Vision-Based Harvesting Robots Based on Improved YOLOv4. Applied Sciences. 2022; 12(6):3088. https://doi.org/10.3390/app12063088
Chicago/Turabian StyleZhu, Changwei, Chujie Wu, Yanzhou Li, Shanshan Hu, and Haibo Gong. 2022. "Spatial Location of Sugarcane Node for Binocular Vision-Based Harvesting Robots Based on Improved YOLOv4" Applied Sciences 12, no. 6: 3088. https://doi.org/10.3390/app12063088
APA StyleZhu, C., Wu, C., Li, Y., Hu, S., & Gong, H. (2022). Spatial Location of Sugarcane Node for Binocular Vision-Based Harvesting Robots Based on Improved YOLOv4. Applied Sciences, 12(6), 3088. https://doi.org/10.3390/app12063088






