Design and Shear Analysis of an Angled Morphing Wing Skin Module
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials
2.1. Design
2.2. Fabrication
3. Methods
3.1. Experiment
3.2. Finite Element Modeling
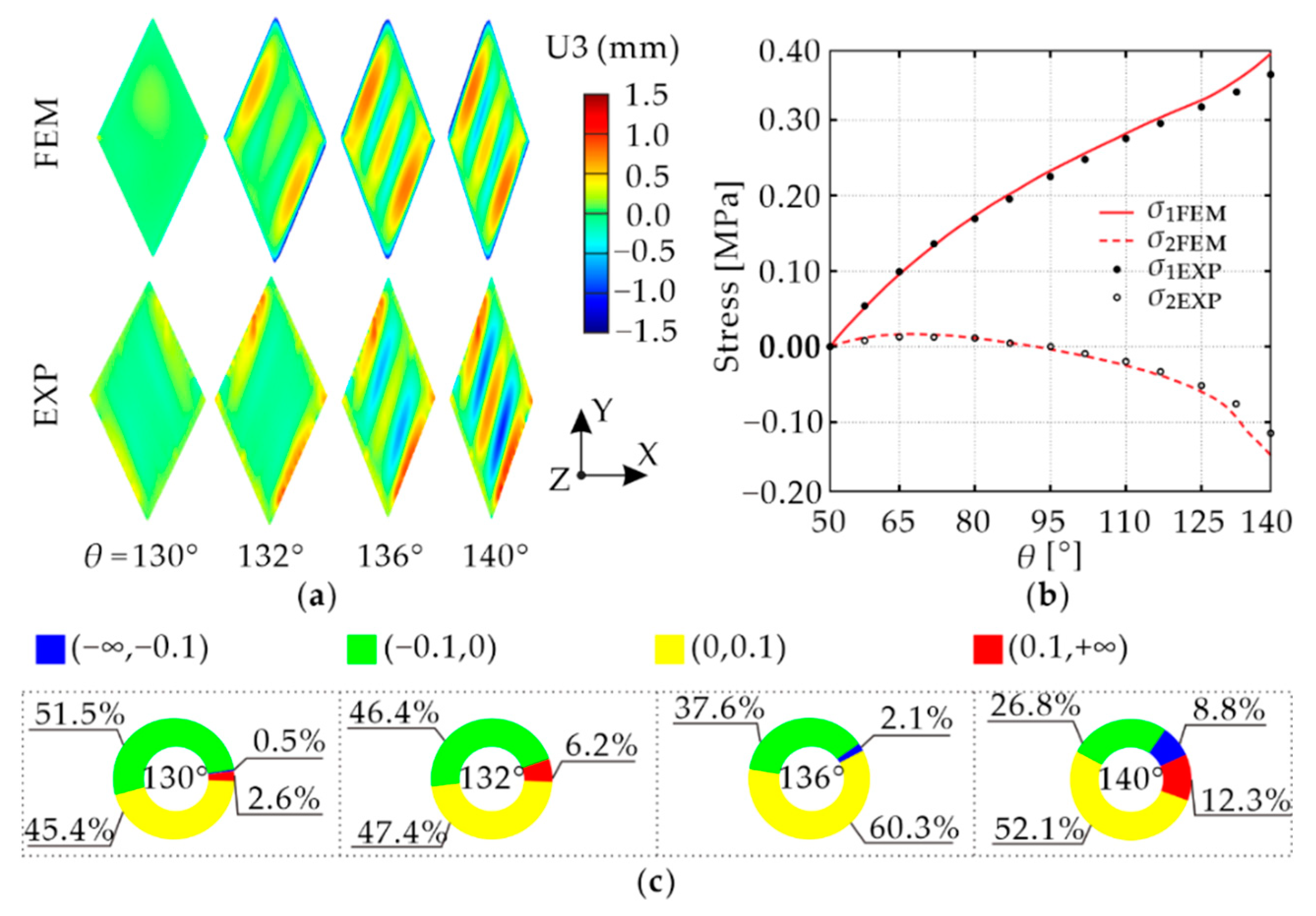
3.3. Validation
4. Results
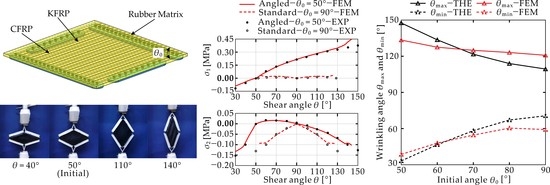
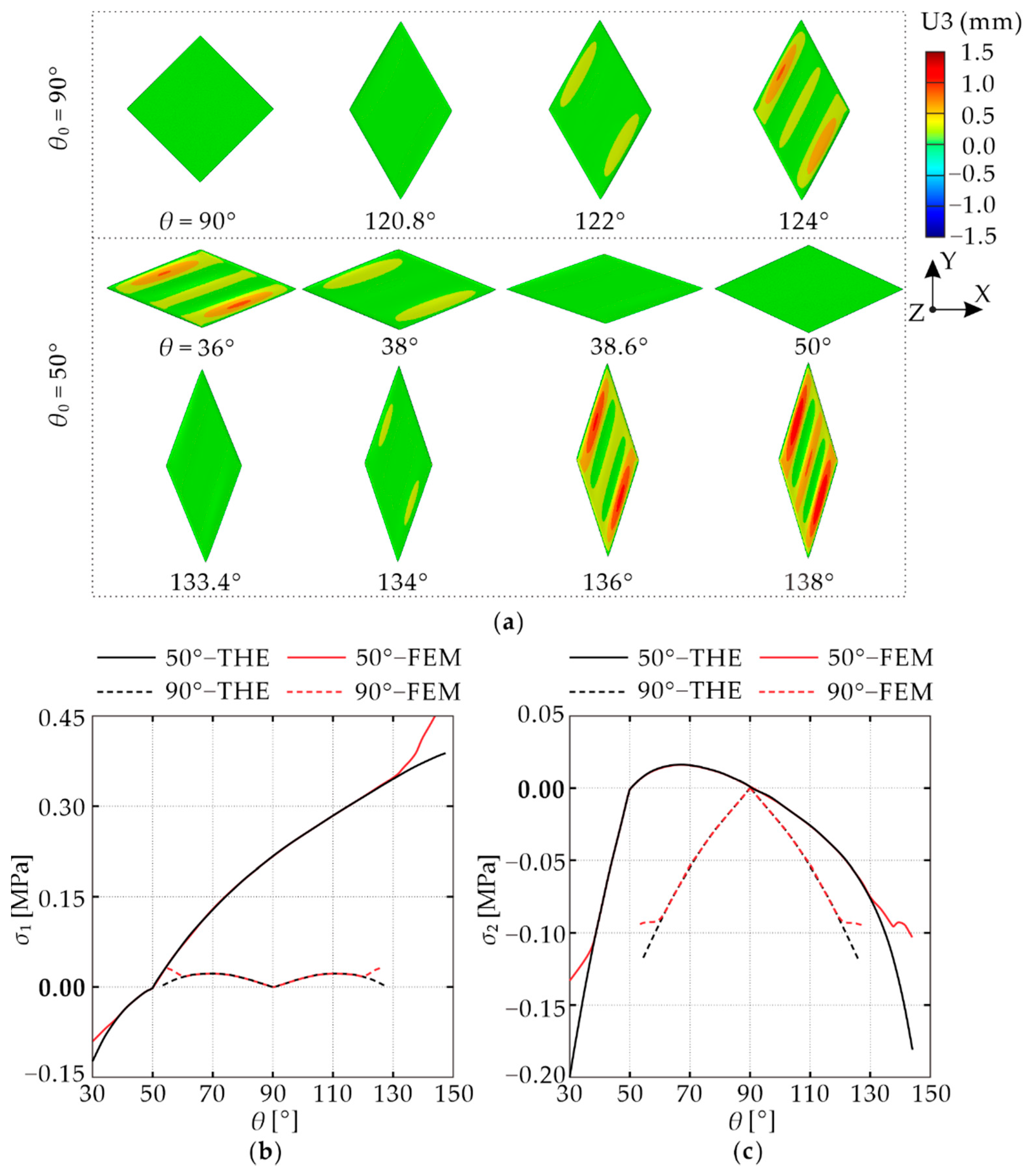
4.1. Comparison of Standard and Angled Skin Modules
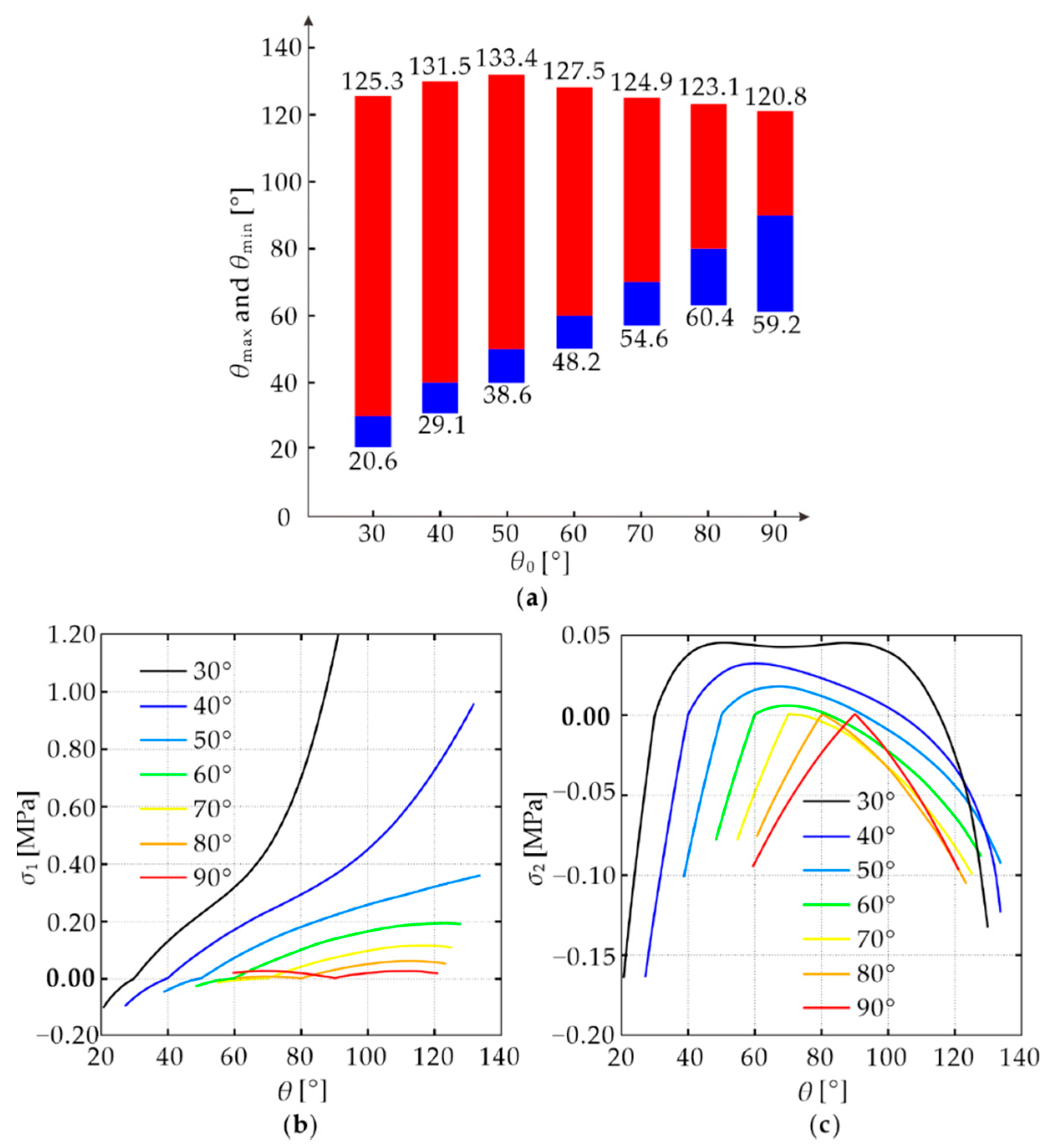
4.2. Effect of the Initial Angle
4.3. Effect of the Hardness of Rubber
4.4. Effect of the CFRP Reinforcement
5. Theoretical Analysis
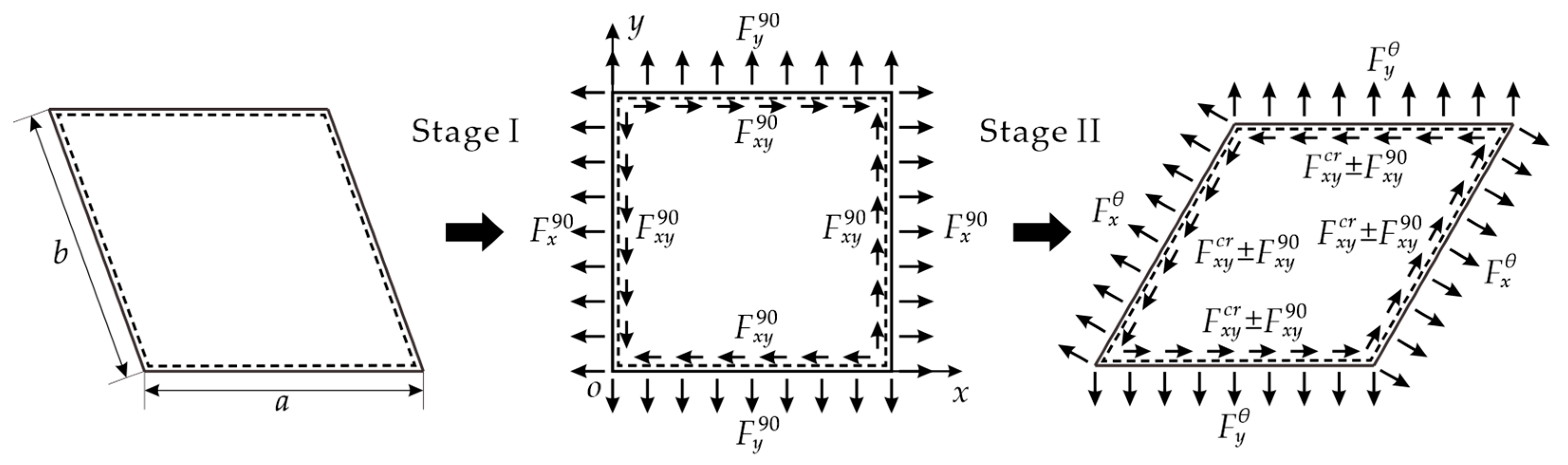
5.1. Theoretical Modeling
- (i)
- The skin is considered as a constructional orthogonal anisotropic plate [36] since the CFRP rods and KFRP fibers are evenly spaced in the rubber. The four edges of the skin are considered to be simply supported. This is close to the realistic boundary condition as the frame provides a limited constraint on the rotation of the skin edge.
- (ii)
- The shear deformation process of the skin is divided into two stages as shown in Figure 11. At stage I, the skin is sheared from the initial angle to 90°. It is known from the previous results that the skin is guaranteed to be wrinkle-free at the end of this stage and is subjected to uniform biaxial in-plane loads and a shear load, denoted as , , and as shown in Figure 11. Note that the dimension of the three loads is force per unit length along the edges of the plate. At stage II, the skin is further sheared in either direction until it wrinkles. At this stage, we consider the skin as a pre-loaded plate and calculate the critical shear force under and . Then and are critical wrinkling forces of the skin in two directions.
- (iii)
- The stresses in the skin are generated only by the rubber since the CFRP rods and KFRP fibers are found from previous results to undergo nearly no deformation before wrinkling.
- (iv)
- The rubber, CFRP rods, and KFPR fibers here are all assumed to be linear elastic materials.
5.2. Comparison with Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| L | Length of the skin module |
| T | Width of the skin module |
| H | Thickness of the skin module |
| l | Distance between the CFRP rods and the skin top surface |
| l1, l2 | Intervals of CFRP rods and KFRP fibers |
| d1, d2 | Diameter of CFRP rods and KFRP fibers |
| θ, θ0 | Morphing angle and initial angle of the skin module |
| θmax, θmin | Maximal and minimal critical wrinkling angles |
| Δθ | Deformation range without wrinkling |
| ρ | Density |
| Er, Ec, Ek | Young’s modulus of rubber, CFRP rods, and KFRP fibers |
| μr, μc, μk | Poisson’s ratio of rubber, CFRP rods, and KFRP fibers |
| C10, C20, C30 | Material constants of rubber |
| σi (i = 1, 2) | Maximal and minimal principal stress |
| W | Strain energy density function |
| S | Cauchy-Green strain tensor |
| I1 | First strain invariant of Cauchy-Green strain tensor |
| λi (i = 1, 2, 3) | Principal extension ratio |
| s0, t0 | Diagonal lengths of the skin module before deformation |
| s, t | Diagonal lengths of the skin module after deformation |
| In-plane loads, and shear load when the skin is sheared to θ | |
| h | Thickness of the skin module after deformation |
| ε1 (i = 1, 2) | Maximal and minimal principal strain |
| σx, σy, τxy | Stress components |
| w | Displacement function |
| a, b | Edge length of the skin module |
| U | Strain energy of the skin module |
| V | Potential energy of the skin module |
| Di (i = 1, 2, 3, k) | Bending stiffness and shear stiffness |
| Amn | Coefficient of displacement function |
| Ic, Ik | Area moment of inertia of the CFRP rods and KFRP fibers |
| Π | Total potential energy |
Appendix A

References
- Jha, A.K.; Kudva, J.N. Morphing aircraft concepts, classifications, and challenges. In Proceedings of the Smart Structures and Materials, San Diego, CA, USA, 15–18 March 2004; SPIE, The International Society for Optics and Photonics: Bellingham, WA, USA, 2004; pp. 213–224. [Google Scholar]
- Blondeau, J.E.; Pines, D.J. Pneumatic morphing aspect ratio wing. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; pp. 3218–3229. [Google Scholar]
- Hetrick, J.A.; Osborn, R.F.; Kota, S.; Flick, P.M.; Pual, D.B. Flight testing of mission adaptive compliant wing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; pp. 92–109. [Google Scholar]
- Ajaj, R.M.; Friswell, M.I.; Bourchak, M.; Harasani, W. Span morphing using the GNATSpar wing. Aerosp. Sci. Technol. 2016, 53, 38–46. [Google Scholar] [CrossRef] [Green Version]
- Weisshaar, T.A. Morphing Aircraft Systems: Historical Perspectives and Future Challenges. J. Aircr. 2007, 50, 337–353. [Google Scholar] [CrossRef]
- Thill, C.; Etches, J.; Bond, I.; Potter, K.; Weaver, P. Morphing skins. Aeronaut. J. 2008, 112, 117–139. [Google Scholar] [CrossRef]
- Sofla, A.Y.N.; Meguid, S.A.; Tan, K.T.; Yeo, W.K. Shape morphing of aircraft wing: Status and challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar] [CrossRef]
- Gandhi, F.; Inthra, P.A. Skin design studies for variable camber morphing airfoils. Smart Mater. Struct. 2008, 17, 015025. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Murugan, S.; Friswell, M.I. Morphing wing flexible skins with curvilinear fiber composites. Compos. Struct. 2013, 99, 69–75. [Google Scholar] [CrossRef]
- Long, J.H.; Hale, M.E.; Mchenry, M.J.; Westneat, M.W. Functions of fish skin: Flexural stiffness and steady swimming of longnose gar Lepisosteus osseus. J. Exp. Biol. 1996, 199, 2139–2151. [Google Scholar] [CrossRef]
- Rediniotis, O.K.; Wilson, L.N.; Lagoudas, D.C. Development of a shape-memory-alloy actuated biomimetic hydrofoil. J. Intell. Mater. Syst. Struct. 2002, 13, 35–49. [Google Scholar] [CrossRef]
- Olympio, K.R.; Gandhi, F. Flexible skins for morphing aircraft using cellular honeycomb cores. J. Intell. Mater. Syst. Struct. 2010, 21, 1719–1735. [Google Scholar] [CrossRef]
- Liu, W.D.; Zhu, H.; Zhou, S.Q.; Bai, Y.L.; Wang, Y.; Zhao, C.H. In-plane corrugated cosine honeycomb for 1D morphing skin and its application on variable camber wing. Chin. J. Aeronaut. 2013, 26, 935–942. [Google Scholar] [CrossRef] [Green Version]
- Olympio, K.R.; Gandhi, F.; Asheghian, L.; Kudva, J. Design of a flexible skin for a shear morphing wing. J. Intell. Mater. Syst. Struct. 2010, 21, 1755–1770. [Google Scholar] [CrossRef]
- Olympio, K.R.; Gandhi, F. Zero Poisson’s ratio cellular honeycombs for flex skins undergoing one-dimensional morphing. J. Intell. Mater. Syst. Struct. 2010, 21, 1737–1753. [Google Scholar] [CrossRef]
- Chen, J.J.; Shen, X.; Li, J.F. Zero Poisson’s ratio flexible skin for potential two-dimensional wing morphing. Aerosp. Sci. Technol. 2015, 45, 228–241. [Google Scholar] [CrossRef]
- Thill, C.; Etches, J.A.; Bond, I.P.; Potter, K.D.; Weaver, P.M. Composite corrugated structures for morphing wing skin applications. Smart Mater. Struct. 2010, 19, 124009. [Google Scholar] [CrossRef]
- Yokozeki, T.; Takeda, S.I.; Ogasawara, T.; Ishikawa, T. Mechanical properties of corrugated composites for candidate materials of flexible wing structures. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1578–1586. [Google Scholar] [CrossRef]
- Ji, F.L.; Zhu, Y.; Hu, J.L.; Liu, Y.; Yeung, L.Y.; Ye, G.D. Smart polymer fibers with shape memory effect. Smart Mater. Struct. 2006, 15, 1547. [Google Scholar] [CrossRef]
- Cho, J.W.; Kim, J.W.; Jung, Y.C.; Goo, N.S. Electroactive shape-memory polyurethane composites incorporating carbon nanotubes. Macromol. Rapid Commun. 2005, 26, 412–416. [Google Scholar] [CrossRef]
- Kim, N.G.; Han, M.W.; Iakovleva, A.; Park, H.B.; Chu, W.S.; Ahn, S.H. Hybrid composite actuator with shape retention capability for morphing flap of unmanned aerial vehicle (UAV). Compos. Struct. 2020, 243, 112227. [Google Scholar] [CrossRef]
- Yu, Y.; Li, X.; Zhang, W.; Leng, J.S. Investigation on adaptive wing structure based on shape memory polymer composite hinge. In Proceedings of the International Conference on Smart Materials and Nanotechnology in Engineering, Harbin, China, 1–4 July 2007; SPIE, The International Society for Optics and Photonics: Bellingham, WA, USA, 2007; pp. 377–383. [Google Scholar]
- Rodrigue, H.; Cho, S.; Han, M.W. Effect of twist morphing wing segment on aerodynamic performance of UAV. J. Mech. Sci. Technol. 2016, 30, 229–236. [Google Scholar] [CrossRef]
- Yin, W.L.; Sun, Q.J.; Zhang, B.; Liu, J.C.; Leng, J.S. Seamless morphing wing with SMP skin. In Advanced Materials Research; Trans Tech Publications Ltd.: Zürich, Switzerland, 2008; pp. 97–100. [Google Scholar]
- Bye, D.R.; McClure, P.D. Design of a morphing vehicle. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1728. [Google Scholar]
- Perkins, D.A.; Reed, J.L.; Havens, J.E. Morphing wing structures for loitering air vehicles. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 12–22 April 2004; p. 1888. [Google Scholar]
- Andersen, G.R.; Cowan, D.L.; Piatak, D.J. Aeroelastic modeling, analysis and testing of a morphing wing structure. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; pp. 359–373. [Google Scholar]
- Kudva, J.N.; Sanders, B.; Florance, J.P.; Garcia, E. Overview of the DARPA/AFRL/NASA smart wing phase II program. Smart Mater. Struct. 2001, 4332, 383–389. [Google Scholar]
- Asheghian, L.; Reich, G.; Enke, A. Shear morphing skins-simulation and testing of optimized design. J. Intell. Mater. Syst. Struct. 2011, 22, 945–960. [Google Scholar] [CrossRef]
- Wu, R.; Sun, J.; Chang, Z.Z.; Bai, R.; Leng, J.S. Elastic composite skin for a pure shear morphing wing structure. J. Intell. Mater. Syst. Struct. 2015, 26, 352–363. [Google Scholar] [CrossRef] [Green Version]
- Mullins, L. Effect of stretching on the properties of rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Moslemi, A.; Neya, B.N.; Amiri, J.V. Benchmark solution for buckling of thick rectangular transversely isotropic plates under biaxial load. Int. J. Mech. Sci. 2017, 131, 356–367. [Google Scholar] [CrossRef]
- Chen, H.J.; Tsai, S.W. Analysis and optimum design of composite grid structures. J. Compos. Mater. 1996, 30, 503–534. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Elsevier: Amsterdam, The Netherlands, 1986; pp. 3–10. ISBN 9780750626330. [Google Scholar]
- Whitney, J.M. Structural Analysis of Laminated Anisotropic Plates; Routledge: Boca Raton, FL, USA, 1987; pp. 41–45. ISBN 9780203738122. [Google Scholar]
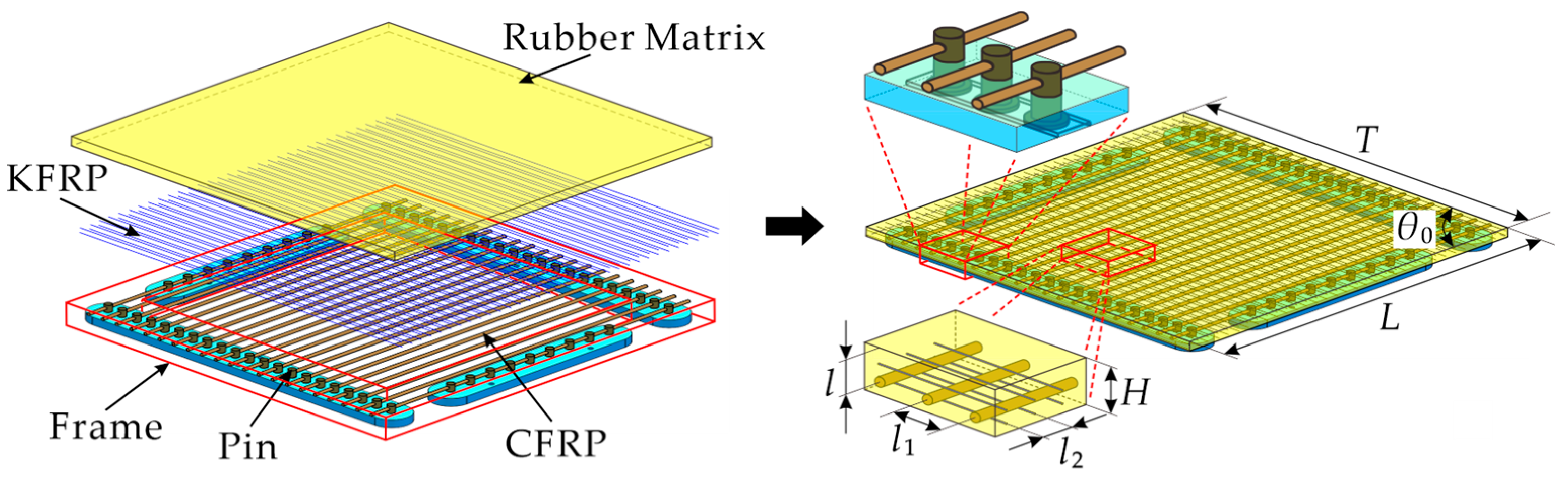
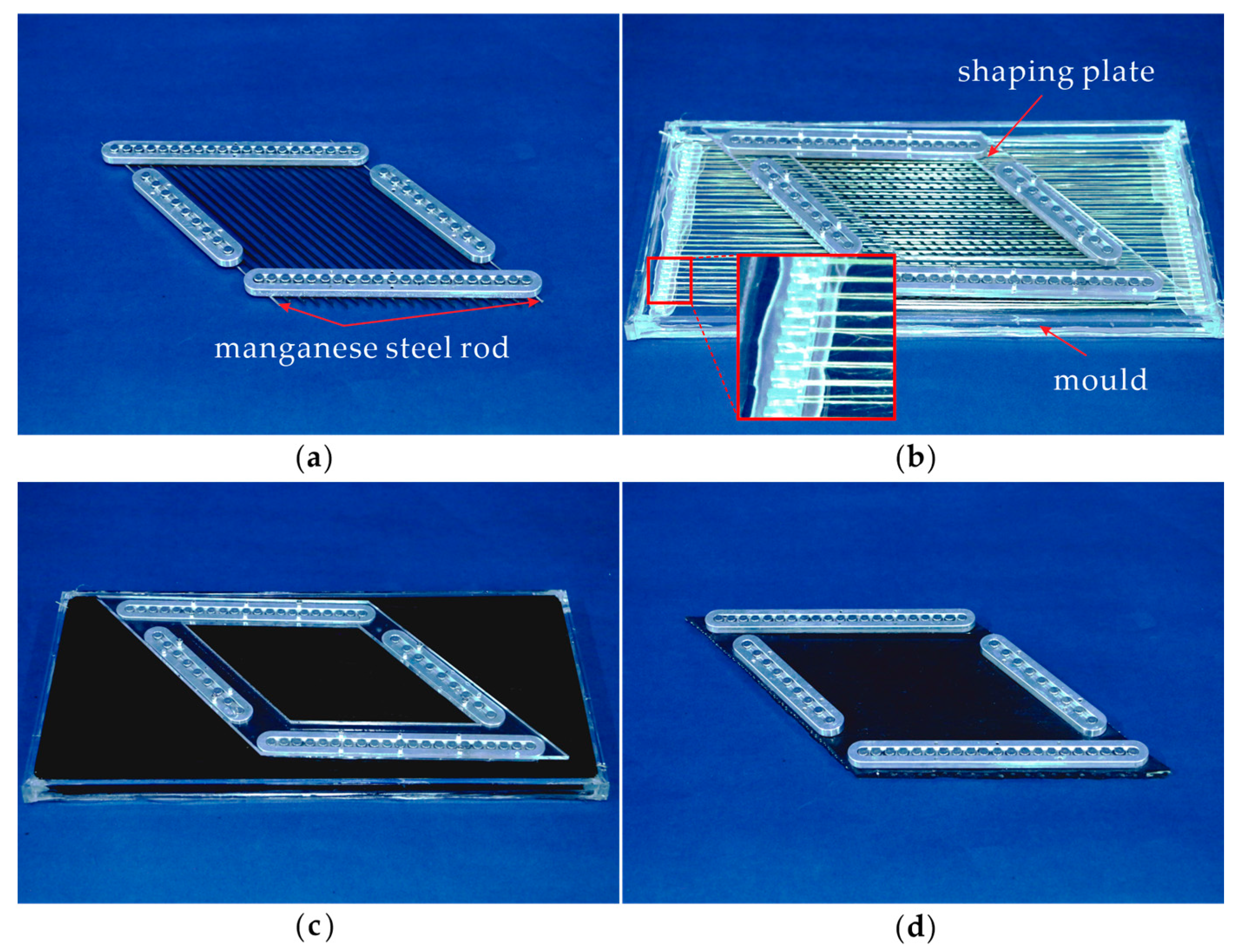





| Parameters | Values |
|---|---|
| Length L | 140 mm |
| Width W | 140 mm |
| Thickness H | 6 mm |
| Distance l | 4.5 mm |
| Interval of CFRP rods l1 | 7 mm |
| Interval of FKRP fibers l2 | 4 mm |
| Diameter of CFRP rods d1 | 1.5 mm |
| Diameter of FKRP fibers d2 | 0.05 mm (400 D) |
| Initial angle θ0 | 50°, 60°, 70°, 80°, 90° |
| Material | ρ (g/cm3) | E (GPa) | μ |
|---|---|---|---|
| CFRP | 1.8 | 210 | 0.3 |
| KFRP | 1.4 | 104 | 0.1 |
| ρ (g/cm3) | C10 | C20 | C30 | D |
|---|---|---|---|---|
| 1.8 | 0.05905 | −0.006268 | 0.0010344 | 0 |
| θ0 (°) | Experiment | FEM | ||||
|---|---|---|---|---|---|---|
| θmax (°) | θmin (°) | Δθ (°) | θmax (°) | θmin (°) | Δθ (°) | |
| 30 | / | / | / | 125.3 | 20.6 | 104.7 |
| 40 | / | / | / | 131.5 | 29.1 | 102.4 |
| 50 | 132.0 | 40.0 | 92.0 | 133.4 | 38.6 | 94.8 |
| 60 | 128.0 | 50.0 | 78.0 | 127.5 | 48.2 | 79.3 |
| 70 | 124.0 | 56.0 | 68.0 | 124.9 | 54.6 | 70.3 |
| 80 | 122.0 | 62.0 | 60.0 | 123.1 | 60.4 | 62.7 |
| 90 | 120.0 | 60.0 | 60.0 | 120.8 | 59.2 | 61.6 |
| Hardness/HS | C10 | C20 | C30 | D |
|---|---|---|---|---|
| 10 | 0.04467 | −0.005278 | 0.0007991 | 0 |
| 20 | 0.10620 | −0.015063 | 0.0029714 | 0 |
| 30 | 0.13025 | −0.018224 | 0.0035482 | 0 |
| 40 | 0.17823 | −0.024546 | 0.0048051 | 0 |
| Group | Ec (GPa) | d1 (mm) | l1 (mm) | L (mm) | Ecd14/l1L2 (N) | θmax (°) | θmin (°) | Δθ (°) |
|---|---|---|---|---|---|---|---|---|
| A | 675 | 1.5 | 7 | 210 | 11.07 | 142.7 | 36.0 | 106.7 |
| 300 | 1.84 | 7 | 210 | 142.4 | 36.2 | 106.2 | ||
| 300 | 1.5 | 3.11 | 210 | 143.0 | 35.7 | 107.3 | ||
| 300 | 1.5 | 7 | 140 | 142.8 | 36.3 | 106.5 | ||
| B | 533 | 1.5 | 7 | 280 | 4.92 | 135.9 | 40.3 | 95.6 |
| 300 | 1.73 | 7 | 280 | 136.0 | 39.8 | 96.2 | ||
| 300 | 1.5 | 3.94 | 280 | 135.1 | 39.3 | 95.8 | ||
| 300 | 1.5 | 7 | 210 | 135.4 | 40.4 | 95.0 | ||
| C | 168 | 1.5 | 7 | 210 | 2.77 | 129.8 | 43.5 | 86.8 |
| 300 | 1.30 | 7 | 210 | 129.6 | 43.2 | 86.4 | ||
| 300 | 1.5 | 12.44 | 210 | 130.1 | 42.9 | 87.2 | ||
| 300 | 1.5 | 7 | 280 | 129.9 | 43.7 | 86.2 | ||
| D | 108 | 1.5 | 7 | 210 | 1.77 | 124.8 | 46.5 | 78.3 |
| 300 | 1.16 | 7 | 210 | 124.9 | 46.2 | 78.7 | ||
| 300 | 1.5 | 19.44 | 210 | 124.5 | 46.7 | 77.8 | ||
| 300 | 1.5 | 7 | 350 | 125.1 | 46.1 | 79.0 |
| θ0 (°) | Theory | FEM | Error | |||
|---|---|---|---|---|---|---|
| θmax (°) | θmin (°) | θmax (°) | θmin (°) | θmax | θmin | |
| 50 | 146.8 | 33.2 | 133.4 | 38.6 | 10.0% | 13.9% |
| 60 | 133.6 | 46.6 | 127.5 | 48.2 | 4.8% | 3.3% |
| 70 | 121.7 | 58.3 | 124.9 | 54.6 | 2.6% | 6.8% |
| 80 | 112.9 | 67.1 | 123.1 | 60.4 | 8.3% | 11.1% |
| 90 | 109.4 | 70.6 | 120.8 | 59.2 | 9.4% | 9.4% |
| Hardness (HS) | Theory | FEM | Error | |||
|---|---|---|---|---|---|---|
| θmax (°) | θmin (°) | θmax (°) | θmin (°) | θmax | θmin | |
| 10 | 151.2 | 28.7 | 138.6 | 35.2 | 9.1% | 18.5% |
| 20 | 133.7 | 46.0 | 130.1 | 41.2 | 2.8% | 11.6% |
| 30 | 132.1 | 47.9 | 128.1 | 42.4 | 3.1% | 12.9% |
| 40 | 129.5 | 49.5 | 127.0 | 44.0 | 2.0% | 12.5% |
| Ecd14/l1L2 (N) | Theory | FEM | Error | |||
|---|---|---|---|---|---|---|
| θmax (°) | θmin (°) | θmax (°) | θmin (°) | θmax | θmin | |
| 11.069 | 151.1 | 28.9 | 142.7 | 36.1 | 5.9% | 19.9% |
| 4.919 | 139.5 | 40.5 | 135.6 | 40.2 | 2.9% | 0.1% |
| 2.767 | 132.8 | 47.1 | 129.8 | 43.3 | 2.3% | 8.8% |
| 1.771 | 128.8 | 48.7 | 124.8 | 46.4 | 3.2% | 4.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Ma, J. Design and Shear Analysis of an Angled Morphing Wing Skin Module. Appl. Sci. 2022, 12, 3092. https://doi.org/10.3390/app12063092
Yu J, Ma J. Design and Shear Analysis of an Angled Morphing Wing Skin Module. Applied Sciences. 2022; 12(6):3092. https://doi.org/10.3390/app12063092
Chicago/Turabian StyleYu, Jinrui, and Jiayao Ma. 2022. "Design and Shear Analysis of an Angled Morphing Wing Skin Module" Applied Sciences 12, no. 6: 3092. https://doi.org/10.3390/app12063092
APA StyleYu, J., & Ma, J. (2022). Design and Shear Analysis of an Angled Morphing Wing Skin Module. Applied Sciences, 12(6), 3092. https://doi.org/10.3390/app12063092