Iterative Dynamic Critical Path Scheduling: An Efficient Technique for Offloading Task Graphs in Mobile Edge Computing

Abstract

Recent years have witnessed a paradigm shift from centralized cloud computing to decentralized edge computing. As a key enabler technique in edge computing, computation offloading migrates computation-intensive tasks from resource-limited devices to nearby devices, optimizing service latency and energy consumption. In this paper, we investigate the problem of offloading task graphs in edge computing scenarios. Previous work based on list-scheduling heuristics is likely to suffer from severe processor time wastage due to intricate task dependencies and data transfer requirements. To this end, we propose a novel offloading algorithm, referred to as Iterative Dynamic Critical Path Scheduling (IDCP). IDCP minimizes the makespan by iteratively migrating tasks to keep shortening the dynamic critical path. Through IDCP, what is managed are essentially the sequences among tasks, including task dependencies and scheduled sequences on processors. Since we only schedule sequences here, the actual start time of each task is not fixed during the scheduling process, which effectively helps to avoid unfavorable schedules. Such flexibilities also offer us much space for continuous scheduling optimizations. Our experimental results show that our algorithm significantly outperforms existing list-scheduling heuristics in various scenarios, which demonstrates the effectiveness and competitiveness of our algorithm.

1. Introduction

Driven by the needs of Internet of Things (IoT), recent years have witnessed a paradigm shift from centralized cloud computing to decentralized mobile edge computing (MEC). As a key enabler technique in edge computing, computation offloading migrates computation-intensive tasks from resource-limited devices to nearby resource-abundant devices on the edge of networks, thereby optimizing various performance metrics such as resource utilization and service latency. In MEC, computation offloading is exploited in various applications and services such as virtual reality (VR) [1], industrial process control [2], forest-fire management [3], UAV surveillance [4,5], health monitoring [6], and intelligent agriculture [7].

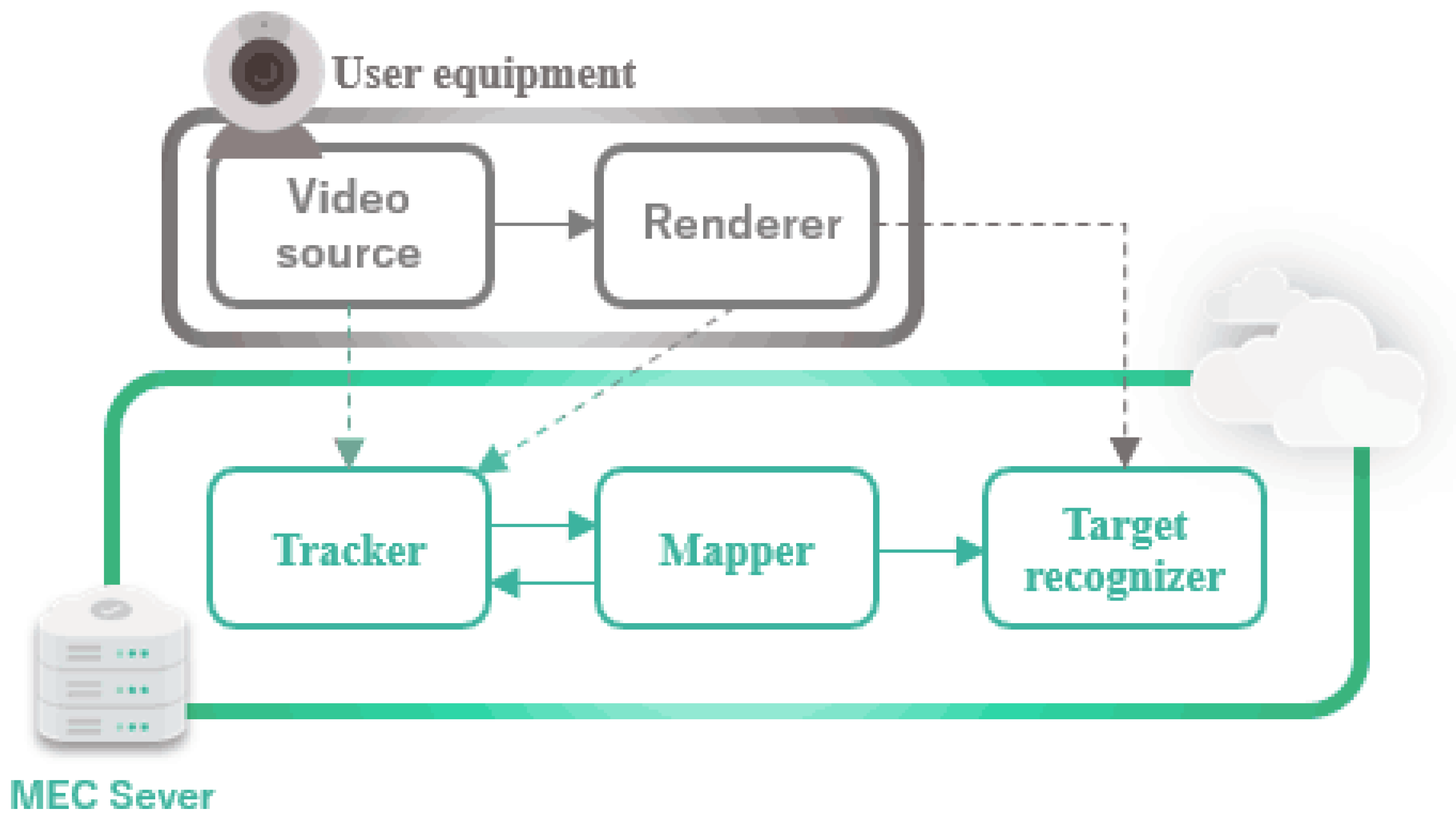
In this paper, we consider the offloading of dependent tasks in a generic edge computing platform consisting of a network of heterogeneous edge devices and servers. The offloading problem in edge scenarios has wide applicability in reality. Many practical applications are composed of multiple procedures/components (e.g., the computation components in an AR application, as shown in Figure 1), making it possible to implement fine-grained (partial) computation offloading. Specifically, the program can be partitioned into two parts with one executed at the mobile device and the other offloaded to the edge for execution. In the partitioning, the dependencies among different procedures/components in many applications cannot be ignored as it significantly affects the procedure of execution and computation offloading. Accordingly, a task graph model is adopted to capture the interdependency among different computation functions and routines in an application.

Although task graphs have wide applicability in practice, the offloading of task graphs receives only limited attention due to the high complexity brought by task dependencies and data transfer requirements among different task nodes of the task graph. A few previous studies have investigated the offloading of task graphs in heterogeneous edge platforms. Most prior work [8,9,10,11] proposed list-scheduling-based constructive heuristics which sequentially assign all task nodes onto processors in a greedy manner, carefully obeying task dependency rules. List-scheduling heuristics are simple and straightforward in algorithm design and implementation. However, the performance of such heuristics may be unsatisfactory, since task dependencies and data-transfer requirements among different task nodes usually cause processors to retain idle and wait, wasting a large amount of time. This is because a node has to wait until all its parent task nodes and the corresponding required data transfer are finished before assigning a processor for it. In addition, in list-scheduling heuristics, task nodes are sequentially assigned in a greedy manner, and once a task has been scheduled, its start time is determined and fixed. In such situations, a task-assignment decision initially may be optimal, but later it may become inefficient and incur severe waiting time after a few other assignment decisions. Therefore, it is highly desirable to design efficient dependent task-offloading approaches which can elegantly handle the challenges brought by complicated task dependencies and data transfer requirements.

Nevertheless, designing elegant algorithms to prevent inefficient assignment decisions and reduce processor waiting times are quite challenging. Due to complicated precedence constraints and data-transfer requirements, it is difficult to make proper scheduling decisions in single steps with global forecasts. To prevent inefficient assignment decisions which cause long processor waiting times, idle times need to be fully utilized. This can be enabled by proper adjustment, such as deferring some task nodes and inserting some other task nodes to avoid making scheduling decisions too early. However, intricate precedence constraints and data-transfer requirements severely complicate the adjustment process. Therefore, an exquisite algorithm which can ease and simplify the adjustment process and thereby empower global perspectives is certainly demanded.

To this end, this paper contributes a novel heuristic for offloading task graphs in mobile edge environments, referred to as Iterative Dynamic Critical Path Scheduling (IDCP). Distinguished from the existing list-scheduling heuristics [8,9,11], IDCP is an iterative algorithm. IDCP minimizes the makespan by iteratively migrating tasks to keep shortening the dynamic critical path, which can dynamically vary depending on the current sequence of the tasks. In IDCP, what is managed are essentially the sequences among tasks, including task dependencies and scheduled sequences on processors. Since we only schedule sequences, the actual start time of each task is not fixed during the scheduling process, while it can be simply calculated after the process terminates. The unfixed start time effectively help to avoid unfavorable schedules which may cause unnecessary processor waiting time. Such flexibilities also offer us much space for continuous scheduling optimizations. In this case, we can easily and efficiently iterate to keep optimizing the makespan.

The rest of this paper is organized as follows. Section 2 reviews related work. Section 3 introduces system models and formulates the problem. Section 4 describe the proposed iterative heuristic algorithm. Section 5 presents performance evaluation and Section 6 summarizes the paper.

2. Related Work

The problem of computation offloading has been studied in recent years and many heuristic algorithms have been proposed. Several survey articles comprehensively reviewed this problem [2,12,13]. Fine-grain resource allocation and scheduling for multiple tasks received much attention. Several studies [14,15,16] investigated the problem of binary task offloading, where each task is executed as a whole either locally at the mobile device or offloaded to the MEC server. Chang et al. [17] proposed a response-time-improved offloading algorithm to make offloading decision with fewer characteristics of continuous uncertain applications. Zhang et al. [18] presented a load-balancing approach for task offloading in vehicular edge computing networks with fiber–wireless enhancement. Barbarossa et al. [15] showed how the optimal resource allocation involves a joint allocation of radio and computation resources via a fully cross-layer approach. Zhang et al. in [14], proposed to minimize energy consumption for executing tasks with soft deadlines. Under the Gilbert–Elliott channel model, they presented optimal data-transmission scheduling by dynamic programming (DP) techniques. This work is extended in [16], where both the local computation and offloading are powered by wireless energy provisioning. Another work [19] formulated a non-cooperative game and presented a fairness-oriented computation offloading algorithm for cloud-assisted edge computing.

In practice, many mobile applications are composed of multiple procedures/components, making it possible to implement fine-grained (partial) computation offloading. Accordingly, partial offloading schemes have been proposed to further optimize MEC performance [8,9,10,11,20]. Geng et al. [8] investigated an energy-efficient task-graph-offloading problem for multicore mobile devices. They designed a critical-path-based heuristic which recursively checks the tasks and moves tasks to the correct CPU cores to save energy. Sundar et al. [9] proposed an heuristic algorithm to minimize the overall application execution cost under task deadlines. Nevertheless, these studies involve list-scheduling-based constructive heuristics, thereby suffering from poor performance due to unfavorable schedules which may cause unnecessary processor waiting times. Further, Kao et al. [10] proposed a polynomial time-approximation algorithm to optimize the makespan under energy budgets for offloading (tree-shape) task graphs on edge devices. However, Ref. [10] relies on an unrealistic assumption that the mobile devices are assumed to possess infinite capacity, i.e., the devices can simultaneously process an infinite number of tasks without reduction in the processing speed for each task. Another work [20] formulated the task-graph-offloading problem via integer linear programming, but no novel solution was presented.

Both the binary offloading and partial offloading strategies investigate resource allocation for a given set of tasks submitted by a single user. For multiuser systems, a number of studies on joint radio- and computational-resource allocation has also been proposed [21,22,23,24,25,26,27]. Chen et al. presented an opportunistic task-scheduling algorithm over co-located clouds in mobile multiuser environments. In [23], the authors considered the multiuser video compression offloading in MEC and minimized the latency in local compression, edge cloud compression and partial compression offloading scenarios. Hong et al. [26] studied a device-to-device (D2D)-enabled multiuser MEC system, in which a local user offloads their computation tasks to multiple helpers for cooperative computation. Zhan et al. [27] proposed a mobility-aware offloading algorithm for multiuser mobile edge computing. These papers studied the assignment of finite radio-and-computational resources on a server among multiple mobile users to achieve system-lever objectives. You et al. [16] studied resource allocation for a multiuser MEC system based on time-division multiple access and orthogonal frequency-division access. Moreover, multiuser cooperative computing [28,29] is also envisioned as a promising technique to improve the MEC performance by offering two key advantages, including short-range transmission via D2D techniques and computation resource sharing. Ref. [30] proposed a method to jointly optimize the transmit power, the number of bits per symbol and the CPU cycles assigned to each user in order to minimize the power consumption at the mobile side. The optimal solution shows that there exists an optimal one-to-one mapping between the transmission power and the number of allocated CPU cycles for each mobile device.

In addition to task offloading, the problem of dependent tasks scheduling on multiprocessor systems has been widely studied [31,32,33,34,35,36]. Kwok et al. [31] proposed an efficient list-scheduling algorithm, called Dynamic Critical-Path scheduling algorithm (DCP), for allocating dependent tasks to homogeneous multiprocessors to minimize the makespan. One valuable feature of DCP is that the start times of the scheduled nodes are unfixed until all nodes have been scheduled. Our IDCP also applies this feature. The differences between DCP and IDCP are that DCP is a constructive heuristic and can only be used for homogeneous multiprocessor scheduling, while IDCP is an iterative heuristic which addresses the offloading problem as task migrations among heterogenous MEC platforms. Moreover, DCP assumed infinite computation capacity while IDCP relaxes this unrealistic assumption for MEC scenarios. In addition, Hu et al. [33] proposed real-time algorithms for dependent task scheduling on time-triggered in-vehicle networks. Another work [36] presented adaptive scheduling algorithms for task graphs in dynamic environments. All the above literature studied constructive heuristic algorithms. In contrast, the algorithm proposed in our paper is an iterative heuristic, offering more flexibility for optimization, that works on heterogeneous edge computing systems.

3. Problem Formulation

This Section introduces the system models and formulates the optimization problem. We consider an edge computing system with a certain number of local processors and MEC servers, as shown in Figure 2. These processors and servers cooperate to compute a set of dependent tasks. Hence, we investigate the problem of offloading dependent tasks in the edge computing system. We begin by listing the notation and terminology in Notation.

In the system, the local processors are typically installed in the mobile users and mobile peers. Each local processor is only capable of executing one task at a time, while other assigned tasks wait in a queue. Nevertheless, each MEC server is able to execute multiple tasks concurrently, depending on how many processors it possesses. We also assume a remote cloud center (RCC) which is able to provide an unlimited amount of computation resources. In other words, the processing cores of the remote cloud center are infinite. Therefore, all the assigned tasks can be performed simultaneously. Let P be the set of all processors and its size be M. Let $f_i$ denote the time taken by processor i to process per unit workload. Let $d_{ij}$ define the delay per unit data transfer from processor i to processor j. It is clear that the value of $f_i$ is much smaller while offloading to RCC, yet the value of $d_{ij}$ is often much higher.

We consider a scenario where a single application must be completed before its deadline $T_{dl}$. The application is partitioned into multiple tasks, whose dependency is modeled as a Directed Acyclic Graph (DAG), as shown in Figure 3. Let $G(v,\epsilon )$ denote a DAG, where v represents the set of task vertices and $\epsilon$ represents the set of directed edges. Each task $v_i$ is assigned with a certain amount of workload, which is represented by $w_{v_i}$. Hence, the execution time of task $v_i$ on processor $p_j$ is

$$T_{ex}\left(v_i\right)=w_{v_i}{f}_{p_j}$$

(1)

Each directed edge $(v_i,v_j)$ in $\epsilon$ indicates that there is some data, denoted as $e_{v_i{v}_j}$, required to be transferred from $v_i$ to $v_j$. Therefore, $v_j$ will not be able to start until $v_i$ finishes. We define $v_i$ to be the parent of $v_j$. Furthermore, if $v_i$ and $v_j$ are scheduled to be executed on processor $p_m$ and processor $p_n$ respectively, the time taken by data transferring is $d_{p_m{p}_n}{e}_{v_i{v}_j}$. However, such time is ignored if $v_i$ and $v_j$ are scheduled on the same processor, since no data transferring is required.

It is assumed that the application starts at a particular local processor and must end at the same local processor. For simplicity, we insert one dummy node at the start of DAG to trigger the application, which is referred to as the entry node hereinafter. It has zero weight and no data to be transferred. Likewise, one dummy node, called the exit node, is inserted at the end of DAG to retrieve the results at the processor where the application started. Therefore, the number of tasks considered is

$$N=\left|v\right|+2$$

(2)

Each task shall be assigned to a position of a processor; hence, the task-scheduling decision involves both the processor mapping and the relative order of tasks on each processor. Let $x_{ijr}$ denote the scheduling decision, which is given as follows:

$$x_{ijr}:\left\{\begin{array}{c}1iftaskiisassignedtoprocessorjinpositionr\hfill \\ 0ifotherwise\hfill \end{array}\right.$$

(3)

The application must start and end at the same local processor, which is denoted as $p_s$, so we have

$$\sum _{r=1}^{L_{p_s}}{x}_{1p_{s}r}=1$$

(4)

$$\sum _{r=1}^{L_{p_s}}{x}_{N{p}_{s}r}=1$$

(5)

Each task can only be assigned to exactly one certain position on one processor, therefore,

$$\sum _{j=1}^M\sum _{r=1}^{L_j}{x}_{ijr}=1,\forall i=1,\dots ,N$$

(6)

where $L_j$ represents the number of available positions on processor j. Furthermore, each position on each processor can only be allocated to at most one task, which is given as:

$$\sum _{i=1}^N{x}_{ijr}\le 1,\forall r=1,\dots ,L_j,j=1,\dots ,M$$

(7)

Each task is required to be assigned sequentially to the available positions on each processor, which is imposed as follows:

$$\sum _{i=1}^N{x}_{ijr}\le \sum _{i=1}^N{x}_{ij(r-1)},\forall r=2,\dots ,L_j,j=1,\dots ,M.$$

(8)

For each task, the earliest time it finishes depends on the finish of all of its parent tasks. Moreover, it is also constrained by the time when the task occupying the last position on the same processor finishes. Hence, we have

$$F{T}_i=max(F{T}_{tx}^{(j,i)},F{T}_{pre\left(i\right)})+T_{ex}\left(i\right),\forall j\in G\left(i\right)$$

(9)

where $pre\left(i\right)$ represents the task scheduled at the last position of i and $G\left(i\right)$ denotes the set of parent tasks of i. We use $F{T}_{tx}^{(j,i)}$ to denote the time when the results from j are received by i, which is given as:

$$F{T}_{tx}^{(i,j)}=F{T}_i+d_{p_i{p}_j}{e}_{ij}$$

(10)

where $p_i$ and $p_j$ represent the processor where i and j are executed respectively.

The finish time of each task executed on local processor j is constrained by:

$$\begin{array}{cc}\hfill & {FT}_i-{FT}_k+C(2-x_{ijr}-x_{kj(r-1)})\ge T_{ex}\left(i\right)\hfill \\ \hfill & \forall i,k=1,\dots ,N,j=1,2,\dots ,M,r=2,\dots ,L_j\hfill \end{array}$$

(11)

where C is set to be a relatively large positive number. It is guaranteed that the finish time of i on processor j is at least equal to the finish time of its preceding task plus the execution time of i. Notice that the value of $2-x_{ijr}-x_{kj(r-1)}$ is equal to 0 if and only if task k and task i are scheduled consecutively on processor j. Moreover, our task-scheduling decision must meet the application deadline, which is imposed by:

$$F{T}_N\le T_{dl}$$

(12)

Our goal is to reasonably schedule the tasks such that the finish time of the application is minimized, which is given by:

$$\begin{array}{c}minF{T}_N,\\ s.t.\mathrm{Equations} \left(4\right)–\left(12\right)\end{array}$$

(13)

4. The IDCP Algorithm

This section describes the design of IDCP in detail, which is shown in Algorithm 1. IDCP works by iteratively adjusting the task-scheduling decision such that the solution is optimized. At every iteration, IDCP executes three steps: (1) node selection; (2) node assignment; and (3) solution update. In step 1, some nodes, which may be critical to the solution quality, are selected. In step 2, the nodes selected are rescheduled to retrieve a better solution. In step 3, the solution is updated based on the new task-scheduling decision. Figure 4 illustrates an example of the node migration steps in one iteration.

Algorithm 1 The IDCP Algorithm

1: Initialization 2: $S^{*}\leftarrow \varnothing$ 3: while exit criteria are not satisfied do 4:    Get $S_n\leftarrow \left\{nodesonthecurrentcriticalpath\right\}$ 5:    while $S_n\ne \varnothing$ do 6:        Select a node $n_i$ from $S_n$ randomly 7:        Get candidate positions for $n_i$ 8:        Calculate $Mobility(n_i,m)$ for all candidate positions 9:        Assign $n_i$ to the candidate position with the maximal $Mobility(n_i,m)$ 10:        Remove $n_i$ from $S_n$ 11:        Update EST and LST for all nodes in $S_n$ 12:        Get the solution S 13:          if S is currently the best then 14:             $S^{*}\leftarrow S$ 15:        end if 16:    end while 17: end while 18: Return $S^{*}$

4.1. Definitions

Following [31], we first give the following definitions.

Definition 1.

The earliest start time (EST) of a node $n_i$ is defined as:

$$EST\left(n_i\right)=\max (ES{T}^G\left(n_i\right),ES{T}^P\left(n_i\right))$$

(14)

where, $ES{T}^G\left(n_i\right)$ is the EST value constrained by $n_i^{\prime }s$ parent nodes; $ES{T}^P\left(n_i\right)$ is the EST value constrained by $pre\left(n_i\right)$. One can write $ES{T}^G\left(n_i\right)$ as follows:

$$ES{T}^G\left(n_i\right)=\underset{n_x\in G\left(n_i\right)}{max}\left(EST\left(n_x\right)+T_{ex}\left(n_x\right)+d_{p_x{p}_i}{e}_{n_x{n}_i}\right)$$

(15)

where $p_x$ and $p_i$ represent the processors where $n_x$ and $n_i$ are executed respectively. Equation (15) states that the EST of a node is no greater than the time when the results from all of its parent nodes are received. $ES{T}^P\left(n_i\right)$ equals to the earliest finish time of the node that is scheduled immediately before $n_i$ on the same processor and can be written as:

$$ES{T}^P\left(n_i\right)=EST\left(pre\left(n_i\right)\right)+T_{ex}\left(pre\left(n_i\right)\right)$$

(16)

If $n_i$ represents the starting dummy node, $ES{T}^P\left(n_i\right)$ = 0. In addition, if $n_i$ has not yet been scheduled, $ES{T}^P\left(n_i\right)$ = 0.

$EST\left(n_i\right)$ can be computed once the EST of all $n_i^{\prime }s$ parents and $pre\left(n_i\right)$ are known. Hence, the EST of all nodes can be calculated by traversing the DAG in a top-down manner beginning from the dummy node we insert at the beginning of DAG. Consequently, when all the EST of $n_i^{\prime }s$ parents and $pre\left(n_i\right)$ are available, the EST of $n_i$ can be computed.

Definition 2.

The latest start time (LST) of a node $n_i$ is defined as:

$$LST\left(n_i\right)=\min (LS{T}^C\left(n_i\right),LS{T}^N\left(n_i\right))$$

(17)

where $LS{T}^C\left(n_i\right)$ is the LST value constrained by $n_i^{\prime }s$ parent nodes. $LS{T}^N\left(n_i\right)$ is the LST value constrained by $nxt\left(n_i\right)$, which denotes the node scheduled immediately after $n_i$ on the same processor. One can write $LS{T}^C\left(n_i\right)$ as follows:

$$LS{T}^C\left(n_i\right)=\underset{n_x\in C\left(i\right)}{min}\left(LST\left(n_x\right)-T_{ex}\left(n_x\right)-d_{p_x{p}_i}{e}_{n_x{n}_i}\right)$$

(18)

where $C\left(i\right)$ represents the set of children nodes of $n_i$. If $n_i$ is the dummy node we insert at the end of DAG, then $LS{T}^G\left(n_i\right)$ = ∞.

$LS{T}^N\left(n_i\right)$ is constrained by the start time of $nxt\left(n_i\right)$. Therefore, one can write $LS{T}^N\left(n_i\right)$ as:

$$LS{T}^N\left(n_i\right)=LST\left(nxt\left(n_i\right)\right)-T_{ex}\left(n_i\right)$$

(19)

If $n_i$ has not yet been scheduled or $n_i$ is the ending dummy node, $LS{T}^N\left(n_i\right)$= $T_{dl}$. Analogously, the LST of all nodes can be calculated by traversing the DAG from bottom to top.

Definition 3.

A critical path of a DAG is a set of nodes and edges, forming a path from the starting dummy node to the ending dummy node, of which the sum of execution time and communication time is the maximum.

According to the definition, the nodes on the critical path are vital to the finish time of the application. Therefore, high priority shall be placed on optimizing the schedule of these nodes. To identify the nodes on the critical path, we simply check the equality of its EST and LST value [31].

4.2. The Algorithm

Before the iterative task-scheduling process, an initial solution needs to be constructed. For the sake of simplicity, as well as the efficiency of IDCP, we adopt HEFT [34] to obtain the initial solution. As in previous statement, the nodes on the critical path are rescheduled at every iteration, offering better chances for improving the current solution. However, the rescheduling operation on each node is highly likely to change the critical path. Hence, a working set is involved to store the nodes on the current critical path.

$$S_n=\left\{n_i\right|if{n}_{i}isonthecurrerntcriticalpath\}$$

(20)

At the start of every iteration, all the nodes on the current critical path are added to $S_n$. Then IDCP iterates to reschedule all the nodes in $S_n$ and update the current solution. Note that every time a node is rescheduled, the solution is updated and the critical path is changed. Thanks to the working set, IDCP is able to focus on critical path we try to optimize at the beginning.

Further, to prevent infinite iterations, we introduce two exit criteria. The first one is the number of iterations. The IDCP simply exits after $NR$ number of iterations. In addition, it may occur that the solution is not improved for $NT$ consecutive times due to local optimum or global optimum. Either way, we choose to exit IDCP.

As stated above, three steps are executed at every iteration, namely node selection, node assignment and solution update, which are detailed respectively in the following subsections.

4.2.1. Node Selection

IDCP iterates to optimize the task-scheduling decision of the initial solution. Therefore, an order in which nodes are rescheduled needs to be determined first. Since the critical path is crucial to the solution quality, we prioritize the nodes on the critical path for scheduling.

As in previous statement, the critical path changes dynamically during the scheduling process, which means nodes on the critical path are not fixed. To reduce the time complexity of the algorithm, we randomly select nodes from the critical path for scheduling.

4.2.2. Node Assignment

As one can see from the definitions of EST and LST, the start time of each node can slide between its EST and LST. Hence, the EST and LST of each node reflect its mobility, which is defined as:

$$Mobility\left(n_i\right)=LST\left(n_i\right)-EST\left(n_i\right)$$

(21)

The value of $Mobility\left(n_i\right)$ implies the flexibility of scheduling on node $n_i$.

Constrained by the dependency of tasks, $n_i$ shall not be scheduled before its parents or after its children. A position that satisfies this constraint is called a candidate position. Let the set of candidate positions of node $n_i$ be $CP\left(n_i\right)$. Let $EST(n_i,m)$ and $LST(n_i,m)$ denote the EST and LST of node $n_i$ if it is scheduled onto the position m among all of its candidate positions respectively, which are given as

$$EST(n_i,m)=max(ES{T}^G\left(n_i\right),EST\left(n_{m-1}\right)+T_{ex}\left(n_{m-1}\right))$$

(22)

$$LST(n_i,m)=min(LS{T}^G\left(n_i\right),LST\left(n_{m+1}\right)-T_{ex}\left(n_m\right))$$

(23)

where $n_{m-1}$ and $n_{m+1}$ denotes the node on the last position and next position of m.

Likewise, let $Mobility(n_i,m)$ represent the slide range of node $n_i$ if it is scheduled onto position m among the candidate positions:

$$Mobility(n_i,m)=LST(n_i,m)-EST(n_i,m)$$

(24)

Among all the candidate positions in $CP\left(n_i\right)$, $n_i$ is scheduled onto the position with the greatest $Mobility(n_i,m)$. In this way, the high flexibility of the node is preserved, offering more room for future optimization. After assigning node $n_i$ to the proper candidate position, $n_i$ is removed from $S_n$.

Theorem 1.

If the current schedule is feasible, the node-assignment operation maintains the feasibility, provided that:

$$Mobility(n_i,m)\ge 0$$

(25)

After the node $n_i$ is scheduled onto a new position m, the EST value of each node can be retained recursively from the entry node since the dependency of tasks has been considered in the node-assignment operation. Similar to EST, the LST value can also be obtained recursively. Accordingly, $n_i$ can be scheduled onto its new position m, with its starting time sliding between the range $[EST(n_i,m),LST(n_i,m)]$, which is valid if $Mobility(n_i,m)\ge 0$. Theorem 1 ensures that the feasibility of the solution is not violated after node-assignment operation is executed.

4.2.3. Update

Since the task-scheduling decision has changed after node assignment operation, the EST and LST values of each node need to be updated. As discussed previously, the EST and LST value of each node can be retrieved by traversing the DAG. After the solution is updated, IDCP is able to evaluate the solution and determine whether to continue working on the current working set or to start the next iteration (line 3 of Algorithm 1).

5. Performance Evaluation

In this section, an evaluation study is carried out to show the performance of the proposed algorithm. For this purpose, three other approaches, namely Infocom-2018 [8], TC-2017 [36] and TPDS-2012 [32], are utilized to compare with IDCP. First, the evaluation setup is presented.

5.1. Evaluation Setup

The system considered in our evaluation study is composed of a remote cloud center, an MEC server and several local processors. For simplicity, each processor is presumed to have an infinite number of available positions. An application, which is composed of multiple dependent tasks, needs to be finished before its deadline. To verify the practicability of the application, we consider three kinds of applications with different DAG topologies: tree, workflow, and random topologies.

To understand the merits of IDCP, three baseline algorithms are adopted to make a comparison, namely:

• Infocom-2018: an efficient offloading algorithm for multicore-based mobile devices proposed in [8], which can minimize the energy consumption while satisfying the completion time constraints of multiple applications;
• TC-2017: an online dynamic-resilience scheduling algorithm called Adaptive Scheduling Algorithm (ASA) proposed in [36], which realistically deals with the dynamic properties of multiprocessor platforms in several ways;
• TPDS-2012: an offloading algorithm for multiprocessor-embedded systems proposed in [32], which is an online scheduling methodology for task graphs with communication edges.

Table 1. Comparison of the algorithms evaluated.

Algorithm	IDCP	Infocom-2018 [8]	TC-2017 [36]	TPDS-2012 [32]
Objective	Total time	Energy	Total time	Total time
Type	Iterative	List scheduling	List scheduling	List scheduling
Online	No	No	Yes	Yes

lists the four algorithms evaluated in our simulations.

The finish time of the application, referred to as application latency, is the only performance metric that interests us. It is defined as the EST value of the exit node, which represents the earliest time when the application can finish. Indubitably, a lower value of the application latency indicates higher performance of the algorithm.

First, we fix the other settings and only vary the number of nodes in range (30, 70), which indicates the scale of the application. The results are represented graphically in Figure 5a–c. Second, the number of nodes is set at 50 while the number of local processors varies in the range [3, 15]. Figure 6a–c depicts the corresponding results. Finally, the number of nodes and local processors are fixed at 50 and 10 respectively, with the delay factor varies between 1 and 5. The delay factor controls the deterioration of the network. The results are presented in Figure 7a–c.

5.2. IDCP Simulation Results

Figure 5a–c shows that IDCP outperforms the other three algorithms significantly, under all three types of applications. It, in turn, verifies that IDCP can adapt to multiple types of applications. The performance of Infocom 2018 and TC 2017 is quite close when applied to our problem. In addition, it can be observed that the more tasks needed to be offloaded, the higher the application latency, which is consistent with intuition.

IDCP also has significant advantages with varying number of local processors, as shown in Figure 6a–c. When the number of local processors varies from 3 to 15, IDCP always achieves the best performance. In particular, when working on workflow DAG, the application latency of IDCP is less than 0.085 on average, but the lowest application latency of the other three algorithms is over 0.13, which means that IDCP improves the performance by at least 150%.

Figure 7a–c shows that when the delay factor varies between 1 and 3, the application latency of IDCP changes rapidly from high to low, and then continues to decrease slowly after the delay factor reaches 3. It indicates that IDCP is quite sensitive to the situation of the network, yet it still achieves greatest performance under all situations. In random DAG situation, when delay factor reaches 5, the application latency of IDCP is less than one-half of the work in TPDS2012. Hence, IDCP reduces application latency by over 200%.

In conclusion, the simulation results show that under different experiment settings, our proposed approach outperforms the three offloading algorithms Infocom-2018, TC-2017, and TPDS-2012 by a clear margin. This is due to the fact that these algorithms are constructive list-scheduling heuristics, which make only limited efforts to search for efficient solutions, while the proposed IDCP algorithm is an iterative algorithm which repeatedly migrates tasks to keep shortening the dynamic critical path such that the total processing time is finally minimized.

The proposed heuristic is fast and flexible, but it is still only an offline algorithm. Accordingly, in future work, we can extend it to an online algorithm so that it can adapt to various dynamic scenarios. In addition, the communication models in this paper do not consider complicated 5G communications. In this case, another future direction is to integrate complex 5G communication models in our algorithm such that the algorithm would better fit future 5G scenarios.

6. Conclusions

In this paper, we have proposed a novel offloading algorithm, referred to as Iterative Dynamic Critical Path (IDCP). IDCP minimizes the makespan by iteratively migrating tasks to keep shortening the dynamic critical path. In IDCP, we essentially managed the sequences among tasks, including task dependencies and scheduled sequences on processors. Since we only scheduled sequences, the actual start time of each task is not fixed during the scheduling process, which effectively helped to avoid unfavorable schedules. Such flexibilities also offer much space for continuous scheduling optimizations. We have conducted extensive experiments to evaluate the performance of IDCP, which have shown that IDCP significantly outperforms existing list-scheduling heuristics under a variety of scenarios.