Mechanical Performance of Curved Link-Slab of Simply Supported Bridge Beam
Abstract
:1. Introduction
2. Theoretical Analysis
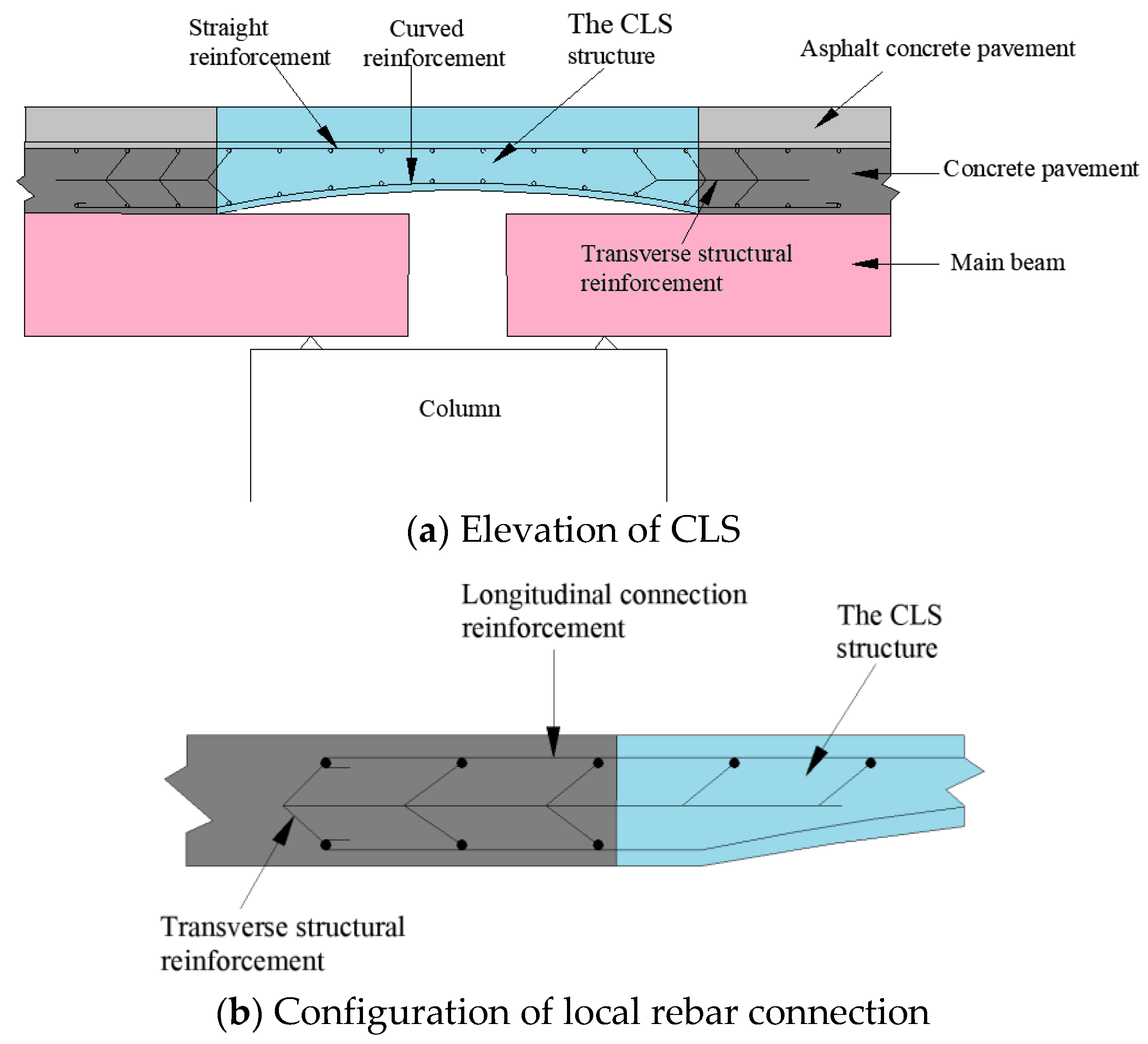
2.1. Overview of CLS
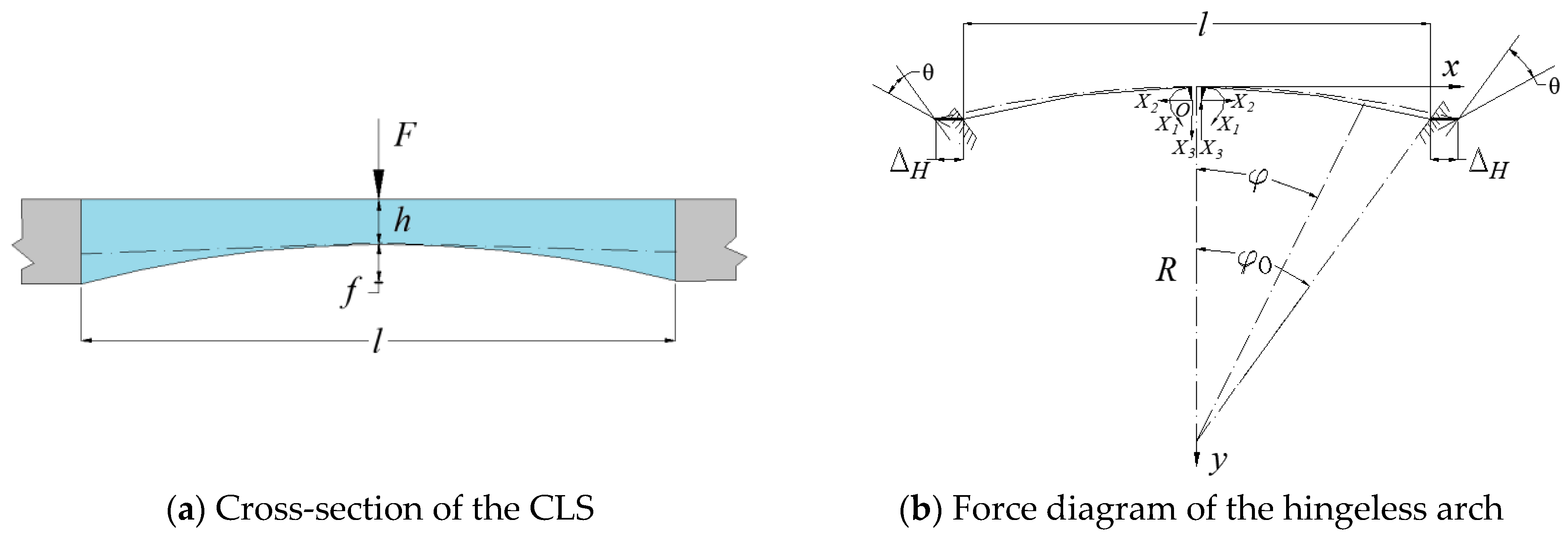
2.1.1. Simplified Hingeless Arch Model
2.1.2. Hingeless Arch Section Characteristics
2.2. Mechanical Analysis of CLS
2.2.1. Vehicle Loading
2.2.2. Vehicle Braking Force
2.2.3. Temperature Gradient
2.2.4. Overall Temperature Change
2.3. Stress Combination on CLS
3. Numerical Analysis of CLS and FLS
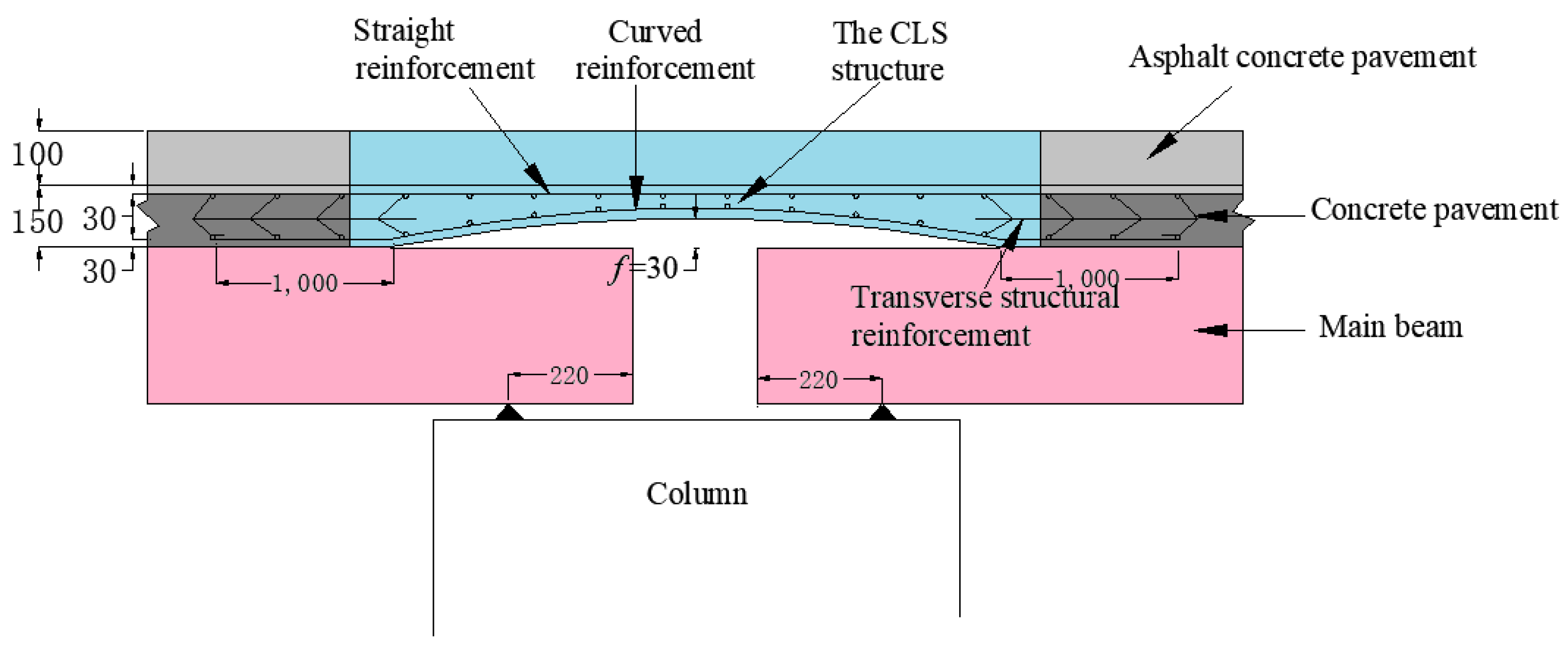
3.1. Project Overview
3.2. Finite Element Modeling
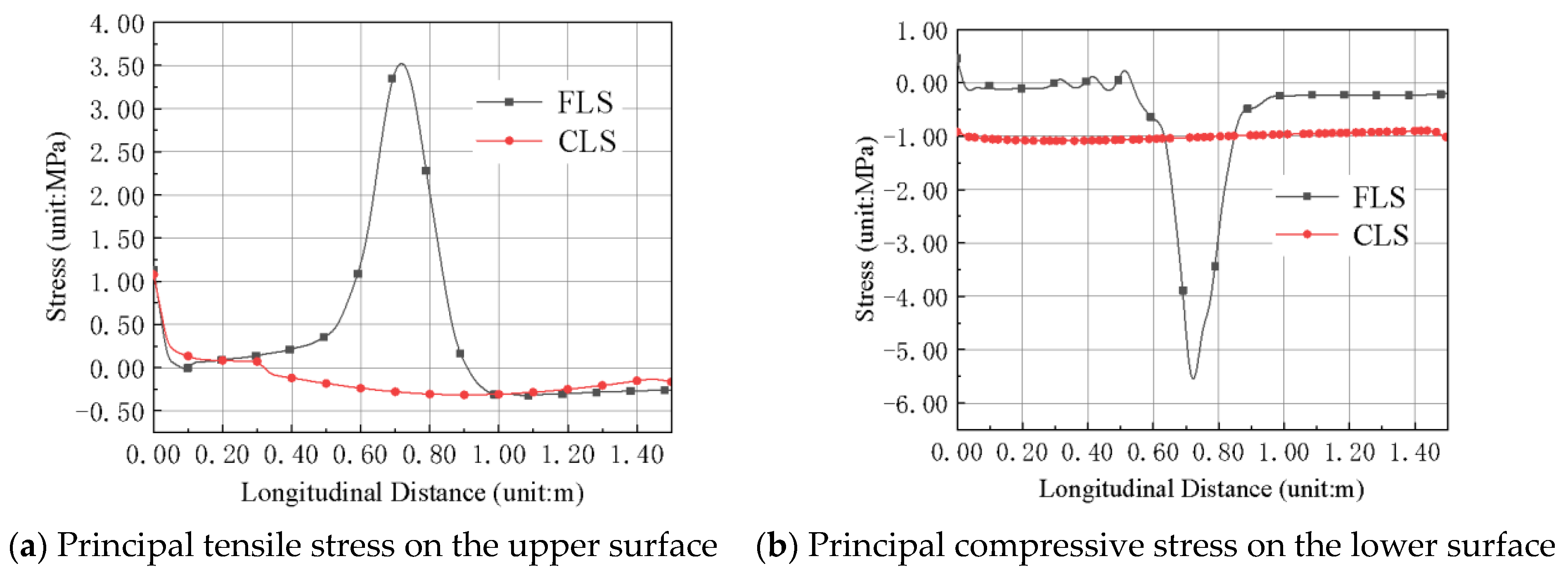
3.3. Data Analysis
3.3.1. The Second Phase Dead Load
3.3.2. Highway Class I Lane Load
3.3.3. Vehicle Braking Force (Right Span)
3.3.4. Overall Heating (15 °C)
3.3.5. Negative Temperature Gradient
4. Sensitivity Analysis of CLS
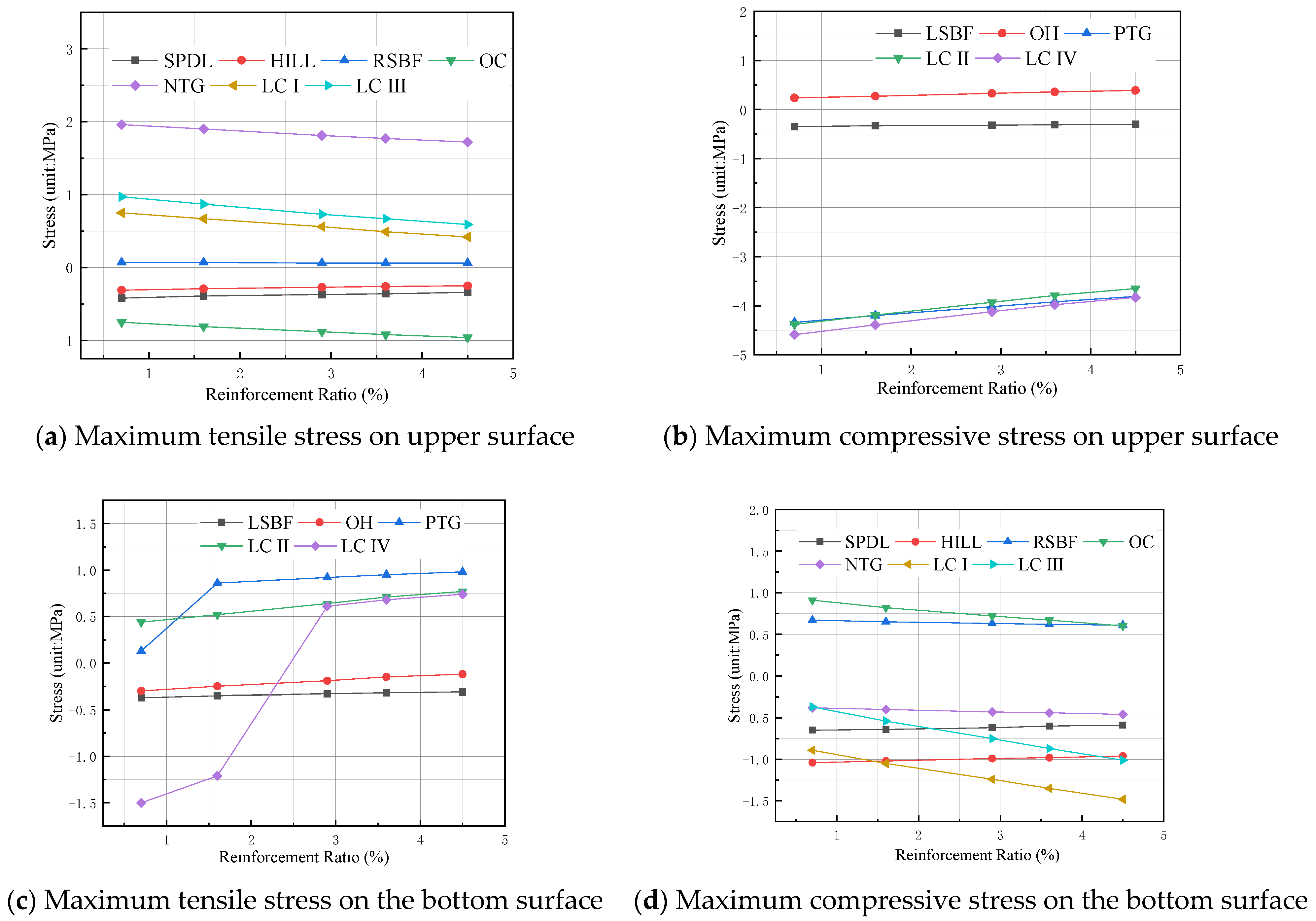
4.1. Reinforcement Ratio of CLS
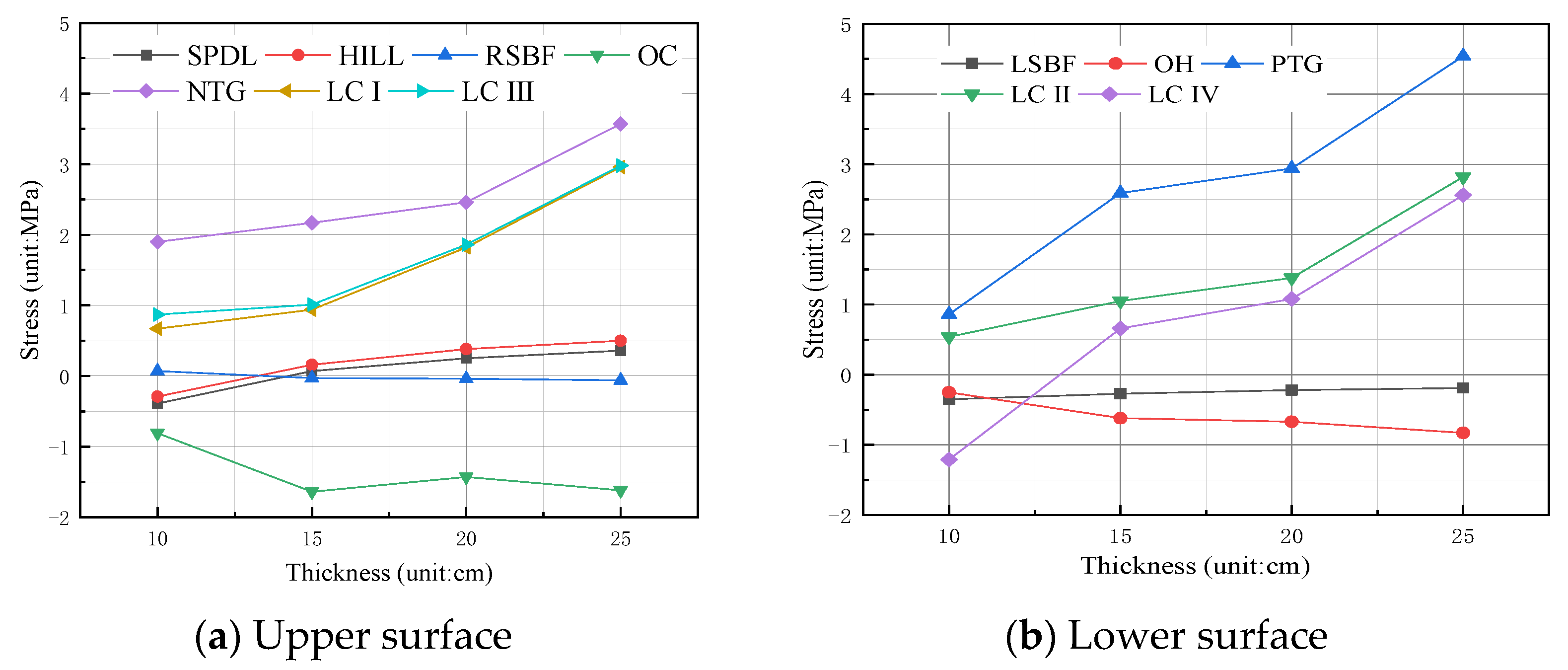
4.2. Pavement Thickness and Surface Material of CLS
4.3. Span of CLS
4.4. Comparison of Numerical and Theoretical Results
5. Concluding Remarks
- The design of the CLS enables the link-slab to form an isolation space with the main girder, which can release the tensile stress in the CLS. In addition, the curve structure weakens the thickness of the link-slab and reduces its bending, and tensile stiffness can better adapt to the deformation of the beam end structure and effectively solves the cracking problem of the link-slab.
- Since both CLS ends are consolidated with the bridge deck pavement, the CLS is simplified into a hingeless arch structure. According to the classical mechanical method, the hingeless arch simplified model is derived based on theoretical deduction. Formulas are derived for the maximum tension and compression stress on the upper and lower surfaces of the mid-span part of the link-slab. In addition, the rationality of the stress formula is verified using the FEM simulation.
- The sensitivity analysis showed that only changing the CLS section’s reinforcement ratio has a limited impact on the CLS. The CLS with asphalt concrete pavement is more reasonable to keep the structure consistent with the overall bridge deck pavement. Based on the combined concrete tensile and compression limits, the CLS thickness should be 15 cm to 20 cm, and its design span should be about 5% to 7.5% of the main beam length.
- The analysis of the refined model relies only on the two-span deck continuous T-shape simply supported girder on a straight bridge. However, this model has certain limitations regarding bridge type and bridge span diameter. Future research should address the force analysis of the inclined and curved bridges with different types and spans of arch deck continuous structure to fully verify the feasibility of the reinforced concrete arch deck. In addition, in the theoretical derivation and numerical analysis, only the force conditions of the continuous arch deck structure were calculated for the second stage constant load, highway class I lane load, vehicle braking force, overall temperature change, and temperature gradient. Future research should further analyze the effect of shrinkage, creep, and uneven settlement of the beam end on the continuous arch deck structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| total area of upper and lower edge steel bars, respectively | |
| area of the concrete section | |
| a, b | upper and lower surfaces of the CLS, respectively |
| B | calculated width of the section |
| b(H) | function of the width of the main beam section along the beam height |
| C | gap between adjacent main beams, and d is the distance between the arch foot and the support |
| CLS e | curved link-slab distance from the bridge support to the beam end |
| E1 | elastic modulus of the main beam at the left end |
| Fz | vehicle braking force |
| Fi | braking force of each abutment |
| h | height of the mid-span section |
| distances from the neutral axis of the upper and lower longitudinal bars to the bottom edge of the cross-section, respectively | |
| Concrete surface thickness design scheme of CLS | |
| h1, h2 | Concrete surface thickness and asphalt surface thickness design scheme of CLS, respectively |
| hc | distance from the neutral axis of the combined cross-section to the bottom of the cross-section |
| H | height of the main beam |
| Hc | distance from the center of the main beam section to the bottom of the beam |
| I, Ic | moments of inertia of the main beam section and the concrete section, respectively |
| li | distance between vehicle axle load Pi and the beam end A |
| moments of inertia for steel bar section at the upper and lower edges, respectively | |
| Ki | integrated thrust stiffness of the i-th bearing and abutment |
| l | CLS span length |
| L | span of the SSB |
| L1 | calculated span of the main beam |
| Pi | vehicle axle load |
| T(H) | temperature change function of the main beam section |
| ys | distance from the elastic center to the vault |
| α | linear expansion coefficient of concrete |
| ratio coefficient of the elastic modulus of steel bar to that of concrete | |
| Δ1c, Δ2c, Δ3c | angular, horizontal, and vertical displacements, respectively |
| ΔH | longitudinal displacement of the CLS due to the corner of the beam end |
| ΔL | horizontal displacement of CLS under braking force |
| Δt | difference between the calculated and ambient temperatures when the bridge is closed |
| σqa | sum of bending and axial tensile stresses under vehicle load |
| σqb | sum of bending and compressive stresses under vehicle load |
| σyka | tensile stress of the right-span vehicle under the braking force |
| σykb | tensile stress of the right-span vehicle under the braking force |
| σfwa | sum of bending and axial tensile stresses under a negative temperature gradient |
| σfwb | sum of bending and compressive stresses under a negative temperature gradient |
| σja | tensile stress under the overall temperature drop |
| σjb | tensile stress under the effect of overall cooling |
| σzwa | sum of bending and compressive stresses under a positive temperature gradient |
| σzwb | sum of bending and axial tensile stresses under a positive temperature gradient |
| σzka | compressive stress under braking force of the left-span vehicle |
| σzkb | compressive stress under the braking force of the left-span vehicle |
| σsa | compressive stress under overall temperature rise |
| σsb | compressive stress under overall heating |
| maximum tensile stress on the CLS upper surface | |
| maximum compressive stress on the CLS upper surface | |
| maximum tensile stress on the CLS lower surface | |
| maximum compressive stress on the CLS lower surface | |
| σs | stress produced by the axial force X2 |
| θ | angular displacement at the end of the main beam |
References
- Chen, B.C.; Zhuang, Y.Z.; Huang, F.Y.; Briseghella, B. Jointless Bridges, 2nd ed.; China Communication Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Matt, P. Status of segmental bridge construction in Europe. J.-Prestress. Concr. Inst. 1983, 28, 104–125. [Google Scholar] [CrossRef]
- Fan, L.C. Prestressed concrete highway bridges in China. Zeitschrift 1984, 12, 15–27. [Google Scholar] [CrossRef]
- Yao, H. Early damage and prevention of continuous expansion joint on reinforced concrete bridge deck. J. Ningbo Univ. (Sci. Technol. Ed.) 2005, 2, 261–263. (In Chinese) [Google Scholar]
- Su, L.; Yang, X.; Hu, Z.L. Analysis of hollow slab bridge diseases and remedial measures for continuous structure of bridge deck. Technol. Highw. Transp. 2005, 2, 100–103. (In Chinese) [Google Scholar]
- Caner, A.; Zia, P. Behavior and design of link slabs for jointless bridge decks. J.-Prestress. Concr. Inst. 1998, 43, 68–81. [Google Scholar] [CrossRef]
- Charuchaimontri, T.; Senjuntichai, T.; Limsuwan, E. Effect of lap reinforcement in link slabs of highway bridges. Eng. Struct. 2008, 30, 546–560. [Google Scholar] [CrossRef]
- Au, A.; Lam, C.; Au, J.; Tharmabala, B. Eliminating deck joints using debonded link slabs: Research and Field Tests in Ontario. J. Bridge Eng. 2013, 18, 768–778. [Google Scholar] [CrossRef]
- Chen, Q.; Abu-Farsakh, M. Mitigating the bridge end bump problem: A case study of a new approach slab system with geosynthetic reinforced soil foundation. Geotext. Geomembr. 2015, 44, 39–50. [Google Scholar] [CrossRef]
- Kim, Y.; Fischer, Y. Performance of bridge deck link slabs designed with ductile engineered cementitious composite. ACI Struct. J. 2004, 101, 792–801. [Google Scholar]
- Ahn, J.-H.; Yoon, J.-H.; Kim, J.-H. Evaluation of the behaviour of abutment-pile connection in integral abutment bridge. J. Constr. Steel Res. 2011, 67, 1134–1148. [Google Scholar] [CrossRef]
- Kendall, A.; Keoleian, G.A.; Helfand, G.E. Integrated life-cycle assessment and life-cycle cost analysis model for concrete bridge deck applications. J. Infrastruct. Syst. 2008, 14, 214–222. [Google Scholar] [CrossRef]
- Saber, A.; Aleti, A.R. Behavior of FRP link slabs in jointless bridge decks. Adv. Civ. Eng. 2012, 2012, 140–148. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Xie, X.; Wang, C.Q. Mechanical performance of arch-type continuous slab-deck on simply-suppoorted girder bridge. J. Zhejiang Univ. (Eng. Sci. Ed.) 2014, 48, 1049–1057. (In Chinese) [Google Scholar]
- Wang, C.Q.; Shen, Y.G.; Wang, G. Tests on the mechanical characteristics of the continuous structure of the hollow slab girder bridge deck. J. Zhejiang Univ. (Eng. Sci. Ed.) 2016, 50, 1438–1445. (In Chinese) [Google Scholar]
- Zhuang, Y.Z.; Xu, L.; Cheng, J.F. Theoretical analysis of the mechanical characteristics of the continuous structure of the simply supported girder bridge deck. China J. Highw. Transp. 2017, 30, 73–85. (In Chinese) [Google Scholar]
- Ministry of Transportation of the People’s Republic of China. Concrete Structure: Concrete Highway Bridge Design; Ministry of Transportation of the People’s Republic of China: Beijing, China, 2008; Volume 2. (In Chinese)
- Ministry of Transportation of the People’s Republic of China. General Code for Design of Highway Bridges and Culverts; JTG D60-2015; Ministry of Transportation of the People’s Republic of China: Beijing, China, 2008. (In Chinese)





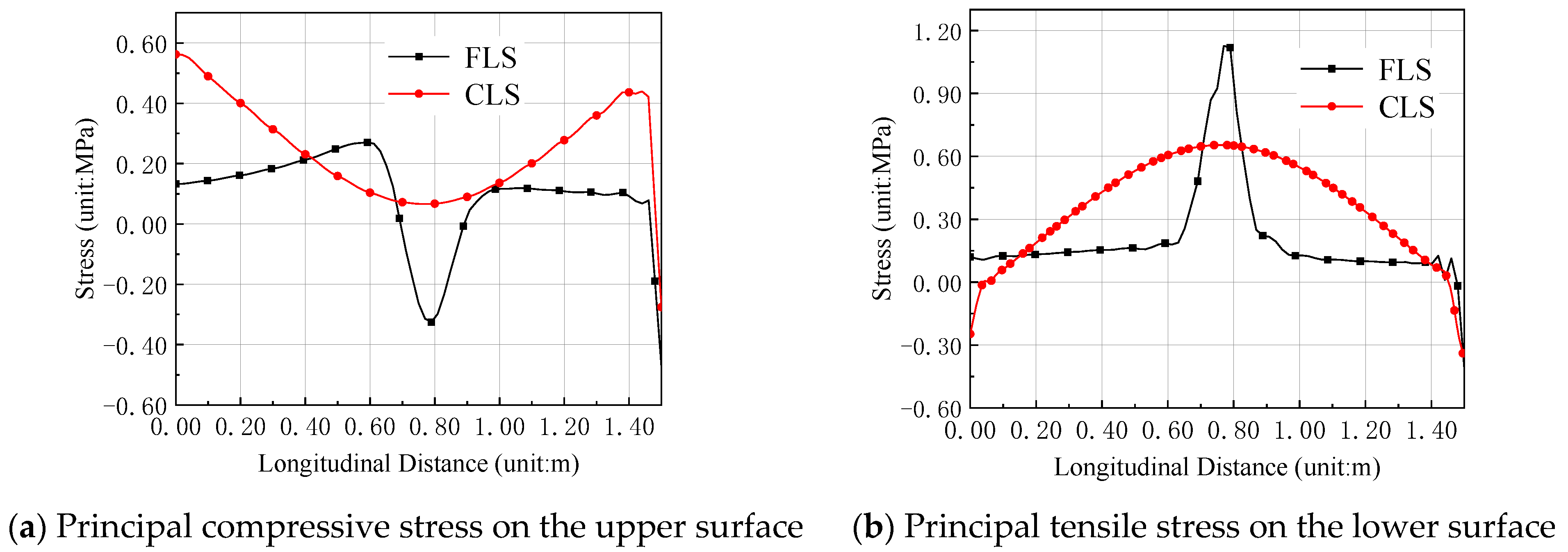
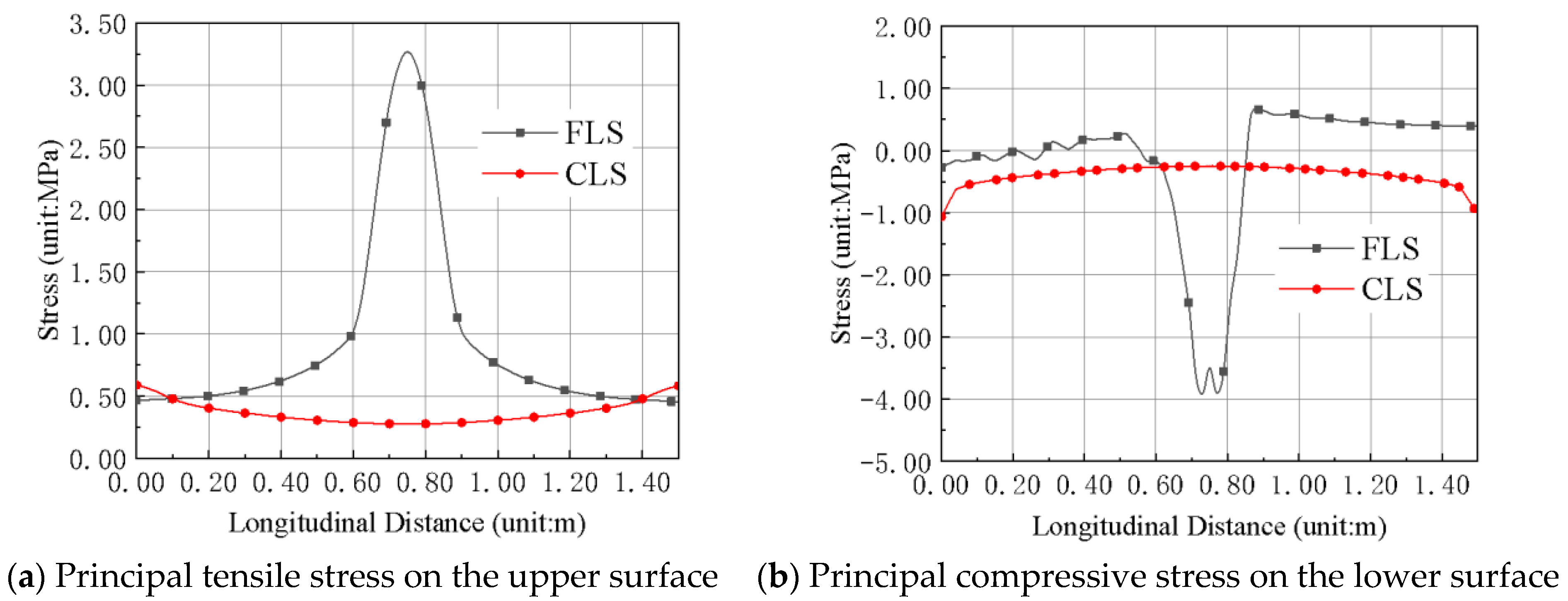
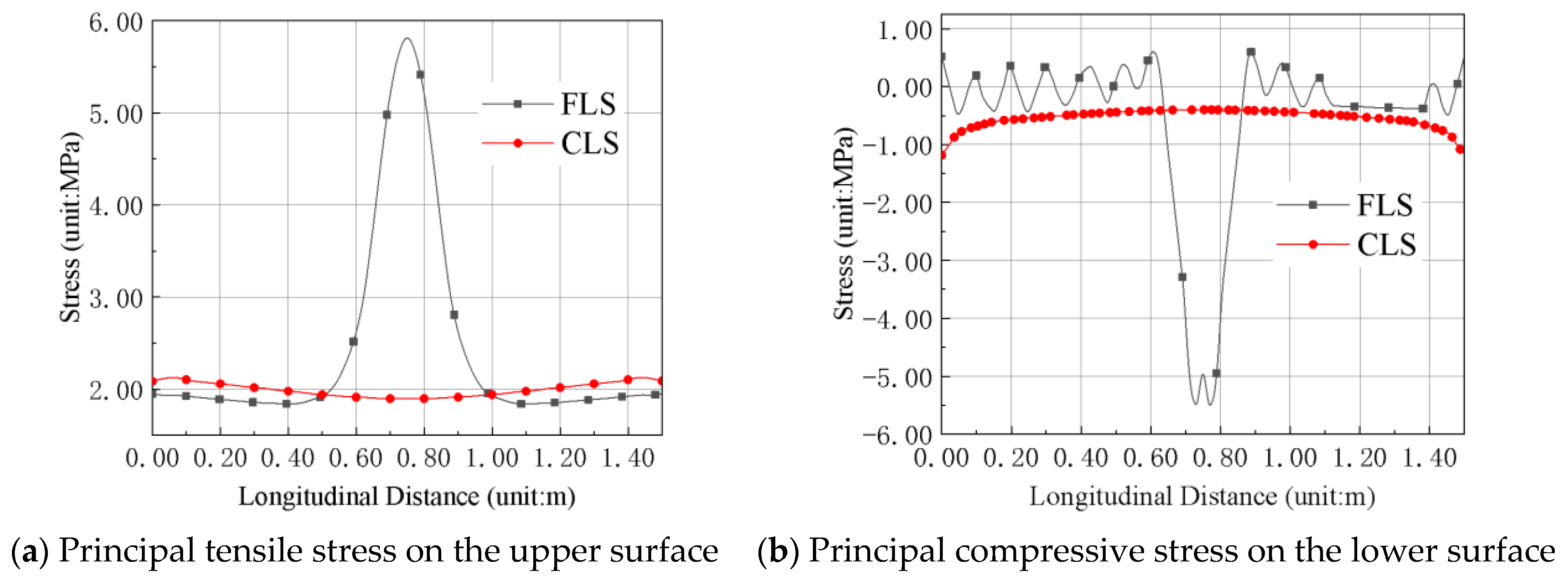


| CLS Position | Ultimate Stress | Stress Combination |
|---|---|---|
| Upper surface | Maximum tensile stress | |
| Maximum compressive stress | ||
| Lower surface | Maximum tensile stress | |
| Maximum compressive stress |
| Stressed Behavior | Stretching Behavior | ||
|---|---|---|---|
| Yield Stress (Pa) | Inelastic Strain | Yield Stress (Pa) | Cracking Strain |
| 17,361,738 | 0 | 2,528,660 | 0 |
| 24,006,564 | 0.000149 | 2,450,951 | 4.57 × 10−5 |
| 28,009,389 | 0.000332 | 2,309,468 | 5.99 × 10−5 |
| 29,779,435 | 0.00058 | 2,151,515 | 7.44 × 10−5 |
| 30,049,200 | 0.000765 | 1,996,698 | 8.89 × 10−5 |
| 28,944,664 | 0.001097 | 1,853,135 | 1.03 × 10−4 |
| 26,531,242 | 0.001466 | 1,723,432 | 1.17 × 10−4 |
| 23,785,962 | 0.001845 | 1,607,646 | 1.30 × 10−4 |
| 21,179,690 | 0.00222 | 1,504,758 | 1.43 × 10−4 |
| 18,877,058 | 0.002586 | 1,413,382 | 1.56 × 10−4 |
| 16,901,892 | 0.002943 | 1,332,091 | 1.68 × 10−4 |
| 15,224,890 | 0.00329 | 1,035,751 | 2.27 × 10−4 |
| 13,802,356 | 0.003631 | 852,075.2 | 2.82 × 10−4 |
| 12,591,282 | 0.003965 | 728,187.4 | 3.36 × 10−4 |
| 11,554,251 | 0.004293 | 639,087.3 | 3.88 × 10−4 |
| 10,660,294 | 0.004618 | 571,847.4 | 4.40 × 10−4 |
| 9,884,318 | 0.004939 | 519,203 | 4.92 × 10−4 |
| 9,206,146 | 0.005257 | 476,782.3 | 5.43 × 10−4 |
| 8,609,569 | 0.005573 | 441,803.6 | 5.94 × 10−4 |
| 6,721,561 | 0.006522 | 412,414.7 | 6.45 × 10−4 |
| 3,994,810 | 0.007495 | 387,334.8 | 6.95 × 10−4 |
| 406,918.3 | 0.008492 | 365,650 | 7.46 × 10−4 |
| 346,690.3 | 7.97 × 10−4 | ||
| 329,953.2 | 8.47 × 10−4 | ||
| 315,054.2 | 8.97 × 10−4 | ||
| 301,693.8 | 9.48 × 10−4 | ||
| 278,688.6 | 1.05 × 10−3 | ||
| 268,700.2 | 1.10 × 10−3 | ||
| Reinforcing Steel Type | Expansion Coefficient | Modulus of Elasticity (MPa) | Elastic Poisson’s Ratio | Plastic Modulus (MPa) | Plastic Poisson’s Ratio |
|---|---|---|---|---|---|
| Prestressed steel bars | 1.2 × 10−5 | 1.95 × 105 | 0.3 | 2.1 × 103 | 0 |
| Ordinary reinforcement steel | 1.2 × 10−5 | 2.0 × 105 | 0.3 | 2.3 × 103 | 0 |
| Numbering | Load Condition |
|---|---|
| 1 | Second Phase Dead Load |
| 2 | Highway I Lane Load |
| 3 | Vehicle Braking Force (Right Span) |
| 4 | Vehicle Braking Force (Left Span) |
| 5 | Overall Cooling 25 °C |
| 6 | Overall Heating 15 °C |
| 7 | Negative Temperature Gradient |
| 8 | Positive Temperature Gradient |
| Load Combination | Load Safety Factor a | ||||||
|---|---|---|---|---|---|---|---|
| DL | P | C&S | CL | TG | TR&F | VBF | |
| I | 1.2 | 1.0 | 1.0 | 1.4 | 0.8 × 1.4 | 0.8 × 1.4 | - b |
| Ⅱ | 1.2 | 1.0 | 1.0 | 0.8 × 1.4 | 1.4 | 1.4 | - b |
| Ⅲ | 1.2 | 1.0 | 1.0 | 1.4 | 0.8 × 1.4 | 0.8 × 1.4 | 0.8 × 1.7 |
| Ⅳ | 1.2 | 1.0 | 1.0 | 0.7 × 1.4 | 1.4 | 1.4 | 0.7 × 1.4 |
| Thickness Design Scheme | Concrete Surface Thickness h1 | Asphalt Surface Thickness h2 | Rise of Curve f | Number of Reinforcement Mesh Layer |
|---|---|---|---|---|
| 1 | 100 | 100 | 30 | 2 |
| 2 | 150 | 100 | 30 | 2 |
| 3 | 200 | 100 | 30 | 2 |
| 4 | 250 | 100 | 30 | 2 |
| 5 | 100 | 0 | 30 | 2 |
| 6 | 150 | 0 | 30 | 2 |
| 7 | 200 | 0 | 30 | 2 |
| 8 | 250 | 0 | 30 | 2 |
| Stress Location | Stress | Type | Stress Value (MPa) |
|---|---|---|---|
| Upper surface | Maximum tensile stress | Theoretical | 1.06 |
| Analysis | 0.97 | ||
| Maximum compressive stress | Theoretical | −4.50 | |
| Analysis | −4.14 | ||
| Lower surface | Maximum tensile stress | Theoretical | 0.86 |
| Analysis | 0.80 | ||
| Maximum compressive stress | Theoretical | −1.16 | |
| Analysis | −1.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Y.; Luo, S.; Easa, S.M.; Zhang, M.; Wang, C. Mechanical Performance of Curved Link-Slab of Simply Supported Bridge Beam. Appl. Sci. 2022, 12, 3344. https://doi.org/10.3390/app12073344
Zhuang Y, Luo S, Easa SM, Zhang M, Wang C. Mechanical Performance of Curved Link-Slab of Simply Supported Bridge Beam. Applied Sciences. 2022; 12(7):3344. https://doi.org/10.3390/app12073344
Chicago/Turabian StyleZhuang, Yizhou, Silv Luo, Said M. Easa, Meng Zhang, and Chengquan Wang. 2022. "Mechanical Performance of Curved Link-Slab of Simply Supported Bridge Beam" Applied Sciences 12, no. 7: 3344. https://doi.org/10.3390/app12073344
APA StyleZhuang, Y., Luo, S., Easa, S. M., Zhang, M., & Wang, C. (2022). Mechanical Performance of Curved Link-Slab of Simply Supported Bridge Beam. Applied Sciences, 12(7), 3344. https://doi.org/10.3390/app12073344







