Dynamical Pseudo-Random Number Generator Using Reinforcement Learning
Abstract
:1. Introduction
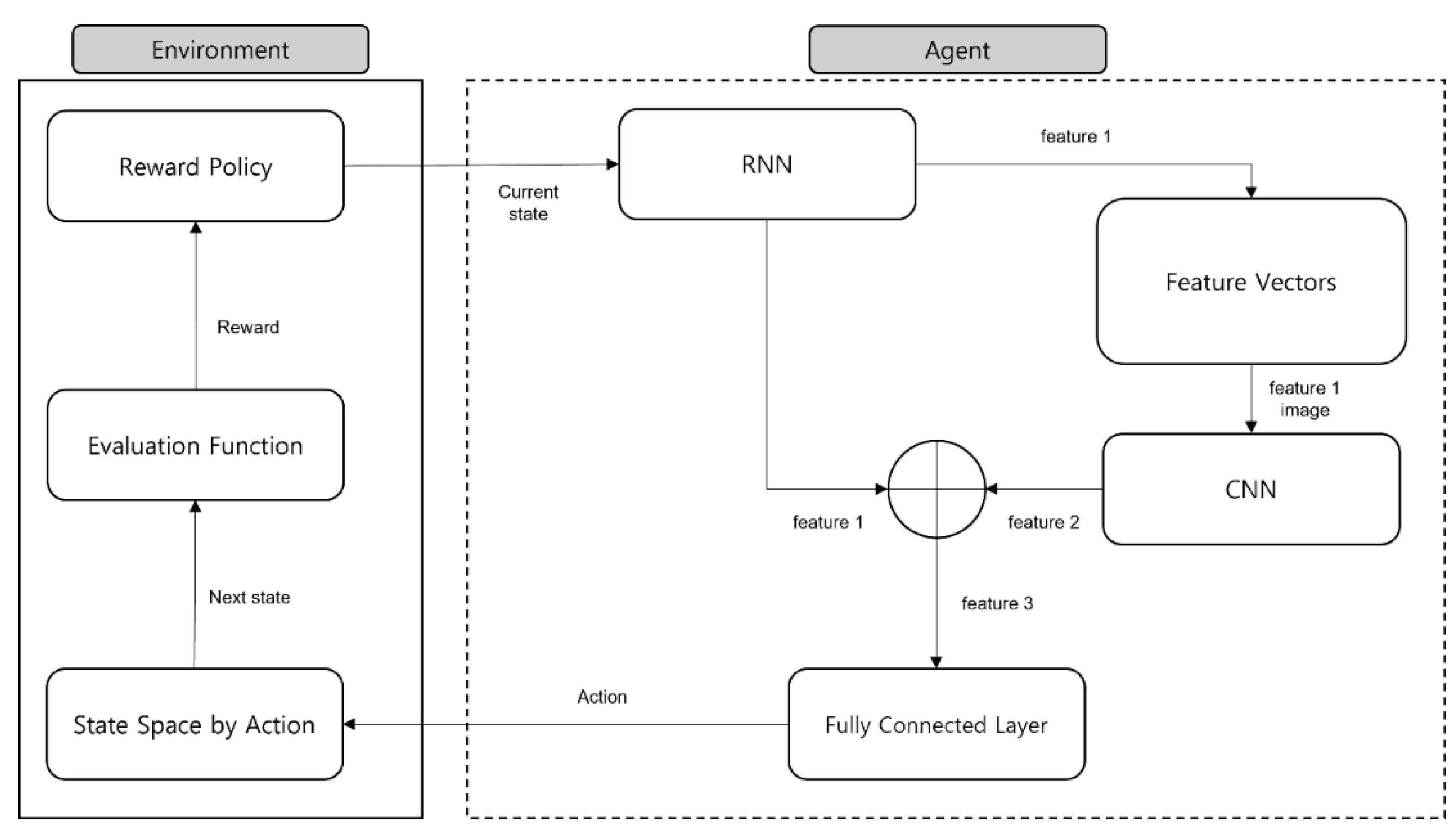
2. Proposed Method
2.1. Environment
2.2. Agent
3. Experiment and Results
3.1. Experiment Configuration
3.2. Average Total Reward with 800 Bits of Random Numbers
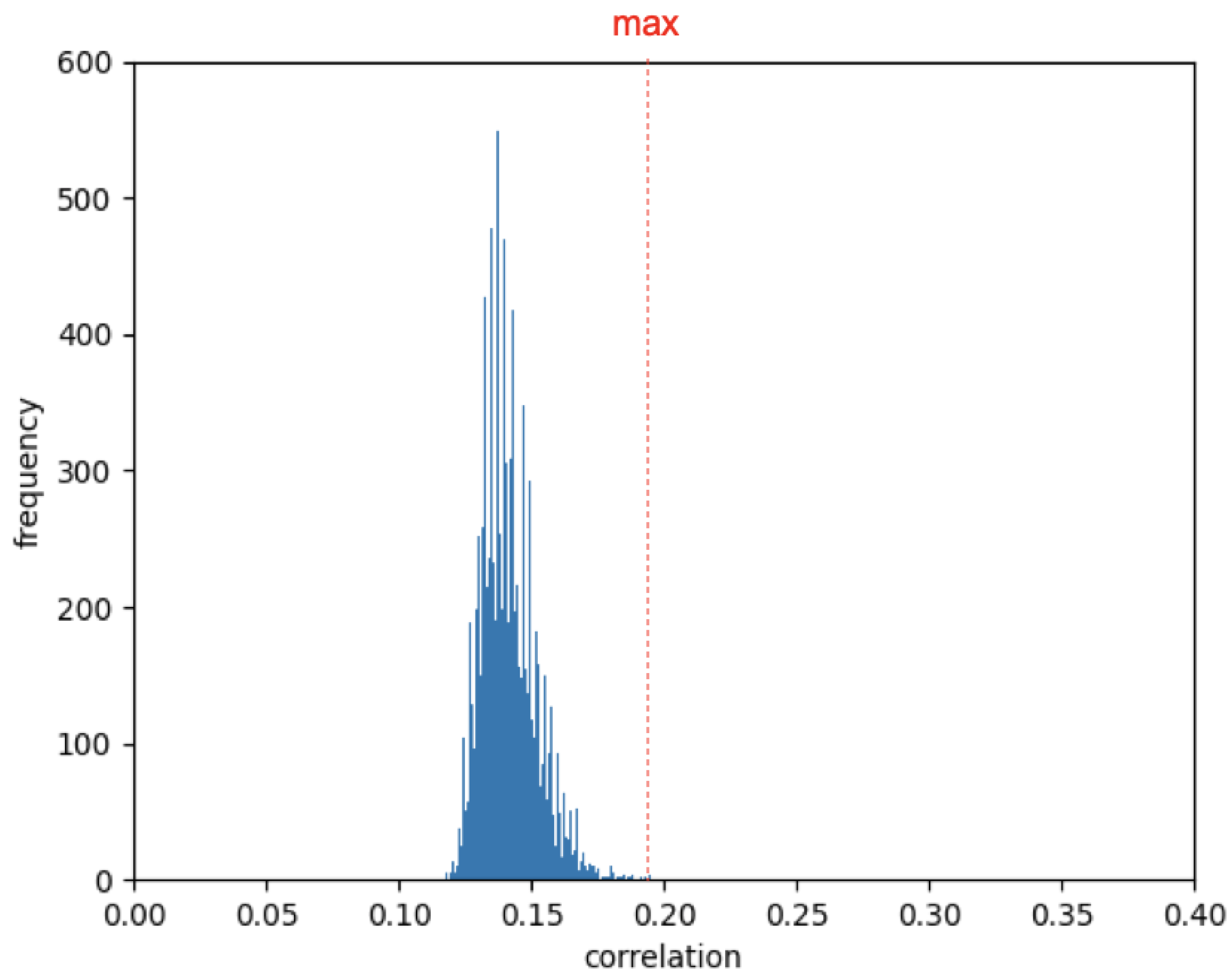
3.3. Different Sequences Even in the Same with 800 Bits of Random Numbers
4. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 124–134. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Barker, E.; Leigh, S.; Levenson, M.; Iii, L.E.B. A statistical test suite for random and pseudorandom number generators for cryptographic applications. NIST Spec. Publ. 2002, 800–822. [Google Scholar]
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum random number generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef] [Green Version]
- Barker, E.B.; Kelsey, J.M. Recommendation for Random Bit Generator (RBG) Constructions; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012.
- Barker, E.B. Guideline for using cryptographic standards in the federal government: Cryptographic mechanisms. NIST Spec. Publ. 2016, 800-175B, 1–82. [Google Scholar] [CrossRef]
- Pasqualini, L.; Parton, M. Pseudo random number generation: A reinforcement learning approach. Procedia Comput. Sci. 2020, 170, 1122–1127. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 1995. [Google Scholar]
- Pseudo Random Number Generation through Reinforcement Learning and Recurrent Neural Networks. Available online: https://github.com/InsaneMonster/pasqualini2020prngrl (accessed on 2 February 2022).
- V100 Tensor Core GPU. Available online: https://www.nvidia.com/en-us/data-center/v100/ (accessed on 2 February 2022).
- Haylock, B.; Peace, D.; Lenzini, F.; Weedbrook, C.; Lobino, M. Multiplexed quantum random number generation. Quantum 2019, 3, 141. [Google Scholar] [CrossRef]

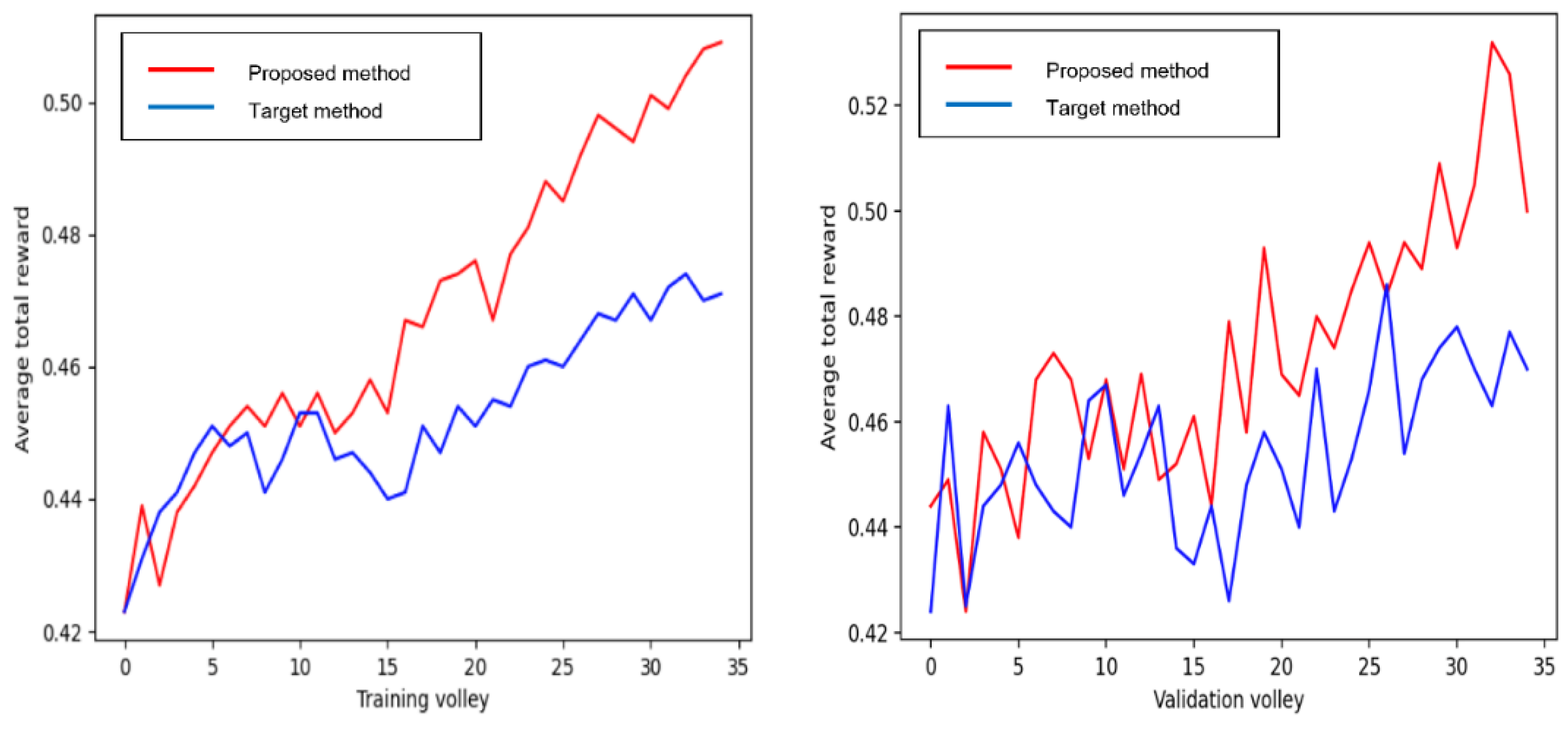
| Maximum Validation Value | Maximum Test Value | Average Test Value | |
|---|---|---|---|
| Proposed method | 0.532 | 0.522 | 0.509 |
| Target method | 0.486 | 0.486 | 0.470 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Kim, K.; Kim, K.; Nam, C. Dynamical Pseudo-Random Number Generator Using Reinforcement Learning. Appl. Sci. 2022, 12, 3377. https://doi.org/10.3390/app12073377
Park S, Kim K, Kim K, Nam C. Dynamical Pseudo-Random Number Generator Using Reinforcement Learning. Applied Sciences. 2022; 12(7):3377. https://doi.org/10.3390/app12073377
Chicago/Turabian StylePark, Sungju, Kyungmin Kim, Keunjin Kim, and Choonsung Nam. 2022. "Dynamical Pseudo-Random Number Generator Using Reinforcement Learning" Applied Sciences 12, no. 7: 3377. https://doi.org/10.3390/app12073377
APA StylePark, S., Kim, K., Kim, K., & Nam, C. (2022). Dynamical Pseudo-Random Number Generator Using Reinforcement Learning. Applied Sciences, 12(7), 3377. https://doi.org/10.3390/app12073377







