Ball Lightning as Plasma Vortexes: A Reinforcement of the Conjecture

Abstract

The idea that ball lightning is a plasma manifestation has been put forth by many authors. One of the major drawbacks of this approach concerns the stability of these structures. After showing the theoretical existence of pure rotating electromagnetic waves in equilibrium, we argue that these can reasonably provide a robust stabilizing scaffolding for the development of ball lightning phenomena.

1. Introduction

The observation of ball lightning has been documented for centuries. Despite all efforts, the development of a full theory remains a challenging subject, and this is particularly true because of the lack of reproducible data. Nevertheless, a series of more or less plausible hypotheses have been proposed in the last few decades, although a widely accepted explanation of this phenomenon has yet to come. Here is an incomplete list of (relatively recent) publications on the subject: [1,2,3,4,5,6,7,8,9]. An up-to-date review paper [10] provides a survey of the latest developments.

These spherical luminous objects of variable size are often associated with thunderstorms, though they look quite stable and last for a relatively long time. They may show up in multiple events in the course of a single electric storm [11]. Nowadays, the widespread use of cameras has increased the chance to catch an event, also from different viewpoints [12], offering support for a more in-depth analysis. Luminous plasmoids have been reproduced in the laboratory [13,14], sharing similarities with natural phenomena. An experiment attempting to generate glowing balls directly from natural thunderstorms was conducted in [15], through a complex apparatus involving the launch of rockets to trigger the events. Occurrences resembling ball lightning were actually observed in some circumstances.

The main features of ball lightning are reported in numerous publications. The balls show up with different appearances and move along rectilinear trajectories, sometimes varying their direction unpredictably. They display an averaged diameter of the order of decimeters and may last up to minutes. They carry a relevant amount of energy and their decay can happen in various fashions.

Several hypotheses have been proposed to explain the physical mechanism of such peculiar structures. Earlier suggestions that ball lightning is comprised of trapped waves of electromagnetic nature were provided in [16]. In particular, many theories try to establish connections with the properties of plasma. In this framework, for instance, ball lightning is regarded as a magnetostatic spherical plasmoid in equilibrium [17]. Stationary conditions for a thin ring have been investigated, for example in [18] for a conducting gas in a magnetic field. In [19], it is assumed that the cohesion inside the balls comes from photon exchange forces. The study of hydrostatic equilibrium for a plasma sphere in microwave fields is a subject developed in [20]. Estimates for the hydrodynamic equilibrium of a ball are provided in [21].

It is argued that the energy stored in plasma balls is far below the one seemingly involved in practice (see [22] and, e.g., the review papers [23,24]). The claims are based on an application of the virial theorem. Actually, explicit estimates of the forces responsible for the thermodynamic equilibrium show inconsistencies with reality. This theoretical restriction can, however, be circumvented, as proposed by several authors. We refer for instance to [25] and the references therein.

Although in this paper we still pursue the idea of a plasma in equilibrium, our approach is rather different from the usual ones. In fact, we are able to show the theoretical existence of electromagnetic rotating waves in toroid regions, which are stable according to magneto-hydrodynamics. This means that their pressure potential assumes zero normal gradient at the surface of the body. The vortexes can be also of Hill’s type, so that they look like spheres, though their topology is that of a ring. In atmosphere, these ensembles of stored energy mix with molecules, so becoming a real plasma. As we shall see, the stability properties of the new object do not descend from physical particles interactions, but from the gluing action of the electromagnetic part, which can hypothetically carry an arbitrary amount of energy.

2. Some Mathematical Facts

According to the classical Maxwell’s equations in vacuum, we have Ampère’s law with no current source term, together with Faraday’s law, namely:

$$\frac{\partial \mathbf{E}}{\partial t}=c^2\mathrm{curl}\mathbf{B}\frac{\partial \mathbf{B}}{\partial t}=-\mathrm{curl}\mathbf{E}$$

(1)

where we denoted by $\mathbf{E}$ the electric field and by $\mathbf{B}$ the magnetic one. Here c is the speed of light. We close the system of equations by requiring the divergences to be zero:

$$\mathrm{div}\mathbf{E}=0\mathrm{div}\mathbf{B}=0$$

(2)

We now show some vector displacements where the fields satisfy the whole set of equations and rotate about an axis. In this example, it is convenient to work in the cylindrical system of coordinates $(r,\varphi ,z)$, where we are able to carry out explicit computations [26,27,28]. In this way, we will be able to explicitly build objects defined on infinite cylinders. Nevertheless, similar constructions can be made for more general geometries (see in particular the review paper [29]), though computations become much more involved and necessitate a numerical approach. We address to Section 3 for more insight.

For an integer $k\ge 1$ and an arbitrary constant $\omega >0$, we define the vector and the scalar potentials:

$$\mathbf{A}=-\frac{1}{\omega }\left(J_{k+1}\left(\omega r\right)sin(c\omega t-k\varphi ),J_{k+1}\left(\omega r\right)cos(c\omega t-k\varphi ),0\right)$$

$$\mathsf{\Phi }=-\frac{1}{\omega }{J}_k\left(\omega r\right)cos(c\omega t-k\varphi )$$

(3)

where $0\le \varphi <2\pi$, $r\ge 0$ and any z. By $J_k$ we denoted the k-th Bessel function, which satisfies the equation:

$$J_k^{″}\left(x\right)+\frac{J_k^{\prime }\left(x\right)}{x}-\frac{k^2{J}_k\left(x\right)}{x^2}+J_k\left(x\right)=0$$

(4)

The above potentials fulfill the Lorenz gauge condition:

$$\mathrm{div}\mathbf{A}+\frac{1}{c}\frac{\partial \mathsf{\Phi }}{\partial t}=0$$

(5)

From the definitions:

$$\mathbf{B}=\frac{1}{c}\mathrm{curl}\mathbf{A}\mathbf{E}=-\frac{1}{c}\frac{\partial \mathbf{A}}{\partial t}-\nabla \mathsf{\Phi }$$

(6)

we get in straightforward way the electromagnetic fields, i.e.,

$$\mathbf{E}=\left(\frac{k{J}_k\left(\omega r\right)}{\omega r}cos(c\omega t-k\varphi ),J_k^{\prime }\left(\omega r\right)sin(c\omega t-k\varphi ),0\right)$$

$$\mathbf{B}=-\frac{1}{c}\left(0,0,J_k\left(\omega r\right)cos(c\omega t-k\varphi )\right)$$

(7)

In these computations we used that: $J_{k+1}^{\prime }\left(x\right)+(k+1)J_{k+1}\left(x\right)/x=J_k\left(x\right)$ and $J_k^{\prime }\left(x\right)-k{J}_k\left(x\right)/x=-J_{k+1}\left(x\right)$. We finally introduce the velocity vector field:

$$\mathbf{V}=\left(0,\frac{c\omega r}{k},0\right)$$

(8)

that actually corresponds to a rotation at constant angular velocity about the z axis.

By direct computation, we can prove a series of very interesting results. We first have:

$$\mathbf{E}\times \mathbf{V}=\left(0,0,c{J}_k\left(\omega r\right)cos(c\omega t-k\varphi )\right)=-c^2\mathbf{B}$$

(9)

This relation is equivalent to that obtainable from a set of rotating (with uniform angular velocity) physical charges, subject to a magnetic field lined up with the z-axis. Such an extension to pure electromagnetic fields is quite a remarkable feat.

Moreover, in the context of magneto-hydrodynamics [30], we have the induction equation:

$$\frac{\partial \mathbf{B}}{\partial t}=\left(0,0,\omega J_k\left(\omega r\right)sin(c\omega t-k\varphi )\right)=\mathrm{curl}(\mathbf{V}\times \mathbf{B})$$

(10)

which makes these type of solutions even more interesting.

Finally we also have Euler’s equation (corresponding to zero mass density):

$$\mathbf{B}\times \mathrm{curl}\mathbf{B}=\frac{1}{c^2}\mathbf{B}\times \frac{\partial \mathbf{E}}{\partial t}=-{\mu }_0\nabla P$$

$$=\frac{\omega }{c^2}\left(J_k\left(\omega r\right)J_k^{\prime }\left(\omega r\right){cos}^2(c\omega t-k\varphi ),k\frac{J_k^2\left(\omega r\right)}{\omega r}sin(c\omega t-k\varphi )cos(c\omega t-k\varphi ),0\right)$$

(11)

with the pressure given by:

$$P=-\frac{1}{2{\mu }_0{c}^2}{J}_k^2\left(\omega r\right){cos}^2(c\omega t-k\varphi )$$

(12)

This also follows from the relation $\mathbf{B}\times \mathrm{curl}\mathbf{B}=\frac{1}{2}\nabla {\left|\mathbf{B}\right|}^2-(\mathbf{B}·\nabla )\mathbf{B}$, by noting that, in our case, the last term vanishes.

Let ${\delta }_k>0$ be a zero of $J_k$ (the smallest one, for example). A meaningful consequence of the above relations is that, in correspondence of the value $r_0={\delta }_k/\omega$, the magnetic field is zero and the electric field is tangential to the cylinder of radius $r_0$ (see (7)). According to (11), the variation in time of $\mathbf{B}$ is zero. In addition, the pressure P and its gradient are also zero on the surface of the cylinder. Hydrodynamically, we are in a situation of equilibrium.

It is possible to add to the previous fields suitable stationary type solutions, and still retain most of the properties. This is the case for instance for the expressions (up to multiplicative constant):

$$\mathbf{E}=\left(\frac{r}{\omega },0,0\right)\mathbf{B}=\left(0,0,-\frac{r^2}{ck}\right)$$

(13)

Ampère’s law takes now the form:

$$\frac{\partial \mathbf{E}}{\partial t}=c^2\mathrm{curl}\mathbf{B}-\rho \mathbf{V}$$

(14)

where $\rho =\mathrm{div}\mathbf{E}=2/\omega$ is constant. Going through the computations, it is possible to show that the modified fields satisfy again (9) and (10). By adjusting P, (11) also holds. Note that, in the new displacement, the gradient of pressure P is not automatically zero at the boundary of a cylinder. On the other hand, we may also consider the following expression, deriving from Lorentz’s law:

$$\frac{D\mathbf{V}}{Dt}+\mu (\mathbf{E}+\mathbf{V}\times \mathbf{B})=\left(\frac{c^2{\omega }^{2}r}{k^2},0,0\right)+\mu \left(\frac{r}{\omega }-\frac{\omega r^3}{k^2},0,0\right)=-\nabla Q$$

(15)

where $\mu$ is a dimensional constant (charge divided by mass), $D\mathbf{V}/Dt=\partial \mathbf{V}/\partial t+(\nabla ·\mathbf{V})\mathbf{V}$, and Q is a potential. Note that the term on the right hand side of (15) can be actually written as a gradient (indeed the first component only depends on r). For $r_0={\delta }_k/\omega$, such a gradient is zero if we impose the relation:

$$\frac{c^2{\omega }^3}{k^2}+\mu \left(1-\frac{{\delta }_k^2}{k^2}\right)=0$$

(16)

Thus, for suitable choices of the parameters we should be able to find situations of electrodynamical equilibrium. The constant $\mu$ depends on the general context and may vary depending on circumstances.

3. Electromagnetic Balls

We expect that all the properties discussed so far still hold for toroid regions, although the proof becomes more challenging. In a very first rough approximation, a slim ring is realized by plying and reconnecting a tract of cylinder. Numerical results show that electromagnetic configurations behaving as vortex rings actually exist [29]. These vortexes can be also of Hill’s type, which means that the annular region can assume the shape of a ball where the inner hole is reduced to a segment. In the introduction, we mentioned a possible scenario where ball lightning is actually a manifestation deriving from vortexes. Note that the stability of these structures, in the framework of fluid dynamics, is a well established fact [31,32,33].

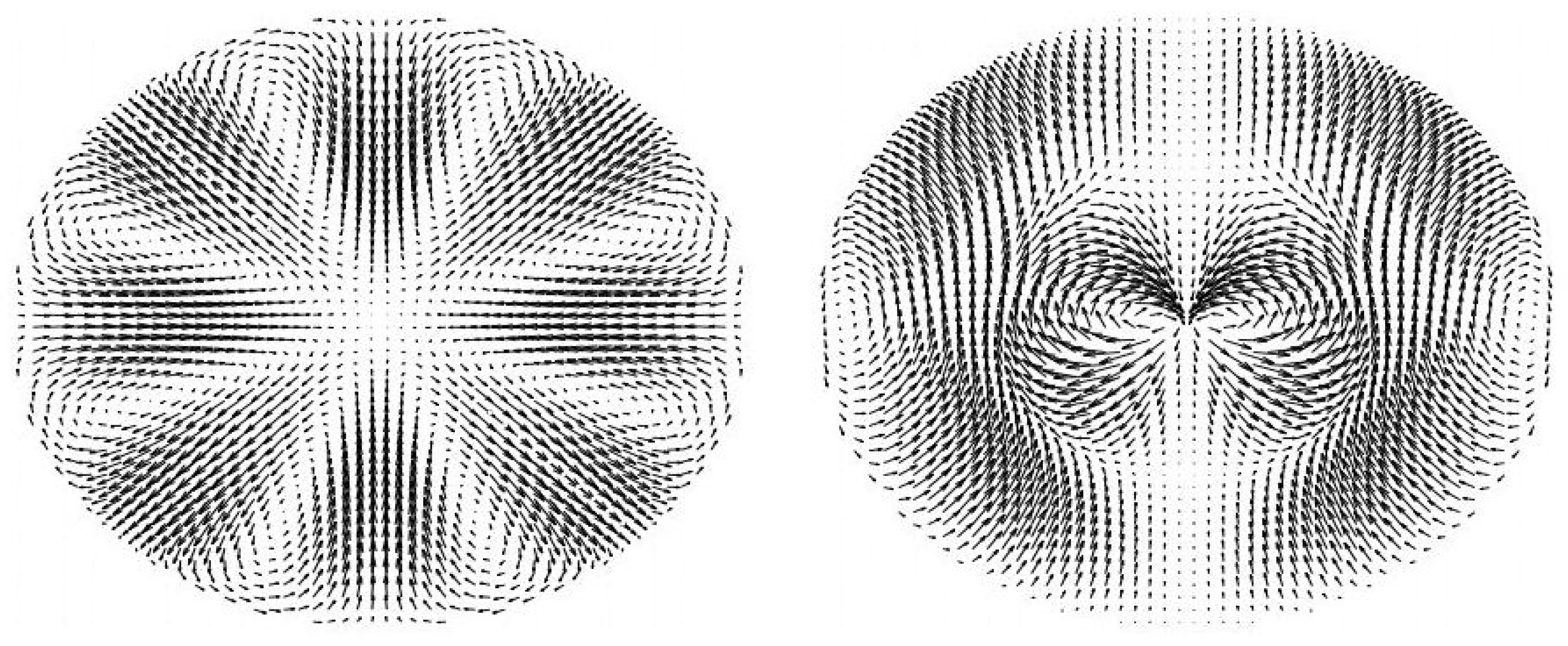
In [34], time-dependent electric fields distributed inside Hill’s type rings are proposed. Solutions are obtained in an ellipsoid by computing certain eigenfunctions of the 3D Laplace’s operator (Figure 1). For special geometrical configurations (for instance when the ratio between the height of the ellipsoid and its major diameter is about 0.7), the eigenvalues are coincident and this automatically allows for the determination of solutions solving the vector wave equation for both the electric and magnetic fields, subject to appropriate boundary constraints. Questions about the stability of these configurations are not addressed in [34]. Since these solutions were computed numerically, we cannot rigorously verify, as we did in the previous section, that they actually satisfy the induction and the Euler’s equations. In particular, the velocity field $\mathbf{V}$ is not clearly defined (reasonably, it should be time dependent). We are, however, confident that suitable stability properties also hold in such situations.

Thus, pure electromagnetic displacements that have the topology of a ring, but confined inside spherical environments, can theoretically exist. In principle, they may display stability properties without the intervention of massive particles. Indeed, we can expect that their magneto-hydrodynamical gradient of pressure assumes zero value on the surface. The size of the body is determined by a series of parameters, as for instance $\omega$ (the frequency of rotation of the signal) or k (the number of modes), as well as geometrical quantities, such as the ratio between the radii of the ring. The structure is self-assembled in order to become a resonant cavity of proper dimensions.

In air, these sources of stored energy mix up with molecules, producing a kind of plasma. Indeed, it has to be remarked that a plasma is naturally associated with rings [35,36]. As was also mentioned in the introduction, it is argued that plasma configurations tend to be strongly unstable without a proper confinement, and so they do not allow ball lightning phenomena to last for long. What we are claiming here is, however, new. We believe that annular lightning can exist in a vacuum. It is invisible however, like vortexes in a swimming pool created by the movement of an immersed body. These stable structures become visible when interacting with a gas (the air of the atmosphere for instance). They drag ions around circular patterns, giving birth to a semi-stable entity. At this point, they start emitting photons, thus losing energy with a relatively slow decay. All the previously consolidated studies concerning the emission spectra remain valid, as well as the considerations regarding possible chemical reactions. Actually, this work is not in contrast with the results that are already known. Note that particles do not necessarily travel quickly within the plasma, contrarily to what happens to the intermediate electromagnetic information which evolves at speeds comparable to that of light.

Referring again to [34], perfect spherical configurations of trapped electromagnetic waves in Hill’s vortexes were shown to exist. It was necessary however to suppose the presence of an annular core inside the sphere (the ratio between the minor radius of this ring and the radius of the embedding sphere was found to be about $1/20$). This geometrical setting would support the theory that plasma is subdivided in various layers of different nature (see [10], Section 2.1), though here the topology remains that of a doughnut. Roughly speaking, the inner part would be the stable one, and the outer part the glowing one.

Plasma is not just the flow of massive charged particles, but a configuration that includes their electromagnetic internal interactions, arranged to form a single entity. Theoretically, the operation of adding electromagnetic components of the type examined so far can be achieved by adjusting a bit the classical modeling equation. A suggestion in this direction is given in [37]. We are assuming here that the pure electromagnetic part can play a nontrivial role in driving and stabilizing the whole structure. Conversely, the movement of particles automatically influences their intermediate space, so generating further fields, and coupling the ingredients indissolubly. In the case of ball lightning, we may argue that the origin of the phenomenon is sustained by high-energetic electromagnetic waves assuming toroid shapes. Only lately, a mixture of waves and massive particles gives rise to the fireballs we actually see. This is true until the final decay, which happens when the internal forces definitely lose equilibrium and the body disappears in various forms of degeneracy. We review some properties of ball lightning in the framework of this idea.

The first observation is borrowed by classical fluid dynamics. In fact, due to viscosity, fluid vortex rings tend to shift naturally in the direction of the axis. This should be reasonably expected to be true also for plasma rings, so their rectilinear movement can acquire a practical explanation. Moreover, these structures are charged so that they may follow invisible electric patterns in the atmosphere, depending on some general conditions of the environment (such as the presence of electric power transmission lines, for instance).

The existence of a global charge can be mainly explained in two ways. The first is classical, i.e., there is a prevalence of positive ions in the plasma. Secondly, as suggested in the previous section, stationary fields such as those in (13) can be part of the pure electromagnetic component. Since this stable part is not made of particles, we cannot invoke repulsion effects caused by Coulomb’s law. Having $\rho$ constant, the object behaves as a rotating uniformly charged dielectric, thus generating a stationary magnetic field (distributed on closed lines inside the body). This exists in conjunction with the rotating wave. The total charge comes from averaging the contribution of the effective physical charges together with a density naturally present at the interior of the ball, probably inherited from the environment in the first instants of formation. The electromagnetic ring can originate from rectilinear lightning passing through an aperture, as happens for classical fluids. The real situation is actually rather complicated, since, as we said, it comes from a mix of various ingredients. Numerical computations should be possible, however. Preliminary estimates have been provided in [38] in order to establish a quantitative match with the intensity of charge actually attributed to ball lightning.

In terms of energy, we can sum up the contribution of the kinetic of the massive particles with that of the pure electrodynamical support. Regarding the second one, from the theoretical viewpoint, the intensity is in principle arbitrary (the displacement being the solution of the linear wave equation), so that it can be adjusted to match the values estimated for the real phenomenon. Remember that, in a vacuum, the electromagnetic energy per unit volume is equal to $\frac{1}{2}{ϵ}_0{\left(\right|\mathbf{E}|}^2+c^2{\left|\mathbf{B}\right|}^2)$, from which it should be possible to evaluate the intensity expected for the fields. For instance, an observed averaged energy of ${10}^8÷{10}^{10}$ J/m${}^2$ ([23,24,39]), relatively to a ball of radius of the order of ${10}^{-1}$ m, would bring us to internal magnetic field strengths as high as tens of Teslas.

Paradoxically, in our model, the presence of matter looks like a source of instability, rather than a condensing factor, being a great deal of the global energy carried by the pure electromagnetic component. As mentioned above, the closed lines of the magnetic field inside the ball are of remarkable strength. Matter is usually permeable to magnetism and this should be sufficient, on a first approximation, to explain how the lines of force tend to reconnect after the passage across a solid object. In fact, it is known from observations that ball lightning has the capability to penetrate through obstacles of various nature, sometimes without creating damages (see for instance the experimental results in [40]).

The influence of the environment forces the ball to dissipate energy, which is expelled through visible photons or radio waves. These last are supposed to carry a frequency which is inversely proportional to the diameter of the ball. The frequencies involved are of the order of some GHz when the size is of the order of decimeters. As a great deal of the energy is gone, the electrodynamical support does not guarantee stability any more. The positive ions tend to repel and the object is soon destroyed.

4. Conclusions

The conjecture that ball lightning is a ring-type plasma phenomenon is reinforced in this paper. It is necessary, however, to emphasize in the model the role of the pure electromagnetic component in which the ions are embedded. As shown with mathematical evidence, there are waves that by themselves assume rotating configurations in magneto-hydrodynamical equilibrium, and may provide for a significant stabilization effect on the whole object.