Multi-Agent Deep Q Network to Enhance the Reinforcement Learning for Delayed Reward System
Abstract
:1. Introduction
2. Related Works
2.1. Q-Learning
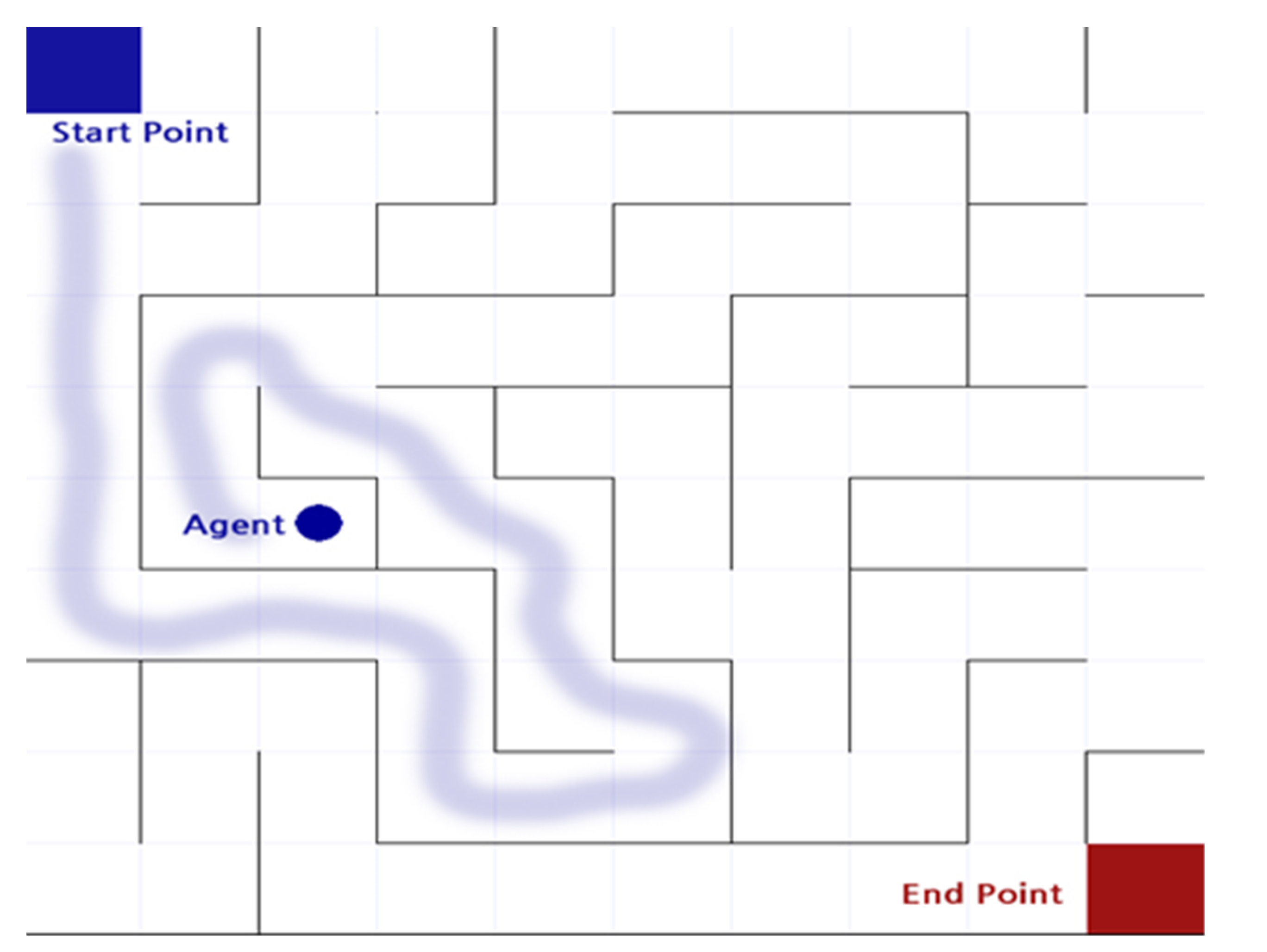
2.2. Maze Finding
 ) from the starting point of the maze to the ending point as shown in Figure 2. The actor can move in only four directions (up/down/left/right) by default, and there is an intuitive rule that walls cannot pass. In this process, the actor is considered to have the best performance in the order of the least amount of time or steps required to reach the destination. Even before reinforcement learning emerged and was studied, there were various studies to automatically perform maze finding [1]. In general, it is implemented in a way that heuristics are applied to recursive functions, etc., and rather than implementing a mechanism to find the destination all at once, the problem was solved by finding the optimal path and weight in repeated experiences [1].
) from the starting point of the maze to the ending point as shown in Figure 2. The actor can move in only four directions (up/down/left/right) by default, and there is an intuitive rule that walls cannot pass. In this process, the actor is considered to have the best performance in the order of the least amount of time or steps required to reach the destination. Even before reinforcement learning emerged and was studied, there were various studies to automatically perform maze finding [1]. In general, it is implemented in a way that heuristics are applied to recursive functions, etc., and rather than implementing a mechanism to find the destination all at once, the problem was solved by finding the optimal path and weight in repeated experiences [1].2.3. The Ping-Pong Game
 ) through the movement of the actor’s paddle (
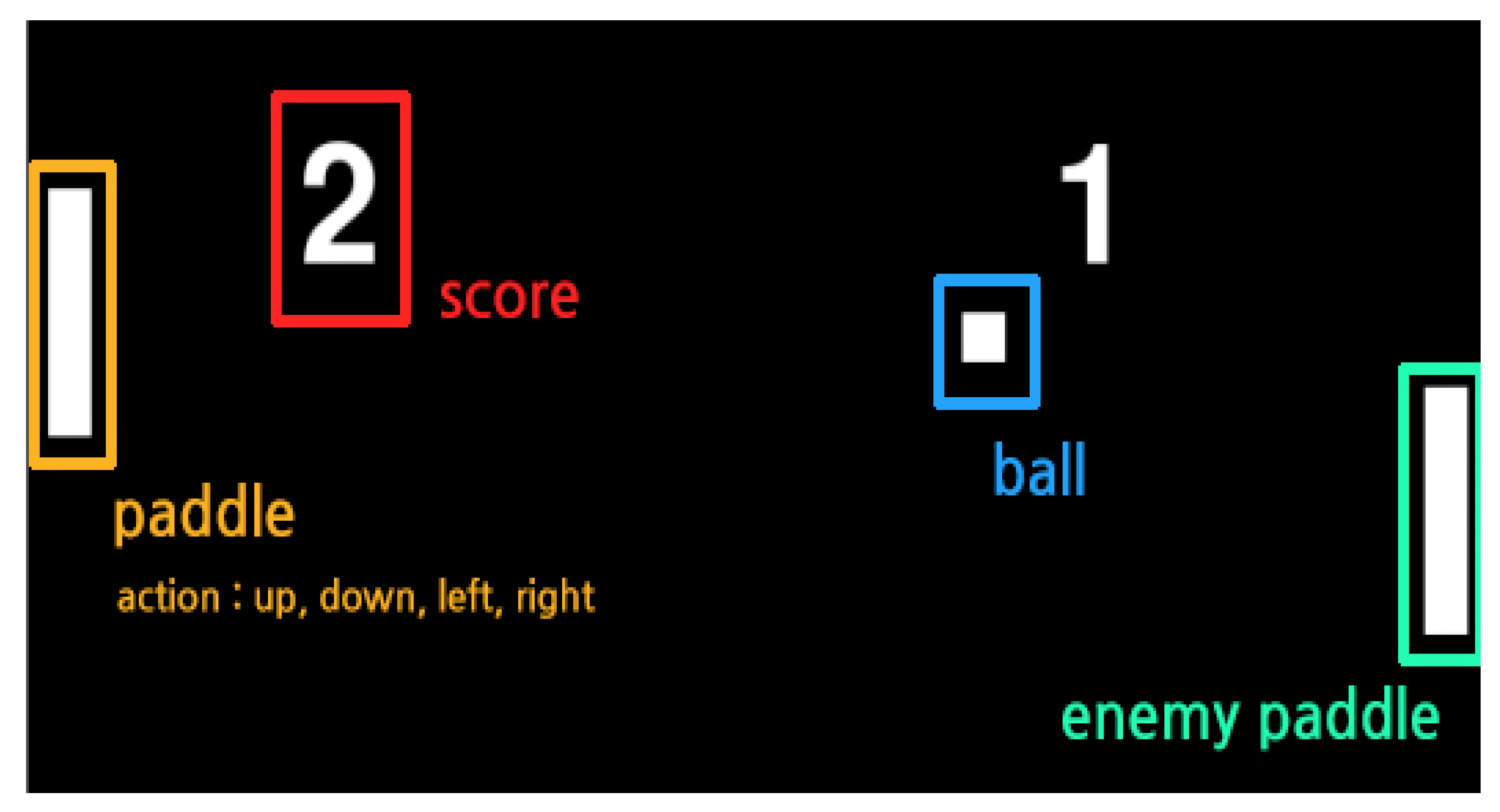
) through the movement of the actor’s paddle (  ), and the ball is sent to a space where the ball cannot be received by the opponent’s paddle as shown in Figure 3. The actor can basically perform one of five actions (top/bottom/left/right/nothing), and the movement is limited to a movement of up/down. The left/right action can be triggered when the ball hits the paddle and pushes the ball strongly in the opponent’s direction. The ball advances through the laws of physics when hitting and is refracted when it touches the top/bottom of the game screen. Therefore, it is important for the actor to strike the ball in a position that the opponent cannot receive while considering these laws of physics. Table 2 shows the rules of the ping-pong game. In applying reinforcement learning to the ping-pong game, both the position of the actor paddle, the position of the ball, and the position of the opponent’s paddle should be considered. It is predicted that, when various objects move like this, the value of the previously performed learning data may be lowered according to the movement of the object. To implement and experiment with a reinforcement learning model with such a direction we implemented using Python, and the opponent’s paddle operates by the rule-based algorithm with heuristics. Therefore, the content of performance evaluation means a confrontation structure between reinforcement learning and rule-based heuristics.
), and the ball is sent to a space where the ball cannot be received by the opponent’s paddle as shown in Figure 3. The actor can basically perform one of five actions (top/bottom/left/right/nothing), and the movement is limited to a movement of up/down. The left/right action can be triggered when the ball hits the paddle and pushes the ball strongly in the opponent’s direction. The ball advances through the laws of physics when hitting and is refracted when it touches the top/bottom of the game screen. Therefore, it is important for the actor to strike the ball in a position that the opponent cannot receive while considering these laws of physics. Table 2 shows the rules of the ping-pong game. In applying reinforcement learning to the ping-pong game, both the position of the actor paddle, the position of the ball, and the position of the opponent’s paddle should be considered. It is predicted that, when various objects move like this, the value of the previously performed learning data may be lowered according to the movement of the object. To implement and experiment with a reinforcement learning model with such a direction we implemented using Python, and the opponent’s paddle operates by the rule-based algorithm with heuristics. Therefore, the content of performance evaluation means a confrontation structure between reinforcement learning and rule-based heuristics.2.4. Multi-Agent System and Reinforcement Learning
3. Proposed Multi-Agent N-DQN
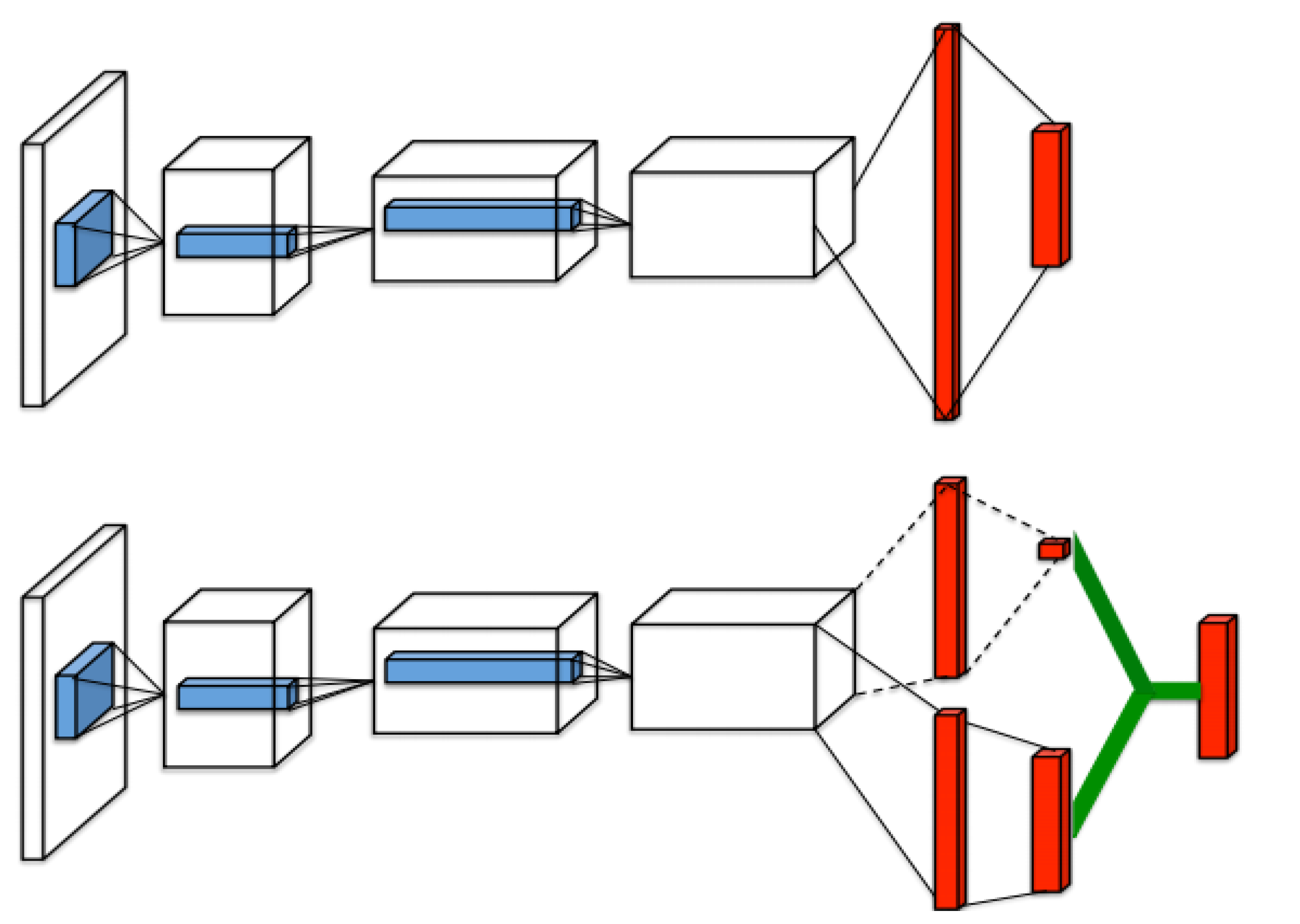
3.1. Proposed Architecture
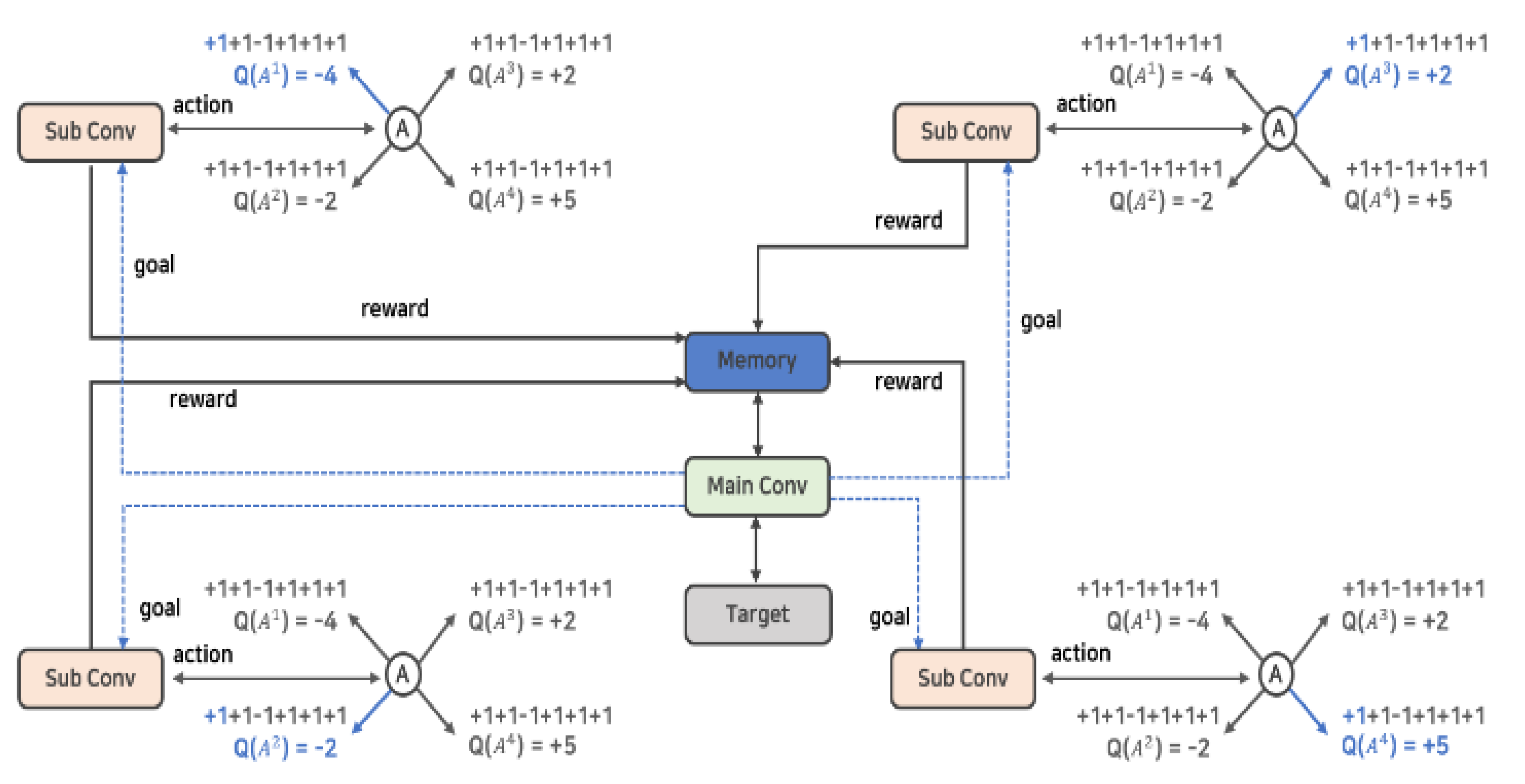
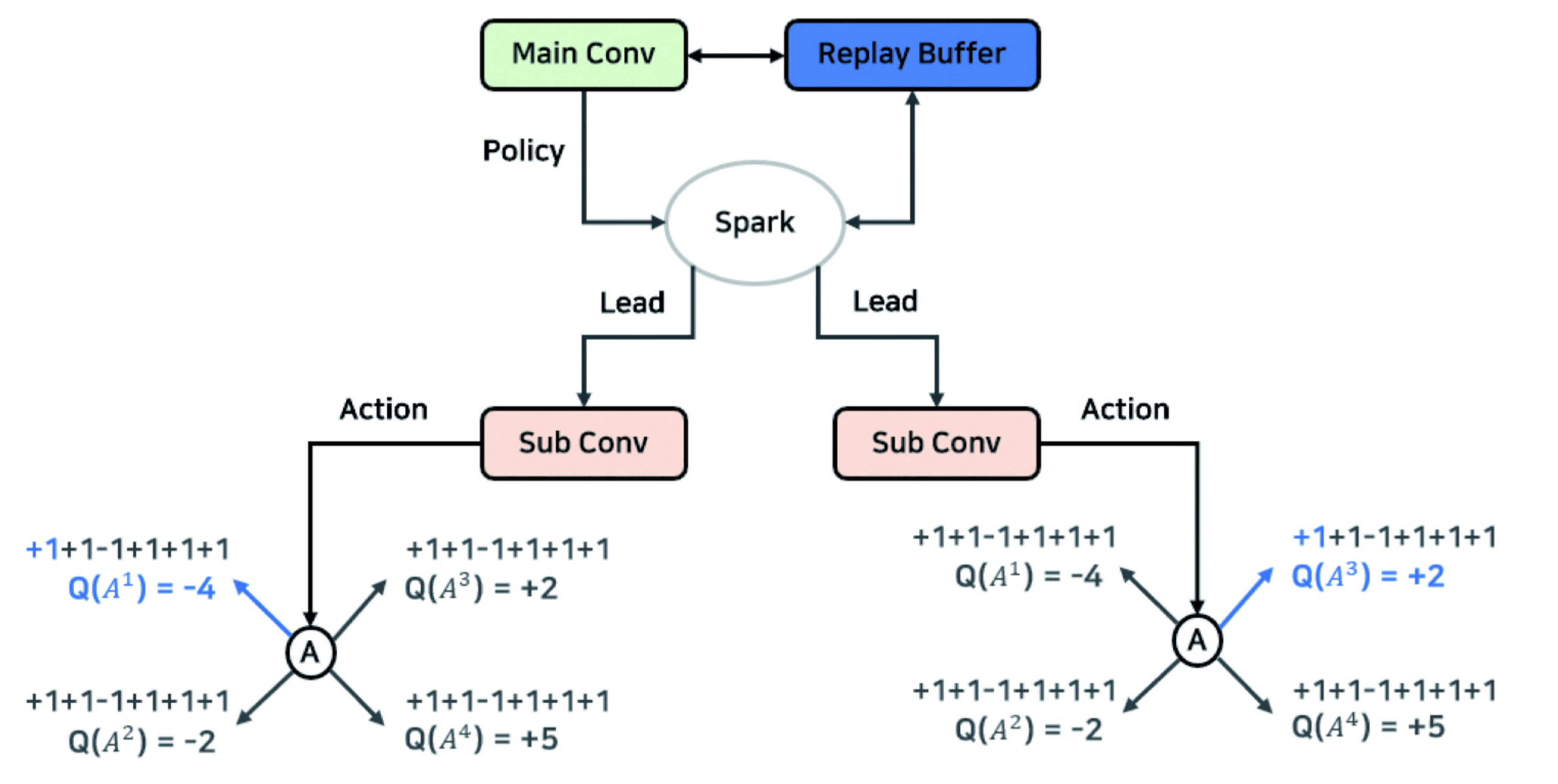
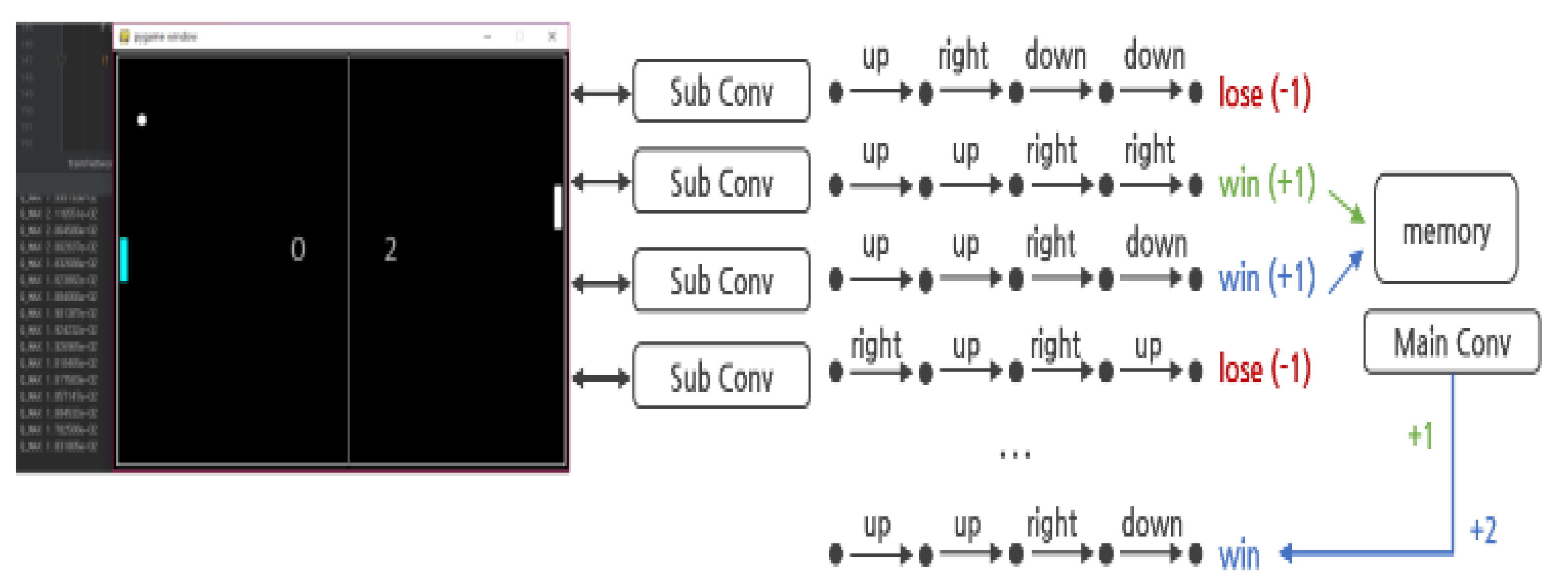
 ) in parallel and has a kind of HDQN-like architecture. In addition, by establishing a policy to control action and learning, each action of several neural networks is controlled. The reward and experience according to the action are shared in one memory, and the best data is selected and prioritized for learning.
) in parallel and has a kind of HDQN-like architecture. In addition, by establishing a policy to control action and learning, each action of several neural networks is controlled. The reward and experience according to the action are shared in one memory, and the best data is selected and prioritized for learning.3.1.1. Hierarchization and Policy
 ) can perform four types of actions. At this time, the sublayer is implemented to perform the action that has not been performed before and without overlapping with other sublayers’ actions by the policy established by the main layer (
) can perform four types of actions. At this time, the sublayer is implemented to perform the action that has not been performed before and without overlapping with other sublayers’ actions by the policy established by the main layer (  ). This implementation policy is to increase learning efficiency by efficiently creating episodes in contrast to the existing reinforcement learning algorithms, and it can be implemented as in Algorithm 1.
). This implementation policy is to increase learning efficiency by efficiently creating episodes in contrast to the existing reinforcement learning algorithms, and it can be implemented as in Algorithm 1. ) takes a non-overlapping action through the history queue H created by the main layer (
) takes a non-overlapping action through the history queue H created by the main layer (  ). History queue H stores state and action records for all episodes stored in the existing replay buffer. Therefore, each sublayer can verify the redundancy of its current target action by checking the history queue H. The existing Q-Learning and DQN algorithms perform random actions to acquire learning data that has not been performed [3]. This is implemented as a process (e-greedy) in which a random number is generated, an action is performed when it is lower
than the threshold, and the process of gradually lowering the value of the threshold is repeatedly performed. Because these procedures rely on random probabilities, their clarity and efficiency are poor [6]. However, multi agent N-DQN does not rely only on random probability through Algorithm 1, but it performs verification and by actively intervening in the creation of learning data through policy, the efficiency of learning can be increased.
). History queue H stores state and action records for all episodes stored in the existing replay buffer. Therefore, each sublayer can verify the redundancy of its current target action by checking the history queue H. The existing Q-Learning and DQN algorithms perform random actions to acquire learning data that has not been performed [3]. This is implemented as a process (e-greedy) in which a random number is generated, an action is performed when it is lower
than the threshold, and the process of gradually lowering the value of the threshold is repeatedly performed. Because these procedures rely on random probabilities, their clarity and efficiency are poor [6]. However, multi agent N-DQN does not rely only on random probability through Algorithm 1, but it performs verification and by actively intervening in the creation of learning data through policy, the efficiency of learning can be increased.| Algorithm 1: Action Control Policy | |
| 1 | Input: number of sublayer N, current states, target action a |
| 2 | Initialize: shared replay memory D to size N ∗ n |
| 3 | Initialize: N action-value function Q with random weights |
| 4 | Initialize: episode history queue H to size N ∗ n |
| 5 | Copy data to H from D For 1, N do For state in H do if state = s then For action in state.action do if action != a then do action else break else do action |
| Algorithm 2: Reward Policy | |
| 1 | Input: current state s, immediate reward r |
| 2 | Initialize: list of lethal state L, dict of reward P |
| 3 | Initialize: the number of reward point K After do action Before return immediate reward r |
| 4 | For k in range (0, K) if s = L[k] then return r += P[L[k]] else return r |
3.1.2. Parallel Processing and Memory Sharing
 ) obtains the value of n number of action-value function Q and stores the result in the shared replay buffer. As such, the learning data shared by several actors enables collecting data faster than a general reinforcement learning algorithm.
) obtains the value of n number of action-value function Q and stores the result in the shared replay buffer. As such, the learning data shared by several actors enables collecting data faster than a general reinforcement learning algorithm.
| Algorithm 3: N-DQN Experience Sharing | |
| 1 | Procedure: training |
| 2 | Initialize: shared replay memory D to size N ∗ n |
| 3 | Initialize: N action-value function Q with random weights |
| 4 | Loop: episode = 1, M do Initialize state s1 For t = 1, T do For each Qn do With probability ϵ select random action at otherwise select at = argmaxa Qn(st, a; θi) Execute action at in emulator and observe rt and st+1 Store transition (st, at, rt, st+1) in D End For Sample a minibatch of transitions (sj, aj, rj, sj+1) from D Set yj: = rj For terminal sj+1 rj + γmax_(a^′) Qn(sj+1, a′; θi) For non-terminal sj+1 Perform a gradient step on (yj − Qn(sj, aj; θi))2 with respect to θ end For |
| 5 | End Loop |
3.1.3. Training Policy
| Algorithm 4: Prioritized Experience Replay | |
| 1. | Input: minibatch k, step-size n, replay period K and size N, exponents α and β, budget T and N action-value function Q |
| 2. | Initialize replay memory H = θ, Δ = 0, = 1 |
| 3. | Observe and choose ~ () |
| 4. | for t = 1 to T do Observe for p = 1 to N do Store transition ( in H with maximal priority = end for if t then for j = 1 to k do Sample transition j ~ P(j) = Compute sampling weight Compute TD-error = Update transition priority Gather weight-change Δ Δ + end for Update weights Δ, reset Δ = 0 From time to time copy weights into target NN end if for p = 1 to N do Choose action ∼ () end for end for |
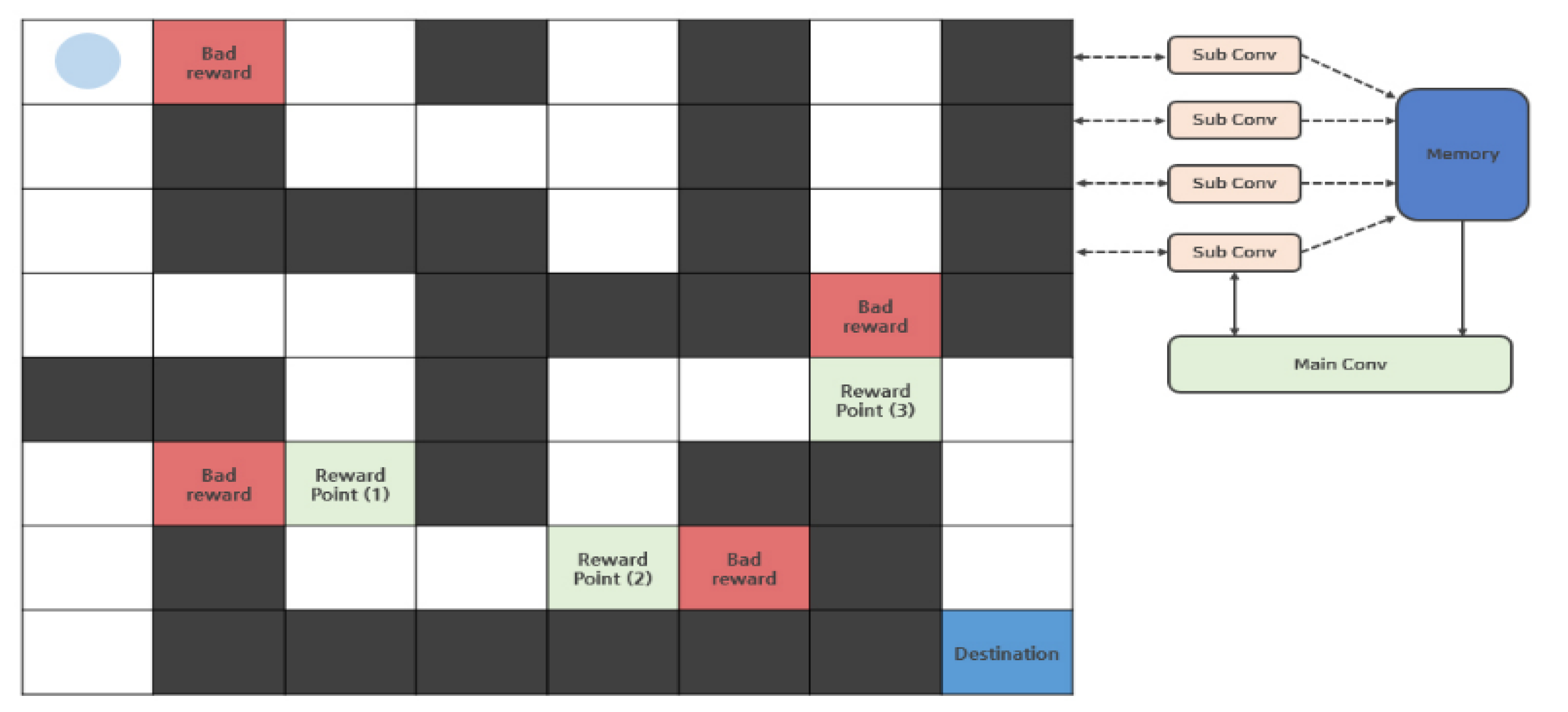
4. Evaluation Results and Analysis with Maze Finding
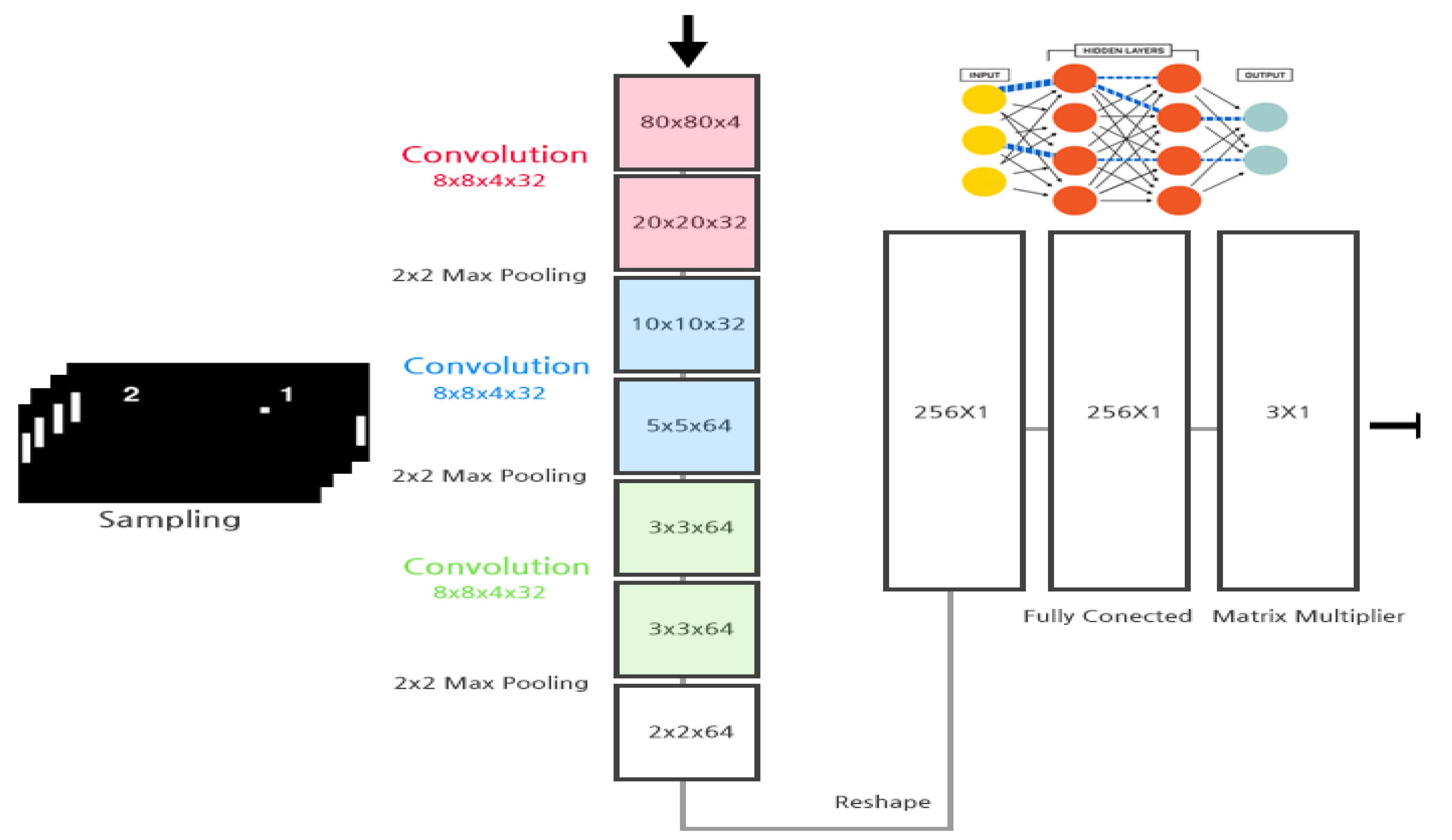
4.1. Environment
4.2. Training Features
4.3. Implement and Performance Evaluation
4.3.1. N-DQN-Based Implementation
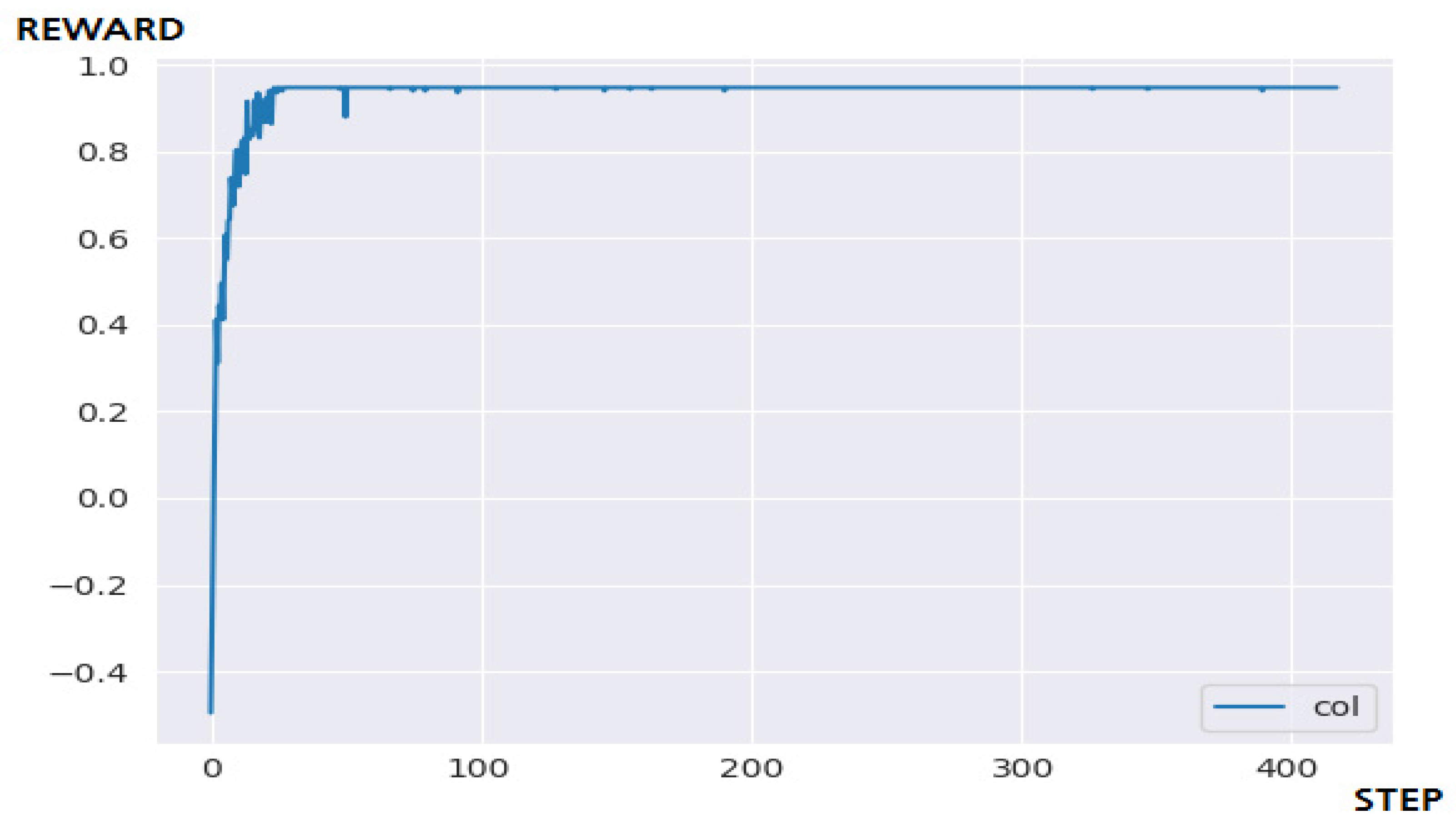
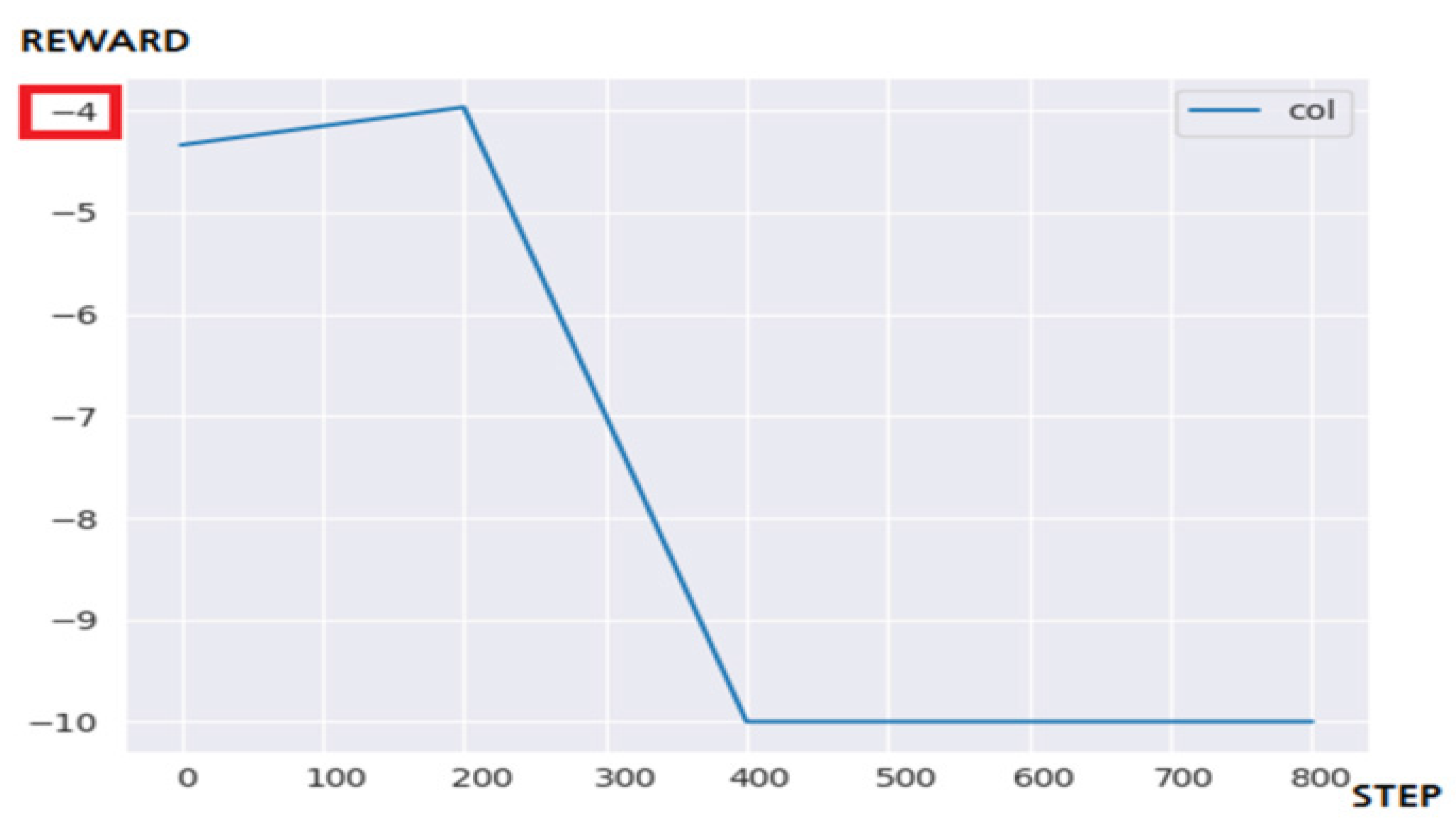
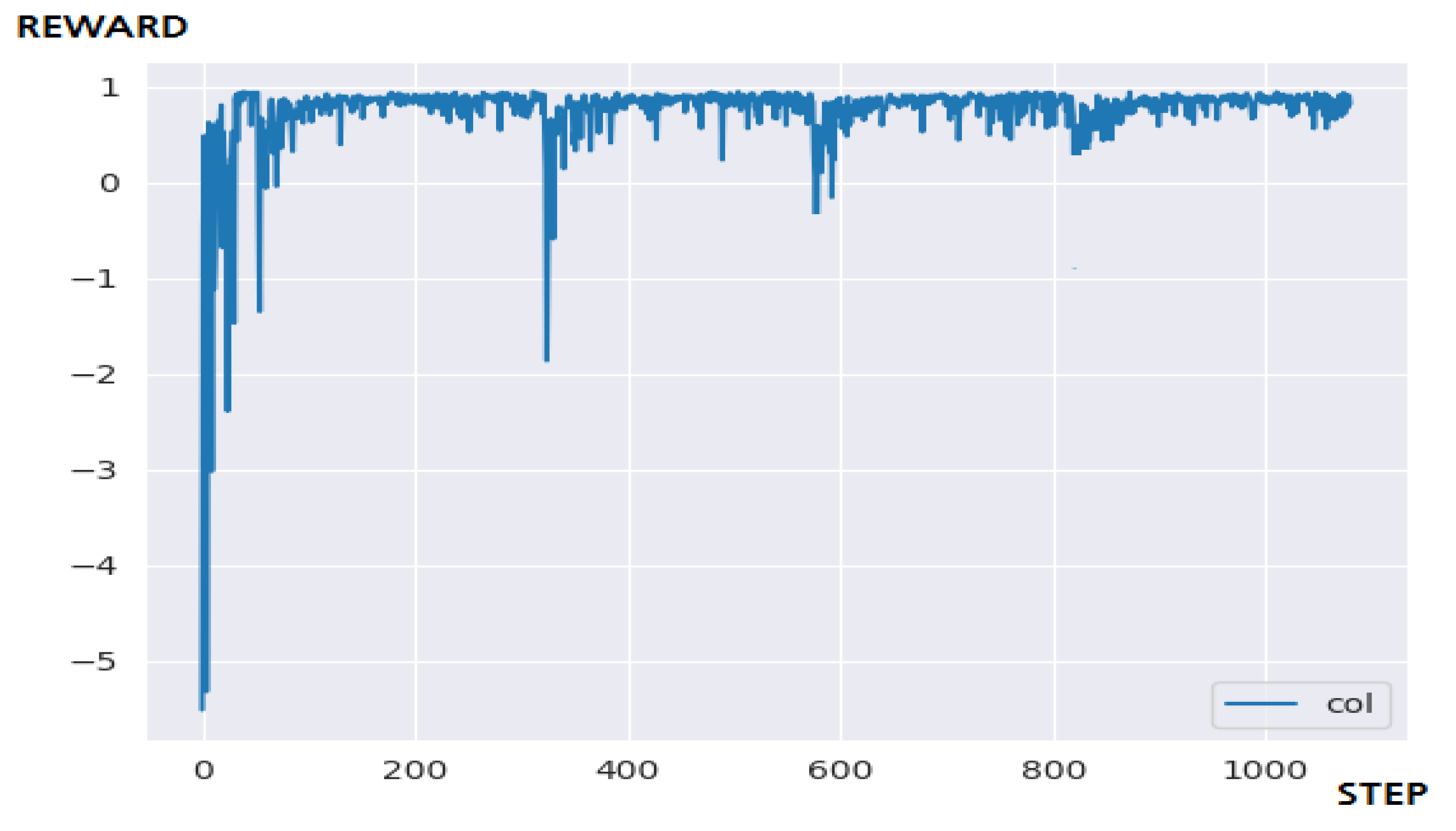
4.3.2. Performance Evaluation and Discussion
5. Evaluation Results and Analysis with Ping-Pong
5.1. Environment
5.2. Training Features
5.3. Implement and Performance Evaluation
5.3.1. N-DQN-Based Implementation
| Algorithm 5: PING-PONG Game’s DQN Training | |
| 1. | Procedure: training |
| 2. | Initialize: replay memory D to size N |
| 3. | Initialize: action-value function Q with random weights |
| 4. | Loop: episode = 1, M do Initialize state s_1 for t = 1, T do With probability ϵ select random action a_t otherwise select a_t = argmax_a Q(s_t,a; θ_i) Execute action a_t in emulator and observe r_t and s_(t + 1) Store transition (s_t,a_t,r_t,s_(t + 1)) in D Sample a minibatch of transitions (s_j,a_j,r_j,s_(j + 1)) from D Set y_j:= r_j for terminal s_(j + 1) r_j + γ*max_(a^′ ) Q(s_(j + 1),a′; θ_i) for non-terminal s_(j + 1) Perform a gradient step on (y_j-Q(s_j,_j; θ_i))^2 with respect to θ end for |
| 5. | End Loop |
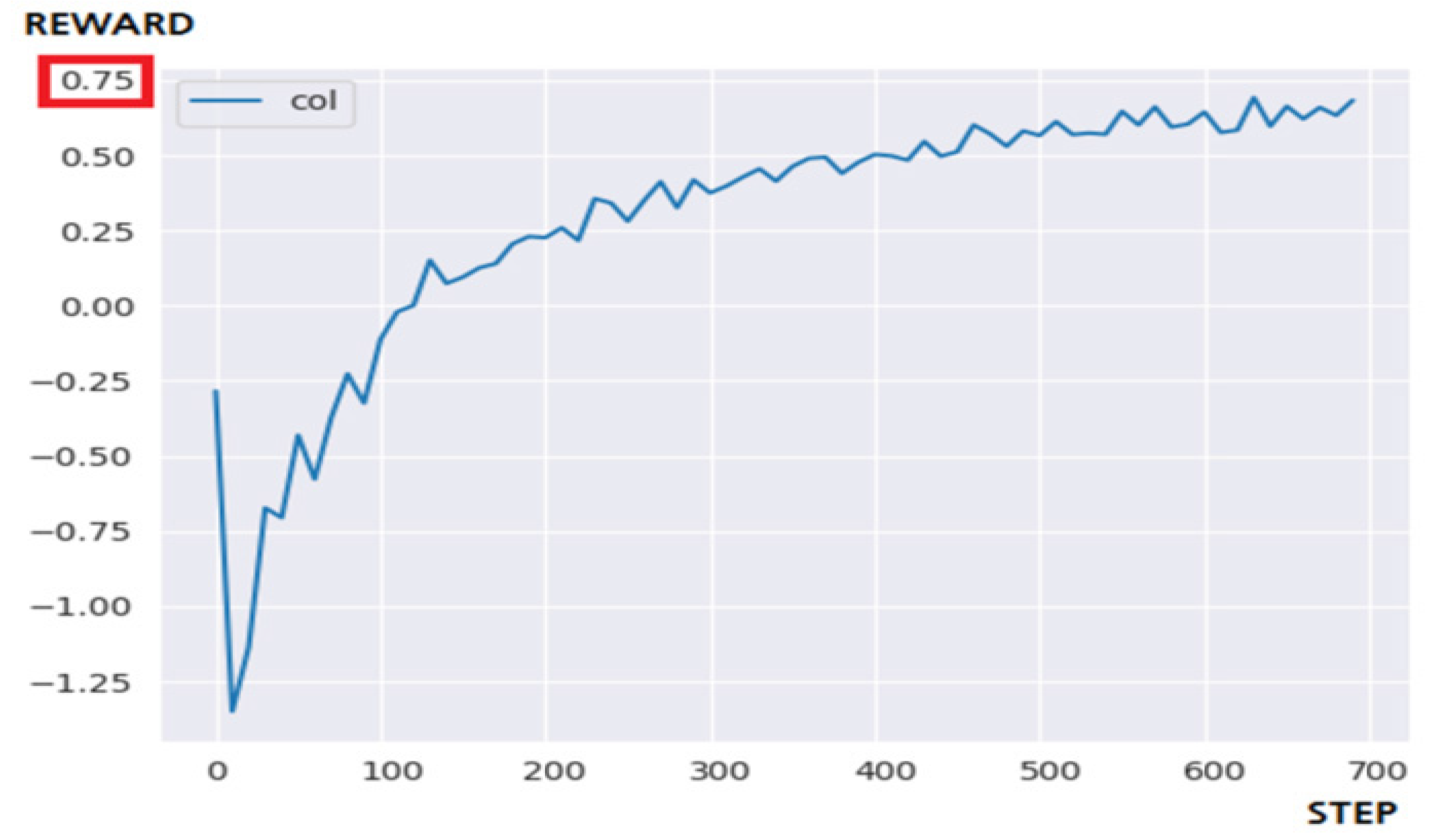
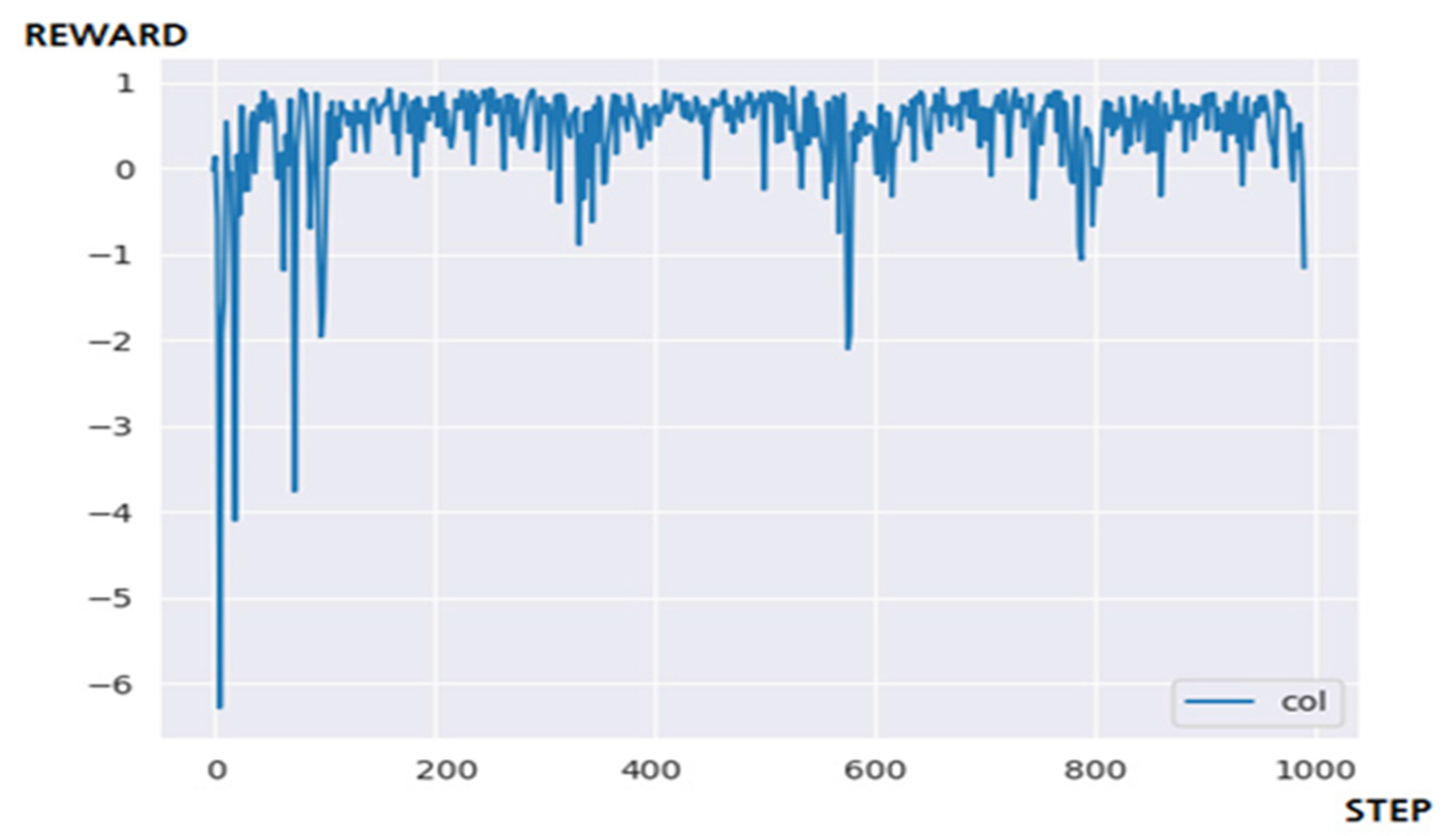
5.3.2. Performance Evaluation and Discussion
6. Conclusions and Future Research
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Boyan, J.A.; Moore, A.W. Generalization in reinforcement learning: Safely approximating the value function. Adv. Neural Inf. Process. Syst. 1995, 369–376. [Google Scholar]
- Kulkarni, T.D.; Narasimhan, K.; Saeedi, A.; Tenenbaum, J. Hierarchical deep reinforcement learning: Integrating temporal abstraction and intrinsic motivation. Adv. Neural Inf. Inf. Process. Syst. 2016, 3675–3683. [Google Scholar]
- Hasselt, H.V. Double Q-learning. Adv. Neural Inf. Process. Syst. 2010, 2613–2621. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Sutton, R.S. Generalization in reinforcement learning: Successful examples using sparse coarse coding. Adv. Neural Inf. Process. Syst. 1996, 8, 1038–1044. [Google Scholar]
- Queyrel, M. Multithreading to Construct Neural Networks 2018. Available online: https://www.slideshare.net/altoros/multithreading-to-construct-neural-networks (accessed on 14 January 2019).
- Purkaitl, N. How to Train Your Neural Networks in Parallel with Keras and ApacheSpark 2018. Available online: https://towardsdatascience.com/how-to-train-your-neural-networks-in-parallel-with-keras-and-apache-spark-ea8a3f48cae6 (accessed on 15 January 2019).
- Lifeomic/Sparkflow. 2018. Available online: https://github.com/lifeomic/sparkflow (accessed on 15 January 2019).
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling network architectures for deep reinforcement learning. arXiv 2015, arXiv:1511.06581. [Google Scholar]
- Tesauro, G. Temporal difference learning and TD-Gammon. Commun. ACM 1995, 38, 58–68. [Google Scholar] [CrossRef]
- O’Doherty, J.P.; Dayan, P.; Friston, K.; Critchley, H.; Dolan, R.J. Temporal difference models and reward-related learning in the human brain. Neuron 2003, 38, 329–337. [Google Scholar] [CrossRef] [Green Version]
- Lyu, S. Prioritized Experience Replay. 2018. Available online: https://lyusungwon.github.io/reinforcement-learning/2018/03/20/preplay.html (accessed on 11 January 2019).
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 2000, 12, 1057–1063. [Google Scholar]
- Tijsma, A.D.; Drugan, M.M.; Wiering, M.A. Comparing exploration strategies for Q-learning in random stochastic mazes. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Saravanan, C. Color image to grayscale image conversion. In Proceedings of the 2010 Second International Conference on Computer Engineering and Applications, Bali Island, Indonesia, 19–21 March 2010. [Google Scholar]
- Kanan, C.; Cottrell, G.W. Color-to-Grayscale: Does the method matter in image recognition? PLoS ONE 2012, 7, e29740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foerster, J.N.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual multi-agent policy gradients. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6379–6390. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the Thirtieth AAAI Conference Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. Int. Conf. Mach. Learn. 2016, 48, 1928–1937. [Google Scholar]
- Osband, I.; Blundell, C.; Pritzel, A.; van Roy, B. Deep exploration via bootstrapped DQN. Adv. Neural Inf. Process. Syst. 2016, 29, 4026–4034. [Google Scholar]
- Oh, J.; Guo, X.; Lee, H.; Lewis, R.L.; Singh, S. Action-conditional video prediction using deep networks in atari games. Adv. Neural Inf. Process. Syst. 2015, 28, 2863–2871. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Wiering, M.A.; van Hasselt, H. Ensemble algorithms in reinforcement learning. IEEE Trans. Syst. Man Cybern. 2008, 38, 930–936. [Google Scholar] [CrossRef] [Green Version]
- Rolls, E.T.; McCabe, C.; Redoute, J. Expected value, reward outcome, and temporal difference error representations in a probabilistic decision task. Cereb. Cortex 2007, 18, 652–663. [Google Scholar] [CrossRef]
- Moore, A.W.; Atkeson, C.G. Prioritized sweeping: Reinforcement learning with less data and less time. Mach. Learn. 1993, 13, 103–130. [Google Scholar] [CrossRef] [Green Version]
- Dayan, P.; Hinton, G.E. Feudal reinforcement learning. Adv. Neural Inf. Process. Syst. 1993, 5, 271–278. [Google Scholar]
- Tesauro, G. Practical issues in temporal difference learning. Adv. Neural Inf. Process. Syst. 1992, 4, 259–266. [Google Scholar]
- Abul, O.; Polat, F.; Alhajj, R. Multiagent reinforcement learning using function approximation. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2000, 4, 485–497. [Google Scholar] [CrossRef]
- Bus¸oniu, L.; De Schutter, B.; Babuska, R. Multiagent reinforcement learning with adaptive state focus. In Proceedings of the 17th Belgian-Dutch Conference on Artificial Intelligence (BNAIC-05), Brussels, Belgium, 17–18 October 2005; pp. 35–42. [Google Scholar]
- Castaño, F.; Haber, R.E.; Mohammed, W.M.; Nejman, M.; Villalonga, A.; Martinez Lastra, J.L. Quality monitoring of complex manufacturing systems on the basis of model driven approach. Smart Struct. Syst. 2020, 26, 495–506. [Google Scholar] [CrossRef]
- Beruvides, G.; Juanes, C.; Castaño, F.; Haber, R.E. A self-learning strategy for artificial cognitive control systems. In Proceedings of the 2015 IEEE International Conference on Industrial Informatics, INDIN, Cambridge, UK, 22–24 July 2015; pp. 1180–1185. [Google Scholar] [CrossRef]




| No. | Rule |
|---|---|
| 1 | The actor can only move in four directions: up/down/left/right |
| 2 | The actor cannot go through walls |
| 3 | The actor must reach his/her destination in the shortest time possible |
| No. | Rule |
|---|---|
| 1 | The actor can perform 5 actions: up/down/left/right/nothing |
| 2 | Up/down is related to movement, and left/right pushes the ball |
| 3 | When the ball touches the upper/lower area of the game screen, it is refracted |
| Category | Contents |
|---|---|
| State | The coordinates of actor’s location (x/y) |
| Action | Up/down is related to movement, and left/right pushes the ball |
| Rewards | +1, on arrival at the goal For movement of each step—(0.1/number of cell) |
| Model | Goal | Need Step | Time Required (400 Step) |
|---|---|---|---|
| Q-Learning | Success | 50 step | 46.7918 s |
| DQN | Fail | 500 step | 57.8764 s |
| N-DQN | Success | 100 step | 66.1712 s |
| Model | Goal | Need Step | Time Required (400 Step) |
|---|---|---|---|
| Q-Learning | Fail | 1200 step | 379.1281 s |
| DQN | Fail | step | 427.3794 s |
| N-DQN | Success | 700 step | 395.9581 s |
| Category | Contents |
|---|---|
| State | Coordinates of the current position of the paddle (x/y) Coordinates of the current position of the ball (x/y) |
| Action | 1 action of up/down/left/right actions |
| Rewards | +1, if the opponent’s paddle misses the ball −1, if the ball is missed by the actor’s paddle, otherwise 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K. Multi-Agent Deep Q Network to Enhance the Reinforcement Learning for Delayed Reward System. Appl. Sci. 2022, 12, 3520. https://doi.org/10.3390/app12073520
Kim K. Multi-Agent Deep Q Network to Enhance the Reinforcement Learning for Delayed Reward System. Applied Sciences. 2022; 12(7):3520. https://doi.org/10.3390/app12073520
Chicago/Turabian StyleKim, Keecheon. 2022. "Multi-Agent Deep Q Network to Enhance the Reinforcement Learning for Delayed Reward System" Applied Sciences 12, no. 7: 3520. https://doi.org/10.3390/app12073520
APA StyleKim, K. (2022). Multi-Agent Deep Q Network to Enhance the Reinforcement Learning for Delayed Reward System. Applied Sciences, 12(7), 3520. https://doi.org/10.3390/app12073520





