Asymmetric Encryption of Invisible Structured Light 3D Imaging
Abstract
:1. Introduction
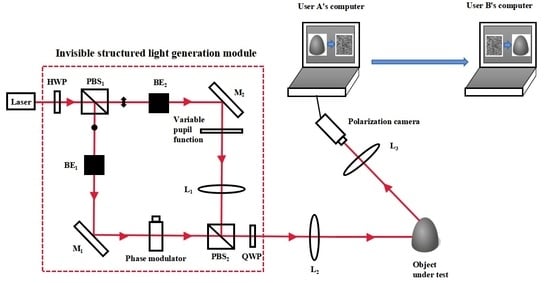
2. Invisible Structured Light 3D Imaging System
2.1. Obtaining the Eight Images for Encryption
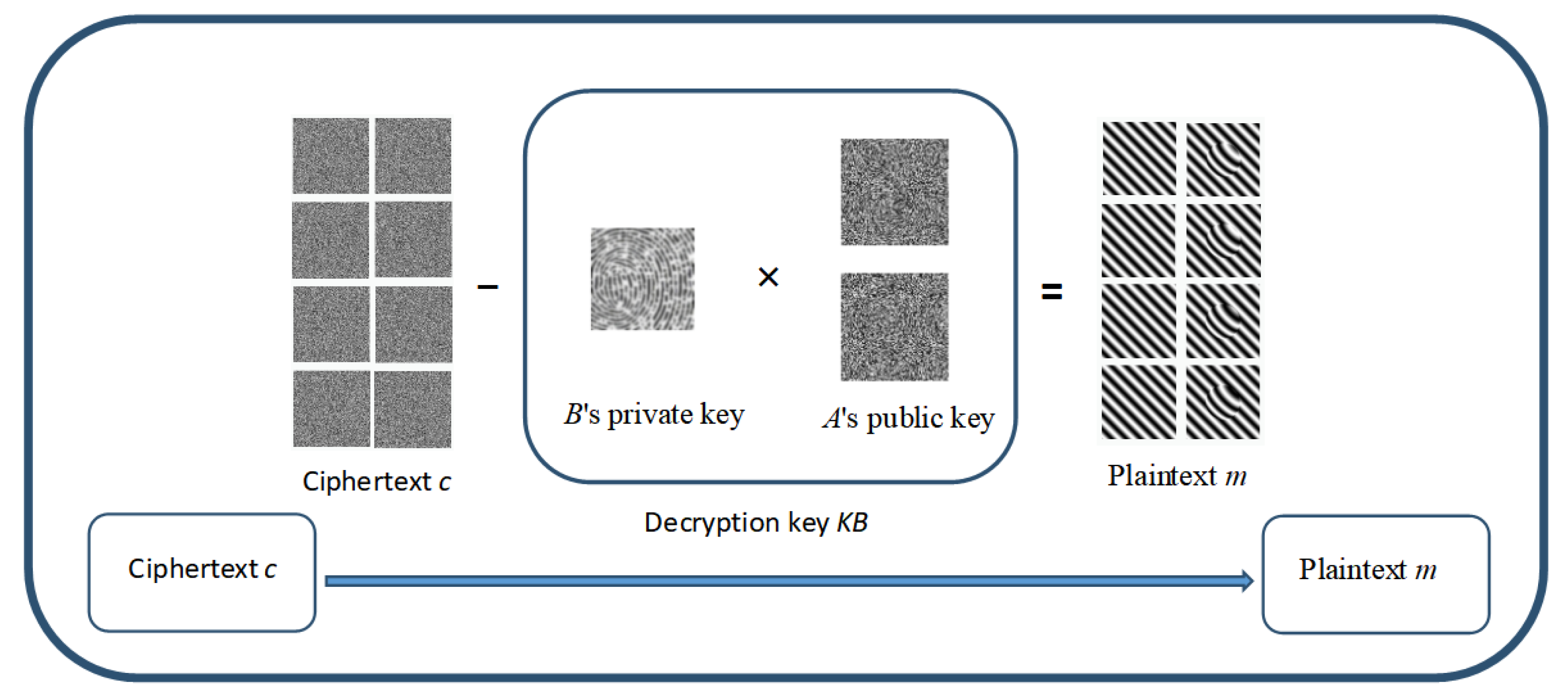
2.2. Encryption Using the Elliptic Curve Encryption Algorithm
2.3. Decryption Using the Elliptic Curve Encryption Algorithm
2.4. Reconstruction of the Three-Dimensional Image of the Measured Object
3. Simulation Results and Performance Analyses
3.1. Encryption Result Analysis
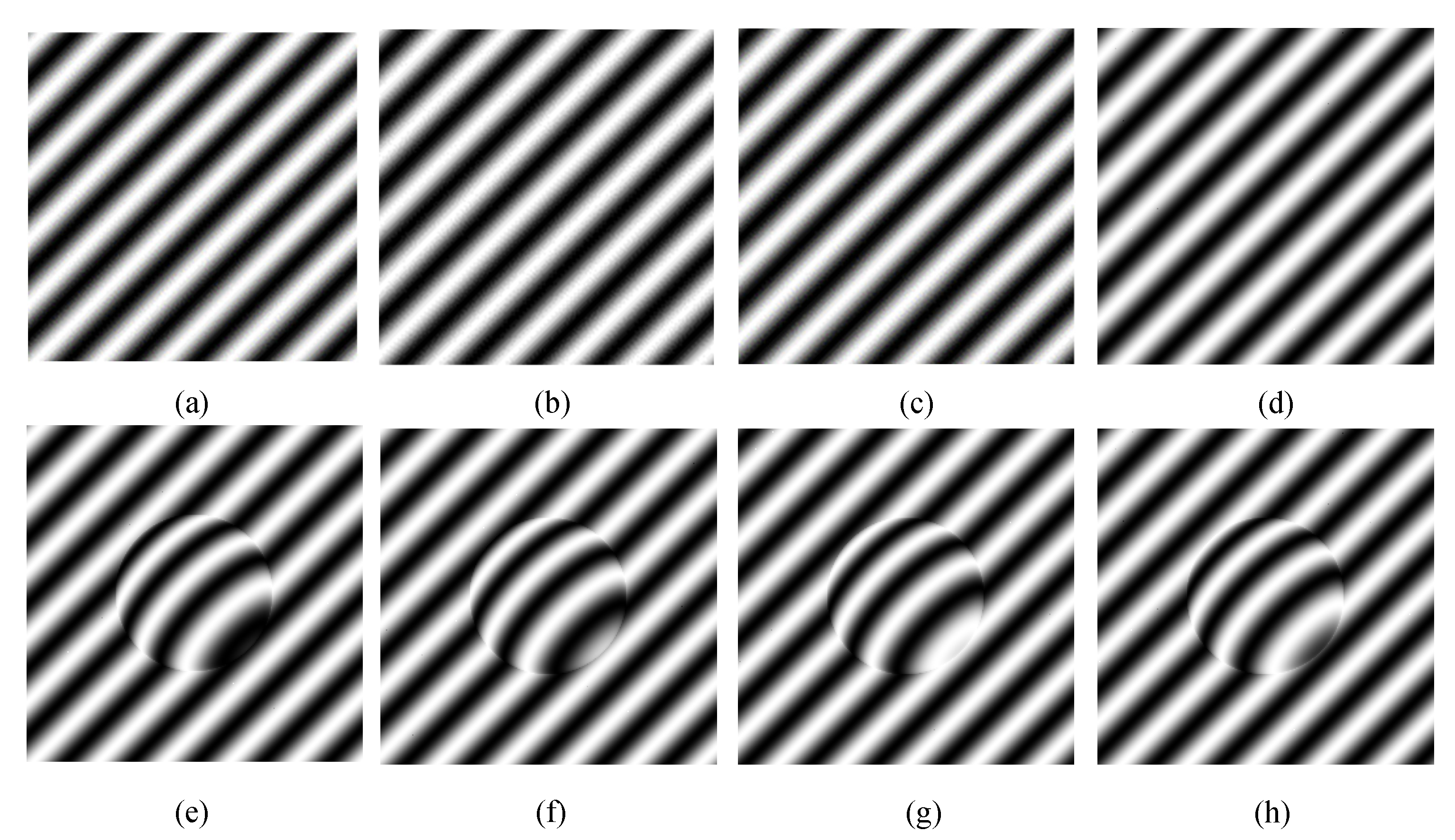
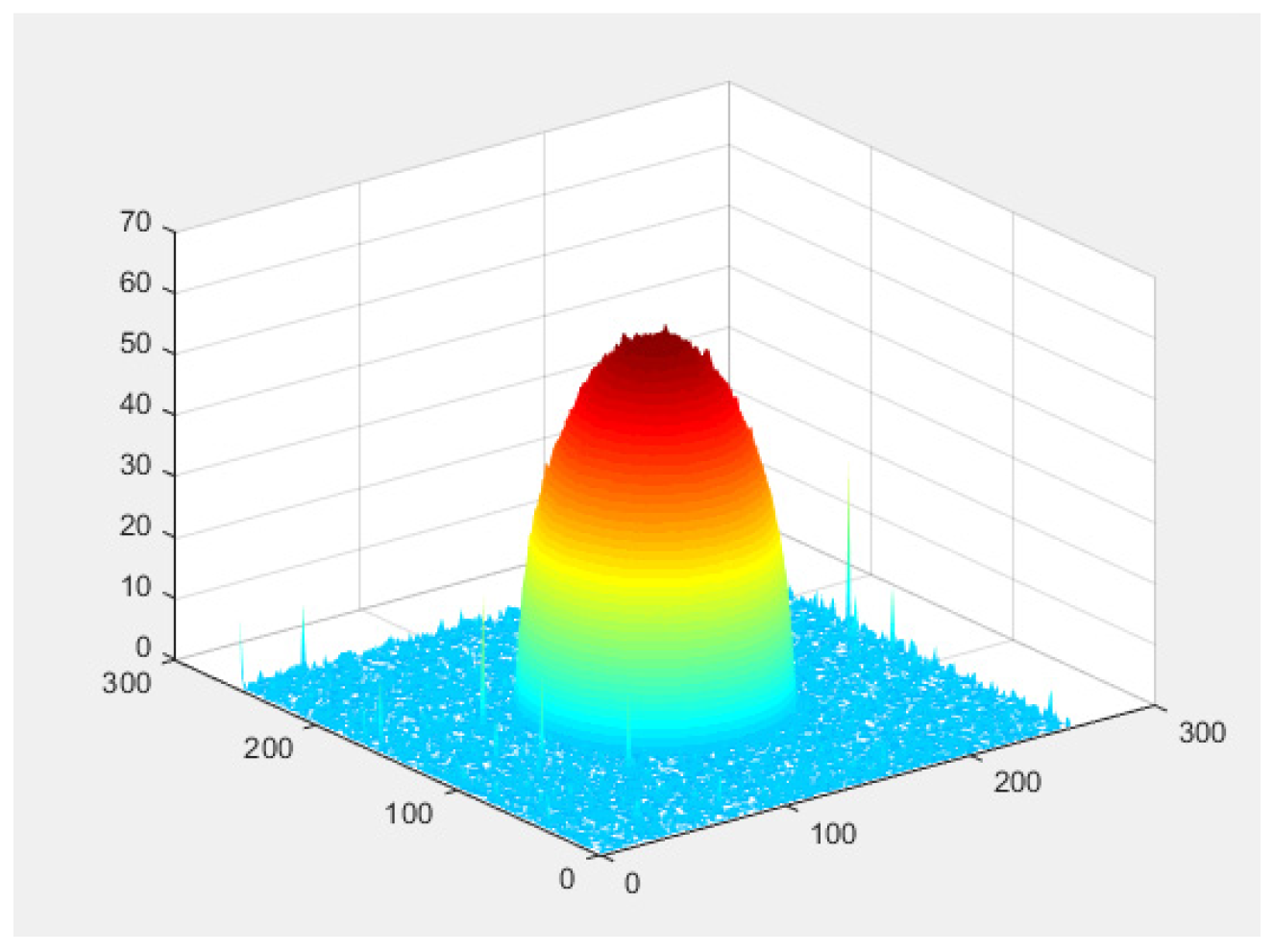
3.2. Analysis of Imaging Results
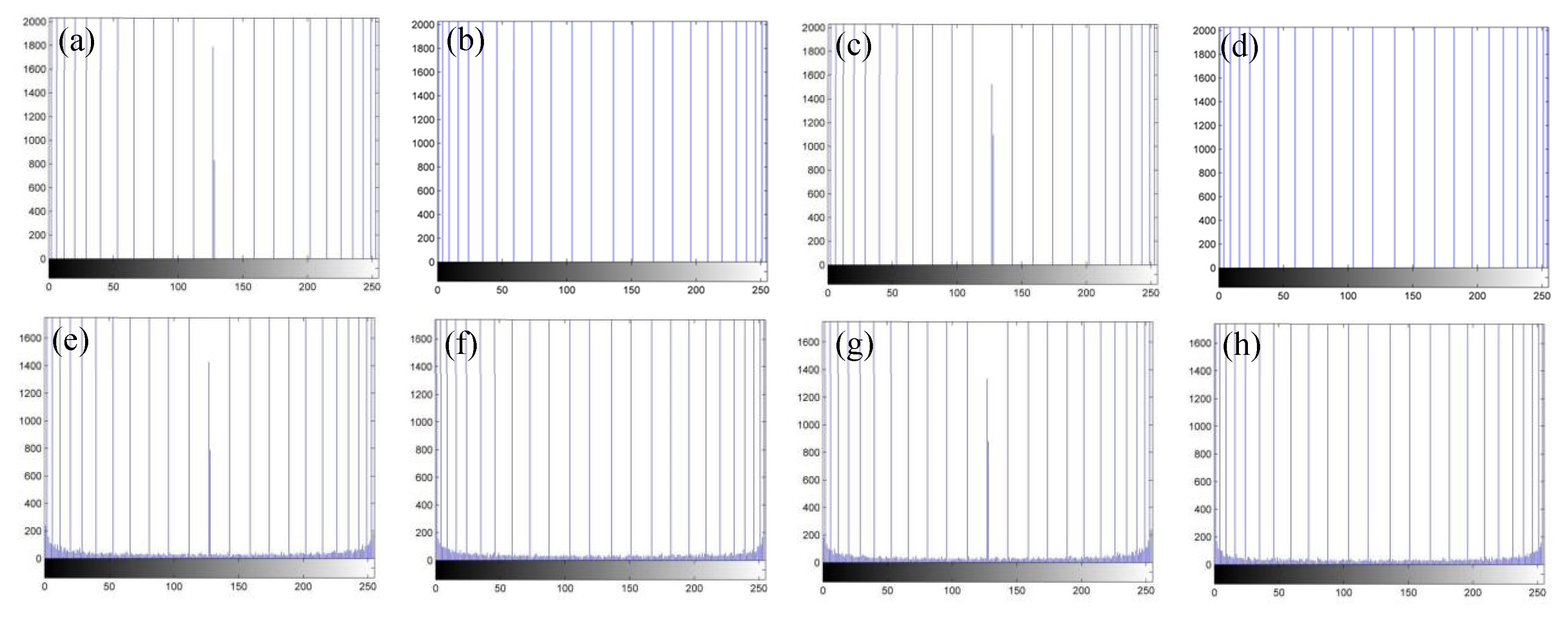
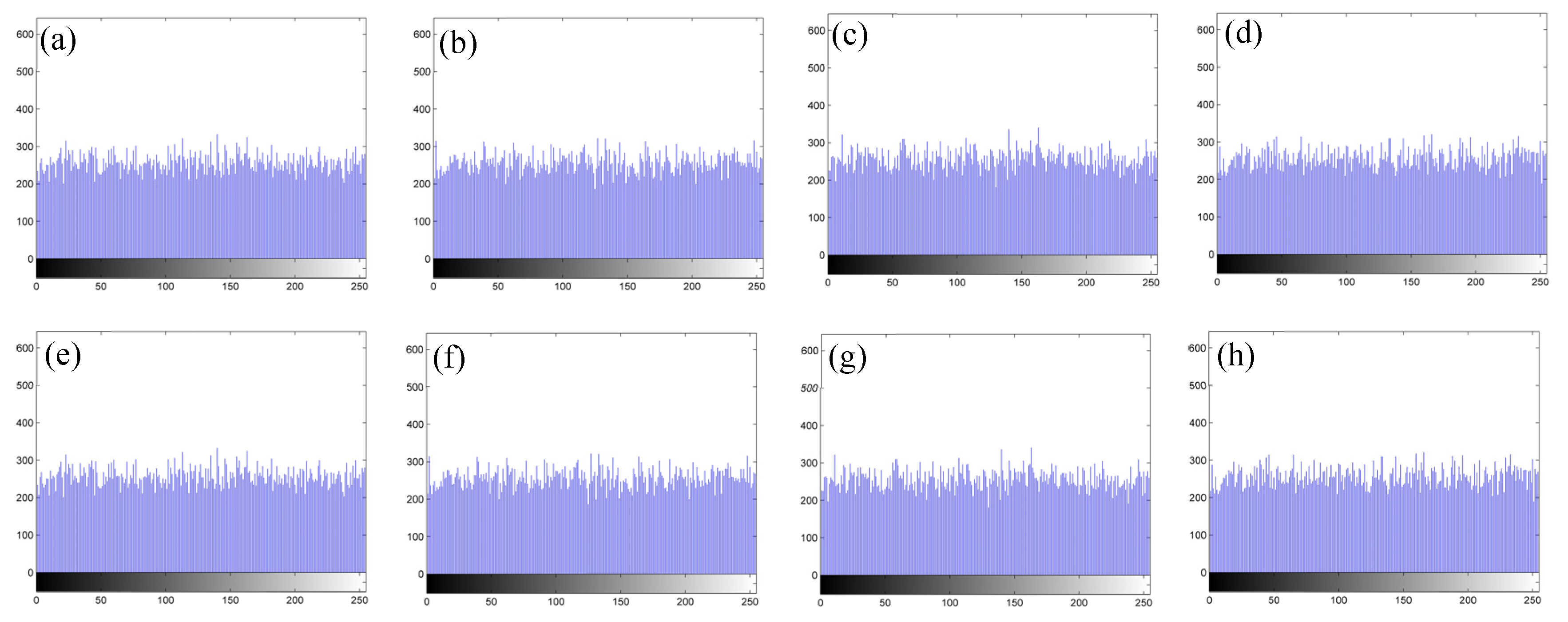
3.3. Histogram Analysis
3.4. Adjacent Pixel Correlation
3.5. Information Entropy Analysis
3.6. Noise Attack Analysis
3.7. Known Plaintext Attack
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Lasers Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Peng, X.; Yin, Y.; Li, A.; Wu, J.; Gao, B.Z. Structured light field 3D imaging. Opt. Express 2016, 24, 20324–20334. [Google Scholar] [CrossRef] [PubMed]
- Sam, V.; Dirckx, J. Real-time structured light profilometry: A review. Opt. Laser Eng. 2016, 87, 18–31. [Google Scholar]
- Feng, S.; Zhang, L.; Zuo, C.; Tao, T.; Chen, Q.; Gu, G. High dynamic range 3D measurements with fringe projection profilometry: A review. Meas. Sci. Technol. 2018, 29, 122001. [Google Scholar] [CrossRef]
- Yang, S.C.; Wu, G.X.; Yan, J.; Luo, H.F.; Zhang, Y.N.; Liu, F. High-accuracy high-speed unconstrained fringe projection pro-filometry of 3D measurement. Opt. Laser Technol. 2020, 125, 106063. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Xie, W.; Ahmed, S.M.; Li, C.R. Defect detection method for rail surface based on line-structured light. Measurement 2020, 159, 107771. [Google Scholar] [CrossRef]
- Guo, X.Z.; Shi, Z.Y.; Yu, B.; Zhao, B.Y.; Li, K.; Sun, Y.Q. 3D measurement of gears based on a line structured light sensor. Precis. Eng. 2020, 61, 160–169. [Google Scholar] [CrossRef]
- Pan, X.; Liu, Z. High-accuracy calibration of line-structured light vision sensor by correction of image deviation. Opt. Express 2019, 27, 4364–4385. [Google Scholar] [CrossRef]
- Jae-Sang, H.; George, T.; Song, Z. High-speed and high-accuracy 3D surface measurement using a mechanical projector. Opt. Express 2018, 26, 1474–1487. [Google Scholar]
- Zeng, Z.; Li, B.; Fu, Y.; Chai, M. Stair phase-coding fringe plus phase-shifting used in 3D measuring profilometry. J. Eur. Opt. Soc. Publ. 2016, 12, 133. [Google Scholar] [CrossRef] [Green Version]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef] [PubMed]
- Qian, K.M. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar]
- Qian, K.M. Two-dimensional windowed Fourier transform for fringe pattern analysis: Principles, applications and imple-mentations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar]
- Zhang, J.; Luo, B.; Su, X.; Li, L.; Li, B.; Zhang, S.; Wang, Y. A convenient 3D reconstruction model based on parallel-axis structured light system. Opt. Lasers Eng. 2020, 138, 106366. [Google Scholar] [CrossRef]
- Yan, Z.; Cheng, J.; Wei, Z.; Fang, J.; Jiang, F.; Chen, S. Rapid detection of weld contour based on compound vision of projection structured light and shape from shading. Int. J. Adv. Manuf. Technol. 2022, 119, 4057–4072. [Google Scholar] [CrossRef]
- Mao, A.; Sun, J.F.; Lu, Z.Y.; Zhou, Y.; Xu, Q.; Lao, C.Z.; He, H.Y.; Xu, M.M. Dynamic Background light interference suppres-sion technology based on invisible structured light three-dimensional imaging. Acta Opt. Sin. 2019, 39, 0711004-1–0711004-12. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Vanstone, S.; Hellman, M. Next generation security for wireless: Elliptic curve cryptography. Comput. Secur. 2003, 22, 412–415. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A. Elliptic Curve Cryptography; Springer: Berlin, Germany, 2011; pp. 194–207. [Google Scholar]
- Sheng, Y.; Xin, Z.; Zhou, D.F. Simultaneous transmission for an encrypted image and a double random-phase encryption key. Appl. Opt. 2007, 46, 3747–3753. [Google Scholar]
- Meng, X.F.; Peng, X.; Cai, L.Z.; Li, A.M.; Gao, Z.M.; Wang, Y.R. Cryptosystem based on two-step phase-shifting interferometry and the RSA public-key encryption algorithm. J. Opt. Pure Appl. Opt. 2009, 11, 085402. [Google Scholar] [CrossRef]
- Bi, H. Aggregation Encryption Method of Social Network Privacy Data Based on Matrix Decomposition Algorithm. Wirel. Pers. Commun. 2021, 5, 1–15. [Google Scholar] [CrossRef]
- Wang, F.; Ni, R.; Wang, J.; Zhu, Z.; Hu, Y. Invertible encryption network for optical image cryptosystem. Opt. Lasers Eng. 2021, 149, 106784. [Google Scholar] [CrossRef]
- Mille, V.S. Use of elliptic curves in cryptography. In Proceedings of the Advances in Cryptology-CRYPTO ‘85, Santa Barbara, CA, USA, 18–22 August 1985; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Koblitz, N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Tawalbeh, L.; Mowafi, M.; Aljoby, W. Use of elliptic curve cryptography for multimedia encryption. IET Inf. Secur. 2013, 7, 67–74. [Google Scholar] [CrossRef]
- Singh, L.D.; Singh, K.M. Medical image encryption based on improved ElGamal encryption technique. Optik 2017, 147, 88–102. [Google Scholar]
- Khoirom, M.S.; Laiphrakpam, D.S.; Themrichon, T. Cryptanalysis of multimedia encryption using elliptic curve cryptography. Optik 2018, 168, 370–375. [Google Scholar] [CrossRef]
- Yan, A.; Wei, Y.; Hu, Z.; Zhang, J.; Tsang, P.W.M.; Poon, T.-C. Optical cryptography with biometrics for multi-depth objects. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]










| Correlation Coefficients | Original Images | |||||||
|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | O6 | O7 | O8 | |
| Horizontal | 0.9921 | 0.9921 | 0.9921 | 0.9921 | 0.9917 | 0.9916 | 0.9917 | 0.9916 |
| Vertical | 0.9921 | 0.9921 | 0.9921 | 0.9921 | 0.9917 | 0.9916 | 0.9917 | 0.9916 |
| Diagonal | 0.9688 | 0.9688 | 0.9688 | 0.9688 | 0.9681 | 0.9680 | 0.9681 | 0.9680 |
| Correlation Coefficients | Ciphertext Images | |||||||
|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
| Horizontal | 0.0000 | 0.0002 | 0.0017 | −0.0005 | 0.0013 | 0.0016 | 0.0006 | 0.0008 |
| Vertical | −0.0056 | −0.0107 | 0.0036 | −0.0055 | −0.0045 | −0.0035 | −0.0001 | −0.0088 |
| Diagonal | 0.0129 | 0.0079 | 0.0117 | 0.0156 | 0.0142 | 0.0064 | 0.0137 | 0.0171 |
| Original Images | Ciphertext Images | Theoretical Value |
|---|---|---|
| 4.6799 | 7.9901 | 8 |
| 4.6838 | 7.9894 | 8 |
| 4.6831 | 7.9891 | 8 |
| 4.6838 | 7.9896 | 8 |
| 5.6854 | 7.9918 | 8 |
| 5.6981 | 7.9912 | 8 |
| 5.6864 | 7.9908 | 8 |
| 5.6981 | 7.9912 | 8 |
| Density of Noise | SSIM | |||||||
|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | O6 | O7 | O8 | |
| 0.1 | 0.9980 | 0.9986 | 0.9980 | 0.9987 | 0.9979 | 0.9987 | 0.9980 | 0.9986 |
| 0.2 | 0.9962 | 0.9968 | 0.9961 | 0.9968 | 0.9960 | 0.9968 | 0.9961 | 0.9969 |
| 0.3 | 0.9937 | 0.9944 | 0.9937 | 0.9945 | 0.9937 | 0.9944 | 0.9936 | 0.9943 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yan, A.; Zhang, H. Asymmetric Encryption of Invisible Structured Light 3D Imaging. Appl. Sci. 2022, 12, 3563. https://doi.org/10.3390/app12073563
Zhang J, Yan A, Zhang H. Asymmetric Encryption of Invisible Structured Light 3D Imaging. Applied Sciences. 2022; 12(7):3563. https://doi.org/10.3390/app12073563
Chicago/Turabian StyleZhang, Jing, Aimin Yan, and Hongbo Zhang. 2022. "Asymmetric Encryption of Invisible Structured Light 3D Imaging" Applied Sciences 12, no. 7: 3563. https://doi.org/10.3390/app12073563
APA StyleZhang, J., Yan, A., & Zhang, H. (2022). Asymmetric Encryption of Invisible Structured Light 3D Imaging. Applied Sciences, 12(7), 3563. https://doi.org/10.3390/app12073563