Modeling Several Optical Components Using Scalar Diffraction Theory
Abstract
:1. Introduction
- With the proposed formalism, we can analyze higher diffraction orders, which is not straightforwardly feasible with conventional geometrical optics.
- The new formalism allows for easily calculating the (1) PSF (point spread function), (2) DTF (optical transfer function), and (3) MTF (modulation transfer function). These three metrics are very meaningful in measuring the optical behavior of various systems. Special interest goes to the optical system of the human eye.
- The system of the human eye is easily covered by our approach.
- Optical performance criteria, as well as image quality criteria, including the optical transfer (OTE), are easily treated by our diffractive approach.
- We can easily treat optical information processing and invariance issues [14].
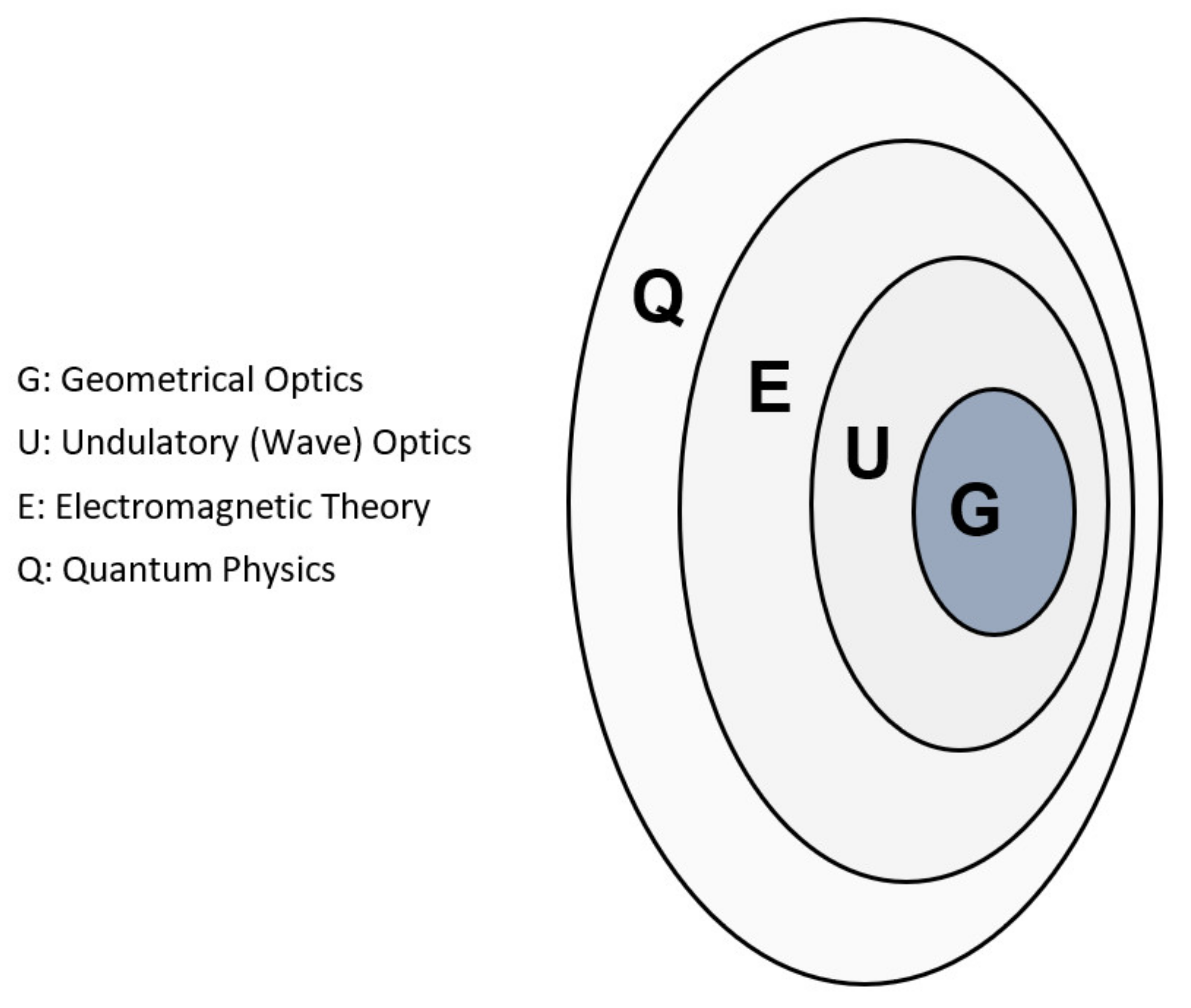
2. Related Works
- The wave direction is given by the normal, to what is referred to as the equiphase planes.
- Rays are assumed to progress in straight lines in a homogeneous medium.
- Power is conserved inside a bundle of rays.
- Reflection and refraction obey the refraction rule.
3. Analysis
- The observation distance is significantly larger than the diffracting objection;
- The angles involved in the diffraction process are small.
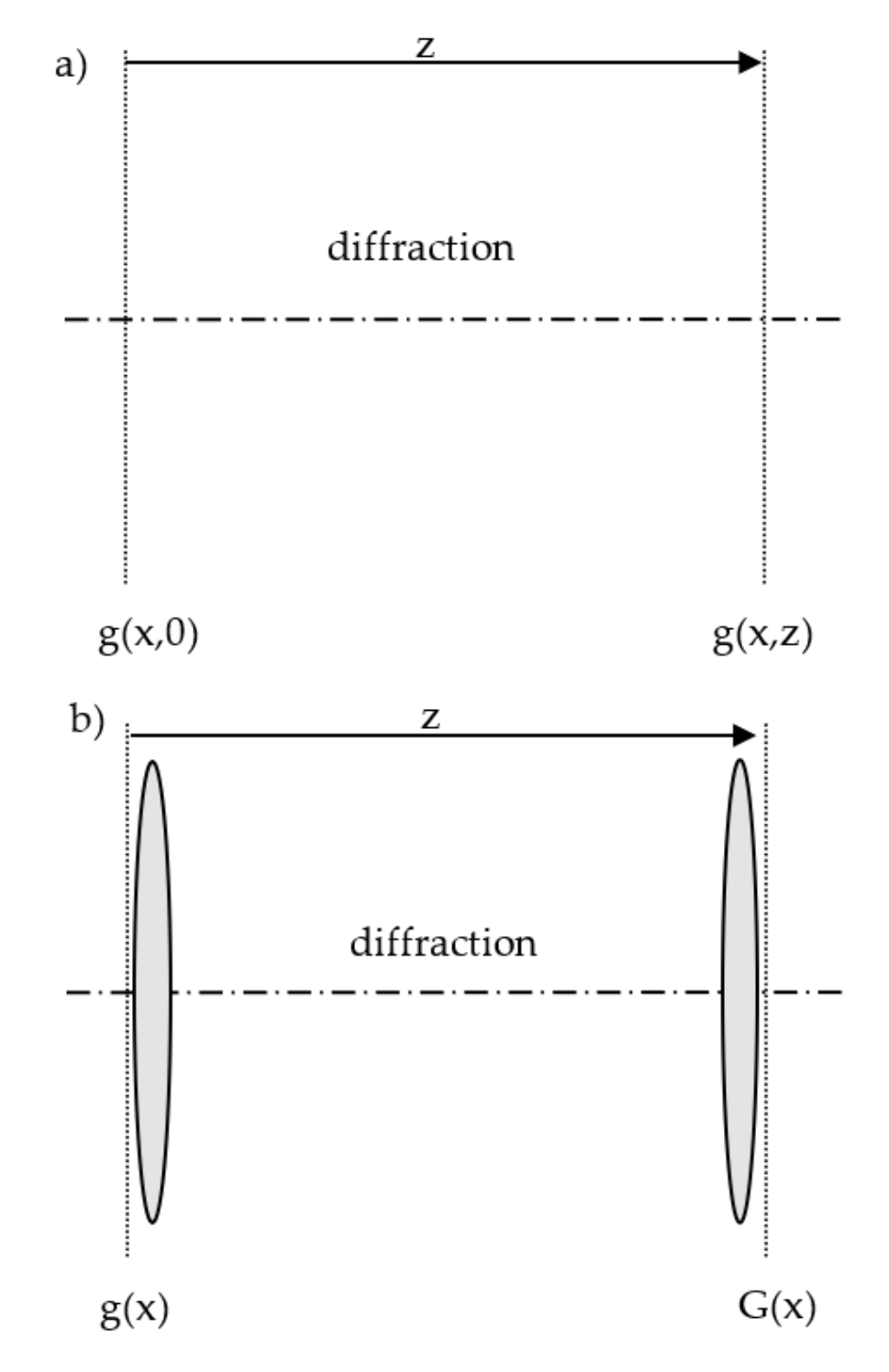
3.1. Fresnel Transform
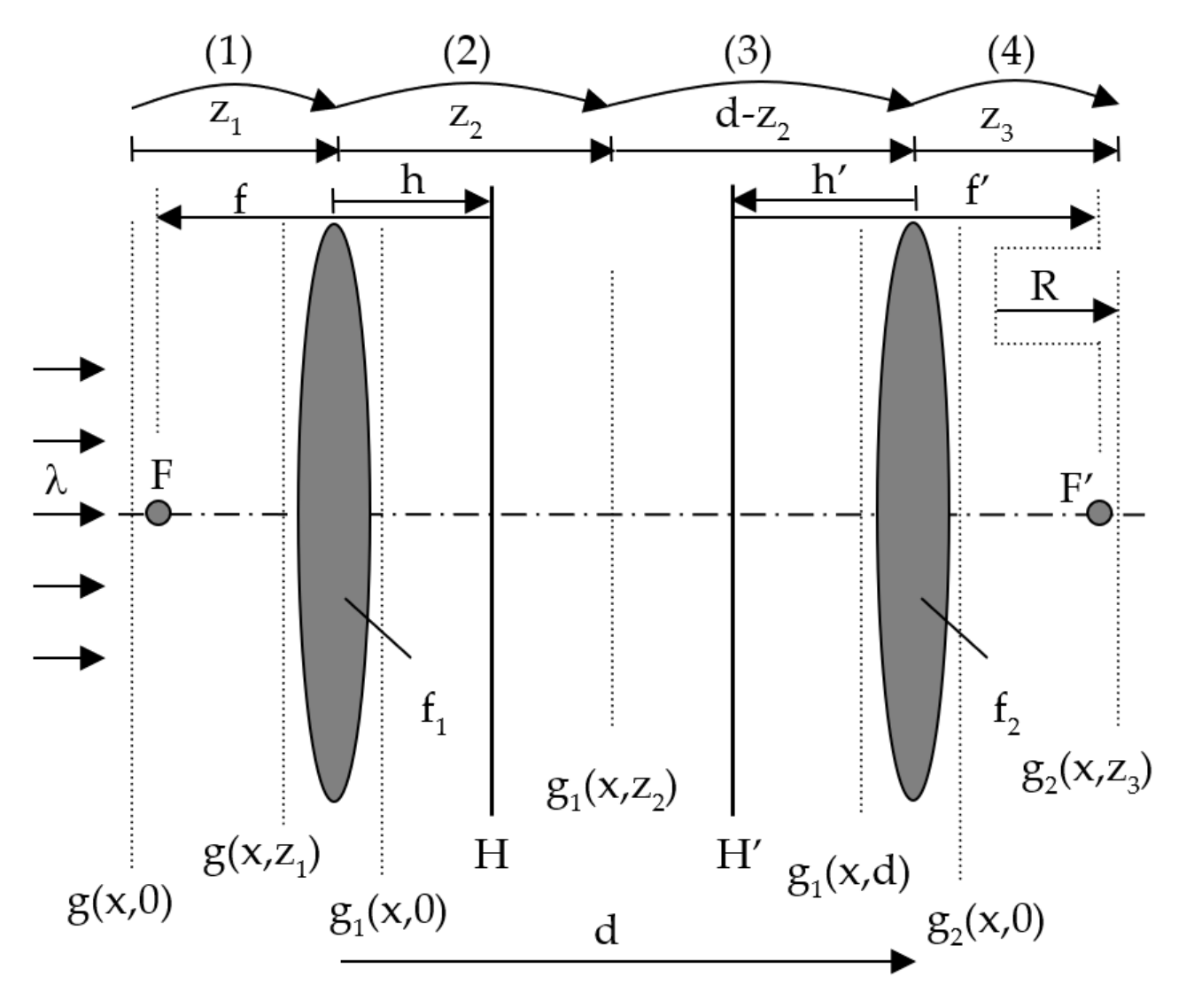
3.2. Compound Systems Using Geometrical Optics
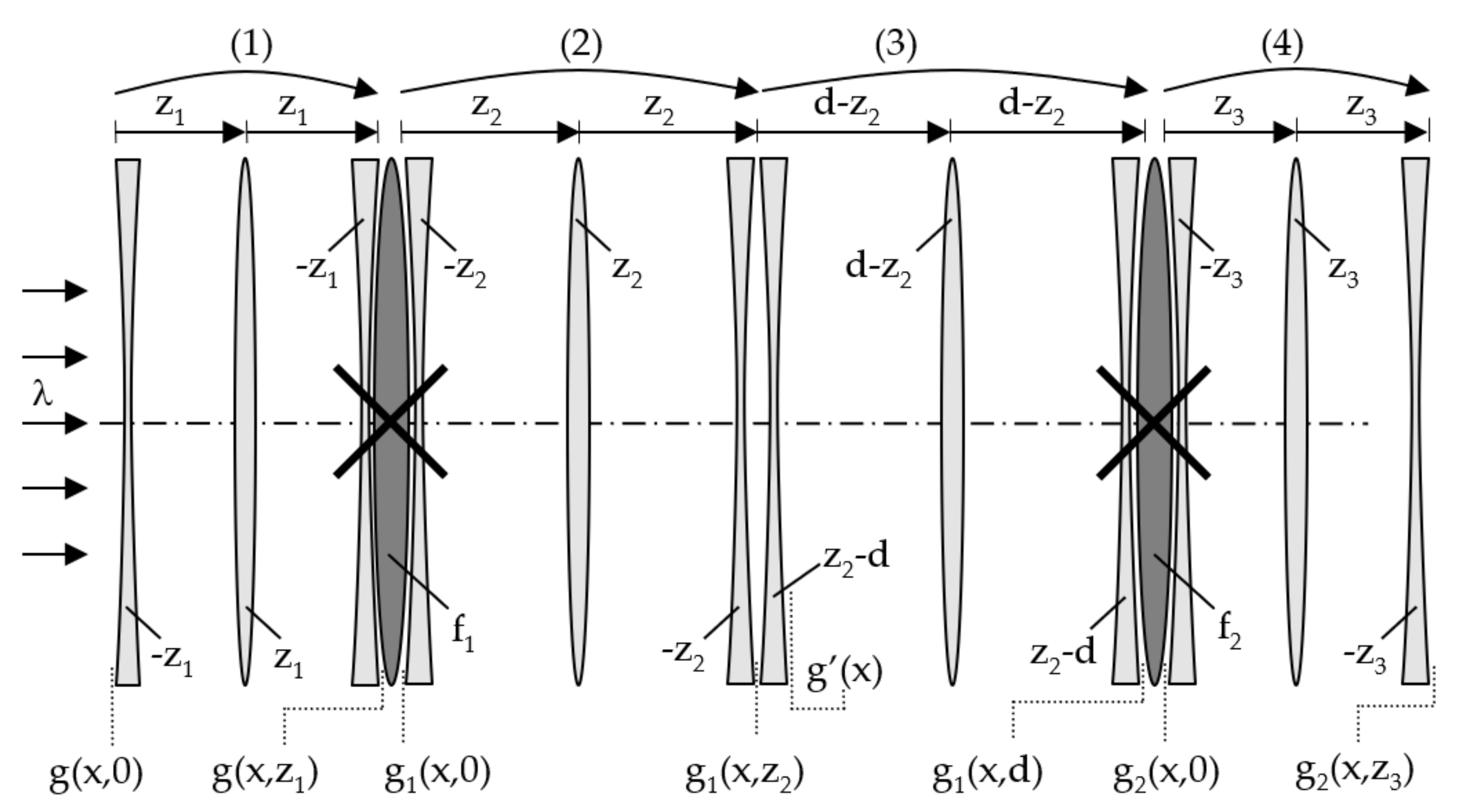
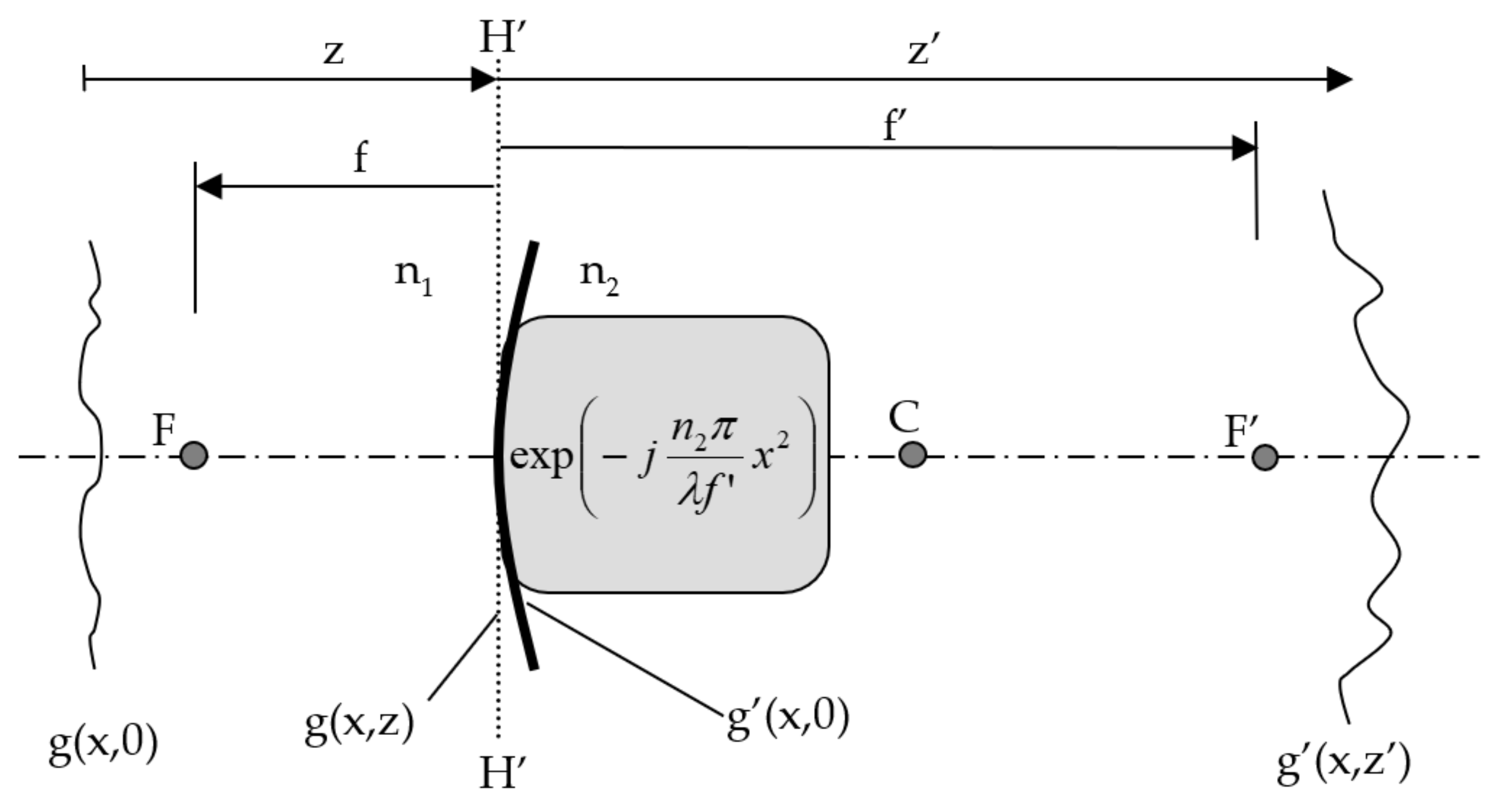
3.3. Difraction-Based Compound System
3.4. A Scalar Theory-Based Compound System
4. Typical Examples of Systems
4.1. Spherical Diopter
4.2. The System of the Human Eye
4.3. Propagation in a Dispersive Optical Fiber
- A: Slowly varying complex amplitude of the pulse envelope,
- α: Absorption coefficient,
- γ: Nonlinearity coefficient,
- β2: 2nd order dispersion coefficient,
- z: Observation distance,
- T: The time measured in a reference frame running with the pulse at the group velocity, vg (T = t-z/vg).
5. Applications
5.1. Analysis and Design of Refractive Devices and Instruments
5.2. Analysis and Synthesis of Diffractive Optical Elements
5.3. Optometry and Opthalmology
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Keller, J.B. Geometrical theory of diffraction. J. Opt. Soc. Am. 1962, 52, 116–130. [Google Scholar] [CrossRef] [PubMed]
- Zghal, M.; Bouali, H.E.; Ben Lakhdar, Z.; Hamam, H. The First Steps for Learning Optics: Ibn Sahl’s, Al-Haytham’s and Young’s Works on Refraction as Typical Examples; SPIE-ETOP: Bellingham, WA, USA, 2007; pp. 38–45. Available online: https://spie.org/etop/2007/etop07fundamentalsII.pdf (accessed on 22 February 2022).
- Luneburg, R.K. Mathematical Theory of Optics; University of California Press: Berkeley, CA, USA, 1964. [Google Scholar]
- Asimellis, G. Wave Optics; SPIE Press: Bellingham, WA, USA, 2020; ISBN 9781510622647. [Google Scholar]
- Young, T. The bakerian lectures. On the theory of light and colours. Philos. Trans. R. Soc. Lond. 1802, 92, 12–48. [Google Scholar]
- Young, T. Outlines of experimentals and inquiries respecting sound and light. Philos. Trans. R. Soc. Lond. 1800, 90, 106–150. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; MacGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Hamam, H.; de la Tocnaye, J.D.B. Programmable joint fractional Talbot computer-generated holograms. J. Opt. Soc. Am. A 1995, 12, 314–324. [Google Scholar] [CrossRef]
- Hamam, H. A direct technique for calculating the profile of aberration of the eye measured by a modified Hartmann–Shack apparatus. Opt. Commun. 2000, 173, 23–36. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 5th ed.; Pergamon Press: London, UK, 1975; pp. 1–18, 665–690. [Google Scholar]
- Tesfa, S. Quantum Optical Processes: From Basics to Applications; Springer: Berlin, Germany, 2021. [Google Scholar]
- Papoulis, A. Pulse compression, fiber communications, and diffraction: A unified approach. J. Opt. Soc. Am. A 1994, 11, 3–13. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; Wiley: Hoboken, NJ, USA, 2021; ISBN 978-1-119-73736-0. [Google Scholar]
- Hamam, H. Rotation Invariant Parallel Signal Processing Using a Diffractive Phase Element for Image Compression. Appl. Sci. 2012, 2, 439–449. [Google Scholar] [CrossRef]
- Grimaldi, F. Physico-Mathesis de Lumine, Coloribus et Irride; Published Just after His Death; Biblio: Bologna, Italy, 1665. [Google Scholar]
- Huygens, C. Traité D’optique; Réédition: Paris, France, 1920. [Google Scholar]
- Uriostegui, K.; Wolf, K.B. 2 × 2 Matrices: Manifolds, Realizations, Applications. Appl. Sci. 2021, 11, 7479. [Google Scholar] [CrossRef]
- Rakich, A. A New Type of Atmospheric Dispersion Corrector Suitable for Wide-Field High-Resolution Imaging and Spectroscopy on Large Telescopes. Appl. Sci. 2021, 11, 6261. [Google Scholar] [CrossRef]
- Chee, S.; Ryu, J.; Choi, H. New Optical Design Method of Floating Type Collimator for Microscopic Camera Inspection. Appl. Sci. 2021, 11, 6203. [Google Scholar] [CrossRef]
- Pascual, E.; Gómez-Pedrero, J.A.; Alonso, J. Improved Analytical Theory of Ophthalmic Lens Design. Appl. Sci. 2021, 11, 5696. [Google Scholar] [CrossRef]
- Sasián, J. Control of Linear Astigmatism Aberration in a Perturbed Axially Symmetric Optical System and Tolerancing. Appl. Sci. 2021, 11, 3928. [Google Scholar] [CrossRef]
- Seo, S.H.; Ryu, J.M.; Hojong Choi, H. Focus-Adjustable Head Mounted Display with Off-Axis System. Appl. Sci. 2020, 10, 7931. [Google Scholar] [CrossRef]
- De Bougrenet de la Tocnaye, J.L.; Hamam, H.; Moignard, R. Light diffraction Device Using Reconfigurable Spatial Light Modulators and the Fractional Talbot Effect. US Patent 5,617,227, 1 April 1997. [Google Scholar]
- Collins, S.A. Lens-system diffraction integral written in terms of matrix optics. J. Opt. Soc. Am. 1970, 60, 1168–1177. [Google Scholar] [CrossRef]
- Hamam, H. Digital holography-based steganography. Opt. Lett. 2010, 35, 4175–4177. [Google Scholar] [CrossRef]
- Gerrard, A.; Burch, J. Introduction to Matrix Methods in Optics; Dover Publications: Mineola, NY, USA, 1994. [Google Scholar]
- Fienup, J.R. Phase retrieval algorithms: A comparision. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [Green Version]
- Hamam, H. Intensity based self-imaging. Appl. Opt. 2010, 49, 2519–2528. [Google Scholar] [CrossRef]
- Gullstrand, A. Appendix II in Handbuch der Physiologischen Optik; Voss: Hamburg, Germany, 1909. [Google Scholar]
- Meyer-Arendt, J.R. Introduction to Classical and Modern Optics, 4th ed.; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Strong, J. Concepts of Classical Optics; W.H. Freeman and Company, Inc.: New York, NY, USA, 1958. [Google Scholar]
- Hamam, H. A new measure for optical performance. Optom. Vis. Sci. 2003, 80, 175–184. [Google Scholar] [CrossRef]
- Emsley, H.H. Visual Optics, 5th ed.; Hatton Press Ltd.: London, UK, 1952. [Google Scholar]
- Guizani, S.; Hamam, H.; Bouslimani, Y.; Cheriti, A. High bit rate optical communications: Limitations and perspectives. IEEE Can. Rev. 2005, 50, 11–15. [Google Scholar]
- Razzak, M.; Guizani, S.; Hamam, H.; Bouslimani, Y. Optical Post-Egalization based on self-imaging. J. Mod. Opt. 2006, 53, 1675–1684. [Google Scholar] [CrossRef]
- Simonet, P.; Hamam, H.; Brunette, I.; Campbell, M. Influence of ametropia on the optical quality of the human eye. Investig. Ophthalmol. Vis. Sci. 2003, 40, S448. [Google Scholar]
- Malacara, D.; Malacara, Z. Handbook of Lens Design; Marcel Dekker Inc.: New York, NY, USA, 1994. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamam, H. Modeling Several Optical Components Using Scalar Diffraction Theory. Appl. Sci. 2022, 12, 3580. https://doi.org/10.3390/app12073580
Hamam H. Modeling Several Optical Components Using Scalar Diffraction Theory. Applied Sciences. 2022; 12(7):3580. https://doi.org/10.3390/app12073580
Chicago/Turabian StyleHamam, Habib. 2022. "Modeling Several Optical Components Using Scalar Diffraction Theory" Applied Sciences 12, no. 7: 3580. https://doi.org/10.3390/app12073580
APA StyleHamam, H. (2022). Modeling Several Optical Components Using Scalar Diffraction Theory. Applied Sciences, 12(7), 3580. https://doi.org/10.3390/app12073580





