1. Introduction
Optoelectronic platform has a wide range of applications in the field of aerospace, such as disaster prevention and rescue, geographic mapping, and precision agriculture [
1,
2]. The line of sight (LOS) is the axis of the optoelectronic sensor lens. The stability of LOS of optoelectronic sensor can ensure the quality of the output image of optoelectronic platform. A high-quality feedback inertial signal is the basis of LOS motion control system in optoelectronic platform [
3]. The processing of inertial sensor signal which affects the stabilization of LOS is an effective method. Gyro and accelerometer are two common inertial space motion sensors [
4]. The LOS stability control of the optoelectronic platform needs the inertial velocity feedback of gyro. Gyro has a fast response but suffers from drift due to accumulated errors. In the application of the motion control method, even if the control command and feedback error are zero, the LOS of optoelectronic still shakes due to gyro drift [
5]. Therefore, the velocity feedback of gyro measurement must be transformed into attitude feedback. In addition, maneuvering acceleration exists in the flight of aircraft. It adversely affects the output of the accelerometer and the angular attitude calculated from it [
6]. Therefore, the attitude estimation based on multi-sensor data fusion method is necessary to improve the attitude control performance of optoelectronic platform.
Many scholars do studies to solve the above problems. An attitude estimation algorithm based on gyro and accelerometer is proposed in reference [
7]. However, the cumulative error of yaw attitude cannot be compensated for due to the lack of magnetometer information. An error data model of accelerometer and gyro is established and the attitude of moving carrier is predicted by Kalman filter [
8,
9]. This method can suppress the attitude divergence caused by gyro drift but it is not applicable to the situation where the motion state changes rapidly. The system has poor robustness because the accelerometer measures the sum of motion acceleration and gravity acceleration when the carrier has maneuvering acceleration [
10]. An extended Kalman filter (EKF) algorithm is applied to integrate accelerometer and magnetometer in [
11]. During the maneuvering period, the estimation error of the maneuvering acceleration is modeled as the sum of a fluctuation error and a sudden change error. However, the magnetometer has measurement error due to electromagnetic interference which affects the measurement accuracy [
12]. An improved adaptive Kalman filter (AKF) based on Sage-Husa time-varying state disturbance estimator is used to estimate the mean and variance of state disturbance, but this method is not stable and easy to diverge [
13].The combination of KF and adaptive Kalman filter is also an effective data fusion method [
14]. Reference [
15] takes GPS/SINS integrated navigation as the background and adopts adaptive filter algorithm for attitude estimation. However, the measurement error of GPS is large when obstructions exist which affects the accuracy of the algorithm [
16]. In addition, it needs to be processed synchronously with inertial sensor which increases the complexity of the algorithm.
In order to solve the above problems, zero speed correction and speed constraint are applied to improve the accuracy and robustness of attitude estimation algorithm [
17]. It means that the accurate detection of motion state of the moving carrier is very important. Reference [
18] uses accelerometer variance and introduces yaw attitude for detection. The motion state is judged by the standard deviation (STD) of
X-axis and
Y-axis data of accelerometer and magnetometer [
19]. These methods are mainly used in vehicle navigation system but there is little research on attitude measurement. In addition, it is difficult to meet the real-time and flexibility requirements of LOS stabilization control system of the optoelectronic platform.
Furthermore, dynamic processes lead to phase lag. If the feedback signal lags behind, the control system is difficult to achieve a high performance [
20]. The purpose of introducing additional signal is reducing the phase lag. Low pass filter (LPF) and high pass filter (HPF) can form a filter to utilize the phase advance information [
21]. However, it is difficult for any input signal to compensate for the phase lag of LPF. A phase-lag-free LPF has been proposed using higher-order signal in [
22]. This method can suppress noise without obvious phase lag.
Although the common data fusion method can effectively suppress the gyro drift, the measurement accuracy is not high due to the influence of maneuver. The application of GPS and magnetometer can suppress the maneuvering acceleration interference effectively. However, GPS is not suitable for suspended platform without movement since it is necessary to establish the correction quantity related to the inertial attitude [
23]. The measurement accuracy of magnetometer is not high due to electromagnetic interference [
12]. In addition, signal filtering will lead to phase lag inevitably. Compensating the phase lag is also effective to improve the performance of the control system. Optoelectronic platforms adopt vibration isolators to isolate the interference from the carrier, such as attitude motion and vibration [
24]. The LOS stability control accuracy of optoelectronic platform can be improved as long as the attitude estimation based on multi-sensor fusion is applied. The contributions of this study are as follows:
(a) An adaptive threshold criterion is designed based on the accelerometer data in the sliding window. The threshold is determined online to judge whether the influence of maneuvering acceleration can be ignored;
(b) Data fusion based on gyro and accelerometer (DFBGA) and suppressing maneuvering acceleration disturbance method (SLAIM) are designed in attitude estimation. Based on adaptive threshold criterion, DFBGA is applied if the influence of maneuvering acceleration can be ignored. SLAIM is applied if the influence of maneuvering acceleration cannot be ignored. It is also adopted in the estimation of yaw attitude because it cannot be measured by accelerometer;
(c) In order to compensate for the phase lag error introduced in the above attitude estimation process based on Kalman filter, a phase-lag-free LPF is proposed to revise the phase lag by applying the higher order signal.
This paper is organized as follows. The problem formulation is introduced in
Section 2. The attitude estimation method design is proposed in
Section 3. Simulations and experiments are described in
Section 4. At last,
Section 5 concludes the paper.
2. Problem Formulation
Body coordinate system and geographic coordinate system should be established as the reference coordinate system for attitude change. The coordinate system determined by the body axis of the carrier is the body coordinate system
and the coordinate system determined by east-north-sky direction is geographic coordinate system
. These two coordinate systems are shown in
Figure 1. The accelerometer can obtain linear acceleration and the gyro can obtain angular velocity in the body coordinate system. The angular attitude and angular velocity in the geographic coordinate system can be obtained by solving the output data of these sensors. Roll angle
is the angular attitude rotating around
-axis, pitch angle
is the angular attitude rotating around
-axis and yaw angle
is the angular attitude rotating around
-axis.
The measured value of gyro is the angular velocity of body coordinate system. It has the advantage of fast response and low cost. However, it suffers from drift due to accumulated errors by integration to obtain angle information. The measured value of accelerometer is the linear acceleration of body coordinate system which does not suffer from zero drift. However, the yaw angle cannot be measured by accelerometer due to the rotation plane of is orthogonal to gravity. Therefore, it is necessary to use the signal processing method of fusing multiple sensor data to improve the accuracy of angular attitude measurement.
3. An Adaptive Attitude Estimation Method Based on Multi-Sensor Fusion
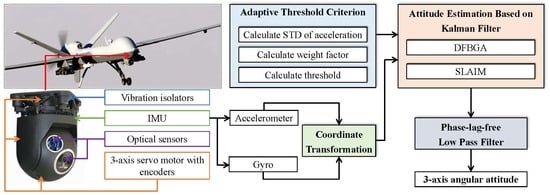
In this study, attitude estimation algorithm flow chart is shown in
Figure 2. It includes four parts: coordinate transformation, adaptive threshold setting, attitude measurement based on Kalman filter, and phase-lag-free LPF.
3.1. Coordinate Transformation
The coordinate transformation for accelerometer output data is shown as follows. If an vector in the inertial space is calculated by unit vector
rotating around 3-axis, attitude rotation matrix
can be expressed as
Record the accelerometer measurement as
,
, and
after unitization
In Equation (2), when the yaw angle
, the roll angle
, and pitch angle
can be calculated as Equations (3) and (4). However, the yaw angle cannot be measured by accelerometer due to the rotation plane is orthogonal to gravity.
The coordinate transformation of gyro output data is shown as follows. Its 3-axis angular velocity is
,
and
,
Therefore, 3-axis angular velocity in the geographic coordinate system can be obtained by
3.2. Adaptive Threshold Criterion
The accelerometer output data are used as the basis to judge the influence of maneuvering acceleration for the attitude estimation of roll angle
and pitch angle
, respectively. Collect the output data of
X-axis and
Y-axis of accelerometer in the conditions of the maneuvering acceleration exists and does not exist. If there are
N groups of data within the sampling interval, the standard deviation(STD) of them can be expressed as
where
is the
i-th output of the single axis of the accelerometer, and
is the average value of
N groups data of the corresponding axis.
Take the
X-axis as an example and collect the output data of
X-axis of accelerometer in two conditions of the same interval. The STD of two conditions are shown in
Figure 3. It shows that the STD of acceleration changes slowly when the maneuvering acceleration does not exist and the STD of the acceleration fluctuates greatly and changes rapidly when the maneuvering acceleration exists.
Based on the above analysis, an adaptive threshold criterion method is adopted. The threshold value
is calculated according to the STD of
x-axis and
y-axis acceleration obtained in the fixed length sliding window, which can be expressed
where
n is the fixed window length which used to calculate the threshold.
is the magnification factor.
is the STD value calculated of each sampling interval in the window time.
is the weight factor and
.
where
i is the serial number in the window time. Compared with
, it can increase the influence of approaching time; compared with
, it will not highlight the approaching time too much to suppress the influence of gross error on the threshold calculation.
If the STD of acceleration calculated in the current period is less than the threshold , it could be considered that the influence of the maneuvering acceleration in the current period can be ignored. Otherwise, it is considered that the influence of the acceleration in the current period cannot be ignored. The threshold setting and the method of judging whether the maneuvering acceleration exists of Y-axis are similar to that of X-axis.
3.3. Attitude Estimation Based on Kalman Filter
The accuracy of the angular attitude calculated by the accelerometer is influenced by the maneuvering acceleration in motion. In addition, the yaw angle cannot be calculated by the output data of the accelerometer. Therefore, two attitude estimation algorithms are designed based on Kalman filter.
For the roll angle and pitch angle , if the STD of the acceleration output data calculated in the current period is greater than the threshold of the corresponding axis, that is the influence of maneuvering acceleration cannot be ignored and for the yaw angle , the angular attitude is calculated by SLAIM. If the STD of the output data of accelerometer calculated in the current period is less than the threshold of the corresponding axis, that is the influence of the maneuvering acceleration can be ignored, the angular attitude is calculated by DFBGA.
3.3.1. Kalman Filter for Inertial Attitude Estimation
Set state equation and measurement equations of random linear discrete system as:
where
is the state variable,
is the measurement variable,
is the non-singular state one step transition matrix,
is the process noise input matrix,
is the control input,
is the random process noise sequence,
is the measurement matrix and
is the measurement noise sequence.
3.3.2. Data Fusion Method of Gyro and Accelerometer
For the angular attitude measurement of roll angle and pitch angle when the influence of maneuvering acceleration can be ignored, the data of gyro and accelerometer are fused to obtain accurate attitude estimation value by Kalman filter.
The roll angle
and pitch angle
are taken as the state variables of Kalman filter, that is the state variables of the state equation in Equation (
10) is
The angular attitude calculated by the accelerometer and the angular velocity calculated by the gyro in the geographic coordinate system are taken as the measurement variables of Kalman filter. The measurement variables of the measurement equation in Equation (10) is
where
and
are the actual roll and pitch angular attitude,
and
are the roll and pitch angular attitude calculated by the accelerometer and
and
are the roll and pitch angular velocity calculated by the gyro at
k-time. In this fusion method, control input
, random process noise sequence
and measurement noise sequence
can be ignored.
3.3.3. Attitude Estimation for Suppressing Maneuvering Acceleration Disturbance
For the angular attitude estimation of roll angle and pitch angle when the influence of maneuvering acceleration cannot be ignored as well as the angular attitude estimation of yaw angle , the attitude error caused by gyro dynamic drift is regarded as a time-varying signal. A more accurate attitude error estimation value is obtained through Kalman filter to compensate for the attitude angle error.
There is an attitude drift error between the angular attitude calculated by the gyro and the actual angular attitude due to the existence of gyro zero drift. The relationship between the actual angular attitude and the calculated angular attitude at moment
k is as follows:
where
,
and
are the actual 3-axis angular attitude at moment
k,
,
, and
are the 3-axis angular attitude calculated by the gyro at moment
k and
,
, and
are the 3-axis angular attitude drift error at moment
k.
The attitude error caused by the zero drift of gyro is related to the motion complexity of the measured carrier and the attitude error accumulates with time when measuring the moving carrier. The motion complexity is described as the change of the angular attitude at moment
k relative to the angular attitude at moment
and the attitude drift error model equation is established as
where
,
and
are the 3-axis angular attitude drift error at moment
k,
,
and
are the 3-axis angular attitude drift error at moment
and
is adjustable parameter. Random process noise sequence
,
and
are determined by the measurement accuracy of the gyro.
The state equation of Kalman filter is established according to the attitude drift error model. The state variable is
In our study, the LPF between the angular attitude calculated by the gyro at moment
k and the first few moments of moment
k is used as the measurement of attitude drift error caused by gyro drift. The measurement variable of attitude drift error is
where
meet the condition
.
are the 3-axis angular attitudes calculated by gyro at moment
, respectively.
3.4. Phase-Lag-Free Low Pass Filter
Phase lag error will be introduced in the above attitude estimation process based on Kalman filter. An additional high-order signal with phase advanced information is introduced to filter the original signal. The phase lag can be compensated for by phase-lag-free LPF.
Define
where
are the 3-axis angular attitude calculated by Kalman filter in
Section 3.3 and
are the 3-axis angular velocity calculated from gyro in
Section 3.1. These two inputs are original signals with noise.
Figure 4 shows the design of this filter. The filter can be described as two sensors which could measure the nearby order information. During data process,
should be the position signal when
is the velocity signal. In addition, if
is the velocity signal,
should be the acceleration signal.
In this research, the signal is low-pass filtered and the phase lag is corrected by . The parameter g is cut off frequency of LPF. The tracking characteristic of output signal is strengthened with the increase in g. If , the relationship is met.
The output of system in
Figure 4 can be expressed as
where
are the 3-axis angular attitude processed by phase-lag-free LPF. It can be seen that the design is composed of LPF and can greatly suppress the input noise from Equation (25).