Blade Shape Optimization and Analysis of a Propeller for VTOL Based on an Inverse Method
Abstract
:1. Introduction
2. Modeling
2.1. VTOL Typical Mission Profile
2.2. Blade Element Momentum Theory
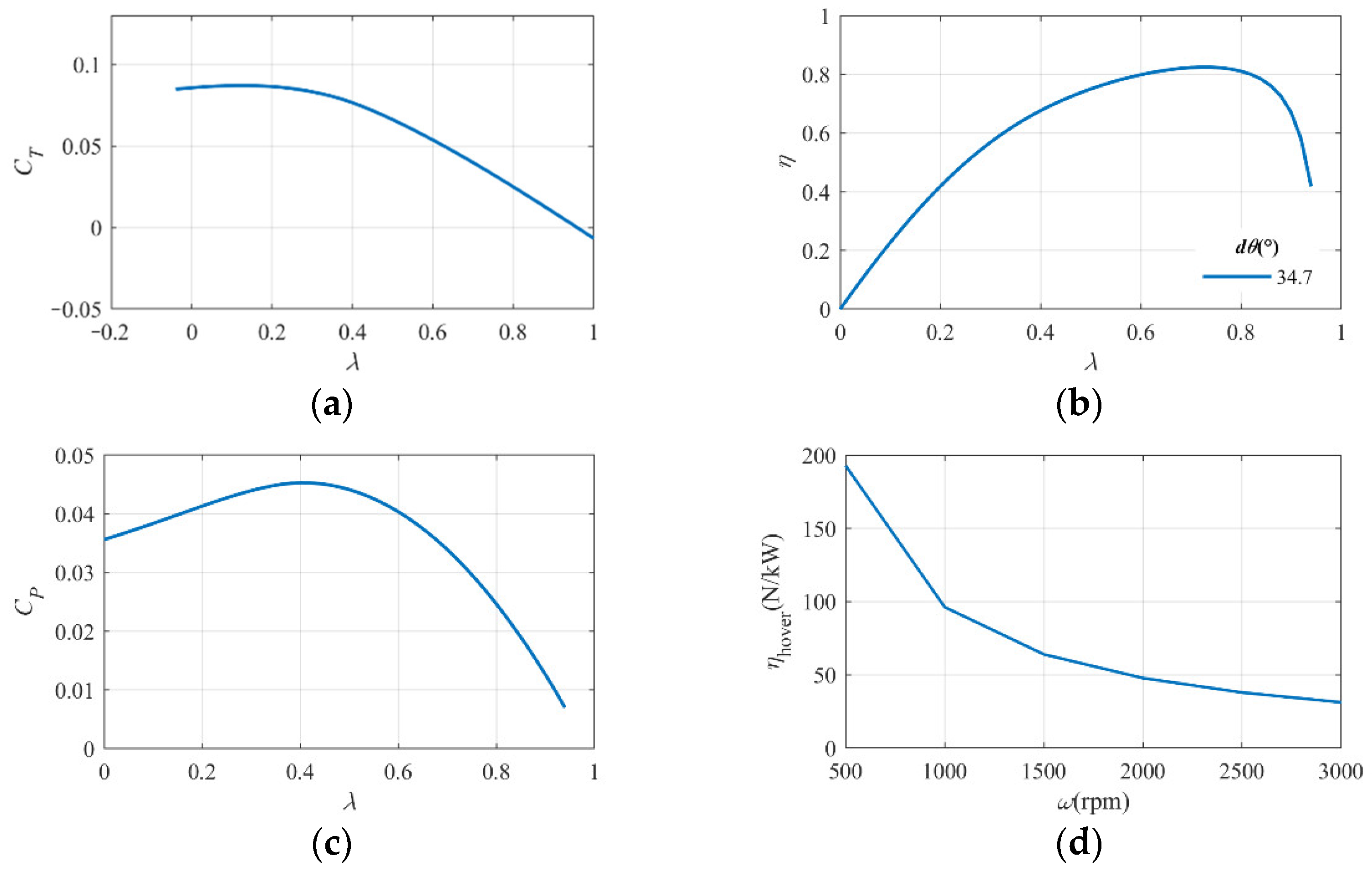
2.2.1. Theory and Numerical Solution
2.2.2. 2D Airfoil Aerodynamics Surrogate Model
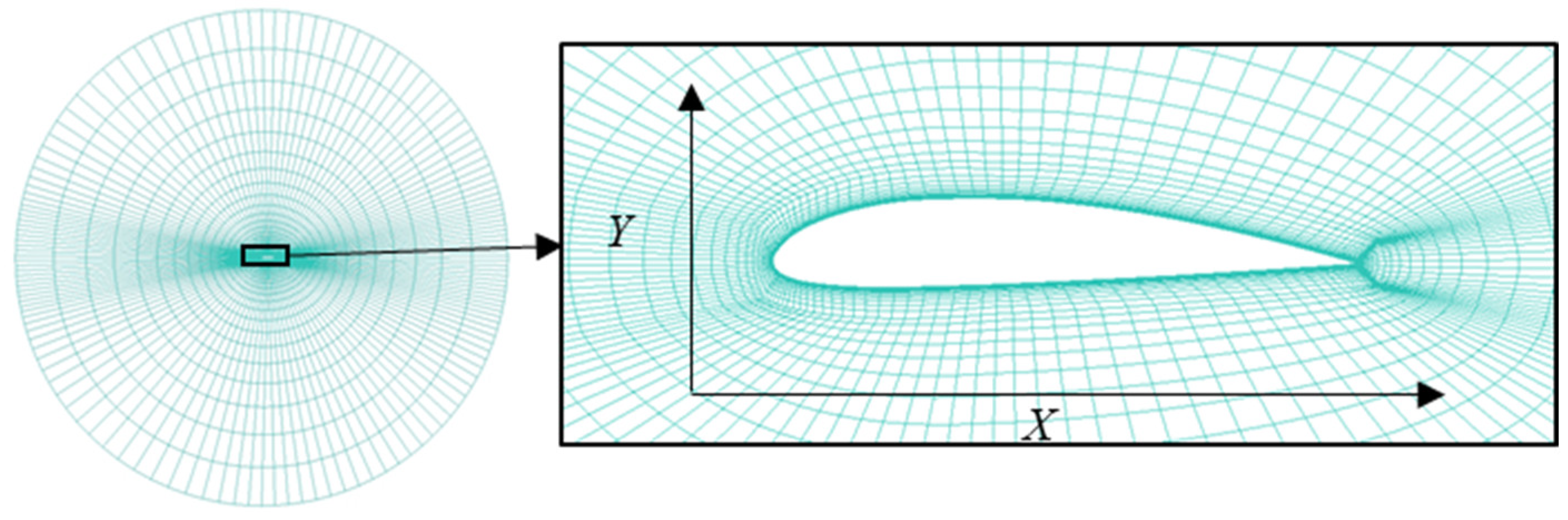
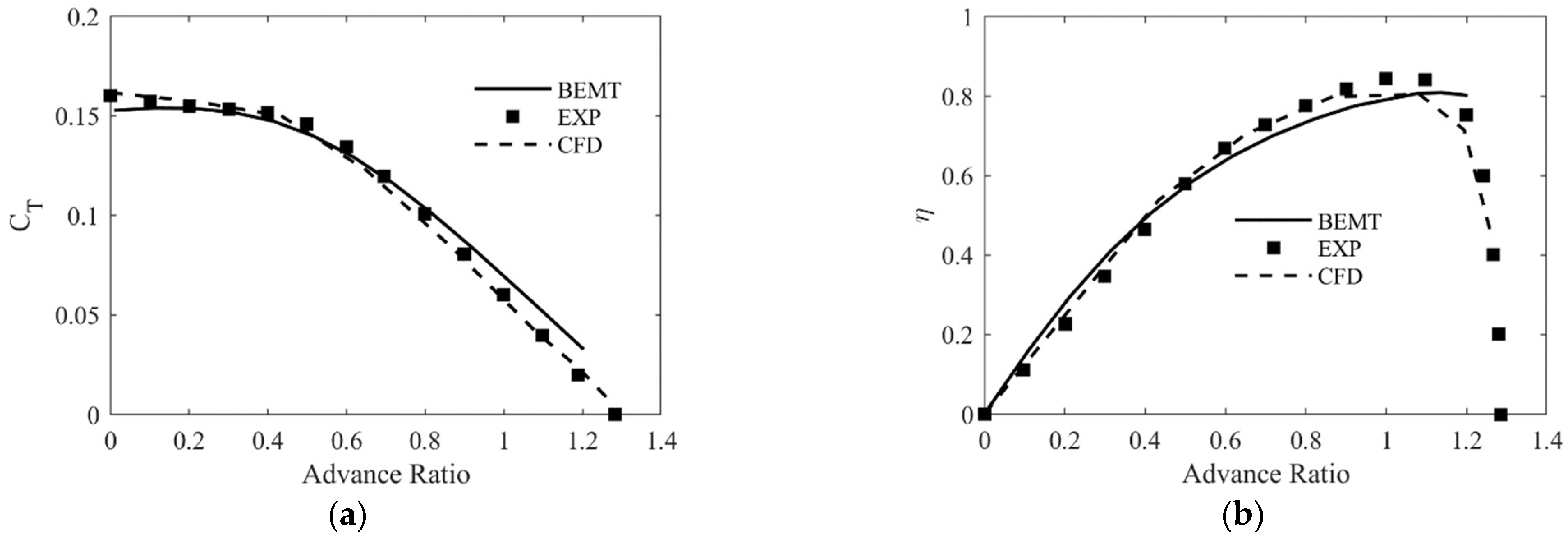
2.2.3. Validation of the BEMT and CFD
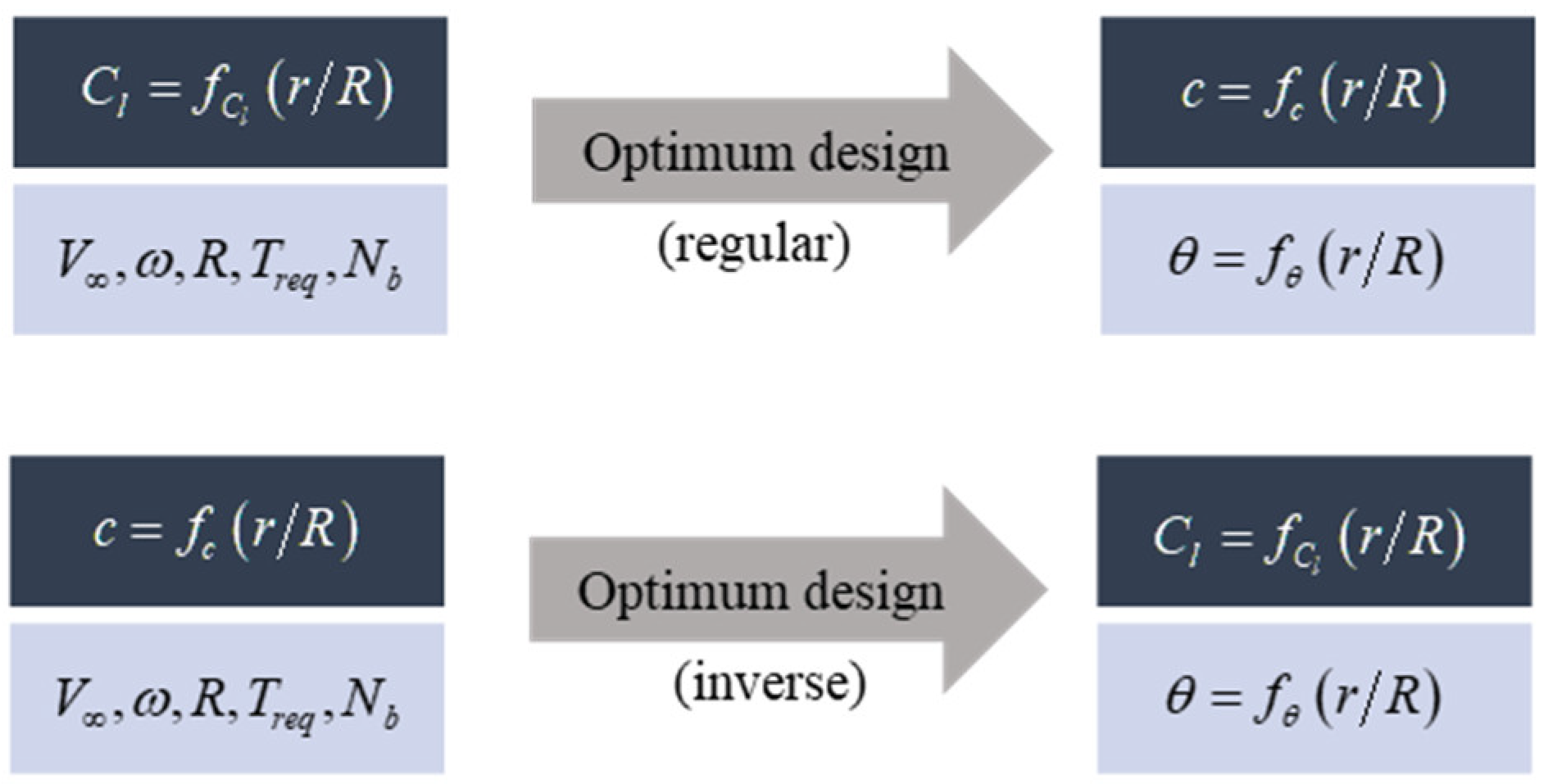
2.3. Propeller Inverse Design Method for the Cruising Stage
2.4. Brushless Motor Modeling
2.5. Non-Cruising Stage Trimming
3. Optimization Problem
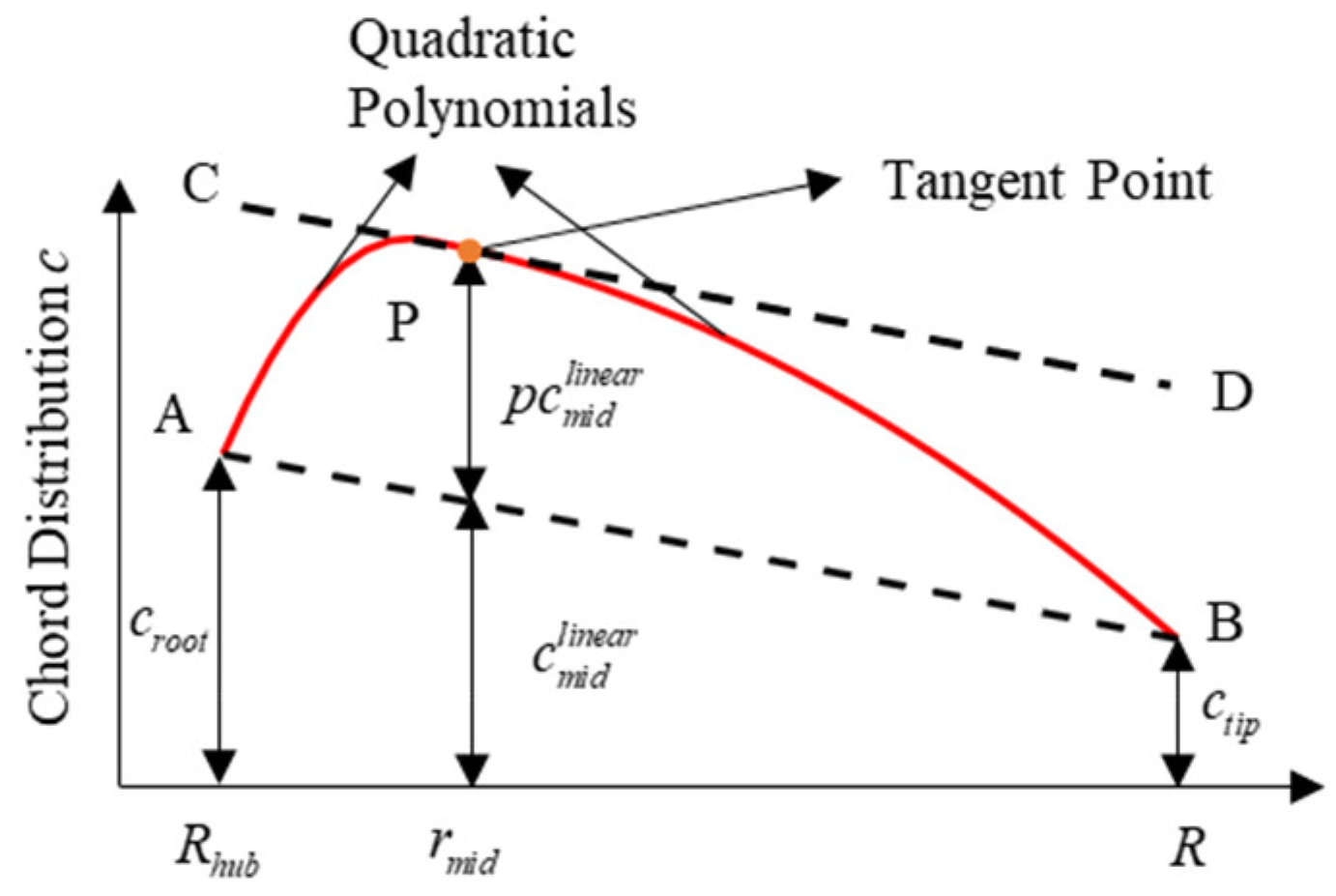
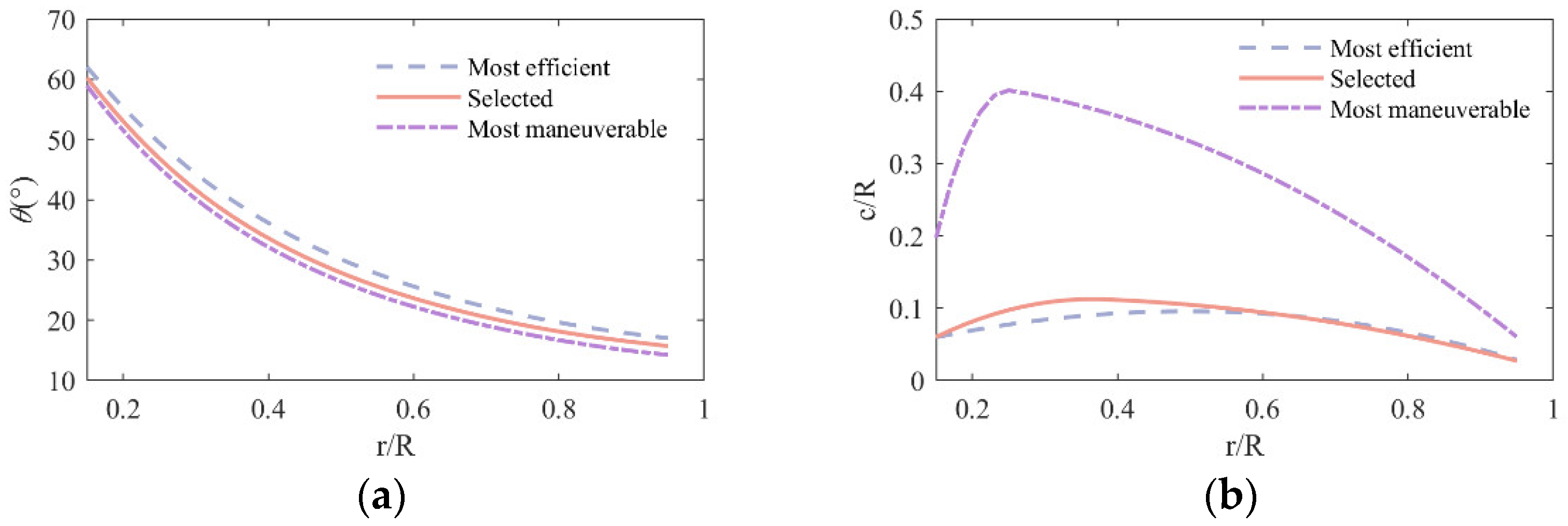
3.1. Chord-Length Distribution Parameterization
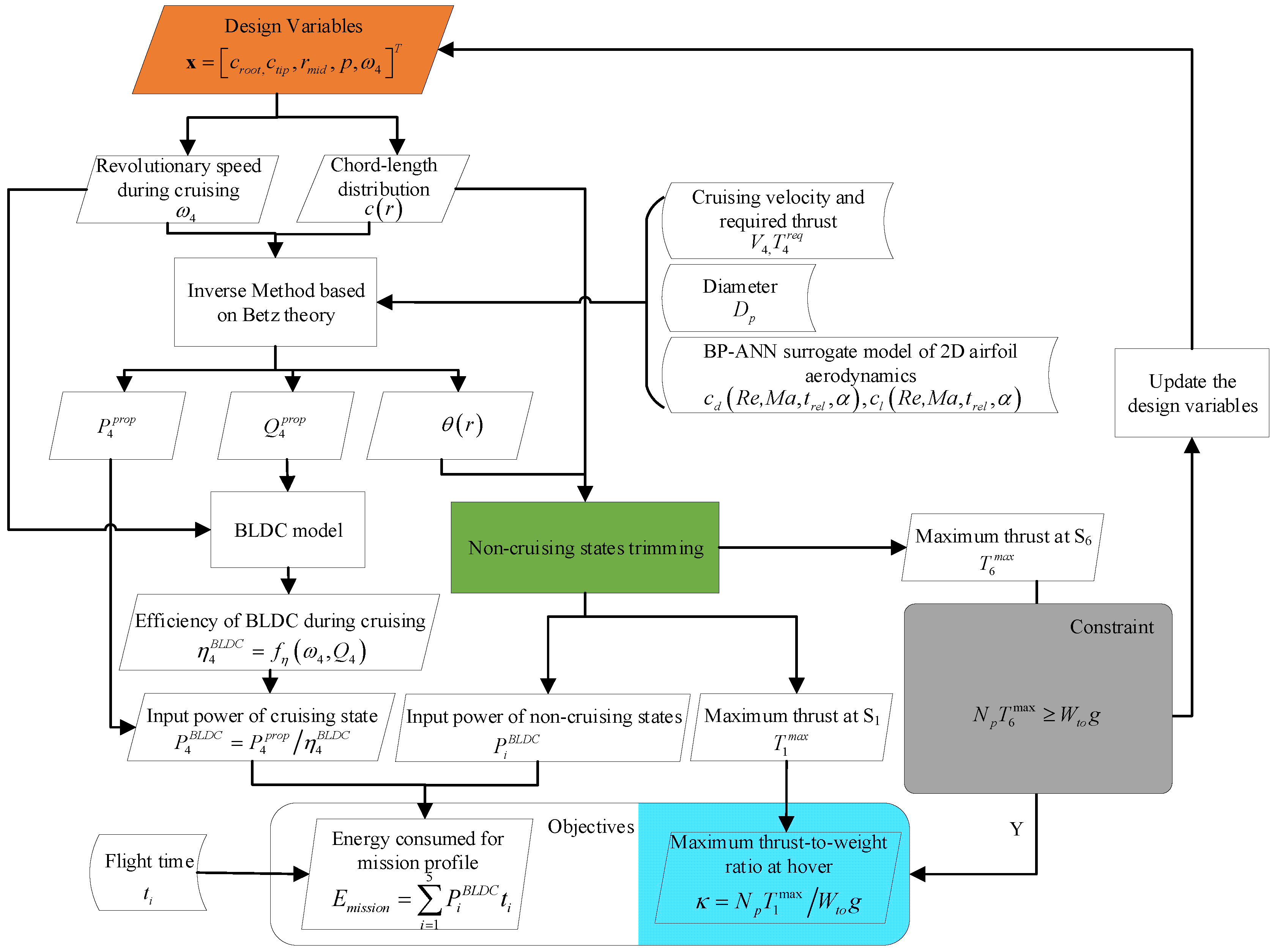
3.2. Optimization Framework for a VTOL Propeller
4. Case Study
4.1. Vahana A3 Tilt-Wing Introduction
4.2. Optimization Result
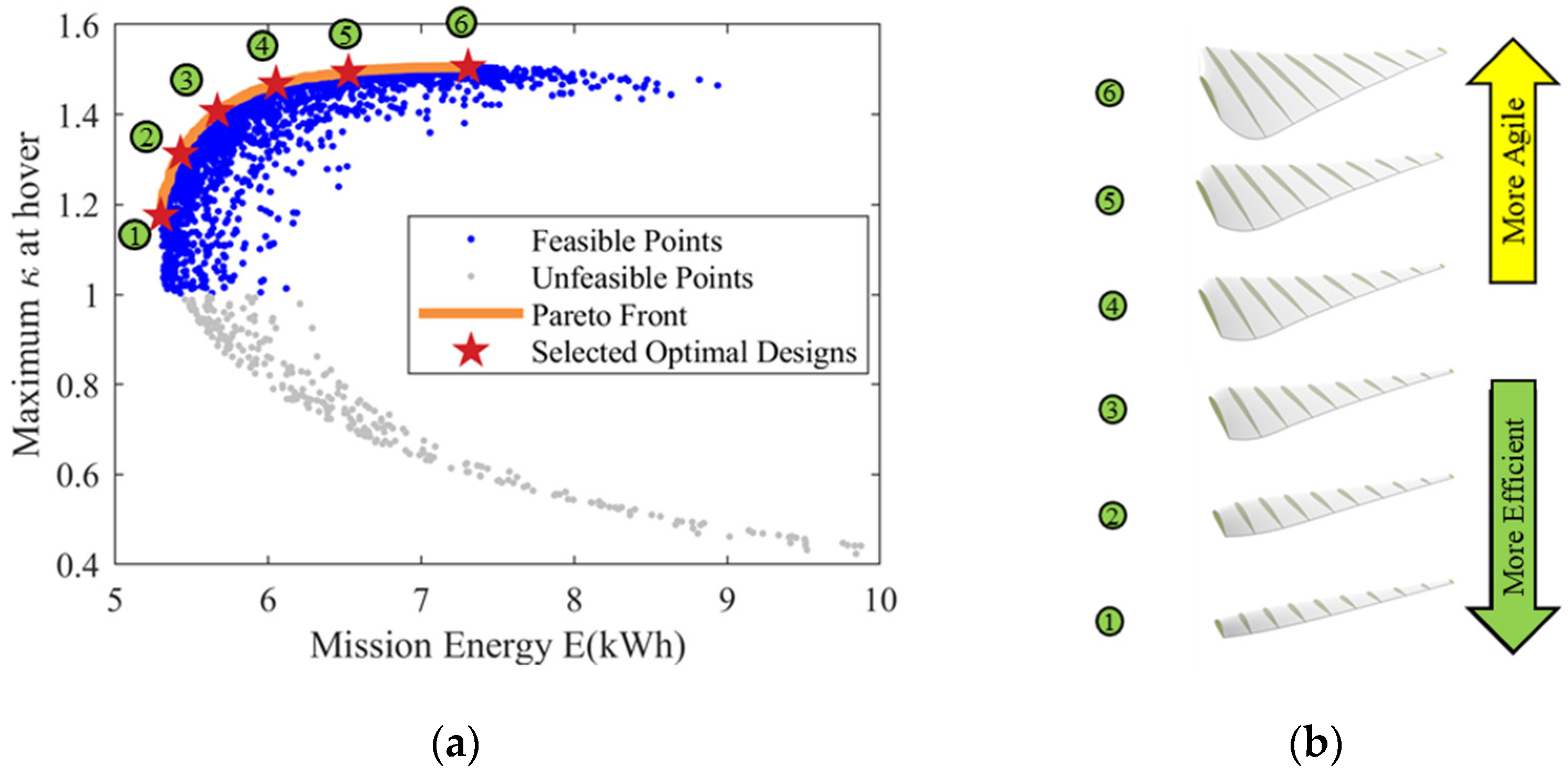
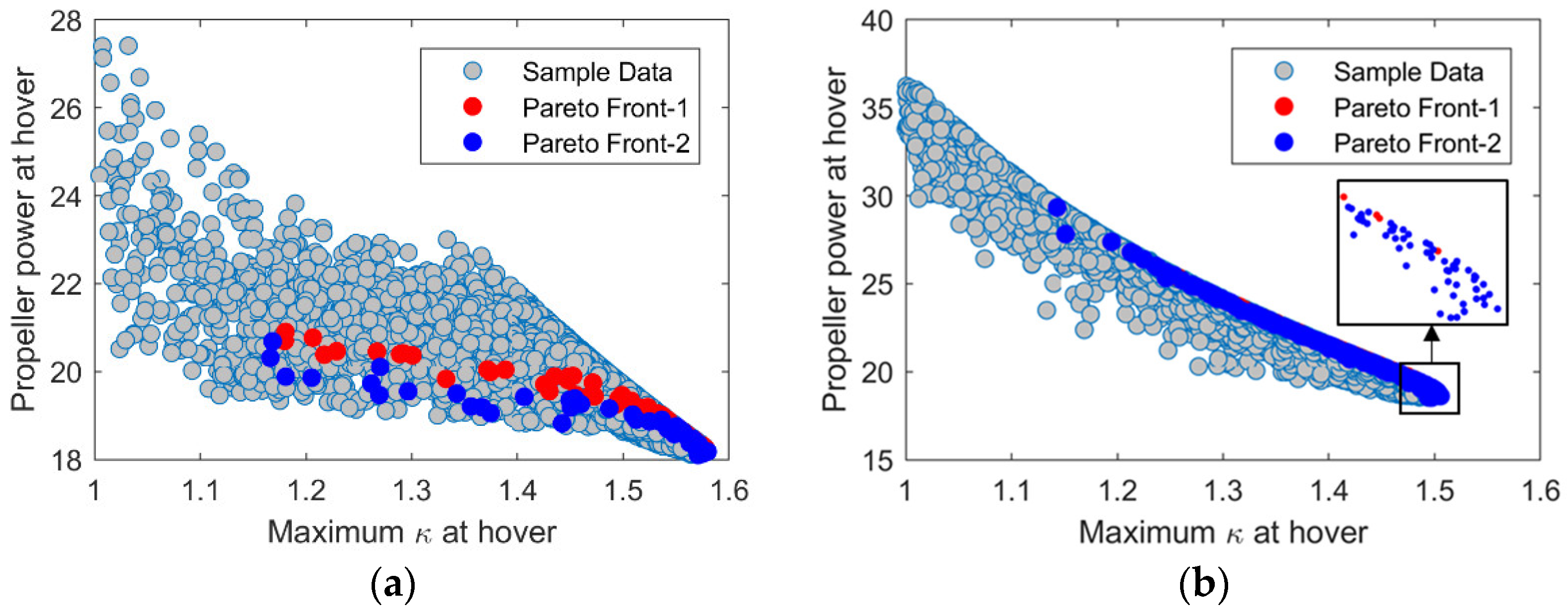
4.2.1. VPP Optimization Result
4.2.2. FPP Optimization Result
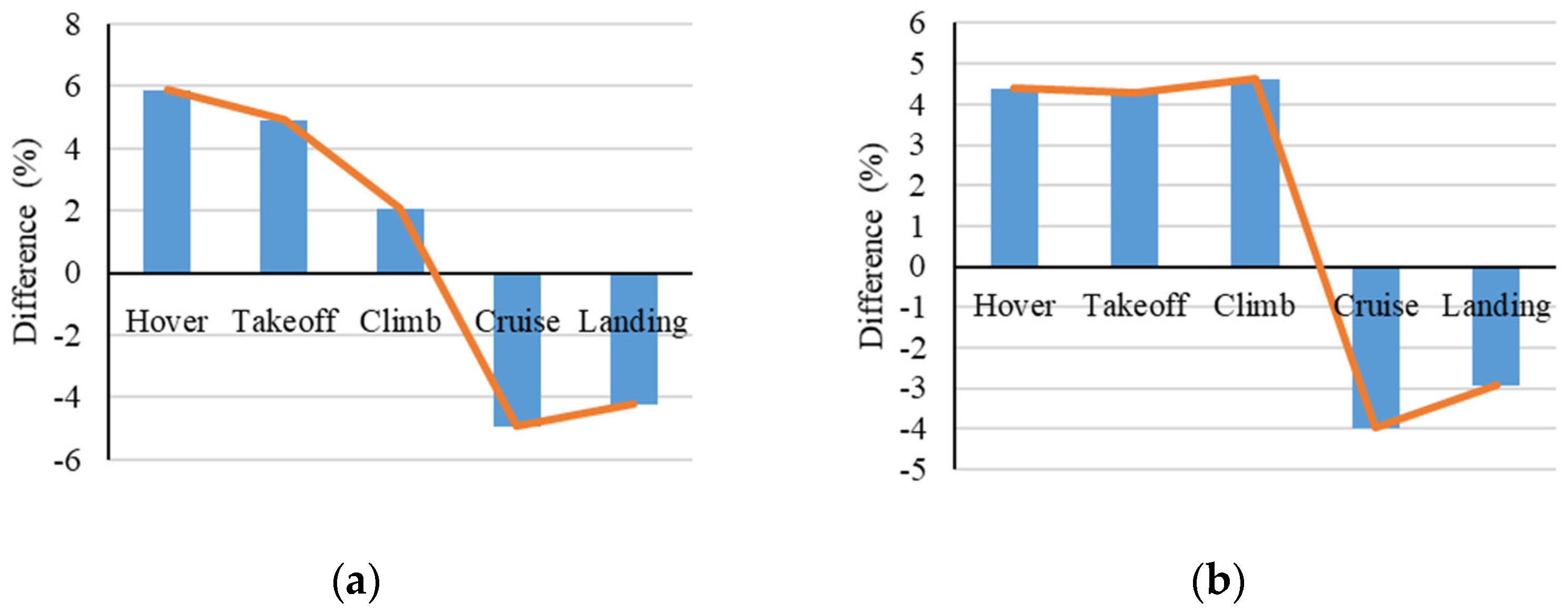
4.2.3. Analysis of the Maximum Thrust-to-Weight Ratio
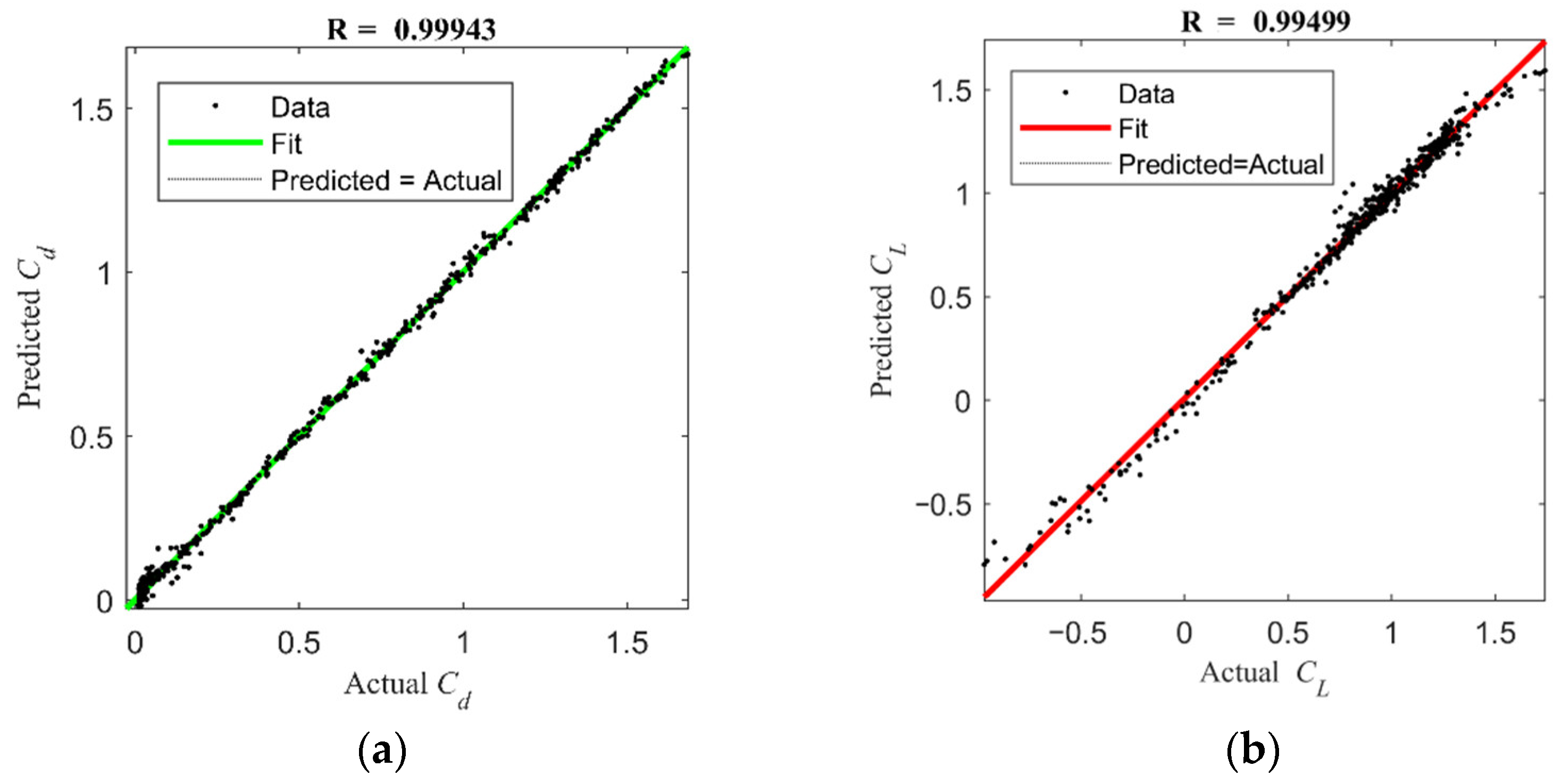
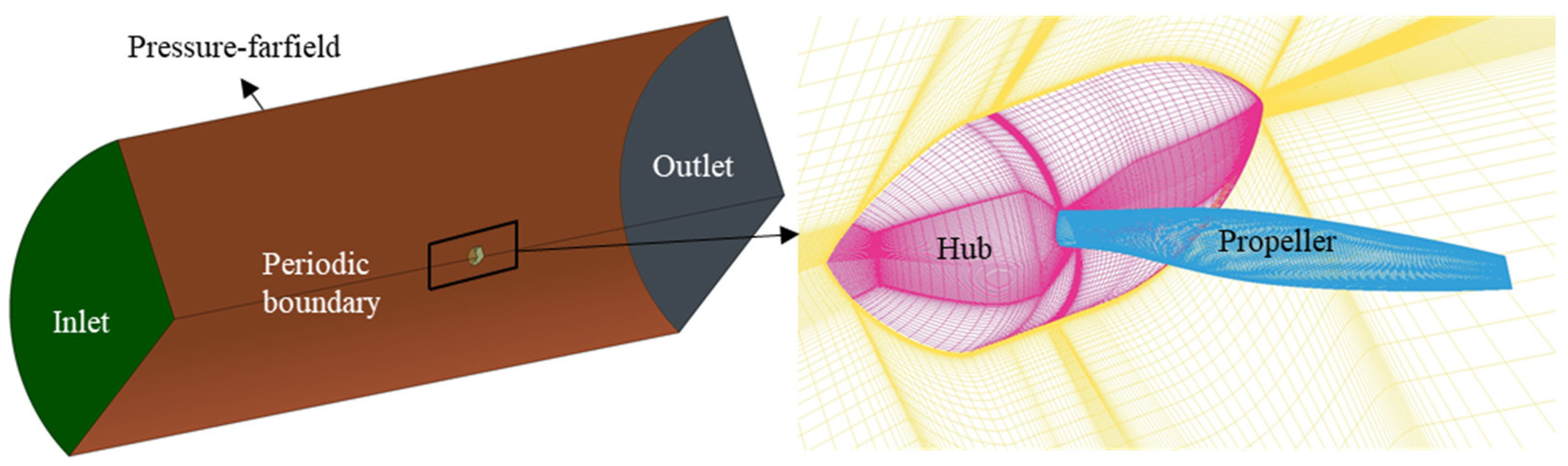
4.2.4. CFD Validation
5. Analysis
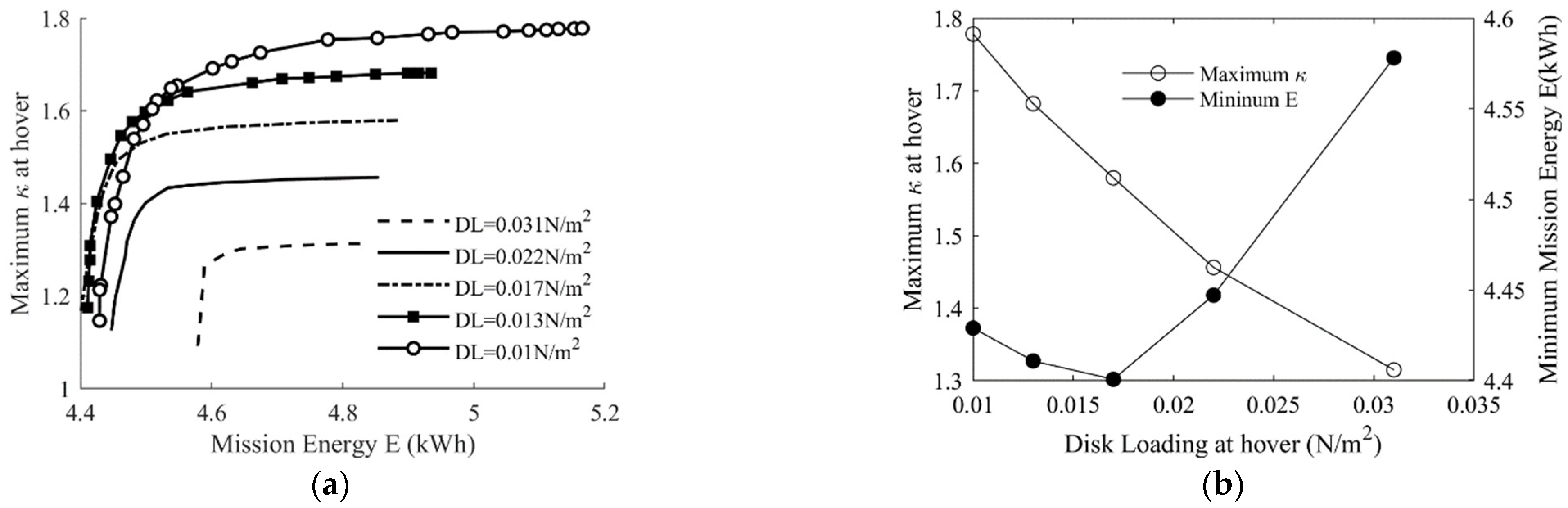
5.1. Analysis of Hover Disk Loading
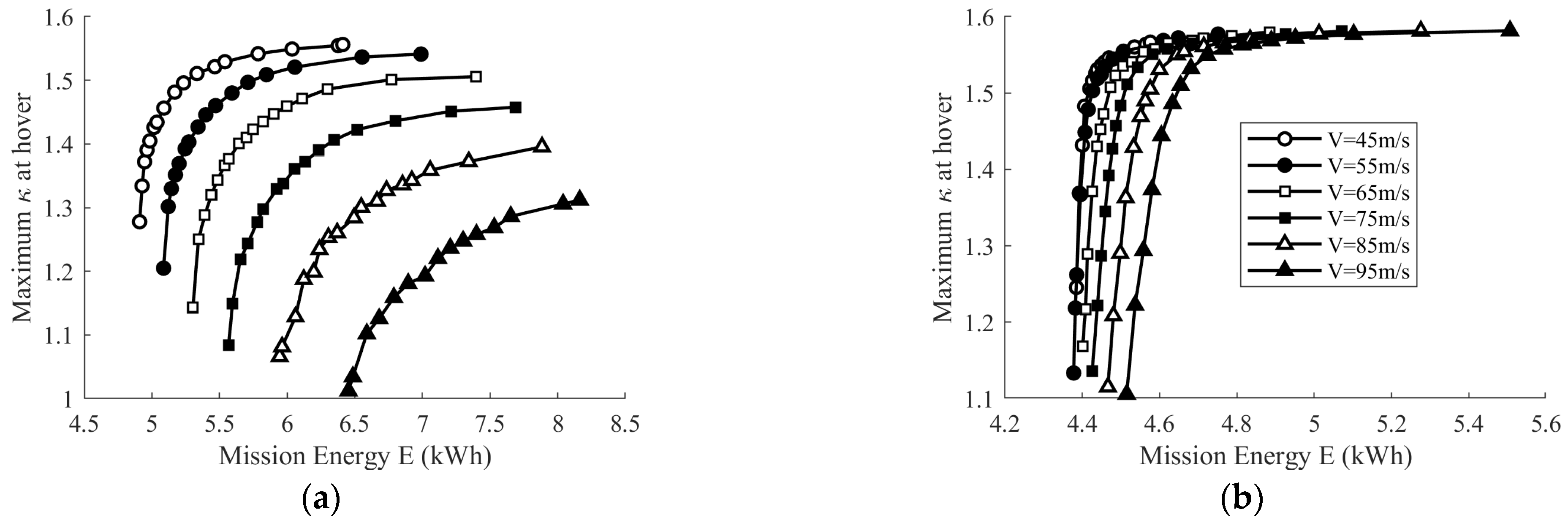
5.2. Analysis of the Cruising Speed
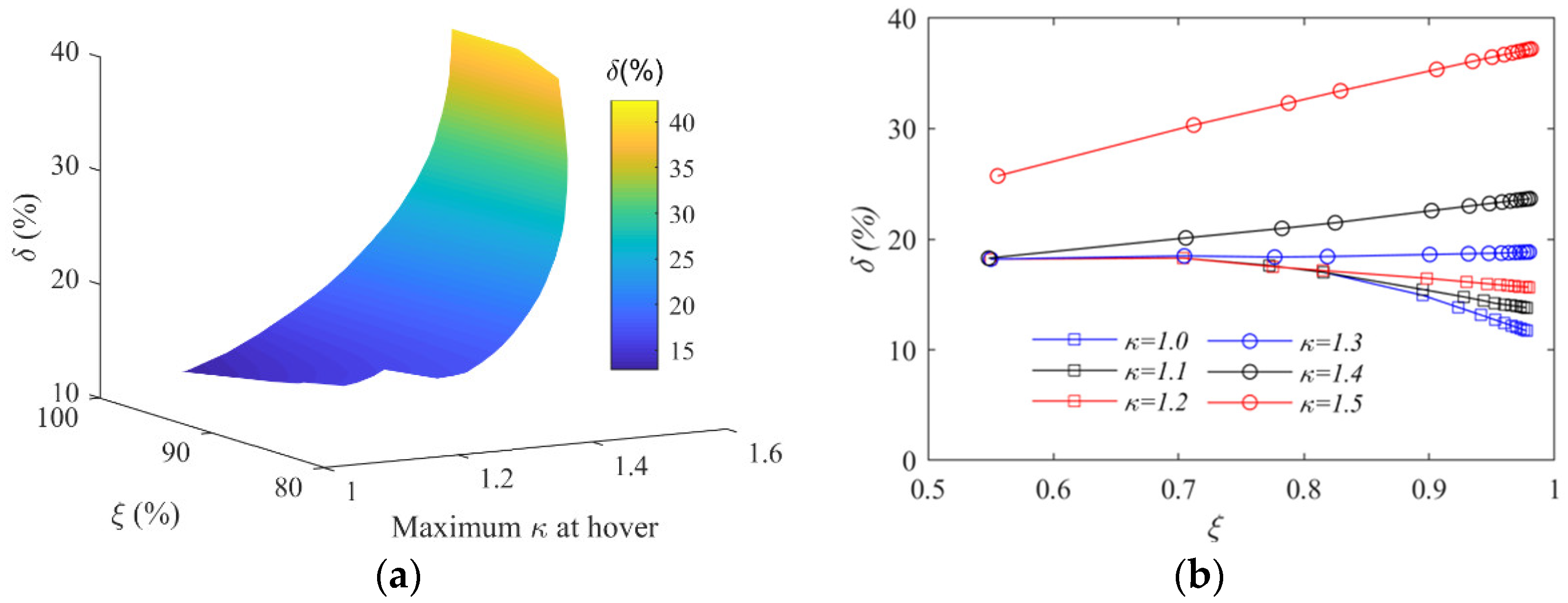
5.3. Analysis of the Level Flight Energy Ratio
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pradeep, P.; Wei, P. Energy Optimal Speed Profile for Arrival of Tandem Tilt-Wing eVTOL Aircraft with RTA Constraint. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- May, M.S.; Milz, D.; Looye, G. Dynamic Modeling and Analysis of Tilt-Wing Electric Vertical Take-Off and Landing Vehicles. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Dickeson, J.J.; Miles, D.; Cifdaloz, O.; Wells, V.L.; Rodriguez, A.A. Robust LPV H∞ gain-scheduled hover-to-cruise conversion for a tilt-wing rotorcraft in the presence of CG variations. In Proceedings of the IEEE Conference on Decision and Control, New York, NY, USA, 9–13 July 2007; pp. 2773–2778. [Google Scholar] [CrossRef]
- Duan, D.; Wang, Z.; Wang, Q.; Li, J. Research on Integrated Optimization Design Method of High-Efficiency Motor Propeller System for UAVs with Multi-States. IEEE Access 2020, 8, 165432–165443. [Google Scholar] [CrossRef]
- Straubinger, A.; Rothfeld, R.; Shamiyeh, M.; Büchter, K.-D.; Kaiser, J.; Plötner, K.O. An overview of current research and developments in urban air mobility—Setting the scene for UAM introduction. J. Air Transp. Manag. 2020, 87, 101852. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Cai, C.; Cai, G. A survey of hybrid Unmanned Aerial Vehicles. Prog. Aerosp. Sci. 2018, 98, 91–105. [Google Scholar] [CrossRef]
- Bell Helicopters. Bell Boeing V-22 Osprey—Bell Helicopter. 2016. Available online: http://www.bellhelicopter.com/military/bell-boeing-v-22#/?tab=features-tab (accessed on 15 February 2022).
- UAVGLOBAL. Bell Eagle Eye. 2015. Available online: http://www.uavglobal.com/bell-eagle-eye/ (accessed on 15 February 2022).
- Montagnani, D.; Tugnoli, M.; Zanotti, A.; Syal, M.; Droandi, G. Analysis of the interactional aerodynamics of the vahana evtol using a medium fidelity open source tool. In Proceedings of the VFS Aeromechanics for Advanced Vertical Flight Technical Meeting, San Jose, CA, USA, 21–23 January 2020; pp. 436–451. [Google Scholar]
- Electric VTOL News. Joby S4. eVTOL News. 2021. Available online: https://evtol.news/joby-s4/ (accessed on 15 February 2022).
- Fredericks, W.J.; Moore, M.D.; Busan, R.C. Benefits of Hybrid-Electric Propulsion to Achieve 4× Cruise Efficiency for a VTOL UAV. In Proceedings of the 2013 International Powered Lift Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar]
- Muraoka, K.; Okada, N.; Kubo, D. Quad Tilt Wing VTOL UAV: Aerodynamic Characteristics and Prototype Flight. In Proceedings of the AIAA Infotech@Aerospace Conference, Seattle, WA, USA, 6–9 April 2009. [Google Scholar]
- Droandi, G.; Gibertini, G. Aerodynamic blade design with multi-objective optimization for a tiltrotor aircraft. Aircr. Eng. Aerosp. Technol. Int. J. 2015, 87, 19–29. [Google Scholar] [CrossRef]
- Leishman, J.; Rosen, K. Challenges in the Aerodynamic Optimization of High-Efficiency Proprotors. J. Am. Helicopter Soc. 2011, 56, 12001–12004. [Google Scholar] [CrossRef]
- Yincheang, N.; Haixin, C. Rapid Aerodynamic Design of Prop-rotor Blade with Optimization. Chin. J. Turbomach. 2019, 61, 19–27. [Google Scholar]
- Kang, H.J. Design Optimization of QTP-UAV Prop-Rotor Blade Using ModelCenter®. J. Aerosp. Syst. Eng. 2017, 11, 36–43. [Google Scholar]
- Chattopadhyay, A.; McCarthy, T.R.; Seeley, C.E. Multiple design point optimization of high-speed proprotors. J. Aircr. 1996, 33, 625–627. [Google Scholar] [CrossRef]
- Mehmood, H.; Nakamura, T.; Johnson, E.N. A maneuverability analysis of a novel hexarotor UAV concept. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 437–446. [Google Scholar] [CrossRef]
- Arellano-Quintana, V.M.; Portilla-Flores, E.A.; Merchan-Cruz, E.A.; Nino-Suarez, P.A. Multirotor design optimization using a genetic algorithm. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1313–1318. [Google Scholar] [CrossRef]
- Mogorosi, T.O.; Jamisola, R.S.; Subaschandar, N.; Mohutsiwa, L.O. Thrust-to-Weight Ratio Optimization for Multi-Rotor Drones Using Neural Network with Six Input Parameters. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 1194–1199. [Google Scholar] [CrossRef]
- Li, K.; Song, Z.; Cai, Z.; Wang, Y. Multi-rotor pseudo-inverse method research based on kernel space. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; IEEE: Piscataway, NJ, USA, 2017; pp. 1418–1422. [Google Scholar] [CrossRef]
- Wang, M.; Diepolder, J.; Zhang, S.; Söpper, M.; Holzapfel, F. Trajectory optimization-based maneuverability assessment of eVTOL aircraft. Aerosp. Sci. Technol. 2021, 117, 106903. [Google Scholar] [CrossRef]
- Chen, G.; Ma, D.; Jia, Y.; Xia, X.; He, C. Comprehensive Optimization of the Unmanned Tilt-Wing Cargo Aircraft with Distributed Propulsors. IEEE Access 2020, 8, 137867–137883. [Google Scholar] [CrossRef]
- Hepperle, M. Inverse Aerodynamic Design Procedure for Propellers Having a Prescribed Chord-Length Distribution. J. Aircr. 2010, 47, 1867–1872. [Google Scholar] [CrossRef]
- Betz, A. Screw Propellers with Minimum Energy Loss; NRC, Division of Mechanical Engineering: Cairo, Egypt, 1958. [Google Scholar]
- Adkins, C.N.; Liebeck, R.H. Design of optimum propellers. J. Propuls. Power 1994, 10, 676–682. [Google Scholar] [CrossRef]
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Liu, P. Aerodynamic Propeller Theory and Application; Beihang University Press: Beijing, China, 2006. [Google Scholar]
- Viterna, L.A.; Janetzke, D.C. Theoretical and Experimental Power from large Horizontal-Axis Wind Turbines; National Aeronautics and Space Administration, Lewis Research Center: Cleveland, OH, USA, 1982. [Google Scholar] [CrossRef] [Green Version]
- Montgomerie, B.; Forskningsinstitut, T. Methods for Root Effects, Tip Effects and Extending the Angle of Attack Range to ±180°, with Application to Aerodynamics for Blades on Wind Turbines and Propellers; Swedish Defence Research Agency: Stockholm, Sweden, 2004. [Google Scholar]
- Hartman, E.P.; Biermann, D. The Aerodynamic Characteristics of Full-Scale Propellers Having 2, 3, 4 Blades of Clark Y and R.A.F. 6 Airfoil Sections; NASA Technical Report 640; NASA: Washington, DC, USA, 1938; no. 640; p. 30. Available online: https://ntrs.nasa.gov/citations/19930091715 (accessed on 8 March 2022).
- Fred, D.H.W.; Weick, E. The Twenty-Foot Propeller Research Tunnel of the National Advisory Committee for Aeronautics; National Advisory Committee for Aeronautics: Washington, DC, USA, 1928. [Google Scholar]
- Gabriel, D.L.; Meyer, J.; Plessis, F.D. Brushless DC motor characterisation and selection for a fixed wing UAV. In Proceedings of the IEEE AFRICON Conference, Livingstone, Zambia, 13–15 September 2011; pp. 13–15. [Google Scholar] [CrossRef]
- Bogusz, P.; Korkosz, M.; Powrózek, A.; Prokop, J.; Wygonik, P. An analysis of properties of the BLDC motor for unmanned aerial vehicle hybrid drive. In Proceedings of the 2015 International Conference on Electrical Drives and Power Electronics (EDPE), Tatranska Lomnica, Slovakia, 21–23 September 2015; pp. 458–464. [Google Scholar] [CrossRef]
- Duan, D.; Pei, J.; Zu, R.; Li, J. Power optimization and control of motor variable-pitch propeller propulsion system. ACTA Aeronaut. Astronaut. Sin. 2021, 42, 623933. [Google Scholar] [CrossRef]
- Droandi, G.; Gibertini, G. Aerodynamic shape optimisation of a proprotor and its validation by means of CFD and experiments. Aeronaut. J. 2015, 119, 1223–1251. [Google Scholar] [CrossRef] [Green Version]
- MAGicALL. Power Your Aircraft to New Heights; MAGiDRIVE: Camarillo, CA, USA, 2018; pp. 211–220. Available online: http://www.magicall.biz/magidrive-datasheet/ (accessed on 10 March 2022).
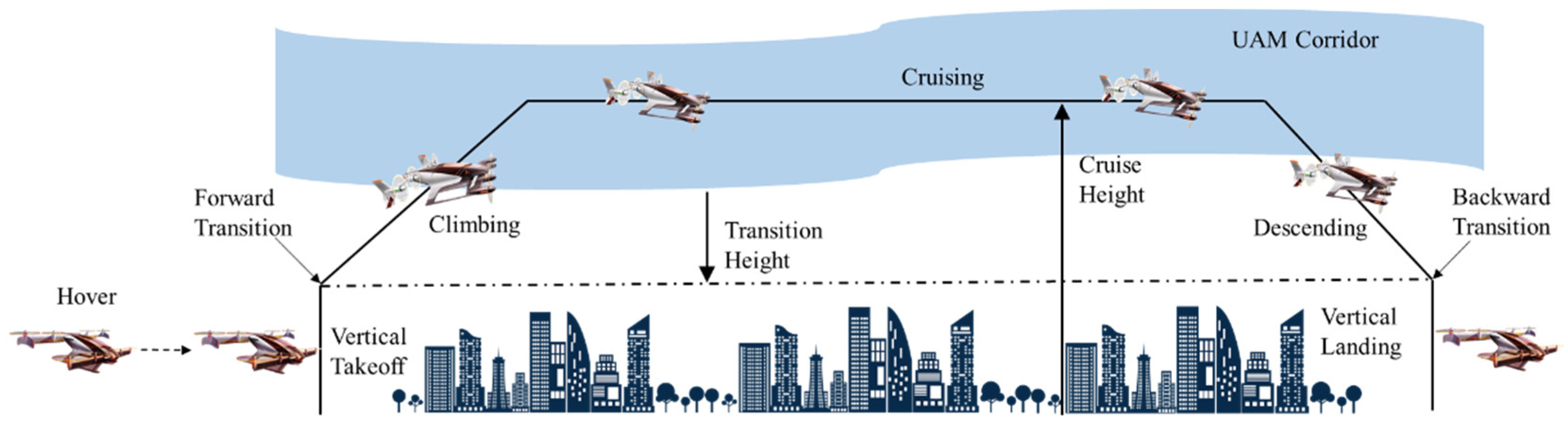
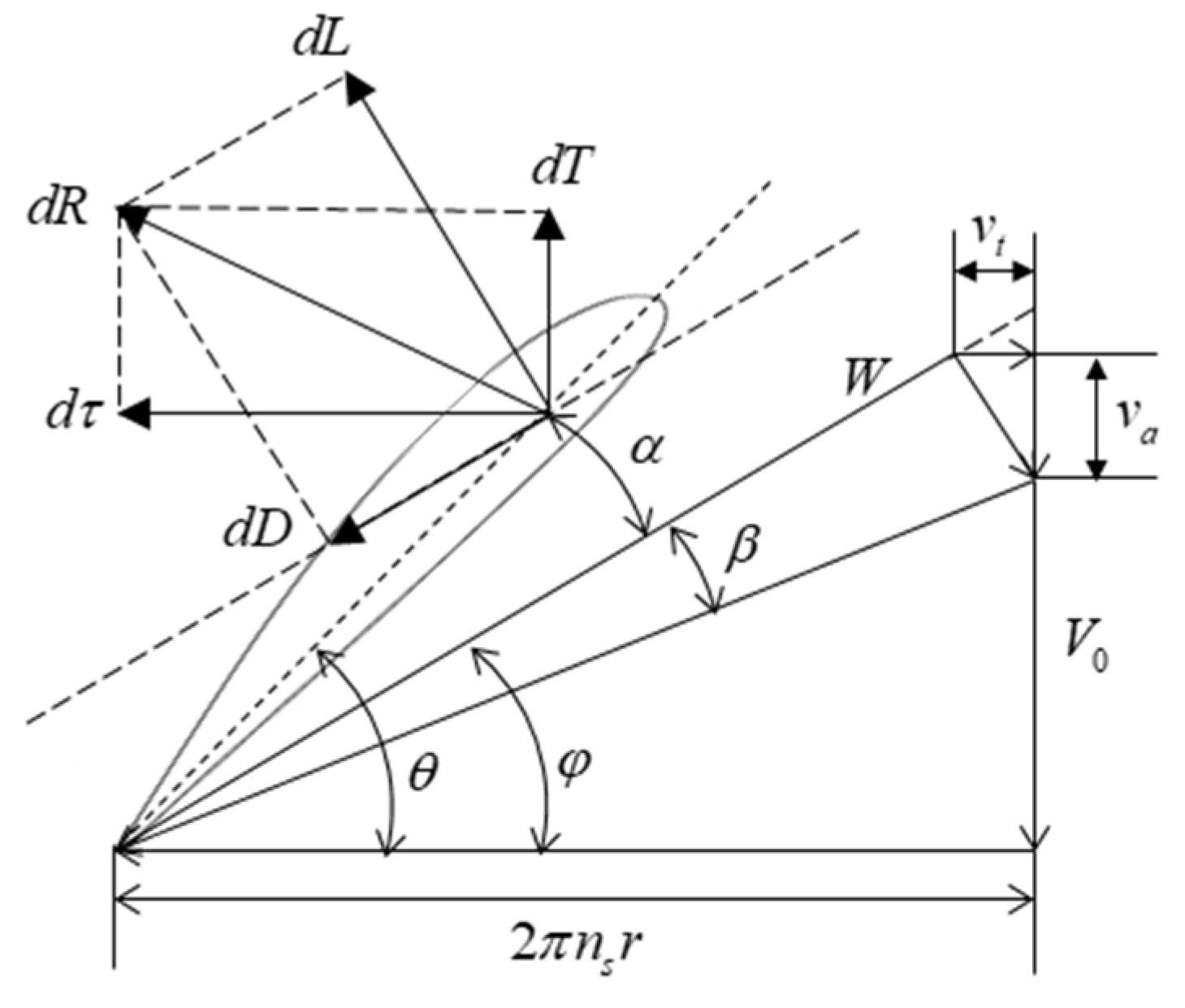
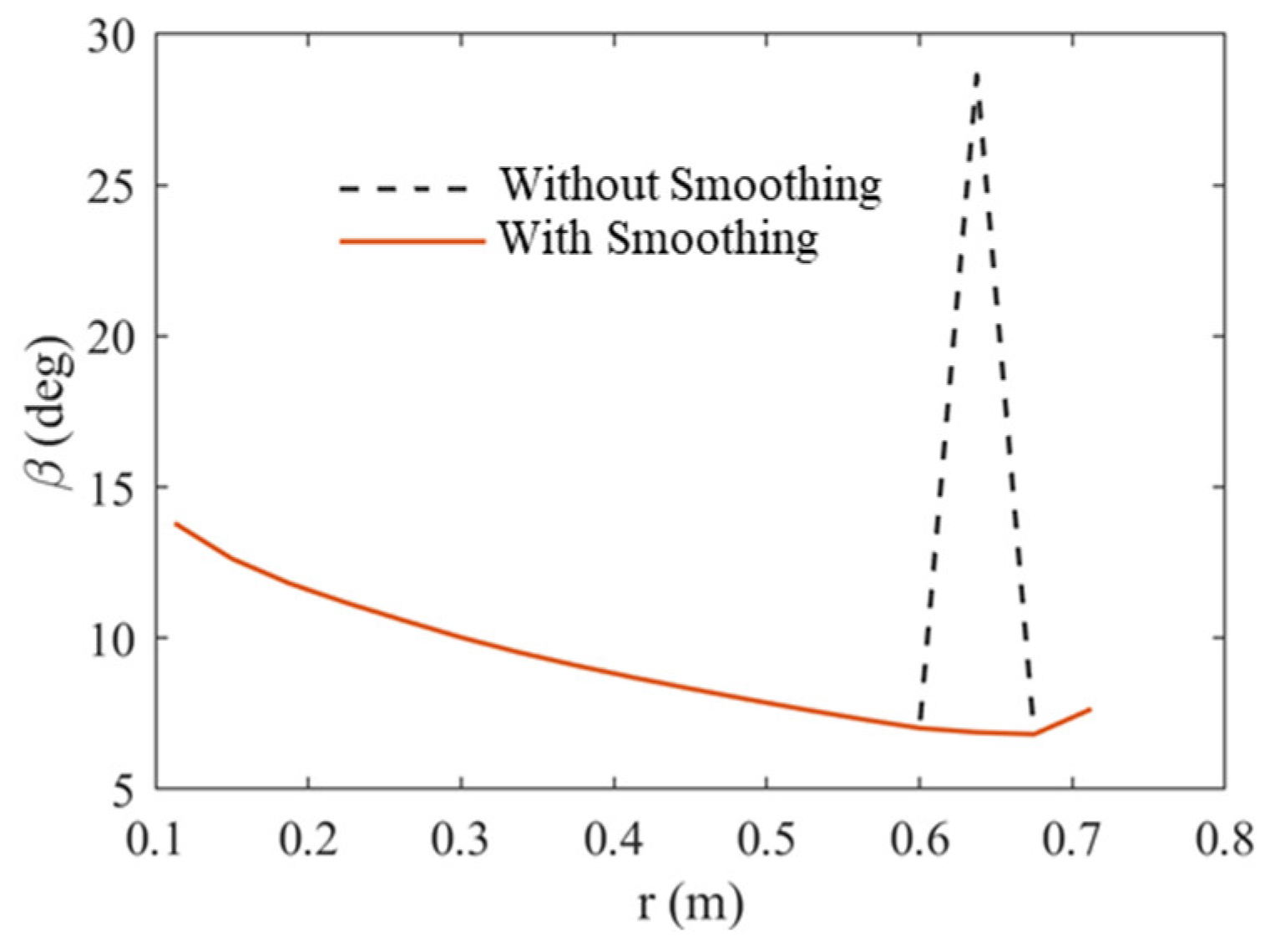
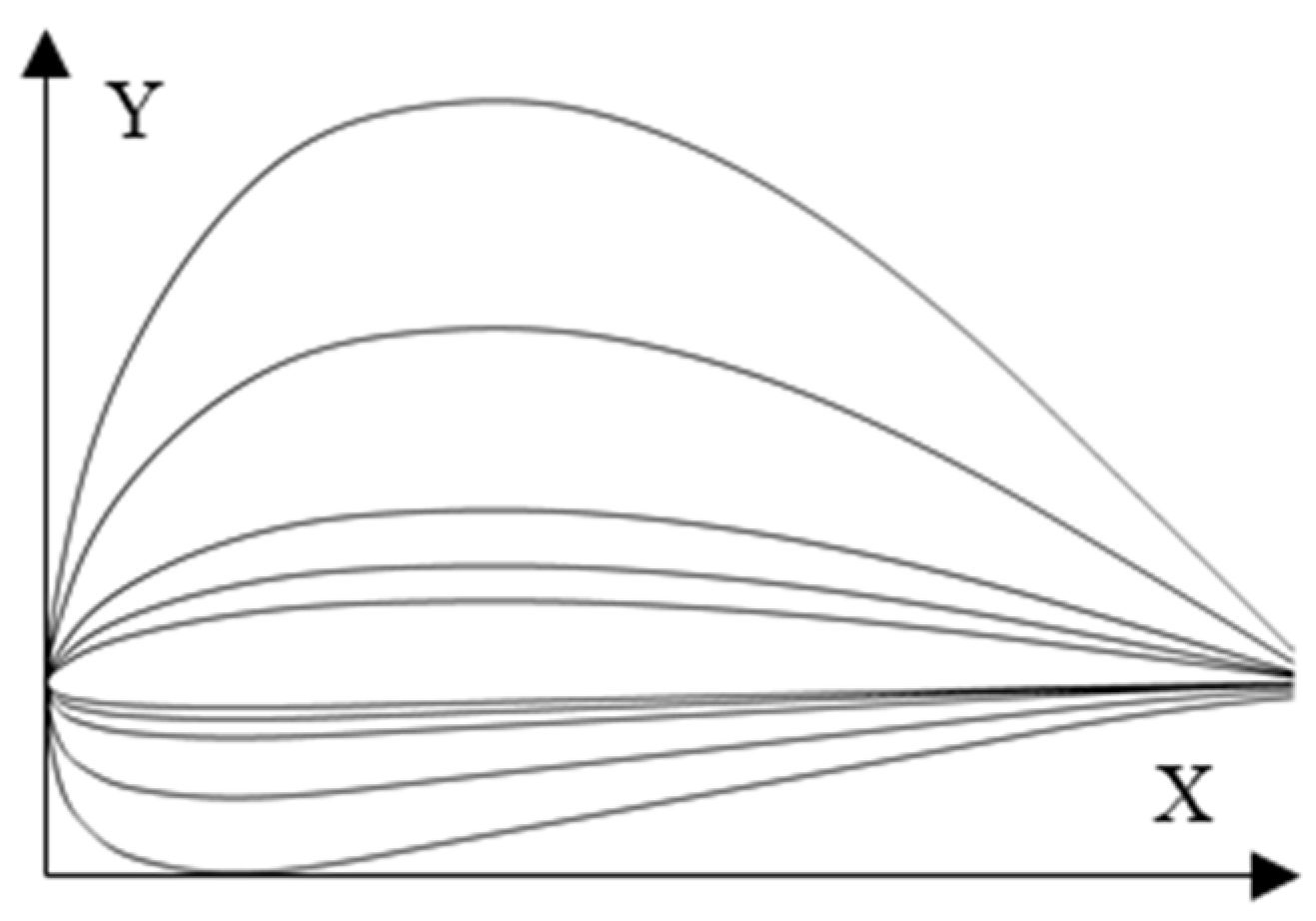

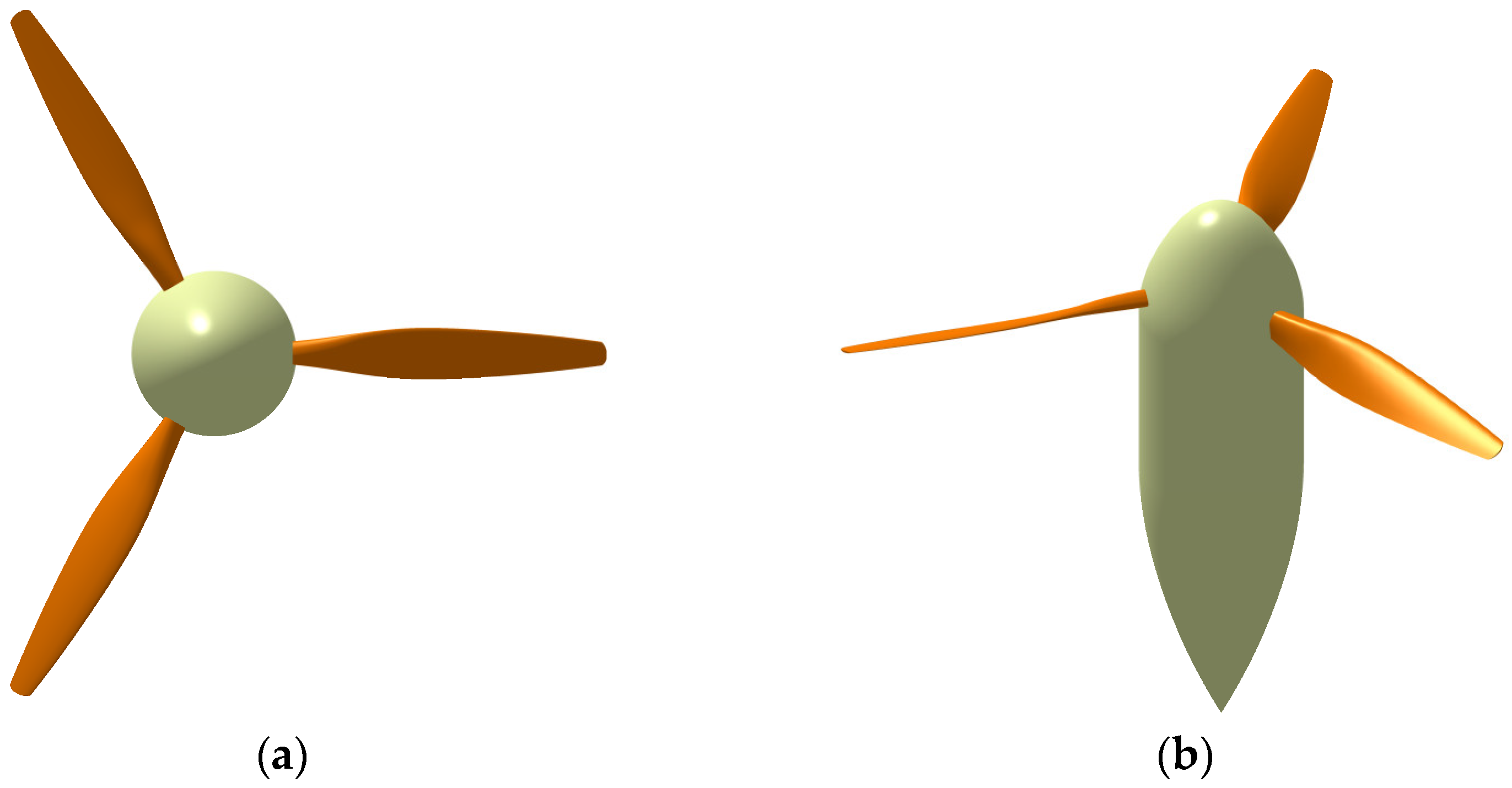

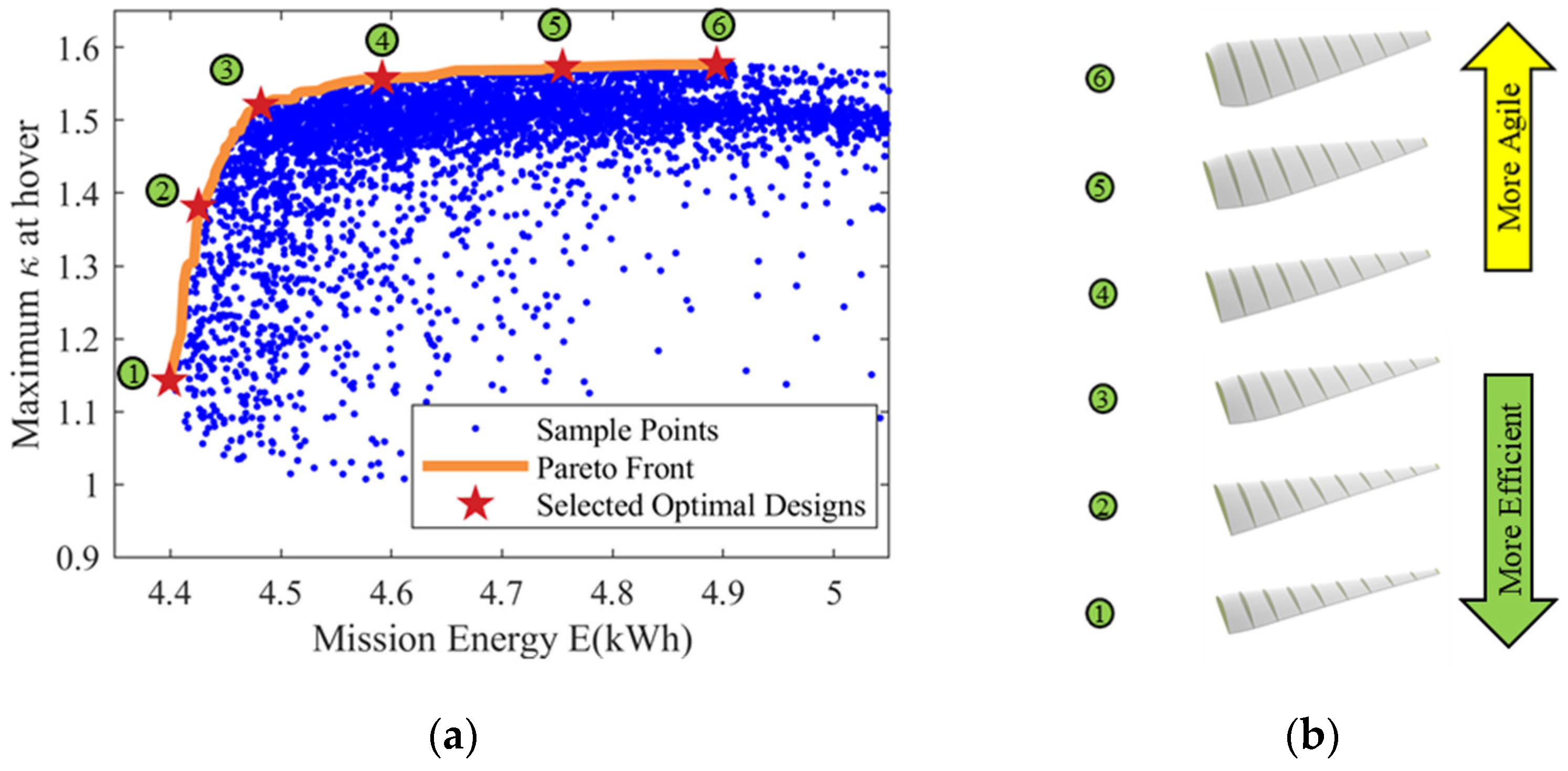

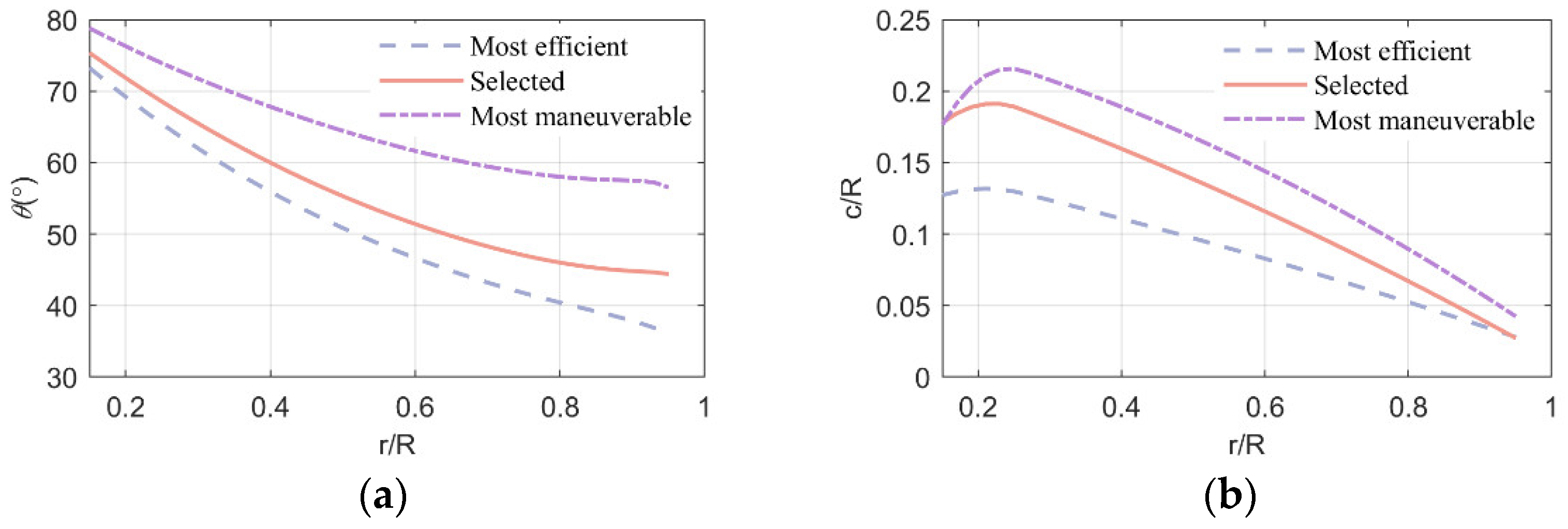
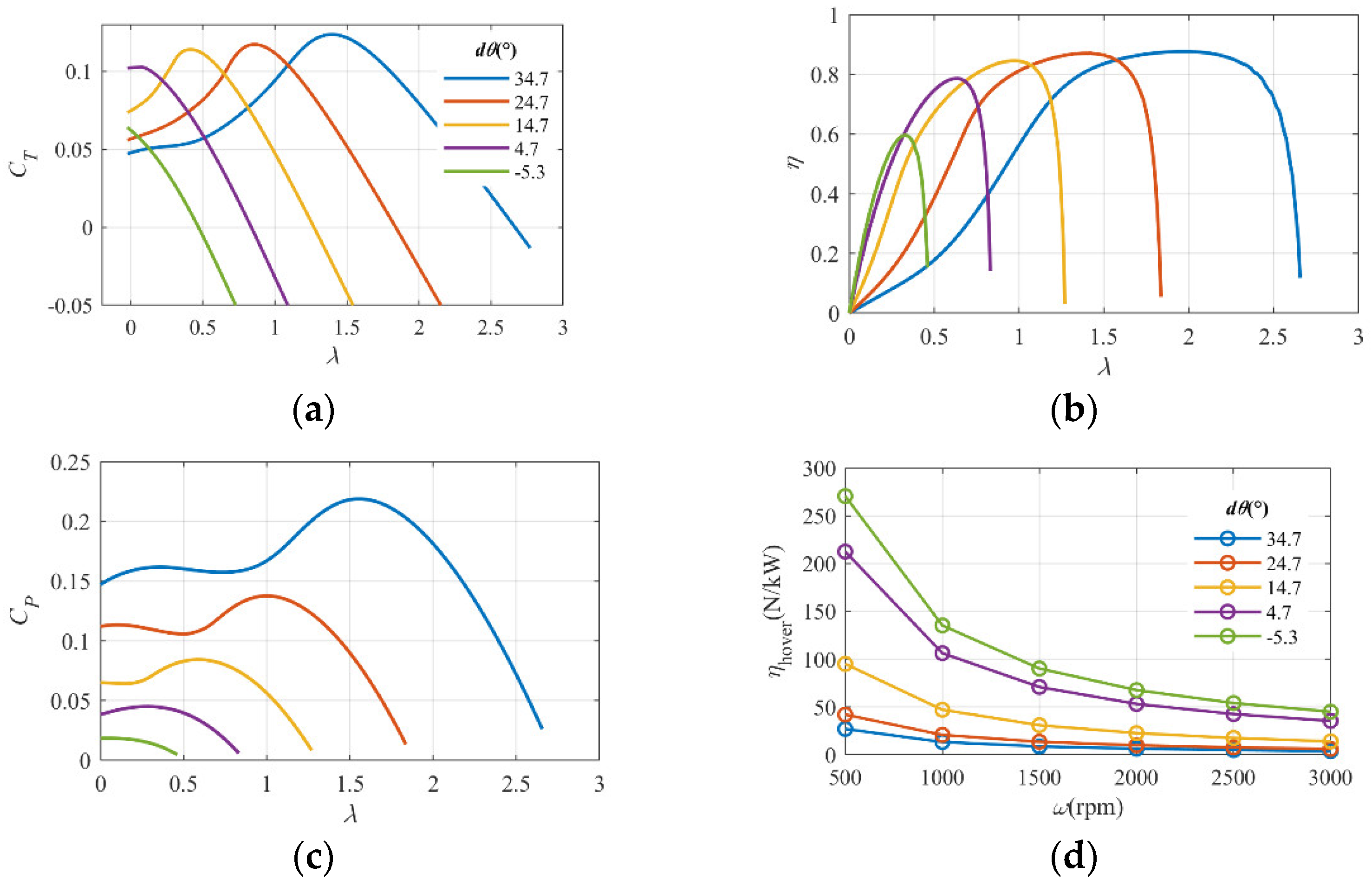
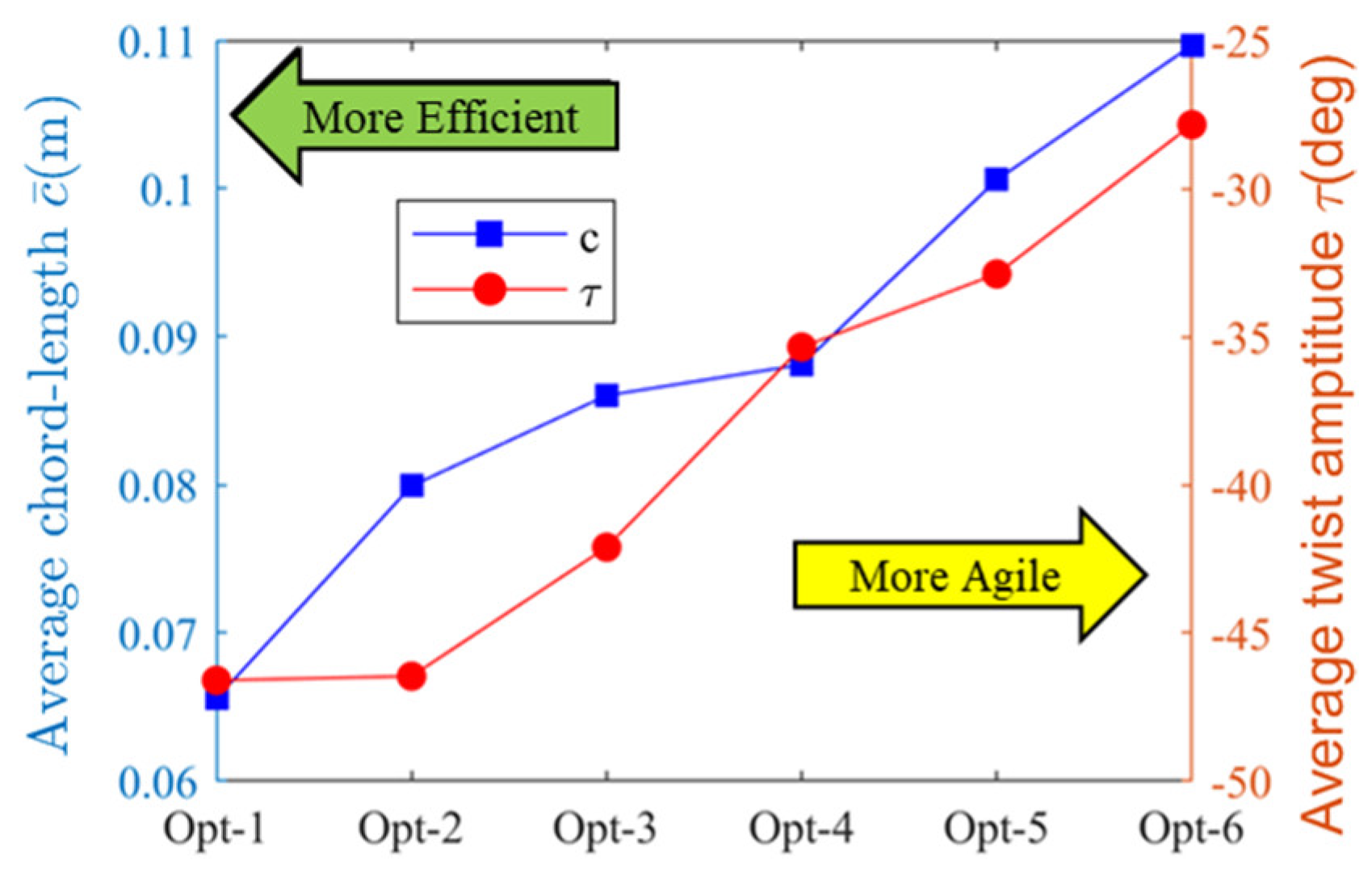



| Flight State | Mission Profile Parameters | ||||
|---|---|---|---|---|---|
| Name | Symbol | Velocity (m/s) | Thrust Required (N) | Time(s) | |
| Cruising | S4 | 65.25 | 155.8 | 920 | |
| Non-Cruising State | Hover | S1 | 0 | 922.4 | 30 |
| Vertical Takeoff | S2 | 3 | 922.4 | 34 | |
| Climbing | S3 | 37 | 169.4 | 124 | |
| Vertical Landing | S5 | −1.5 | 922.4 | 67 | |
| Vertical Climb with Maximum Velocity | S6 | 10 | 922.4 | - | |
| Given Parameters | Estimated Parameters | ||
|---|---|---|---|
| 40 | 8.0 | ||
| 5500 | 0.25 | ||
| 200 | 2.0 | ||
| 24~800 | |||
| Design Variables | Range | Design Variables | Range |
|---|---|---|---|
| VPP | FPP | Advantage of VPP | |
|---|---|---|---|
| 4.399 | 5.303 | −17.05% | |
| 1.577 | 1.505 | 4.57% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X.; Ma, D.; Zhang, L.; Liu, X.; Cong, K. Blade Shape Optimization and Analysis of a Propeller for VTOL Based on an Inverse Method. Appl. Sci. 2022, 12, 3694. https://doi.org/10.3390/app12073694
Xia X, Ma D, Zhang L, Liu X, Cong K. Blade Shape Optimization and Analysis of a Propeller for VTOL Based on an Inverse Method. Applied Sciences. 2022; 12(7):3694. https://doi.org/10.3390/app12073694
Chicago/Turabian StyleXia, Xinglu, Dongli Ma, Liang Zhang, Xing’an Liu, and Keran Cong. 2022. "Blade Shape Optimization and Analysis of a Propeller for VTOL Based on an Inverse Method" Applied Sciences 12, no. 7: 3694. https://doi.org/10.3390/app12073694
APA StyleXia, X., Ma, D., Zhang, L., Liu, X., & Cong, K. (2022). Blade Shape Optimization and Analysis of a Propeller for VTOL Based on an Inverse Method. Applied Sciences, 12(7), 3694. https://doi.org/10.3390/app12073694






