A Lyapunov Stability Analysis of Modified HOSM Controllers Using a PID-Sliding Surface Applied to an ABS Laboratory Setup
Abstract
:1. Introduction
- A modified HOSM controller using a PID-sliding surface was designed.
- The convergence and stability of the controller were proven rigorously using a theoretical analysis based on the Lyapunov function.
- The proposed controller was implemented in an ABS laboratory setup, and the results were compared with a PID-like controller.
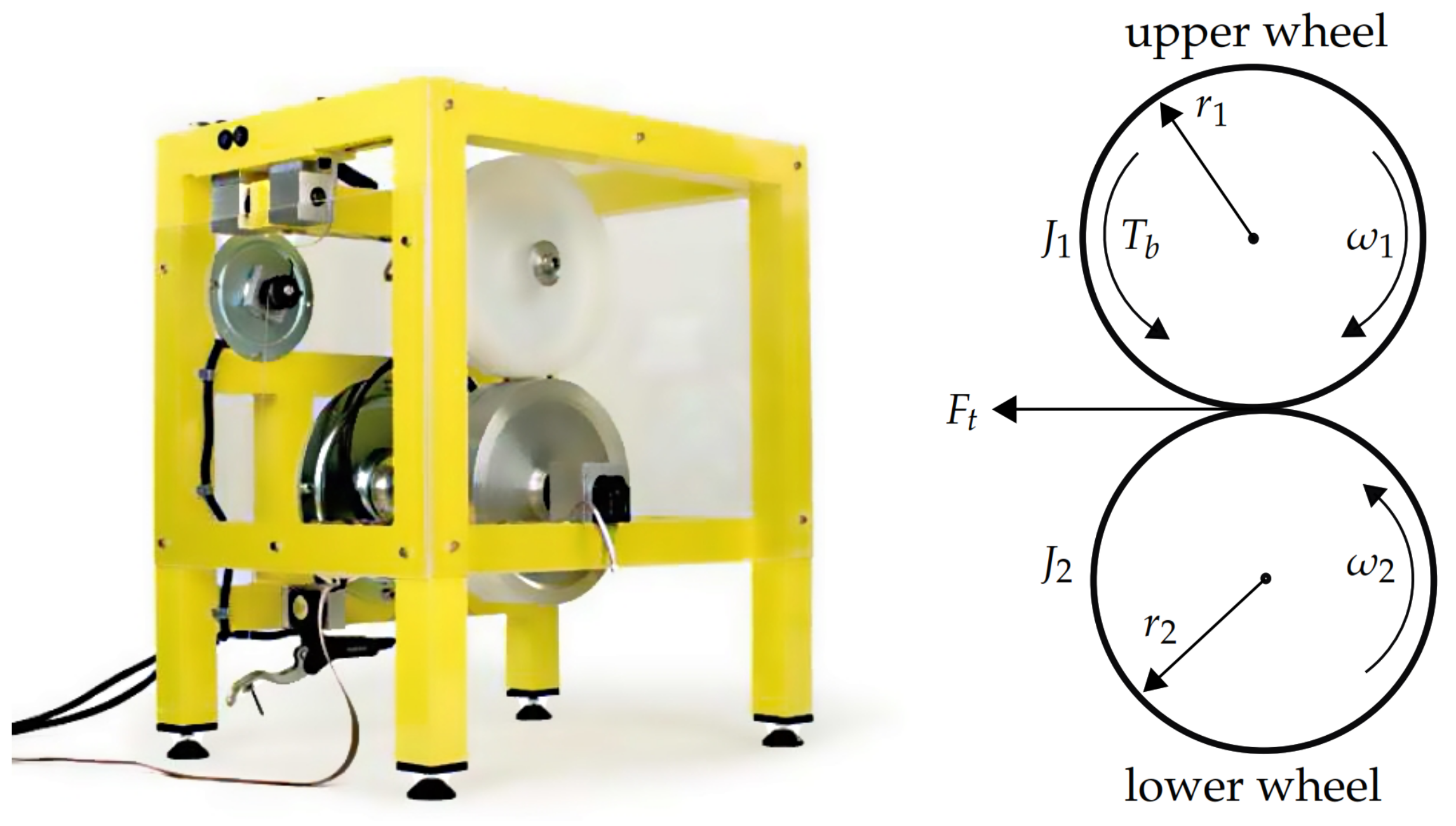
2. Mathematical Model of the Experimental ABS Laboratory Setup
Mathematical Model of the Experimental ABS Laboratory Setup
3. A Modified HOSM Controller Using a PID-Sliding Surface for an ABS Laboratory Setup
3.1. Design of the PID-Sliding Surface
3.2. Design of the Modified HOSM Control Using a PID-Sliding Surface
4. Simulation Results
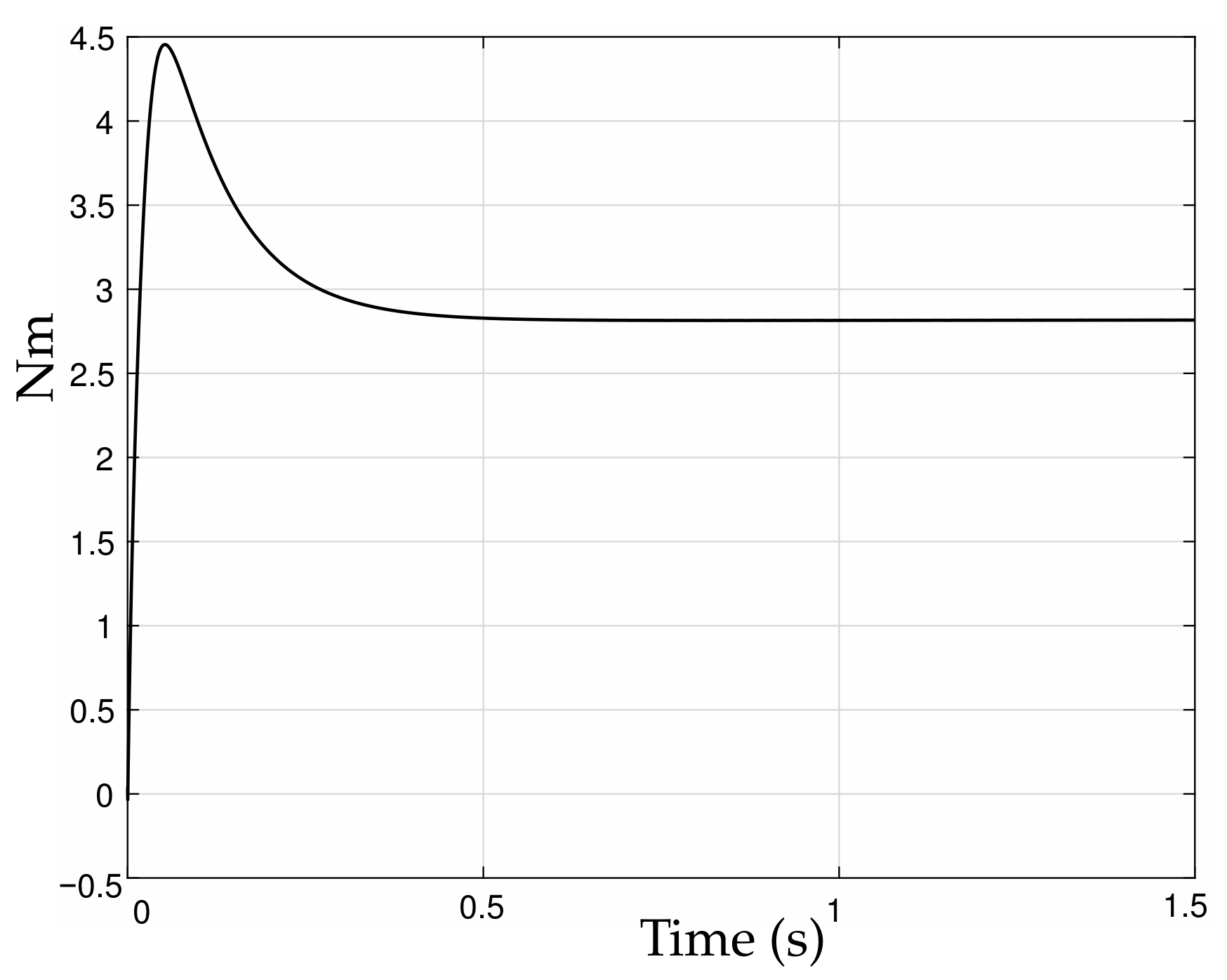
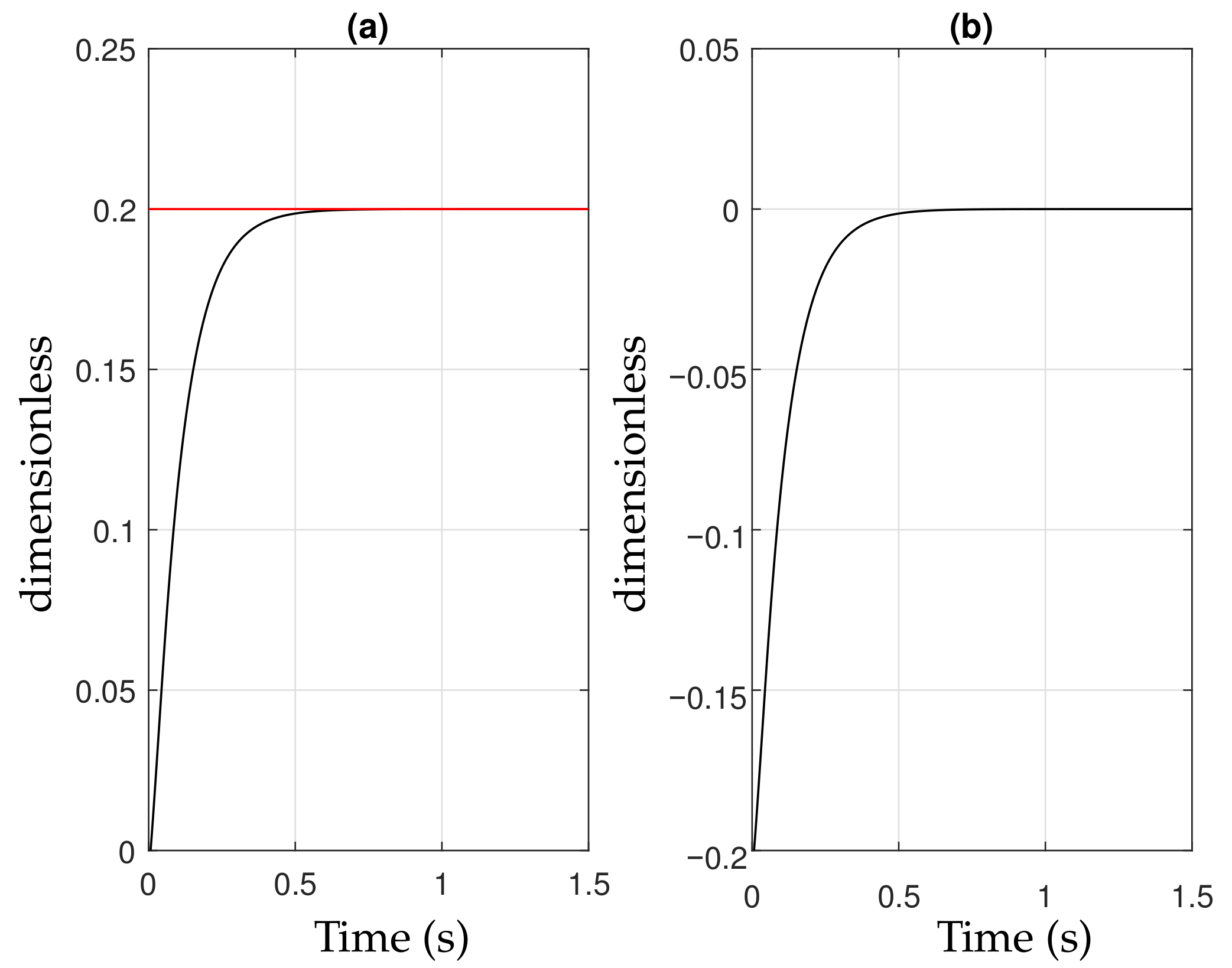
4.1. Numerical Simulation Result
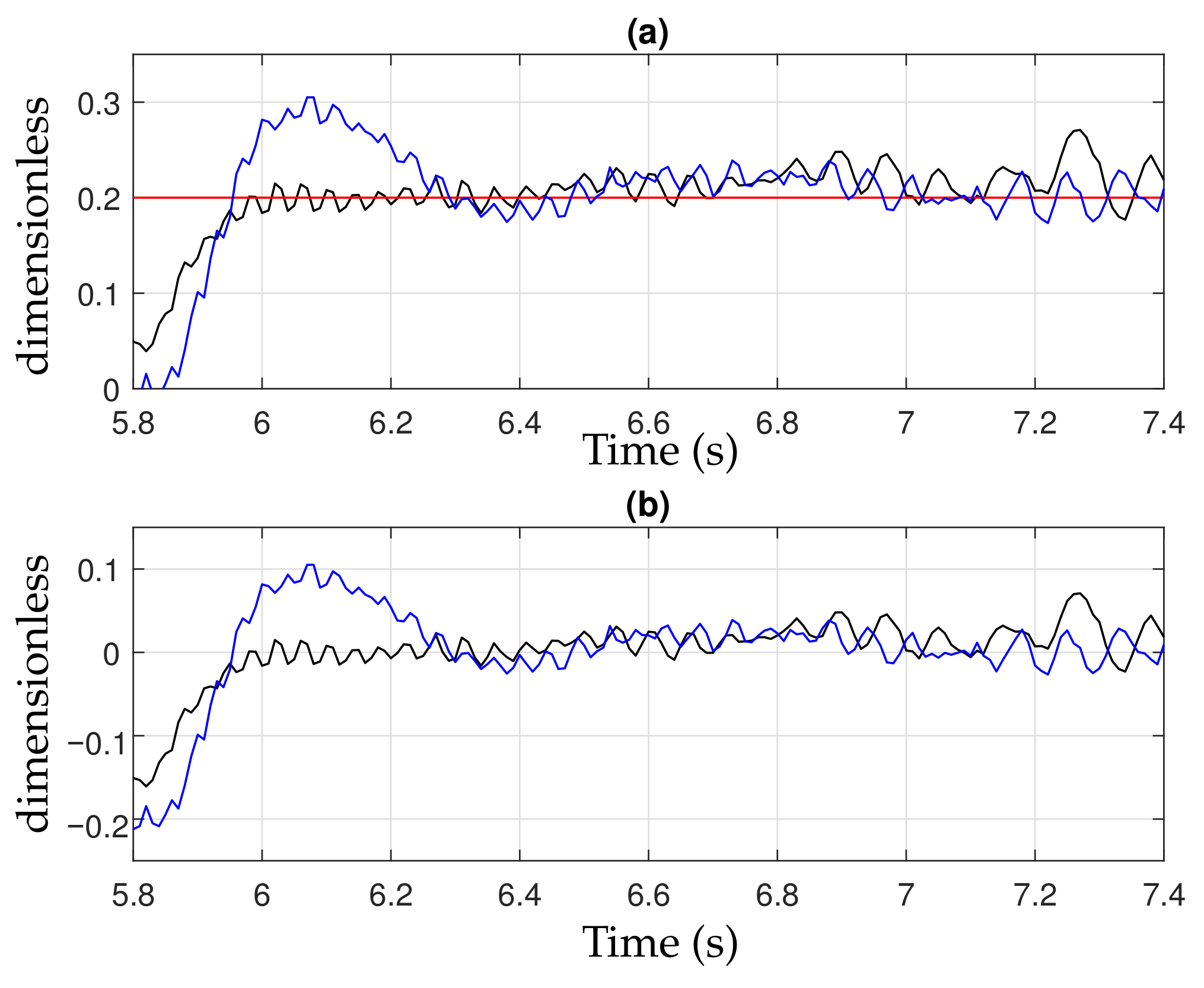
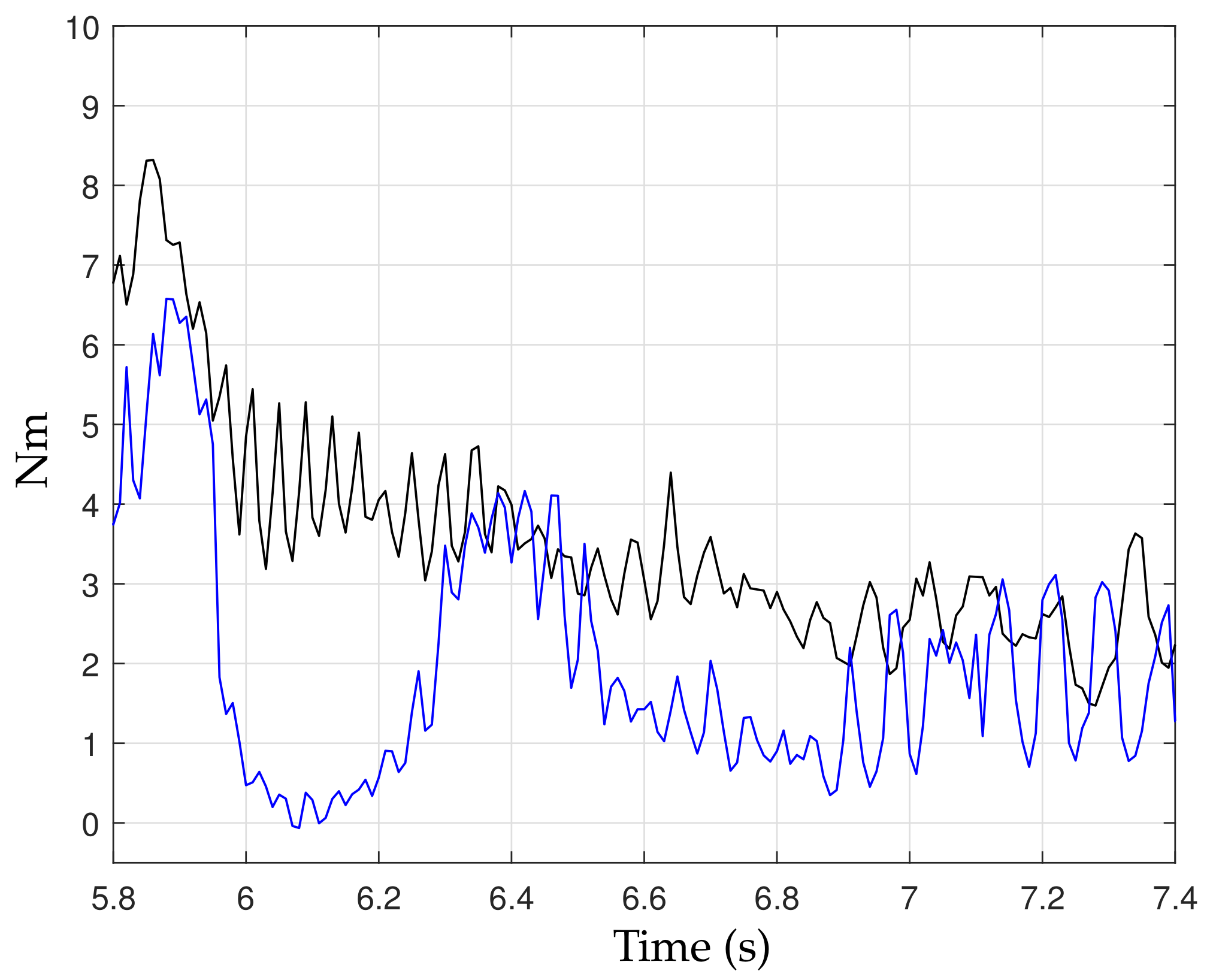
4.2. Experimental Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Emelyanov, S.V.; Korovin, S.K.; Levantovsky, L.V. Higher order sliding regimes in the binary control systems. Doklady Akademii Nauk Russ. Acad. Sci. 1986, 287, 1338–1342. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and High Order Sliding Mode Control. J. Franklin Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Fridman, L.; Moreno, J.; Iriarte, R. Sliding Modes after the First Decade of the 21st Century: State of the Art; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2011; Volume 412, pp. 113–149. [Google Scholar]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory and Application; Taylor and Francis Ltd.: London, UK, 1999. [Google Scholar]
- Fridman, L.; Levant, A. Higher Order Sliding Modes. In Sliding Mode Control in Engineering; Perruquetti, W., Barbot, J.P., Eds.; CRC Press: New York, NY, USA, 2002; pp. 53–101. [Google Scholar]
- Fridman, L.; Shtessel, Y.; Edwards, C.; Yan, X.G. Higher order sliding mode observer for state estimation and input reconstruction in nonlinear systems. Int. J. Robust Nonlinear Control 2008, 18, 399–413. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity approach to High–Order Sliding Mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Angulo, M.; Moreno, J.; Fridman, L. The differentiation error of noisy signals using the generalized super–twisting differentiator. In Proceedings of the 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 7383–7388. [Google Scholar]
- Liu, J.; Gao, L.; Zhang, J.; Yan, F. Super-twisting algorithm second-order sliding mode control for collision avoidance system based on active front steering and direct yaw moment control. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2020, 235, 43–54. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Shi, J.; Huang, Y.; Chen, H. An Adaptive backstepping sliding mode controller to improve Vvehicle maneuverability and stability via torque vectoring control. IEEE Trans. Veh. Technol. 2020, 69, 2598–2612. [Google Scholar] [CrossRef]
- Etienne, L.; Acosta-Lúa, C.; Di Gennaro, S.; Barbot, J.P. A super-twisting controller for active control of ground vehicles with lateral tire-road friction estimation and CarSim validation. Int. J. Control Autom. Syst. 2020, 18, 1177–1189. [Google Scholar] [CrossRef]
- Cappelli, M.; Castillo-Toledo, B.; Di Gennaro, S. Nonlinear control of pressurized water reactors with uncertainties estimation via high order sliding mode. J. Franklin Inst. 2021, 358, 1308–1326. [Google Scholar] [CrossRef]
- Gutiérrez-Oribio, D.; Mercado-Uribe, A.; Moreno, J.A.; Fridman, L. Reaction wheel pendulum control using fourth-order discontinuous integral algorithm. Int. J. Robust Nonlinear Control 2020, 31, 185–206. [Google Scholar] [CrossRef]
- Blas, L.A.; Dávila, J.; Salazar, S.; Bonilla, M. Robust trajectory tracking for an uncertain UAV based on active disturbance rejection. IEEE Control Syst. Lett. 2022, 6, 1466–1471. [Google Scholar] [CrossRef]
- Zhai, J.; Li, Z. Fast–exponential sliding mode control of robotic manipulator with super-twisting method. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 489–493. [Google Scholar] [CrossRef]
- Guo, X.G.; Ahn, C.K. Adaptive fault-tolerant pseudo PID sliding–mode control for high–speed train with integral quadratic constraints and actuator saturation. IEEE Trans. Intel. Transp. Syst. 2020, 22, 7421–7431. [Google Scholar] [CrossRef]
- Zakia, U.; Moallem, M.; Menon, C. PID-SMC controller for a 2-DOF planar robot. In Proceedings of the International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 7–9 February 2019; pp. 1–5. [Google Scholar]
- Gu, G.Y.; Li, C.X.; Zhu, L.M.; Fatikow, S. Robust tracking of nanopositioning stages using sliding mode control with a PID sliding surface. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Besacon, France, 8–11 July 2014; pp. 973–977. [Google Scholar]
- Eker, I. Second–order sliding mode control with PI sliding surface and experimental application to an electromechanical plant. Arab. J. Sci. Eng. 2012, 37, 1969–1986. [Google Scholar] [CrossRef]
- Khan, A.H.; Li, S. Sliding mode sontrol with PID sliding surface for active vibration damping of pneumatically actuated soft robots. IEEE Acces 2020, 8, 88793–88800. [Google Scholar] [CrossRef]
- Navarrete-Guzmán, A.; Vaca-García, C.C.; Di Gennaro, S.; Acosta-Lúa, C. HOSM controller using PI sliding manifold for an integrated active control for wheeled vehicles. Math. Probl. Eng. 2021, 2021, 5482421. [Google Scholar]
- Nilav-Aydina, M.; Cobanb, R. PID sliding surface-based adaptive dynamic second-order fault-tolerant sliding mode control design and experimental application to an electromechanical system. Int. J. Control 2020, 1–10. [Google Scholar] [CrossRef]
- Kang, B.; Miao, Y.; Liu, F. A second-order sliding mode controller of quad–rotor UAV based on PID sliding mode surface with unbalanced load. J. Syst. Sci. Complex. 2021, 34, 520–536. [Google Scholar] [CrossRef]
- ABS. The Laboratory Anti-Lock Braking System, User’s Manual; Inteco Ltd.: Krakow, Poland, 2006. [Google Scholar]
- Al-Mola, M.H.; Mailah, M.; Samin, P.M.; Muhaimin, A.H.; Abdullah, M.Y. Performance comparison between sliding mode control and active force control for a nonlinear anti–lock brake system. WSEAS Trans. Syst. Control 2014, 9, 101–107. [Google Scholar]
- Martinez-Gardea, M.; Mares Guzmán, I.J.; Di Gennaro, S.; Acosta Lúa, C. Experimental comparison of linear and nonlinear controllers applied to an antilock braking system. In Proceedings of the IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; pp. 71–76. [Google Scholar]
- Acosta-Lúa, C.; Di Gennaro, S.; Sánchez-Morales, M.E. An adaptive controller applied to an anti–lock braking system laboratory. Dyna 2016, 83, 69–77. [Google Scholar] [CrossRef]
- Acosta–Lúa, C.; Di Gennaro, S.; Sanchez Morales, M.E. Nonlinear adaptive controller applied to an antilock braking system with parameters variations. Int. J. Control Autom. Syst. 2017, 15, 2043–2052. [Google Scholar] [CrossRef]
- Precup, R.E.; Spataru, S.V.; Radac, M.B.; Petriu, E.M.; Preitl, S.; David, R.C. Experimental results of model–based fuzzy control solutions for a laboratory antilock braking system. In Human—Computer Systems Interaction: Backgrounds and Applications 2; Springer: Berlin/Heidelberg, Germany, 2012; pp. 223–234. [Google Scholar]
- Radac, M.B.; Precup, R.E.; Preitl, S.; Tar, J.K.; Petriu, E.M. Linear and fuzzy control solutions for a laboratory anti–lock braking system. In Proceedings of the 6th IEEE International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 26–27 September 2008; pp. 26–27. [Google Scholar]
- Khanesar, M.A.; Kayacan, E.; Teshnehlab, M.; Kaynak, O. Extended Kalman filter based learning algorithm for type–2 fuzzy logic systems and its experimental evaluation. IEEE Trans. Ind. Electron. 2012, 59, 4443–4455. [Google Scholar] [CrossRef]
- Topalov, A.V.; Kayacan, E.; Oniz, Y.; Kaynak, O. Neuro–fuzzy control of antilock braking system using variable structure–systems based learning algorithm. In Proceedings of the International Conference on Adaptive and Intelligent Systems, Klagenfurt, Austria, 24–26 September 2009; pp. 1–6. [Google Scholar]
- Martinez-Gardea, M.; Mares Guzmán, I.J.; Acosta Lúa, C.; Di Gennaro, S.; Vázquez Álvarez, I. Design of a nonlinear observer for a laboratory antilock braking system. J. Control Eng. Appl. Inf. 2015, 17, 105–112. [Google Scholar]
- Acosta Lúa, C.; Di Gennaro, S.; Castillo-Toledo, B.; Martinez-Gardea, M. Dynamic control applied to a laboratory antilock braking system. Math. Probl. Eng. 2015, 2015, 896859. [Google Scholar] [CrossRef]
- Martinez-Gardea, M.; Acosta-Lúa, C.; Vázquez-Álvarez, I.; Di Gennaro, S. Event–triggered linear control design for an antilock braking system. In Proceedings of the IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 4–6 November 2015; pp. 1–6. [Google Scholar]
- Chereji, E.; Mircea-Bogdan, R.; Alexandra-Iulia, S.S. Sliding mode control algorithms for anti–lock braking systems with performance comparisons. Algorithms 2021, 14, 2. [Google Scholar] [CrossRef]
- Acosta-Lúa, C.; Di Gennaro, S.; Barbot, J.P. Nonlinear control of an antilock braking system in the presence of tire–road friction uncertainties. J. Franklin Inst. 2022, 359, 2608–2626. [Google Scholar] [CrossRef]
- Bosch, R. Bosch Automotive Handbook, 8th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pacejka, H. Tyre and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Ȧmströng, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tunning; ISA—The instrumentation, Systems, and Automation Society: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second–order sliding mode controllers and observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 6th ed.; Pearson: New York, NY, USA, 2009. [Google Scholar]


| Symbol | Value | Unit |
|---|---|---|
| 0.0995 | m | |
| 0.0990 | m | |
| kg m | ||
| kg m | ||
| kg m/s | ||
| kg m/s | ||
| 1 | ||
| 15.24 | ||
| 6.21 | ||
| c | 20.37 | s |
| 0.415 | ||
| D | 23 | |
| C | 1.68 | |
| B | 28 |
| Symbol | Parameter | Value |
|---|---|---|
| Gain in modified HOSM | 2.62 | |
| Gain in modified HOSM | 0.9 | |
| Gain in modified HOSM | 1.7 | |
| Gain in modified HOSM | 10 | |
| PID-sliding surface | 5.5 | |
| PID-sliding surface | 20 | |
| PID-sliding surface | 0.015 | |
| PID-like controller gain | 32 | |
| PID-like controller gain | 15 | |
| PID-like controller gain | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García Torres, C.J.; Ferré Covantes, L.A.; Vaca García, C.C.; Estrada Gutiérrez, J.C.; Guzmán, A.N.; Acosta Lúa, C. A Lyapunov Stability Analysis of Modified HOSM Controllers Using a PID-Sliding Surface Applied to an ABS Laboratory Setup. Appl. Sci. 2022, 12, 3796. https://doi.org/10.3390/app12083796
García Torres CJ, Ferré Covantes LA, Vaca García CC, Estrada Gutiérrez JC, Guzmán AN, Acosta Lúa C. A Lyapunov Stability Analysis of Modified HOSM Controllers Using a PID-Sliding Surface Applied to an ABS Laboratory Setup. Applied Sciences. 2022; 12(8):3796. https://doi.org/10.3390/app12083796
Chicago/Turabian StyleGarcía Torres, Christopher Javier, Luis Adrián Ferré Covantes, Claudia Carolina Vaca García, Juan Carlos Estrada Gutiérrez, Antonio Navarrete Guzmán, and Cuauhtémoc Acosta Lúa. 2022. "A Lyapunov Stability Analysis of Modified HOSM Controllers Using a PID-Sliding Surface Applied to an ABS Laboratory Setup" Applied Sciences 12, no. 8: 3796. https://doi.org/10.3390/app12083796
APA StyleGarcía Torres, C. J., Ferré Covantes, L. A., Vaca García, C. C., Estrada Gutiérrez, J. C., Guzmán, A. N., & Acosta Lúa, C. (2022). A Lyapunov Stability Analysis of Modified HOSM Controllers Using a PID-Sliding Surface Applied to an ABS Laboratory Setup. Applied Sciences, 12(8), 3796. https://doi.org/10.3390/app12083796








