Thermophysical Characterization of a Thermoregulating Interior Coating Containing a Bio-Sourced Phase Change Material
Abstract
:1. Introduction
2. Thermal Characterization
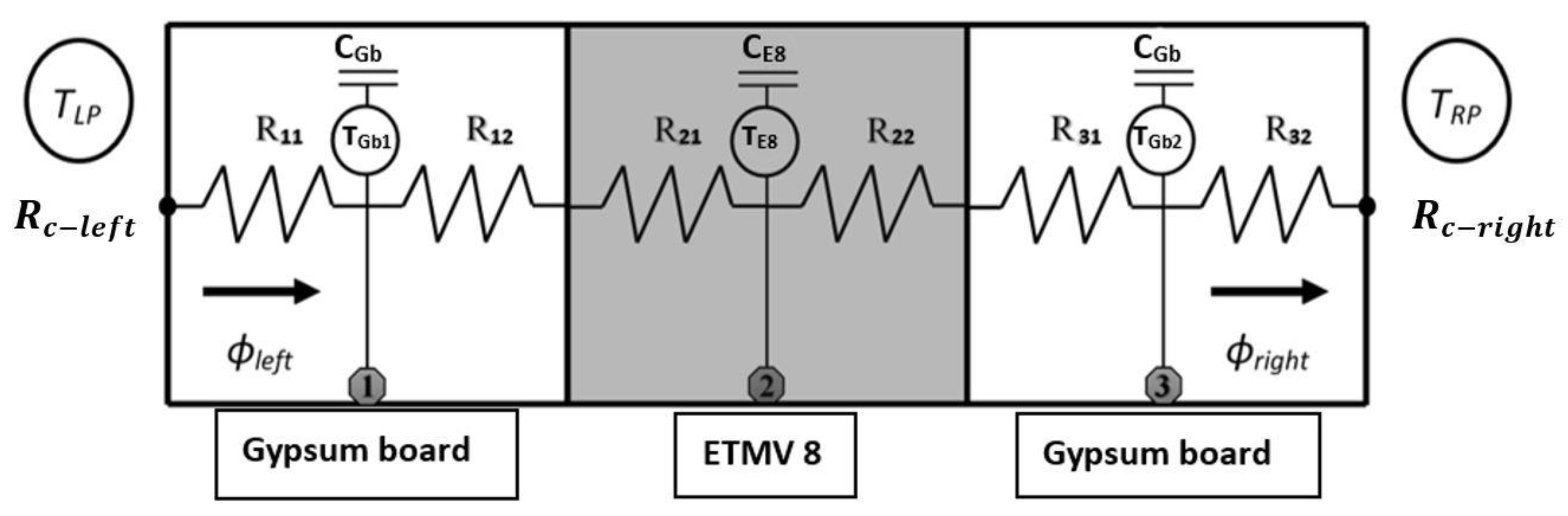
2.1. ETMV 8 Sample
2.2. Experimental Measurement Method
3. Numerical Modeling on Python
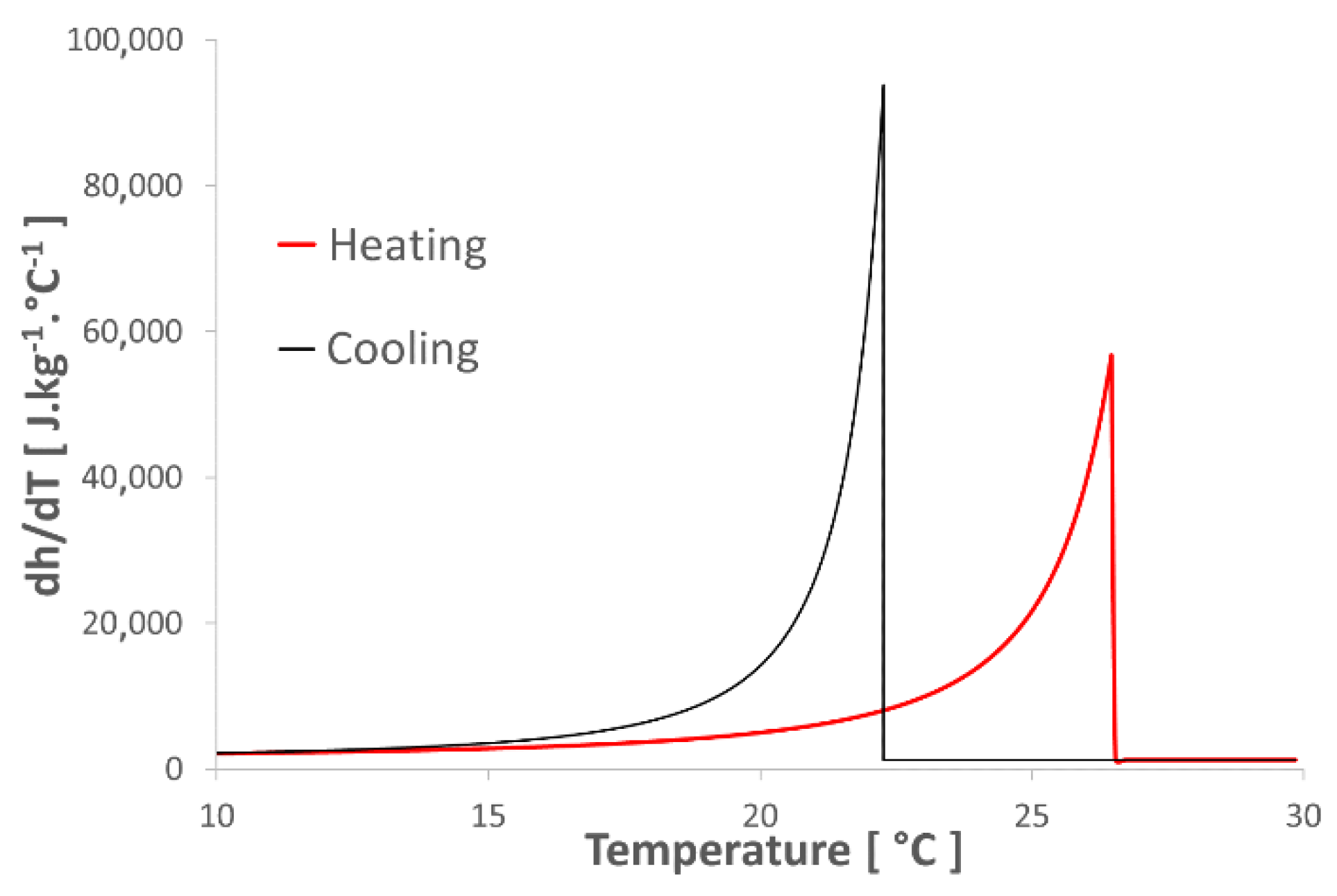
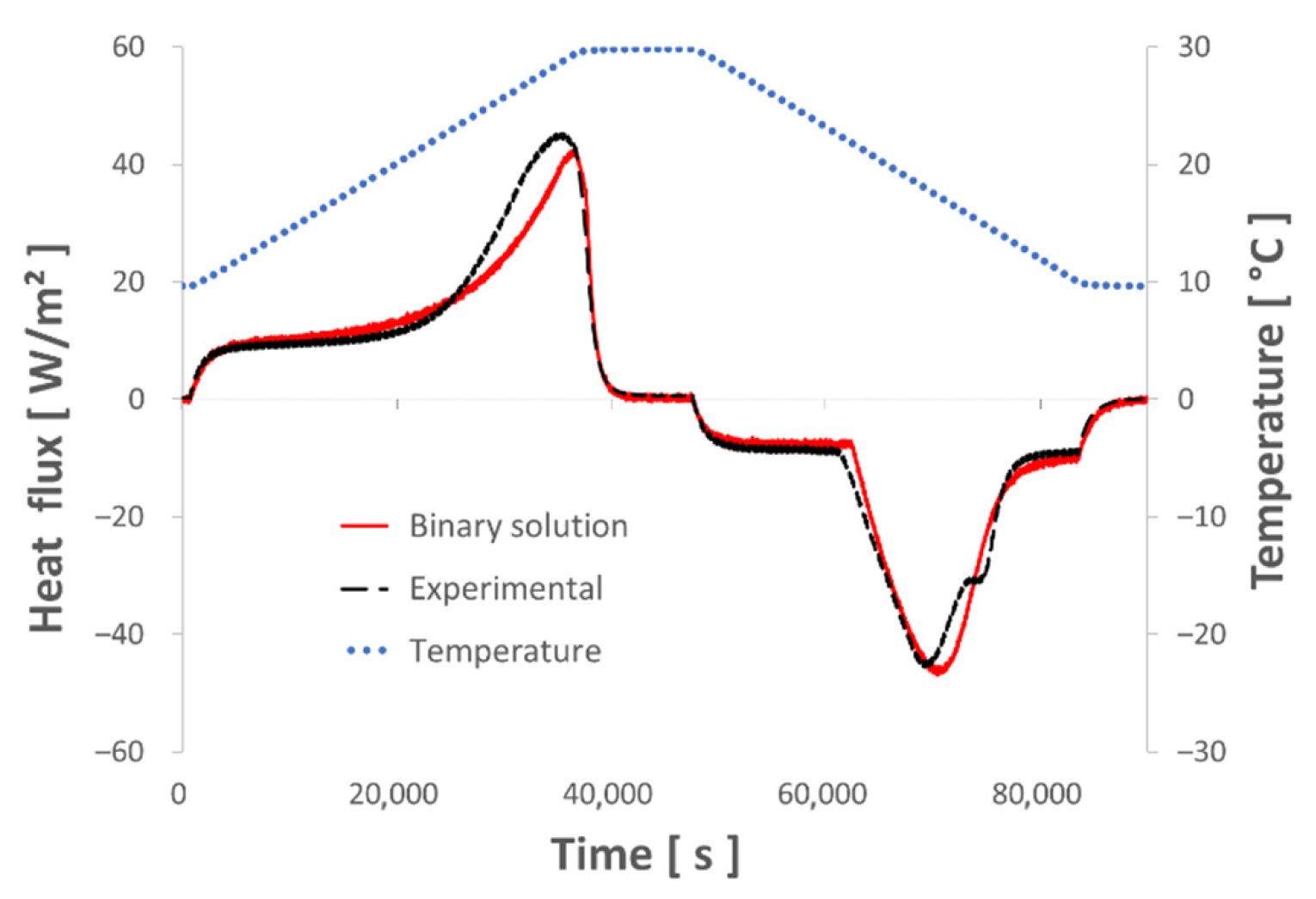
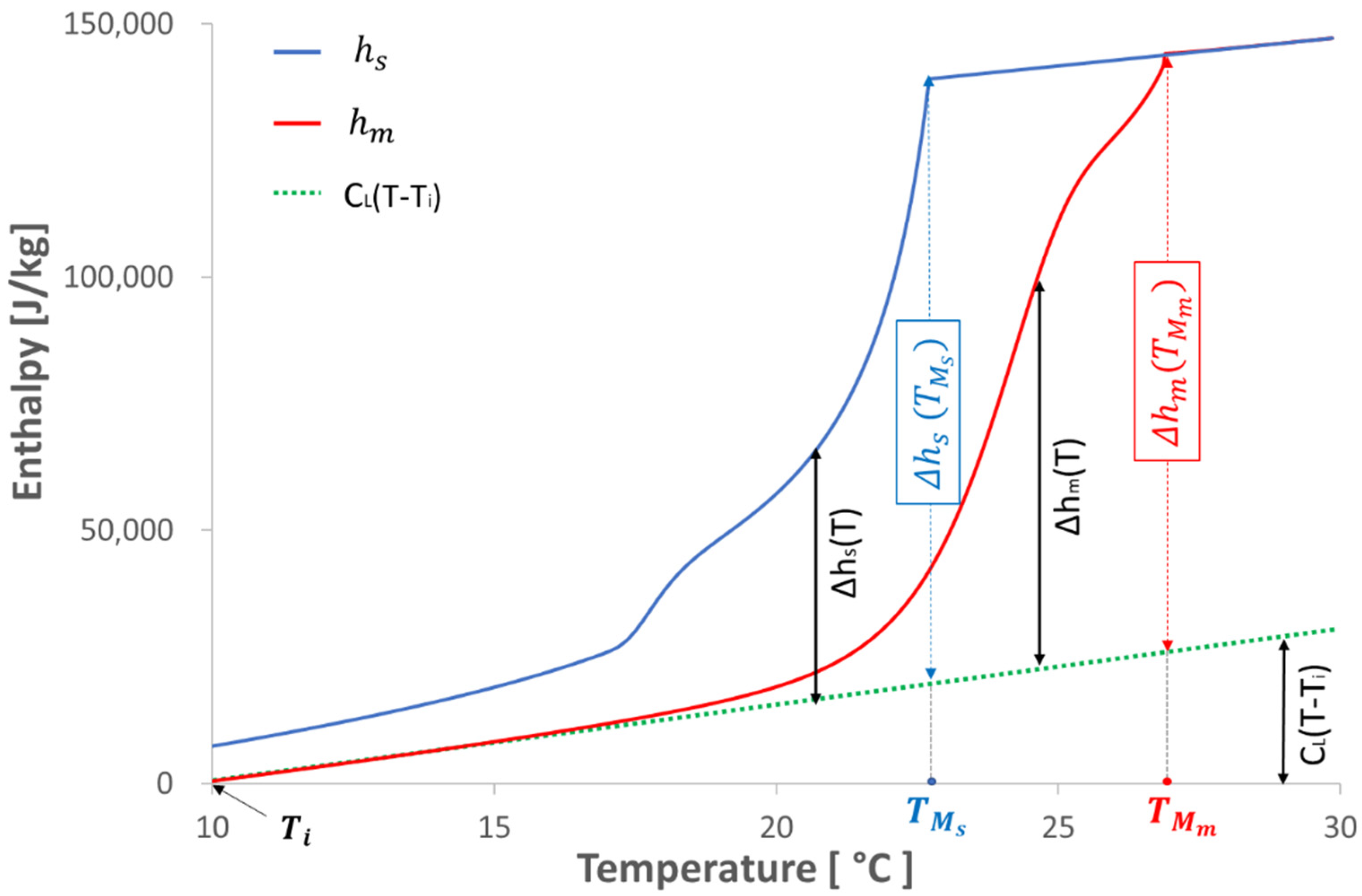
3.1. Binary Solution Model and Its Limitations
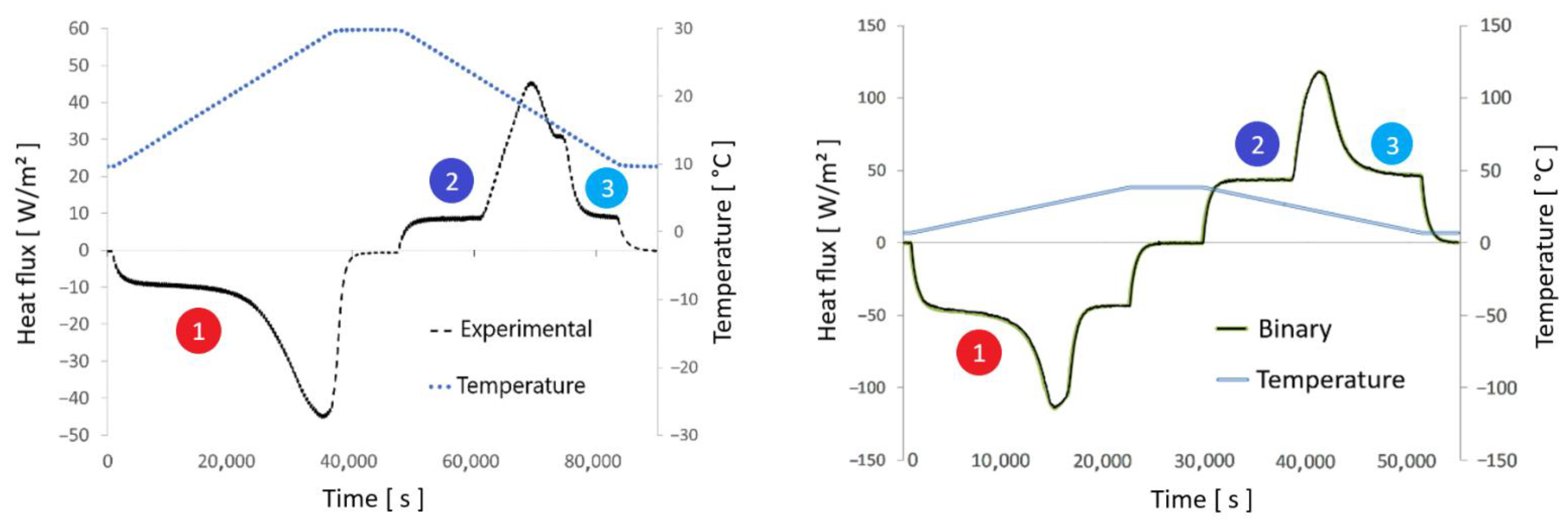
 ), a nearly identical curve of thermal flux measured on both the ETMV 8 sample and the binary solution can be observed. Concerning the solidification phase, two common points between the two bodies essentially stand out, namely the levels at the beginning (
), a nearly identical curve of thermal flux measured on both the ETMV 8 sample and the binary solution can be observed. Concerning the solidification phase, two common points between the two bodies essentially stand out, namely the levels at the beginning (  ) and end of solidification (
) and end of solidification (  ). It should also be noted that during the solidification phase, except for the second peak of thermal flux identified for the ETMV 8 coating, the curves are on the whole similar. All these elements serve to reinforce the choice of a binary solution model to analyze the coating behavior.
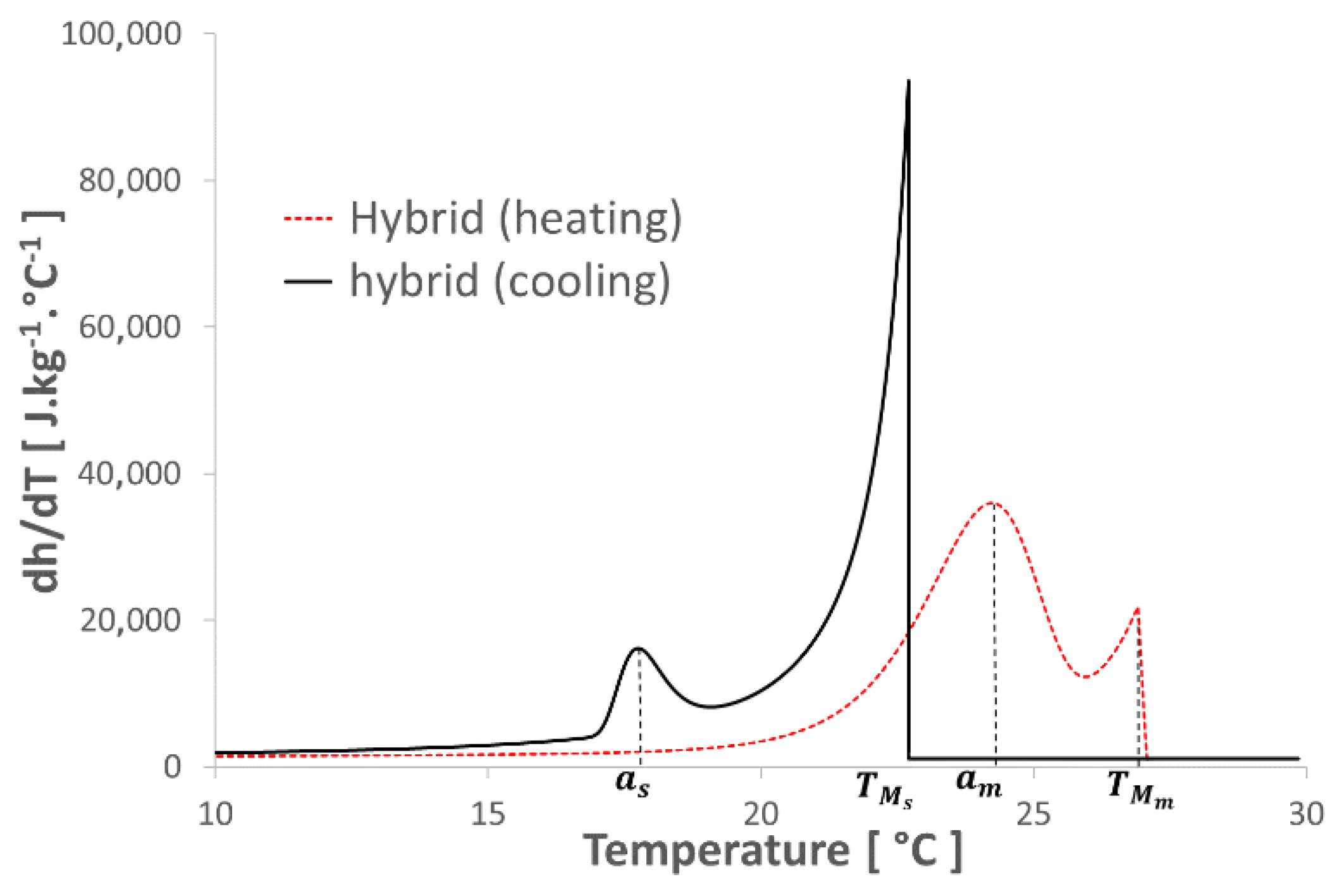
). It should also be noted that during the solidification phase, except for the second peak of thermal flux identified for the ETMV 8 coating, the curves are on the whole similar. All these elements serve to reinforce the choice of a binary solution model to analyze the coating behavior.3.2. New Hybrid Model
4. Results and Discussion
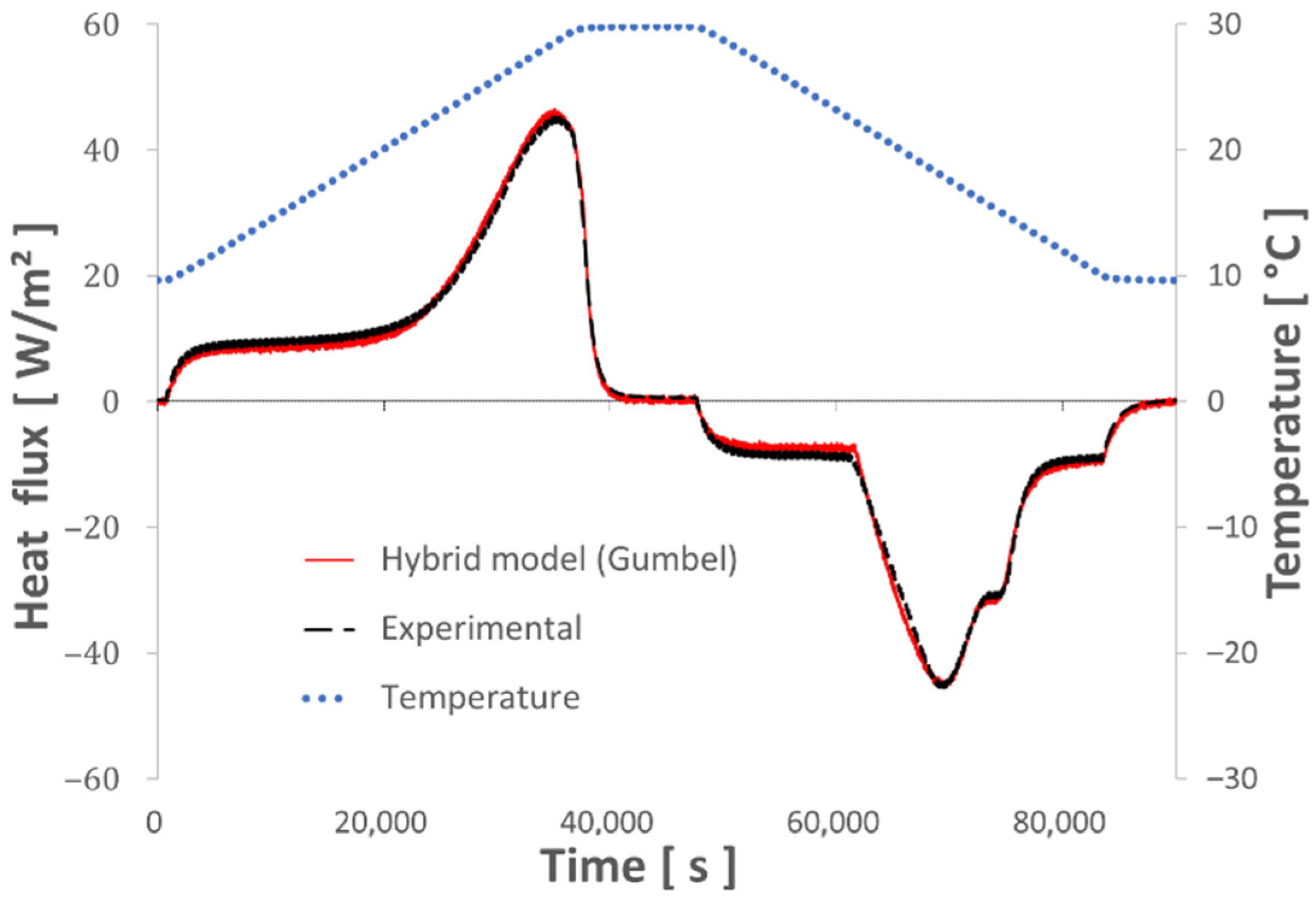
4.1. Optimization of the Numerical Model Parameters
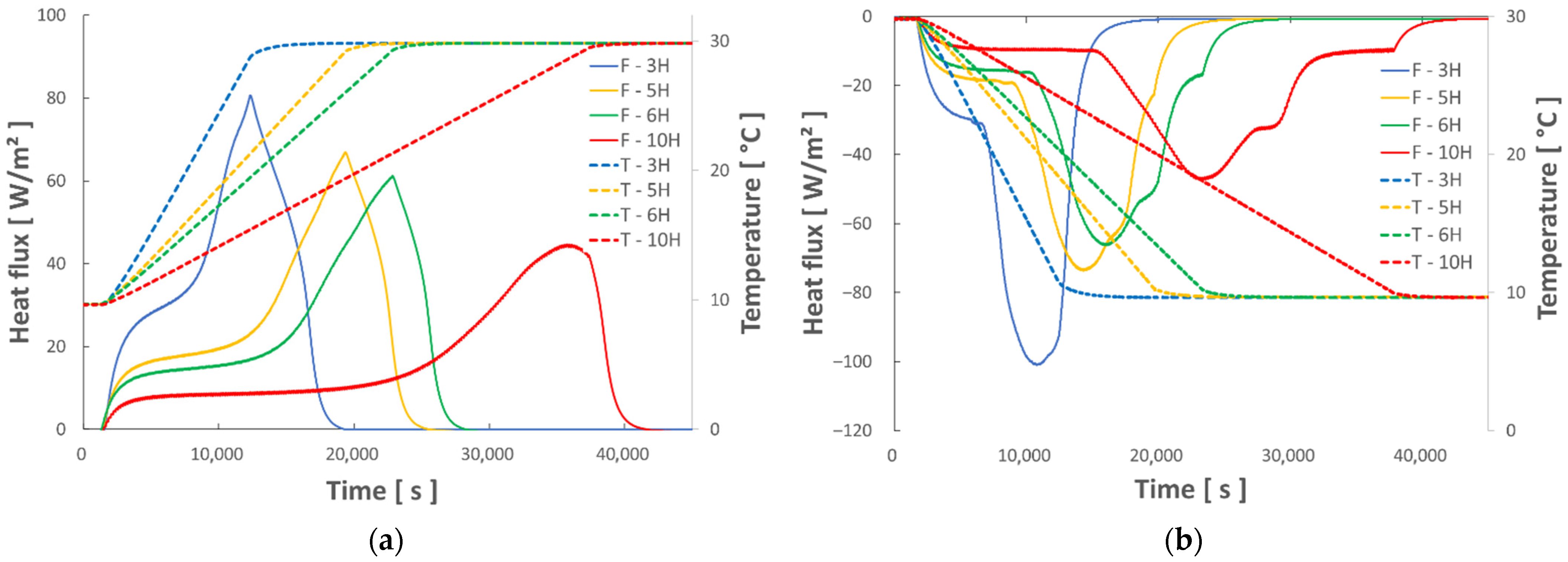
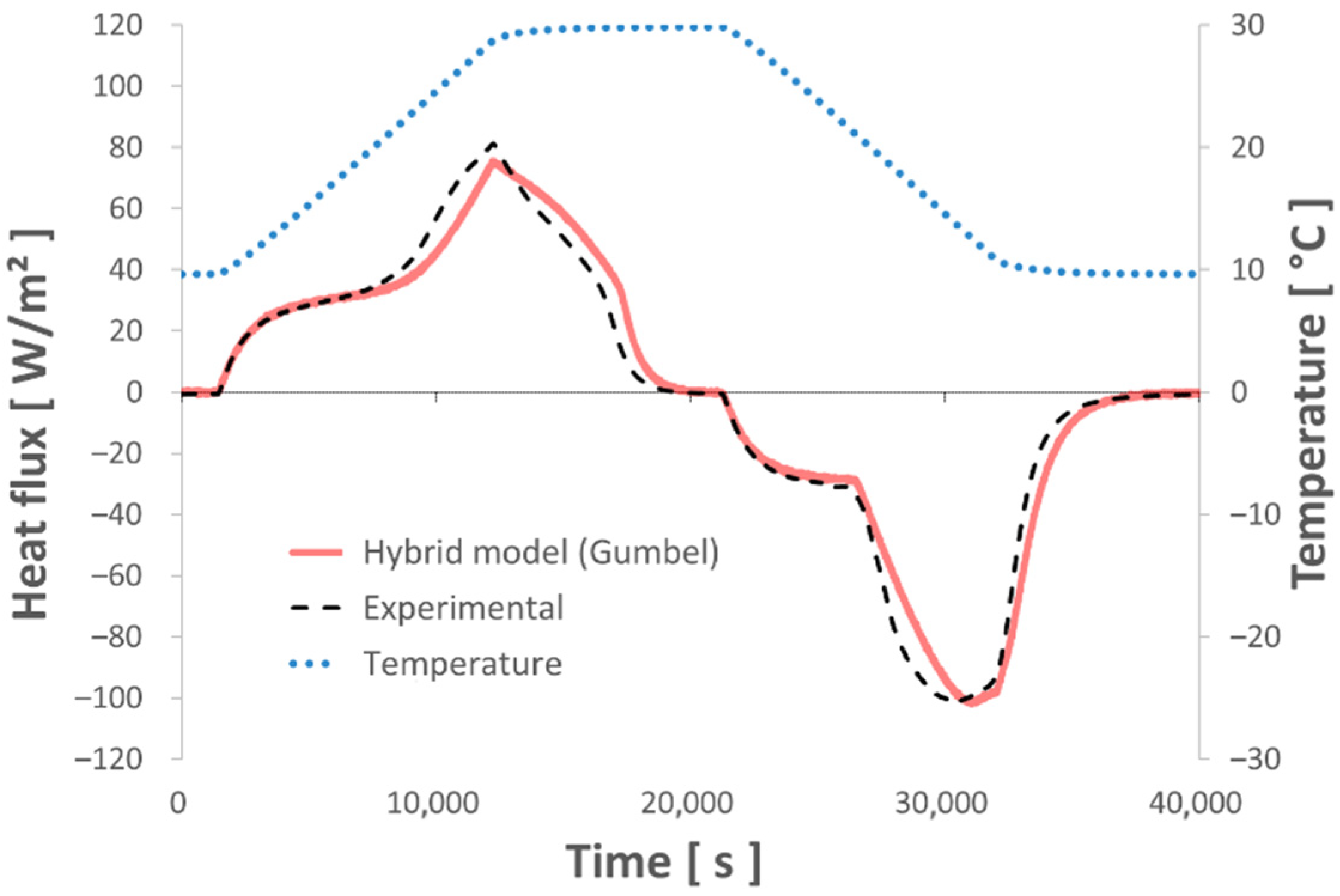
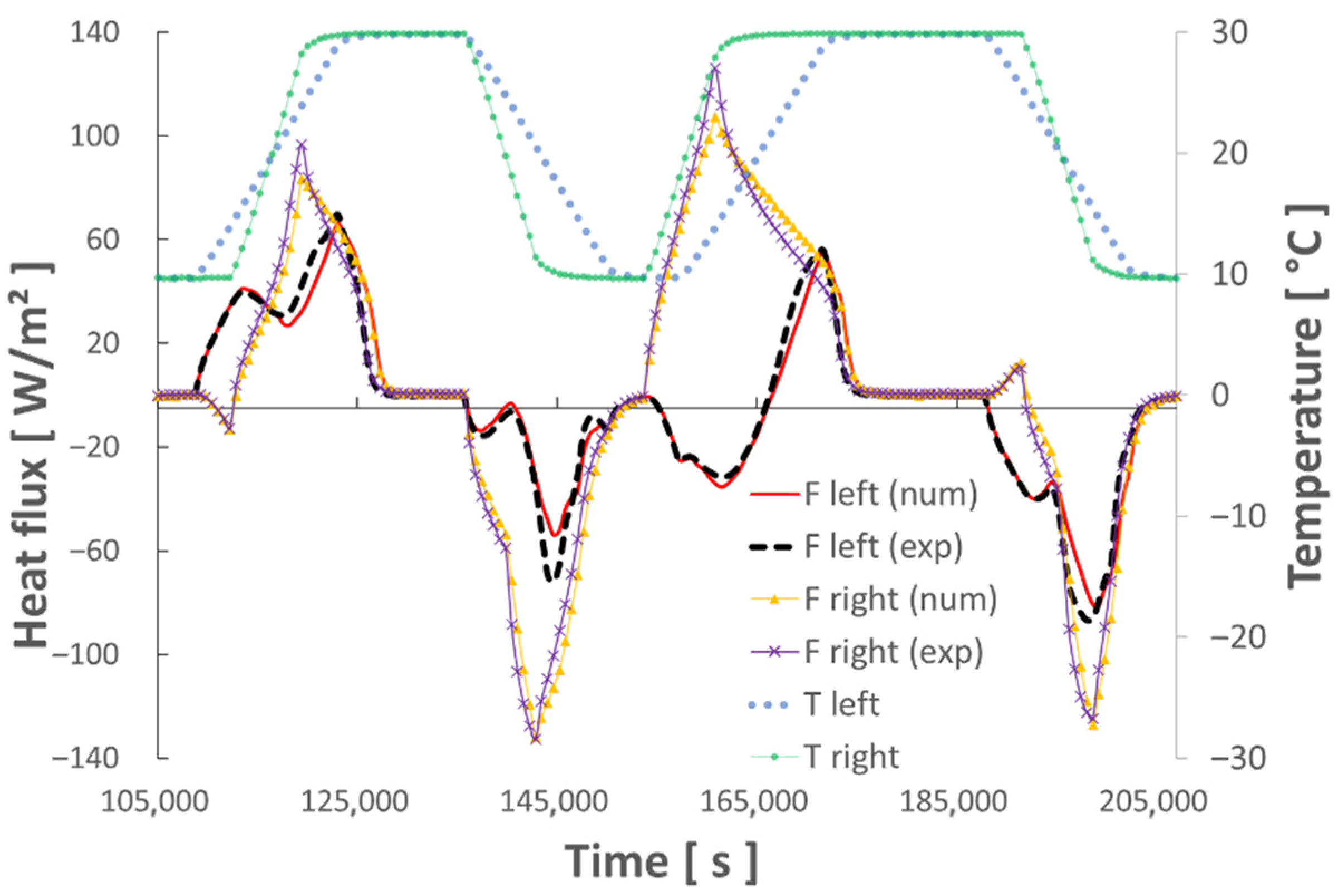
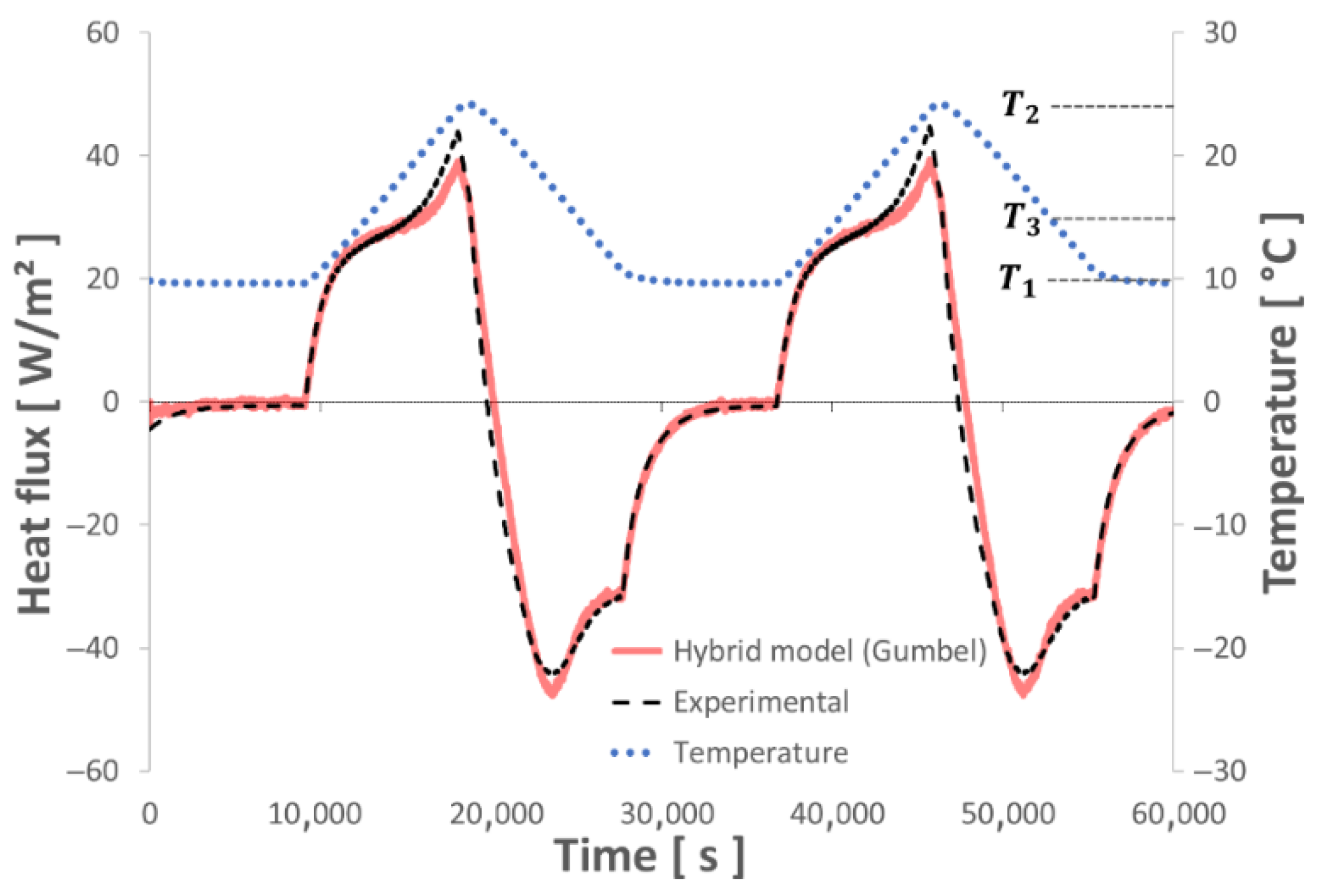
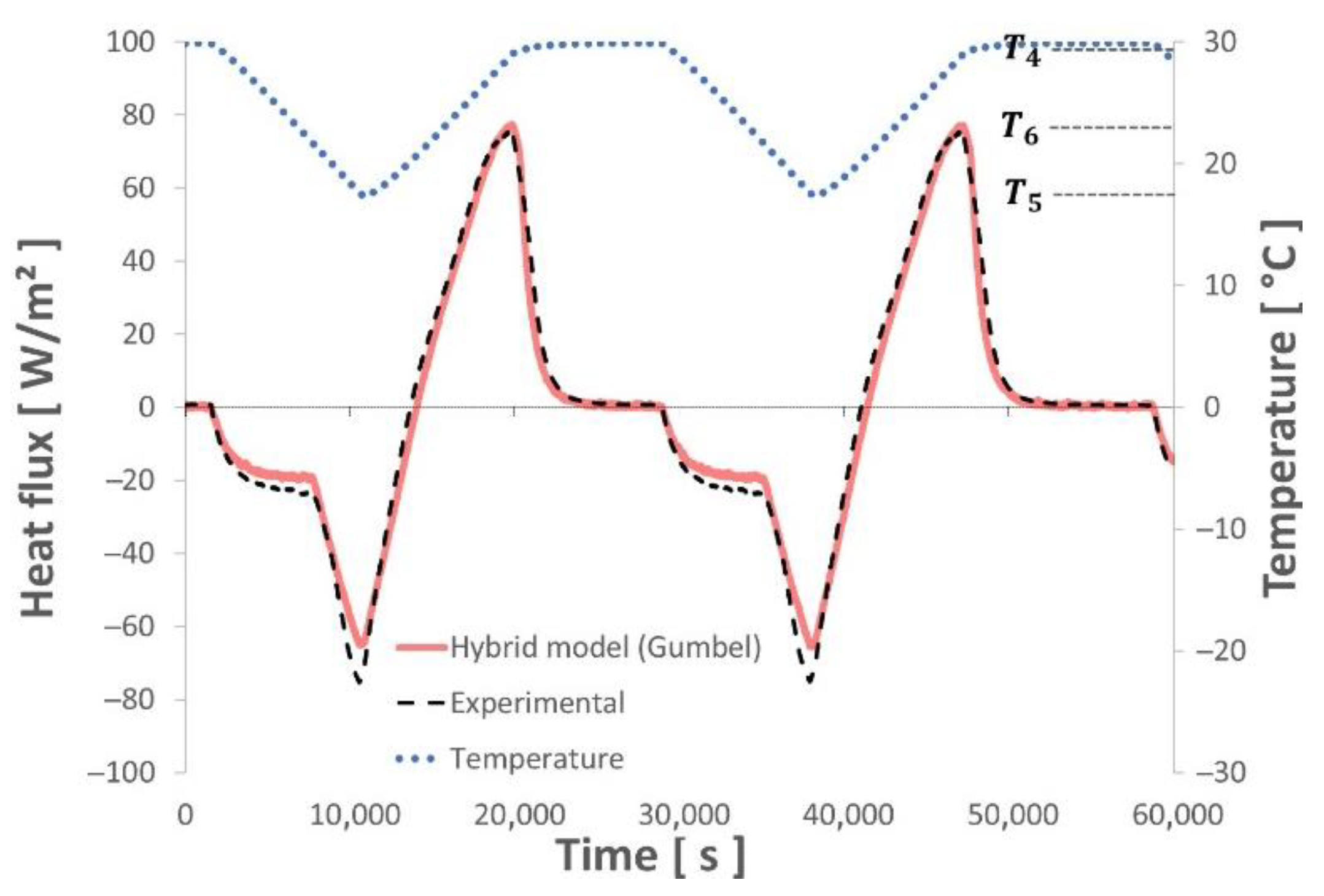
4.2. Test of the Numerical Model with Various Thermal Sollicitations
5. Energy Balance and Error Analysis
5.1. Energy Balance
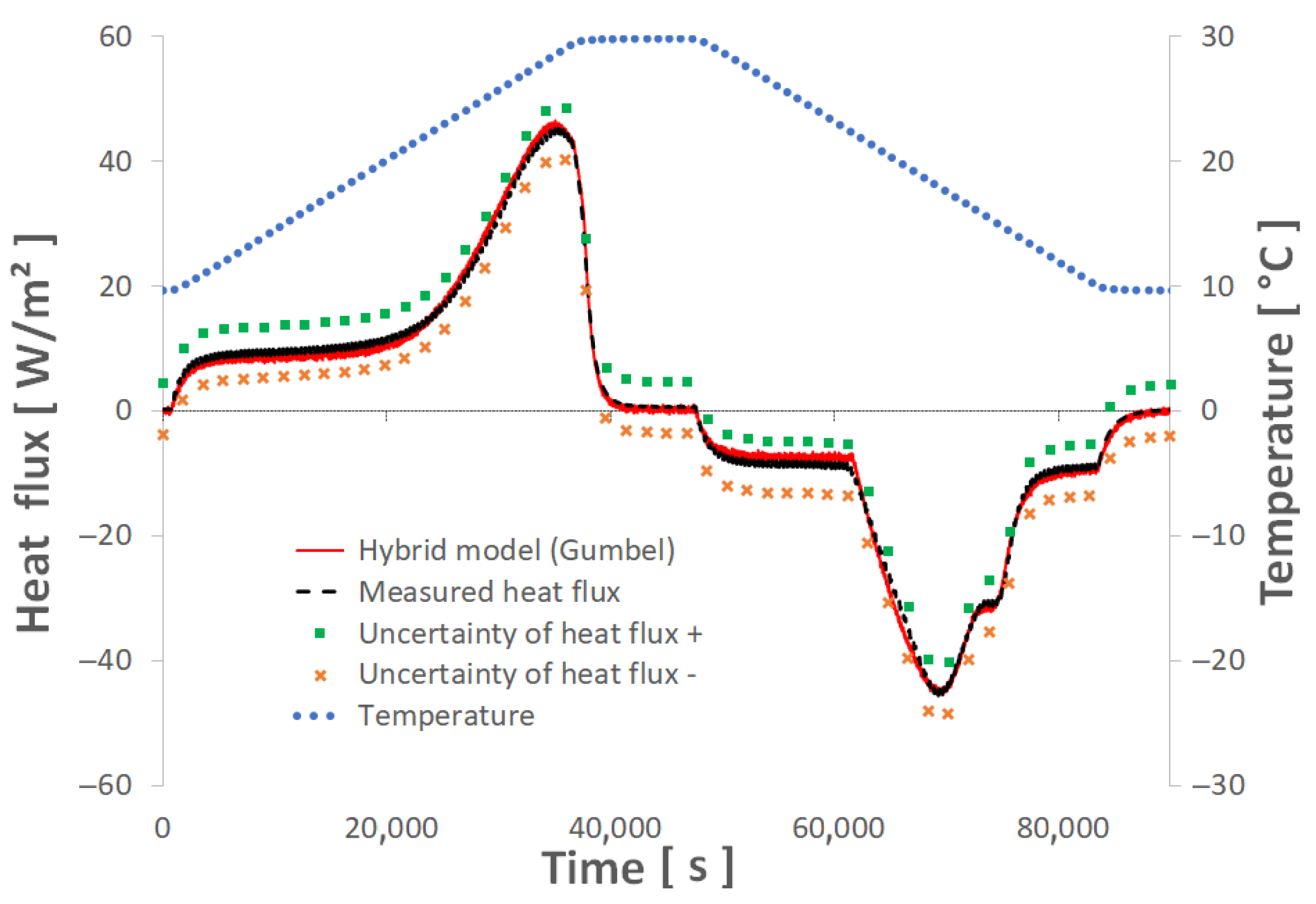
5.2. Evaluation of Errors Related to Uncertainties
6. Conclusions
- This new hybrid model, associating the enthalpy of a binary solution with Gumbel’s Law equations, succeeds in describing the thermal behavior of the studied composite material (gypsum board + micro-encapsulated PCM) with high accuracy even when subjected to undercooling.
- The various dynamic thermal loads (ramps) between 10° and 30 °C depict the different thermal behaviors well represented by the hybrid model. The energy balances performed between these two temperature levels show a good level of repeatability and measurement accuracy.
- This model also takes into account the partial melting/solidification of the PCM, which can occur during its use in a building subjected to meteorological constraints.
- The model has successfully characterized the thermophysical properties of the coating incorporating PCM and, in particular, the latent heat contained in the material. By knowing that the coating is loaded with 70% PCM and in comparison, with the DSC measurements conducted by the manufacturer, the latent heat identified by characterization could be verified.
- An error calculation was used to determine uncertainties of around 4%, which appears acceptable for our application.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| a | parameter for the Gumbel function axis (°C) |
| b | parameter for the form of the Gumbel function (°C) |
| C | heat capacity (J·K−1) |
| cS | specific heat capacity when PCM is in the solid state (J·kg−1·K−1) |
| specific heat capacity when PCM is in the liquid state (J·kg−1·K−1) | |
| e | thickness (m) |
| liquid fraction of the hybrid model | |
| liquid fraction of the binary model | |
| Gumbel function | |
| objective function | |
| Rc- | Thermal contact resistance |
| h | specific enthalpy (J·kg−1) |
| LA | latent heat (J·kg−1) |
| m | mass (kg) |
| n | mesh number |
| Q | energy transferred (J) |
| R | resistance (m2·K·W−1) |
| S | surface area (m2) |
| T | temperature (°C) |
| t | time (s) |
| U | uncertainty |
| Greek symbols | |
| ρ | density (kg.m-3) |
| ɸ | heat flux (W) |
| ψ | latent heat distribution coefficients between the binary function and the Gumbel function |
| λ | thermal conductivity |
| Subscripts | |
| A | melting of pure substance |
| cal | calculation |
| exp | experimentation |
| left | left side of the sample |
| LP | left plate |
| M | end of melting |
| m | during the melting phase |
| mod | acquisition module |
| right | right side of the sample |
| RP | right plate |
| s | during the solidification phase |
References
- Ministry of Ecological Transition (France). Data and Statistical Studies for Climate Change, Energy, Environment, Housing, and Transport. Available online: https://www.statistiques.developpement-durable.gouv.fr/ (accessed on 2 February 2022).
- Abhat, A. Low temperature latent heat thermal energy storage: Heat storage materials. Sol. Energy 1983, 30, 313–332. [Google Scholar] [CrossRef]
- Hasnain, S.M. Review on sustainable thermal energy storage technologies, Part I: Heat storage materials and techniques. Energy Convers. Manag. 1998, 39, 1127–1138. [Google Scholar] [CrossRef]
- Ibrahim, D.; Marc, A.R. Thermal Energy Storage; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Farid, M.M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Swanson, T.D.; Birur, G.C. NASA thermal control technologies for robotic spacecraft. Appl. Therm. Eng. 2003, 23, 1055–1065. [Google Scholar] [CrossRef] [Green Version]
- Hasan, A.; Hejase, H.; Abdelbaqi, S.; Assi, A.; Hamdan, M.O. Comparative Effectiveness of Different Phase Change Materials to Improve Cooling Performance of Heat Sinks for Electronic Devices. Appl. Sci. 2016, 6, 226. [Google Scholar] [CrossRef] [Green Version]
- Renteria, J.D.; Nika, D.L.; Balandin, A.A. Graphene Thermal Properties: Applications in Thermal Management and Energy Storage. Appl. Sci. 2014, 4, 525–547. [Google Scholar] [CrossRef] [Green Version]
- Frusteri, F.; Restuccia, G.; Vasta, S.; Leonardi, V. Thermal conductivity measurement of a PCM based storage system containing carbon fibers. Appl. Therm. Eng. 2005, 25, 1623–1633. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Thermal characterization of nitrates and nitrates/expanded graphite mixture phase change materials for solar energy storage. Energy Convers. Manag. 2013, 73, 86–94. [Google Scholar] [CrossRef]
- Khudhair, A.M.; Farid, M.M. A review on energy conservation in building applications with thermal storage by latent heat using phase change materials. Energy Convers. Manag. 2004, 45, 263–275. [Google Scholar] [CrossRef]
- Salyer, I.O.; Sircar, A.K. Phase change materials for heating and cooling of residential buildings and other applications. In Proceedings of the 25th Intersociety Energy Conversion Engineering Conference, Reno, NV, USA, 12–17 August 1990. [Google Scholar]
- Shapiro, M.; Shapiro, M. Development of the Enthalpy Storage Materials, Mixture of Methyl Stearate and Methyl Palmitate; Subcontract Report to Florida Solar Energy Center; NREL: Golden, CO, USA, 1989. [Google Scholar]
- Liston, L.C. Using Mixtures of Fatty Acid Methyl Esters as Phase Change Materials for Concrete; Purdue University: West Lafayette, IN, USA, 2015; p. 199. [Google Scholar]
- Nikolić, R.; Marinović-Cincović, M.; Gadžurić, S.; Zsigrai, I.J. New materials for solar thermal storage—Solid/liquid transitions in fatty acid esters. Sol. Energy Mater. Sol. Cells 2003, 79, 285–292. [Google Scholar] [CrossRef]
- Li, L.; Yu, H.; Wang, X.; Zheng, S. Thermal analysis of melting and freezing processes of phase change materials (PCMs) based on dynamic DSC test. Energy Build. 2016, 130, 388–396. [Google Scholar] [CrossRef]
- Höhne, G.; Hemminger, W.; Flammersheim, H.-J. Differential Scanning Calorimetry; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Richardson, M.J. Quantitative aspects of differential scanning calorimetry. Thermochim. Acta 1997, 300, 15–28. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y. A simple method, the T-history method, of determining the heat of fusion, specific heat and thermal conductivity of phase-change materials. Meas. Sci. Technol. 1999, 10, 201. [Google Scholar]
- Feng, G.; Huang, K.; Xie, H.; Li, H.; Liu, X.; Liu, S.; Cao, C. DSC test error of phase change material (PCM) and its influence on the simulation of the PCM floor. Renew. Energy 2016, 87, 1148–1153. [Google Scholar] [CrossRef]
- Thonon, M.; Fraisse, G.; Zalewski, L.; Pailha, M. Towards a better analytical modelling of the thermodynamic behaviour of phase change materials. J. Energy Storage 2020, 32, 101826. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Que, L.; Zhang, X.; Ji, J.; Gao, L.; Xie, W.; Liu, L.; Ding, X. Numerical Simulation and Experimental Research Progress of Phase Change Hysteresis: A Review. Energy Build. 2021, 253, 111402. [Google Scholar] [CrossRef]
- Gibout, S.; Franquet, E.; Haillot, D.; Bédécarrats, J.P.; Dumas, J.P. Challenges of the Usual Graphical Methods Used to Characterize Phase Change Materials by Differential Scanning Calorimetry. Appl. Sci. 2018, 8, 66. [Google Scholar] [CrossRef] [Green Version]
- Zalewski, L.; Franquet, E.; Gibout, S.; Tittelein, P.; Defer, D. Efficient Characterization of Macroscopic Composite Cement Mortars with Various Contents of Phase Change Material. Appl. Sci. 2019, 9, 1104. [Google Scholar] [CrossRef] [Green Version]
- Delcroix, B.; Kummert, M.; Daoud, A. Thermal Behavior Mapping of a Phase Change Material Between the Heating and Cooling Enthalpy-temperature Curves. Energy Procedia 2015, 78, 225–230. [Google Scholar] [CrossRef] [Green Version]
- Thonon, M.; Fraisse, G.; Zalewski, L.; Pailha, M. Analytical Modelling of PCM Supercooling Including Recalescence for Complete and Partial Heating/Cooling Cycles. Appl. Therm. Eng. 2021, 190, 116751. [Google Scholar] [CrossRef]
- Barz, T.; Emhofer, J.; Marx, K.; Zsembinszki, G.; Cabeza, L.F. Phenomenological Modelling of Phase Transitions with Hysteresis in Solid/Liquid PCM. J. Build. Perform. Simul. 2019, 12, 770–788. [Google Scholar] [CrossRef] [Green Version]
- Sam, M.N.; Caggiano, A.; Mankel, C.; Koenders, E. A Comparative Study on the Thermal Energy Storage Performance of Bio-Based and Paraffin-Based PCMs Using DSC Procedures. Materials 2020, 13, 1705. [Google Scholar]
- Fabiani, C.; Pisello, A.L.; Barbanera, M.; Cabeza, L.F.; Cotana, F. Assessing the Potentiality of Animal Fat Based-Bio Phase Change Materials (PCM) for Building Applications: An Innovative Multipurpose Thermal Investigation. Energies 2019, 12, 1111. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Jeong, S.G.; Chung, O.; Kim, S. Bio-based PCM/carbon nanomaterials composites with enhanced thermal conductivity. Sol. Energy Mater. Sol. Cells 2014, 120, 549–554. [Google Scholar] [CrossRef]
- Castellón, C.; Medrano, M.; Roca, J.; Cabeza, L.F.; Navarro, M.E.; Fernández, A.I.; Lázaro, A.; Zalba, B. Effect of microencapsulated phase change material in sandwich panels. Renew. Energy 2010, 35, 2370–2374. [Google Scholar] [CrossRef]
- Toppi, T.; Mazzarella, L. Gypsum based composite materials with micro-encapsulated PCM: Experimental correlations for thermal properties estimation on the basis of the composition. Energy Build. 2013, 57, 227–236. [Google Scholar] [CrossRef]
- Winco Technologies Technopôle Saint-Brieuc, Inertek. Winco Technol. 2020, 10. Available online: https://www.winco-tech.com/fr/accueil/ (accessed on 10 February 2020).Winco Technologies Technopôle Saint-Brieuc, Inertek. Winco Technol. 2020, 10.
- Tittelein, P.; Gibout, S.; Franquet, E.; Johannes, K.; Zalewski, L.; Kuznik, F.; Dumas, J.-P.; Lassue, S.; Bédécarrats, J.-P.; David, D. Simulation of the thermal and energy behaviour of a composite material containing encapsulated—PCM: Influence of the thermodynamical modelling. Appl. Energy 2015, 140, 269–274. [Google Scholar] [CrossRef]
- Younsi, Z.; Zalewski, L.; Lassue, S.; Rousse, D.R.; Joulin, A. A Novel Technique for Experimental Thermophysical Characterization of Phase—Change Materials. Int. J. Thermophys. 2011, 32, 674–692. [Google Scholar] [CrossRef]
- Joulin, A.; Younsi, Z.; Zalewski, L.; Lassue, S.; Rousse, D.R.; Cavrot, J.-P. Experimental and numerical investigation of a phase change material: Thermal-energy storage and release. Appl. Energy 2011, 88, 2454–2462. [Google Scholar] [CrossRef]
- Mussatti, E.; Merlini, C.; Barra, G.; Guths, S.; Oliveira, A.; Siligardi, C. Evaluation of the Properties of Iron Oxide-Filled Castor Oil Polyurethane. Mater. Res. 2013, 16, 65–70. [Google Scholar] [CrossRef] [Green Version]
- Alifanov, O.M. Iterative Regularization of Inverse Problems. In Inverse Heat Transfer Problems; Alifanov, O.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 227–328. [Google Scholar]
- Karkri, M.; Jarny, Y.; Mousseau, P. Inverse heat transfer analysis in a polymer melt flow within an extrusion die. Inverse Probl. Sci. Eng. 2005, 13, 355–375. [Google Scholar] [CrossRef]
- Franquet, E.; Gibout, S.; Tittelein, P.; Zalewski, L.; Dumas, J.-P. Experimental and theoretical analysis of a cement mortar containing microencapsulated PCM. Appl. Therm. Eng. 2014, 73, 30–38. [Google Scholar] [CrossRef]
- Bastani, A.; Haghighat, F.; Kozinski, J. Designing building envelope with PCM wallboards: Design tool development. Renew. Sustain. Energy Rev. 2014, 31, 554–562. [Google Scholar] [CrossRef]
- Hu, H.; Argyropoulos, S.A. Mathematical modelling of solidification and melting: A review. Modelling Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar]
- Nabavitabatabayi, M.; Haghighat, F.; Moreau, A.; Sra, P. Numerical analysis of a thermally enhanced domestic hot water tank. Appl. Energy 2014, 129, 253–260. [Google Scholar] [CrossRef]
- Liu, M.; Sun, Y.; Bruno, F. A review of numerical modelling of high-temperature phase change material composites for solar thermal energy storage. J. Energy Storage 2020, 29, 101378. [Google Scholar] [CrossRef]
- Maréchal, W. Utilisation de Méthodes Inverses Pour la Caractérisation de Matériaux à Changement de Phase (MCP). Ph.D. Thesis, University of Pau, Pau, France, 2014. [Google Scholar]
- Weisstein, E.W.; Gumbel Distribution. Wolfram MathWorld. Available online: https://mathworld.wolfram.com/GumbelDistribution.html (accessed on 2 February 2022).
- Gómez, Y.M.; Bolfarine, H.; Gómez, H.W. Gumbel distribution with heavy tails and applications to environmental data. Math. Comput. Simul. 2019, 157, 115–129. [Google Scholar] [CrossRef]
- Merlin, K. Caractérisation Thermique d’un Matériau à Changement de Phase Dans une Structure Conductrice. Ph.D. Thesis, University of Nantes, Nantes, France, 2016. [Google Scholar]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Krömer, P.; Platos, J.; Snasel, V. Differential evolution for the optimization of low-discrepancy generalized Halton sequences. Swarm Evol. Comput. 2020, 54, 100649. [Google Scholar] [CrossRef]
- Jin, X.; Xu, X.; Zhang, X.; Yin, Y. Determination of the PCM melting temperature range using DSC. Thermochim. Acta 2014, 595, 17–21. [Google Scholar] [CrossRef]
- Gschwander, S.; Haussmann, T.; Hagelstein, G.; Solé, A.; Cabeza, L.F.; Diarce, G.; Hohenauer, W.; Lager, D.; Ristic, A.; Rathgeber, C.; et al. Standardization of PCM Characterization via DSC. In Proceedings of the 13th International Conference on Energy Storage, Beijing, China, 19–21 May 2015. [Google Scholar]
- Chandrasekharan, R.; Lee, E.S.; Fisher, D.E.; Deokar, P.S. An Enhanced Simulation Model for Building Envelopes with Phase Change Materials—ProQuest. ASHRAE Trans. 2013, 119, 1–10. [Google Scholar]
- Bony, J.; Citherlet, S. Numerical model and experimental validation of heat storage with phase change materials. Energy Build. 2007, 39, 1065–1072. [Google Scholar] [CrossRef]
- Moreles, E.; Huelsz, G. Comparison of two hysteresis models of phase change materials (PCMs) for application in building envelopes. In Proceedings of the Conference on first UG-ASME-SOMIM Symposium of Energies and Thermal Sciences, Guanajuato, Mexico, 9–10 February 2016. [Google Scholar]
- Biswas, K.; Shukla, Y.; Desjarlais, A.; Rawal, R. Thermal characterization of full-scale PCM products and numerical simulations, including hysteresis, to evaluate energy impacts in an envelope application. Appl. Therm. Eng. 2018, 138, 501–512. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, R.; Heiselberg, P.; Johra, H. Modeling PCM Phase Change Temperature and Hysteresis in Ventilation Cooling and Heating Applications. Energies 2020, 13, 6455. [Google Scholar] [CrossRef]
- Delabrouille, J.C.; Rinck, E. Surfusion de l’étain, influence la pureté du métal. In Weekly Reports of the Sessions of the Academy of Sciences; CRAS: Paris, France, 1965; Volume 2, pp. 131–141. [Google Scholar]
- Dumas, J.-P.; Babin, L. Etude de la Rupture de Métastabilitsme et du Polymorphisme de Corps Organiques. Ph.D. Thesis, Université de Pau et des Pays de l’Adour, Pau, France, 1976. [Google Scholar]
- Bedecarrats, J.-P. Etude des Transformations des Matériaux à Changements de Phase Encapsulés Destinés au Stockage du Froid. Ph.D. Thesis, Université de Pau et des Pays de l’Adour, Pau, France, 1993. [Google Scholar]
- Meyn, L. An uncertainty propagation methodology that simplifies uncertainty analyses. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar]
- Wang, Y.; Dai, J.; Xiao, P. Research on Measurement Technology of Thermophysical Properties for Full-Scale Phase Change Material Product in a Container. Appl. Sci. 2019, 9, 2422. [Google Scholar] [CrossRef] [Green Version]
- Keithley. Model 2700 Multimeter/Data Acquisition System (User’s Manual); Keithley Instruments: Cleveland, OH, USA, 2015. [Google Scholar]
- TC SA. Thermocouple and Resistance Thermometry, Version 6.0; Institut International du Froid: Paris, France, 1999. [Google Scholar]


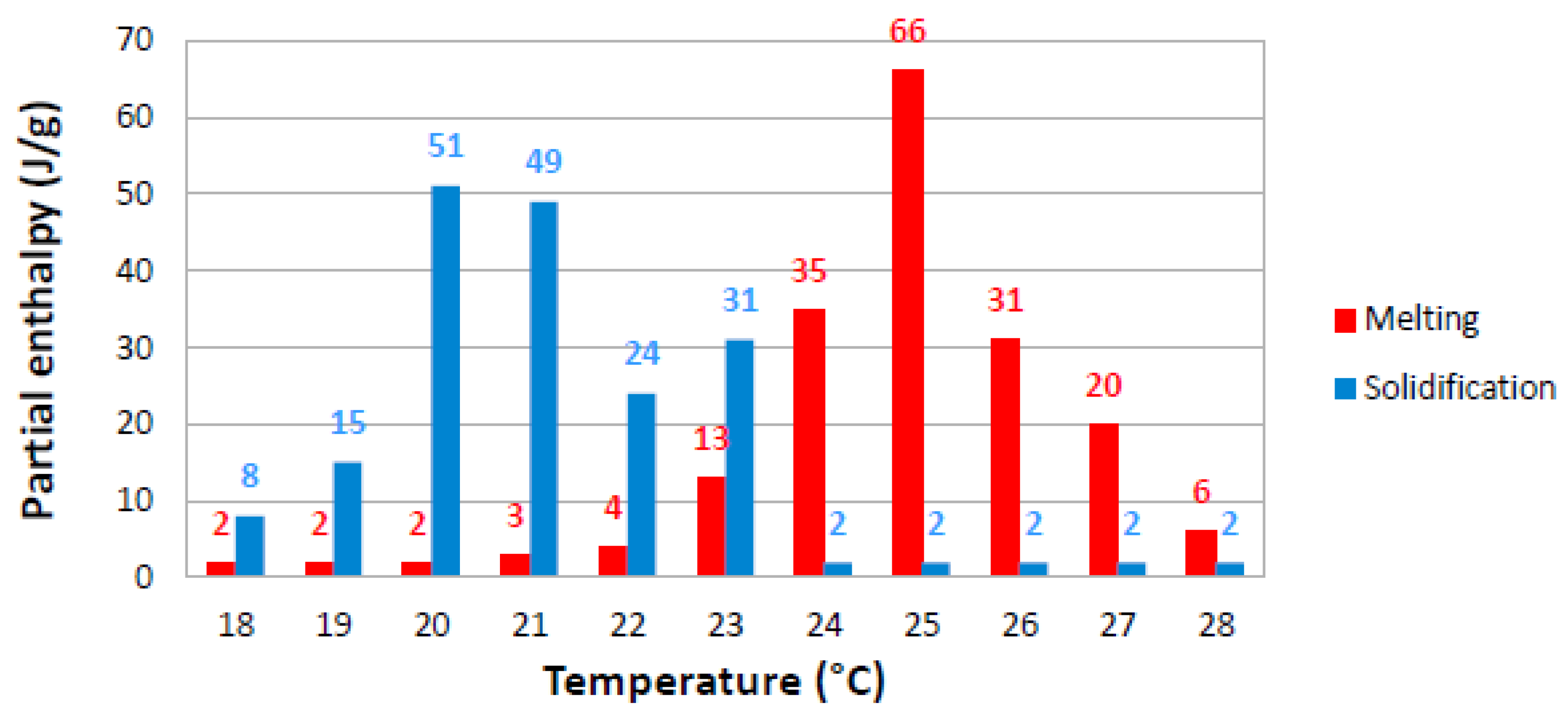

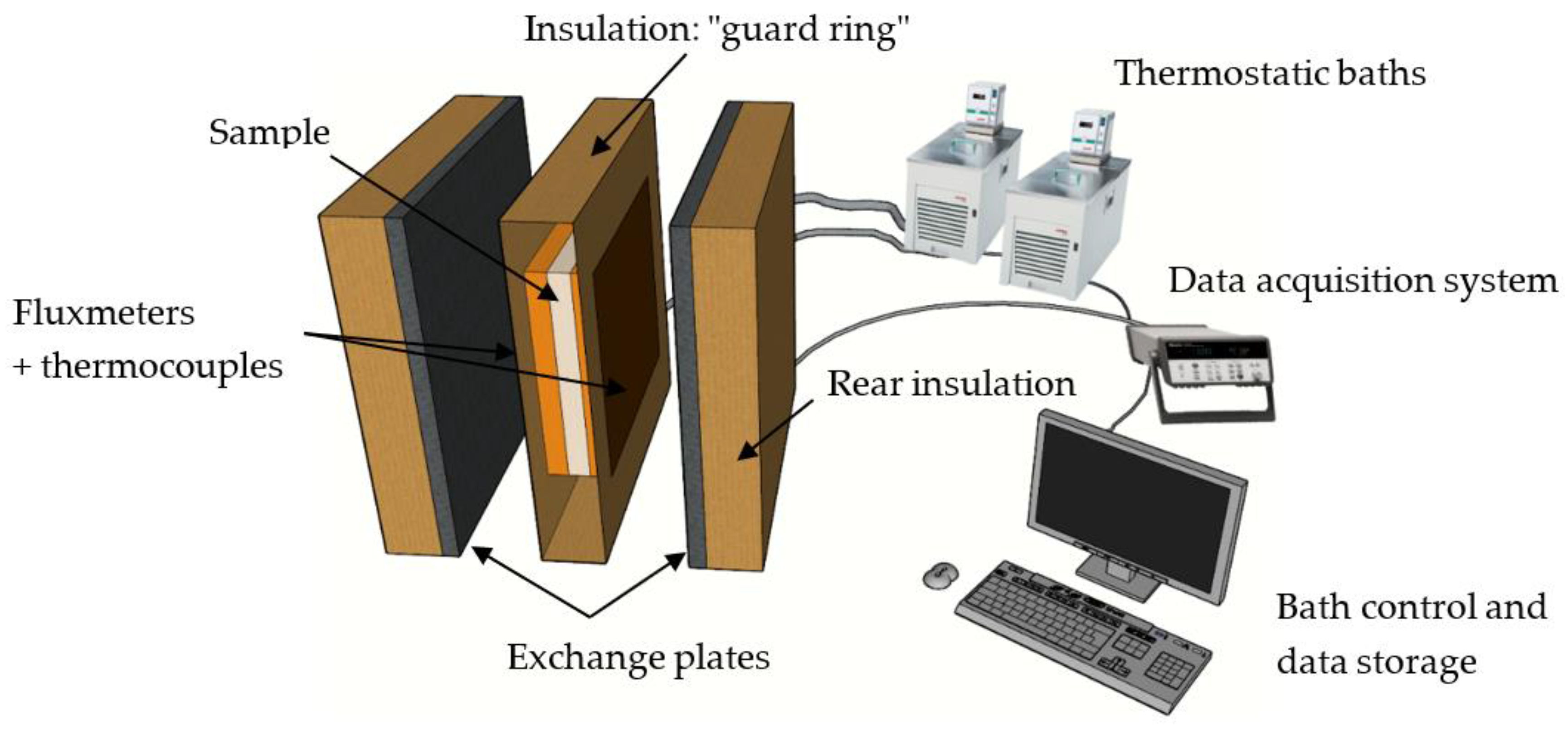




| Chemical | Thermodynamic | Economic |
|---|---|---|
| Chemically stable | Melting point | Inexpensive |
| Non-flammable Non-explosive Non-corrosive | High latent heat of melting High conductivity and density Limited supercooling Volume variation during phase transition | Easy to produce Available in large quantities Durability |
| Material | Composition [%] | Density [kg·m−3] |
|---|---|---|
| Coating Inertek 23 ETMV 8 | 30 70 100 | 650 350 610 |
| = 0.30 W·m−1·°C−1 | = 1071 J·kg−1·°C−1 | ρ = 815 kg·m−3 |
| = 29.02 | = 23.94 | = 0.135 | = 1213 | LA = 126,300 |
| = 26.89 | = 0.128 | CL = 1124 |
| = 81,942 | am = 24.18 | bm = 0.98 |
| = 12,300 | as = 17.74 | bs = 0.4 |
| Experimental | |||
|---|---|---|---|
| Loading | Melting [J] | Solidification [J] | Difference [%] |
| 3-h ramp | 136,233 | 135,727 | 0.37 |
| 6-h ramp | 134,579 | 135,850 | 0.94 |
| 10-h ramp | 135,770 | 135,937 | 0.12 |
| Max difference [%] | 1.2 | 0.2 | |
| Numerical | |||
|---|---|---|---|
| Loading | Melting [J] | Solidification [J] | Difference [%] |
| 3-h ramp | 137,232 | 133,968 | 2.38 |
| 6-h ramp | 137,235 | 133,978 | 2.37 |
| 10-h ramp | 137,225 | 133,922 | 2.41 |
| Difference [%] | 1.0 10−2 | 4.0 10−2 | |
| Heat flux | Component | Designation | Uncertainty [W/m2] | Comment |
| Captec fluxmeter | Uɸ | 2.04 | For 100 W·m−2 | |
| Data acquisition system | Umod,ɸ | 0.0009 | [64] | |
| Compound uncertainty | Uc,ɸ | 2.04 | (Equation (20)) | |
| Temperature | Component | Designation | Uncertainty [°C] | Comment |
| T-type thermocouple | UT | 0.5 | [65] | |
| Data acquisition system | Umod, T | 0.001 | [64] | |
| Compound uncertainty | Uc,T | 0.5 | (Equation (21)) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toifane, H.; Tittelein, P.; Cherif, Y.; Zalewski, L.; Leuck, H. Thermophysical Characterization of a Thermoregulating Interior Coating Containing a Bio-Sourced Phase Change Material. Appl. Sci. 2022, 12, 3827. https://doi.org/10.3390/app12083827
Toifane H, Tittelein P, Cherif Y, Zalewski L, Leuck H. Thermophysical Characterization of a Thermoregulating Interior Coating Containing a Bio-Sourced Phase Change Material. Applied Sciences. 2022; 12(8):3827. https://doi.org/10.3390/app12083827
Chicago/Turabian StyleToifane, Hachmi, Pierre Tittelein, Yassine Cherif, Laurent Zalewski, and Hervé Leuck. 2022. "Thermophysical Characterization of a Thermoregulating Interior Coating Containing a Bio-Sourced Phase Change Material" Applied Sciences 12, no. 8: 3827. https://doi.org/10.3390/app12083827
APA StyleToifane, H., Tittelein, P., Cherif, Y., Zalewski, L., & Leuck, H. (2022). Thermophysical Characterization of a Thermoregulating Interior Coating Containing a Bio-Sourced Phase Change Material. Applied Sciences, 12(8), 3827. https://doi.org/10.3390/app12083827







