A Deterministic Methodology Using Smart Card Data for Prediction of Ridership on Public Transport
Abstract
:1. Introduction
2. Smart Card Data and Public Transport Network
3. Methodology
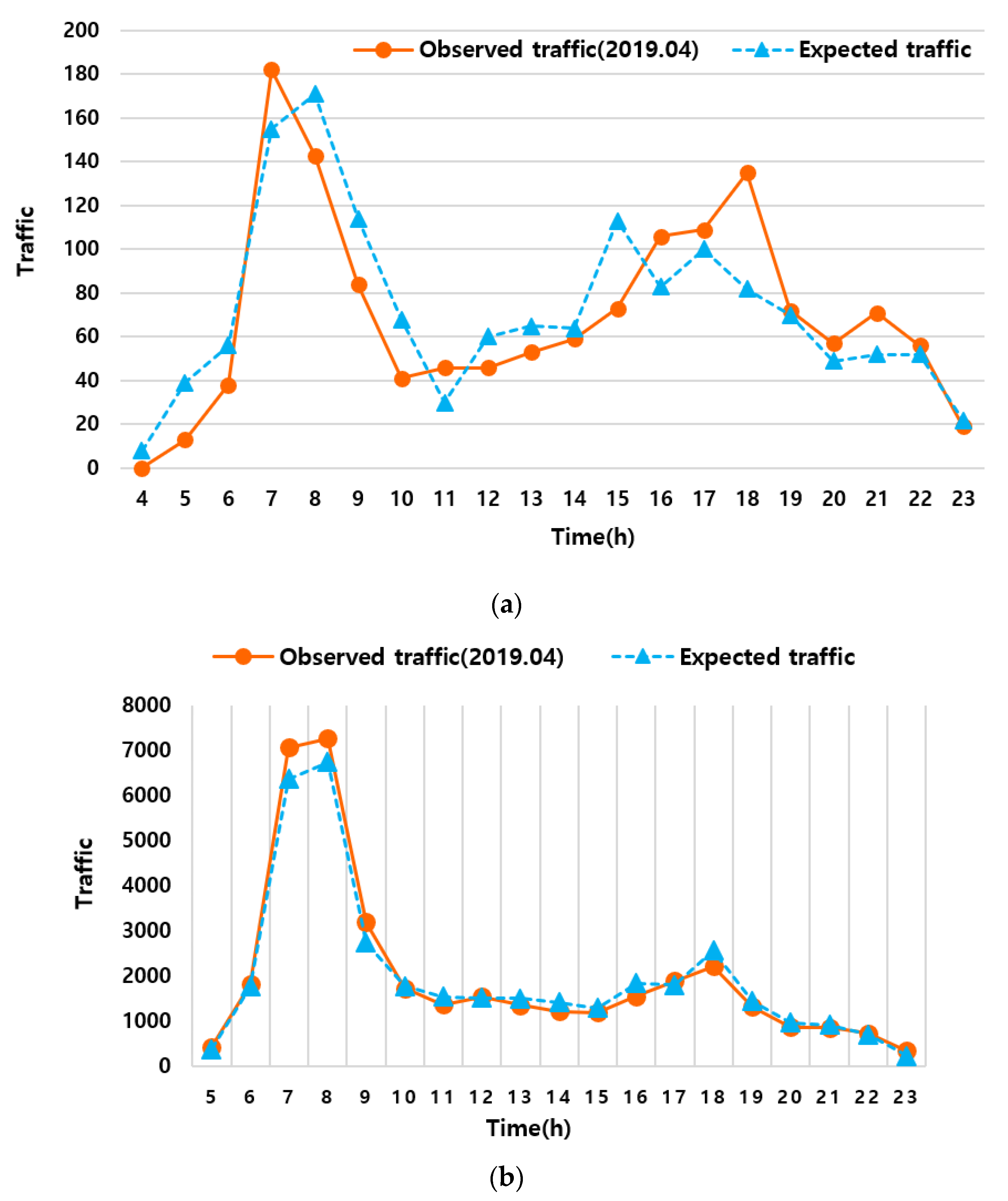
4. Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, T.; Sun, D.; Jing, P.; Yang, K. Smart card data mining of public transport destination: A literature review. Information 2018, 9, 18. [Google Scholar] [CrossRef] [Green Version]
- Kieu, L.M.; Bhaskar, A.; Chung, E. A modified density-based scanning algorithm with noise for spatial travel pattern analysis from smart card AFC data. Transp. Res. Part C Emerg. Technol. 2015, 58, 193–207. [Google Scholar] [CrossRef]
- Han, G.; Sohn, K. Activity imputation for trip-chains elicited from smart-card data using a continuous hidden Markov model. Transp. Res. Part B Methodol. 2016, 83, 121–135. [Google Scholar] [CrossRef]
- Bagchi, M.; White, P.R. The potential of public transport smart card data. Transp. Policy 2005, 125, 464–474. [Google Scholar] [CrossRef]
- Pelletier, M.P.; Trépanier, M.; Morency, C. Smart card data use in public transit: A literature review. Transp. Res. Part C Emerg. Technol. 2011, 19, 557–568. [Google Scholar] [CrossRef]
- Ma, X.; Wu, Y.J.; Wang, Y.; Chen, F.; Liu, J. Mining smart card data for transit riders’ travel patterns. Transp. Res. Part C Emerg. Technol. 2013, 36, 1–12. [Google Scholar] [CrossRef]
- Zhao, J.; Qu, Q.; Zhang, F.; Xu, C.; Liu, S. Spatio-temporal analysis of passenger travel patterns in massive smart card data. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3135–3146. [Google Scholar] [CrossRef]
- Agard, B.; Morency, C.; Trépanier, M. Mining public transport user behaviour from smart card data. IFAC Proc. Vol. 2006, 39, 399–404. [Google Scholar] [CrossRef]
- Munizaga, M.; Devillaine, F.; Navarrete, C.; Silva, D. Validating travel behavior estimated from smartcard data. Transp. Res. Part C Emerg. Technol. 2014, 44, 70–79. [Google Scholar] [CrossRef]
- Ali, A.; Kim, J.; Lee, S. Travel behavior analysis using smart card data. KSCE J. Civ. Eng. 2016, 20, 1532–1539. [Google Scholar] [CrossRef]
- Munizaga, M.A.; Palma, C. Estimation of a disaggregate multimodal public transport Origin–Destination matrix from passive smartcard data from Santiago, Chile. Transp. Res. Part C Emerg. Technol. 2012, 24, 9–18. [Google Scholar] [CrossRef]
- Alsger, A.A.; Mesbah, M.; Ferreira, L.; Safi, H. Use of smart card fare data to estimate public transport origin–destination matrix. Transp. Res. Rec. 2015, 2535, 88–96. [Google Scholar] [CrossRef]
- Tao, S.; Rohde, D.; Corcoran, J. Examining the spatial–temporal dynamics of bus passenger travel behaviour using smart card data and the flow-comap. J. Transp. Geogr. 2014, 41, 21–36. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, S.; Sohn, H.G. Relationship between spatio-temporal travel patterns derived from smart-card data and local environmental characteristics of Seoul, Korea. Sustainability 2018, 10, 787. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Zhang, F.; Tu, L.; Xu, C.; Shen, D.; Tian, C.; Li, Z. Estimation of passenger route choice pattern using smart card data for complex metro systems. IEEE Trans. Intell. Transp. Syst. 2016, 18, 790–801. [Google Scholar] [CrossRef]
- Anderson, M.K.; Nielsen, O.A.; Prato, C.G. Multimodal route choice models of public transport passengers in the Greater Copenhagen Area. EURO J. Transp. Logist. 2017, 6, 221–245. [Google Scholar] [CrossRef]
- Kim, J.; Corcoran, J.; Papamanolis, M. Route choice stickiness of public transport passengers: Measuring habitual bus ridership behaviour using smart card data. Transp. Res. Part C Emerg. Technol. 2017, 83, 146–164. [Google Scholar] [CrossRef]
- Cascajo, R.; Garcia-Martinez, A.; Monzon, A. Stated preference survey for estimating passenger transfer penalties: Design and application to Madrid. Eur. Transp. Res. Rev. 2017, 9, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, O.A. A stochastic transit assignment model considering differences in passengers utility functions. Transp. Res. Part B Methodol. 2000, 34, 377–402. [Google Scholar] [CrossRef]
- van Oort, N.; Drost, M.; Brands, T.; Yap, M. Data-driven public transport ridership prediction approach including comfort aspects. In Proceedings of the 13th Conference on Advanced Systems in Public Transport Conference, Rotterdam, The Netherlands, 20 July 2015. [Google Scholar]
- van Oort, N.; Brands, T.; de Romph, E. Short-term prediction of ridership on public transport with smart card data. Transp. Res. Rec. 2015, 2535, 105–111. [Google Scholar] [CrossRef]
- Xue, R.; Sun, D.J.; Chen, S. Short-term bus passenger demand prediction based on time series model and interactive multiple model approach. Discret. Dyn. Nat. Soc. 2015, 2015, 682390. [Google Scholar] [CrossRef] [Green Version]
- Menon, A.K.; Lee, Y. Predicting short-term public transport demand via inhomogeneous Poisson processes. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 2207–2210. [Google Scholar]
- Santanam, T.; Trasatti, A.; Van Hentenryck, P.; Zhang, H. Public Transit for Special Events: Ridership Prediction and Train Optimization. arXiv 2021, arXiv:2106.05359. [Google Scholar]
- Lawson, C.T.; Muro, A.; Krans, E. Forecasting bus ridership using a “Blended Approach”. Transportation 2021, 48, 617–641. [Google Scholar] [CrossRef] [Green Version]
- Patel, Y.; Firat, C.; Childers, T.; Sartipi, M. Ridership Prediction of New Bus Routes at Stop Level by Modelling Socio-economic Data using Supervised Machine Learning Methods. In Proceedings of the Transportation Research Board 100th Annual Meeting, Washington, DC, USA, 5–29 January 2021. [Google Scholar]
- Spiess, H.; Florian, M. Optimal strategies: A new assignment model for transit networks. Transp. Res. Part B Methodol. 1989, 23, 83–102. [Google Scholar] [CrossRef]
- Andersen, J.L.E.; Landex, A. Catchment areas for public transport. WIT Trans. Built Environ. 2008, 101, 175–184. [Google Scholar]
- Delling, D.; Pajor, T.; Werneck, R.F. Round-based public transit routing. Transp. Sci. 2015, 49, 591–604. [Google Scholar] [CrossRef] [Green Version]
- Jeon, I.; Nam, H.; Jun, C. A schedule-based public transit routing algorithm for finding K-shortest paths considering transfer penalties. J. Korea Inst. Intell. Transp. Syst. 2018, 17, 72–86. [Google Scholar] [CrossRef]
- Barabino, B.; Lai, C.; Olivo, A. Fare evasion in public transport systems: A review of the literature. Public Transp. 2020, 12, 27–88. [Google Scholar] [CrossRef]
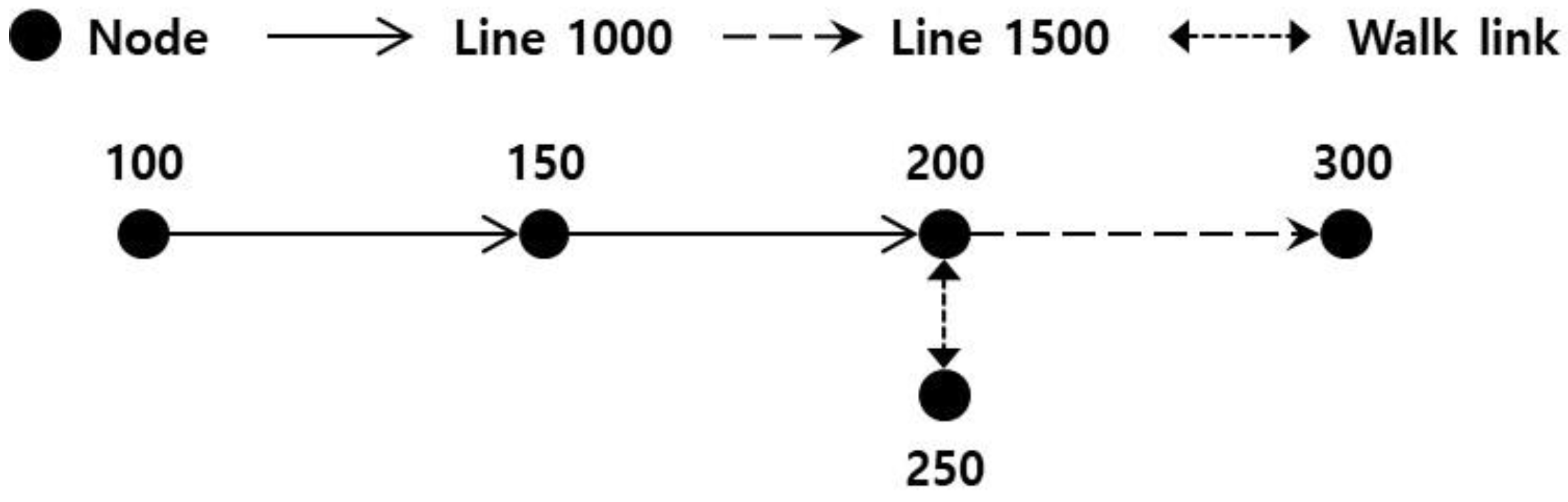
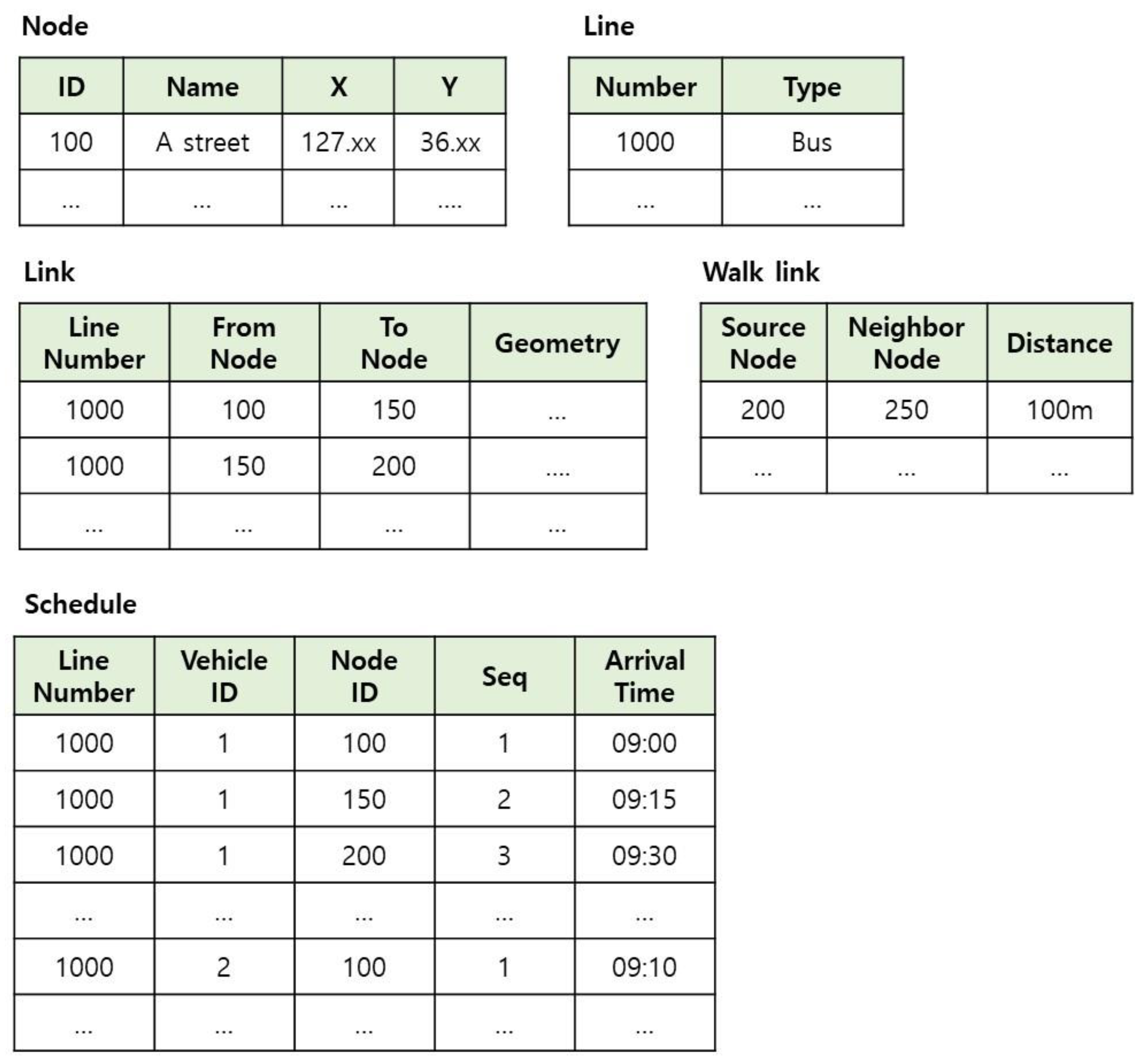
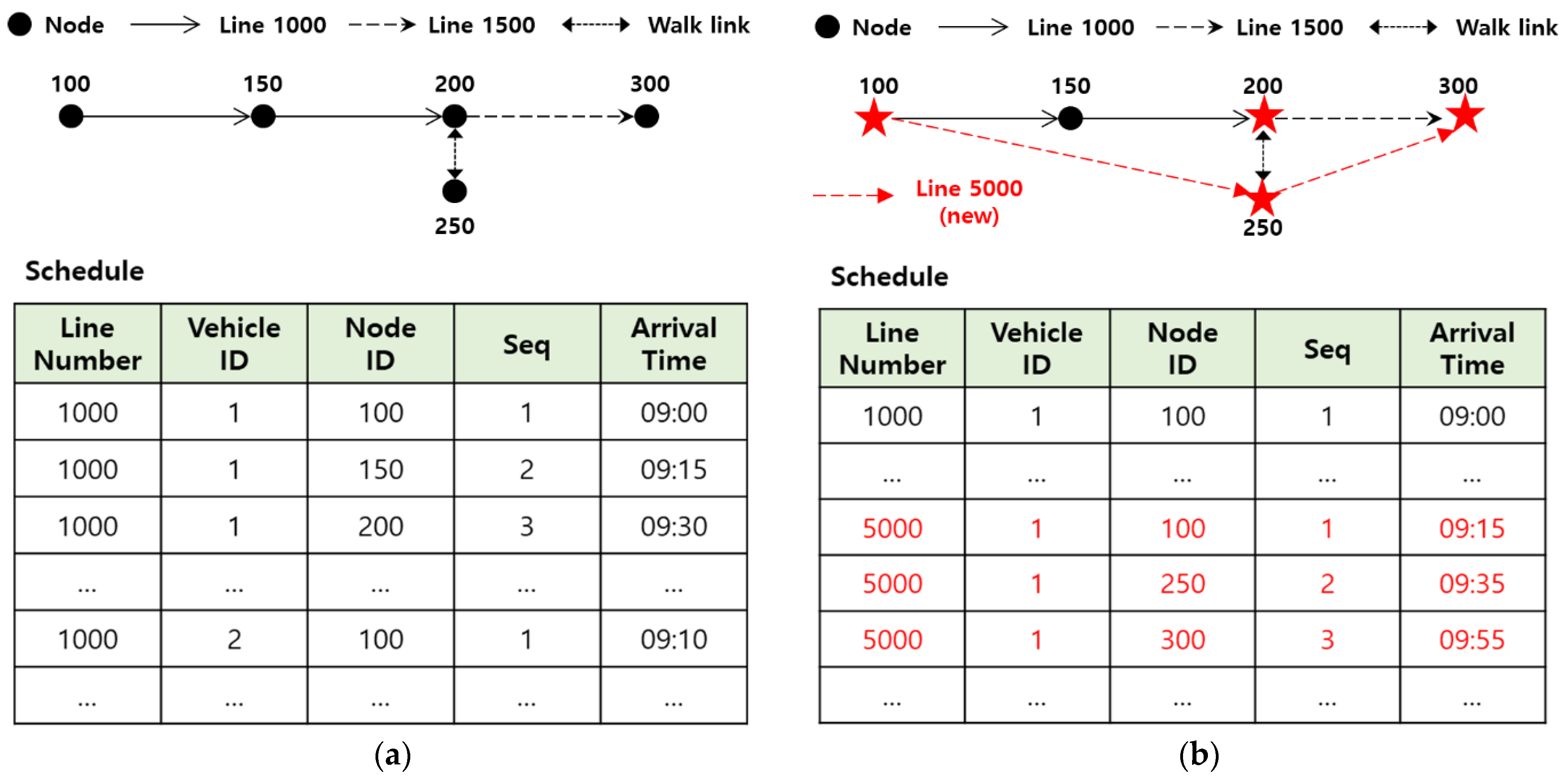
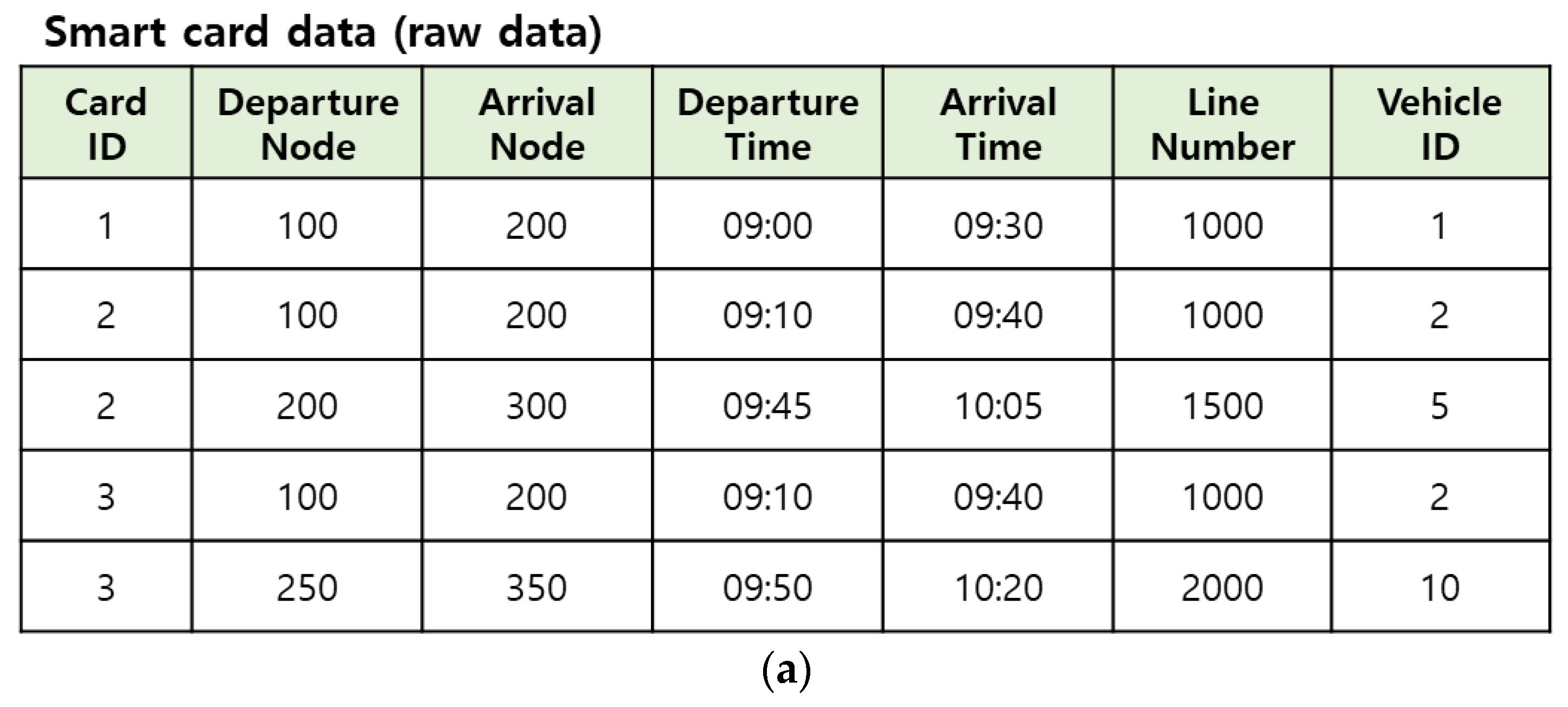
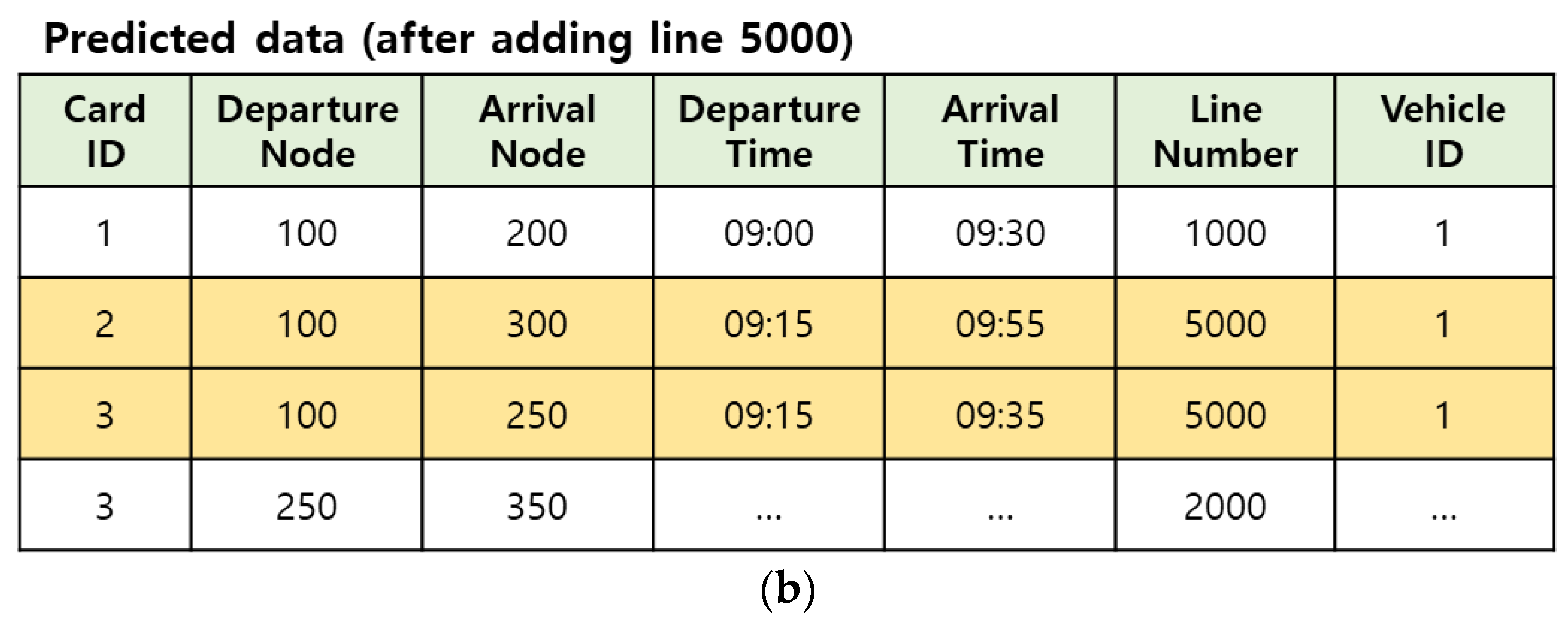

| Card ID | Departure Node | Arrival Node | Departure Time | Arrival Time | Line Number | Vehicle ID | Card Type |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 200 | 09:00 | 09:30 | 1000 | 1 | Senior |
| 2 | 100 | 200 | 09:10 | 09:40 | 1000 | 2 | Teenager |
| 2 | 200 | 300 | 09:45 | 10:05 | 1500 | 5 | Teenager |
| 3 | 100 | 200 | 09:10 | 09:40 | 1000 | 2 | Adult |
| 3 | 250 | 350 | 09:50 | 10:20 | 2000 | 10 | Adult |
| Scenario | Daily Average Ridership per Node | Average Ridership per Hour | ||
|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |
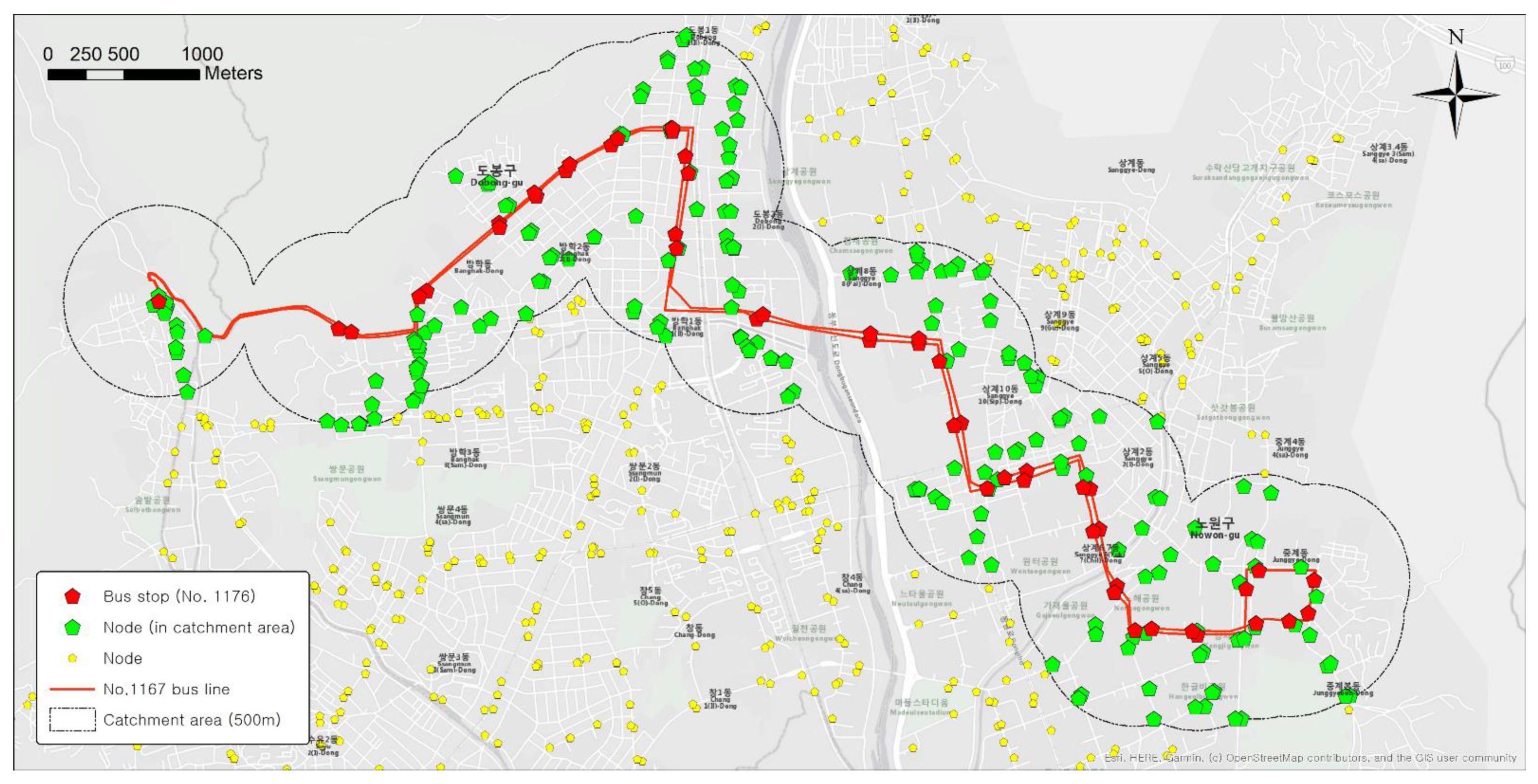
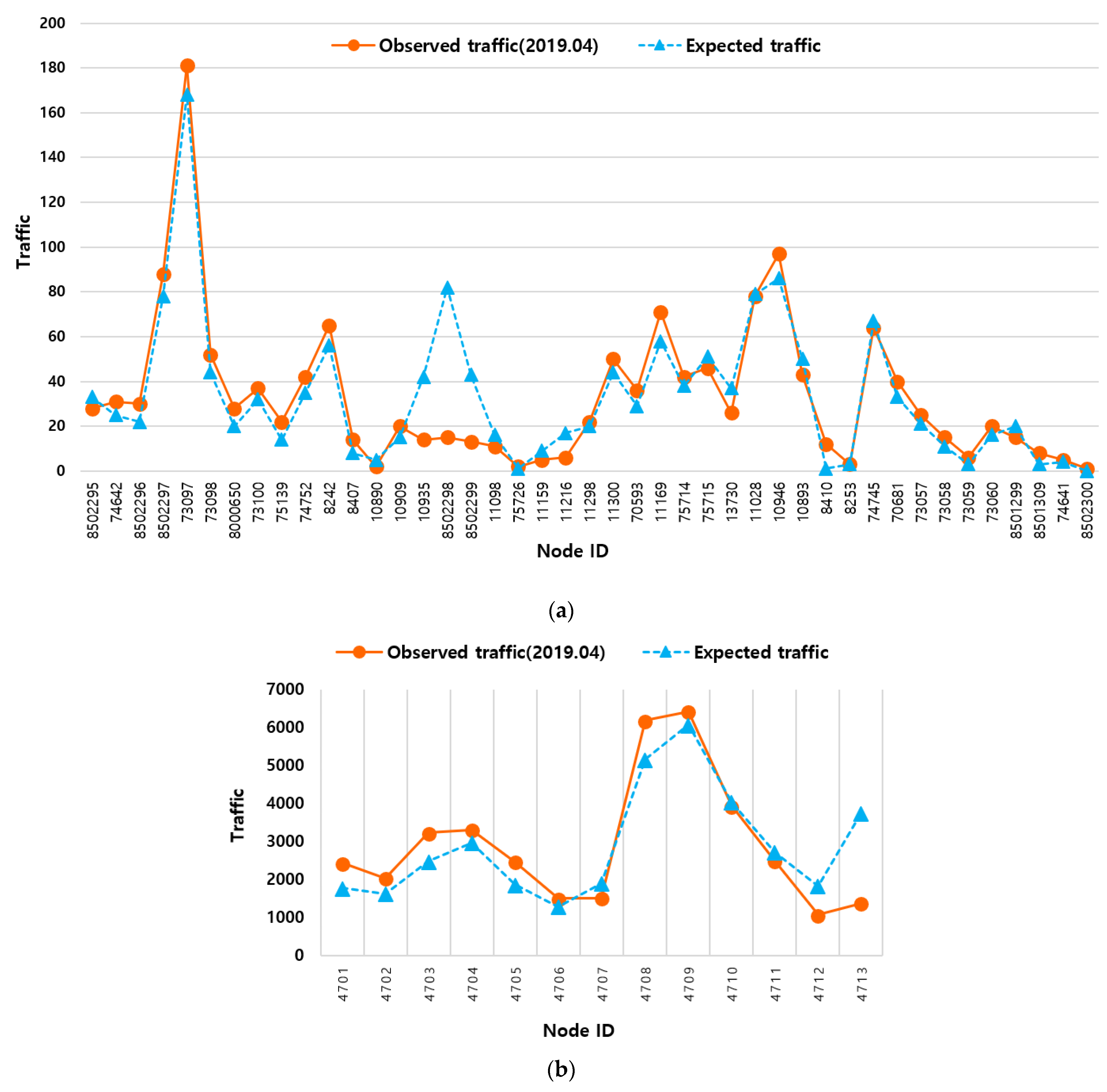
| Bus No. 1167 | 8.4 | 13.7 | 18.6 | 22.7 |
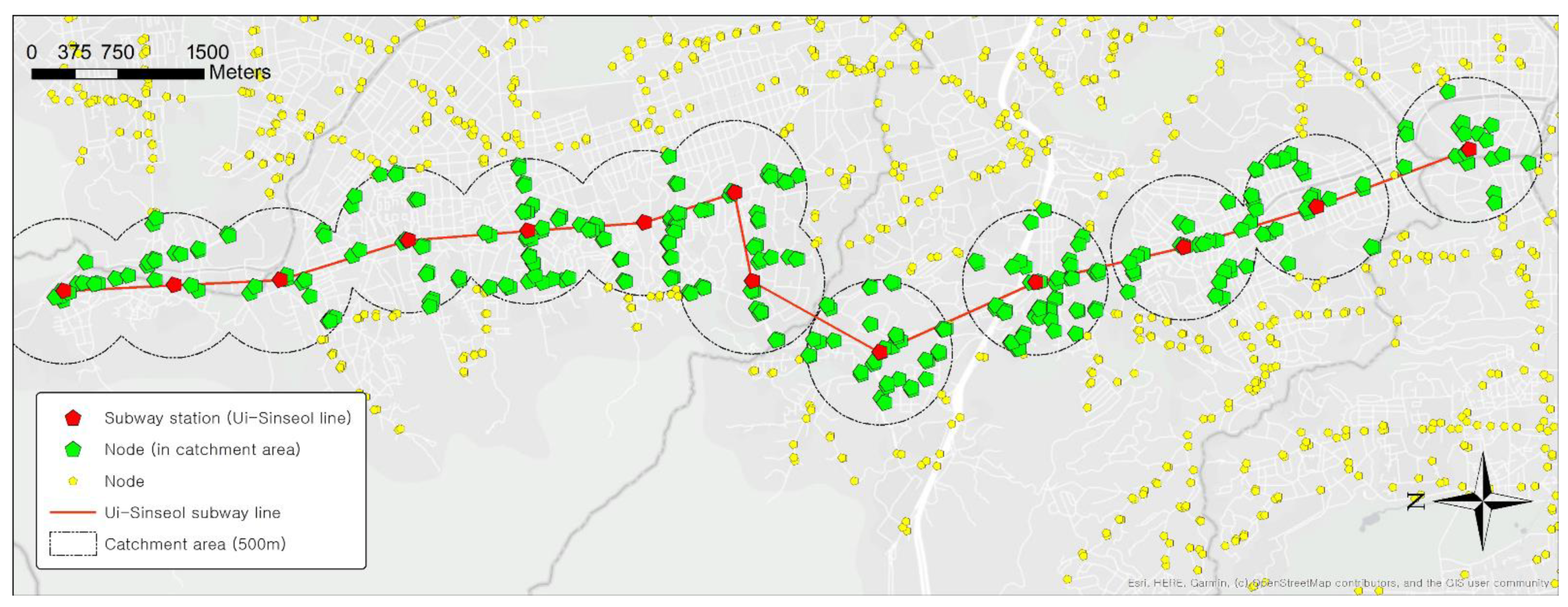
| Ui-Sinseol subway line | 682.6 | 1080.3 | 190.8 | 264.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Jeon, I.; Jun, C. A Deterministic Methodology Using Smart Card Data for Prediction of Ridership on Public Transport. Appl. Sci. 2022, 12, 3867. https://doi.org/10.3390/app12083867
Lee M, Jeon I, Jun C. A Deterministic Methodology Using Smart Card Data for Prediction of Ridership on Public Transport. Applied Sciences. 2022; 12(8):3867. https://doi.org/10.3390/app12083867
Chicago/Turabian StyleLee, Minhyuck, Inwoo Jeon, and Chulmin Jun. 2022. "A Deterministic Methodology Using Smart Card Data for Prediction of Ridership on Public Transport" Applied Sciences 12, no. 8: 3867. https://doi.org/10.3390/app12083867
APA StyleLee, M., Jeon, I., & Jun, C. (2022). A Deterministic Methodology Using Smart Card Data for Prediction of Ridership on Public Transport. Applied Sciences, 12(8), 3867. https://doi.org/10.3390/app12083867






