A Neural Network-Based Method for Respiratory Sound Analysis and Lung Disease Detection

Abstract

Background: Respiratory sound analysis represents a research topic of growing interest in recent times. In fact, in this area, there is the potential to automatically infer the abnormalities in the preliminary stages of a lung dysfunction. Methods: In this paper, we propose a method to analyse respiratory sounds in an automatic way. The aim is to show the effectiveness of machine learning techniques in respiratory sound analysis. A feature vector is gathered directly from breath audio and, thus, by exploiting supervised machine learning techniques, we detect if the feature vector is related to a patient affected by a lung disease. Moreover, the proposed method is able to characterise the lung disease in asthma, bronchiectasis, bronchiolitis, chronic obstructive pulmonary disease, pneumonia, and lower or upper respiratory tract infection. Results: A retrospective experimental analysis on 126 patients with 920 recording sessions showed the effectiveness of the proposed method. Conclusion: The experimental analysis demonstrated that it is possible to detect lung disease by exploiting machine learning techniques. We considered several supervised machine learning algorithms, obtaining the most interesting performance with the neural network model, with an F-Measure of 0.983 in lung disease detection and equal to 0.923 in lung disease characterisation, increasing the state-of-the-art performance.

1. Introduction

Lung diseases are among the most prevalent causes of death worldwide, according to recent statistics (https://www.who.int/gard/publications/The_Global_Impact_of_Respiratory_Disease.pdf accessed on 8 February 2022).

As a matter of fact, chronic obstructive pulmonary disease plagues more than two hundred million persons around the world (http://www.who.int/gard/publications/GARD_Manual/en/ accessed on 8 February 2022), with sixty-five million with moderate or severe lung disease [1]. This is higher than the values reported for other diseases, such as hypertension and hypercholesterolaemia. Furthermore, misdiagnosis is also common [1].

Auscultation represents the practice of listening to the body’s internal sounds, usually using a stethoscope [2]. It is typically performed for the purposes of analysing the circulatory and respiratory systems (for instance, heart and breath sounds) [3,4]. Clearly, an expert doctor is required to detect lung disease using this method. In fact, the possibility that untrained doctors may incorrectly recognize the anomalies, which may be due to a lack of calibration of the instrument but also to the noisy environment, is very high using this method, as shown in [5]: this represents the reason that there is a growing interest in software aimed at analysing and detecting lung disease via pulmonary sounds.

Respiratory sounds in this context can represent important indicators of health from a respiratory point of view. In fact, sounds generated when a patient is breathing are directly related to the movement of air, which can clearly vary according to lung tissue and secretions [6]. Assuming that breathing varies according to the health of the lungs, it may be possible to automatically identify a lung disease by analysing the breath sounds gathered from a stethoscope.

For these reasons, we design an approach to automatically identify lung diseases by analysing respiratory sounds. We propose a two-step supervised machine learning approach able to (i) detect whether audio gathered from digital stethoscopes is related to a healthy patient or a patient afflicted by a (generic) lung disease and to (ii) recognise the specific lung disease.

We experiment with several supervised machine learning algorithms, finding the best one for detecting respiratory sound issues. The aim is to show that machine learning techniques can be successfully employed for the detection of lung pathologies in an automatic and non-invasive way. As a matter of fact, in order to generate the prediction from the proposed approach, we only require the audio registration from the digital stethoscope for the patient, without any invasive examination. For this reason, the proposed method can be considered also for rapid screening.

We itemize the distinctive points introduced in the manuscript below:

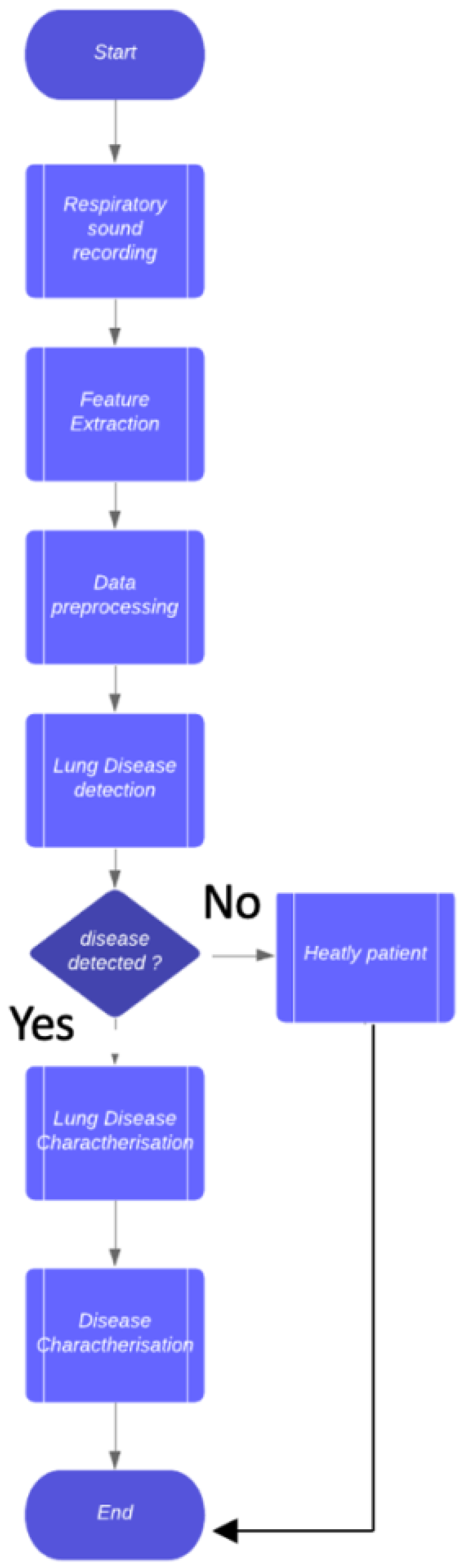
• a two-step method composed of a classifier is proposed: the first one aims to discriminate between healthy patients and patients affected by a generic lung disease, while the second model is devoted to detecting the specific lung disease;
• we exploit a feature vector directly obtained from respiratory sounds, which, to the best of the authors’ knowledge, has never been previously considered;
• in the experimental analysis, we use two datasets, obtained from real-world patients, composed of respiratory sounds, collected and labelled from two different institutions (the first one in Portugal and the second one in Greece);
• for conclusion validity, we analyse the effectiveness of the considered feature vector with different supervised machine learning techniques, by showing that machine learning can be helpful in the automatic detection of lung diseases;
• we obtain an F-Measure of 0.983 in lung disease detection;
• we obtain an F-Measure equal to 0.923 in lung disease characterisation, i.e., in the discrimination between asthma, bronchiectasis, bronchiolitis, chronic obstructive pulmonary disease, pneumonia, and lower or upper respiratory tract infection.

The paper proceeds in the following way: in Section 2, we present the approach that we propose for the automatic analysis of respiratory sounds; Section 3 presents the experimental analysis outcomes; Section 4 aims to explore the current literature in the context of respiratory sound analysis by exploiting machine learning techniques, and, finally, the conclusions and future research lines are presented in the last section.

2. Materials and Methods

In this section, we describe the method that we designed to detect and characterise lung diseases directly from respiratory sounds.

2.1. Materials

Ethical approval was obtained from patients involved in the study. The dataset considered to experimentally evaluate the proposed method was collected by two different and independent research teams located in two countries: Portugal and Greece. The dataset includes 920 annotated respiratory audio recordings of varying length (i.e., from 10 s to 90 s). The audio was obtained from 126 different patients (namely, 46 women and 80 men) with 5.5 h of sound recordings related to 6898 respiratory cycles. The audio samples are related to clean breaths and also noisy audio simulating real-world situations with the related annotation about healthy or lung disease cases. The patients’ ages are categorised as children, adults, and the elderly [7], by considering patients ranging from 1 to 83 years. In detail, of the 126 patients considered, 1 patient was affected by asthma, 7 by bronchiectasis, 6 by bronchiolitis, 64 by chronic obstructive pulmonary disease (i.e., COPD), 2 by infection of the lower respiratory tract (i.e., LRTI), 6 by pneumonia, and 14 by infection of the upper respiratory tract (i.e., URTI), for a total of 100 patients affected by lung disease, and the remaining 26 were healthy patients. Annotation of sounds by respiratory experts is the considered the most common and reliable method for evaluating the robustness of algorithms for detecting adventitious respiratory sounds [8].

Two respiratory physiotherapists and a doctor, with experience in recognizing visual–auditory crackles and wheezing, independently annotated the sound files in terms of the presence (or the absence) of adventitious sounds and identification of respiratory phases [7]. In the case of divergent judgments, the diagnosis was decided by a majority vote.

The dataset is freely available for research purposes (https://www.kaggle.com/vbookshelf/respiratory-sound-database accessed on 8 February 2022).

2.2. Methods

In Figure 1, we depict the workflow related to the method that we propose.

The audio sessions related to the breath of the patient are recorded exploiting, for instance, digital stethoscopes [9]. As a matter of fact, nowadays, electronic stethoscopes convert the acoustic sound waves obtained through the chest piece into electrical signals that are successively amplified for better listening [10].

Once we obtained the audio sample related to the patient’s breath, we computed a set of numeric values, i.e., a feature vector directly computed on the breath sound sample.

In detail, the following features were computed:

• Chromagram (CR): this feature is related to a chromagram representation automatically gathered from a waveform ($F1$ feature);
• Root Mean Square (RMS): this feature (i.e., RMS) is related the value of the mean square as the root that is obtained for each audio frame that is gathered from the sound sample under analysis ($F2$ feature);
• Spectral Centroid (SC): this feature is symptomatic of the “centre of mass” for a sound sample and is obtained as the mean related to the frequencies of the audio ($F3$ feature);
• Bandwidth: it is related the bandwidth of the spectrum ($F4$ feature);
• Spectral Roll-Off (SR): it is expressed as the frequency related to a certain percentage of the total spectral of the energy ($F5$ feature);
• Tonnetz (T): it is computed from the the tonal centroid ($F6$ feature).
• Mel-Frequency Cepstral Coefficient: this feature (i.e., MEL), whose acronym is related to a feature vector (ranging from 10 to 20 different numerical features 10–20), is devoted to representing the shape of a spectral envelope ($F7$ feature);
• Zero Crossing Rate (ZCR): this value is related to the rate of an audio time series ($F8$ feature);
• Poly (P): it is computed as the fitting coefficient related to an nth-order polynomial ($F9$ feature).

Mathematical details about the feature vector that we considered can be found in [11,12,13,14]. We consider this feature set due to its demonstrated effectiveness in performing other tasks involving supervised machine learning—for instance, the classification and segmentation of audio files into generic classes as speech [15], music [16], and silence [17,18,19]. The idea is to obtain a numeric vector for each audio sample; as a matter of fact, machine learning typically works with numerical values.

Once the feature vector is obtained, these values are converted into a CSV file (i.e., Data preprocessing in Figure 1). In particular, the authors developed a script by exploiting the Java programming language that aimed to automatically extract the numeric features from each audio sample and to generate a CSV file, where, in each row, there are the numerical features from a single audio sample. With the script, the authors verified whether, for each audio sample considered in the dataset, all the numeric features had been correctly extracted, with the aim of avoiding inconsistencies.

We consider raw features in the feature vector. We are aware that feature normalization is beneficial in many cases; as a matter of fact, it improves the numerical stability of the model and often reduces the training time. However, it can harm the performance of distance-based clustering algorithms by assuming the equal importance of features. If there are inherent importance differences between features, typically, we do not exploit the normalisation of the features. For instance, neural networks can counteract standardization in the same way as regressions. Therefore, in theory, data standardization should not affect the performance of a neural network. These are the reasons that we do not consider feature normalisation.

This CSV file is sent to the lung disease detection module. In this module, we consider supervised machine learning: we adopt several supervised classification algorithms to obtain models devoted to predicting whether the feature vector belongs to a healthy patient or he/she exhibits a generic lung disease. In detail, in this work, we evaluate the effectiveness in lung disease detection of four different supervised machine learning algorithms (to enforce the conclusion validity): k-nearest neighbours (i.e., kNN), support vector machine (i.e., SVM), neural network, and logistic regression. We aim to show that machine learning algorithms can be exploited to automatically solve the lung disease prediction task.

We exploit these supervised machine learning classification algorithms considering that, in different domains, they were successfully applied—for instance, in glioblastoma detection [20] and in vehicular insurance contexts [21].

The next step, shown in Figure 1, related to the lung disease detection module, aimed to mark the feature vector as healthy or disease. If the prediction for the feature vector under analysis is healthy, the proposed method diagnosed the patient as healthy. Otherwise, the feature vector is sent to the disease characterisation module that aims to predict, from the feature vector previously analysed to detect the generic lung disease, the lung disease typology. In detail, our approach is devoted to predicting whether a feature vector belongs to one of the following lung disease categories: asthma [22], bronchiectasis [23], bronchiolitis [24], COPD [25], LRTI, pneumonia [24], URTI [25].

In a nutshell, the working mechanism of the proposed method relies on two different modules, i.e., the lung disease detection and the lung disease characterisation. The first module outputs a binary class for the feature vector under analysis (i.e., healthy or disease), while the second module marks the feature vector under analysis (i.e., the audio samples obtained from the patient) with one of following labels related to specific lung diseases: asthma, bronchiectasis, bronchiolitis, COPD, LRTI, pneumonia, and URTI (it represents a multi-class model).

2.3. Study Design

For the evaluation of the effectiveness of the proposed approach for the automatic analysis of respiratory sounds, we propose an experiment consisting of three stages: the first stage is represented by a discussion of the descriptive statistics related to the population of the patients under analysis; the second stage is an analysis related to the classification results, aimed to show if the exploited sound features are able to discriminate healthy patients and patients afflicted by lung disease; and the third stage is a graphical analysis aimed to compare the models built through different classifiers. The classification analysis was accomplished with Orange, a software providing several implementations for supervised machine learning algorithms [26].

3. Study Evaluation

The outcomes of our experimental analysis are presented according to the study design division: descriptive statistics, classification performance, and model analysis.

3.1. Experiment Settings

This section is devoted to presenting the experiment that we performed to build both the lung disease detection and the lung disease characterisation models.

Relating to the learning of the first model, i.e., the lung disease detection one, we consider $T_{detection}$ as a set of labels {($M_{detection}$, $l_{detection}$)}, where each $M_{detection}$ is the label that is associated with a $l_{detection}$∈ {healthy, disease}.

With regard to the lung disease characterisation model training, we defined $T_{characterisation}$ as a set of labelled instances {($M_{characterisation}$, $l_{characterisation}$)}, where each $M_{characterisation}$ is the label that is related to a different lung disease $l_{characterisation}$∈ {$asthma$, $bronchietactasis$, $bronchiolitis$, $COPD$, $LRTI$, $pneumonia$, and $URTI$}.

For the two models that we consider, i.e, $M_{detection}$ and $M_{characterisation}$, we build a numeric vector of features F $\in R_y$, where y represents the feature number exploited in the learning phase ($y=10$).

In detail, with respect to the training phase, the k-fold cross-validation is exploited. We explain this process as follows: the instances of the dataset are split in a random way into a set denoted as k.

In order to test the effectiveness of both the models that we propose, the procedure described below is considered:

• generation of set for the training, i.e., T⊂D;
• generation of an evaluation set $T^{\prime }=D÷$ T;
• execution of the model training T;
• application of the model previously generated to each element of the $T^{\prime }$ set.

For both the classifications, we considered the full feature set exploiting the kNN, SVM, neural network, and logistic regression [27] classification algorithms. Regularisation is used in machine learning as a solution to overfitting by reducing the variance of the ML model under consideration. Regularisation can be implemented in multiple ways by either modifying the loss function, sampling method, or the training approach itself. With the aim to avoid overfitting, we exploited the cross-validation: in this way, the whole dataset was evaluated in the testing step. The k-fold cross-validation procedure involves splitting the training dataset into k folds. The first k-1 folds are used to train a model, and the holdout k-th fold is used as the test set. This process is repeated and each of the folds is given an opportunity to be used as the holdout test set. A total of k models are fit and evaluated, and the performance of the model is calculated as the mean of these runs. The procedure has been shown to give a less optimistic estimate of model performance on small training datasets than a single train/test split. A value of k = 10 has been shown to be effective across a wide range of dataset sizes and model types. We considered a version of k-fold cross-validation that preserves the imbalanced class distribution in each fold. It is called stratified k-fold cross-validation and will enforce the class distribution in each split of the data to match the distribution in the complete training dataset. In other words, the folds are selected so that each fold contains roughly the same proportions of class labels of the original dataset.

Below, we explain the parameters that we considered for the models’ training: for the kNN, SVM, neural network, and logistic regression algorithms, we considered a batch size (i.e., the number of instances to process if batch prediction is being performed) equal to 100. With batch, we are referring to a term used in machine learning and it is related to the number of training examples utilized in one iteration. Moreover, for the kNN model, we set the number of neighbours equal to 1. Relative to the neural network, we considered (in addition to a batch size of 100) an architecture composed of one convolutional layer with patch size 5 × 5 and pool size 2 × 2, each with 100 feature maps, respectively. In order to tune the hyperparameters, we exploited the Exhaustive Grid Search provided by the Orange data mining tool. In particular, we exploited the GridSearch CV, which exhaustively considers all parameter combinations in order to find the best ones.

3.2. Descriptive Statistics

Descriptive statistics are represented by descriptive coefficients, which aim to summarize a set of numerical data. The idea is to graphically show whether the considered features assume different values, respectively, for the healthy and disease population and for the lung disease distributions (i.e., asthma, bronchiectasis, bronchiolitis, COPD, LRTI, pneumonia, and URTI).

For feature representation, a scatterplot is considered, i.e., a type of visual representation exploiting Cartesian coordinates to show values for two features. Additionally, we considered a scatterplot as other studies have exploited it for graphical and immediate impact regarding the potential effectiveness of the proposed feature set for lung disease characterisation. We present four different scatterplots, but closer explanation can be made also for the other plots. The rationale behind the adoption of scatterplots is to empirically demonstrate that the distribution of features is different for healthy and lung disease-affected patients: as a matter of fact, the more the numerical value assumed by the features is similar for a class to be identified, but at the same time it is different from the value assumed by the features for another class, the more the machine learning algorithms will be able to create models with good discriminatory ability.

Figure 2 and Figure 3 show the scatterplots related to the lung disease detection (i.e., with $l_{detection}$∈ {healthy, disease}).

In detail, Figure 2 shows the scatterplot for the $F3$ (i.e., Spectral Centroid) and $F2$ (i.e., Root Mean Square) features.

As emerges from the scatterplot in Figure 2, the healthy distributions (i.e., the red points) are highly concentrated in the lower left corner if compared to the blue ones (i.e., the values obtained for the disease instances), occupying a much larger space in the scatterplot.

In Figure 3 is depicted the scatterplot related to the feature $F4$ (i.e., Bandwidth) and the feature $F5$ (i.e., Spectral Roll-Off).

Similar considerations can be made; in fact, the distribution of the healthy points is more localised in comparison with the disease ones. From this observation, it emerges that the disease instances with respect to the $F4$ and $F5$ features are ranging in an interval that is wider than the healthy instances.

Clearly, the more that the points of the healthy and disease cases are distant (i.e., the two distributions do not overlap), the more the classification algorithms will be able to generate effective models.

Figure 4 and Figure 5 are related to the scatterplots of the lung disease detection (i.e., with $l_{characterisation}$∈ {asthma, bronchiectasis, bronchiolitis, COPD, LRTI, pneumonia, and URTI}).

In particular, Figure 4 shows the scatterplot for the $F8$ (i.e., Zero Crossing Rate) and $F4$ features (i.e., Bandwidth).

We note that the widest area is covered by the COPD instances, symptomatic of the fact that the $F8$ and $F4$ features range in a wider interval if compared to the remaining features.

For the instances of the remaining lung diseases, particularly pneumonia and asthma, the range is in a similar interval, as confirmed by the instances overlapping.

Figure 5 shows the scatterplot for the $F9$ (i.e., Poly) and $F3$ features (i.e., Spectral Centroid).

Similarly to the considerations made for the scatterplots in Figure 4, the COPD instances cover a more extended area in the scatterplot, confirming that the values of these instances are ranging in a wide interval. Moreover, we confirm that the instances related to asthma and pneumonia are ranging in similar numeric values.

3.3. Classification Performance

To evaluate the performance of the proposed models, three different metrics are computed: these metrics are the specificity, the sensitivity, and the F-Measure.

The sensitivity of a test is the proportion of people who test positive among all those who actually have the disease, and it is defined as:

$$\mathit{Sensitivity}=\frac{tp}{tp+fn}$$

where tp indicates the number of true positives and fn indicates the number of false negatives.

The specificity of a test is the proportion of people who test negative among all those who actually do not have the disease, and it is defined as:

$$\mathit{Specificity}=\frac{tn}{tn+fp}$$

where tn indicates the number of true negatives and fp is related to the number of false positives.

The F-Measure represents the weighted average between the specificity and the sensitivity metrics:

$$F\text{-}Measure=2\ast \frac{Specificity\ast Sensitivity}{Specificity+Sensitivity}$$

Table 1. Lung disease detection classification results.

Model	F-Measure	Specificity	Sensitivity
kNN	0.981 (0.993)	0.965 (0.988)	0.997 (0.999)
SVM	0.983 (0.994)	0.966 (0.990)	1.000 (1.000)
Neural Network	0.983 (0.991)	0.979 (0.988)	0.988 (0.995)
Logistic Regression	0.979 (0.988)	0.976 (0.986)	0.982 (0.992)

contains the results of the classification of the lung disease detection model. In parentheses, we indicate the performance on the training model.

As emerges from the results depicted in Table 1, the proposed method reaches a specificity score between 0.965 and 0.979 and a sensitivity score between 0.997 and 1. For the lung disease detection task, the model that achieves the most interesting performance is the one built with the neural network.

With regard to the lung disease characterisation model, the results are shown in

Table 2. Lung disease characterisation results.

Model	F-Measure	Specificity	Sensitivity
kNN	0.892 (0.932)	0.883 (0.927)	0.908 (0.939)
SVM	0.872 (0.936)	0.890 (0.931)	0.907 (0.938)
Neural Network	0.923 (0.948)	0.917 (0.941)	0.931 (0.958)
Logistic Regression	0.892 (0.916)	0.886 (0.906)	0.904 (0.929)

. In parentheses, we indicate the performance on the training model.

In this case, the average ranges from 0.883 (with the kNN model) to 0.917 (with the neural network model), while the sensitivity, on average, ranges from 0.907 (with the SVM classification algorithm) to 0.931 (with the neural network classification algorithm). The algorithm obtaining the best performance is the neural network.

From the classification results, it emerges that for, both the models (i.e., lung disease detection and characterisation), the algorithm obtaining the best performance is the neural network.

In

Table 3. Lung disease characterisation confusion matrix. We use the Be and Bl notations to indicate bronchiectasis and bronchiolitis pulmonary disease, respectively.

	Actual Class
		Asthma	Be	Bl	COPD	LRTI	Pneumonia	URTI
Predicted	Asthma	1	0	0	0	0	0	0
class	Be	0	6	1	0	0	0	0
	Bl	0	0	6	0	0	0	0
	COPD	0	1	0	60	1	1	1
	LRTI	0	0	0	0	2	0	0
	Pneumonia	0	0	0	0	0	6	0
	URTI	0	0	0	2	0	0	14

, we show the confusion matrix for the lung disease characterisation for the neural network model, the one obtaining the best performance.

From the confusion matrix results shown in the table, we computed, for each disease, the metrics shown in

Table 4. Lung disease characterisation classification result from the single disease. We use the Be and Bl notations to indicate bronchiectasis and bronchiolitis pulmonary disease, respectively.

Class	F-Measure	Specificity	Sensitivity
Asthma	1	1	1
Be	10.92	1	0.86
Bl	0.92	0.86	1
COPD	0.96	0.97	0.95
LRTI	0.80	0.67	1
Pneumonia	0.92	0.86	1
URTI	0.90	0.93	0.88

. From this analysis, it emerges that the proposed method achieves interesting performance in disease detection.

3.4. Model Analysis

To confirm the effectiveness of the neural network models for the lung disease detection task, below, we present the receiver operating characteristic (i.e., roc) analysis plot.

The roc analysis plot, shown in Figure 6, is generated by drawing the rate related to the rate of the true positive feature vector and the rate of the false positive feature vector by considering different thresholds.

As shown in Figure 6, the roc curve related to the neural network model exhibits the best prediction trend; in fact, the closer the curve comes to the 45-degree diagonal of the roc space in Figure 6, the less accurate the test is (as shown by the kNN roc curve).

This confirms the effectiveness of the neural network model for lung disease detection from respiratory audio sessions. As a matter of fact, there are several advantages in the adoption of the neural network architecture. For instance, different from the kNN, the SVM, and the logistic regression algorithms, they offer the possibility to perform incremental updates with stochastic gradient descent (differently, for instance, from decision trees, which consider inherently batch-learning algorithms). Moreover, they are able to model more arbitrary functions (for instance, nonlinear interactions) and, for this reason, they can often be more accurate. Relating to the disadvantages, neural networks certainly require a longer learning time (if compared, for instance, to the decision tree algorithm), but considering that learning is carried out only once, this does not represent a problem in the adoption of the proposed method in a real-world context.

4. Related Work

The current state-of-the-art in the application of supervised learning for pulmonary diseases is reported in this section.

The authors in [28] classify respiratory sounds as normal and pulmonary emphysema by analysing a dataset composed of 168 subjects. They obtain an accuracy score ranging from 87.4% to 88.7%.

The authors in [29] reached a detection rate of 0.92 in the discrimination between healthy and pathological crackles by exploiting supervised machine learning.

A support vector machine model is discussed by researchers in [30] to discriminate pneumonia and congestive heart failure. In total, 257 patients are analysed by the authors, reaching a detection rate between 0.82 and 0.87.

A detection rate equal to 0.9 is obtained by the authors in [31]. They propose the adoption of the support vector machine algorithm with the aim to distinguish between healthy lung sounds and non-healthy ones.

Researchers in [32] exploited Empirical Mode Decomposition (EMD), which is a time domain, and computed the Instantaneous Frequency (IF) for the detection of disease starting from lung sounds. Other research papers presented Short-Time Fourier Transform (STFT) results, from which signal features can be extracted, such as peak frequency [33], local maxima, peak coexistence, discontinuity [34], mean, amplitude deviation, local maximum, discontinuity criteria [35], mean and median frequency, spectral crest factor, entropy, relative power factor, and high-order frequency moment. Another approach used is to change the STFT as an image and then to perform processing such as image processing [33,35]. The advantages of STFT are that it is computationally simple and allows the easy observation of the frequency of the signal each time. The drawbacks of this method are the relatively low resolution and the uncertainty of the time when the frequency occurs because the frequencies are calculated at specified intervals. Another TF domain method used is Wigner–Ville Distribution, exploited by several researchers, i.e., [36,37], to show the differences between normal lung sounds and pathological lung sounds. Another approach is to identify wheeze sounds in pulmonary audio, as discussed by researchers in [38], obtaining a detection ratio equal to 0.95 in the detection of lung disease-affected patients. Neural networks (NNs) are exploited by researchers in [39] in lung disease detection, obtaining an accuracy score equal to 71.81% using a deep neural network trained with respiratory sounds based on Mel spectrogram features.

The authors in [40] explore whether the application of a convolutional neural network in the deep learning context can assist medical experts by providing a detailed and rigorous analysis of the medical respiratory audio data for chronic obstructive pulmonary disease detection. They exploit features such as MFCC, Mel spectrogram, Chroma, and Chroma CENS. The proposed method is able to predict the severity of the disease identified, such as mild, moderate, or acute, obtaining an accuracy score equal to 93%.

Researchers in [41] propose a method proposed aimed to transform the characteristic vectors from reconstructed signals into reconstructed signal energy for lung disease detection. They consider linear discriminant analysis, which aimed to reduce the dimension of characteristic vectors. They consider a neural network to carry out lung sound recognition, where comparatively high-dimensional characteristic vectors and low-dimensional vectors are set as input and lung sound categories as output, with an accuracy score ranging between 82.5% and 92.5%.

Table 5. State of the art comparison in lung disease classification; (N.A. stands for data not available).

Research	Features	Performance
Charleston et al. [32]	IMF	N.A.
Rizal et al. [33]	BP-NN	98.33%
Mondal et al. [42]	ELM, SVM	92.86%
Gnitecki et al. [43]	fractal	N.A.
Ayari et al. [44]	width	98.3%
Alsmadi et al. [45]	K-NN	N.A.
Hadjileontiadis et al. [46]	Lacunarity	99%
Kahya et al. [47]	AR coefficient	67%
Charleston et al. [48]	Time-variant AR	N.A.
Yamashita et al. [49]	MFCC	83%
Torre et al. [38]	NMF	95%
Acharya et al. [39]	MEL	71%
Srivastava et al. [40]	CNN	93%
Shi et al. [41]	NN	92.5%
Our method	CR,RMS,SC,SR,ZCR,MEL,T,P	98%

shows a comparison of the state of the art in automatic lung disease detection, in terms of features extracted and performance obtained.

As shown from the comparison in Table 5, the proposed method (last row in Table 5) obtains detection performance equal to 98%. The only methods [33,38,44,46] obtaining performance slightly higher than the one we obtained consider the binary detection between healthy patients and patients affected by lung disease. Differently, the method we propose is aimed at discriminating between healthy and disease-affected patients, but it is also devoted to the identification of the specific lung disease.

From the analysis of the current state-of-the-art literature, it emerges that researchers are mostly focused on the binary discrimination between healthy patients and patients with lung diseases, while the proposed method is also devoted to detecting the lung disease with a feature set never previously considered in the lung disease detection context. Moreover, the performances are lower in comparison to the ones we achieved by using the neural network classification algorithm. Another novelty is represented by the lung disease characterisation, i.e., the automatic detection of the specific lung disease. We highlight also that, to the best of the authors’ knowledge, the proposed feature set has not been exploited in the previous literature.

5. Conclusions and Future Works

In this paper, an approach for respiratory disease detection and characterisation is proposed. By considering respiratory sessions stored in audio format, a feature vector is directly gathered from the audio file. Thus, the proposed numeric feature vector is sent to a supervised model that aims to identify whether the feature vector is related to a patient who is healthy or one with a generic lung disease. If the patient is labelled with a (generic) lung disease, the same feature vector is the input for a second classifier aimed to characterise the lung disease. Experiments with different machine learning algorithms demonstrated that the model obtaining the most interesting prediction performance is the one built with the neural network algorithm (for both the steps). The main finding of the proposed approach is that it is possible to exploit a two-step classifier to detect the lung a disease at a fine grain, not only to simply discriminate between healthy and lung disease-affected patients. In detail, we obtain the best results by exploiting the neural network classifier, with an F-Measure equal to 0.983 for the task related to the discrimination between healthy patients and patients affected by a generic lung disease, and an F-Measure of 0.923 for the lung disease detection (in particular, we discriminate between the following lung diseases: asthma, bronchiectasis, bronchiolitis, chronic obstructive pulmonary disease, pneumonia, and lower or upper respiratory tract infection).

As future work, it could be of interest to explore whether deep learning [50] and model checking techniques can be helpful to obtain better performance, but also whether feature normalisation can help in improving performance. Moreover, further future works include the localisation in the audio session of the exact point where the lung disease is detected.