Abstract
The displacement and stress-based error estimates in a posteriori error recovery of compressible and nearly-incompressible elastic finite element solutions is investigated in the present study. The errors in the finite element solutions, i.e., in displacement and stress, at local and global levels are computed in L2-norm of quantity of interest, namely, displacements and gradients. The error estimation techniques are based on the least square fitting of higher order polynomials to stress and displacement in a patch comprising of node/elements surrounding and including the node/elements under consideration. The benchmark examples of compressible and incompressible elastic bodies, with known solutions employing triangular discretization schemes, are implemented to measure the finite element errors in displacements and gradients. The mixed formulation involving displacement and pressure is used for incompressible elastic analysis. The performance of error estimation is measured in terms of convergence properties, effectivity and mesh required for predefined precision. The error convergence rate, in FEM original solution, recovered solution using displacement recovery-based and stress-based error recovery technique for stresses, are obtained as (1.9714, 2.8999, and 2.5018) and (0.9818, 1.7805, and 1.4952) respectively for compressible and incompressible self-loaded elastic plate benchmark example using higher order triangular elements. It is concluded from the study that displacement fitting technique for extracting higher order derivatives shows a very effective technique for recovery of compressible and nearly-incompressible finite element analysis errors.
1. Introduction
The finite element method is the most used computational tool for analyzing industrial problems. However, the errors are inherent in the finite element solution due to discretization of the problem area into subdomains. The other sources of errors in the finite element solution are due to the mathematical model for the problem definition, the algorithm employed for solving system equations, and the method employed for computing derivatives of state variable and round-off due to the machine precision. The attention of error control in the finite element solution has been on the discretization error which is due to incomplete satisfaction of the governing equations and boundary conditions. The recent interest in the finite element method is to minimize the discretization error which is due to incomplete satisfaction of the governing equations and boundary conditions [1]. The review on various applications of the finite element method are presented in [2]. Though advancement are made in the finite element method, there are areas which needed further attention [3]. Several techniques are developed to recover the field variables or gradients and to improve the accuracy of finite element solution. The different types of error estimation techniques are developed for finite element analysis [4]. Among the developed error estimation procedures, the post-processed or recovery type error estimation techniques are easy to implement in the codes and provide local errors as well [5]. In a posteriori error estimation, the recovery of finite element solution error using the least squares interpolation technique is made by fitting a higher order polynomial to the field variable or field variable derivatives over a suitable patch. The difference between the field variable or field variable derivatives from the finite element results and projected field variable or field variable derivatives from the recovery analysis results provides the measure of the error which should be represented in appropriate scale measure or norms. The energy norms and L2-norm are commonly used. The energy norms represent the error in the rate of energy dissipation while the L2-norm of field variable or field variable derivatives express straightforward physical meaning. The super-convergent patch recovery (SPR) technique or so-called Zienkiewicz and Zhu (ZZ) recovery technique recovers the error in the stress field by interpolating the stress fields over the super-convergent stress (Gauss) points [6]. They have estimated stress recovery-based recovered error in energy norm. In the present study, the stress and displacement-based recovered errors are computed in L2-norm. The alternative patch recovery scheme recovers stress fields by incorporating the equilibrium and boundary conditions [7]. Boroomand and Zienkiewicz [8] have presented a recovery by equilibrium in patches (REP) recovery technique. The ZZ recovery (SPR) method is modified by Gu et al. [9] by considering the integration point as a sampling point and using additional nodes and weighted average procedure. The improvement of the SPR technique (SPR-C technique) is proposed by Rodenas et al. [10] using additional constraint equations. The recovery of finite element linear elasticity exact solutions for nonconforming elements using the residual method considering the set of Neumann data is due to Kim and Lee [11]. Mohite and Upadhyay [12] have proposed the recovery of the exact solution of the displacement field and strains using the energy predictions over the element patches. Nadal et al. [13] have presented an explicit-type recovery technique for the linear elasticity problem using smooth solution.
Rajendran and Liew [14] have used best-t procedure to predict the optimal stress sampling points for the patch recovery of nodal stresses. They have found that Gaussian quadrature points are better candidates for patch recovery in comparison to Barlow points. Duflot and Bordas [15] have presented a global field variable derivative recovery technique in L2-norm for extended finite elements. A dual error estimator for the conforming finite element technique, developed using the explicit residual and the enhanced Zienkiewicz–Zhu (ZZ) error estimator, is presented by Cai et al. [16]. Zhang et al. [17] have proposed an approximation technique to create a continuous field and implemented the mesh refinement procedure to obtain a uniform error distribution over the domain. Dong et al. [18] proposed an error estimator based on element energy projection technique for adaptive finite element analysis. Sharma et al. [19] have presented a procedure to recover the stress solution error for low-order 3D finite elements and the recovered stress field satisfies the equilibrium in an average sense. The mesh free recovery technique using the element free Galerkin (EFG) method has also been developed to recover the finite element solution error. A mesh free error recovery technique to recover the displacement field of elastic finite element analysis is proposed by Ahmed [20]. The performance of mesh free MLS interpolation-based a posteriori error recovery technique is investigated by Ahmed et al. [21] considering different discretization scheme, recovery points, and recovered derivative of field variables. They found that effectivity of proposed mesh free a posteriori error technique for stress extraction is comparable to ZZ error technique. Hauret et al. [22] have proposed a finite element meshing scheme for the incompressible elasticity problems giving optimal convergence with mesh refinement. The scheme consists of the combination of a mesh pattern and a choice of interpolation that guarantees optimal convergence of displacements and pressures. Lehrenfeld and Reusken [23] have extended the unfitted finite element method and have demonstrated a converged L2-error analysis of the method applied to an interface problem.
To smooth out the derivative at inter-element boundaries or nodes, better approximated derivatives at nodes are required, and to calculate the derivative at any point in the element domain, a better approximate displacement field is needed. This can be achieved by least square fit of the computed Gauss point stress or displacement using the higher degree polynomial over node patches. The difference between the displacement/stress/strain from the finite element results and projected displacement/stress/strain from post-processed results provides the error in the finite element solution. Most of the existing study paid attention to the recovery of errors in stresses employing node-based patches, and errors are represented in energy norms. The present study represents the errors at local and global level in quantity of interest, i.e., displacement or gradients based on L2-norm. The study considers larger patch size, i.e., element-based patch, to recover the errors in displacement to improve the effectiveness of a posteriori error recovery technique at domain boundaries. The effectiveness of L2-norm-based error estimators are also investigated for the adaptive finite element analysis of incompressible elastic problems. Therefore, the present study is a contribution to further investigate the least squares interpolation-based a posteriori error recovery technique for recovery of stress and displacement using larger patch size, and implemented to compressible and incompressible elastic problems. The elastic benchmark examples of compressible and incompressible elastic bodies, with linear and quadratic triangular discretization schemes, are solved to quantify the finite element error in displacement or gradients. The quality of error estimation in a posteriori recovery techniques are enumerated and matched in terms of convergence properties, effectivity, and adaptively updated meshes for predefined precision. The adaptively updated meshes are used to compare the distribution pattern of errors in displacements, stresses, and strains over the problem domains. The error recovery technique using the least squares interpolation method for displacement and stress are described in literature [24] and the same is followed in the study.
2. Least Squares Interpolation-Based Zienkiewicz–Zhu (ZZ) Stress Recovery Technique
The ZZ patch error recovery technique [6] adopts that the node values of field variable derivatives (σ) belong to a polynomial expansion of the same complete order as of the basis function, and is valid over a node patch in a mesh (Figure 1 and Figure 2). The following polynomial expansion may be used for each component of stress:
where P(x) is the polynomial basis function, x = (xi, yi) are the sampling points coordinates, and a is the unknown parameters.
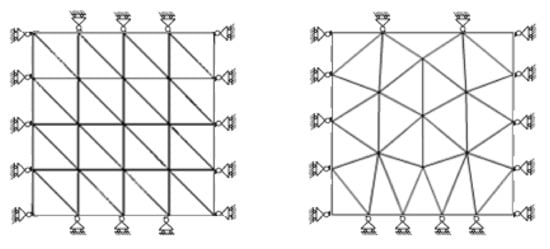
Figure 1.
Plate domain: regular/irregular discretization schemes with boundary conditions.
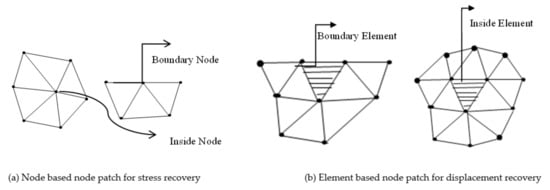
Figure 2.
Node based Patches for stress error recovery and Element based Patches for displacement error recovery.
The following functional is minimized for least square fitting of σh values over the node patch:
The following equation is obtained after solving for a:
where , , and np are the number of nodes in a patch.
3. Least Squares Interpolation-Based Displacement Recovery Technique
The recovery of field variable (displacement) is obtained by least squares fit of the computed nodal field variable (u) using a higher order polynomial over an element patch (Figure 1). The following functional is minimized for least square fitting:
where in which a is the vector of unknown parameters au and av, and .
Minimization condition of πf (a) implies that a satisfies the following relation:
Equation (5), in simplified form, can be written as:
where and
4. L2-Norm-Based Error Quantification and Mesh Improvement
The error in computed state variable or gradients, i.e., displacement (u), stress (σ) or strain (ε), eu* (or eσ*, eε*) is equal to the difference between the exact (or recovered) values of u (or σ, ε) and respective numerical values, uh (or σh, εh), i.e.,
The norms are used to measure the finite element solution errors. L2-norm giving integral measure of the error directly for state variable or gradients may be defined as follows:
where Ω represents problem domain.
The effectivity (θ) of the computed solution error is defined as the ratio of evaluated error and exact error. When the mesh size approaches to zero, the problem effectivity (θ) converges to one for an asymptotically exact error estimator [5]. The accuracy (η) of a finite element solution may be defined as follows:
The solution is satisfactory if accuracy (η) is within the aimed accuracy (ηallowable). If solution accuracy is more than the aimed accuracy, the mesh may be adaptively improved. The permissible global error is given as follows:
The allowable error in the ith element is calculated using the following relation:
The element modification parameter ξi guides the refinement:
If ξi is greater than 1, improvement of mesh is needed. The modified element size (hmod) is found with the help of the following equation:
5. Benchmark Example Applications
5.1. Application to Compressible Elastic Plate
The finite element formulation for compressible elastic problem described by Ahmed [20] is followed in this study. The performance of the stress and displacement recovery techniques is demonstrated through the convergence characteristics, and required meshes for intended precision in the case of a two-dimensional compressible elastic body subjected to body forces. The elements and node connectivity data are prepared as an input for regular triangular elements’ discretization of the problem domain. An in-house preprocessor is developed to discretize the problem domain into irregular linear and quadratic triangular elements. The plate domain is discretized by triangular elements in regular and irregular mode as shown in Figure 1. The number of nodes for three fineness levels in regular discretization are (25, 289 and 1089) and (81, 625 and 2401) respectively for linear and quadratic triangles whereas for irregular discretization, the number of nodes are (23, 326 and 1329) and (74, 735 and 2804) respectively for linear and quadratic triangles. Figure 2 shows the node patches used in least square fitting for displacement and stress error recovery. The example was used by Zienkiewicz and Zhu [6]. It presents no singularity so that theoretical rate of convergence of the proposed recovery techniques can be easily verified with other recovery techniques.
Domain = Ω [0 × 0] × [1 × 1], u = v = 0 on Γ
Exact solution:
Body forces:
The α and β are constant and are given by the following relations:
where u, v are the displacement in x and y direction, E and ν is the Modulus of elasticity and Poisson’s Ratio respectively with a value of 1.0 N/mm2 and 0.3 [20].
α = E·ν/[(1 − 2·ν) (1 + ν)]; β = E/[2·(1 + ν)]
The error estimation quality results, i.e., error convergence and global effectivity in finite element solution, and recovered solution employing displacement and stress error recovery with increasing order of triangular element (regular/irregular) fineness, are given in Table 1, Table 2, Table 3 and Table 4. The finite element solution absolute errors of plate problem, i.e., the difference between the exact (or recovered) values of u (or σ, ε) and respective finite element analysis values, uh (or σh, εh) are computed using the Equation (7) and the solution errors are represented in L2-norm of stresses, displacement, and strains using Equations (8)–(10). Figure 3 depicts the rate of convergence of error at increased order of fineness, i.e., at 1/16 and 1/36 mesh size under displacement and stress error recovery procedures in linear and quadratic triangular elements.

Table 1.
Error in displacement and strain (L2-Norm) and global effectivity (θ) in compressible elastic square plate example considering displacement recovery technique.

Table 2.
Error in stress (L2-Norm) and global effectivity (θ) in compressible elastic square plate example considering displacement and stress recovery techniques.

Table 3.
Error in displacement, strain and stress (L2-Norm), and global effectivity (θ) in compressible elastic square plate example considering displacement and stress recovery technique.

Table 4.
Error in displacement, strain and stress (L2-Norm), and global effectivity (θ) in compressible elastic square plate example considering displacement and stress recovery techniques.
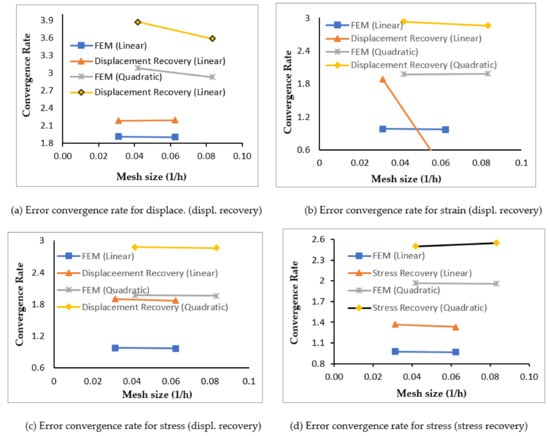
Figure 3.
Error convergence rate for different quantity in compressible elastic square plate example considering displacement and stress recovery techniques, and using linear and quadratic triangular elements.
For comparison of results of finite element analysis errors of stresses in L2-norm, they are also matched with errors of stresses in energy norm (Zienkiewicz–Zhu technique). The ZZ recovery technique-based error estimation quality results in energy norm, i.e., error convergence and global effectivity are presented in Table 5 [24]. Table 5 also shows the displacement recovery-based results in energy norm for comparison purposes [20].

Table 5.
Error in Stress (Energy Norm) and global effectivity (θ) in compressible elastic square plate example considering ZZ stress and displacement recovery techniques [20,24].
The adaptive analysis results are obtained for mesh required for target error limit for stresses, displacement, and strains. Table 6 and Table 7 show global errors (FEM and processed), the number of element (N), and degrees of freedom (DOF) in refined meshes, obtained from the linear and quadratic elements of the initial mesh, to bring accuracy to the target level. The required adaptive meshes for aimed accuracy in various L2-norms, namely stresses, displacement, and strains, using the least square stress, and displacement recovery-based error estimation for linear and quadratic elements are portrayed in Figure 4 and Figure 5.

Table 6.
Global errors (FEM and processed, L2-Norm) and number of element (N) with DOF of adaptively refined meshes (considering displacement and stress recovery-based analysis (linear triangle, 3% target error).

Table 7.
Global errors (FEM and processed, L2-Norm) and number of element (N) with DOF of adaptively refined meshes considering displacement and stress recovery based analysis (quadratic triangle, 1% target error).

Figure 4.
Adaptive mesh required for 3% target error (L2-Norm) in compressible elastic square plate example solution variables considering displacement and stress recovery techniques (Initial regular linear triangular mesh: N = 580, DOF = 652).
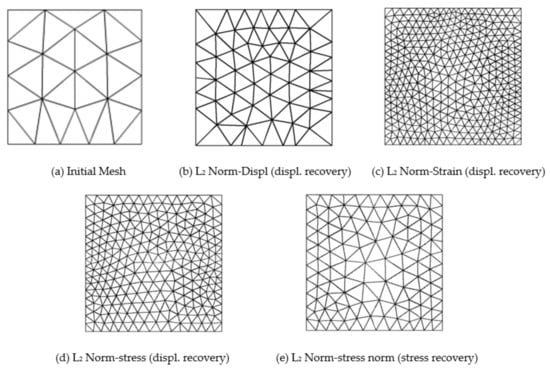
Figure 5.
Adaptive mesh required for 1% target error (L2-Norm) in compressible elastic square plate example solution variables considering displacement and stress recovery techniques (Initial regular quadratic triangular mesh: N = 28, DOF = 146).
5.2. Application to Compressible Elastic Plate with Rigid Circular Inclusion
The proposed recovery techniques and mesh improvement procedures are also used in the example problem of an infinite elastic plate having a rigid circular inclusion. The exact solution for elastic plate example is known [5]. It represents a typical case where all derivatives of the exact solution are continuous and bounded on solution domain, and on its boundary. The plate example is solved under the action of a unit in-plane traction applied in the x-direction.
where r2 = y2 + x2 and σ∞ is the uniaxial traction applied at infinity.
Due to symmetry, only the upper left square quadrant of the plate is modeled and discretized with linear and quadratic triangular elements (Figure 6). The error convergence with mesh refinement and global effectivity of error estimation using displacement and stress-based recovery technique for various domain discretization is given in Table 8. The finite element solution error is measured in stress-based L2-norm. The global errors (FEM and processed), and the required number of element (N) and degrees of freedom (DOF) for target accuracy using the linear and quadratic elements mesh are given in Table 9. The meshes required for predefined accuracy using the stress and displacement recovery-based error estimation for linear and quadratic elements are depicted in Figure 7 and Figure 8.
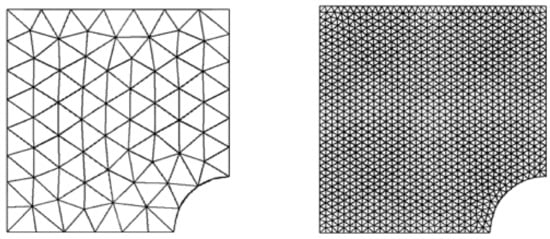
Figure 6.
Plate with rigid circular inclusion domain.

Table 8.
Error in Stress (L2-Norm) and global effectivity (θ) in compressible elastic square plate with circular inclusion example considering displacement and stress recovery techniques.

Table 9.
Global errors (FEM and processed L2-Norm) and number of element (N) with DOF of adaptively refined meshes considering displacement and stress recovery-based analysis.
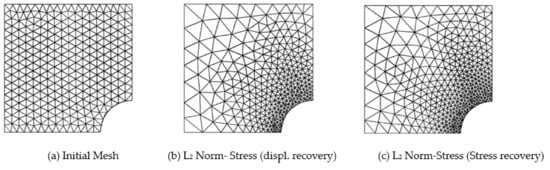
Figure 7.
Adaptive mesh required for 3% target error (L2-Norm) in compressible elastic square plate with circular inclusion example solution variables considering displacement and stress recovery techniques (Initial regular linear triangular mesh: N = 548, DOF = 618).
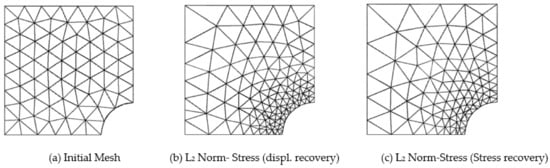
Figure 8.
Adaptive mesh required for 1% target error (L2-Norm) in compressible elastic square plate with circular inclusion example solution variables considering displacement and stress recovery techniques (Initial regular quadratic triangular mesh: N = 124, DOF = 558).
5.3. Application to Incompressible Elastic Plate
The mixed formulation involving displacement and pressure is used for incompressible elastic analysis [25]. The equilibrium and boundary condition for the incompressible elastic problem can be defined as:
The constitutive equation, stress (σ) and strain (ε) relation, is written as:
where Ω is an incompressible elastic body bounded domain, u is the displacement field, p is the pressure, and λ, μ are the Lame constants. Lame constants are defined as:
in which and are given tractions and displacements on Γt, Γu boundaries respectively.
λ = E/2(1 + ν)]; μ = E·ν/[(1 − 2·ν) (1 + ν)]
The two-dimensional incompressible elastic problem subjected to body forces with known solution is implemented to investigate the effectiveness and performance of recovery techniques in terms of convergence properties and required precision adaptive meshes. The domain discretization with triangular elements and node patches for error recovery are shown in Figure 1 and Figure 2. The example was taken by Zienkiewicz and Zhu [26] for recovery technique effectiveness demonstration.
Domain = Ω [0 × 0] × [1 × 1], u = v = 0 on Γ
Exact solution:
Body forces:
The rate of error convergence in finite element solution, recovered solution employing displacement/gradient error recovery with various element mesh density, and effectivity of error estimation are given in Table 10. The global errors (FEM and processed) and the required number of element (N) and degrees of freedom (DOF) for target accuracy using the higher order triangular elements’ mesh is given in Table 11. The lower order triangular element will not converge the solution error in incompressible elastic problems. The meshes required for aimed accuracy using the stress/displacement recovery-based error estimation for quadratic triangular elements are shown in Figure 9.

Table 10.
Error in stress (L2-Norm) and global effectivity (θ) in incompressible elastic square plate example considering displacement and stress recovery technique for Quadratic Triangular mesh (Regular/irregular).

Table 11.
Global errors (FEM and processed, L2-Norm) and number of elements (N) with DOF of adaptively refined meshes considering displacement and stress recovery-based analysis.

Figure 9.
Adaptive mesh required for 1% target error (L2-Norm) incompressible elastic square plate example solution variables considering displacement and stress recovery techniques (Initial regular quadratic triangular mesh: N = 1349, DOF = 5608).
6. Discussion
This study presents the a posteriori error estimations of finite element solutions based on recovery of displacement and stress. The benchmark examples of compressible and incompressible elastic bodies are implemented to demonstrate the effectiveness and efficiency of the recovery techniques. The error estimation techniques are based on the least square fitting of higher order polynomials to stress and displacement in a patch comprising of node/elements surrounding and including the node/elements under consideration. The error estimations at global and elemental levels have been presented in the L2-norms of quantity of interest, i.e., displacement, strain, and stress. The quality of error estimation in a posteriori recovery techniques are enumerated and matched in terms of convergence properties, effectivity, and adaptively updated meshes for predefined precision. The computational results of error convergence and effectivity with various densities of triangular meshing are given in Table 1, Table 2, Table 3, Table 4, Table 5, Table 8, and Table 10 respectively for elastic square plate, elastic plate with circular inclusion, and incompressible elastic square plate. It is clear from the tables that the order of error obtained with displacement and stress recovery techniques is much lower than the FEM solution error, and the error convergence is also higher when compared to the FEM solution error with an increase in the element density. It can be concluded that the displacement-based recovery technique gives more accurate stress than the stress-based recovery technique specially for boundary node where a smaller number of points are available, and displacement-based recovery technique has higher effectivity than the stress-based recovery technique.
The rates of error convergence using stress and displacement recovery technique at different fineness levels for displacements, strains, and stresses errors are plotted in Figure 3. It can be observed from Figure 3 that displacement-based recovery technique results higher convergence at different fineness levels as compared to stress-based recovery technique, especially for the error recovery of state variable derivatives. The convergence rate of error with increased fineness levels for regular linear triangular elements, in original finite element solution of compressible elastic plate example for displacements, strains, and stresses, and recovered solution for displacements, strains, and stresses using displacement recovery method are found respectively as (1.9394, 2.1539), (0.9799, 1.8898), and (0.9765, 1.9012). The error convergence rate for regular quadratic triangular elements, in finite element solution for displacements, strains, and stresses, and recovered solution for displacements, strains, and stresses using displacement recovery are found respectively as (3.0473, 3.7215), (1.9869, 2.9010), and (1.9714, 2.8999). The error convergence rates are obtained in finite element results using stress recovery method for stresses as (0.9765, 1.3710) and (1.9714, 2.5018) respectively for linear and quadratic triangular elements. The higher error convergence rate is observed by employing displacement-based recovery technique for compressible and incompressible elastic problems in comparison to stress- based recovery technique. The error convergence rates are obtained in finite element results of incompressible elastic plate example using displacement and stress recovery method as (0.9818, 1.7805, and 1.4952) for stresses with quadratic triangular elements’ discretization. It can be seen from the analysis results that the compressible elastic problems exhibit lower convergence rate of error as compared to incompressible elastic problems for both displacement and stress-based recovery approaches.
The required adaptive meshing for predefined precision are presented in tables and figures. Table 6, Table 7, Table 9 and Table 11 show global errors (FEM and post-processed), the number of elements and DOF in adaptive meshing, obtained with the linear and quadratic elements of the initial mesh respectively for elastic square plate, elastic plate with circular inclusion, and incompressible elastic square plate. The application of the displacement and stress-fitting technique-based error estimation (L2-norm-based error estimator), for guiding the improvement of meshing scheme to obtain the predefined precision in finite element analysis, is also demonstrated. Results of the adaptive refinement, for aimed error limits of displacement and gradients, are obtained for displacement and stress-fitting techniques. The aimed error of 3% is set for adaptive finite element analyses employing linear element discretization and a target error of 1% is fixed for adaptive analyses employing quadratic elements. The initial meshes are adaptively improved to bring the gradient error within the predefined precision and to distribute the error equally among all the elements. The adaptively improved meshes also indicate the distribution pattern of the errors in the problem domain. From the adaptive mesh plots, it is clear that the errors are more on corners and edges as compared to the interior of the compressible and incompressible elastic plate domain. It is concluded that the adaptive finite element analysis may predict the gradients’ high error zones and can be used to improve the reliability and effectivity of solutions to the problem.
7. Conclusions
The further developments in recovery of displacement and stress in a posteriori error estimations of finite element solutions is carried out in this study. The error estimation techniques are based on the least square fitting of higher order polynomials to stress and displacement in a patch comprising of node/elements surrounding and including the node/elements under consideration. The error estimations at global and elemental levels have been presented in the L2-norms of quantity of interest, i.e., displacement, strain, and stress. The benchmark examples of compressible and incompressible elastic bodies are implemented to demonstrate the effectiveness and efficiency of the recovery techniques. The elastic benchmark examples are discretized with linear and quadratic triangular meshing schemes. The quality of error estimation in a-posteriori recovery techniques are enumerated and matched in terms of convergence properties, effectivity, and adaptively updated meshes for predefined precision. It is observed that displacement-based recovery technique gives more accurate stress than stress-based recovery technique specially for boundary node where a smaller number of points are available, and displacement-based recovery technique has higher effectivity than the stress-based recovery technique. The error convergence rate is also higher by employing the displacement-based recovery technique for compressible and incompressible elastic problems. The compressible elastic problems exhibit lower convergence rate of error as compared to incompressible elastic problems for both displacement- and stress-based recovery approaches. The error convergence rate, in FEM original solution, recovered solution using displacement recovery- based and stress-based error recovery technique for stresses, are obtained as (1.9714, 2.8999, and 2.5018) and (0.9818, 1.7805, and 1.4952) respectively for compressible and incompressible self-loaded elastic plate benchmark example using higher order triangular elements’ meshing. It is concluded that the adaptive finite element analysis may predict the gradients’ high error zones, and can be used to improve the reliability and effectivity of compressible and incompressible problem.
Author Contributions
Conceptualization, M.A. and D.S.; methodology, M.A.; software, D.S.; validation, S.A. and N.B.K.; formal analysis, M.A. and S.A.; investigation, M.A.; resources, S.A.; data curation, N.B.K.; writing—original draft preparation, M.A.; writing—review and editing, S.A. and N.B.K.; visualization, S.A.; supervision, D.S.; project administration, N.B.K.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Research Project (small group) under grant number [R.G.P1 /90/42].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the Dean, Faculty of Engineering, for his valuable support and help.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Taus, M.; Rodin, G.J.; Hughes, T.R.; Scott, M.A. Isogeometric boundary element methods and patch tests for linear elastic problems: Formulation, numerical integration, and applications. Comput. Methods Appl. Mech. Eng. 2019, 357, 112591. [Google Scholar] [CrossRef]
- Cen, S.; Wu, C.J.; Li, Z.; Shang, Y.; Li, C. Some advances in high-performance finite element methods. Eng. Comput. 2019, 36, 2811–2834. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C. Achievement and Some Unsolved Problems of Finite Element Method. Int. J. Numer. Meth. Eng. 2000, 47, 9–28. [Google Scholar] [CrossRef]
- Gratsch, T.; Bathe, K. A posteriori error estimation technique in practical finite element analysis. Comput. Struct. 2005, 83, 75–90. [Google Scholar] [CrossRef] [Green Version]
- Zienkiewicz, O.C.; Zhu, J.Z. Simple error estimator and adaptive procedure for practical engineering analysis. Int. J. Numer. Meth. Eng. 1987, 24, 337–357. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. The Super-convergent patch recovery and a posteriori error estimates, Part I, The Error Recovery technique. Int. J. Numer. Meth. Eng. 1992, 33, 1331–1364. [Google Scholar] [CrossRef]
- Wiberg, N.E.; Abdulwahab, F.; Ziukas, S. Enhanced superconvergent patch recovery incorporating equilibrium and boundary conditions. Int. J. Numer. Meth. Eng. 1994, 37, 3417–3440. [Google Scholar] [CrossRef]
- Boroomand, B.; Zienkiewicz, O.C. Recovery by equilibrium in patches (REP). Int. J. Numer. Meth. Eng. 1997, 40, 137–164. [Google Scholar] [CrossRef]
- Gu, H.; Zong, Z.; Hung, K.C. A modified super-convergent patch recovery method and its application to large deformation problems. Finite Elem. Anal. Des. 2004, 40, 665–687. [Google Scholar] [CrossRef]
- Rodenas, J.J.; Tur, M.; Fuenmayor, F.J.; Vercher, A. Improvement of the super-convergent patch recovery technique by the use of constraint equations: The SPR-C technique. Int. J. Numer. Meth. Eng. 2007, 70, 705–727. [Google Scholar] [CrossRef]
- Kim, K.; Lee, H. A posteriori Error Estimator for non-conforming finite element methods of the linear elasticity problem. J. Comput. Appl. Math. 2010, 235, 186–202. [Google Scholar] [CrossRef] [Green Version]
- Mohite, P.M.; Upadhyay, C.S. Adaptive finite element based shape optimization in laminated composite plates. Comput. Struct. 2015, 153, 19–35. [Google Scholar] [CrossRef]
- Nadal, E.; Dıez, P.; Ródenas, J.J.; Tur, M.; Fuenmayor, F.J. A recovery-explicit error estimator in energy norm for linear elasticity. Comput. Methods Appl. Mech. Eng. 2015, 287, 172–190. [Google Scholar] [CrossRef] [Green Version]
- Rajendran, S.; Liew, K.M. Optimal stress sampling points of plane triangular elements for patch recovery of nodal stresses. Int. J. Numer. Meth. Eng. 2003, 58, 579–607. [Google Scholar] [CrossRef]
- Duflot, M.; Bordas, S. A posteriori error estimation for extended finite elements by an extended global recovery. Int. J. Numer. Meth. Eng. 2008, 76, 1123–1138. [Google Scholar] [CrossRef]
- Cai, D.; Cai, Z. A hybrid a posteriori error estimator for conforming finite element approximations. Comput. Methods Appl. Mech. Eng. 2018, 339, 320–340. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L.; Zhao, L.; Tang, G. An adaptive remeshing procedure for discontinuous finite element limit analysis. Int. J. Numer. Meth. Eng. 2018. 116, 287–307. [CrossRef]
- Dong, Y.; Yuan, S.; Xing, Q. Adaptive finite element analysis with local mesh refinement based on a posteriori error estimate of element energy projection technique. Eng. Comput. 2019, 36, 2010–2033. [Google Scholar] [CrossRef]
- Sharma, R.; Zhang, J.; Langelaar, M.; van Keulen, F.; Aragón, A.M. An improved stress recovery technique for low-order 3D finite elements. Int. J. Numer. Meth. Eng. 2018, 114, 88–103. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M. Techniques for Mesh Independent Displacement Recovery in Elastic Finite Element Solutions. Trans. Famena 2021, XLV-2, 41–58. [Google Scholar] [CrossRef]
- Ahmed, M.; Singh, D.; AlQadhi, S.; Thanh, N.V. Moving Least Squares Interpolation Based A-Posteriori Error Technique in Finite Element Elastic Analysis. Comput. Modeling Eng. Sci. 2021, 129, 167–189. [Google Scholar] [CrossRef]
- Hauret, P.; Kuhl, E.; Ortiz, M. Diamond elements: A finite element/discrete-mechanics approximation scheme with guaranteed optimal convergence in incompressible elasticity. Int. J. Numer. Meth. Eng. 2007, 72, 253–294. [Google Scholar] [CrossRef]
- Lehrenfeld, C.; Reusken, A. L2-error analysis of an isoparametric unfitted finite element method for elliptic interface problems. J. Numer. Math. 2019, 27, 85–99. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Singh, D.; AlQadhi, S.; Alrefae, M.A. Improvement of the Zienkiewicz–Zhu Error Recovery Technique Using a Patch Configuration. Appl. Sci. 2021, 11, 8120. [Google Scholar] [CrossRef]
- Nakshatrala, K.B.; Masud, A.; Hjelmstad, K.D. On finite element formulations for nearly incompressible linear elasticity. Comput Mech. 2008, 41, 547–561. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Lui, Y.C.; Huang, G.C. Error Estimates and convergence rate for various incompressible elements. Int. J. Numer. Meth. Eng. 1989, 28, 2192–2202. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).