Compressed Sensing Super-Resolution Method for Improving the Accuracy of Infrared Diagnosis of Power Equipment
Abstract
:1. Introduction
2. SR Basic Model of Compressed Sensing
3. Blur Kernel Estimation
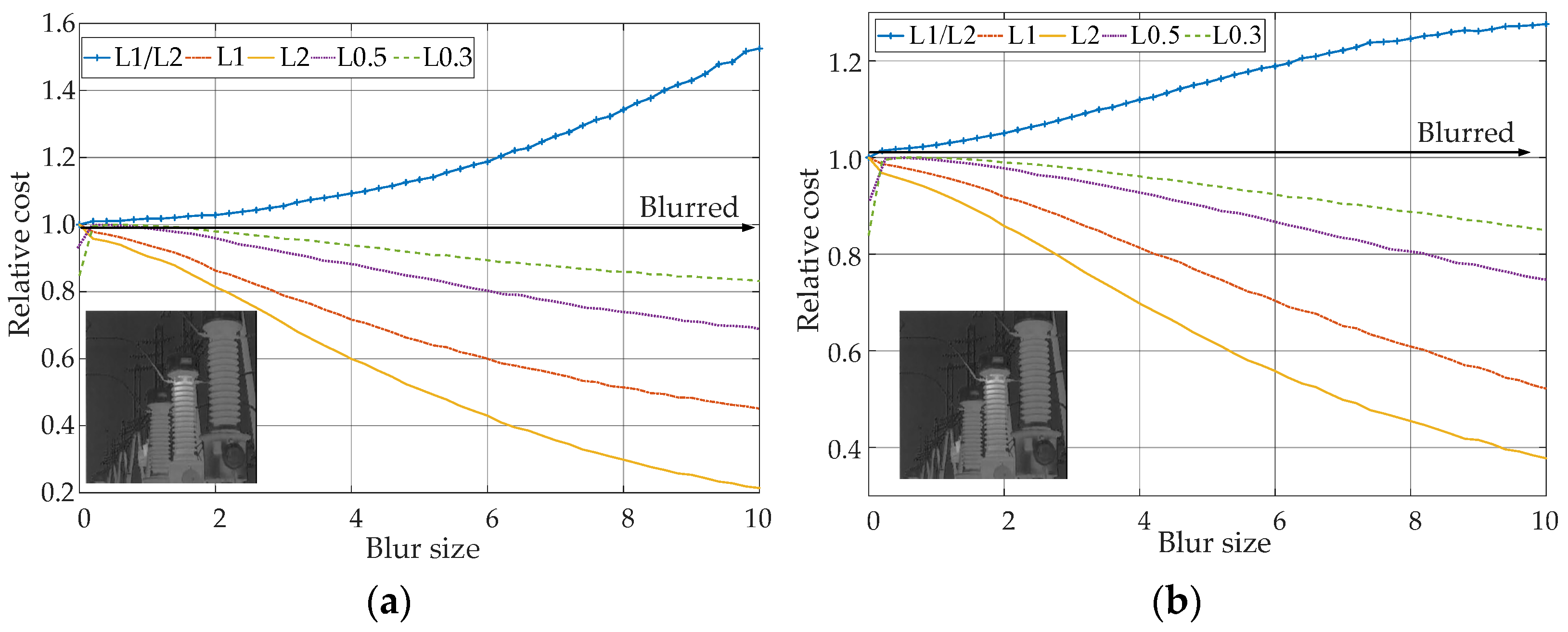
3.1. Gradient Norm Ratio Priori
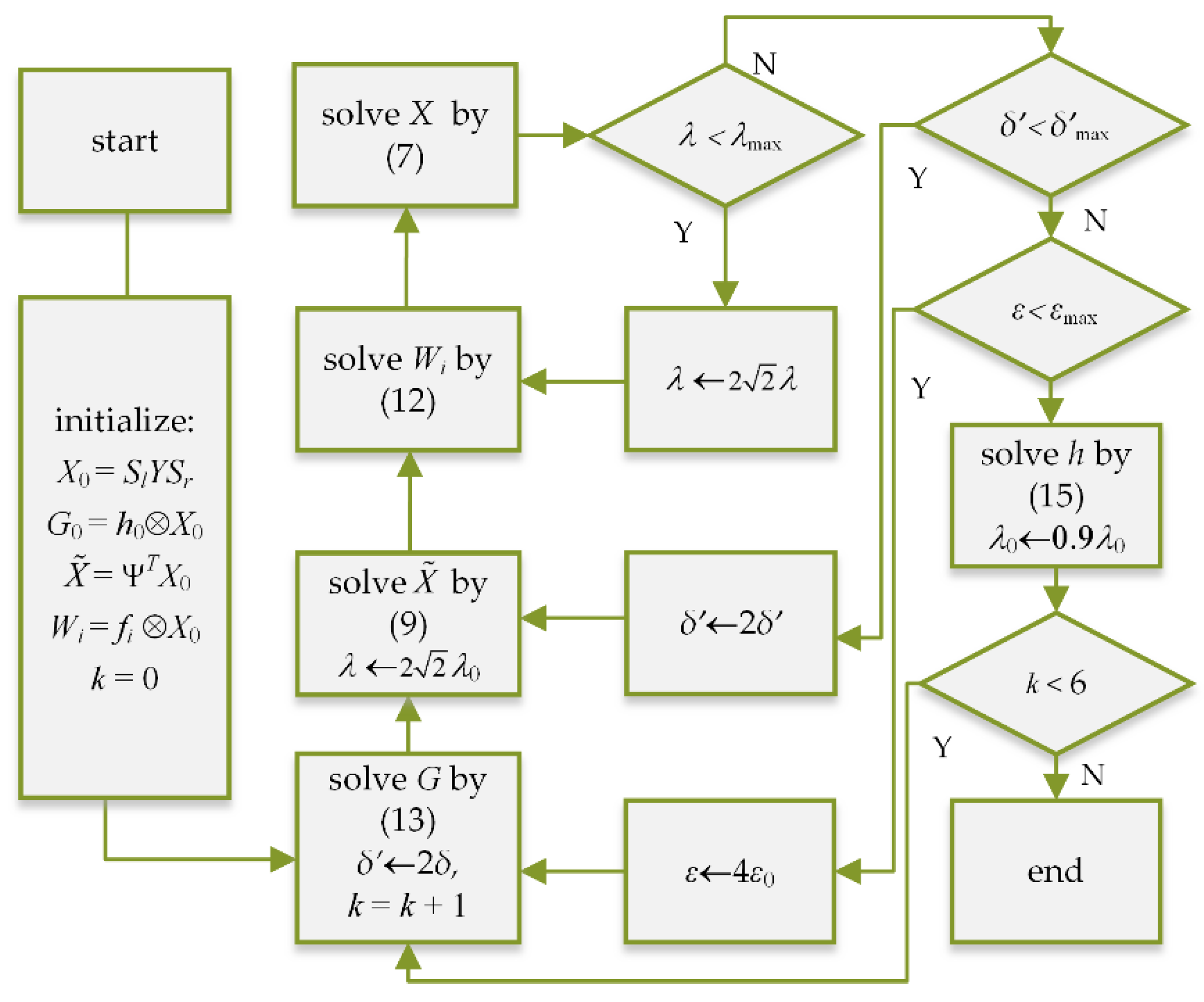
3.2. Blure Kernel Estimation Algorithm
3.2.1. Intermediate Latent Image X Estimation
3.2.2. Blur Kernel h Estimation
4. Image SR Reconstruction
4.1. Objective Function
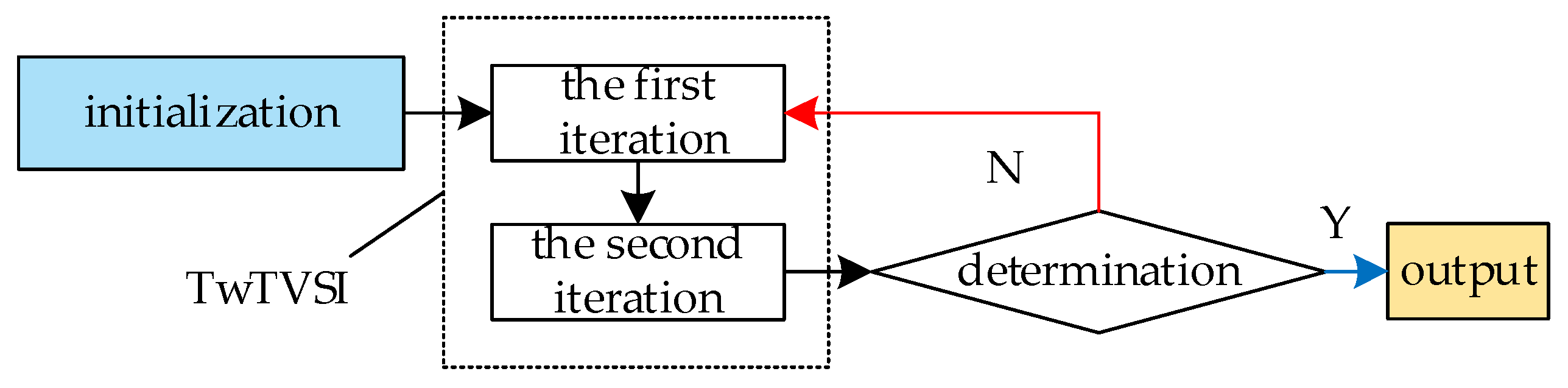
4.2. Optimization Solution
- Initialize and separately.
- The first iteration: Use gradient descent to solve the TV regular term to get , .
- The second iteration: is obtained by using the proximal gradient method from for the sparse regular term according to Equation (27). Perform the
- Judgment: when is less than the error constraint , or is greater than the maximum number of iterations , stop the iteration, when it is otherwise, we set and go back to step 2.
- Output: high resolution image .
5. Experiment and Result Analysis
5.1. Experimental Data and Evaluation Paramenters
5.2. Infrared Image Reconstruction Experiment
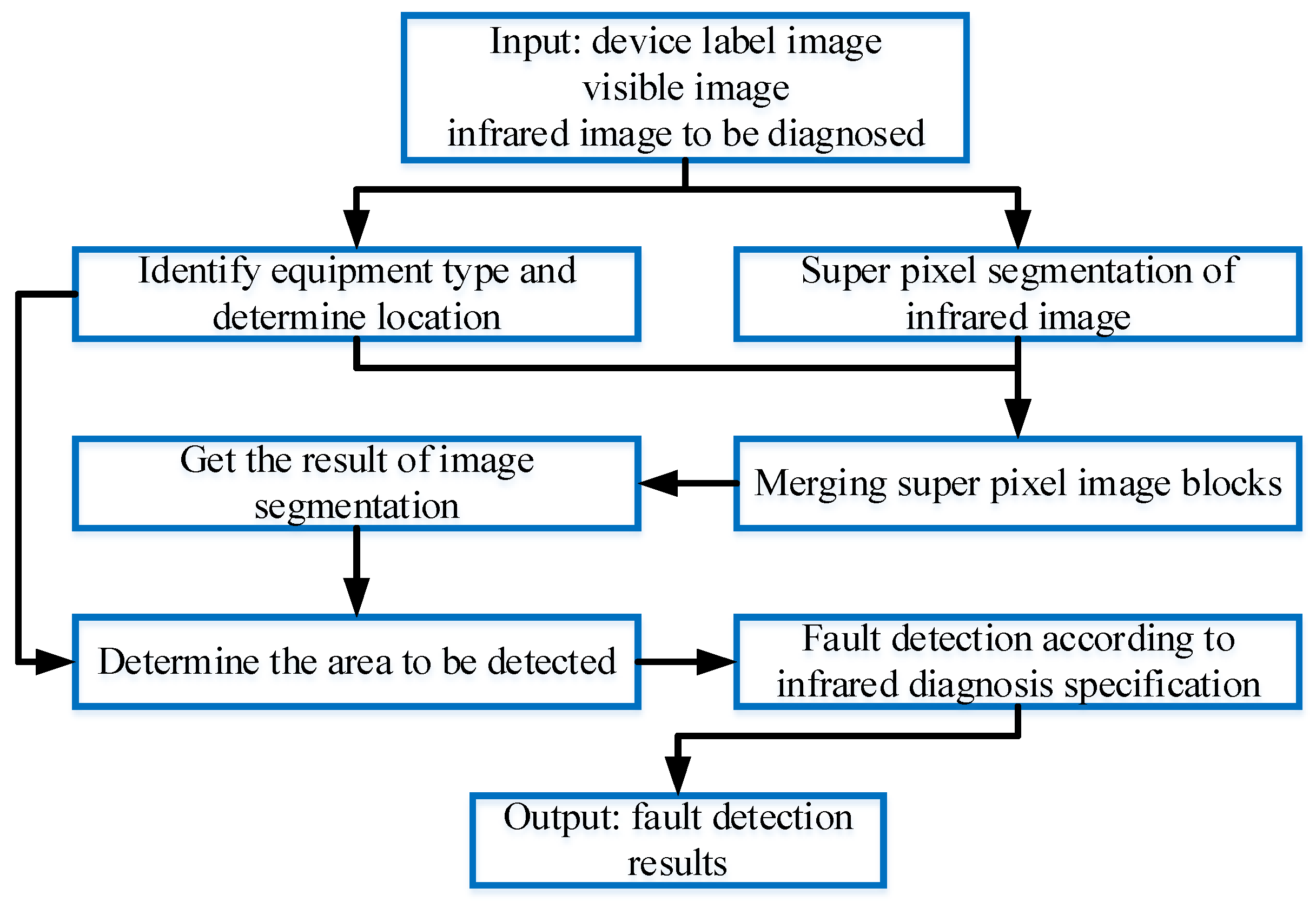
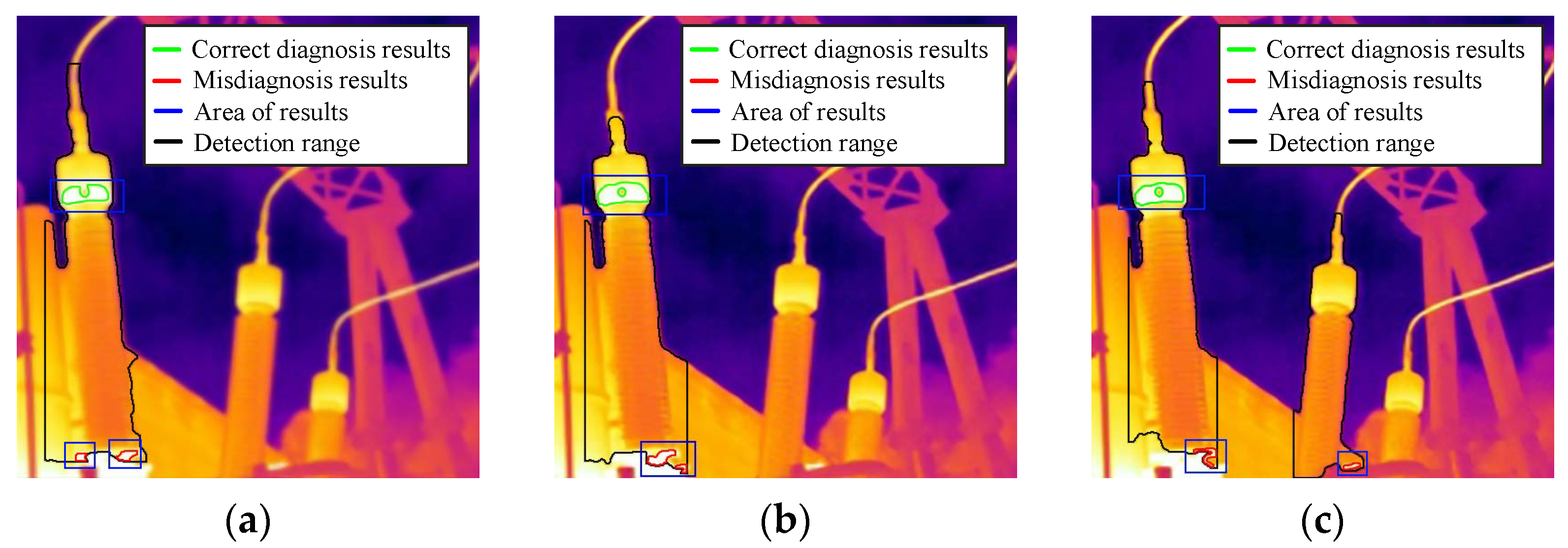
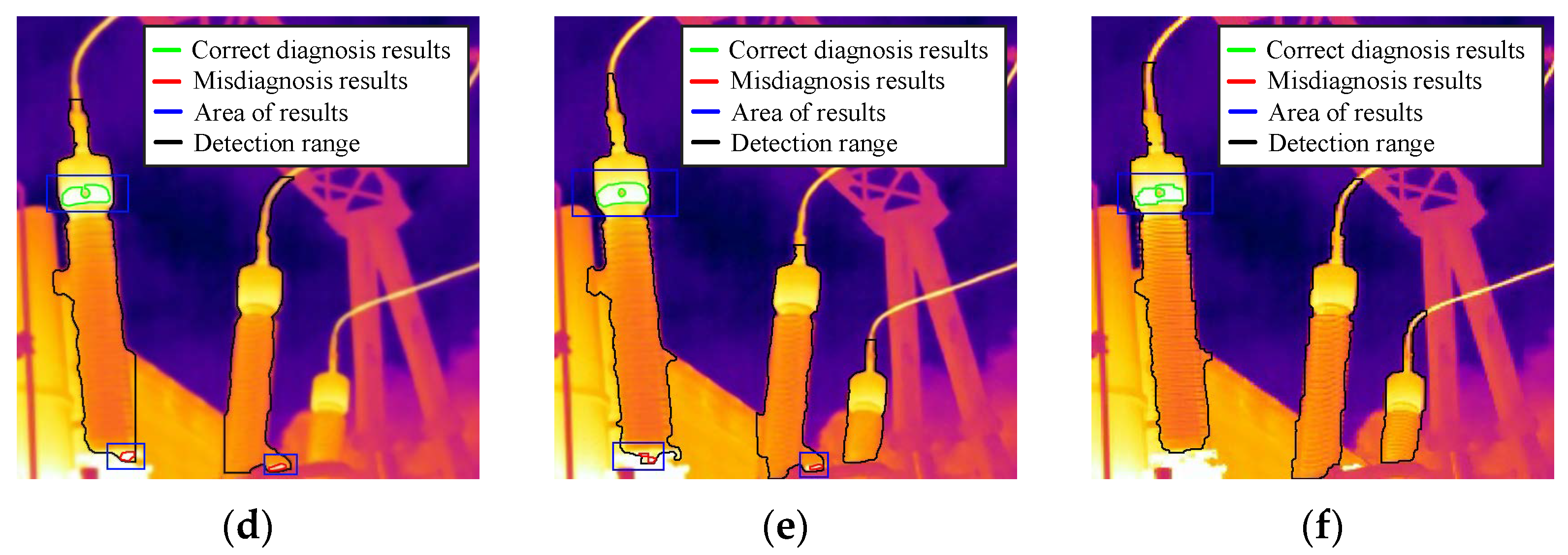
5.3. Comparative Experiment of Image Recognition
5.4. Comparative Experiment of Image Recognition
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lin, Y.; Zhang, W.; Zhang, H.; Bai, D.; Li, J.; Xu, R. An intelligent infrared image fault diagnosis for electrical equipment. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 1829–1833. [Google Scholar]
- Li, X. Design of Infrared Anomaly Detection for Power Equipment Based on YOLOv3. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 2291–2294. [Google Scholar]
- Wang, Y.; Chen, Q.; Zhang, N.; Feng, C.; Teng, F.; Sun, M.; Kang, F. Fusion of the 5G Communication and the Ubiquitous Electric Internet of Things: Application Analysis and Research Prospects. Power Syst. Technol. 2019, 43, 1575–1585. [Google Scholar]
- Zhao, S.; Zhao, H.; Shou, P. Discussion on Key Technology and Operation & Maintenance of Intelligent Power Equipment. Autom. Electr. Power Syst. 2020, 44, 1–10. [Google Scholar]
- Lozanov, Y.; Tzvetkova, S. A methodology for processing of thermographic images for diagnostics of electrical equipment. In Proceedings of the 2019 11th Electrical Engineering Faculty Conference (EEFC), Varna, Bulgaria, 11–14 September 2019; pp. 1–4. [Google Scholar]
- Li, Y.; Zhao, K.; Ren, F.; Wang, B.; Zhao, J. Research on Super-Resolution Image Reconstruction Based on Low-Resolution Infrared Sensor. IEEE Access 2020, 8, 69186–69199. [Google Scholar] [CrossRef]
- Huo, W.; Tuo, X.; Zhang, Y.; Huang, Y. Balanced Tikhonov and Total Variation Deconvolution Approach for Radar For-ward-Looking Super-Resolution Imaging. IEEE Geosci. Remote. Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Batz, M.; Eichenseer, A.; Kaup, A. Multi-image super-resolution using a dual weighting scheme based on Voronoi tessellation. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2822–2826. [Google Scholar]
- Wang, L.; Lin, Z.; Deng, X.; An, W. Multi-frame image super-resolution with fast upscaling technique. arXiv preprint 2017, arXiv:1706.06266. [Google Scholar]
- Rasti, P.; Demirel, H.; Anbarjafari, G. Improved iterative back projection for video super-resolution. In Proceedings of the 2014 22nd Signal Processing and Communications Applications Conference (SIU), Trabzon, Turkey, 23–25 April 2014; pp. 552–555. [Google Scholar]
- Li, L.; Xie, Y.; Hu, W.; Zhang, W. Single image super-resolution using combined total variation regularization by split Bregman Iteration. Neurocomputing 2014, 142, 551–560. [Google Scholar] [CrossRef]
- Kato, T.; Hino, H.; Murata, N. Multi-frame image super resolution based on sparse coding. Neural Networks 2015, 66, 64–78. [Google Scholar] [CrossRef]
- Greaves, A.; Winter, H. Multi-frame video super-resolution using convolutional neural networks. IEEE Trans Multimed. 2017, 8, 76–85. [Google Scholar]
- Hayat, K. Multimedia super-resolution via deep learning: A survey. Digit. Signal Process. 2018, 81, 198–217. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Zhang, L.; Lukac, R.; Shi, G. Sparse representation-based image interpolation with nonlocal autoregressive model-ing. IEEE Trans. Image Process. 2013, 22, 1382–1394. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wu, H.; Pan, C. Fast Image Upsampling via the Displacement Field. IEEE Trans. Image Process. 2014, 23, 5123–5135. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Q.; Bao, F.; Zhang, C. Single-image super-resolution based on rational fractal interpolation. IEEE Trans. Image Process. 2018, 27, 3782–3797. [Google Scholar]
- Manjón, J.V.; Coupe, P.; Buades, A.; Fonov, V.; Collins, D.L.; Robles, M. Non-local MRI upsampling. Med Image Anal. 2010, 14, 784–792. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Ge, Q.; Wang, Q.; Lin, Z.; Deng, S.; Li, B. Nonparametric Blind Super-Resolution Using Adaptive Heavy-Tailed Priors. J. Math Imaging Vis. 2019, 61, 885–917. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S. Blind single image super resolution with low computational complexity. Multimed. Tools. Appl. 2017, 76, 7235–7249. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Dong, C.; Loy, C.C. Recovering Realistic Texture in Image Super-Resolution by Deep Spatial Feature Transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, GA, USA, 17–19 June 2018; pp. 606–615. [Google Scholar]
- Zoph, B.; Le, V. Neural architecture search with reinforcement learning. arXiv preprint 2016, arXiv:1611.01578. [Google Scholar]
- Efrat, N.; Glasner, D.; Apartsin, A.; Nadler, B.; Levin, A. Accurate blur models vs. image priors in single image su-per-resolution. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, NSW, Australia, 1–8 December 2013; pp. 2832–2839. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Xu, L.; Lu, C.; Xu, Y.; Jia, J. Image smoothing via L0 gradient minimization. In Proceedings of the 2011 SIGGRAPH Asia Conference, Hong Kong, China, 13–15 December 2011; pp. 1–12. [Google Scholar]
- Zhang, H.; Hager, W.W. A Nonmonotone Line Search Technique and Its Application to Unconstrained Optimization. SIAM J. Optim. 2004, 14, 1043–1056. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.; Lee, S. Fast Motion Deblurring. ACM Trans. Graph. 2009, 28, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Liu, B.; Zhao, H. Research on Blind Super-Resolution Technology for Infrared Images of Power Equipment Based on Compressed Sensing Theory. Sensors 2021, 21, 4109. [Google Scholar] [CrossRef] [PubMed]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
- Patel, M.I.; Thakar, V.K.; Shah, S.K. Image registration of satellite images with varying illumination level using HOG descriptor based SURF. Procedia Comput. Sci. 2016, 93, 382–388. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Li, Z.; Huang, B. Linear Spectral Clustering Superpixel. IEEE Trans. Image Process. 2017, 26, 3317–3330. [Google Scholar] [CrossRef]
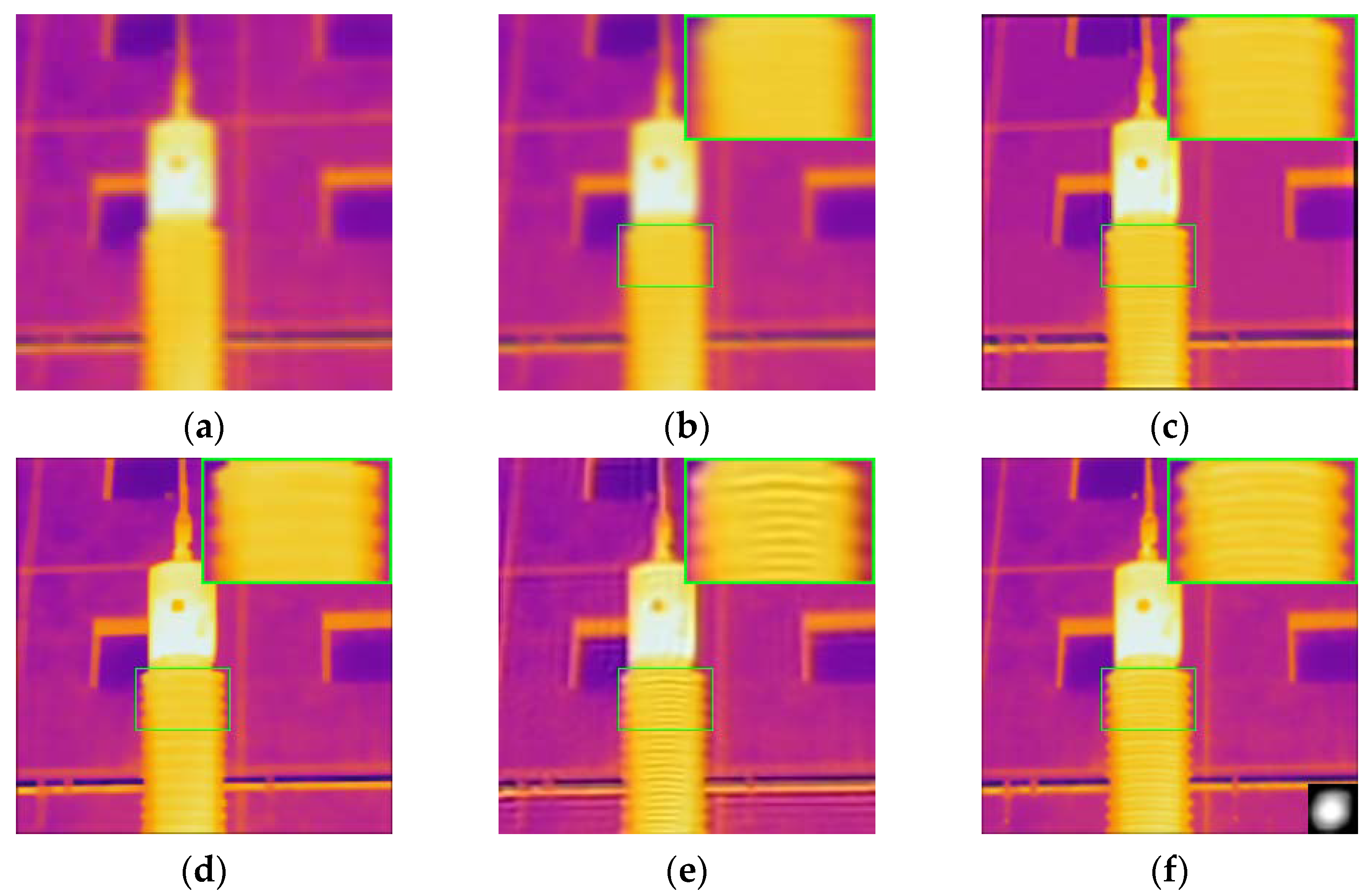

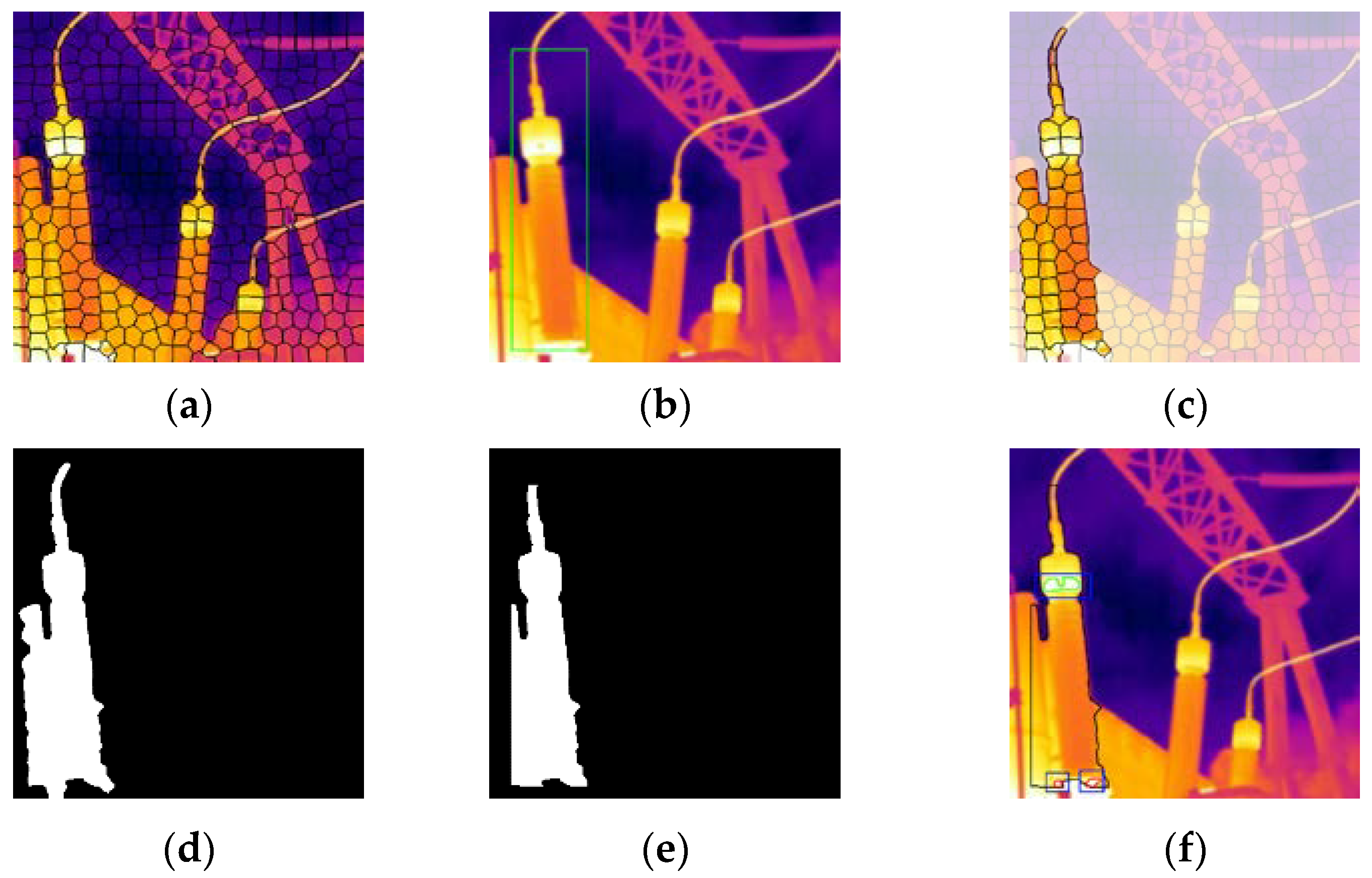

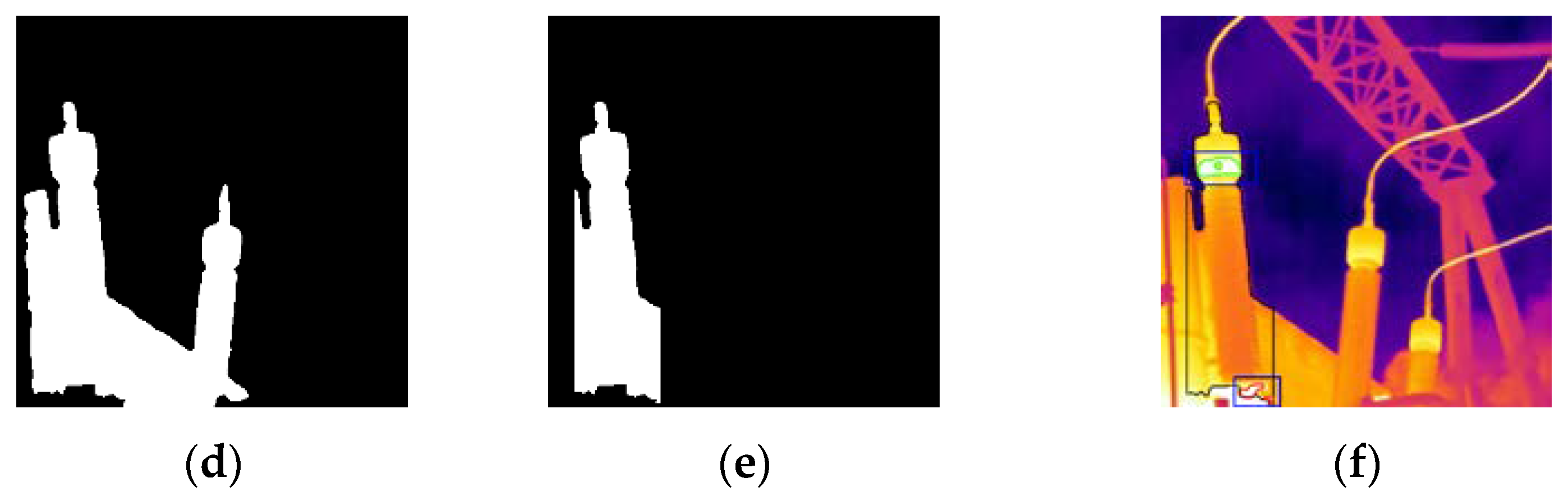


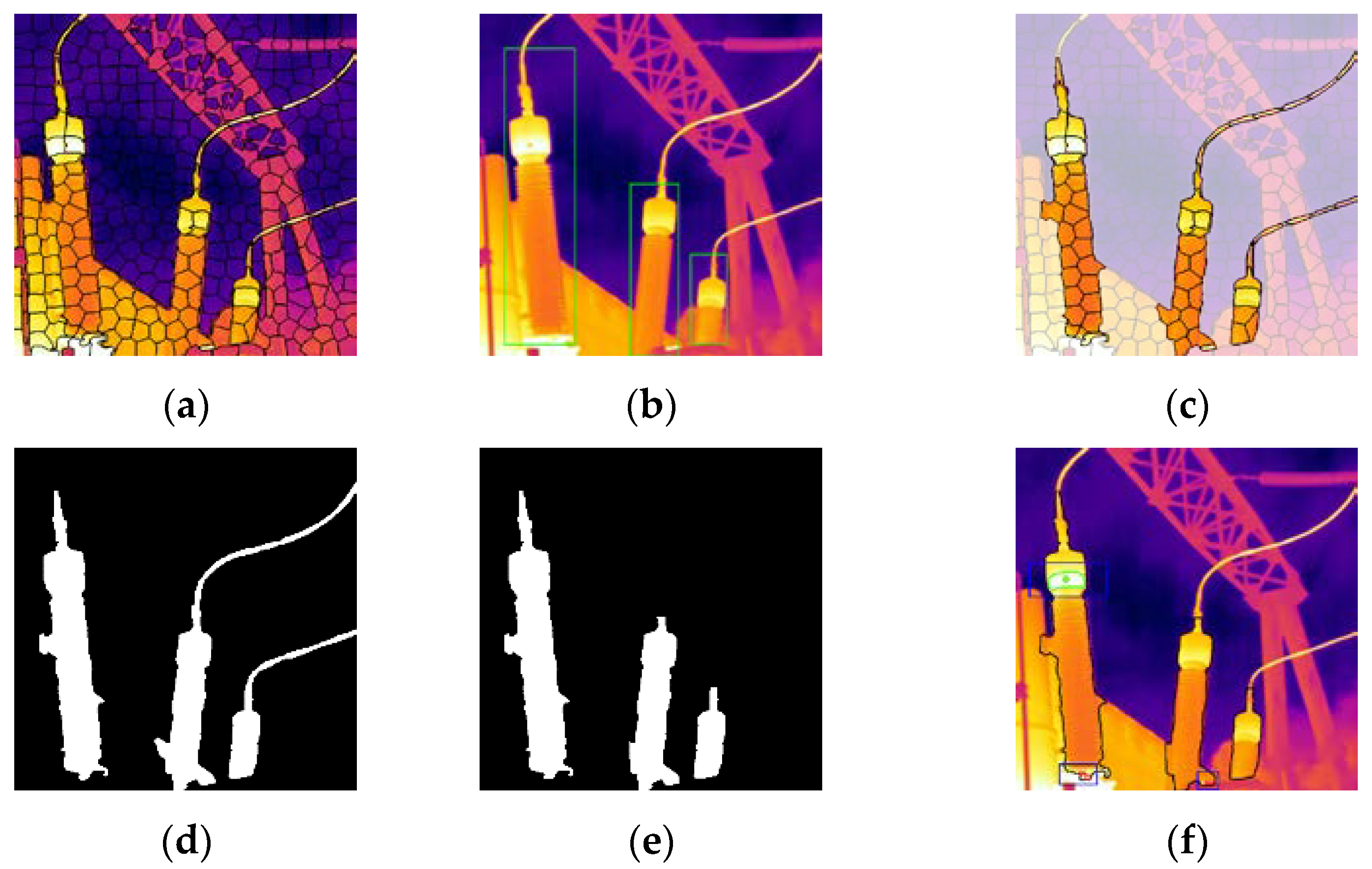

| Image Number | Keys | Shao | Li | Kim | Ours |
|---|---|---|---|---|---|
| 1 | 19.775 | 27.041 | 30.884 | 29.349 | 32.264 |
| 2 | 22.088 | 29.501 | 34.080 | 32.242 | 35.862 |
| 3 | 21.673 | 29.864 | 34.454 | 35.397 | 37.037 |
| 4 | 18.224 | 20.516 | 23.267 | 25.403 | 24.967 |
| 5 | 18.663 | 26.544 | 29.113 | 28.802 | 30.924 |
| 6 | 17.382 | 25.653 | 26.671 | 26.239 | 28.594 |
| 7 | 24.436 | 34.371 | 35.125 | 37.538 | 42.723 |
| 8 | 20.335 | 26.411 | 34.929 | 27.216 | 32.857 |
| Image Number | Keys | Shao | Li | Kim | Ours |
|---|---|---|---|---|---|
| 1 | 5.504 | 6.203 | 6.111 | 6.048 | 6.276 |
| 2 | 6.597 | 6.419 | 6.653 | 6.706 | 6.948 |
| 3 | 6.318 | 6.581 | 6.738 | 6.442 | 6.281 |
| 4 | 5.530 | 5.603 | 5.762 | 5.891 | 5.806 |
| 5 | 6.103 | 6.143 | 6.249 | 6.543 | 6.698 |
| 6 | 5.609 | 5.581 | 5.609 | 5.191 | 5.792 |
| 7 | 6.742 | 6.764 | 6.865 | 6.782 | 6.876 |
| 8 | 5.713 | 5.862 | 5.790 | 5.983 | 5.316 |
| Image Number | LR | Keys | Shao | Li | Kim | Ours |
|---|---|---|---|---|---|---|
| 1 | 257 | 278 | 351 | 377 | 385 | 405 |
| 2 | 219 | 248 | 309 | 328 | 334 | 365 |
| 3 | 153 | 164 | 210 | 223 | 221 | 252 |
| 4 | 256 | 276 | 351 | 375 | 379 | 416 |
| 5 | 185 | 209 | 267 | 282 | 292 | 326 |
| Reconstruction Algorithm | Correct Matching Rate of Feature Points | ||||
|---|---|---|---|---|---|
| Image 1 | Image 2 | Image 3 | Image 4 | Image 5 | |
| LR | 52.38 | 48.78 | 51.15 | 50.22 | 53.79 |
| Keys’ | 55.95 | 50.70 | 52.37 | 53.84 | 54.34 |
| Shao’s | 61.52 | 59.56 | 64.56 | 61.88 | 64.75 |
| Li’s | 71.03 | 71.76 | 71.79 | 69.75 | 70.91 |
| Kim’s | 74.23 | 72.62 | 76.65 | 76.36 | 74.48 |
| Ours | 82.13 | 83.40 | 81.04 | 83.25 | 84.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, J.; Wang, L. Compressed Sensing Super-Resolution Method for Improving the Accuracy of Infrared Diagnosis of Power Equipment. Appl. Sci. 2022, 12, 4046. https://doi.org/10.3390/app12084046
Wang Y, Zhang J, Wang L. Compressed Sensing Super-Resolution Method for Improving the Accuracy of Infrared Diagnosis of Power Equipment. Applied Sciences. 2022; 12(8):4046. https://doi.org/10.3390/app12084046
Chicago/Turabian StyleWang, Yan, Jialin Zhang, and Lingjie Wang. 2022. "Compressed Sensing Super-Resolution Method for Improving the Accuracy of Infrared Diagnosis of Power Equipment" Applied Sciences 12, no. 8: 4046. https://doi.org/10.3390/app12084046
APA StyleWang, Y., Zhang, J., & Wang, L. (2022). Compressed Sensing Super-Resolution Method for Improving the Accuracy of Infrared Diagnosis of Power Equipment. Applied Sciences, 12(8), 4046. https://doi.org/10.3390/app12084046





