Fractal Contact Mechanics Model for the Rough Surface of a Beveloid Gear with Elliptical Asperities
Abstract
:1. Introduction
2. A New Fractal Characterization Approach for a Rough Surface Texture
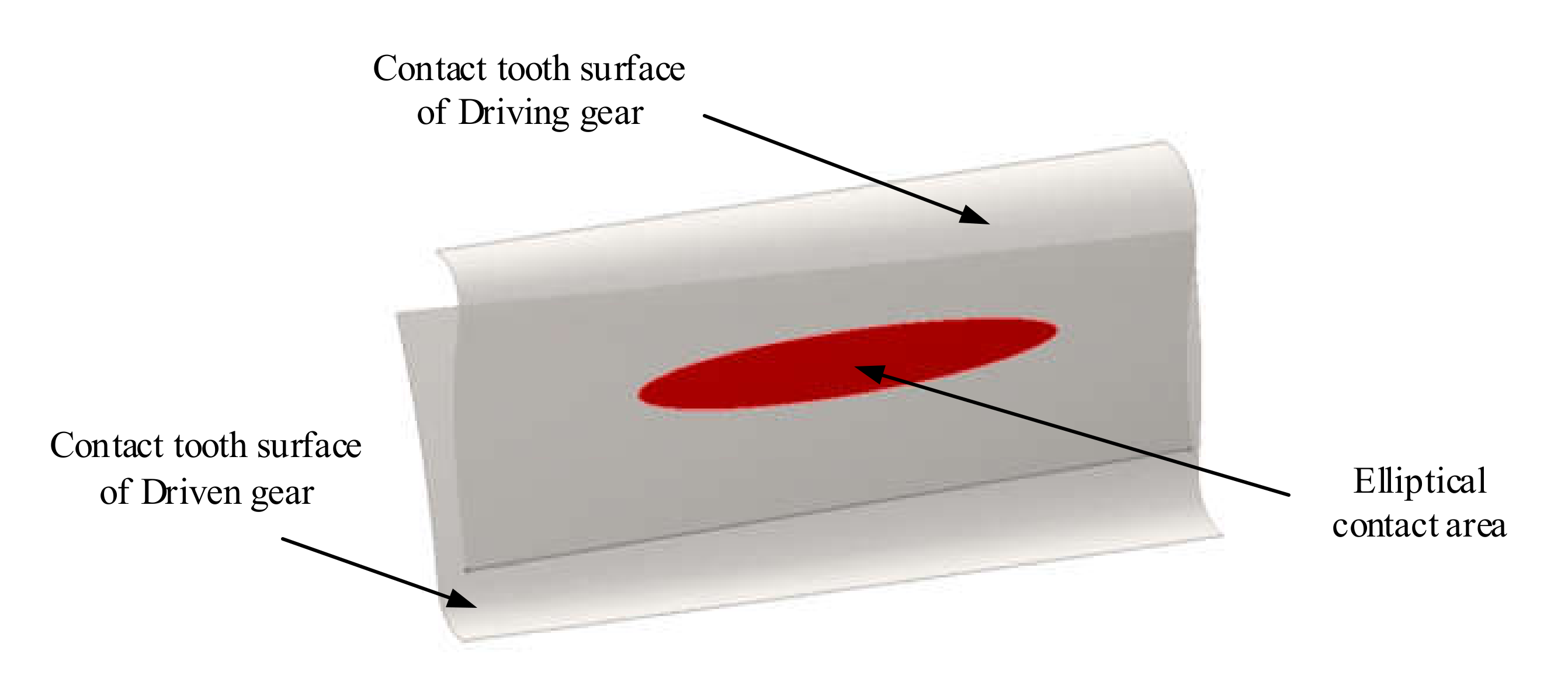
3. Contact Mechanics Model of Elliptical Asperity with Rough Tooth Surface
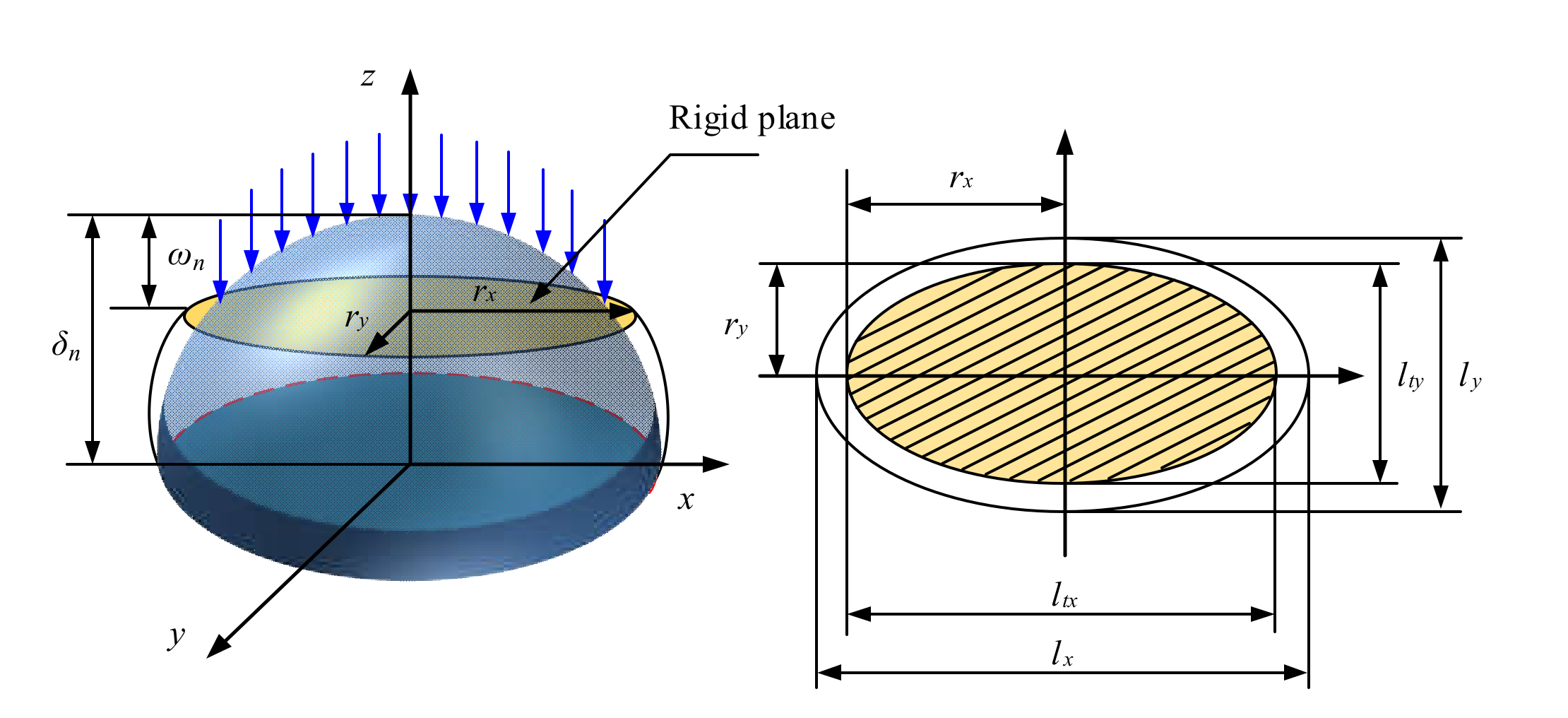
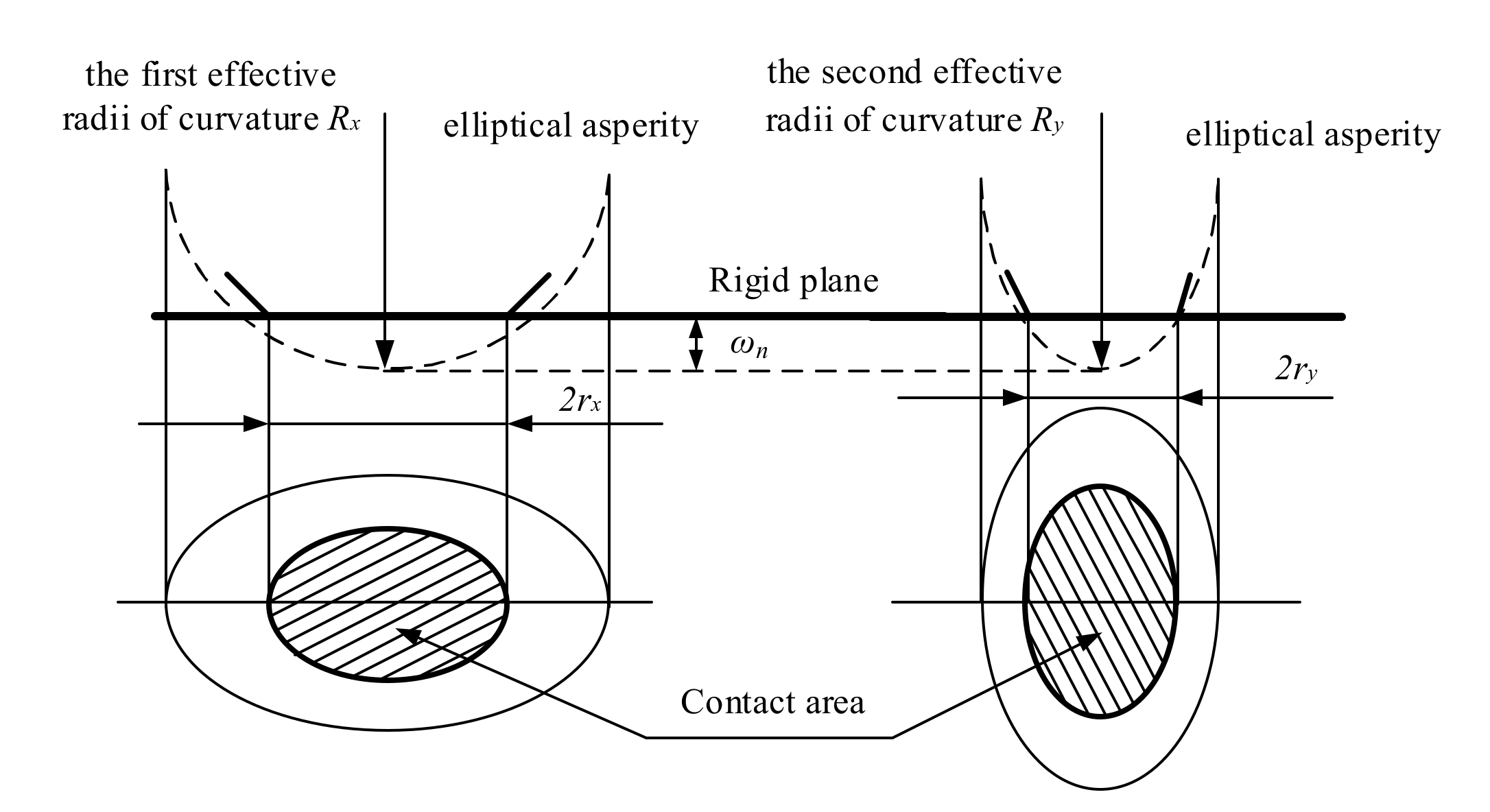
3.1. Geometric Model of Single Elliptical Asperity
3.2. Contact Mechanics Model of Single Elliptical Asperity
3.2.1. Elastic Contact of Elliptical Asperity
3.2.2. Elastic–Plastic Contact of Elliptical Asperity
3.2.3. Plastic Contact of Elliptical Asperity
3.3. Modified Model of the Island Area Distribution Function for a Point Contact
3.3.1. Contact Area Distribution Function
3.3.2. Elliptical Contact Area Distribution Function
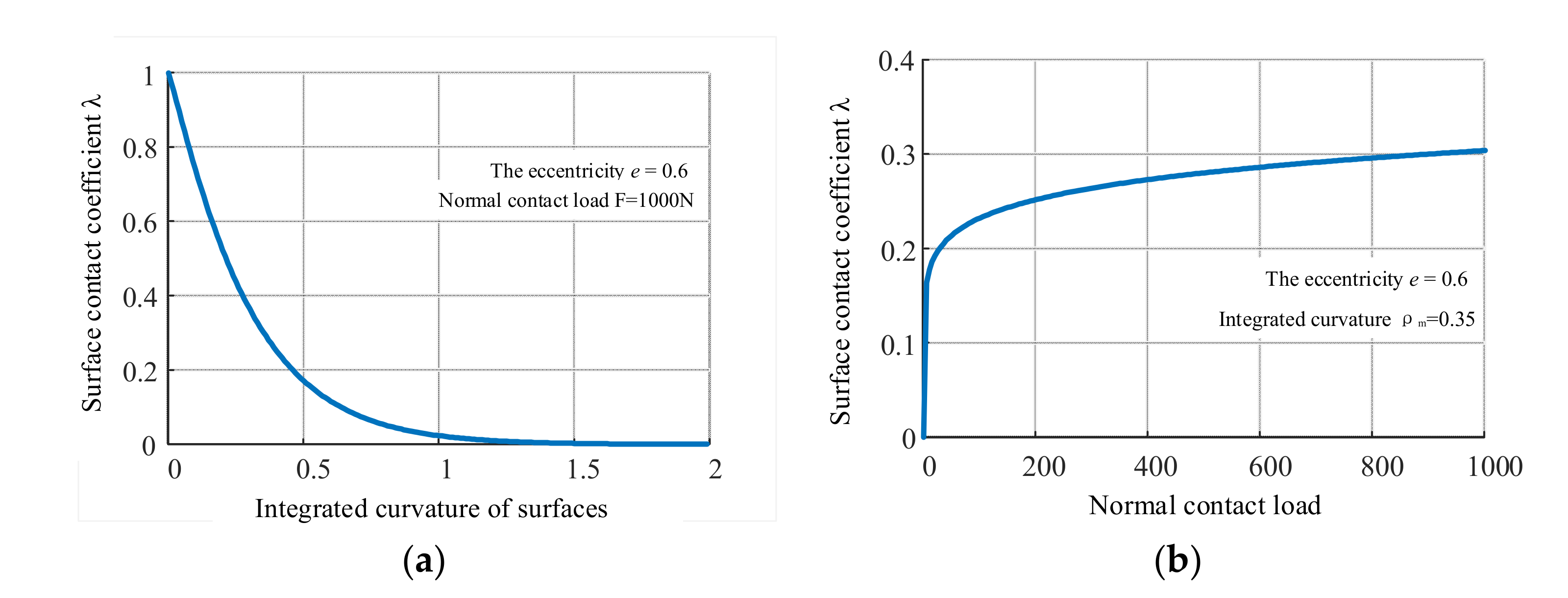
3.3.3. Contact Coefficient of the Elliptical Area of a Beveloid Gear
4. The Fractal Contact Model for Rough Curved Surfaces with Elliptical Asperities
4.1. Real Contact Area and Contact Load
4.1.1. Real Contact Area
4.1.2. Real Contact Load
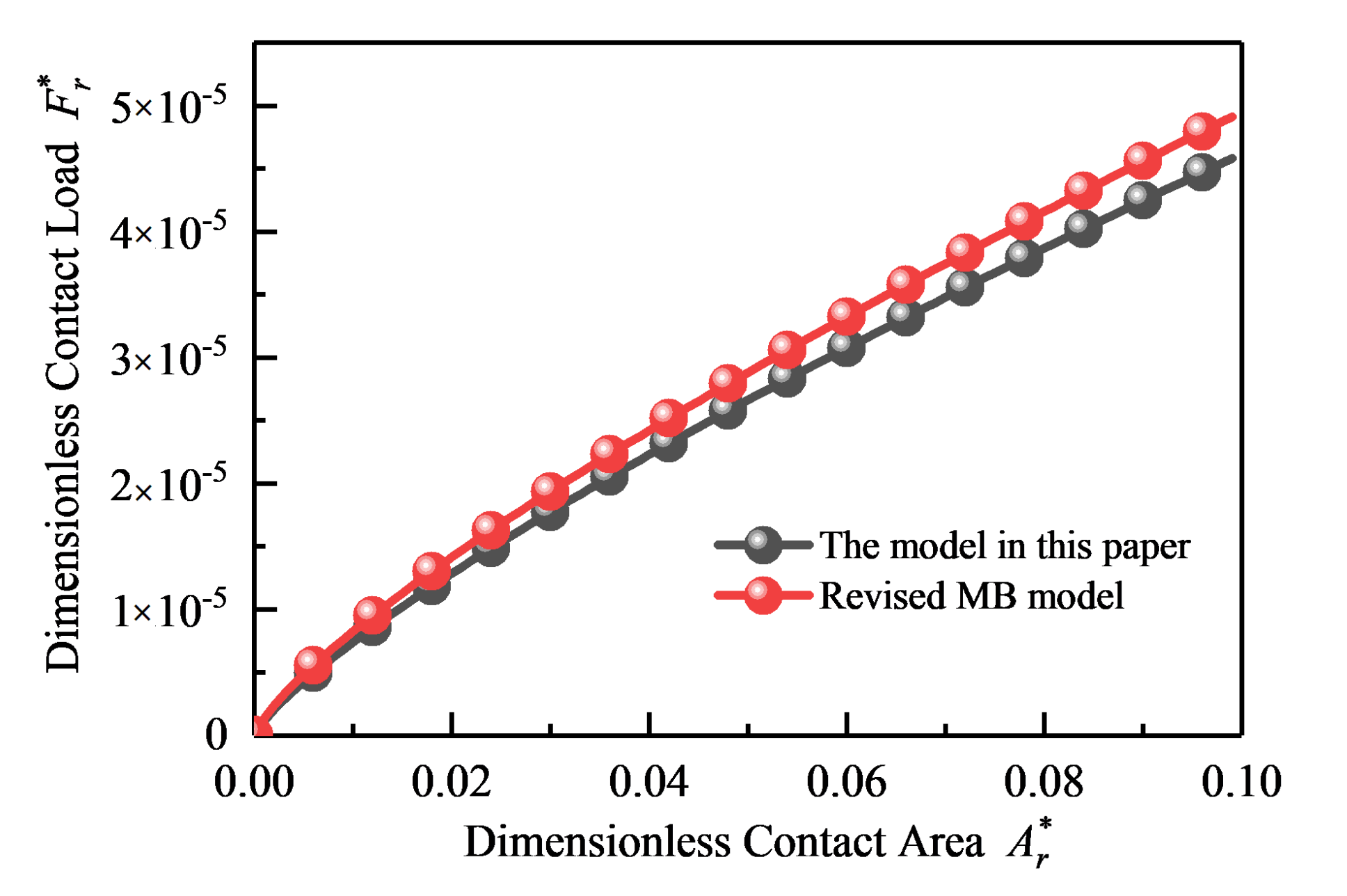
4.1.3. The Relationship between the Real Contact Area and the Real Contact Load
4.2. Calculation of the Contact Stiffness of Rough Tooth Surfaces
4.2.1. Contact Stiffness Model of a Single Elliptical Asperity
4.2.2. Contact Stiffness Model of a Rough Surface
5. Numerical Analysis and Discussion of Results
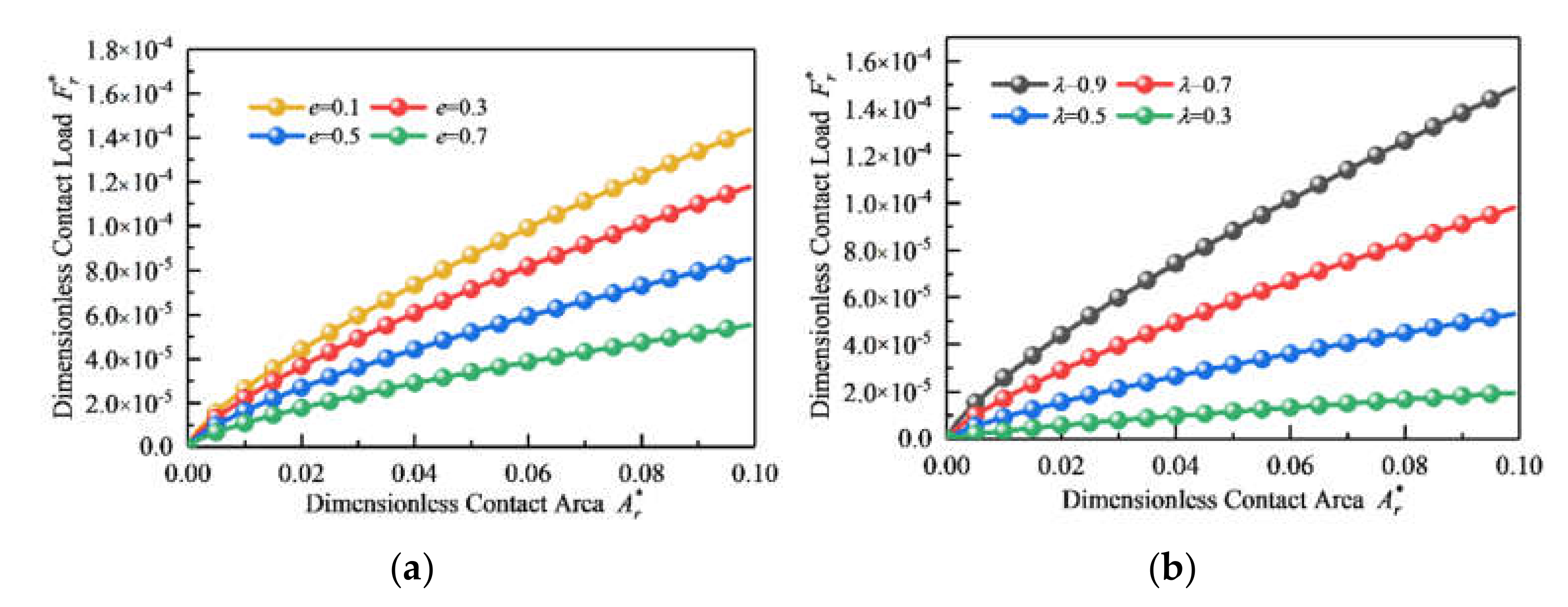
5.1. Effect of Fractal Parameters and Eccentricity on Contact Area
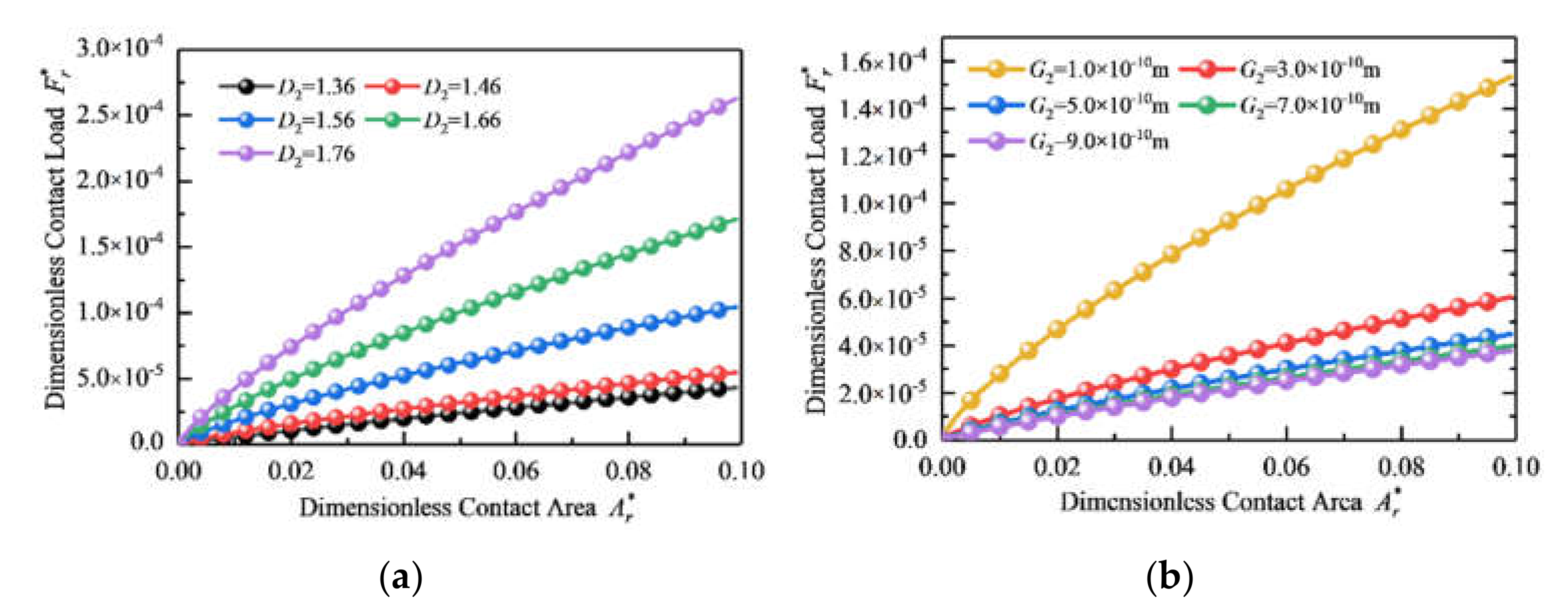
5.2. Effect of Fractal Parameters on the Contact Load
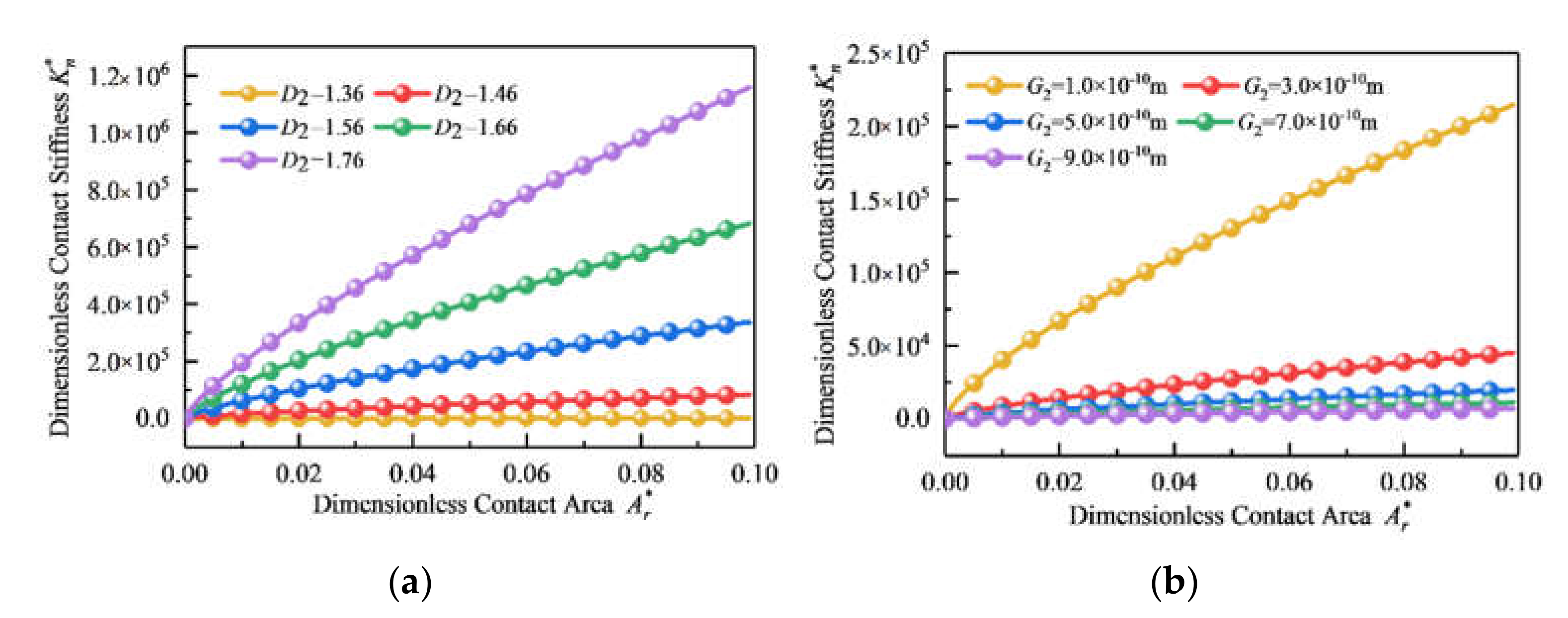
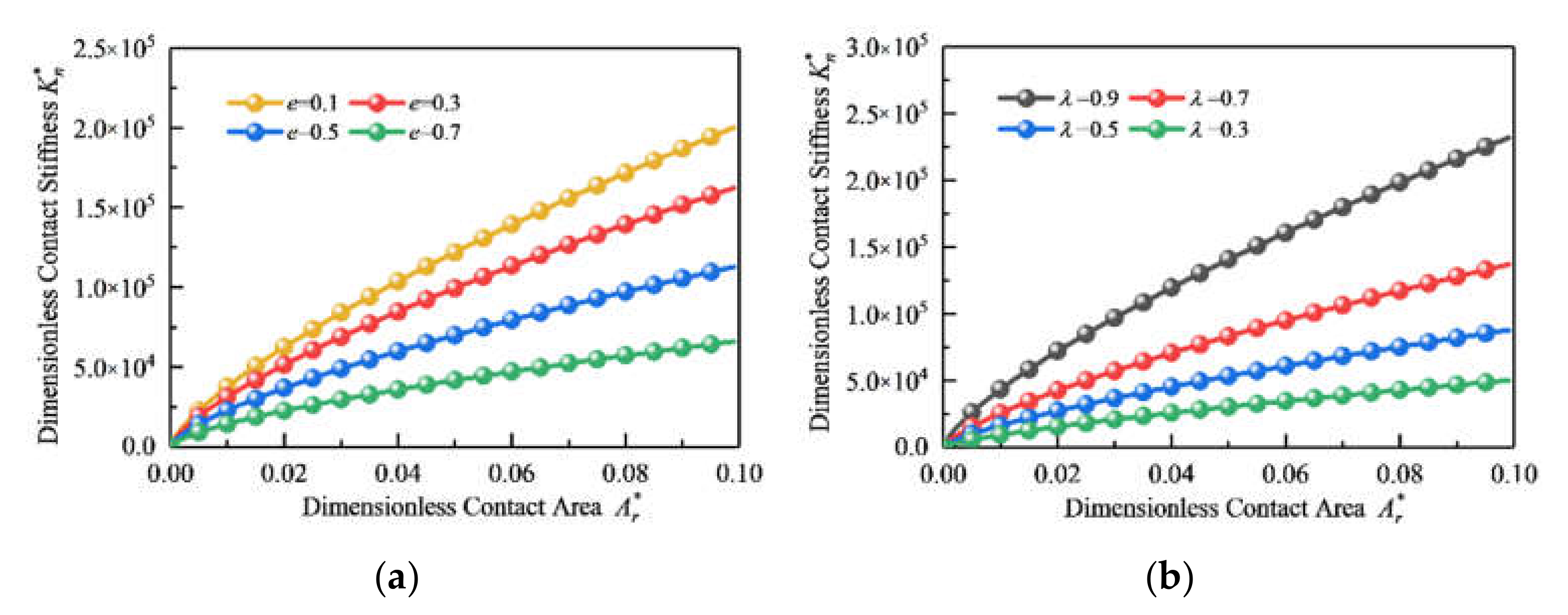
5.3. Effect of Fractal Parameters on Normal Contact Stiffness
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. 1966, 295, 300–319. [Google Scholar]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surface. ASME J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Bhushan, B.; Majumdar, A. Elastic-plastic contact model for bifractal surfaces. Wear 1992, 153, 53–64. [Google Scholar] [CrossRef]
- Chang, W.R.; Etsion, I.; Bogy, D.B. An elastic-plastic model for the contact of rough surfaces. ASME J Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An asperity micro-contact model incorporating the transition from elastic deformation to fully plastic flow. J. Tribol. 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic–plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef] [Green Version]
- Kogut, L.; Etsion, I. A static friction model for elastic-plastic contacting rough surfaces. J. Tribol. 2004, 126, 34–40. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A finite element study of elasto-plastic hemispherical contact against a rigid flat. J. Tribol. Trans. ASME 2005, 127, 343–354. [Google Scholar] [CrossRef] [Green Version]
- Jackson, R.L.; Streator, J.L. A multi-scale model for contact between rough surfaces. Wear 2006, 261, 1337–1347. [Google Scholar] [CrossRef]
- Sun, J.J.; Ji, Z.B.; Zhang, Y.Y.; Yu, Q.P.; Ma, C.B. A Contact Mechanics Model for Rough Surfaces Based on a New Fractal Characterization Method. Int. J. Appl. Mech. 2018, 10, 1850069. [Google Scholar] [CrossRef]
- Morag, Y.; Etsion, I. Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces. Wear 2007, 262, 624–629. [Google Scholar] [CrossRef]
- Yuan, Y.; Cheng, Y.; Liu, K.; Gan, L. A revised Majumdar and Bushan model of elastoplastic contact between rough surfaces. Appl. Surf. Sci. 2017, 425, 1138–1157. [Google Scholar] [CrossRef]
- Yuan, Y.; Gan, L.; Liu, K.; Yang, X.H. Elastoplastic contact mechanics model of rough surface based on fractal theory. Chin. J. Mech. Eng. 2017, 30, 207–215. [Google Scholar] [CrossRef]
- Yu, Q.; Sun, J.; Ji, Z. Mechanics Analysis of Rough Surface Based on Shoulder-Shoulder Contact. Appl. Sci. 2021, 11, 8048. [Google Scholar] [CrossRef]
- Pan, W.J.; Li, X.P.; Wang, L.L.; Guo, N.; Mu, J.X. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification. Eur. J. Mech. A-Solids 2017, 66, 94–102. [Google Scholar] [CrossRef]
- Pan, W.J.; Song, C.X.; Ling, L.Y.; Qu, H.Y.; Wang, M.H. Unloading contact mechanics analysis of elastic-plastic fractal surface. Arch. Appl. Mech. 2021, 91, 2697–2712. [Google Scholar] [CrossRef]
- Zhou, H.; Long, X.H.; Meng, G.; Liu, X.B. A stiffness model for bolted joints considering asperity interactions of rough surface contact. J. Tribol. Trans. ASME 2021, 114, 011501. [Google Scholar] [CrossRef]
- Wang, R.Q.; Zhu, L.D.; Zhu, C.X. Research on fractal model of normal contact stiffness for mechanical joint considering asperity interaction. Int. J. Mech. Sci. 2017, 134, 357–369. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.J.; Shi, X.H.; Ma, S.L.; Cai, A.J. Contact Stiffness Model of Joint Surface Considering Continuous Smooth Characteristics and Asperity Interaction. Tribol. Lett. 2021, 69, 43. [Google Scholar] [CrossRef]
- Cohen, D.; Kligerman, Y.; Etsion, I. The Effect of Surface Roughness on Static Friction and Junction Growth of an Elastic-Plastic Spherical Contact. J. Tribol. Trans. ASME 2009, 131, 021404. [Google Scholar] [CrossRef]
- Cohen, D.; Kligerman, Y.; Etsion, I. A model for contact and static friction of nominally flat rough surfaces under full stick contact condition. J. Tribol. -Trans. ASME 2008, 130, 031401. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Z.S.; Jin, F.; Fan, X.H. Normal Contact Model for Elastic and Plastic Mechanics of Rough Surfaces. ACTA Mech. Solida Sin. 2019, 32, 148–159. [Google Scholar] [CrossRef]
- Xiao, H.F.; Sun, Y.Y.; Chen, Z.G. Fractal modeling of normal contact stiffness for rough surface contact considering the elastic-plastic deformation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 11. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.Y.; Zhao, D.; Wu, S.J. A revised contact stiffness model of rough curved surfaces based on the length scale. Tribol. Int. 2021, 164, 107206. [Google Scholar] [CrossRef]
- Kragelskii, I.V.; Mikhin, N.M. Handbook of Friction Units of Machines; ASME Press: New York, NY, USA, 2002. [Google Scholar]
- Horng, J.H. An elliptic elastic-plastic asperity microcontact model for rough surfaces. ASME J. Tribol. 1998, 120, 82–88. [Google Scholar] [CrossRef]
- Jamari, J. An Elliptic Elastic-Plastic Asperity Micro-Contact Model. Rotasi J. Tek. Mesin 2006, 8, 1–5. [Google Scholar]
- Jeng, Y.R.; Wang, P.Y. An elliptic microcontact model considering elastic, elastoplastic, and plastic deformation. ASME J. 2003, 125, 232–240. [Google Scholar]
- Wen, Y.Q.; Tang, J.Y.; Zhou, W.; Zhu, C.C. A new elliptical microcontact model considering elastoplastic deformation. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2018, 232, 1352–1364. [Google Scholar] [CrossRef]
- Jamari, J.; Schipper, D.J. An elastic-plastic contact model of ellipsoid bodies. Tribol. Lett. 2006, 21, 262–271. [Google Scholar] [CrossRef]
- Lan, W.; Fan, S.; Fan, S. A fractal model of elastic-plastic contact between rough surfaces for a low-velocity impact process. Int. J. Comput. Methods 2021, 18, 2150039. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, F.; Liu, P.; Fan, H. Research on fractal model of normal contact stiffness between two spheroidal joint surfaces considering friction factor. Tribol. Int. 2016, 87, 253–264. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.S.; Yu, H.C. A spherical conformal contact model considering frictional and microscopic factors based on fractal theory. Chaos Solitons Fractals 2018, 111, 96–107. [Google Scholar] [CrossRef]
- Wang, H.H.; Jia, P.; Wang, L.Q.; Yun, F.H.; Wang, G.; Liu, M.; Wang, X.Y. Modeling of the Loading-Unloading Contact of Two Cylindrical Rough Surfaces with Friction. Appl. Sci. 2020, 10, 742. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Li, H.; Dengqiu, M.; Yongqiao, W.; Jian, C. Sliding Friction Contact Stiffness Model of Involute Arc Cylindrical Gear Based on Fractal Theory. Int. J. Eng. 2017, 30, 109–119. [Google Scholar]
- Zhao, Z.F.; Han, H.Z.; Wang, P.F.; Ma, H.; Zhang, S.H.; Yang, Y. An improved model for meshing characteristics analysis of spur gears considering fractal surface contact and friction. Mech. Mach. Theory 2021, 158, 104219. [Google Scholar] [CrossRef]
- Mao, H.C.; Sun, Y.G.; Xu, T.T.; Yu, G.B. Numerical Calculation Method of Meshing Stiffness for the Beveloid Gear considering the Effect of Surface Topography. Math. Probl. Eng. 2021, 2021, 8886792. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D.H. A Multivariate Weierstrass-Mandelbrot Function. Proc. R. Soc. A Math. Phys. Eng. Sci. 1985, 400, 331–350. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1982; pp. 35–45. [Google Scholar]

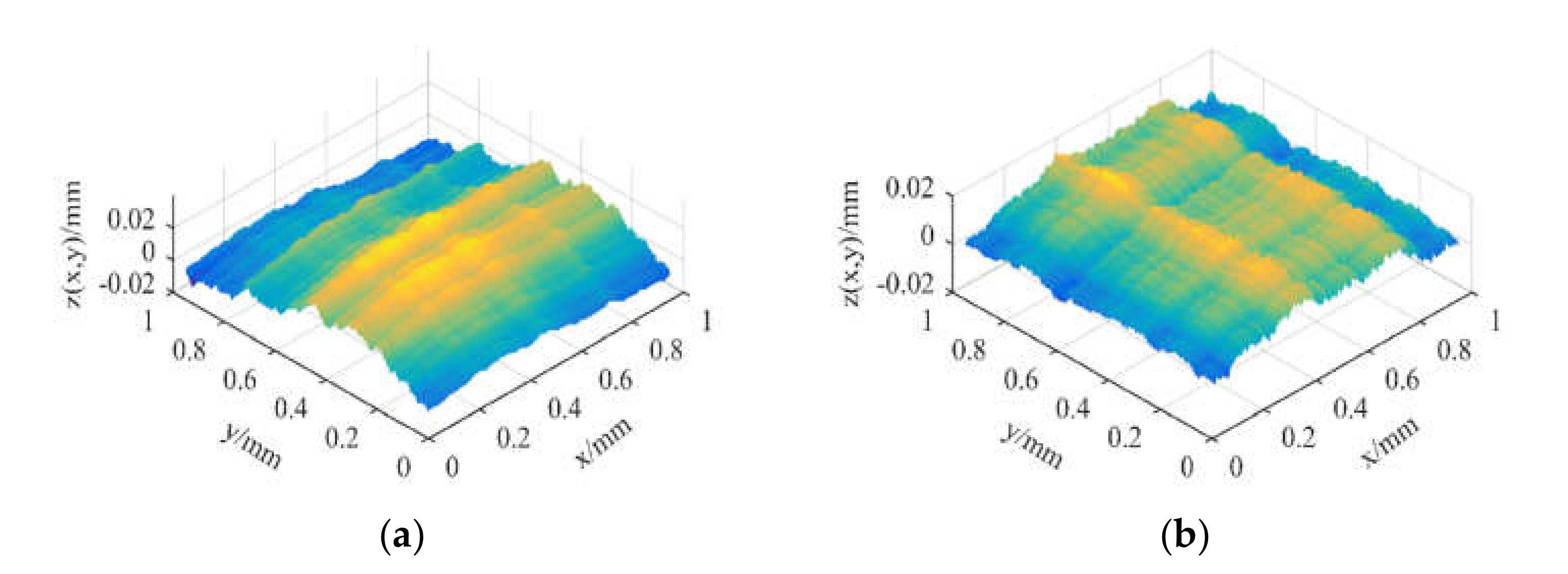




| Parameters | Profile 1 | Profile 2 |
|---|---|---|
| Fractal dimension D | 1.3–1.8 | 1.3–1.8 |
| Characteristic scale G (m) | 1.0 × 10−10 | 1.0 × 10−10 |
| Young’s modulus E (Pa) | 2.06 × 1011 | |
| Poisson’s ratio ν | 0.26 | |
| Plastic yield stress σy (Pa) | 235 × 106 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, G.; Mao, H.; Jiang, L.; Liu, W.; Valerii, T. Fractal Contact Mechanics Model for the Rough Surface of a Beveloid Gear with Elliptical Asperities. Appl. Sci. 2022, 12, 4071. https://doi.org/10.3390/app12084071
Yu G, Mao H, Jiang L, Liu W, Valerii T. Fractal Contact Mechanics Model for the Rough Surface of a Beveloid Gear with Elliptical Asperities. Applied Sciences. 2022; 12(8):4071. https://doi.org/10.3390/app12084071
Chicago/Turabian StyleYu, Guangbin, Hancheng Mao, Lidong Jiang, Wei Liu, and Tupolev Valerii. 2022. "Fractal Contact Mechanics Model for the Rough Surface of a Beveloid Gear with Elliptical Asperities" Applied Sciences 12, no. 8: 4071. https://doi.org/10.3390/app12084071
APA StyleYu, G., Mao, H., Jiang, L., Liu, W., & Valerii, T. (2022). Fractal Contact Mechanics Model for the Rough Surface of a Beveloid Gear with Elliptical Asperities. Applied Sciences, 12(8), 4071. https://doi.org/10.3390/app12084071






