Analysis of Slip Failure Characteristics and Support Deformation Law of Structural Planes and Rock Foundation Pits with Developed Karst Caves
Abstract
:1. Introduction
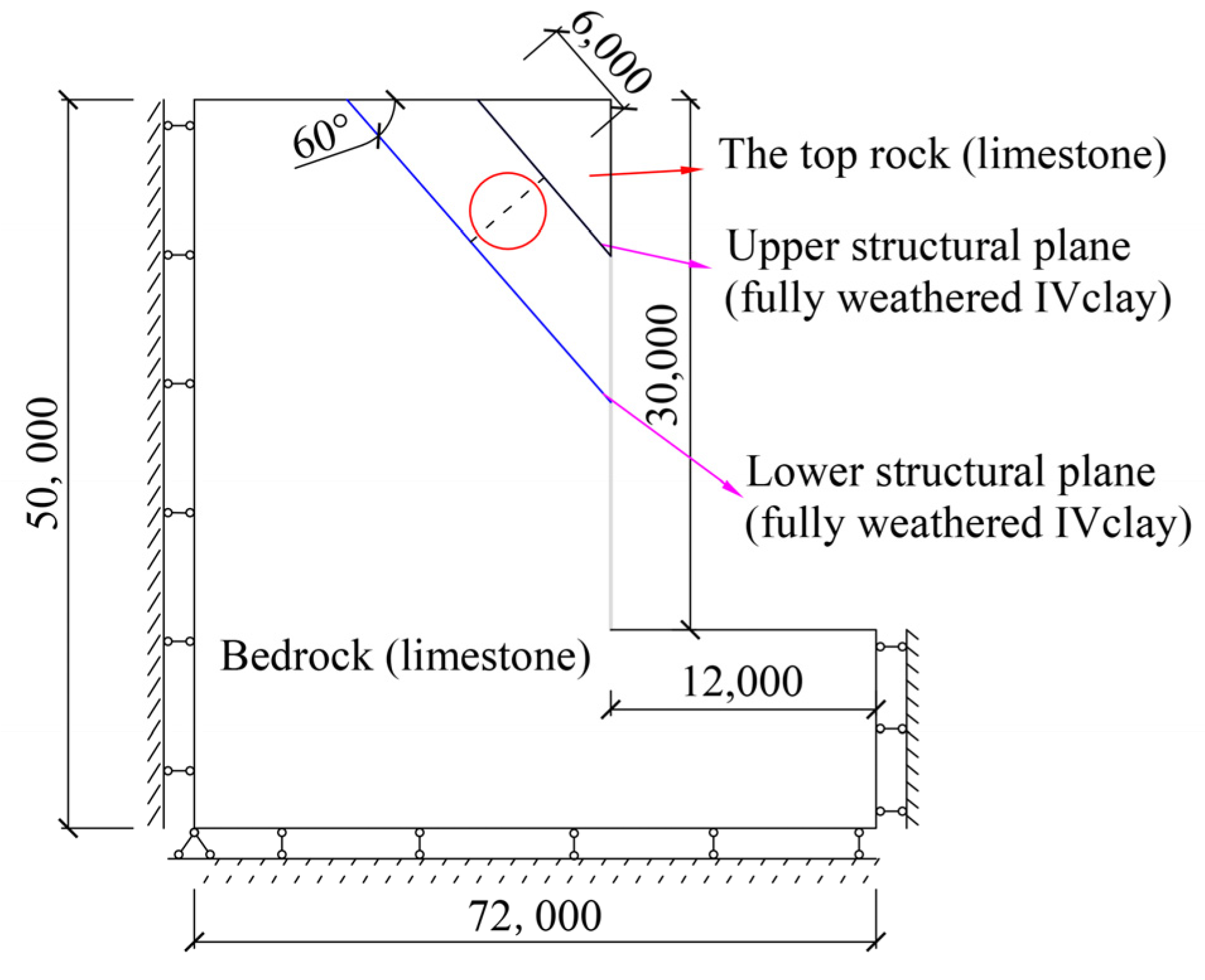
2. Analysis of the Influence of Rock Slopes of Deep Foundation Pits with Karst Caves and Structural Planes on the Failure Mode
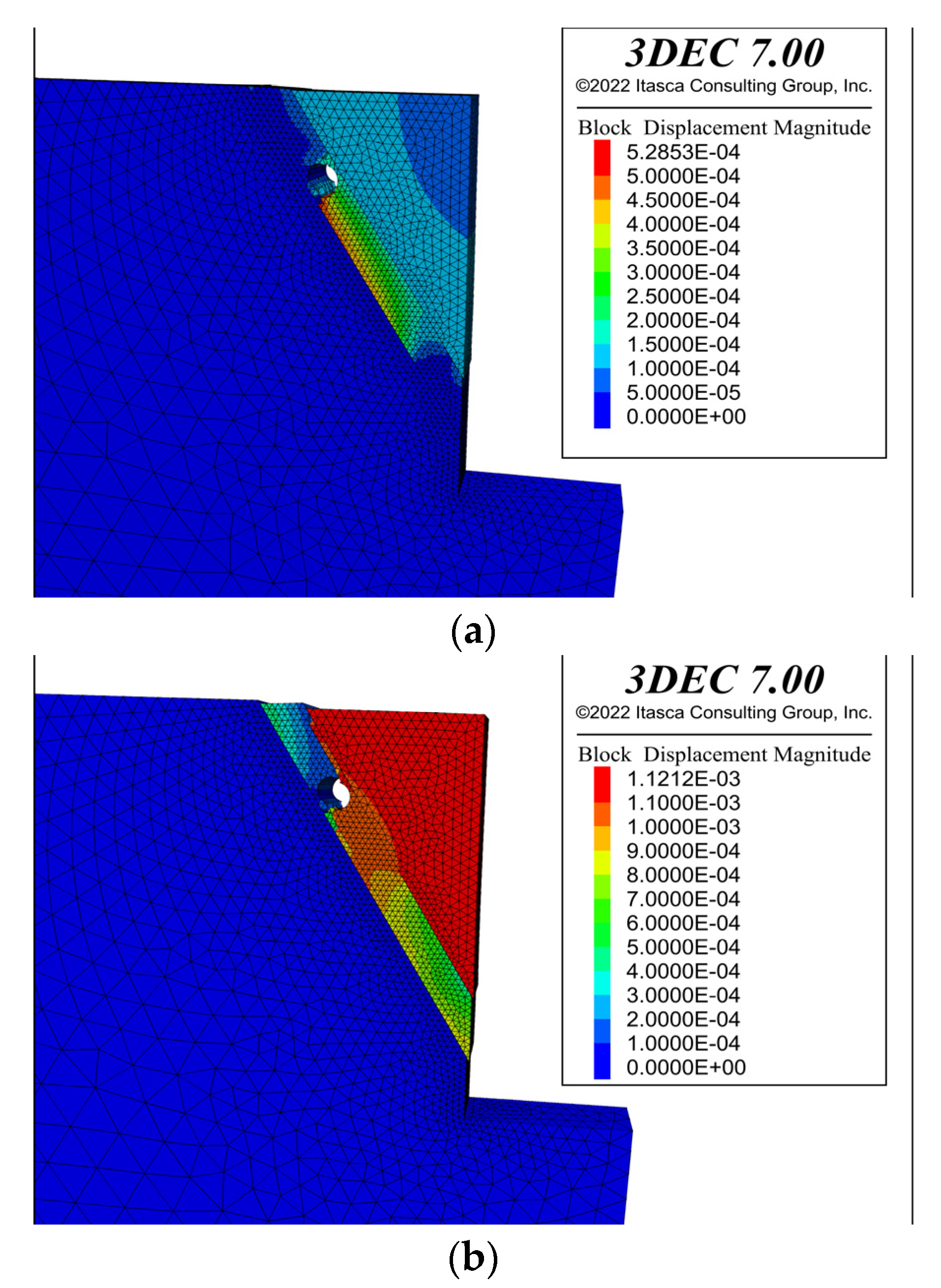
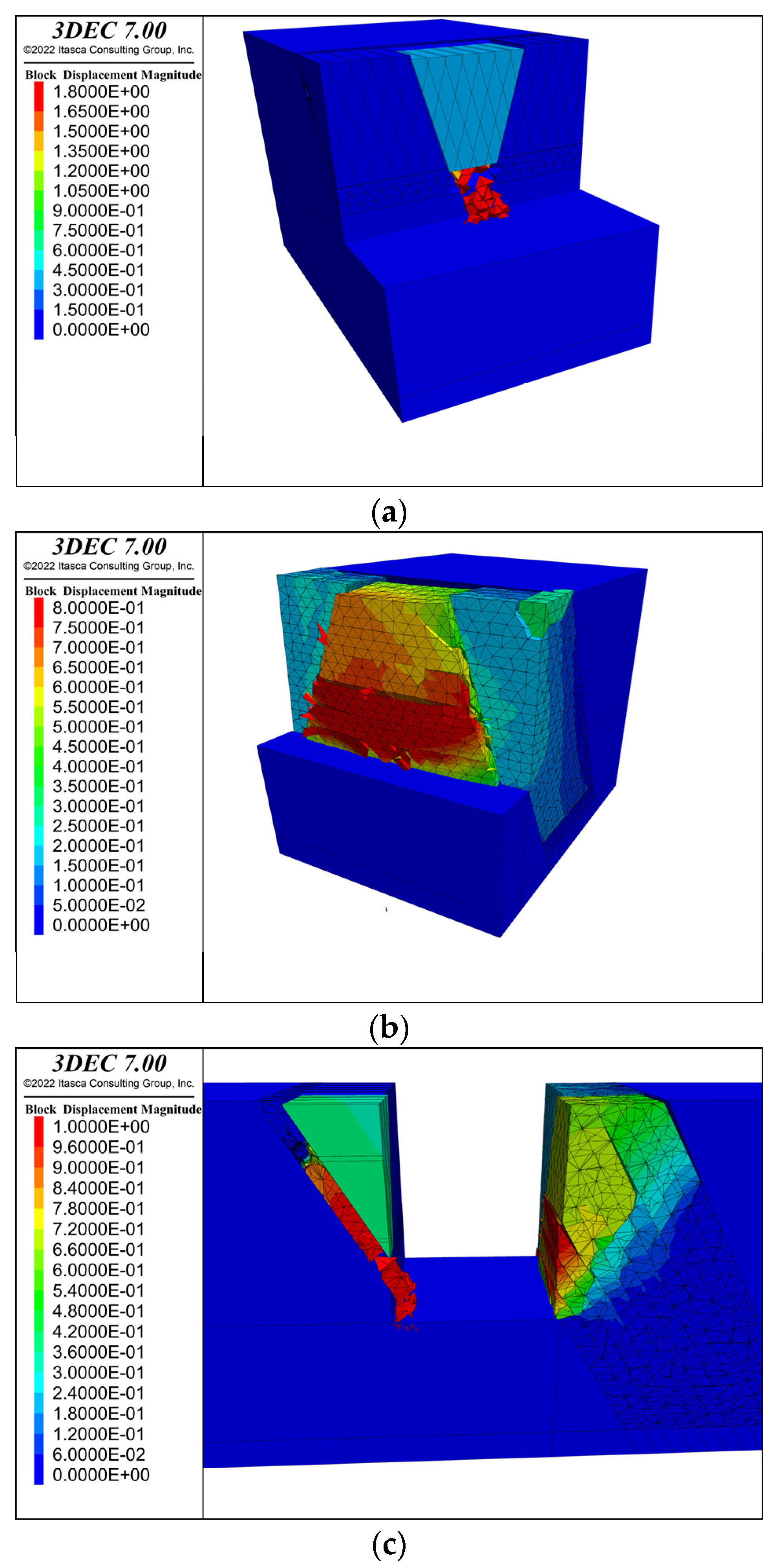
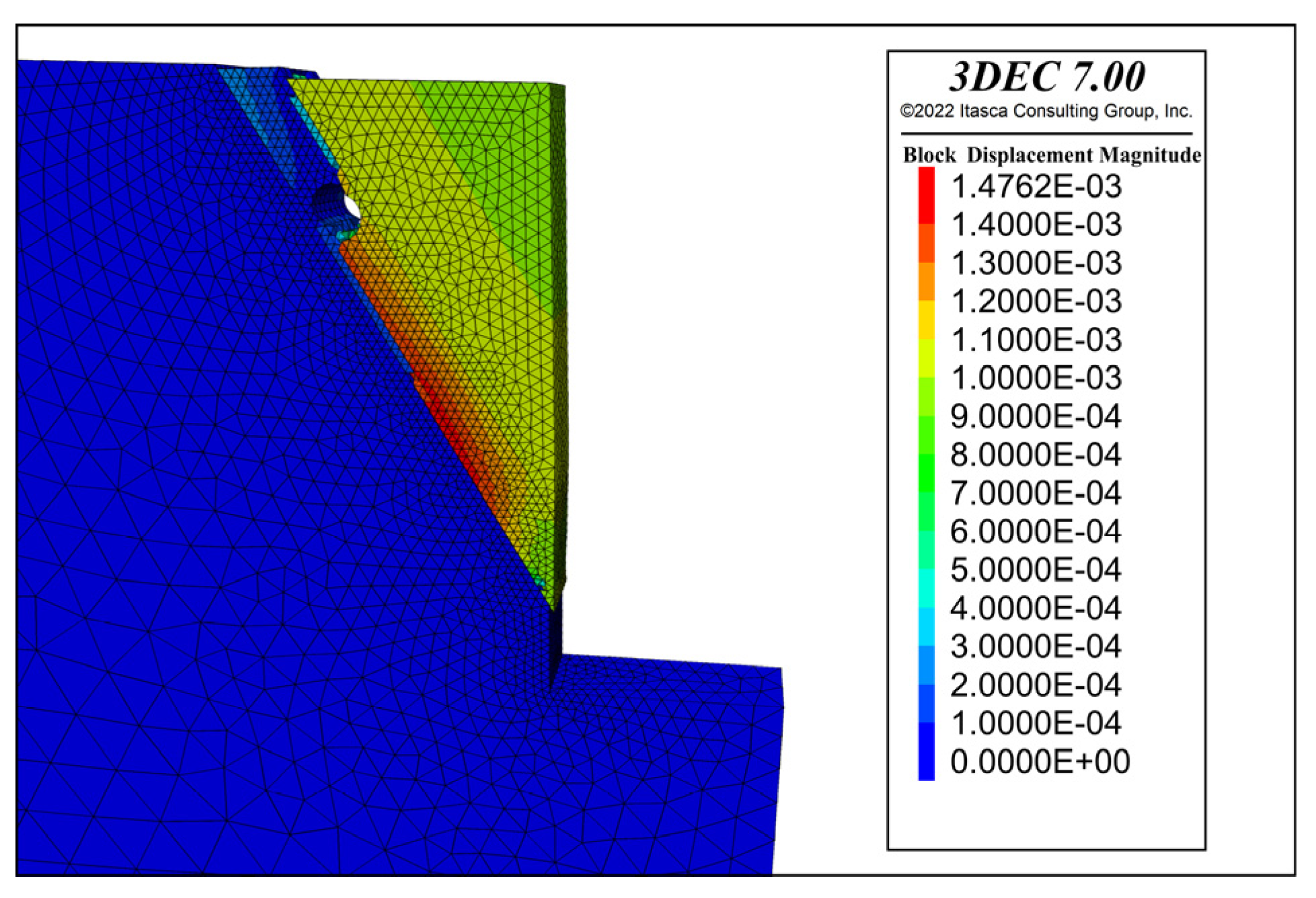
3. Numerical Simulation of Pile-Anchor Support Technology for Rock Slopes of Deep Foundation Pits
4. Numerical Simulation of Pile-Bracing Support Technology for Rock Slopes of Deep Rock Foundation Pits
5. Contrastive Analysis of Different Supporting Schemes of Rock Slopes of Deep Foundation Pits
5.1. Supporting Analysis of the Pile Bracing Structure of the Rock Foundation Pit
5.2. Analysis of the Combined Support of the Pile-Bracing Anchor of the Rock Foundation Pit
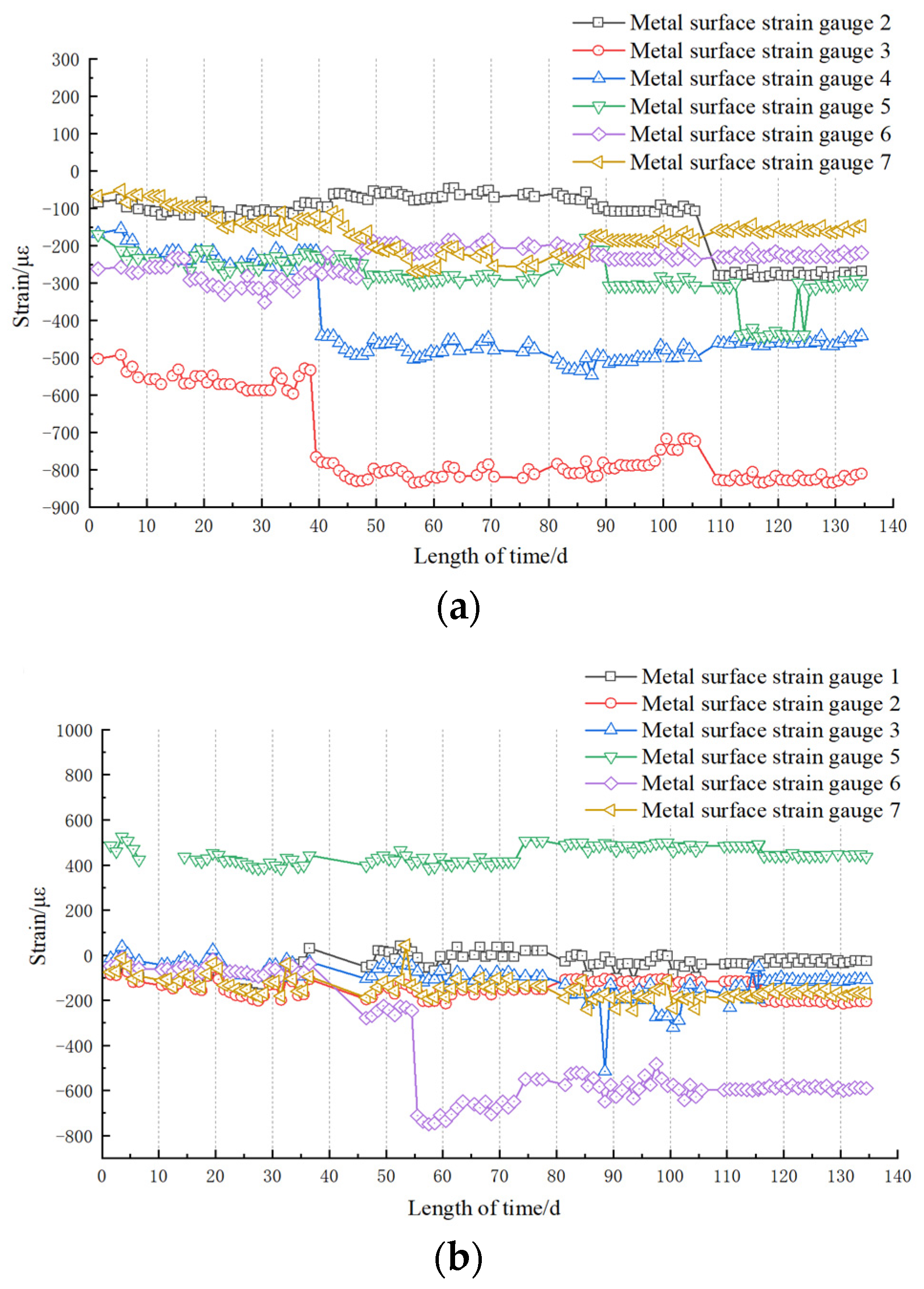
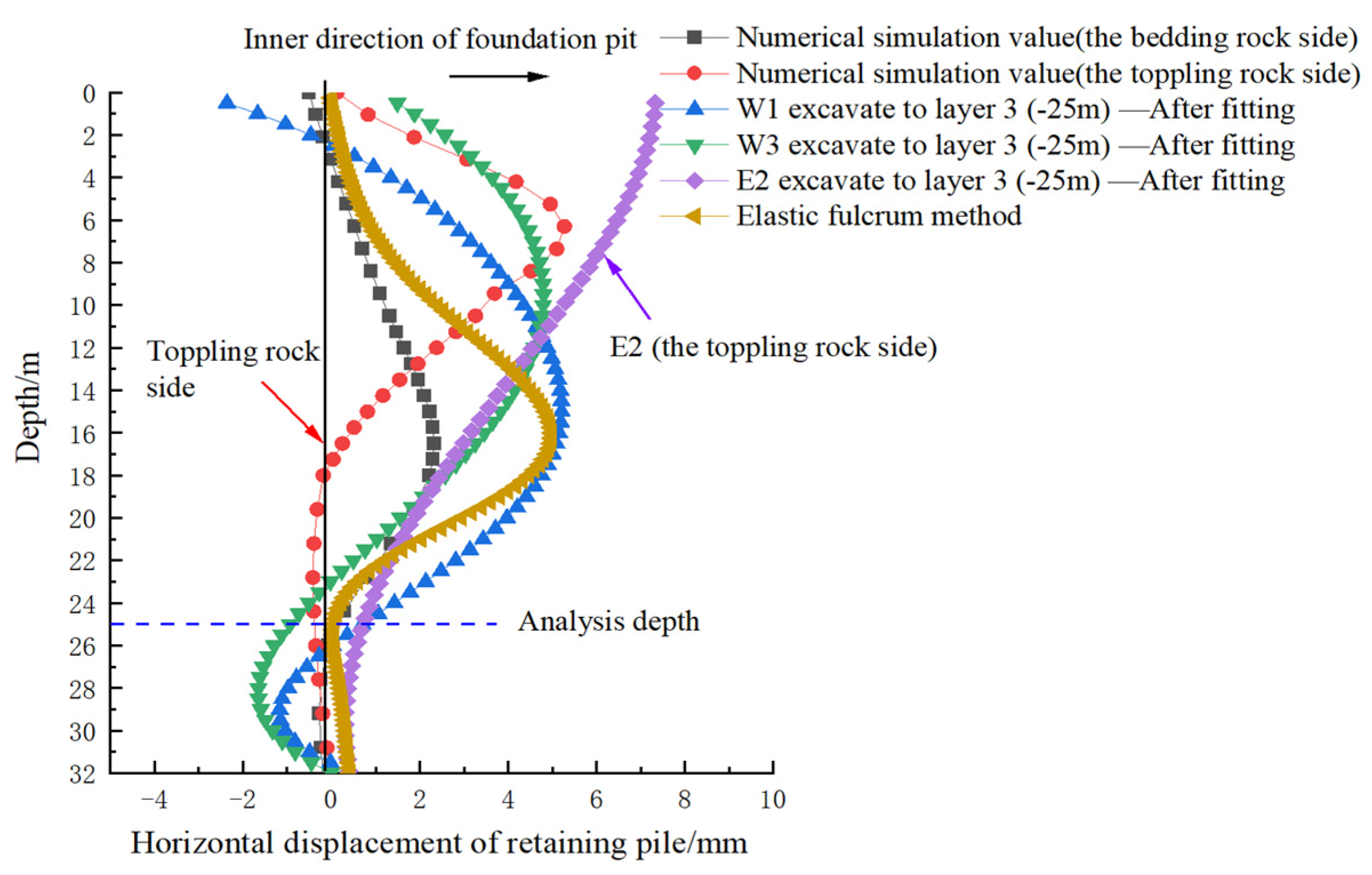
6. Analysis Based on the Foundation Pit Project of Sanhuan South Road Station of Xuzhou Metro Line 3
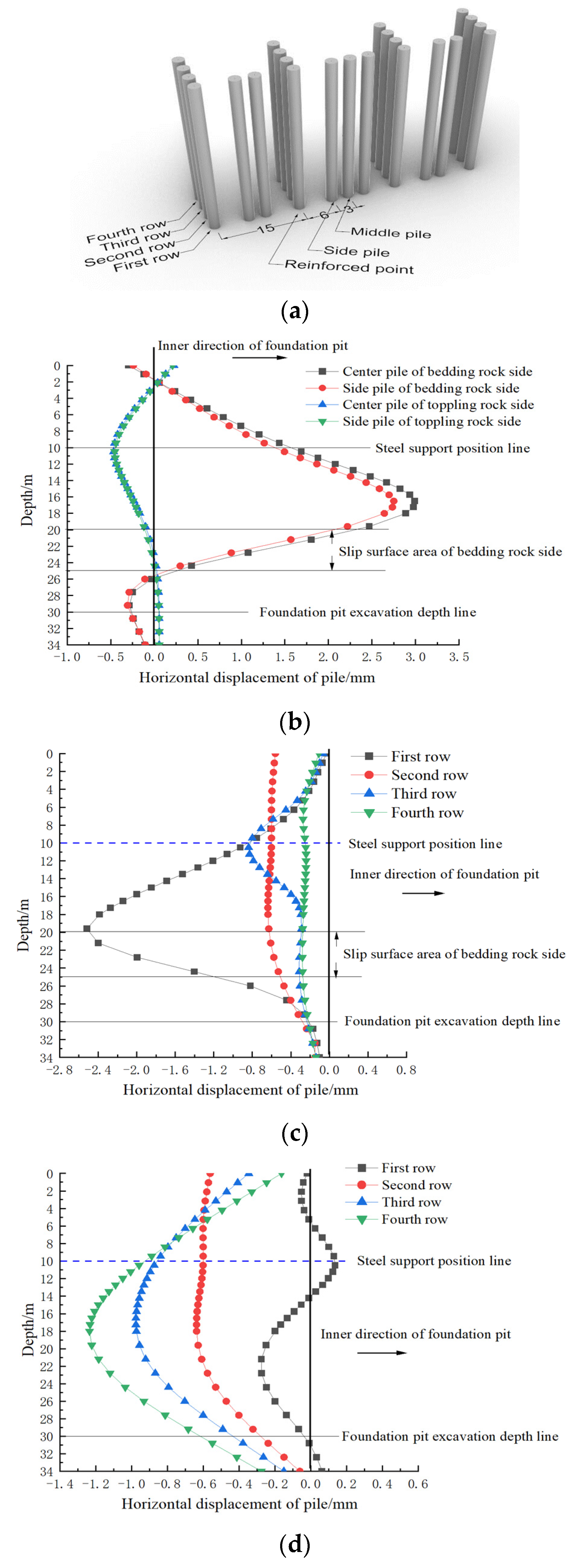
7. Analysis of Optimizing the Foundation Pit Supporting System Based on the Space Effect
8. Conclusions
- (1)
- For bedding rock slopes, the failure on the bedding rock side is prone to be affected by karst caves and thus changes the final sliding path to form a broken line landslide, while arc-shaped toppling failure is prone to be formed on the toppling rock side.
- (2)
- For bedding rock foundation pits, it is recommended to use prestressed anchor cables in conjunction with the anchor cables, which can reduce the maximum displacement by about 12%, while the anchor cable spacing needs to be strictly controlled to maximize the supporting effect of the anchor cables. However, the additional bending load from anchor cables on the pile body on the toppling rock side should be taken into consideration.
- (3)
- For the foundation pit side slope with a long longitudinal distance, the sectionalized support of the retaining pile could effectively restrict the deformation of the retaining structure and the range of rock landslides. Taking three times the spacing of piles as an example, the maximum displacement of the retaining piles in the bedding direction can be reduced by about 13% under the same spacing of piles.
- (4)
- On the basis of spatial effect support, the top of the foundation pit on the bedding rock side can be provided with a tie beam for overall reinforcement to maintain the integrity of the support structure. The tie beam can replace the anchor cable, and its support effect can reduce the maximum horizontal displacement by 13% compared with the pile anchor support in the toppling slope.
- (5)
- For the foundation pit side slope with sectionalized support, if the requirement of final displacement control on the bedding rock side could not be met, prestressed anchor cables could be set above the slip surface, which can further control the deformation of the pile body, while the toppling rock side slope can basically meet the maximum displacement requirements by adopting the sectionalized support design. At the same time, the spacing of piles in the bedding rock side can be extended by 0.5 times as that of the toppling side.
- (6)
- When using anti-sliding piles to divide the foundation pit section, it is necessary to calculate the stability against sliding of the anti-sliding piles so as to ensure that the integral damage will not occur.
- (7)
- From the results of monitoring and numerical simulation, the foundation pit of Sanhuan South Road Station is in a safe state. If the traditional pile-anchor support method is adopted, the spacing between piles can be enlarged by three times or the local stability can be improved by using the sectional support method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raghuvanshi, T.K. Plane failure in rock slopes—A review on stability analysis techniques. J. King Saud Univ. Sci. 2019, 31, 101–109. [Google Scholar] [CrossRef]
- Tang, H.; Yong, R.; Eldin, M.A.M.E. Stability analysis of stratified rock slopes with spatially variable strength parameters: The case of Qianjiangping landslide. Bull. Eng. Geol. Environ. 2017, 76, 839–853. [Google Scholar] [CrossRef]
- Kamaruszaman, N.; Jamaluddin, T.A. Rock slope stability assessment by using RMRB and SMR methods for future development around Gunung Lang, Ipoh, Perak. AIP Conf. Proc. 2016, 1784, 060029. [Google Scholar]
- Liu, T.; Liu, H. Design and construction of foundation pits in rock area in Qingdao. Chin. J. Geotech. Eng. 2010, 32, 499–503. [Google Scholar]
- Liu, J.; Zhang, D.; Liu, J. Stability analysis of a rock slope and optimized design of its support scheme. J. Water Resour. Archit. Eng. 2013, 11, 94–98. [Google Scholar]
- Bai, X.; Chen, X.; Zhang, M. “Pile—Steel Support—Anchor” System for Foundation in Rock-Soil Layer. Soil Mech. Found. Eng. 2019, 55, 425–432. [Google Scholar] [CrossRef]
- Liu, X.; Li, B. Analysis of Supporting Analysis of supporting mechanism of micro-steel-pipe piles in rock foundation pit. Rock Soil Mech. 2012, 33, 217–222. [Google Scholar]
- Hou, J.; Tang, Q.; Liu, J. Experimental study on super-deep rock foundation pit under complex environmental condition. Build. Struct. 2021, 51, 132–137. [Google Scholar]
- An, C.; Liang, Y.; Wang, L.; Deng, S.; Sun, Z.; Fan, B.; Zheng, L. Three-dimensional optimization design for the direction angle of anchor cable reinforcement in wedge rock slope. Rock Soil Mech. 2020, 41, 2765–2772. [Google Scholar]
- Zhou, Y.; Wang, X.; Zhu, Y.; Li, J.; Jiang, X. Monitoring and numerical simulation of an interbedding high slope composed of soft and hard strong-weathered rock. Rock Soil Mech. 2018, 39, 2249–2258. [Google Scholar]
- Li, J.; Liu, B.; Wang, Z.; Fan, G. Design and construction of deep foundation pit supporting in rock slop of Chongqing area. Constr. Technol. 2008, 37, 104–109. [Google Scholar]
- Li, J.; Peng, Z.; Li, Y.; Liu, M.F. Application of Bolt-shotcrete Support in Rock Slope Protecting. Soil Eng. Found. 2008, 22, 30–32. [Google Scholar]
- Chen, J.; Tang, H.; Li, X. Some problems on anchor-shotcrete reinforcement application in rock slop. Earth Sci. 2001, 26, 357–360. [Google Scholar]
- Chen, B.; Fan, Q.; Wei, G. Combined Application of Shotcrete-bolt and Pre-anchor Support in Rock Slope Engineering. Subgrade Eng. 2006, 3, 45–46. [Google Scholar]
- Xiao, J.; Zhong, Y.; Zhu, L. Support technology of deep foundation excavation in heavy miscellaneous fill-rock layers. Constr. Technol. 2013, 42, 59–62. [Google Scholar]
- Zhou, T.; Hua, Y. Stability analysis of layered cutting slope soil nailing support structure based on strength reduction method. Rock Soil Mech. 2008, 29, 417–420. [Google Scholar]
- Huang, D.; Ma, H.; Meng, Q.; Song, Y. Study on toppling mechanism and affecting factors of Anti-dip rock slopes with soft-hard interbedded structure. J. Eng. Geol. 2021, 29, 602–616. [Google Scholar]
- Yao, Y.; Zhang, G.; Chen, H.; Wang, M.; Bao, L.; Chang, Z. Study on the failure mechanisms of counter-tilt rock slopes with layered cataclastic structure. Chin. J. Rock Mech. Eng. 2021, 40, 365–381. [Google Scholar]
- Zheng, Y.; Zhao, S.; Deng, W. Numerical simulation on failure mechanism of rock slope by strength reduction FEM. Chin. J. Rock Mech. Eng. 2003, 22, 1943–1952. [Google Scholar]
- Zhang, H.; Zhu, D.; Wang, P.; Wen, H. Analysis of Deformation and Failure Mechanism of Bedding Rock Slope. Highway 2021, 66, 67–71. [Google Scholar]
- Raghuvanshi, T.K.; Ibrahim, J.; Ayalew, D. Slope stability susceptibility evaluation parameter (SSEP) rating scheme—An approach for landslide hazard zonation. J. Afr. Earth Sci. 2014, 99, 595–612. [Google Scholar] [CrossRef]
- Hamza, T.; Raghuvanshi, T.K. GIS based landslide hazard evaluation and zonation—A case from Jeldu District, Central Ethiopia. J. King Saud Univ. Sci. 2017, 29, 151–165. [Google Scholar] [CrossRef] [Green Version]
- Ilawe, N.V.; Zimmerman, J.A.; Wong, B.M. Breaking Badly: DFT-D2 gives sizeable errors for tensile strengths in palladium-hydride solids. J. Chem. Theory Comput. 2015, 11, 5426–5435. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Park, J.H.; Soon, A. Assessing the influence of van der Waals corrected exchange-correlation functionals on the anisotropic mechanical properties of coinage metals. Phys. Rev. B 2016, 94, 024108. [Google Scholar] [CrossRef] [Green Version]
- Abdellah, W.; Abdelhaffez, G.; Saleem, H. Stability assessment of underground openings using different rock support systems. Rudarsko-geološko-Naftni Zbornik 2019, 35, 49–63. [Google Scholar]
- Asker, K.; Fouad, M.T.; Bahr, M.; El-Attar, A. Numerical analysis of reducing tunneling effect on viaduct piles foundation by jet grouted wall. Min. Miner. Depos. 2021, 15, 75–86. [Google Scholar] [CrossRef]
- Liu, W.; Li, T.; Wan, J. Deformation Characteristic of a Supported Deep Excavation System: A Case Study in Red Sandstone Stratum. Appl. Sci. 2022, 12, 129. [Google Scholar] [CrossRef]
- Yang, X.H.; Wu, F.W.; Chen, T.; Liu, X. Analysis of Monitoring Results of a Deep Foundation Pit with Pile-Anchor Retaining Structure. Adv. Civil Ind. Eng. IV 2014, 580–583, 28–33. [Google Scholar] [CrossRef]
- Nehrii, S.; Nehrii, T.; Zolotarova, O.; Volkov, S. Investigation of the geomechanical state of soft adjoining rocks under protective constructions. Rudarsko-geološko-Naftni Zbornik 2021, 36, 61–71. [Google Scholar] [CrossRef]

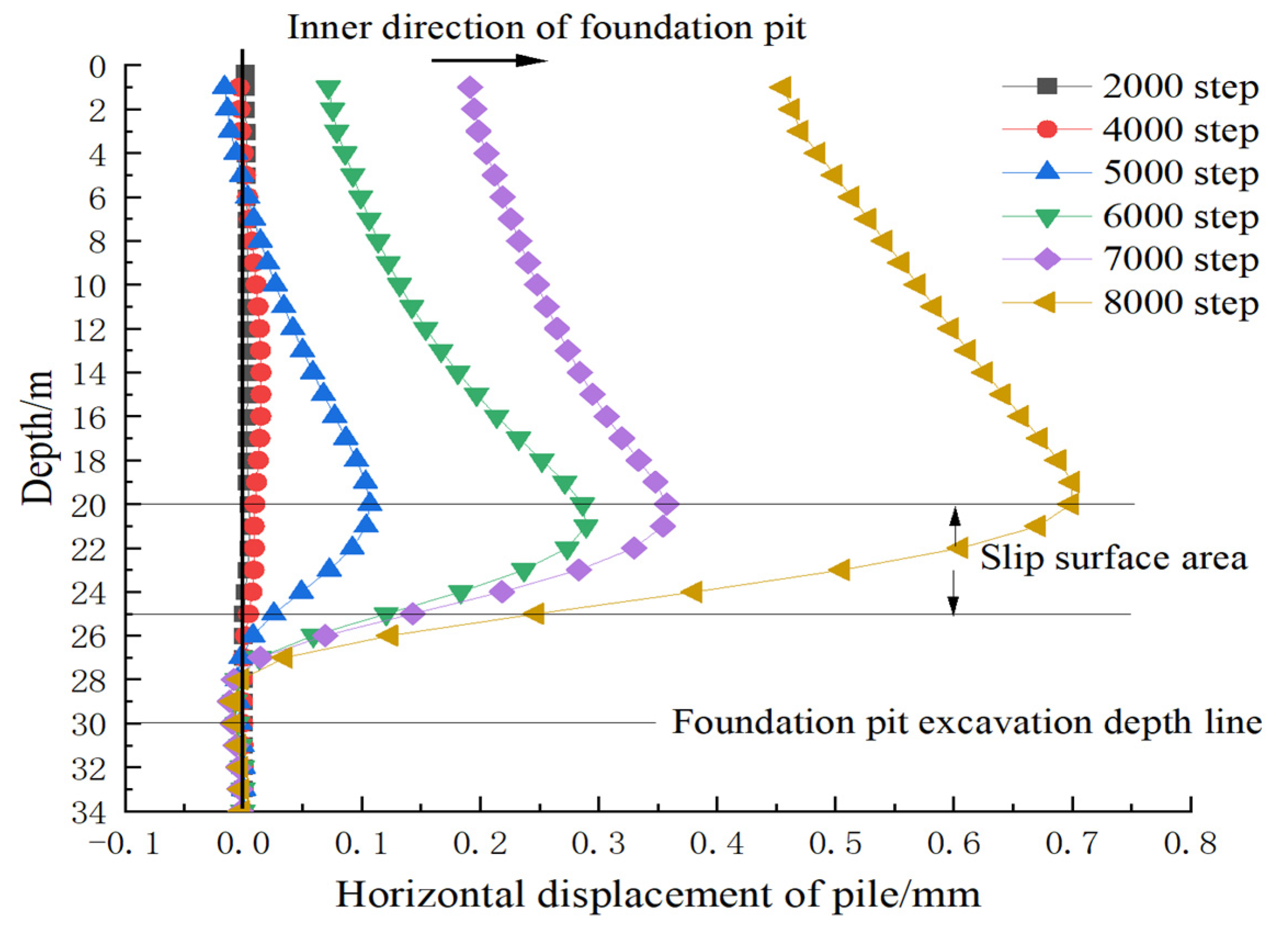
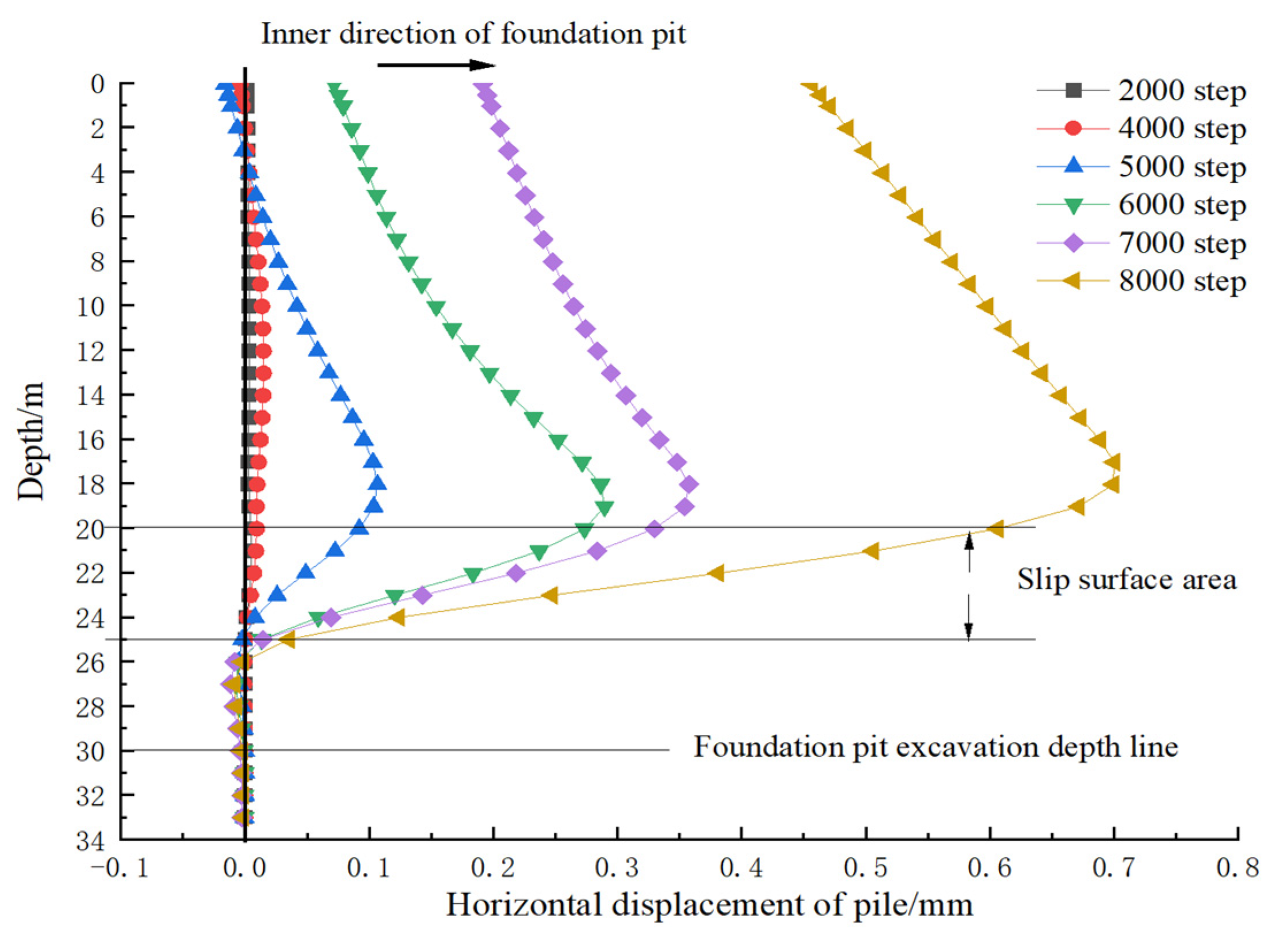

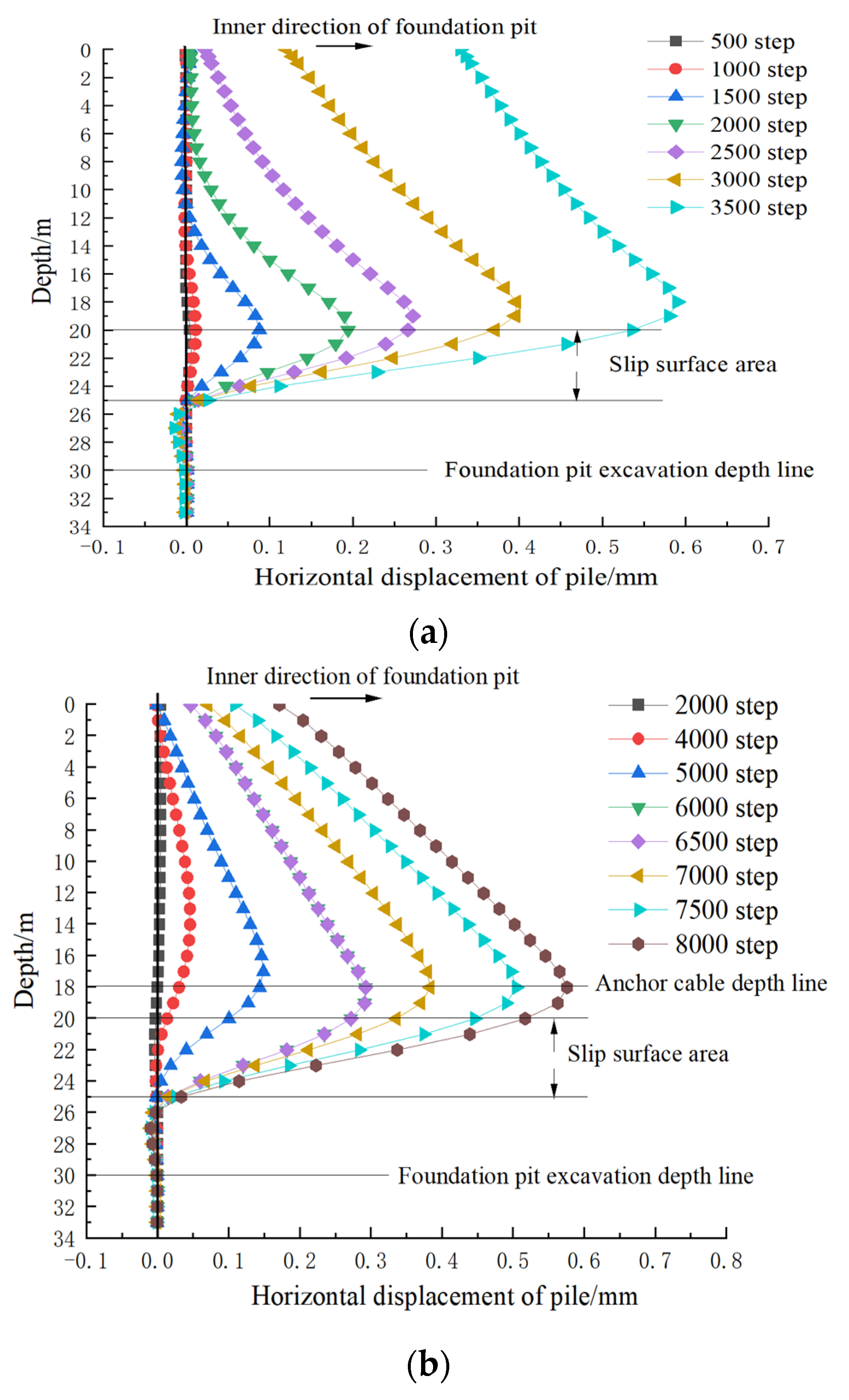
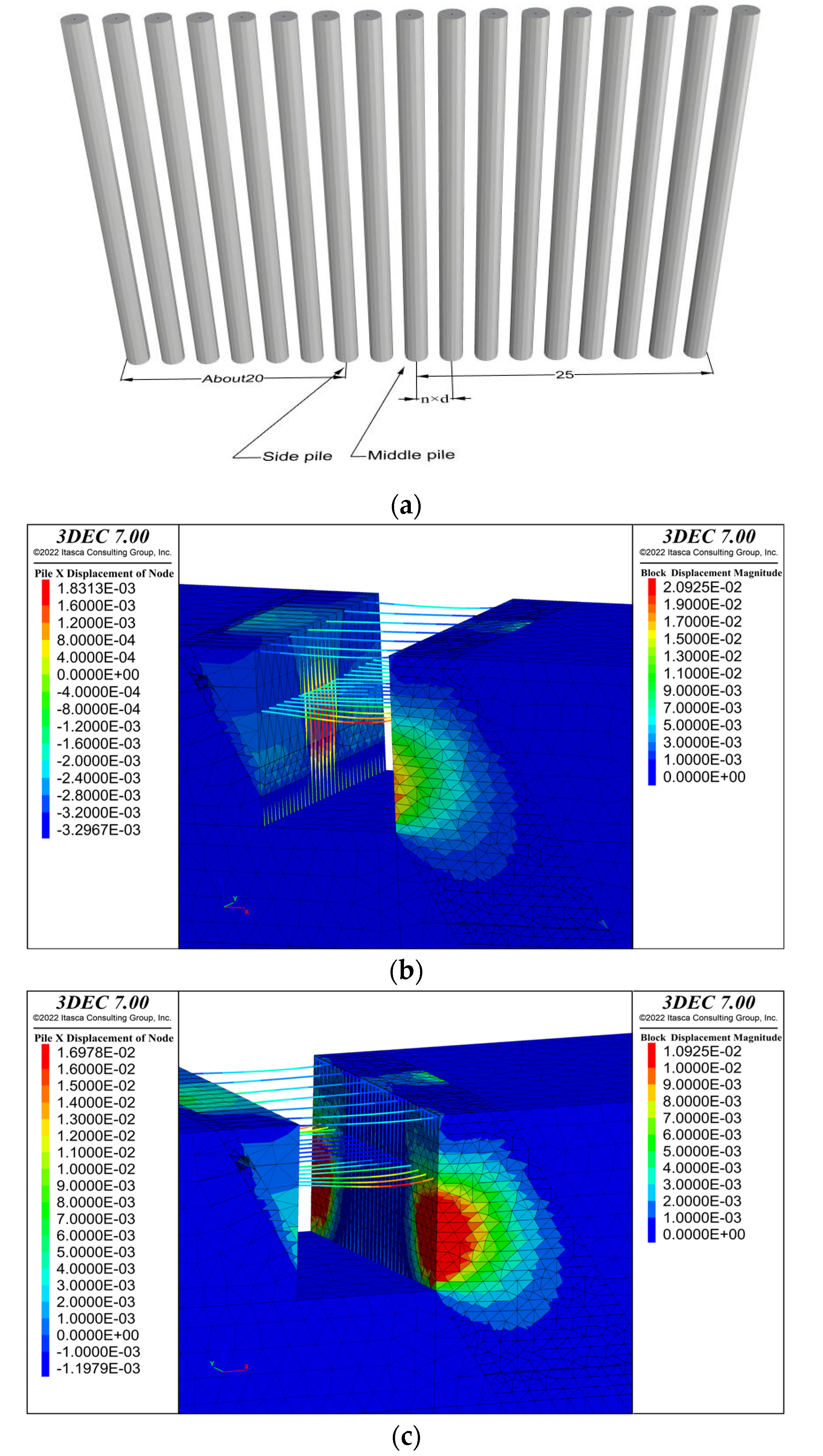
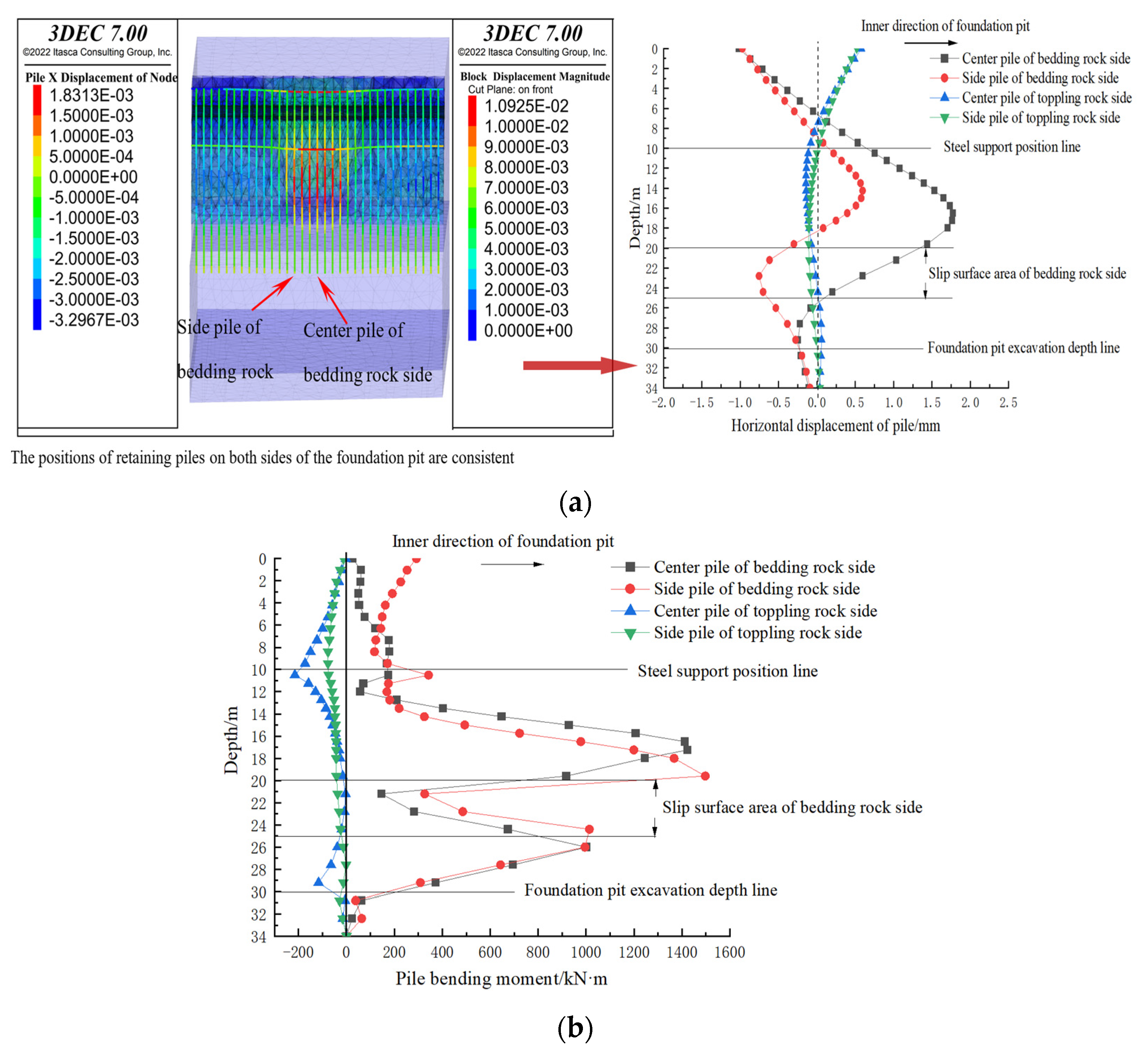
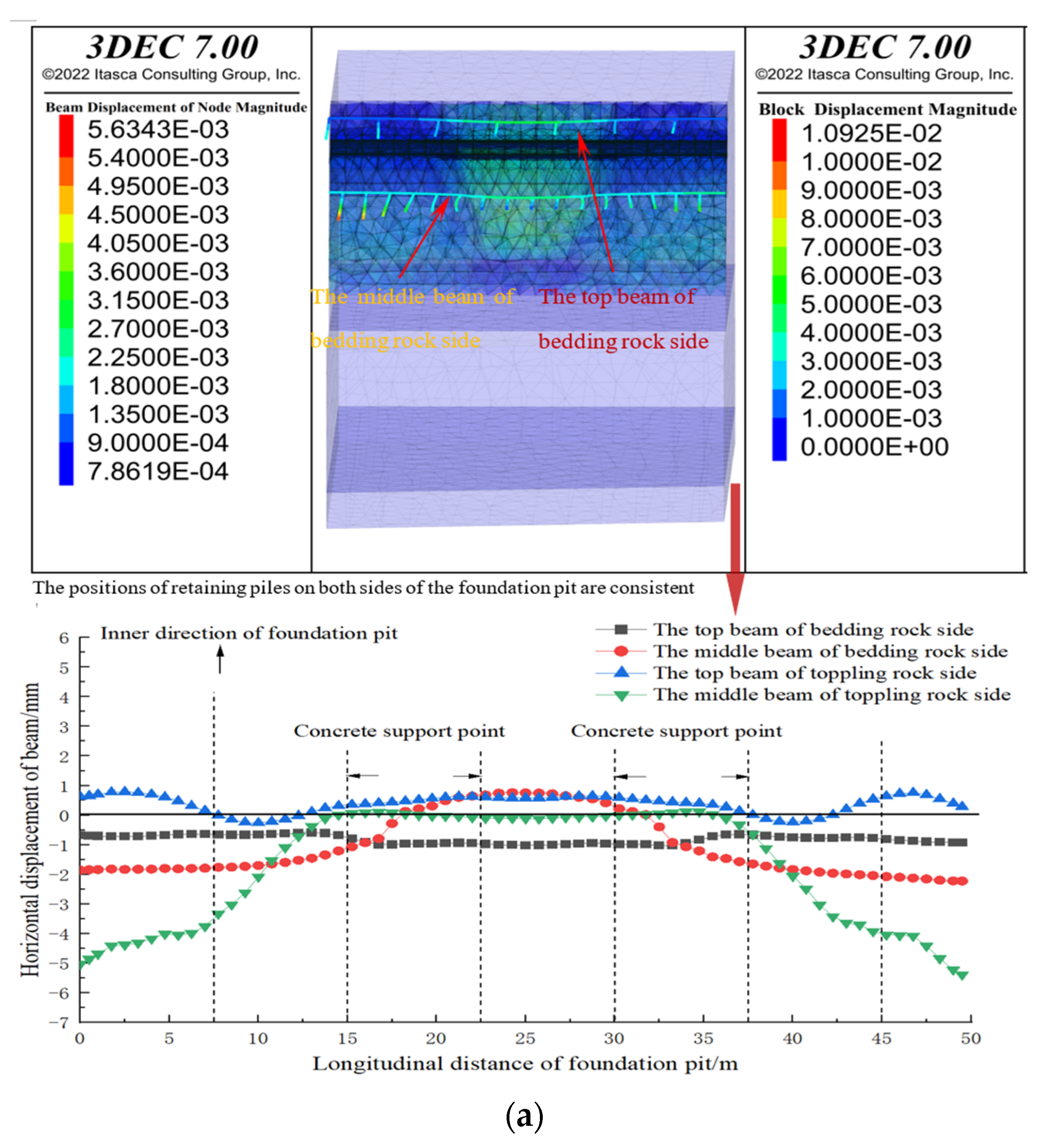
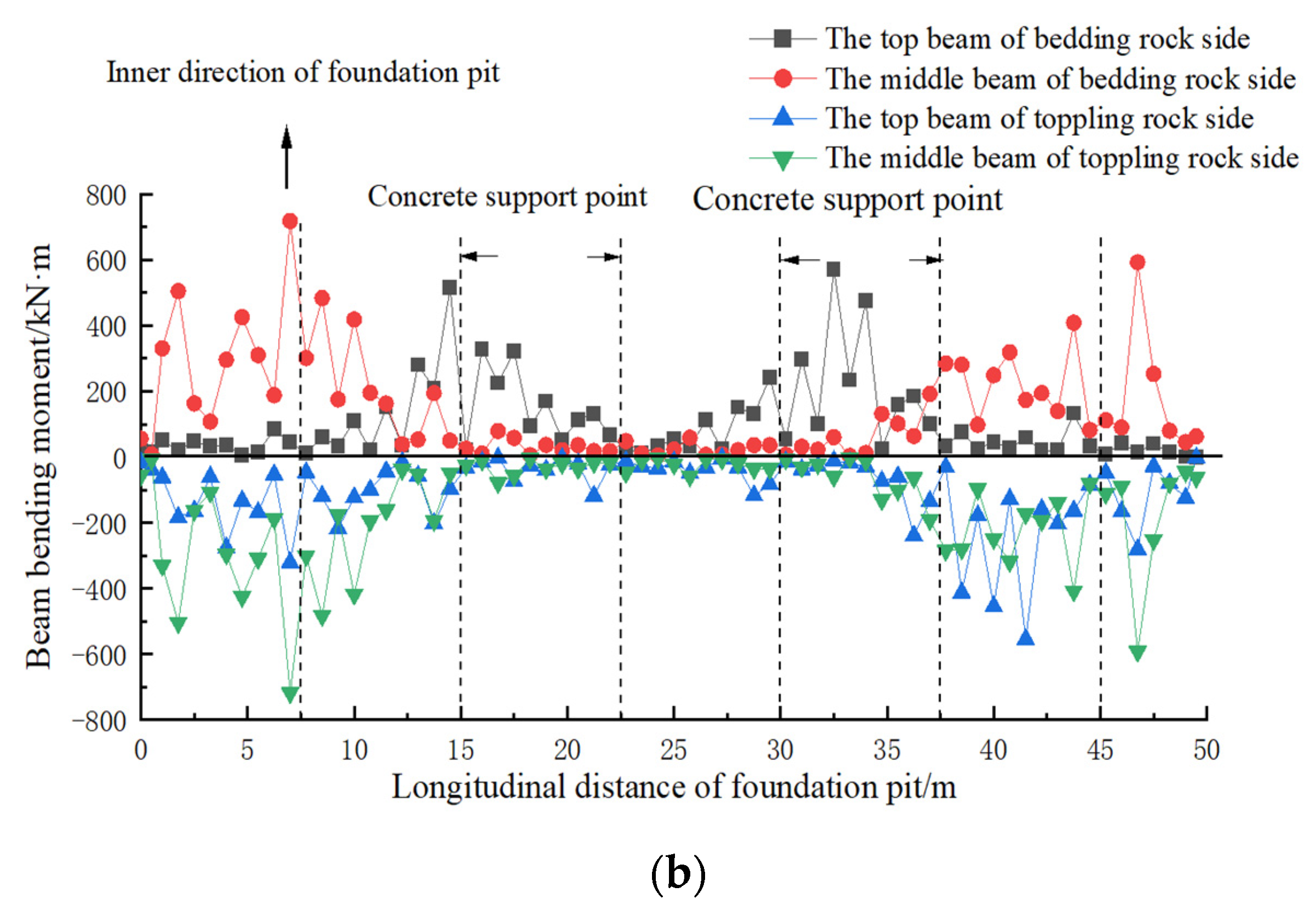

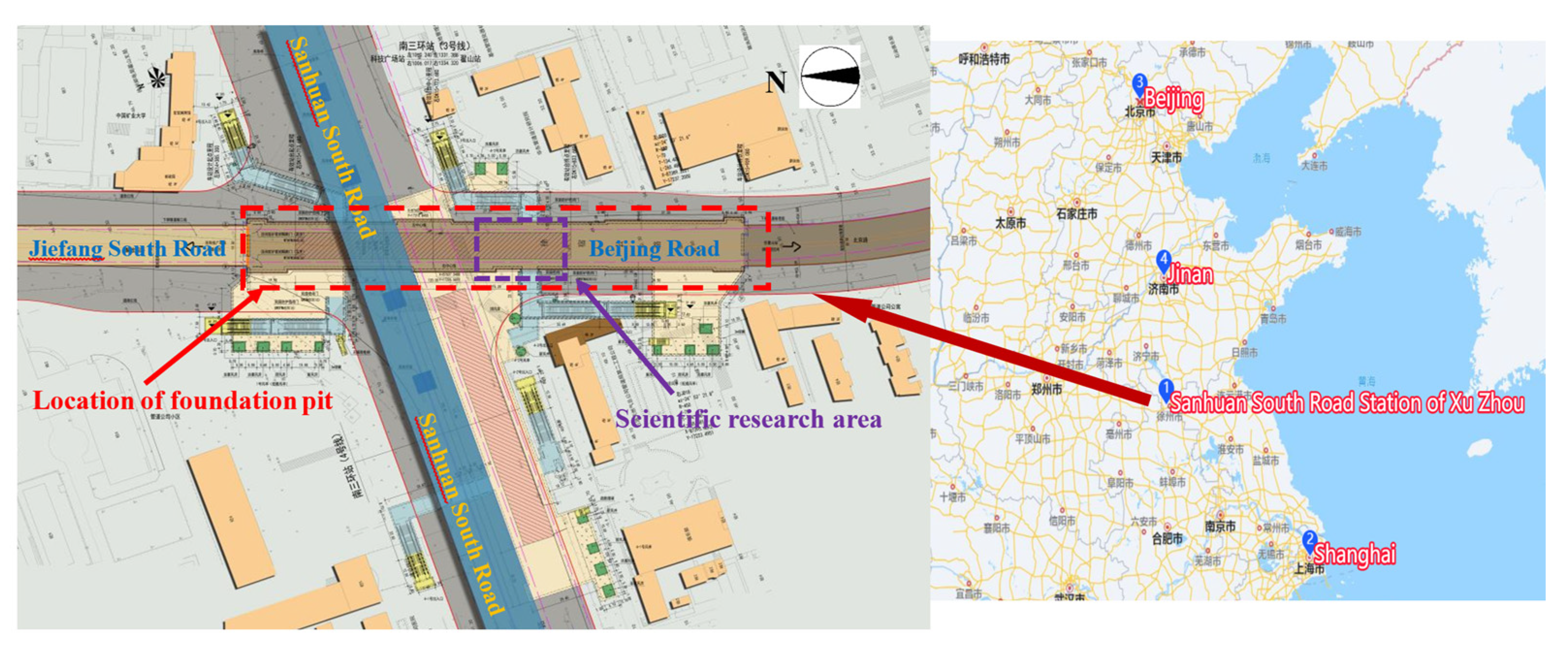





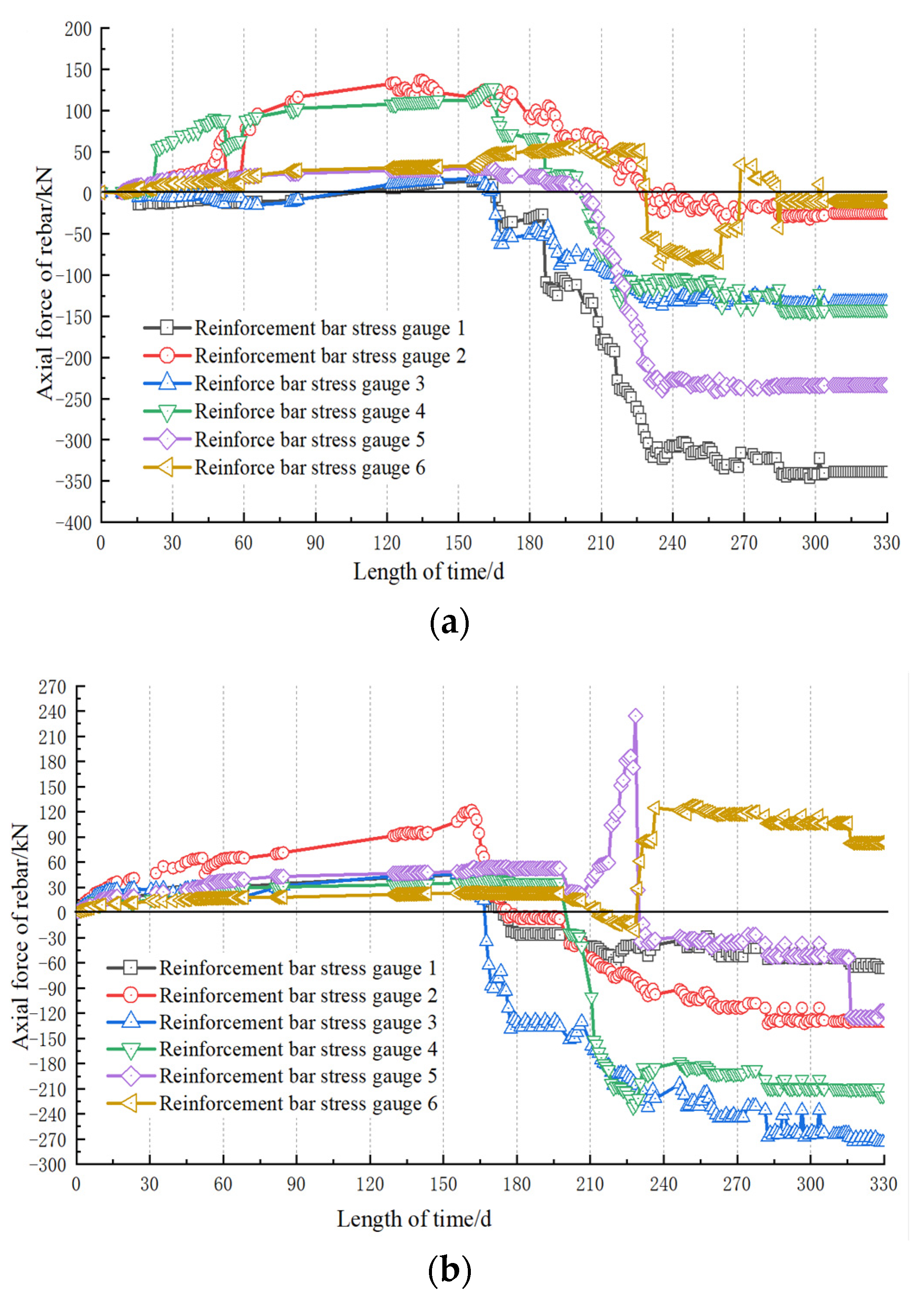
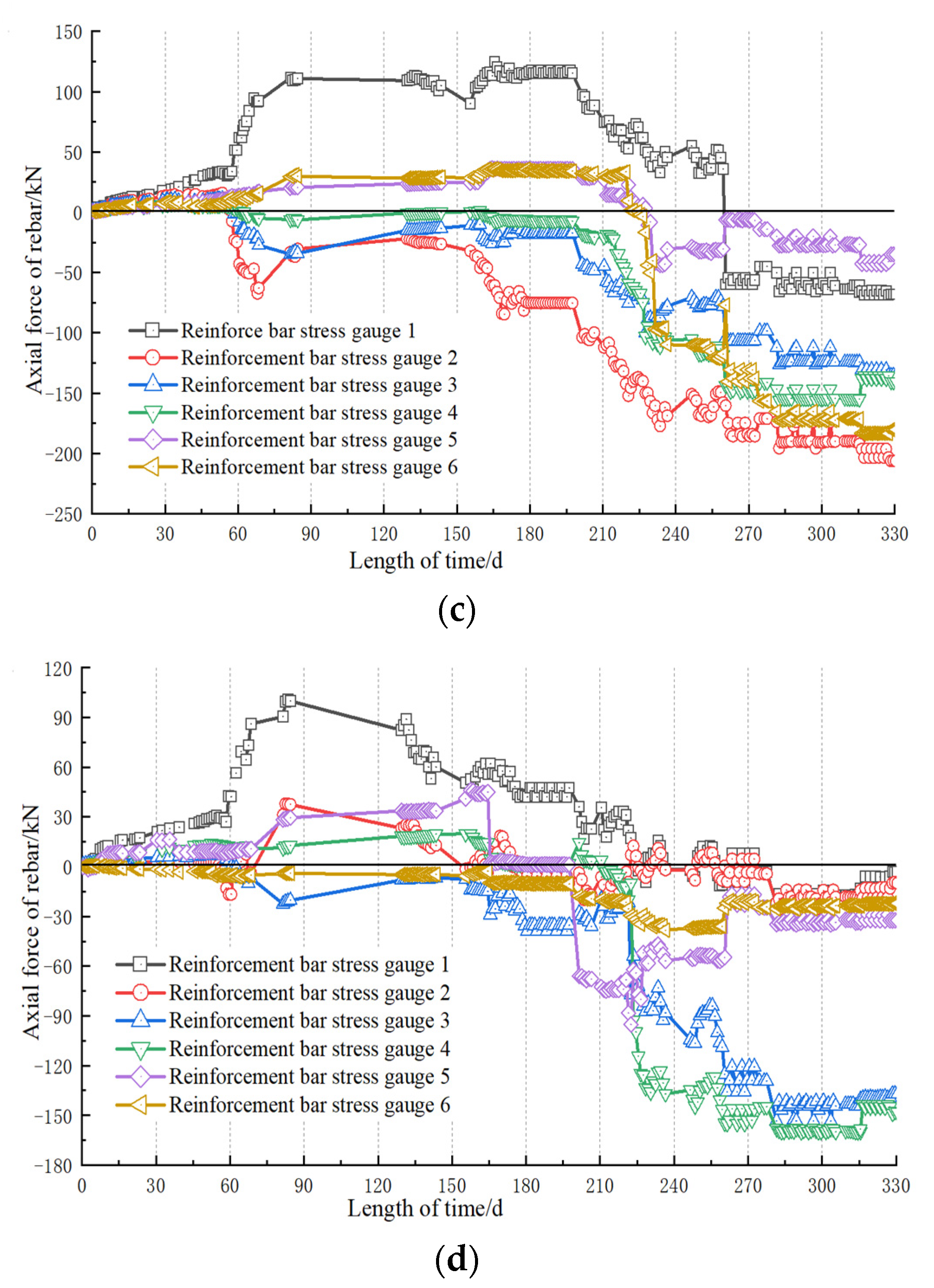

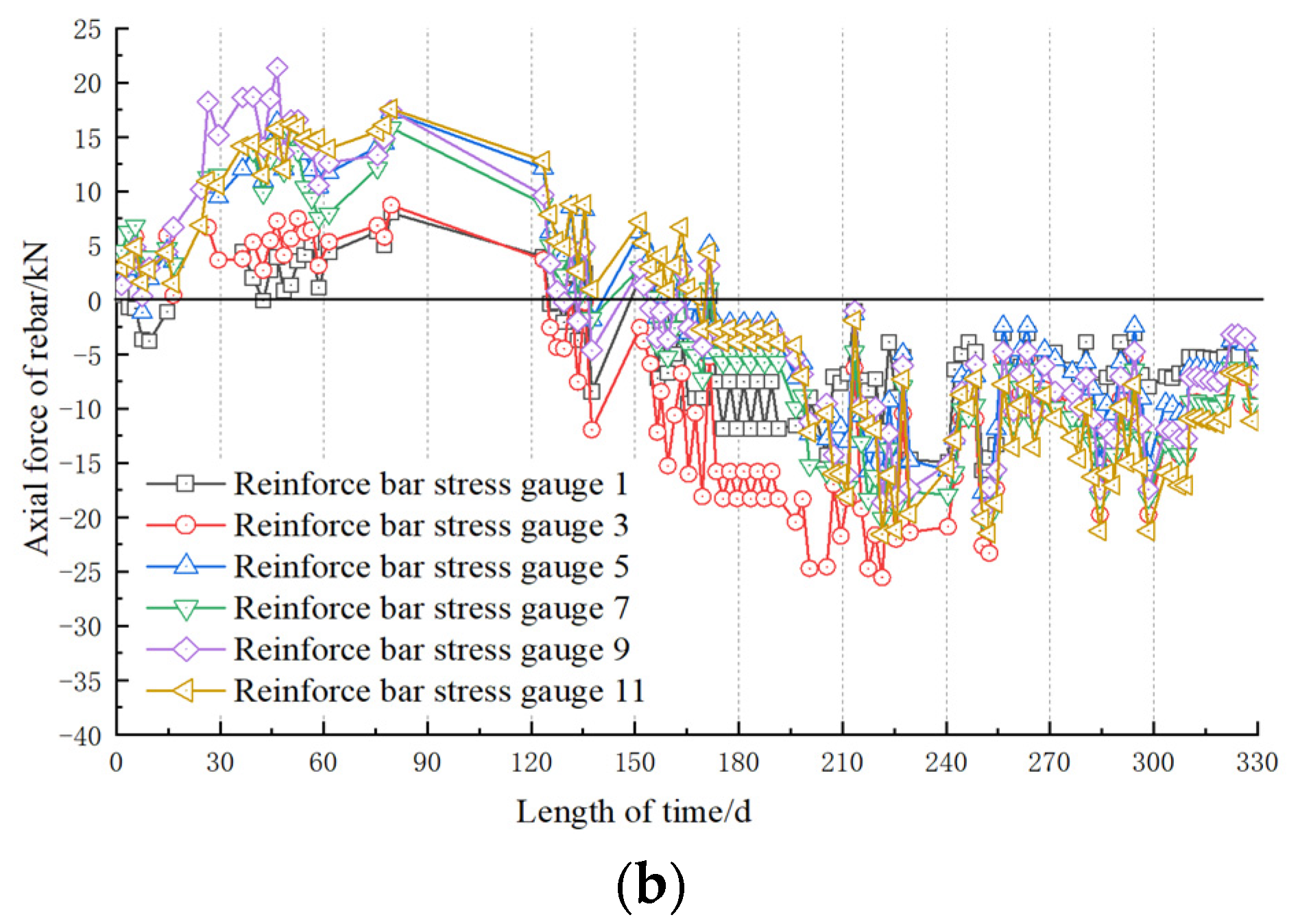


| Description | Density (kg/m³) | Young’s Modulus (Pa) | Poisson’s Ratio | Cohesion (Pa) | Internal Friction Angle (°) | Compressive Strength (Pa) |
|---|---|---|---|---|---|---|
| Limestone | 2300 | 21.0 × 109 | 0.22 | 3.0 × 106 | 30 | 1.0 × 106 |
| Description | Normal Stiffness (Pa) | Shear Stiffness (Pa) | Cohesion (Pa) | Angle of Internal Friction (°) | Compressive Strength (Pa) |
|---|---|---|---|---|---|
| Structural plane IV | 2.0 × 109 | 1.0 × 109 | 2.0 × 105 | 15 | 1.0 × 105 |
| Description | Density (kg/m³) | Young’s Modulus (Pa) | Poisson’s Ratio | Cohesion (Pa) | Internal Friction Angle (°) | Compressive Strength (Pa) |
|---|---|---|---|---|---|---|
| Limestone | 2680 | 21.18 × 109 | 0.17 | 3.0 × 106 | 34 | 1.0 × 106 |
| The Type of Support | The Basic Parameters | Basic Law of Displacement Increase/Decrease after Pile Spacing Change in Bedding Slope (on the Basis of the Previous Level) | ||
|---|---|---|---|---|
| The Pile Diameter (m) | Pile Spacing (Multiple of Pile Diameter) | Longitudinal Length of Model (m) | ||
| Pile-bracing | 1.0 | 1.5, 2.0, 3.0, 4.0 | 50 | 1.5 times to 2 times displacement increase by about 12.5%. 2 times to 3 times displacement increase by about 40%. 3 times to 4 times displacement increase by about 18%. |
| Pile-brace-anchor combination | 1.0 | 4.0 | 50 | Displacement is reduced by about 12% compared to 4.0 times of the pile-bracing structure. |
| Sectionalized support | 1.0 | 3.0 | 50 | Sparse-dense pile: displacement is reduced by about 14% compared with 3.0 times of pile-bracing. Sparse-dense pile and tie beam: displacement is reduced by 13% compared with 3.0 times of pile-bracing. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Wang, Y. Analysis of Slip Failure Characteristics and Support Deformation Law of Structural Planes and Rock Foundation Pits with Developed Karst Caves. Appl. Sci. 2022, 12, 4076. https://doi.org/10.3390/app12084076
Xu J, Wang Y. Analysis of Slip Failure Characteristics and Support Deformation Law of Structural Planes and Rock Foundation Pits with Developed Karst Caves. Applied Sciences. 2022; 12(8):4076. https://doi.org/10.3390/app12084076
Chicago/Turabian StyleXu, Jin, and Yansen Wang. 2022. "Analysis of Slip Failure Characteristics and Support Deformation Law of Structural Planes and Rock Foundation Pits with Developed Karst Caves" Applied Sciences 12, no. 8: 4076. https://doi.org/10.3390/app12084076
APA StyleXu, J., & Wang, Y. (2022). Analysis of Slip Failure Characteristics and Support Deformation Law of Structural Planes and Rock Foundation Pits with Developed Karst Caves. Applied Sciences, 12(8), 4076. https://doi.org/10.3390/app12084076






