Influence of Vegetation Filter Strip on Slope Runoff, Sediment Yield and Nutrient Loss
Abstract
:1. Introduction
2. Materials and Methods
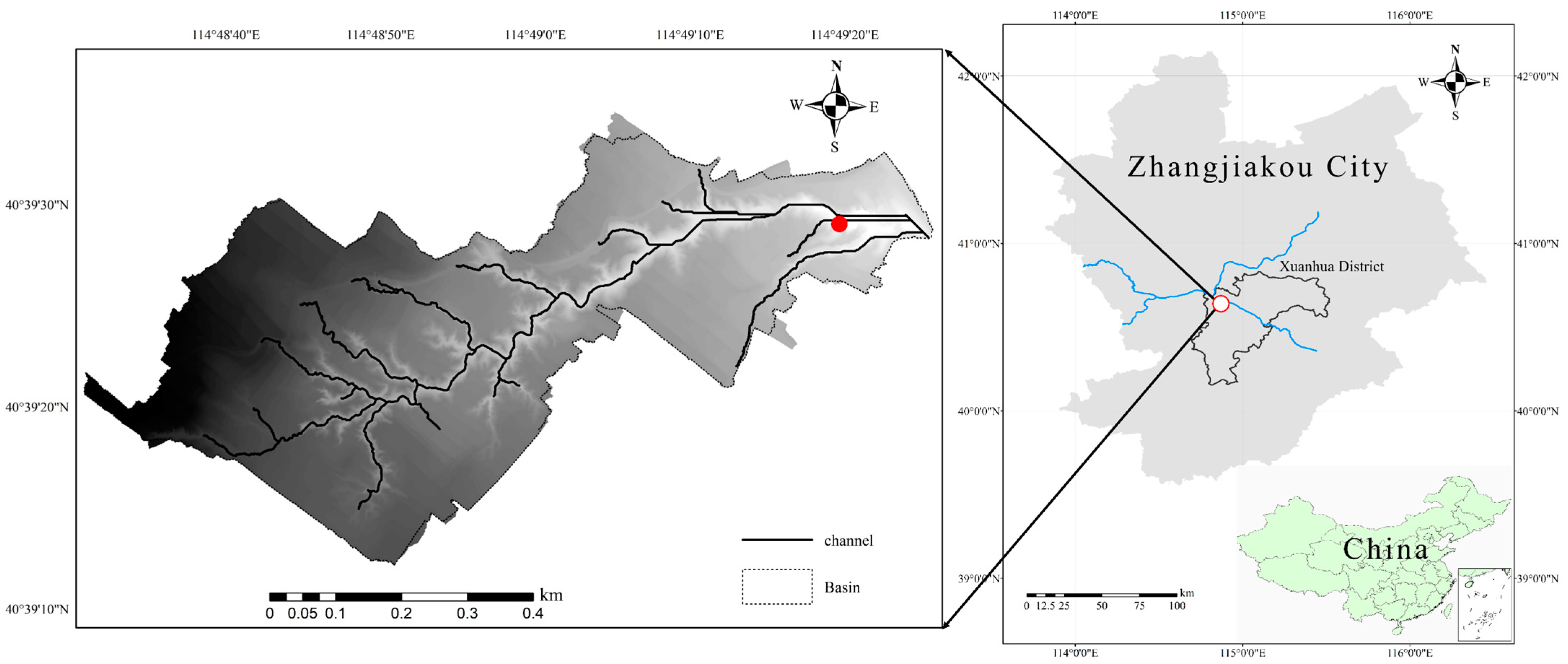
2.1. Study Area
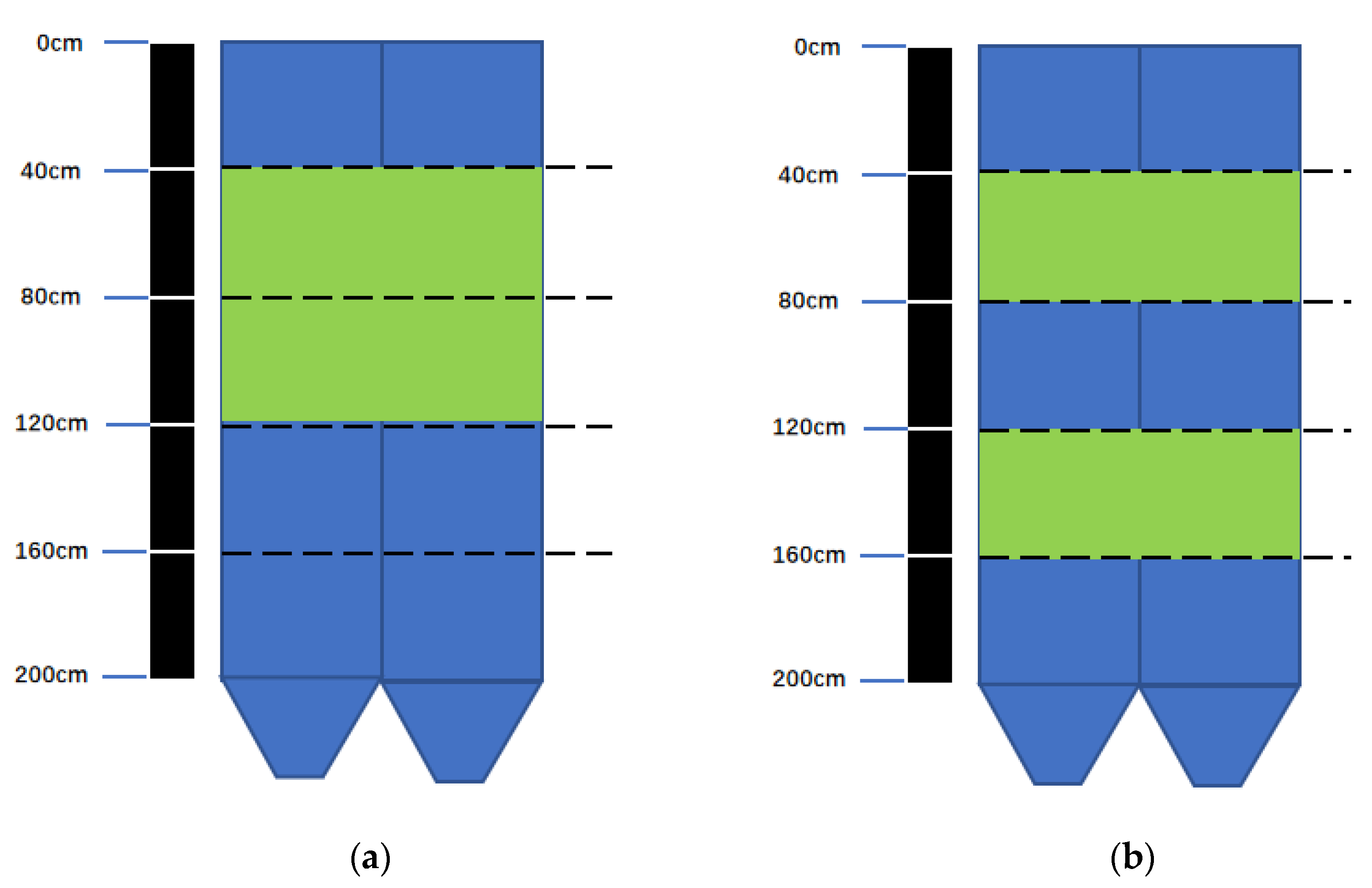
2.2. Experimental Design and Measurement
2.3. Data Analysis
2.3.1. Multiple Regressions
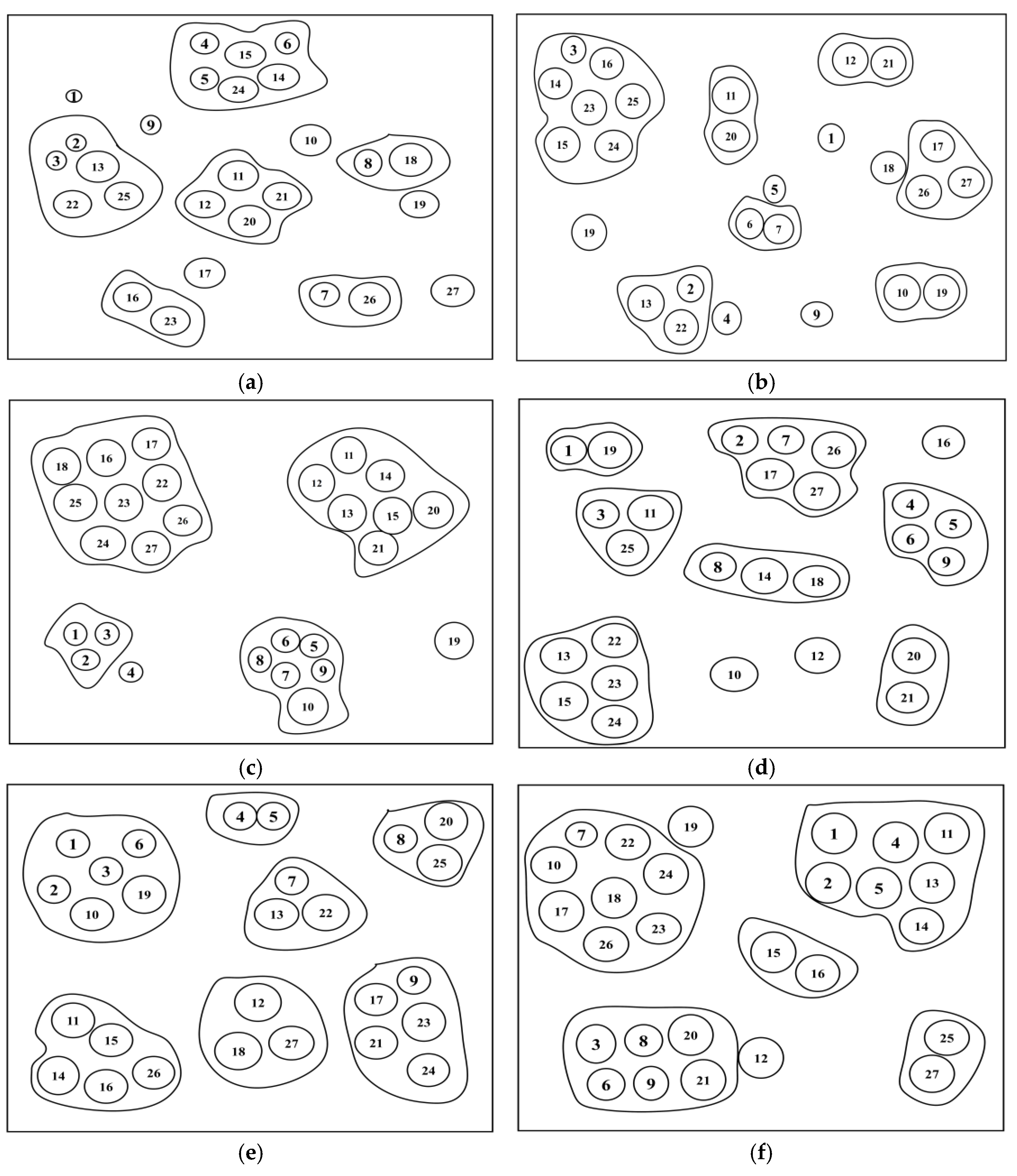
2.3.2. Cluster Analysis
3. Results
3.1. The Effects of VFS on Runoff Production and Sediment Yield
3.1.1. The Effects of the VFS on Runoff Production
3.1.2. The Effects of the VFS on Sediment Yield
3.2. The Effects of the VFS on Nutrient Loss
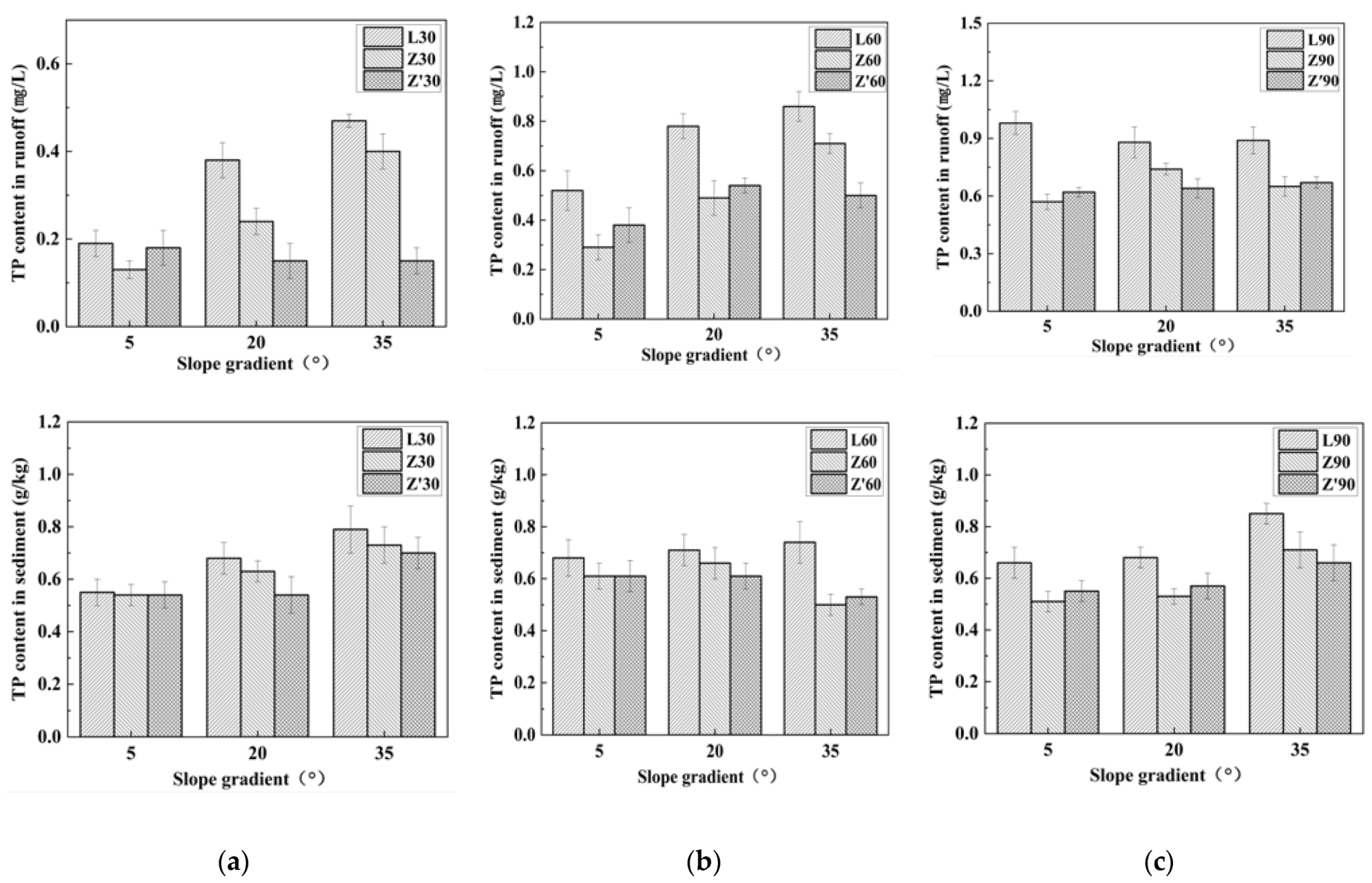
3.2.1. The Effects of the VFS on TP Loss
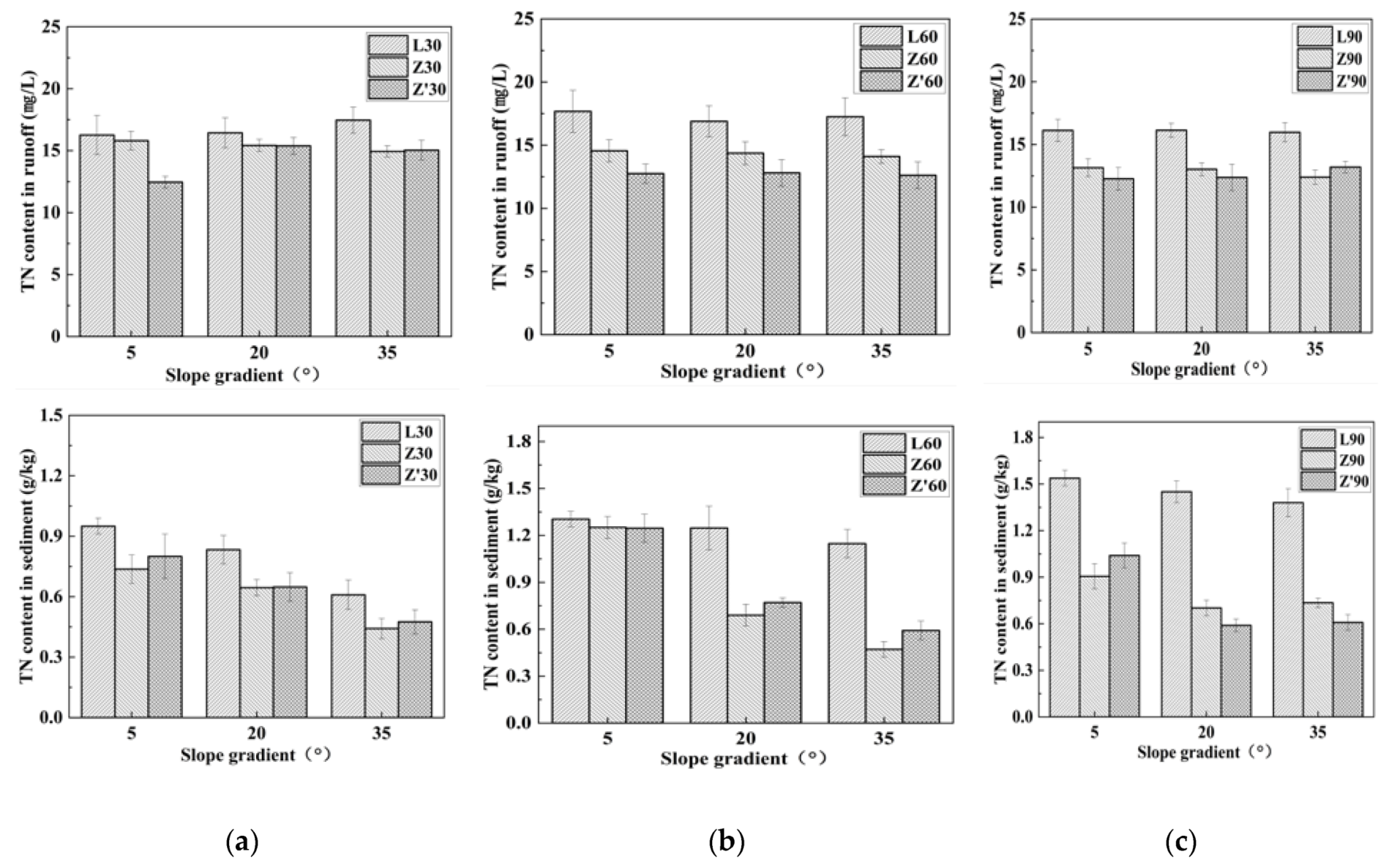
3.2.2. The Effects of the VFS on TN Loss
4. Discussion
4.1. Relationships between Erosion Indexes and Infuencing Factors
4.2. The Offset Effect of Influencing Factors on Erosion Control
5. Conclusions
- (1)
- For the slope area of eroded gully with severe soil erosion and loss, under the condition of certain width of vegetation filter strip, setting vegetation filter strip can effectively reduce soil erosion and nutrient loss on slope surface. However, the effect of the two setting modes of VFS was affected by rainfall intensity and slope gradient, and the best choice can be made under known meteorological and topographic conditions.
- (2)
- During the whole rainfall process, within the same time interval after the stable runoff yield, there were also great differences in runoff yield, sediment quantity and nutrient content, and the change of each index over time was not completely stable. This may be related to the change of slope topography during rainfall. However, it was possible to find the same variation trend of the same index in different combinations of rainfall intensity, slope gradient and vegetation coverage.
- (3)
- Multiple regression analysis was used to describe the correlation between vegetation, rainfall intensity and slope and erosion indexes. The three factors had significant effects on runoff sediment yield, TP loss in runoff and TN loss in sediment. There was no significant difference in the amount of runoff and sediment yield between the two vegetation setting modes. The TN loss in sediment on the bare land was mainly affected by the rainfall intensity, while the vegetation covered slope was affected by the slope gradient obviously. When the slope was covered with vegetation, rainfall intensity and slope had no significant effect on the content of TP loss in sediment.
- (4)
- Based on the heterogeneity analysis of data mining method, this study believed that the effects of rainfall intensity, slope gradient and vegetation setting mode on soil and water loss on slope can be equal or offset. In general, setting vegetation can offset the effect of rainfall intensity and slope gradient, but the effect of vegetation was not obvious under extreme conditions (heavy rainfall and steep slope), and it was also not obvious under light rainfall intensity, which may be due to the small amount of sediment yield, leading to little difference in various indicators. In some cases, the combined action of VFS and slope can offset the influence of rainfall intensity on soil erosion. In general, the influence of rainfall intensity was dominant in most cases.
- (5)
- This research mainly analyzed the correlation between rainfall intensity, slope and vegetation and erosion through multiple regression, and used cluster analysis to study the offsetting effect among the factors affecting erosion. However, the analysis in this research was limited by the experiment performed under restricted conditions. Future experiments may be carried out using other dominant plant species such as Salsola found in the study area, and investigation can be made to further explore the mutual influence or offset effect among the different factors on erosion control in subsequent studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Doulabian, S.; Toosi, A.S.; Calbimonte, G.H.; Tousi, E.G.; Alaghmand, S. Projected climate change impacts on soil erosion over Iran. J. Hydrol. 2021, 598, 126432. [Google Scholar] [CrossRef]
- Kervroëdan, L.; Armand, R.; Rey, F.; Faucon, M. Trait-based sediment retention and runoff control by herbaceous vegetation in agricultural catchments: A review. Land Degrad. Dev. 2021, 32, 1077–1089. [Google Scholar] [CrossRef]
- Safwan, M.; Alaa, K.; Omran, A.; Quoc, B.P.; Nguyen, T.T.L.; Van, N.T.; Duong, T.A.; Endre, H. Predicting soil erosion hazard in Lattakia Governorate (W Syria). Int. J. Sediment Res. 2021, 36, 207–220. [Google Scholar] [CrossRef]
- Francipane, A.; Fatichi, S.; Ivanov, V.Y.; Noto, L.V. Stochastic assessment of climate impacts on hydrology and geomorphology of semiarid headwater basins using a physically based model: Climate impact on semiarid basins. J. Geophys. Res. Earth Surf. 2015, 120, 507–533. [Google Scholar] [CrossRef] [Green Version]
- Mekonnen, M.; Keesstra, S.; Stroosnijder, L.; Baartman, J.; Maroulis, J. Soil Conservation through Sediment Trapping: A Review: Individual, Combined and Integrated Sediment Trapping. Land Degrad. Dev. 2015, 26, 544–556. [Google Scholar] [CrossRef]
- Prosdocimi, M.; Cerdà, A.; Tarolli, P. Soil water erosion on Mediterranean vineyards: A review. CATENA 2016, 141, 1–21. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Fox, G.A.; Sabbagh, G.J. Parameter Importance and Uncertainty in Predicting Runoff Pesticide Reduction with Filter Strips. J. Environ. Qual. 2010, 39, 630–641. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Grieneisen, M.L.; Zhang, M. Predicting pesticide removal efficacy of vegetated filter strips: A meta-regression analysis. Sci. Total Environ. 2016, 548–549, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Pan, D.; Gao, X.; Wang, J.; Yang, M.; Wu, P.; Huang, J.; Dyck, M.; Zhao, X. Vegetative filter strips-Effect of vegetation type and shape of strip on run-off and sediment trapping. Land Degrad. Dev. 2018, 29, 3917–3927. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, M.; Zhang, J. Beryllium-7 in vegetation, soil, sediment and runoff on the northern Loess Plateau. Sci. Total Environ. 2018, 626, 842–850. [Google Scholar] [CrossRef]
- Luo, M.; Pan, C.; Cui, Y.; Guo, Y.; Wu, Y. Effects of Different Aboveground Structural Parts of Grass Strips on the Sediment-Trapping Process. Sustainability 2021, 13, 7591. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, Z.; Xia, J.; Liang, Z.; Yang, J.; Chen, X.-A. Impact of grass traits on the transport path and retention efficiency of nitrate nitrogen in vegetation filter strips. Agric. Water Manag. 2021, 253, 106931. [Google Scholar] [CrossRef]
- Wang, T.; Fan, Y.; Xu, Z.; Kumar, S.; Kasu, B. Adopting cover crops and buffer strips to reduce nonpoint source pollution: Understanding farmers’ perspectives in the US Northern Great Plains. J. Soil Water Conserv. 2021, 76, 475–486. [Google Scholar] [CrossRef]
- Fox, G.; Muñoz-Carpena, R.; Purvis, R.A. Controlled laboratory experiments and modeling of vegetative filter strips with shallow water tables. J. Hydrol. 2018, 556, 1–9. [Google Scholar] [CrossRef]
- Flanagan, K.; Branchu, P.; Ramier, D.; Gromaire, M.-C. Evaluation of the relative roles of a vegetative filter strip and a biofiltration swale in a treatment train for road runoff. Water Sci. Technol. 2016, 75, 987–997. [Google Scholar] [CrossRef]
- Lambrechts, T.; François, S.; Lutts, S.; Muñoz-Carpena, R.; Bielders, C.L. Impact of plant growth and morphology and of sediment concentration on sediment retention efficiency of vegetative filter strips: Flume experiments and VFSMOD modeling. J. Hydrol. 2014, 511, 800–810. [Google Scholar] [CrossRef]
- Duan, J.; Liu, Y.-J.; Wang, L.-Y.; Yang, J.; Tang, C.-J.; Zheng, H.-J. Importance of grass stolons in mitigating runoff and sediment yield under simulated rainstorms. CATENA 2022, 213, 106132. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Ma, X. How biochar, horizontal ridge, and grass affect runoff phosphorus fractions and possible tradeoffs under consecutive rainstorms in loessial sloping land? Agric. Water Manag. 2021, 256, 107121. [Google Scholar] [CrossRef]
- Carluer, N.; Lauvernet, C.; Noll, D.; Muñoz-Carpena, R. Defining context-specific scenarios to design vegetated buffer zones that limit pesticide transfer via surface runoff. Sci. Total Environ. 2017, 575, 701–712. [Google Scholar] [CrossRef] [PubMed]
- García-Serrana, M.; Gulliver, J.; Nieber, J.L. Infiltration capacity of roadside filter strips with non-uniform overland flow. J. Hydrol. 2017, 545, 451–462. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Huang, J.; Wu, P.; Gao, X. The dynamic effects of pastures and crop on runoff and sediments reduction at loess slopes under simulated rainfall conditions. CATENA 2014, 119, 1–7. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, J.; Huang, Y.; Wang, G.; Zhang, M. Effects of Vegetation Stems on Hydraulics of Overland Flow Under Varying Water Discharges. Land Degrad. Dev. 2016, 27, 748–757. [Google Scholar] [CrossRef]
- Pan, D.; Gao, X.; Dyck, M.; Song, Y.; Wu, P.; Zhao, X. Dynamics of runoff and sediment trapping performance of vegetative filter strips: Run-on experiments and modeling. Sci. Total Environ. 2017, 593–594, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Gilley, J.E.; Eghball, B.; Kramer, L.A.; Moorman, T.B. Narrow Grass Hedge Effects on Runoff and Soil Loss. J. Soil Water Conserv. 2000, 55, 190–196. [Google Scholar] [CrossRef]
- Wu, J.Y.; Huang, D.; Teng, W.J.; Sardo, V.I. Grass hedges to reduce overland flow and soil erosion. Agron. Sustain. Dev. 2010, 30, 481–485. [Google Scholar] [CrossRef]
- Durán-Zuazo, V.H.; Pleguezuelo, C.R.; Panadero, L.A.; Raya, A.M.; Martínez, J.F.; Rodríguez, B.C. Soil Conservation Measures in Rainfed Olive Orchards in South-Eastern Spain: Impacts of Plant Strips on Soil Water Dynamics. Pedosphere 2009, 19, 453–464. [Google Scholar] [CrossRef]
- Lambrechts, T.; De Braekeleer, C.; Fautsch, V.; Iserentant, A.; Rentmeesters, G.; Lutts, S.; Bielders, C.L. Can vegetative filter strips efficiently trap trace elements during water erosion events? A flume experiment with contaminated sediments. Ecol. Eng. 2014, 68, 60–64. [Google Scholar] [CrossRef]
- Jianqiang, W.; Shenfa, H.; Yuchi, H.; Hongyang, W. Effects of pollutant loads and vegetation biomass of buffer strips on runoff purification. Chin. J. Environ. Eng. 2008, 2, 1425–1429. [Google Scholar]
- Blanco-Canqui, H.; Gantzer, C.J.; Anderson, S.H.; Alberts, E.E.; Thompson, A.L. Grass Barrier and Vegetative Filter Strip Effectiveness in Reducing Runoff, Sediment, Nitrogen, and Phosphorus Loss. Soil Sci. Soc. Am. J. 2004, 68, 1670–1678. [Google Scholar] [CrossRef]
- Dillaha, T.A.; Reneau, R.; Mostaghimi, S.; Lee, D. Vegetative Filter Strips for Agricultural Nonpoint Source Pollution Control. Trans. Am. Soc. Agric. Eng. 1989, 32, 0513–0519. [Google Scholar] [CrossRef]
- Li, H.; Deng, N.; Yang, Y.; Shi, D. Clarification Efficiency of Vegetative Filter Strips to Several Pollutants in Surface Runoff. Trans. Chin. Soc. Agric. Eng. 2010, 26, 81–86. [Google Scholar]
- She, D.L.; A., L.B.; Chen, Q.; Han, X. Effects of vegetative filter strip on overland flow nitrogen and phosphorus intercepting under different inflow conditions. J. Appl. Ecol. 2018, 29, 3425–3432. [Google Scholar]
- Klatt, S.; Kraus, D.; Kraft, P.; Breuer, L.; Wlotzka, M.; Heuveline, V.; Haas, E.; Kiese, R.; Butterbach-Bahl, K. Exploring impacts of vegetated buffer strips on nitrogen cycling using a spatially explicit hydro-biogeochemical modeling approach. Environ. Model. Softw. 2017, 90, 55–67. [Google Scholar] [CrossRef]
- Dosskey, M.; Helmers, M.; Eisenhauer, D. A design aid for determining width of filter strips. J. Soil Water Conserv. 2008, 63, 232–241. [Google Scholar] [CrossRef]
- Srivastava, A.N.; Kantardzie, M. Data Mining: Concepts, Models, Methods, and Algorithms. J. Comput. Inf. Sci. Eng. 2005, 5, 394–395. [Google Scholar] [CrossRef]
- Duchemin, M.; Hogue, R. Reduction in agricultural non-point source pollution in the first year following establishment of an integrated grass/tree filter strip system in southern Quebec (Canada). Agric. Ecosyst. Environ. 2009, 131, 85–97. [Google Scholar] [CrossRef]
- McDowell, R.; Sharpley, A.N. Soil phosphorus fractions in solution: Influence of fertiliser and manure, filtration and method of determination. Chemosphere 2001, 45, 737–748. [Google Scholar] [CrossRef]
- Wen, Y.F.; Gao, P.; Mu, X.M.; Zhao, G.J.; Sun, W.Y. Experimental Study on Runoff and Sediment Yield in Runoff Plot Under Field Simulated Rainfall Condition. Res. Soil Water Conserv. 2018, 25, 23–29. [Google Scholar] [CrossRef]
- Pan, C.; Ma, L.; Wainwright, J.; Shangguan, Z. Overland flow resistances on varying slope gradients and partitioning on grassed slopes under simulated rainfall. Water Resour. Res. 2016, 52, 2490–2512. [Google Scholar] [CrossRef] [Green Version]
- Otto, S.; Vianello, M.; Infantino, A.; Zanin, G.; Di Guardo, A. Effect of a full-grown vegetative filter strip on herbicide runoff: Maintaining of filter capacity over time. Chemosphere 2008, 71, 74–82. [Google Scholar] [CrossRef]
- Yang, F.S.; Cao, M.M.; Li, H.E.; Yang, X.D.; Sun, S.Z.; Zhang, H.M. Modeling the Sediment Retention Effect of the Vegetative Filter Strip Composed of Seabuckthorn-Shrub and Herbaceous Vegetation. J. Arid. Land Resour. Environ. 2017, 31, 71–75. [Google Scholar] [CrossRef]
- Schmitt, T.J.; Dosskey, M.G.; Hoagland, K.D. Filter Strip Performance and Processes for Different Vegetation, Widths, and Contaminants. Pap. Nat. Resour. 1999, 28, 1479–1489. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Zheng, F.; Wen, L.; Han, Y.; Hu, W. Impacts of rainfall intensity and slope gradient on rill erosion processes at loessial hillslope. Soil Tillage Res. 2016, 155, 429–436. [Google Scholar] [CrossRef]
- Qian, J.; Zhang, L.; Wang, W.; Liu, Q. Simulated Rainfall Experiment on the Nitrogen Loss in Sloping Vegetable Fields Under Different Conditions of Fertilization. J. Soil Water Conserv. 2015, 29, 248–253. [Google Scholar] [CrossRef]
- Han, D.; Deng, J.; Gu, C.; Mu, X.; Gao, P.; Gao, J. Effect of shrub-grass vegetation coverage and slope gradient on runoff and sediment yield under simulated rainfall. Int. J. Sediment Res. 2021, 36, 34–42. [Google Scholar] [CrossRef]
- Cerdan, O.; Govers, G.; Le Bissonnais, Y.; Van Oost, K.; Poesen, J.; Saby, N.; Gobin, A.; Vacca, A.; Quinton, J.; Auerswald, K.; et al. Rates and spatial variations of soil erosion in Europe: A study based on erosion plot data. Geomorphology 2010, 122, 167–177. [Google Scholar] [CrossRef]
- Hayat, W.; Khan, S.; Hayat, M.T.; Pervez, R.; Ahmad, S.; Iqbal, A. The effect of deforestation on soil quality in Lesser-Himalayan community forests of Abbottabad, Pakistan. Arab. J. Geosci. 2021, 14, 1919–1933. [Google Scholar] [CrossRef]
- Niu, X.-Y.; Wang, Y.-H.; Yang, H.; Zheng, J.-W.; Zou, J.; Xu, M.-N.; Wu, S.-S.; Xie, B. Effect of Land Use on Soil Erosion and Nutrients in Dianchi Lake Watershed, China. Pedosphere 2015, 25, 103–111. [Google Scholar] [CrossRef]
- Watson, D.A.; Laflen, J.M. Soil Strength, Slope, and Rainfall Intensity Effects on Interrill Erosion. Trans. ASAE 1986, 29, 0098–0102. [Google Scholar] [CrossRef]
- Akbarimehr, M.; Jalilvand, H. Considering the Relationship of Slope and Soil Loss on Skid Trails in the North of Iran (A Case Study). J. For. Sci. 2013, 78, 339–344. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Zhang, X.; Hu, X. Runoff and soil erosion as affected by plastic mulch patterns in vegetable field at Dianchi lake’s catchment, China. Agric. Water Manag. 2013, 122, 20–27. [Google Scholar] [CrossRef]
- Rose, C.W.; Hogarth, W.L.; Ghadiri, H.; Parlange, J.-Y.; Okom, A. Overland flow to and through a segment of uniform resistance. J. Hydrol. 2002, 255, 134–150. [Google Scholar] [CrossRef]
- Kemper, D.; Dabney, S.; Kramer, L.; Dominick, D.; Keep, T. Hedging against Erosion. J. Soil Water Conserv. 1992, 47, 284–288. [Google Scholar]
- Baudry, J.; Bunce, R.; Burel, F. Hedgerows: An international perspective on their origin, function and management. J. Environ. Manag. 2000, 60, 7–22. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, Q.; Wang, H.; Wu, J.; Yu, D. The effects of grass hedges and micro-basins on reducing soil and water loss in temperate regions: A case study of Northern China. Soil Tillage Res. 2012, 122, 22–35. [Google Scholar] [CrossRef]
- Hargrave, A.P.; Shaykewich, C.F. Rainfall induced nitrogen and phosphorus losses from Manitoba soils. Can. J. Soil Sci. 1997, 77, 59–65. [Google Scholar] [CrossRef]
- Dabney, S.; Liu, Z.; Lane, M.; Douglas, J.; Zhu, J.; Flanagan, D. Landscape benching from tillage erosion between grass hedges. Soil Tillage Res. 1999, 51, 219–231. [Google Scholar] [CrossRef]
- Bhattarai, R.; Kalita, P.K.; Patel, M.K. Nutrient transport through a Vegetative Filter Strip with subsurface drainage. J. Environ. Manag. 2009, 90, 1868–1876. [Google Scholar] [CrossRef]
- Andraski, B.J.; Mueller, D.H.; Daniel, T.C. Phosphorus Losses in Runoff as Affected by Tillage. Soil Sci. Soc. Am. J. 1985, 49, 1523–1527. [Google Scholar] [CrossRef]
- Snyder, J.K.; Woolhiser, D.A. Effects of Infiltration on Chemical Transport into Overland Flow. Trans. ASAE 1985, 28, 1450–1457. [Google Scholar] [CrossRef]
- Wei, W.S.; Tong, J.X.; Yang, R.; Zhang, X.W.; Yun, L.J. Experimental Study on the Migration of Solutes in Soil Under Simulated Rainfall. China Rural. Water Hydropower 2016, 9, 168–173. [Google Scholar] [CrossRef]
- Campo-Bescós, M.A.; Muñoz-Carpena, R.; Kiker, G.A.; Bodah, B.W.; Ullman, J.L. Watering or buffering? Runoff and sediment pollution control from furrow irrigated fields in arid environments. Agric. Ecosyst. Environ. 2015, 205, 90–101. [Google Scholar] [CrossRef] [Green Version]
- Meng, Q.; Fu, B.; Tang, X.; Ren, H. Effects of land use on phosphorus loss in the hilly area of the Loess Plateau, China. Environ. Monit. Assess. 2008, 139, 195–204. [Google Scholar] [CrossRef]
- Kuo, Y.-M.; Muñoz-Carpena, R. Simplified modeling of phosphorus removal by vegetative filter strips to control runoff pollution from phosphate mining areas. J. Hydrol. 2009, 378, 343–354. [Google Scholar] [CrossRef]
- Lovell, S.T.; Sullivan, W.C. Environmental benefits of conservation buffers in the United States: Evidence, promise, and open questions. Agric. Ecosyst. Environ. 2006, 112, 249–260. [Google Scholar] [CrossRef]



| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Rain intensity mm/h | 30 | 60 | 90 | 30 | 60 | 90 | 30 | 60 | 90 |
| Vegetation coverage type | L | L | L | Z | Z | Z | Z′ | Z′ | Z′ |
| Vegetation Coverage Type | Rainfall Intensity (mm/h) | TP in Runoff (mg) | TP in Sediment (g) | TN in Runoff (mg) | TN in Sediment (g) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope (°) | Slope (°) | Slope (°) | Slope (°) | ||||||||||
| 5 | 20 | 35 | 5 | 20 | 35 | 5 | 20 | 35 | 5 | 20 | 35 | ||
| L | 30 | 1.017 | 4.978 | 6.450 | 0.002 | 0.009 | 0.029 | 99.279 | 226.009 | 245.110 | 0.004 | 0.004 | 0.004 |
| 60 | 8.475 | 15.503 | 18.332 | 0.012 | 0.051 | 0.071 | 308.764 | 339.164 | 362.296 | 0.011 | 0.011 | 0.011 | |
| 90 | 30.438 | 37.812 | 42.738 | 0.074 | 0.299 | 0.624 | 499.226 | 721.918 | 765.869 | 0.023 | 0.023 | 0.023 | |
| Z | 30 | 0.469 | 1.640 | 2.978 | 0.001 | 0.004 | 0.018 | 59.306 | 99.326 | 110.360 | 0.023 | 0.023 | 0.023 |
| 60 | 4.049 | 9.538 | 13.878 | 0.008 | 0.028 | 0.029 | 198.789 | 271.852 | 272.594 | 0.090 | 0.090 | 0.090 | |
| 90 | 8.984 | 17.377 | 25.208 | 0.027 | 0.131 | 0.250 | 197.454 | 320.725 | 483.819 | 0.108 | 0.108 | 0.108 | |
| Z’ | 30 | 0.577 | 1.277 | 1.304 | 0.001 | 0.004 | 0.022 | 43.015 | 119.691 | 128.178 | 0.169 | 0.169 | 0.169 |
| 60 | 5.500 | 8.608 | 9.463 | 0.007 | 0.028 | 0.030 | 182.819 | 208.062 | 257.174 | 0.681 | 0.681 | 0.681 | |
| 90 | 8.307 | 19.405 | 24.234 | 0.026 | 0.144 | 0.196 | 159.286 | 379.565 | 471.516 | 1.040 | 1.040 | 1.040 | |
| Erosion Index | Regression Equation | Determination Coefficient R2 | p Value | N |
|---|---|---|---|---|
| Sediment (g) | Y = −288.547 + 4.478 × R + 5.229 × S + 86.496 × V0 + 2.516 × V1 | 0.617 | 0.000 | 54 |
| Runoff (L) | Y = −13.743 + 0.387 × R + 0.348 × S + 7.422 × V0 – 0.035 × V1 | 0.850 | 0.000 | 54 |
| TP in runoff (mg/L) | Y = −0.172 + 0.008 × R + 0.006 × S + 0.223 × V0 + 0.044 × V1 | 0.839 | 0.000 | 54 |
| TP in sediment (g/kg) | Y = 0.510 + 0.004 × S + 0.118 × V0 + 0.020 × V1 | 0.434 | 0.000 | 54 |
| TN in runoff (mg/L) | Y = 14.769−0.028 × R + 0.011 × S + 3.454 × V0 + 0.812 × V1 | 0.697 | 0.000 | 54 |
| TN in sediment (g/kg) | Y = 0.675 + 0.005 × R – 0.012 × S + 0.413 × V0 – 0.014 × V1 | 0.714 | 0.000 | 54 |
| Erosion Index | Vegetation Coverage Type | Mean | Regression Equation | Determination Coefficient R2 | p Value | N |
|---|---|---|---|---|---|---|
| Sediment (g) | L | 171.232 a | Y = −416.856 + 7.100 × R + 8.323 × S | 0.682 | 0.000 | 18 |
| Z | 87.252 b | Y = −193.807 + 3.399 × R + 3.938 × S | 0.706 | 0.000 | 18 | |
| Z’ | 84.736 b | Y = −180.704 + 3.255 × R + 3.661 × S | 0.700 | 0.000 | 18 | |
| Runoff (L) | L | 23.882 a | Y = −11.687 + 0.504 × R + 0.306 × S | 0.893 | 0.000 | 18 |
| Z | 16.425 b | Y = −11.157 + 0.347 × R + 0.377 × S | 0.858 | 0.000 | 18 | |
| Z’ | 16.460 b | Y = −10.784 + 0.336 × R + 0.388 × S | 0.868 | 0.000 | 18 | |
| TP in runoff (mg/L) | L | 0.648 a | Y = −0.040 + 0.010 × R + 0.006 × S | 0.865 | 0.000 | 18 |
| Z | 0.469 b | Y = −0.085 + 0.007 × R + 0.009 × S | 0.878 | 0.000 | 18 | |
| Z’ | 0.425 c | Y = −0.067 + 0.008 × R +0.001 × S | 0.942 | 0.000 | 18 | |
| TP in sediment (g/kg) | L | 0.701 a | Y = 0.583 + 0.001 × R + 0.005 × S | 0.626 | 0.001 | 18 |
| Z | 0.603 b | Y = 0.599 – 0.001 × R + 0.004 × S | 0.284 | 0.081 | 18 | |
| Z’ | 0.583 b | Y = 0.572 + 0.000 × R + 0.002 × S | 0.212 | 0.168 | 18 | |
| TN in runoff (mg/L) | L | 16.754 a | Y = 18.224 – 0.017 × R + 0.003 × S | 0.216 | 0.161 | 18 |
| Z | 14.112 b | Y = 17.334 – 0.042 × R−0.019 × S | 0.910 | 0.000 | 18 | |
| Z’ | 13.300 b | Y = 14.448 – 0.027 × R + 0.040 × S | 0.471 | 0.008 | 18 | |
| TN in sediment (g/kg) | L | 1.165 a | Y = 0.656 + 0.011 × R – 0.006 × S | 0.930 | 0.000 | 18 |
| Z | 0.739 b | Y = 0.856 + 0.003 × R – 0.013 × S | 0.628 | 0.001 | 18 | |
| Z’ | 0.752 b | Y = 1.020 + 0.002 × R – 0.016 × S | 0.696 | 0.000 | 18 |
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rainfall intensity (mm/h) | 30 | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||||
| 60 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||||
| 90 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||||
| Slope gradient (°) | 5 | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||||
| 20 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||||
| 35 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||||
| Vegetation coverage type | L | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||||
| Z | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||||
| Z′ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Meng, Q.; You, Q.; Huang, T.; Zhang, X. Influence of Vegetation Filter Strip on Slope Runoff, Sediment Yield and Nutrient Loss. Appl. Sci. 2022, 12, 4129. https://doi.org/10.3390/app12094129
Zhang H, Meng Q, You Q, Huang T, Zhang X. Influence of Vegetation Filter Strip on Slope Runoff, Sediment Yield and Nutrient Loss. Applied Sciences. 2022; 12(9):4129. https://doi.org/10.3390/app12094129
Chicago/Turabian StyleZhang, Huayong, Qiang Meng, Qinjing You, Tousheng Huang, and Xiumin Zhang. 2022. "Influence of Vegetation Filter Strip on Slope Runoff, Sediment Yield and Nutrient Loss" Applied Sciences 12, no. 9: 4129. https://doi.org/10.3390/app12094129
APA StyleZhang, H., Meng, Q., You, Q., Huang, T., & Zhang, X. (2022). Influence of Vegetation Filter Strip on Slope Runoff, Sediment Yield and Nutrient Loss. Applied Sciences, 12(9), 4129. https://doi.org/10.3390/app12094129







