Avoiding Obstacles via Missile Real-Time Inference by Reinforcement Learning

Abstract

In the contemporary battlefield where complexity has increased, the enhancement of the role and ability of missiles has become crucial. Thus, missile guidance systems are required to be further developed in a more intelligent and autonomous way to deal with complicated environments. In this paper, we propose novel missile guidance laws using reinforcement learning, which can autonomously avoid obstacles and terrains in complicated environments with limited prior information and even without the need of off-line trajectory or waypoint generation. The proposed guidance laws are focused on two mission scenarios: the first is with planar obstacles, which is used to cope with maritime operations, and the second is with complex terrain, which is used to cope with land operations. We present the detailed design processes for both scenarios, including a neural network architecture, reward function selection, and training method. Simulation results are provided to show the feasibility and effectiveness of the proposed guidance laws and some important aspects are discussed in terms of their advantages and limitations.

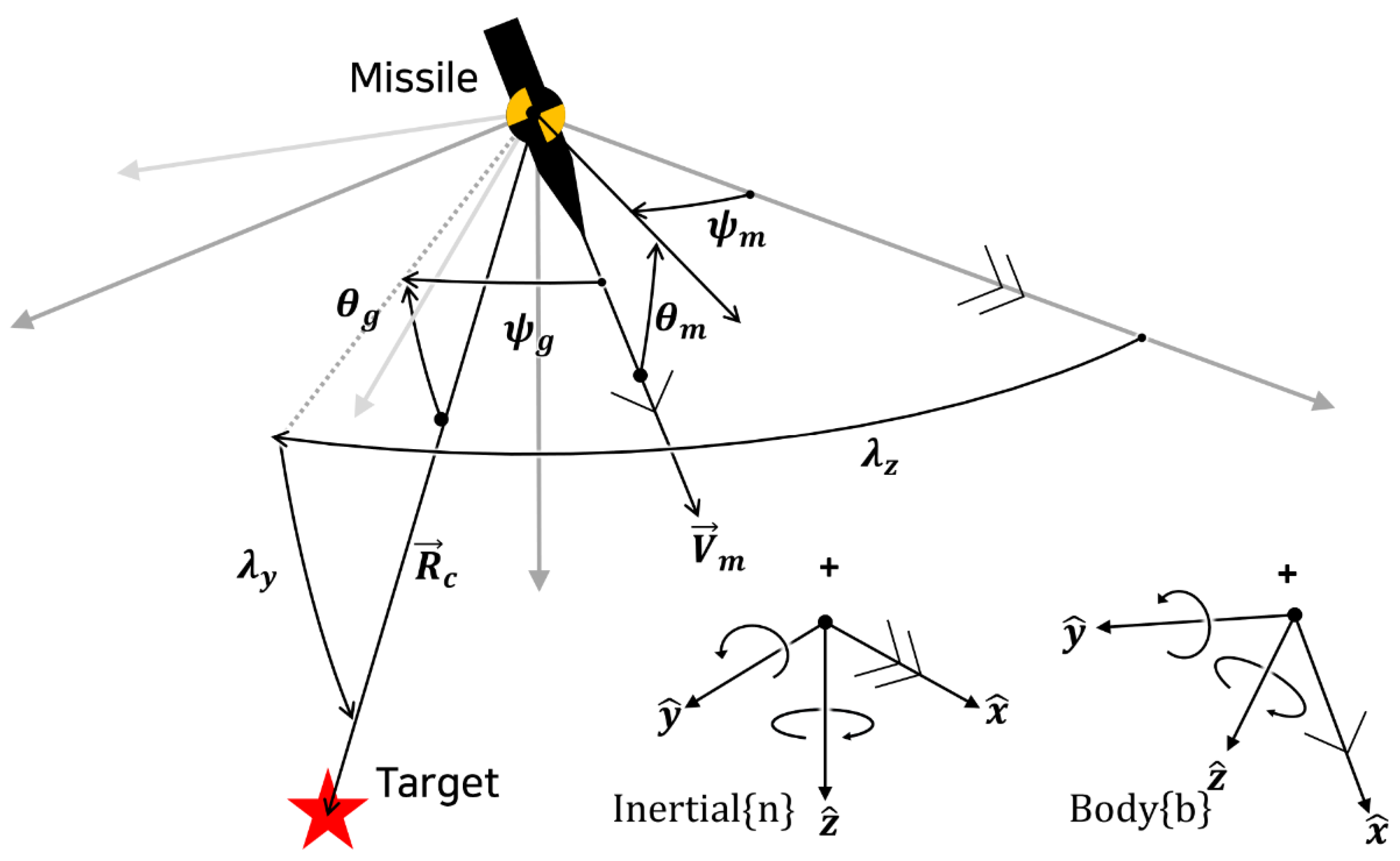
1. Introduction

Many studies on missiles that deal with complex and complicated mission profiles have been carried out. This is not only because there is military demand, which needs to overcome the complicated engagement scenarios, but also because researchers have expected the demands in advance. A guided missile is generally based on PNG (Proportional Navigation Guidance), which is widely known as quasi-optimal for interceptor guidance [1,2,3,4]. Many guidance laws for various objectives have been derived by using PNG. Zhou et al. [5,6,7,8,9] concerned jamming and deception to the friendly missile. They showed a simultaneous impact engagement profile by introducing impact time control guidance (ITCG). They pointed out the limitation of jammers which can only work well under the one-to-one correspondence of seeker–jammer interaction. ITCG has been continuously developed from the initial study on planar engagement space [9] to many improved guidance laws. Some studies of terminal angle constraint guidance (TACG) have also been carried out by constraining the approaching angle on the terminal phase [7,10,11,12]. Those studies are based on the fact that the performance of the missile can be enhanced if the missile is able to strike the specific vulnerable part of the target.

Meanwhile, we also looked into studies of obstacle avoidance guidance for fixed-wing aircrafts, since missile and fixed-wing aircrafts share similar dynamic properties. Ma [13] proposed a real-time obstacle avoidance method for a fixed-wing unmanned aerial vehicle (UAV). He showed a good performance of trajectory planning in a three-dimensional dynamic environment by using rapidly exploring random tree (RRT). Wan [14] proposed a novel collision avoidance algorithm for cooperative fixed-wing UAV. Each UAV generates three different possible maneuvers and predicts the planned trajectories. The algorithm manipulates the planned trajectories of UAVs, decides whether each combination of trajectories is good for collision avoidance or not, and activates the chosen maneuver when the collision comes closer.

Recently, reinforcement learning (RL) has attracted a lot of attention in the optimization and design of guidance in various fields. Yu and Mannucci [15,16] used RL for fixed-wing UAVs to implement collision avoidance tasks. They showed that they reduced the probability of UAVs’ collision with many simulation experiments. Furthermore, there are some prior studies for missile guidance via reinforcement learning. Gaudet [17] argued that RL working under a stochastic environment could make the logic more robust. They presented an RL-based missile guidance law and its framework for a missile homing phase via Q learning. They also presented a framework for interceptor guidance law design, which is able to infer guidance commands with only line-of-sight angles via Proximal policy optimization (PPO) in [18]. However, they dealt with a small and limited environment. Hong [19] expanded the environment further to cover a whole planar environment and set the fair comparison condition. They presented an RL-based missile guidance law for a wide range of environments and showed some advantageous features.

In practice, some missiles have the ability to avoid anti-missile systems and obstacles. Harpoons, for example, guide themselves to a sea-skimming maneuver to hide from radar detection. In the terminal phase, the missile kicks into the high for pop-up maneuver and prevents the mission failure due to CIWS (close-in weapon system) counteraction. It is also able to avoid the known obstacles such as friendly ships or islets by following the predefined waypoints. Such capabilities of missile guidance could raise the mission success rate, since it makes missile defense systems difficult to properly counter.

Several algorithms for obstacle avoidance have already been suggested in the literature to guide the missile to the target in complicated environments containing mountainous areas, islets, and ships. They were achieved by following the predefined trajectory, which requires a complete map of the operation field. Their approaches obviously limit the operation environment and requires too much prior information.

In this paper, we propose novel missile guidance laws using reinforcement learning, which can autonomously avoid obstacles and terrains in complicated environments with limited prior information and even without the need of off-line trajectory or waypoint generation. Our guidance laws are operating in real-time inference with less computational burdens and are also able to determine the probability of mission failure, which provides the missile some time to quit the mission safely when a mission is predicted as a failure.

This paper is organized as follows. Section 2 explains some basic missile dynamics and discusses environment modeling in which missile guidance laws are trained and operated. In Section 3, we present details of neural network architecture, reward function design, and training methodology. In Section 4, some numerical simulations are provided and the performance of proposed guidance laws is evaluated. Concluding remarks are given in Section 5.

2. Missile Dynamics and Environment Modeling

2.1. Problem Formulation

This paper introduces two engagement scenarios: the first is two-dimensional real-time obstacle avoidance and the second is overcoming three-dimensional real-time terrain for a missile. The target in both scenarios is assumed to be static. In both scenarios, the missiles should satisfy their core objective, which is to strike the target, while satisfying additional objectives for each scenario explained below.

2.1.1. Scenario A: 2D Obstacle Avoidance

This scenario focuses on the anti-ship missile with sea-skimming and waypoint navigation maneuvers. It considers the possible existence of friendly objects that should not be hit or specific objects that can be utilized to increase the survivability and success rate of the mission [20]. Previously proposed guidance laws have obvious limitations because they need all the placement and map information of the objects in the battlefield. In this paper, we propose a two-dimensional anti-ship missile guidance law that hits the target while avoiding obstacles without any prior information of their placement and map in the battlefield. The proposed guidance law, however, needs an extra onboard seeker that will be explained later.

2.1.2. Scenario B: Overcoming 3D Rough Terrain

This scenario considers the cruise missile flying through complicated terrain. When a missile flies toward a target over a mountain or rough terrain, it is better to keep a low altitude to avoid exposure to enemy defense systems. In this paper, we propose a guidance law that overcomes complicated terrain while keeping the missile altitude under the highest ridge where the enemy radar station most likely exists. We focused on the missile to have less information for active guidance to show the possibility of the RL-based guidance law. In this paper, it is assumed that it is possible to measure the distance of any pinpoint in front of the missile. Although previously impossible, the monocular depth estimation method with AI inference presented in Refs. [21,22] makes forward distance measurement no longer impossible while maintaining the small space occupancy of the missile head.

2.2. Missile Dynamics

The missile equations of motion is given by the pseudo-5DOF model as follows:

$$V_m=\left|\overrightarrow{V_m}\right|$$

(1)

$$\dot{\psi }=\frac{a_{m_y}}{V_{m}cos{\theta }_m}$$

(2)

$$\dot{\theta }=-\frac{a_{m_z}+gcos{\theta }_m}{V_m}$$

(3)

$${\psi }_m\left(t\right)={\int }_0^t{\dot{\psi }}_{m}dt+{\psi }_m\left(0\right)$$

(4)

$${\theta }_m\left(t\right)={\int }_0^t{\dot{\theta }}_{m}dt+{\theta }_m\left(0\right)$$

(5)

$$C_b^n=\left[\begin{array}{ccc}cos{\psi }_{m}cos{\theta }_m& -sin{\psi }_m& cos{\psi }_{m}sin{\theta }_m\\ sin{\psi }_{m}cos{\theta }_m& cos{\psi }_m& sin{\psi }_{m}sin{\theta }_m\\ -sin{\theta }_m& 0& cos{\theta }_m\end{array}\right]$$

(6)

$$V_m=C_b^n{V}_M^b$$

(7)

$$R_m=R\left(0\right)+{\int }_0^t{C}_b^n{V}_m^{b}dt$$

(8)

where ${\theta }_g\mathrm{and}{\psi }_g$ are the elevation look angle and the azimuth look angle, respectively, ${\lambda }_y\mathrm{and}{\lambda }_z$ are the line of sight angle of the y-axis and z-axis under inertial frame, respectively, $V_m$ is the velocity vector of a missile, $R_c$ is the line of sight vector, and ${\theta }_m\mathrm{and}{\psi }_m$ are the pitch and yaw attitude of the missile, respectively. The geometry of the model is showed in Figure 1.

2.3. Environment Modeling

2.3.1. Environment Modeling for Scenario A

The environment for scenario A contains obstacles as shown in Figure 2. The missile is launched from the coordinate origin and obstacles are formulated inside sector B between sector A and sector C. Sector A is an arc with a radius of 1000 m and Sector B is the area beyond sector A surrounded by an arc with a radius equal to the distance between the missile and the target. Sector C is an open space beyond the target.

Table 1. Target position and missile speed for scenario A.

$\left|{\mathit{R}}_{{\mathit{T}}_0}\right|$ [m]	${\mathit{L}}_0$ [rad]	${\mathit{\varphi }}_0$ [rad]	${\mathit{V}}_{\mathit{m}}$ [m/s]
$[5000,\mathrm{10,000}]$	$\left[\frac{-\pi }{2},\frac{\pi }{2}\right]$	$[0,2\pi ]$	$[200,400]$

shows the numerical intervals for the parameters related to the target position and missile speed.

In Table 1, $\left|R_{T_0}\right|$ is the initial distance between the missile and the target, $L_0$ is the missile initial look angle to the target, ${\Phi }_0$ is the initial line of sight angle to the target, and $V_m$ is the speed of the missile, respectively. The numerical values for the parameters are randomly selected within these numerical intervals.

Obstacles are modeled as rectangles. Ships are modeled as one rectangle and islands are modeled as multiple rectangles. The numerical intervals of various parameters for the rectangular geometry are given in

Table 2. The rectangle parameters.

${\mathit{R}}_{\mathbf{Ob}}$ [m]	${\mathit{\varphi }}_{\mathbf{Ob}}$ [rad]	$\Gamma$	l [m]	$\mathit{\kappa }$ [rad]	${\mathit{n}}_{\mathit{O}}$
$\left[{10}^3,\left|R_{T_0}\right|\right]$	$\left[0,\pi \right]$	$\left[\frac{1}{3},3\right]$	$\left[60,400\right]$	$\left[0,\frac{\pi }{2}\right]$	$\left[0,60\right]$

.

In Table 2, $R_{Ob}$ is the distance between the coordinate origin and the center of an obstacle, ${\varphi }_{Ob}$ represents heading toward the center of an obstacle from the coordinate origin, $\Gamma$ (height/width) is the aspect ratio of a rectangle, l is the length of the main line (line parallel to the x axis when the yaw angle of the rectangle $\kappa$ is zero), and $n_O$ represents the number of all the rectangles in the environment, respectively. The target is also modeled as a rectangle, and the parameters are as shown in

Table 3. Target geometry.

${\mathit{R}}_{\mathbf{Ob}}$ [m]	${\mathit{\varphi }}_{\mathbf{Ob}}$ [rad]	$\Gamma$	l [m]	$\mathit{\kappa }$ [rad]	${\mathit{n}}_{\mathit{O}}$
$\left|R_{T_0}\right|$	${\pi }_0$	1	40	$\left[0,\frac{\pi }{2}\right]$	1

.

Figure 3 shows the geometry of a rectangular obstacles.

In Figure 3, $P_{out}$ and $P_{in}$ are a set of points outside and inside of obstacles, respectively. For any point in sector B, it needs to be determined whether it belongs to an obstacle or not. The determination algorithm starts from getting the vertices of an obstacle as follows:

$$v_c=\left[\begin{array}{c}{R}_{Ob}cos{\varphi }_{Ob}\\ R_{Ob}sin{\varphi }_{Ob}\end{array}\right]$$

(9)

$$C_O^n=\left[\begin{array}{cc}cos\kappa & -sin\kappa \\ sin\kappa & cos\kappa \end{array}\right]$$

(10)

$$\begin{array}{cc}\hfill M& =\left[\begin{array}{cccc}{v^{\prime }}_1& {v^{\prime }}_2& {v^{\prime }}_3& {v^{\prime }}_4\end{array}\right]\hfill \\ \hfill & =C_O^n\left[\begin{array}{cccc}{\displaystyle \frac{l}{2}}& -{\displaystyle \frac{l}{2}}& -{\displaystyle \frac{l}{2}}& {\displaystyle \frac{l}{2}}\\ {\displaystyle \frac{\Gamma l}{2}}& {\displaystyle \frac{\Gamma l}{2}}& -{\displaystyle \frac{\Gamma l}{2}}& -{\displaystyle \frac{\Gamma l}{2}}\end{array}\right]\hfill \end{array}$$

(11)

$$M=\left[\begin{array}{cccc}{v}_1& v_2& v_3& v_4\end{array}\right]=M^{\prime }+\left[\begin{array}{cccc}{v}_c& v_c& v_c& v_c\end{array}\right]$$

(12)

The column of matrix $M^{\prime }$ consists of coordinates of vertices of a rectangular obstacle relative to its center $v_c$. The column of matrix M, therefore, represents the coordinates of vertices of the obstacle. The method for determining whether an arbitrary point $p_a$ belongs to $P_{out}$ or $P_{in}$ is as follows:

$$\left\{\begin{array}{cc}{p}_a\in P_{out}\hfill & {\displaystyle \mathrm{if}\Gamma l^2={\displaystyle \frac{1}{2}}\sum _{\{i,j\}\subset \{1,2,3,4\}}det\left|\begin{array}{ccc}{p}_{a_x}& p_{a_y}& 1\\ v_{i_x}& v_{i_y}& 1\\ v_{j_x}& v_{j_y}& 1\end{array}\right|}\hfill \\ p_a\in P_{in}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

where:

$$M=\left[\begin{array}{cccc}{v}_{1_x}& v_{2_x}& v_{3_x}& v_{4_x}\\ v_{1_y}& v_{2_y}& v_{3_y}& v_{4_y}\end{array}\right],p_a=\left[\begin{array}{c}{p}_{a_x}\\ p_{a_y}\end{array}\right]$$

During the training time, we used the algorithm above to randomly generate rectangle obstacles and determined if the target was far enough from each obstacle. If not, we canceled the generation and ran the same process again until none of the rectangular obstacles overlapped the target. We also used this algorithm to ensure that at every step the missile positions were not overlapped by all rectangular obstacles and to determine whether the missiles hit the target.

2.3.2. Environment Modeling for Scenario B

For scenario B, the three-dimensional rough terrain environments are generated as visualized in Figure 4.

The environment has a planar size of 10,000 m for both the x- and y-axis, and the limitation of height is the highest peak. For each episode, the missile agent must hit the target without colliding with the terrain but while maintaining spatial limits. To formulate the mountainous area, numerical values within the range shown in

Table 4. Parameters of mountainous environment.

${\Lambda }_{{\mathit{M}}_{\mathit{i}}}$ [m]	${\mathit{x}}_{{\mathit{M}}_{\mathit{i}}}$ [m]	${\mathit{y}}_{{\mathit{M}}_{\mathit{i}}}$ [m]	${\mathit{\sigma }}_{{\mathit{M}}_{\mathit{i}}}$
$[0,400]$	$[-3000,3000]$	$[-5000,5000]$	$[5\times {10}^5,{10}^6]$

are randomly chosen.

With the parameters above, the following function generates the height map of the field:

$$f(x,y)=\sum _{i=0}^{n_{\Lambda }}-{\Lambda }_{M_i}exp\left\{-\frac{{(x-x_{M_i})}^2+{(y-y_{M_i})}^2}{{\sigma }_{M_i}}\right\}$$

(14)

where $n_{\Lambda }$ is the total number of peaks and ${\Lambda }_{M_i}$ is the minimum height of the ith peak. The height of the ith peak is higher than the value ${\Lambda }_{M_i}$ due to the effect of the value of the surrounding peaks. $x_{M_i}$ and $y_{M_i}$ represent the planar position of the ith peak on the x and y axis, respectively. ${\sigma }_{M_i}$ is the deviation, which shows a more widely spread mountain shape as its magnitude increases.

2.4. Missile Seeker Modeling

The sensor considered in this paper is able to detect the obstacles by measuring the distance to the closest reflection of 5 pinpoints for scenario A and 15 pinpoints for scenario B. The sensors may obtain the information by a sequential search point scan or by a monocular depth estimation.

2.4.1. Seeker for Scenario A

For seekers for scenario A, we modeled the obstacle detector with a simple algorithm using the geometry shown in Figure 5, where lines $\overline{B_0{B}_1}$, $\overline{B_0{B}_2}$, $\overline{B_0{B}_3}$, $\overline{B_0{B}_4}$, and $\overline{B_0{B}_5}$ represent the beam for distance acquisition.

Initial numerical values for the algorithm are as shown in

Table 5. Initial value for the beam formation.

$\overline{\mathit{B}}$ [m]	$\mathit{\xi }$ [rad]
10,000	$\pi /6$

.

In Table 5, $\overline{B}$ is the maximum sensing distance, which is the length of a 2D obstacle detector segment line and $\xi$ is the angle displacement from the center beam to the most outer beam. Each tip $B_{\iota }$ is defined as Equations (15) and (16):

$$n_m\in \left\{n\left|\frac{n_{beam}}{2}<\frac{n_{beam}}{2}+1,n\in \mathbb{Z}\right.\right\}$$

(15)

$$B_{\iota }=C_b^n·C\left(\widehat{z},\frac{2\xi (n_m-\iota )}{n_{beam}-1}\right)·\left(\begin{array}{c}{10}^4\\ 0\end{array}\right)$$

(16)

where $n_{beam}$ is the quantity of beams which is an odd number. Each beam can be modeled as an equation of line. The equation of a line having two dots $(x_1,y_1)$ and $(x_2,y_2)$ on the line is as follows:

$$y-y_1=\left(\frac{y_2-y_1}{x_2-x_1}\right)(x-x_1)=m(x-x_1)$$

(17)

Furthermore, this equation can be used for modeling the line of obstacle rectangles. Suppose an obstacle rectangle d with line segments $\overline{v_1^d{v}_2^d}$, $\overline{v_2^d{v}_3^d}$, $\overline{v_3^d{v}_4^d}$, and $\overline{v_4^d{v}_1^d}$. Then, the intersection with a line extending from segment $\overline{v_k^d{v}_l^d}$ with slope $m_v^d$ and a beam line extended from segment $\overline{B_0{B}_i}$ with slope $m_B$ is as follows:

$$p_{i-kl}^d={\left(\begin{array}{cc}-m_v^d& 1\\ -m_B& 1\end{array}\right)}^{-1}\left(\begin{array}{c}-v_{ky}^d-m_v^d{v}_{kx}^d\\ -B_{iy}-m_B{B}_{ix}\end{array}\right)$$

(18)

Thus, the set of the whole intersection of beam line extended from segment $\overline{B_0{B}_i}$ with all lines extended from line segments of all obstacles are as follows:

$$\check{I}=\bigcup _{d=1}^{n_O}\left(\bigcup _{\{k,l\}\subset \{1,2,3,4\}}{p}_{i-kl}^d\right)$$

(19)

$$\left\{\begin{array}{cc}{p}_{i-kl}^d\in I_i\hfill & \mathrm{if}\begin{array}{c}{v}_{x_{min}}\le p_{{i-kl}_x}^d\le v_{x_{max}}^d\hfill \\ \&v_{y_{min}}\le p_{{i-kl}_y}^d\le v_{y_{max}}^d\hfill \\ \&B_{x_{min}}\le p_{{i-kl}_x}^d\le B_{x_{max}}^d\hfill \\ \&B_{y_{min}}\le p_{{i-kl}_y}^d\le B_{y_{max}}^d\hfill \end{array}\hfill \\ p_{i-kl}^d\in I_i^c\hfill & otherwise\hfill \end{array}\right.$$

(20)

where:

$$v_{x_{min}}^d=min(v_{k_x}^d,v_{l_x}^d),v_{x_{max}}^d=max(v_{k_x}^d,v_{l_x}^d)$$

$$B_{x_{min}}^d=min(B_{k_x}^d,B_{l_x}^d),B_{x_{max}}^d=max(B_{k_x}^d,B_{l_x}^d)$$

$$p_{i-kl}^d\in {\check{I}}_i$$

This set, however, contains a lot of invalid intersections, such as ${\mu }_6$ to ${\mu }_9$ in Figure 5. Real intersection ${\mu }_{B_i}$ for the sensor should be an intersection with the line segments and only detects the closest one as follows:

$${\mu }_{B_i}=\left\{\begin{array}{cc}\underset{\mu \in I_i}{argmin}\parallel \mu -B_0\parallel ,\hfill & I_i\ne \varnothing \hfill \\ B_i,\hfill & I_i=\varnothing \hfill \end{array}\right.$$

(21)

Then, the distance measured by beam i, $D_{B_i}$, is as follows:

$$D_{B_i}=\parallel \mu -B_0\parallel$$

(22)

2.4.2. Seeker for Scenario B

For scenario B, we assume an additional seeker that has a total of 15 beams, which consist of 5 columns and 3 rows. The geometry of the seeker beams are shown in Figure 6 and its numerical values are given in

Table 6. Numerical values for beam formulation on scenario B.

${\overline{\mathit{\psi }}}_{\mathit{B}}$ [rad]	${\overline{\mathit{\theta }}}_{\mathit{B}}$ [rad]	${\mathit{l}}_{\mathit{B}}$ [m]
$\pi /3$	$\pi /24$	$2\times {10}^3$

.

We suppose the direction vector ${\widehat{B}}_i$ of an ith beam of the seeker is parallel to the x-axis of a coordinate system ${\beta }_i$. Then, the direction cosine matrix represents the rotation from the body to the coordinate system for each beam, which is given by Equation (23):

$$C_{{\beta }_i}^b=\left[\begin{array}{ccc}cos{\overline{\psi }}_{i}cos{\overline{\theta }}_i& -sin{\overline{\psi }}_i& cos{\overline{\psi }}_{i}sin{\overline{\theta }}_i\\ sin{\overline{\psi }}_{i}cos{\overline{\theta }}_i& sin{\overline{\psi }}_i& sin{\overline{\psi }}_{i}cos{\overline{\theta }}_i\\ -sin{\overline{\theta }}_i& 0& cos{\overline{\theta }}_i\end{array}\right]$$

(23)

where ${\overline{\psi }}_i$ and ${\overline{\theta }}_i$ are the elements of combination of a set $\Phi$ that consists of an ordered pair. The ith order of the pair is lined up by ascending order for the value of $\overline{\theta }$ at first, then by ascending order for the value of $\overline{\psi }$.

$$\Phi =\bigcup _{\begin{array}{c}\overline{\psi }\in \left\{-{\overline{\psi }}_B,-{\overline{\psi }}_B/2,0,{\overline{\psi }}_B/2,{\overline{\psi }}_B\right\}\\ \overline{\theta }\in \left\{-{\overline{\theta }}_B,0,{\overline{\theta }}_B,\right\}\end{array}}\left(\overline{\psi },\overline{\theta }\right)$$

(24)

Then, the direction vector of the i^th beam on the body frame and that on the inertial frame are as follows:

$${\widehat{B}}^b=C_{{\beta }_i}^b·{\left(\begin{array}{ccc}1& 0& 0\end{array}\right)}^T$$

(25)

$$\widehat{B}=C_b^n·{\widehat{B}}^b$$

(26)

We have used the algebraic method to obtain the distance of the 2D obstacle environment. However, this is not a good method to obtain distances to obstacles of the environment of scenario B. The obstacles of scenario B are formulated with non-linear complicated formula Equation (14), so the computation is not simple, unlike the planar scenario. Thus, here we obtain the distance to the terrain reflection D by the Algorithm 1 in a numerical way.

Algorithm 1: Beam reflection—Scenario B

$N\leftarrow l_B/10+1$

$n\leftarrow 10$

$S\leftarrow 0$

$s\leftarrow 0$

$boo{l}_c\leftarrow True$

if $z_R<f(x_R,y_R)$ then

$boo{l}_c\leftarrow False$

$S\leftarrow N-1$

while $j<N-1$ do

$boo{l}_E\leftarrow True$

$R_B\leftarrow R+\widehat{B}·S·j$

if $z_{R_E}>f(x_{R_E},y_{R_E})$ then

$S\leftarrow j$

$boo{l}_E\leftarrow False$

break

end if

end while

if $boo{l}_E\ne True\&boo{l}_c\ne True$ then

while $j<n-1$ do

$R_B\leftarrow R_B-\widehat{B}·s$

if $z_{R_E}\le f(x_{R_E},y_{R_E})$ then

$S\leftarrow i$

break

end if

end while

end if

end if

$D\leftarrow S·10$

if $boo{l}_E\ne True\&boo{l}_c\ne True$ then

$D\leftarrow D-S+1/2$

else if $boo{l}_E=True$ then

$D\leftarrow l_B$

end if

3. Architecture Design and Training

Figure 7 shows the architecture of the artificial neural network for scenarios A and B, where the left one is the actor network and the right one is the critic network. Each network is composed of nine hidden layers and each layer contains hundreds of neurons, as shown in Figure 7. All layers use hyperbolic activation functions. The actor network has 14 and 24 states as inputs for scenarios A and B, respectively, and has 1 and 2 outputs as actions for scenarios A and B, respectively. Actions, which are the missile maneuver acceleration, are limited to the feasible range. Actions are then normalized and fed into the critic network to evaluate the policy along with the states. The critic networks is updated with the loss function of Mean Square Error (MSE), and the policy is updated via TD3PG [23]. TD3PG stands for Twin Delayed Deep Deterministic Policy Gradient and is one of the most advanced algorithms of RL. TD3PG was developed to ease the limitation of Deep Deterministic Policy Gradient (DDPG) [24,25], which sometimes overestimated the value of the state-action.

The environments for both scenarios have the following termination conditions:

1

Collision: is activated when the agent hits the object that should not be hit;

2

Escape: is activated when the agent is going outside of the environment;

3

Excess altitude: is activated when the agent exceeds the altitude limit set in advance and is only for scenario B;

4

Time over: is activated when the episode takes more time than it is supposed to;

5

Out of sight: is activated when the target is outside of the field of view of the seeker of the agent;

6

Hit: is activated when the agent is close enough to the target.

In the training session, the environment of each episode is randomly generated under the given constraints. This randomness makes the guidance law robust by letting the agent experience a varying environment. Further training details for each scenario will be described below.

3.1. Training Details for Scenario A

For scenario A, the agent has 14 inputs, which are the distance to the target R, its rate $\dot{R}$, look angle to the target $L_t$, the very previous look angle $L_{t-1}$, 5 beam length reflected of obstacle detector, and their one-step previous values. The reason for having values of one-step backward is to let the agent recognize the rate somehow. The termination rewards for each episode are shown in

Table 7. Termination rewards for scenario A.

Termination Condition	Reward
1	−500
2	−500
4	−500
5	$-500+0.1\frac{|R_0|}{|R_f|}$
6	$+200+0.1\frac{|R_0|}{|R_f|}$

.

Where $R_0$ and $R_f$ represent the initial distance to the target and the final distance to the target at which the episode terminated, respectively. If multiple termination conditions are satisfied at the same time, the condition in the largest ordinal number is applied. The reward for the termination condition 1–5 starts with −500, since we want the agent to be able to predict mission failure as it should not happen for a missile to hit obstacles involving friendly ships. The reward function is designed by:

$$r_{t{d}_A}=-\frac{a_M^{2}dt}{2500}-\frac{\dot{R}}{200}+\frac{n_O}{30}$$

(27)

where each term has its own purpose. The first term is to minimize the maneuver energy and the second term is to get the missile closer to the target. The third term is to encourage the agent to be more rewarded in a more difficult environment. Furthermore, it takes positive rewards over time to encourage the agent to create a detour route in a situation where the agent faces obstacles. Figure 8 shows the learning curve of the agent during training, which illustrates that the agent learns reliably and reaches its maximum reward after about 400 episodes.

3.2. Training Details for Scenario B

For scenario A, the agent has 23 inputs, which are the distance to the target R, its rate $\dot{R}$, azimuth, and elevation look angle to the target $L_t$, the very previous look angle $L_{t-1}$, the attitude of the missile ${\theta }_m$, ${\psi }_m$, 15 beam length reflected of obstacle detector, and their one-step previous values.

Table 8. Termination rewards for scenario B.

Termination Condition	Reward
1	0
2	$0.1·\frac{|R_0|}{|R_f|}$
3	0
4	0
5	$0.1·\frac{|R_0|}{|R_f|}$
6	$+200+0.1\frac{|R_0|}{|R_f|}$

shows the termination reward for each episode.

In Table 8, $R_0$ and $R_f$ represent the initial distance to the target and the final distance to the target at which the episode terminated, respectively. If multiple conditions are satisfied, the reward in the condition with the larger ordinal number is applied. Meanwhile, training only with the termination reward is very inefficient because unless there is some guide to the target as step reward, the agent tries too many attempts to get sparse reward in the vast environment. Thus, we have set the step reward as follows:

$$r_{t{d}_B}=-\frac{a_m·a_{m}dt}{2500}-\frac{\dot{R}}{200}+\frac{z_{R_m}}{{\Lambda }_{max}}+\frac{n_{\Lambda }}{20}$$

(28)

where $z_{R_m}$ is the z-axis element of missile inertial position, ${\Lambda }_{max}$ is the highest altitude of the top of the mountainous terrain, and $n_{\Lambda }$ is the number of peaks. The first term of the right hand reduces the maneuver acceleration of the missile to suppress excessive maneuvers and to save energy; the second term guides the movement of the missile to have direction heading toward the target. The third term forces the missile to keep a low altitude and so suppresses the possibility of being detected. The fourth term provides a certain amount of reward for each step so that the total reward at the end of the episode increases as the episode gets longer, helping the missile create a detour trajectory.

The learning curve in Figure 9 shows that the reward increases in a stable manner as training progresses. After around episode 3100, we lowered the learning rate so that the guidance law is fine-tuned. Eventually, after training, the missile tends to move in the direction of the topographic valley and turn its head toward the target while keeping the altitude as low as possible.

4. Results and Discussions

4.1. Simulation Results

4.1.1. Simulation Results of Scenario A

In scenario A, the obstacle avoidance guidance law shows a mission success rate of 0.96 in 10,000 Monte Carlo simulations. As it aims to operate with limited information, some episodes seem to fail and not be able to determine proper behavior with the given sparse information. This problem will be addressed in more detail in the next section.

The test set of the environment in Figure 10 has a total of 50 obstacles. The initial look angle is randomly selected between $-\pi /2$ to $\pi /2$. Figure 10 shows several missile trajectories reaching the target while avoiding obstacles. Each missile initially moves in a direction where an obstacle is not detected; then, it tends to move closer to the obstacles and avoid them if it detects an obstacle nearby. Since the agent has no memory, the agent should decide its action only using the state at the moment and it seems to decide the direction not to encounter another obstacle soon. In some episodes, the agent seems to take advantage of the fact that there is no obstacle behind the target. The missile moves to the rear of the target, and hits the target from the rear.

The episode in Figure 11 has four times more dense obstacles than the one in Figure 10. However, it can be seen from Figure 11 and Figure 12 that the proposed guidance law avoids all obstacles and hits the target.

4.1.2. Simulation Results of Scenario B

Figure 13 and Figure 14 show the missile trajectories generated by guidance law for scenario B.

The 3D terrain avoidance guidance shows a success rate of 0.90 in overcoming topographic features in 10,000 Monte Carlo simulations. It seems that the missiles rarely strike the terrain, but they sometimes appear to try to exceed their altitude limit. This suggests that inference is difficult in certain situations due to limited information and maneuver acceleration. This problem will be addressed in more detail in the next section. However, in most routes, the missiles fly along the valleys of mountainous terrain toward the target site, overcoming the terrain. Figure 15 and Figure 16 show a single trajectory of an episode and its state-action plot, respectively.

While the missile initially moves in the target direction, terrain features are detected from the bottom on the right at about 1 s, and the missile tries to avoid this by giving the y-axis positive direction acceleration. After that, the mountain on the left is detected at about 5 s, giving negative y-axis acceleration to overcome it at about 10 s, and applying negative acceleration to avoid the mountain left being detected again at around 12 s. Finally, the missile overcomes every topological feature and strikes the target.

4.2. Discussions

The most obvious limitation of guidance law design, based on reinforcement learning, is that its operation mechanism cannot be explained. This is a problem found in most deep learning approaches. Udrescu [26] and Mott [27] aimed to formulate policy as an interpretable one, yet they just glimpsed the notable features. It is almost impossible to be fully aware of the action of a neural network which is commonly described as a black box. Therefore, we discuss some limitations and outcomes for the specific situations.

4.2.1. Limitations and Outcomes of Scenario A

The guidance designed for scenario A has some episodes where the mission fails, as shown in Figure 17. The missile agent appears to be trapped in the surrounding obstacles, and attempts to escape from there with full maneuver acceleration, but it fails to function properly, which is confirmed by the plots in Figure 18. In this situation, the last subplot in Figure 18 shows that the critic network predicts mission failure by negatively valuing the critic value 2 s before impact. This predictive capability comes from the reward function, which is designed so that the agent takes a large negative reward for the termination that does not strike the target. It can give missiles some time to proactively respond to situations in which their mission is likely to fail.

In this way, the critic network produces a negative critic value if it predicts an adverse situation in advance without developing additional decision algorithms. On the other hand, an agent continuously produces a positive critic value if the critic network predicts success of the mission even though the environment seems hard to handle. For example, the environment in the episode mission shown in Figure 11 looks complex and hard to complete, but the critic network continuously produces a positive critic value, as shown in Figure 19, and predicts its mission success.

4.2.2. Limitation of Scenario B

For scenario B, an episode of a failed mission is depicted in Figure 20.

Figure 20 consists of three snapshots of sequential moments of mission failure, from left to right. As the missile agent approaches the center of a peak, it tends to pass through the top of the peak without generating a detour command when the look angle to the target is close to zero. This seems to happen in a situation where it is difficult to pursue higher rewards no matter which direction is chosen, left or right. Since the highest peak is in a straight line in the direction the missile is headed after the first peak, and the missile flies by at that height, the seeker does not detect anything ahead and instructs the missile to fly forward. In this situation, it seems that there is not enough information to select a specific command, and eventually the episode ends, as it does not detect obstacles at that high altitude and meets the termination condition.

5. Conclusions

This paper presents novel missile guidance laws using reinforcement learning. Design processes of guidance laws are explained in detail in terms of neural network architecture, reward function selection, and train method. The proposed guidance laws are focused on two scenarios. For scenario A, two-dimensional obstacle avoidance, the guidance law is designed in the way to avoid planar obstacles until it reaches the target. It avoids most obstacles by real-time inference of trained networks with limited information compared to existing algorithms with similar purposes. Meanwhile, failure can be predicted through critic network which is naturally generated during the learning process. Thus, it allows the missile to take action before a missile makes a fatal disaster, such as hitting friendly ships. For the 3D terrain avoidance, which is scenario B, a missile guidance law based on RL is designed to overcome terrain features through real-time inference. It keeps its altitude low to ensure it is not seen by radar on the top of the field while striking the target.

In summary, the proposed RL-based missile guidance laws are not only able to strike the targets while avoiding obstacles and topographic features with limited information, but also able to determine the probability of the success rate, i.e., whether the mission is achievable or not. Numerical simulations show their effectiveness with some inherent limitations.