All-Optical Tuning of Fano Resonance for Quasi-BIC and Terahertz Sensing Applications

Abstract

The bound states in the continuum (BIC) support anomalous resonances in the optical or terahertz band with a theoretically infinite quality factor. Therefore, it has great application prospects in the field of sensors. However, the current regulation of BIC mainly relies on the asymmetry of the material structure, which requires high processing technology. The structure can hardly be effectively adjusted once it is formed. In this work, we propose a new metasurface consisting of an array rectangular hole structure combined with aluminum and photosensitive silicon, which supports quasi-BIC to achieve ultrasensitive sensing in the terahertz range. By introducing photosensitive silicon, the asymmetry of the structure is efficiently controlled by the light field, thus realizing the bidirectional continuous control from quasi-BIC to BIC-like states. Through the optimization of the structure, a class of highly sensitive terahertz sensing based on optical tuning is finally proposed. The narrow-band quasi-BIC resonance is sensitive to medium thickness and refractive index, and compared with pure metal structure, the sensitivity and dynamic range can be increased by 2.60 times and 2.63 times, respectively. Due to the high slope of the Fano lineshape, sensitivity can reach 9.41 GHz/RIU and 0.65 GHz/μm, respectively. Furthermore, this feasible and practical structure provides an ideal platform for highly sensitive sensing.

1. Introduction

Terahertz (THz) sensing technology has the advantages of low photon energy, strong penetrability, wide frequency band, and strong anti-interference ability, and has shown great application potential in non-destructive testing [1], label-free genetic diagnostics [2], and biomedical imaging [3]. However, the sensitivity of THz sensing is not high at present, due to the lack of high-power radiation sources and the weak intermolecular or intramolecular vibration of analytes in THz band, which greatly limits its development in the sensing field.

Resonant metasurfaces structures can effectively enhance the local optical field and promote the interaction between light and matter at specific frequencies, thus becoming an effective way to improve sensitivity [4]. This requires the introduction of asymmetry in the geometric cell tailoring of the subwavelength structural platform so as to form Fano resonance, in which an asymmetric linear shape is generated by the interference coupling between a continuous state mode with a wide resonance bandwidth and a discrete state mode with a narrow resonance bandwidth [5,6,7]. Recently, a variety of asymmetric structures have been derived, including ring/disk cavities, holes, dolmen structures, and compound sub-structures [8,9,10]. However, these require high processing accuracy, which needs to reach the order of 100 nanometers.

In recent years, the concept of BIC originated from the concept of quantum mechanics and was gradually introduced into metasurface structures. The ideal BIC structure theoretically does not produce radiation leakage, has an infinite Q factor, and extremely narrow resonance [11,12], so it has great potential in sensing, lasing, filters, and nonlinear optics [13,14]. However, for sensing, the ideal BIC is usually hidden in the normally propagating electromagnetic spectrum and cannot be identified [15]. Therefore, in practical applications, it is necessary to perturb the symmetry-protected BIC state to convert it into a quasi-BIC mode in order to construct a radiation channel with the outside. Among them, the quasi-BIC structure constructed by toroidal dipole (TD) not only has a high Q factor but also can strengthen the interaction between light and matter through the near-field enhancement effect, thus providing a unique advantage for sensing [5,16,17].

Quasi-BICs have been realized in symmetric dielectric dimer/trimeric nanobar structures [18]; asymmetric dipole rods [5], pillars [19], rings [16]; and other metasurface structures. In addition to introducing symmetry breaking in the structure, the method of inducing the quasi-BIC state can also change the absorption of the material or adjust the incident angle of the light source [16,19]. The above-mentioned tuning methods are all called parametric tuning BIC. In general, the closer the system is to the BIC state, the greater the influence of asymmetry on it. The micron-scale deviation will even cause the Q factor to decrease by an order of magnitude. Once the structure is determined, it can only support a single BIC state. This is undoubtedly a great challenge to the manufacturing process. In addition, the surface roughness, limited area, and material properties of the sample can lead to unpredictable radiative and non-radiative losses during design, hence the device needs to be dynamically tuned. To overcome this issue, methods based on electrical or optical dynamic BIC modulate of metasurfaces have been gradually developed in recent years. Yao et al. introduced structured graphene into the metal metasurfaces to form graphene-metal metasurfaces, tuned the Fermi energy of graphene to change the free electron concentration to adjust it from semiconductor-like to metal-like, and finally realized free switching between BIC and quasi-BIC of resonance mode [20]. Fan et al. used optical doping (or optical pumping) methods to induce free-carrier changes in semiconducting dielectric materials in all-dielectric subsurfaces, achieving spectral conversion from quasi-BIC to BIC and amplitude modulation of the transmission spectrum [21,22]. Mikheeva et al. took advantage of the photosensitive properties of arsenic trisulfide to prepare metasurfaces structures and fine-tune the Fano resonance by light absorption [23]. Taking advantage of the photoconductive properties of the material, the Q factor can be dynamically controlled by adjusting the pump flow rate of external light excitation, which not only has high precision but also has a fast response. It provides a new way for real-time modulate of active metamaterial devices.

Therefore, in this paper, a porous metal subsurface is introduced to form a metasurfaces structure, and a structured photosensitive silicon material is introduced into the porous metal structure. Taking advantage of its photoconductive properties, the electron concentration can be tuned from a semiconductor-like to a metal-like by adjusting the electron concentration by an optical field. Through the optimization of the structure, the transformation of the ideal BIC into the Fano quasi-BIC resonance mode with high Q factor is realized in the THz band. Finally, a highly sensitive sensing based on quasi-BIC resonance was proposed by taking advantage of its quasi-BIC resonance properties. The highly sensitive detection of surface area medium thickness and refractive index is achieved, which provides a new method for high sensitivity THz sensing.

2. Materials and Methods

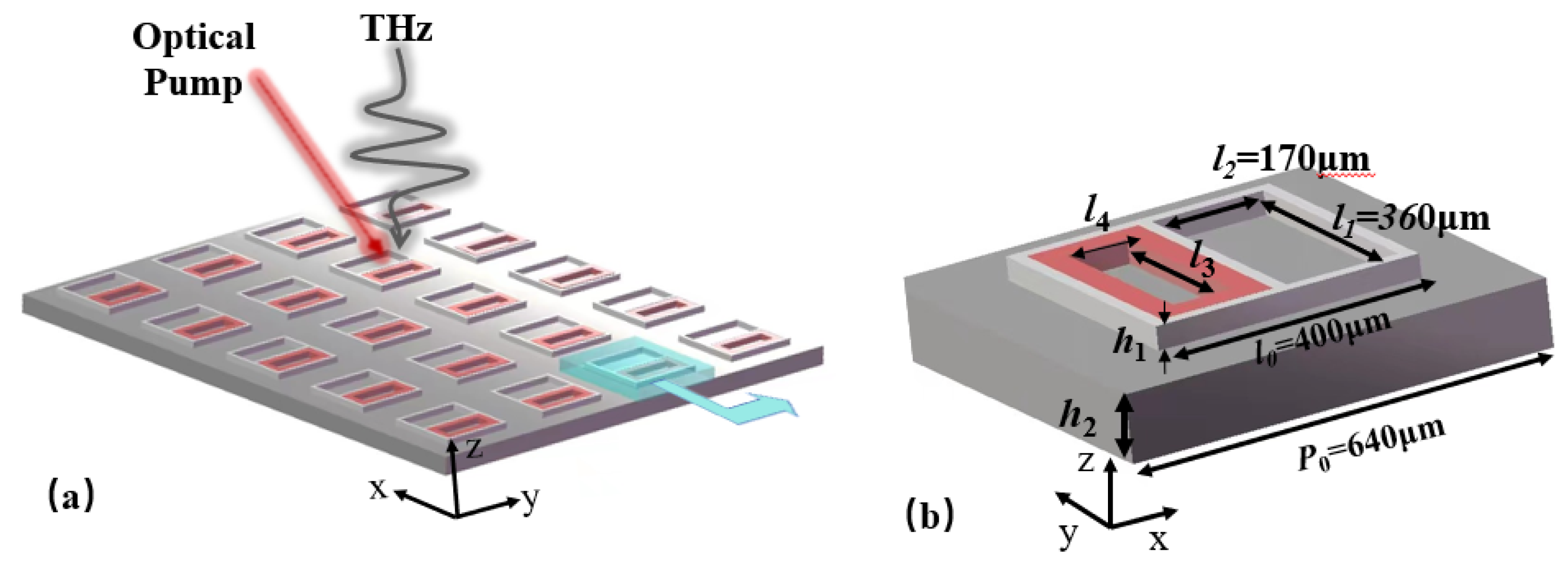
Figure 1a shows a schematic diagram of the proposed THz metastructure. A typical section of the metasurfaces was fabricated on PolyTetraFluoroEthylene (PTFE), and the inset shows the enlarged geometry of the unit cell. A single resonator is 640 × 640 μm, the length and width l₀ of the metal-aluminum structure are both 400 μm, and the array size is 400 × 400 μm. There are two rectangular openings on the metal aluminum, and the upper part is a fixed opening with a size of 360 × 170 μm. In order to verify the structural asymmetry, the lower inner boundary is filled with aluminum or photosensitive silicon material with a width of 0–40 μm. As shown in Figure 1b, when red photosensitive silicon with width of 40 μm is introduced into the lower rectangular opening, the internal length and width are l₃ = 280 μm and l₄ = 90 μm, respectively. Both Si and Al material parameters can be referenced from the Palik Refractive Index database values so that the optical properties of this structure can be simulated and analyzed. In order to excite a significant resonant response, the polarization direction of the incident light must be along the asymmetric axis [24]. The parameters of the materials in the model are shown in the following

Table 1. Material properties of the metasuface used in the model [24,25].

Material	Relative Permittivity	Conductivity (S/m)	Relative Permeability	Refractive Index
PolyTetraFluoroEthylene (PTFE)	2.08	0	1	1.4
Aluminum	1	3.8 × 107	1.000021	1
Photosensitive Silicon	11.9	0~5 × 105	1	3.4

.

The aluminum material as a perfect electrical conductor with conductivity about 10⁷ S/m in the THz band. The optical excitation uses the optical pump and terahertz probe (OPTP) method to control the modulate process by applying femtosecond pulsed laser stimulation (wavelength 800 nm, repetition rate 1 kHz, pulse width 100 fs). The photosensitive silicon material acts as the active medium. When the photon energy (1.55 eV) is larger than the silicon band gap (1.1 eV) of external optical excitation pumping, the light-induced free carriers can change the electrical conductivity of the silicon resonator surface, enabling the modulate from semiconductor-like to metal-like. The conductivity of silicon in the absence of illumination is set to σ = 0 S/m in the simulation. With the increase of pump light intensity, the conductivity increases from 0 to 5 × 10⁵, correspondingly.

To validate the response of the designed metamaterial, numerical simulations based on the Ansys 3D High Frequency Simulation Software (HFSS) is employed. Periodic boundary conditions are employed along the x and y-directions and the perfectly matched boundary condition is used in the z-direction in the free space. The normal-incidence x-polarized THz wave is applied as the excitation. Furthermore, this design is realized on the assumption that the incident terahertz wave is the plane wave [26]. According to the equivalence principle, the field and source inside the periodic boundary can be replaced by the only field and source outside, so the Maxwell equations are solved on the boundary [27].

3. Results and Discussion

Next, we investigated the effect of different structural parameters on the transmission spectrum to optimize the sensing structure. In this structure, photosensitive silicon is not introduced firstly, and the asymmetry of the upper and lower structures is mainly realized by filling the aluminum structure in the lower frame. The asymmetry along the y-direction is represented by the asymmetry parameter Δl. Specifically, ∆l = 0 means that the upper and lower holes are equal in size, both 360 × 170 μm. When a rectangular frame structure with equal width is introduced into the lower hole, the asymmetric parameter ∆l = (l₁ − l₃)/2. As shown in Figure 1b, when the size of the lower hole is 280 × 90 μm, Δl = 40 μm. This means that symmetry breaking elements are introduced.

In the wave system, the incompatibility of resonant states for coupling with energy radiating channels leads to the formation of the bound states. In general, when the antisymmetric modes persist in the in-plane symmetry structures and cannot couple to the symmetric plane waves propagating as the radiation channel, which is also known as symmetry-protected BIC (SP-BIC) [15]. The energy in the resonator is trapped without leakage to the continuum. While when the structure is no longer symmetrical, the radiation channels are established between non-radiated bound states and the free space continuum, it results in more incident light radiating to free space, which manifests as resonance peaks in the transmittance spectra.

In this paper, the simulation results of the asymmetric structure are shown in Figure 2a. It can be seen that when Δl = 0, the structure is symmetrical and the system state is in the BIC state, which means that no energy leaks from the bound state to the free space continuum. With the increase of Δl, the asymmetry also gradually increases, and the transmission intensity also reaches the maximum at 40 μm. At this time, our structure breaks the symmetry to the greatest extent and reaches the quasi-resonant state. The interference between the discrete bound states supported by the microstructure and the continuous radiation in free space forms the Fano resonance lineshape with almost constant resonance positions [17,28]. It can be seen from the fitting that the Q value reaches a maximum of 1130.

In addition, structural parameters such as height and shape also affect resonance properties. The asymmetric parameter ∆l = 40 μm is set to continue the research of subsequent numerical simulation. As shown in Figure 2b, increasing the size l of the array of metal aluminum deposited on the silicon substrate from 400 to 560 μm, the resonance frequency gradually decreases, and the intensity of the Fano resonance peak also decreases gradually. As shown in Figure 2c, when the height h₁ of the aluminum structure is gradually decreased, the Fano resonance peak is gradually enhanced, but the peak position is almost unchanged. Similarly,, with the decrease of the substrate thickness h₂, the resonance peak is weakly enhanced, and the resonance frequency gradually increases, showing a weak blue shift in Figure 2d. It can be seen that the change in the structure height has the similar effect on the resonance than the change caused by the base thickness. According to the above simulation results, the final selection parameters are as follows: the upper inner hole size is l₁ × l₂ = 360 × 170 μm, the lower inner hole size is l₃ × l₄ = 280 × 90 μm, and the asymmetric parameters Δl = 40 μm, l₀ = 400 μm, h₁ = 30 μm, h₂ = 100 μm.

As can be seen from Figure 2, there are two types of methods to improve sensitivity. One is to increase the asymmetry by increasing the width of the aluminum inner hole, and the other is to reduce the volume of the metal structure, such as reducing the area or reducing the thickness. The mechanism is speculated that the ability to confine the electric field is weakened as the volume of the aluminum structure decreases, and the binding effect on energy is weakened, which leads to resonance leakage and enhances the resonance strength. This can be attributed to the enhancement of asymmetry and the weakening of the binding effect on energy.

The transition from BIC to quasi-BIC characteristic response is seen in the simulations in Figure 3a, and the trajectories given are simulation results for different Δl. As Δl gradually decreases, the overall spectrum exhibits the red-shifted. However, there is only a slight red shift in the Fano resonance peak position, the spectral linewidth is gradually narrowed, and the transmission intensity is gradually reduced, which reflects the decrease in the leakage rate of the quasi-BIC. With ∆l decreases to zero, the resonance linewidth and the transmission disappears until the upper and lower structures are completely symmetrical. As shown in Figure 3b, the SP-BIC state increases with increasing Q-factor. Thus, it can be seen as a significant method for designing and tuning the resonance Q-factor and linewidth at quasi-BIC mode. It is worth noting that although the Q-factor is maximized when infinitely close to the BIC state, and slight perturbations result in infinitely low leakage of the BIC, resulting in weak transmission intensity. Due to the limitation of the resolution of the equipment and the signal-to-noise ratio, Δl = 40 μm with obvious transmission is still selected for research.

After that, the resonance phenomenon was investigated under the variation of electric field and current, as shown in Figure 4. To observe the localization of the energy more clearly, the color and size of the current arrows represent the amplitude distribution on the surface. Figure 4a shows that the resonance is suppressed when the structure is symmetric. As shown in Figure 4b, the flow of the current is mainly along the y-axis and presents a symmetrical distribution. When the symmetry is broken, as shown in Figure 4c, localization also occurs on both sides of the structure along the x-axis. At the same time, the local enhancement is particularly evident at the outer edge of l₁ above the aluminum structure. It can be seen that the enhancement effect can be attributed to two reasons. Firstly, the asymmetry of the structure leads to the generation of oscillating currents, which leads to the accumulation of charges mainly in the smaller aluminum frame. Due to the edge effect, the charge will accumulate at the position of l₁ above the aluminum resonant ring, as well as the left and right sides, as shown in Figure 4d. Secondly, the increase in the size of the conductive structure weakens the confinement of electromagnetic waves, resulting in a corresponding weakening of resonance. Therefore, by comparing Figure 4b,d, it can be found that when the size of the metal frame is increased, the enhancement of the current is no longer obvious.

As shown in Figure 1b, when the size of the structure is optimized, the aluminum inner frame is changed to photosensitive silicon, and the electrical conductivity can be controlled by light intensity, realizing the continuous modulate of the BIC processes. Interestingly, when the conductivity is 0, although the size of the conductive structure does not change, a strong enhancement effect of the Fano lineshape appears on the photosensitive Si-metal subsurface, as shown in Figure 5a. However, with the gradually increase of the conductivity and the substantial increase of its free electron concentration, the conductive properties of photosensitive silicon will change from semiconductor-like to metal-like. When the conductivity is 1000–2000 S/m, the BIC-like state is approximately reached, and the enhancement effect is suppressed. It is easy to understand as the conductivity is further enhanced. When the electron concentration is high, the conductive properties of photosensitive silicon are similar to those of metals, and the interaction strength of photosensitive silicon with THz waves is comparable to that of metal with THz waves. At this point, the presence of photosensitive silicon can be regarded as a metal. This greatly enhances the asymmetry of the device, resulting in progressive enhancement of the Fano lineshape.

In order to further explore the mechanism of optical modulation of the structure by photosensitive silicon, three types of structures with conductivity of 0 S/m, 2000 S/m and 500,000 S/m were selected, and the distribution of electric field and surface current in the xy plane was observed, as shown in Figure 6. In Figure 6a,b, when there is no light irradiation, the conductivity of the photosensitive silicon structure is 0, so the silicon structure can be regarded as an insulator, and metal aluminum is the main resonant structure. However, the discontinuous boundary between the photosensitive silicon and the metal makes the current in the metal aluminum asymmetric in the x-direction, which greatly enhances the oscillating current of the underlying metal structure, and the enhancement effect of the current at the lower edge of the metal frame becomes more and more obvious. As the conductivity increases to 2000 S/m, the discontinuity between photosensitive silicon and metal becomes smaller in Figure 6c,d. The entire resonant structure is made symmetrical along the x-direction, and then the current along the x-direction is suppressed in Figure 6d, resulting in a BIC-like state.

As shown in Figure 6e,f, when the conductivity is further increased up to 500,000 S/m, the photosensitive silicon can be regarded as a metal, gradually. The discontinuity between it and the metal basically disappears, making the whole resonant structure and the surface current asymmetric again in the x-direction, which leads to the reappearance of the quasi-BIC state. This is similar to Figure 4d wherein the current concentration effect mainly occurs in the upper metal frame with smaller structure size. It can be seen that when the structure is controlled by photosensitive silicon, and will go through three stages. Firstly, the photosensitive silicon promotes the confinement of electromagnetic waves by the metal structure tightly bound to it when initially non-conductive, resulting in the enhancement of the underlying resonant structure. Secondly, when partially conducting, the upper and lower structures are gradually symmetrical, and a BIC-like state appears. Finally, the area of the metal structure is increased when it is approximated as a conductor, so that its electric field concentration effect mainly occurs in the square structure above with smaller area.

Finally, we observe the sensitivity of the proposed THz sensing by varying the refractive index and the thickness of the analyte, respectively. As shown in Figure 7a, we analyze the effect of external media with different thicknesses (h_f) on the transmission spectrum. When the filling structure gap and the surrounding dielectric thickness increase from 15 μm to 35 μm, there is a clear red shift in the resonance peak position. When the refractive index is from 1.23 to 1.87 that is shown in Figure 7b, the resonant peak position also has an obvious red shift. However, the increase of the thickness and refractive index has little effect on the Q value of the resonance peak and the spectral contrast.

In refractive index sensing, the sensitivity is:

$$S=df/dn\left(\mathrm{GHz}/\mathrm{RIU}\right)$$

(1)

where df and dn are the frequency offset and the refractive index difference or thickness difference. Quasi-BIC Fano resonance sensitivities were 3.62 GHz per refractive index unit (RIU) and 0.25 GHz per micrometer, respectively. Although the sensitivity is not dominant compared with other similar sensors, the biggest advantage of the Fano lineshape is the steepness of the slope of the resonance peak. Taking refractive index sensing as an example, when using light intensity for sensing measurements, the sensitivity can be calculated by the ratio of the change in light intensity amplitude to the change in refractive index [29]:

$$\frac{dI}{dn}=\frac{df}{dn}\times \frac{dI}{df}$$

(2)

It can be seen from the formula that there are two parts multiplied together. The first part of the formula is the conventional sensitivity, which characterizes the sensitivity by the amount of frequency drift. It mainly related to the change of the refractive index, and has nothing to do with the lineshape. The second part is related to the resonance lineshape. The steep slope (dI/df) of the Fano resonance help to increase the sensitivity (dI/dp). As Figure 8 shows, it can be seen that the slope of Fano resonance will increase sharply at a conductivity of 500,000 S/m, so the sensing sensitivity can be greatly enhanced about 2.60 times higher than the aluminum filling. In this way, the sensitivity of the Fano resonant structure with photosensitive silicon can reach 9.41 GHz per refractive index unit (RIU) and 0.65 GHz per micron, respectively. Moreover, compared with filled aluminum, the transmission intensity of Fano linear region of photosensitive silicon structure is increased by 2.63 times, which means that the dynamic range of the sensor is also improved. What’s more important is that the lineshape can be freely adjusted and controlled by using this structure, meanwhile the sensitivity can be optimized. Therefore, this method opens the window for ultra-high-sensitivity sensing applications.

4. Conclusions

The BIC or quasi-BIC state supports anomalous resonances in the optical or terahertz band with a theoretically infinite quality factor, so it has great potential in sensing, lasing, filters and nonlinear optics. The conventional method of regulating BIC by introducing symmetric breaking elements is static, which means that once the structure is formed, it only supports one kind of state. This undoubtedly limits the application of BIC or quasi-BIC in practice. This paper presents a novel metasurface consisting of an array rectangular hole structure combined with aluminum and photosensitive silicon. It can realize dynamic regulation by adjusting the pump light power. More importantly, it can achieve bidirectional continuous control from quasi-BIC to BIC-like states with high precision and high response. Then, the mechanism of the modulate process is analyzed in detail through the distribution of electric field and current. And through the optimization of the structure, a terahertz sensing structure with highly sensitive based on optical tuning is finally designed. The narrow-band quasi-BIC resonance is sensitive to medium thickness and refractive index. Due to the high slope of Fano lineshape, sensitivity can reach 9.41GHz/RIU and 0.65 GHz/μm, respectively. And compared with pure metal structure, the sensitivity and dynamic range can be increased by 2.60 times and 2.63 times, respectively. Furthermore, this feasible and practical structure provides an ideal platform for highly sensitive sensing and nonlinear optical control.