Truncated Newton Kernel Ridge Regression for Prediction of Porosity in Additive Manufactured SS316L
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
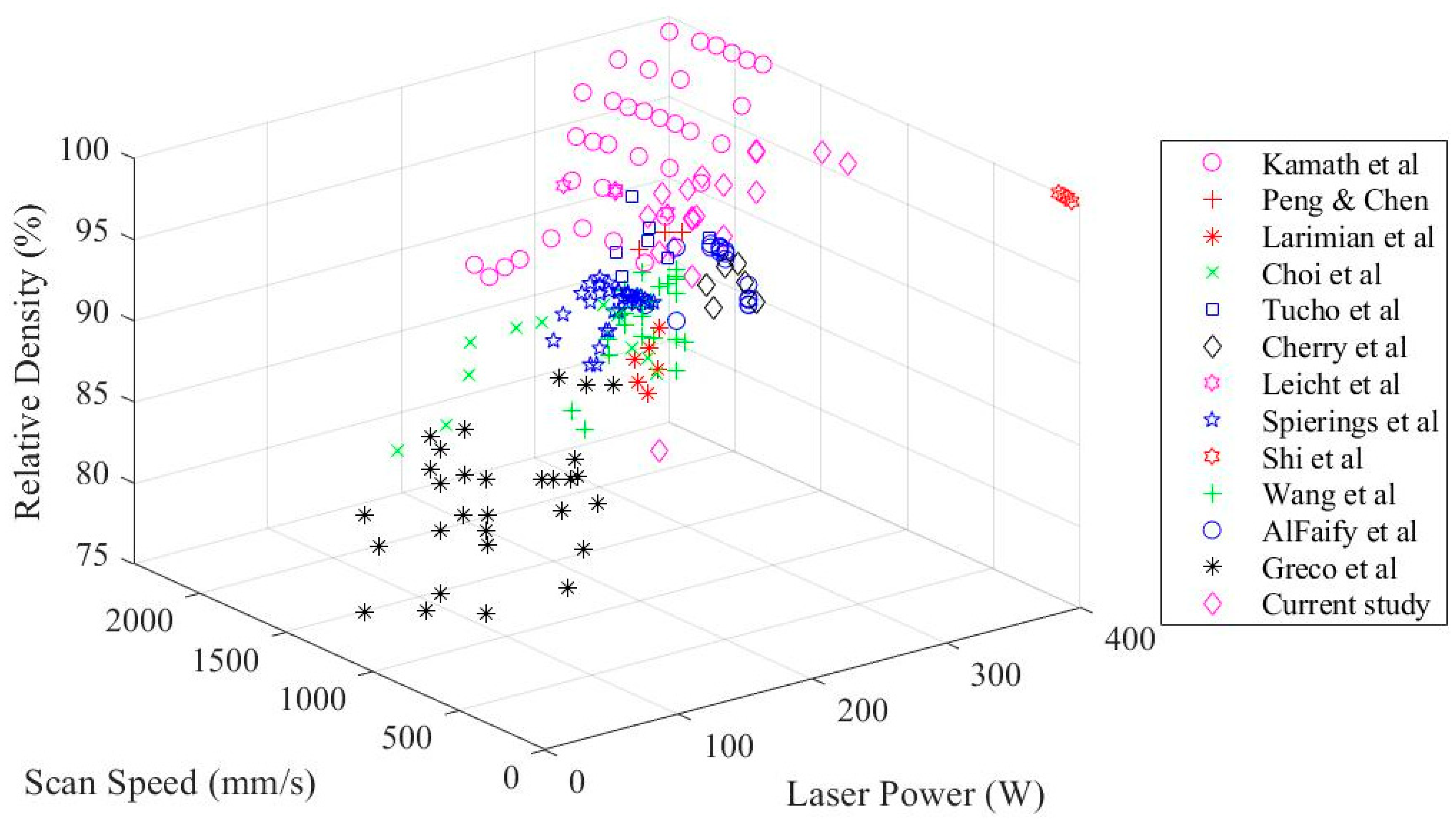
2.2. Experimental Results from the Literature
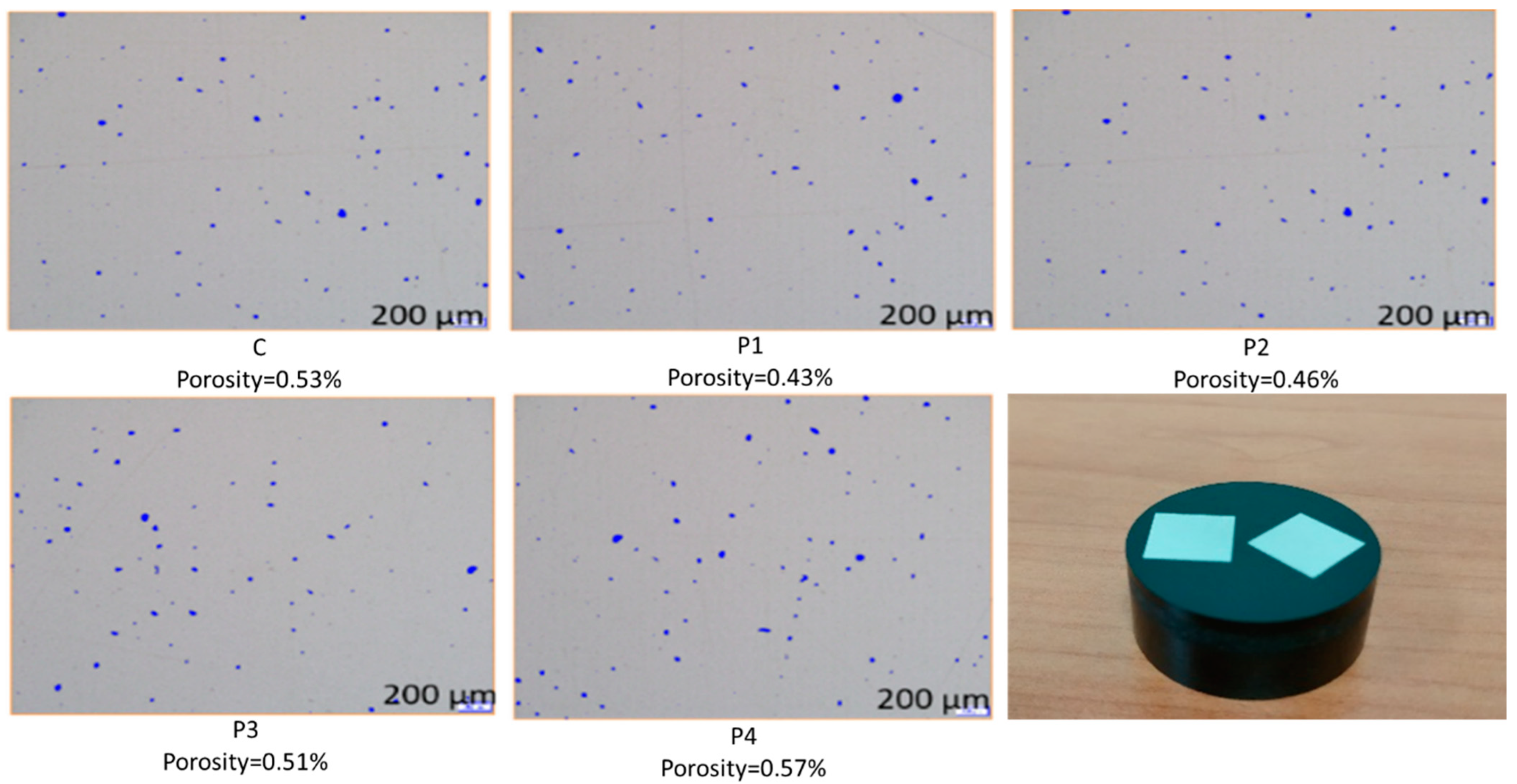
2.3. Experimental Procedure and Density Measurement
3. Applied Regression Models and Modelling
3.1. Ridge Regression (RR)
3.2. Kernel Ridge Regression (KRR)
3.3. Support Vector Regression (SVR)
3.4. Data Preparation and Model Evaluation
3.4.1. Data Pre-Processing
3.4.2. Model Evaluation with 10-Fold Cross-Validation
4. Results and Discussion
4.1. Analysis of Data Plots
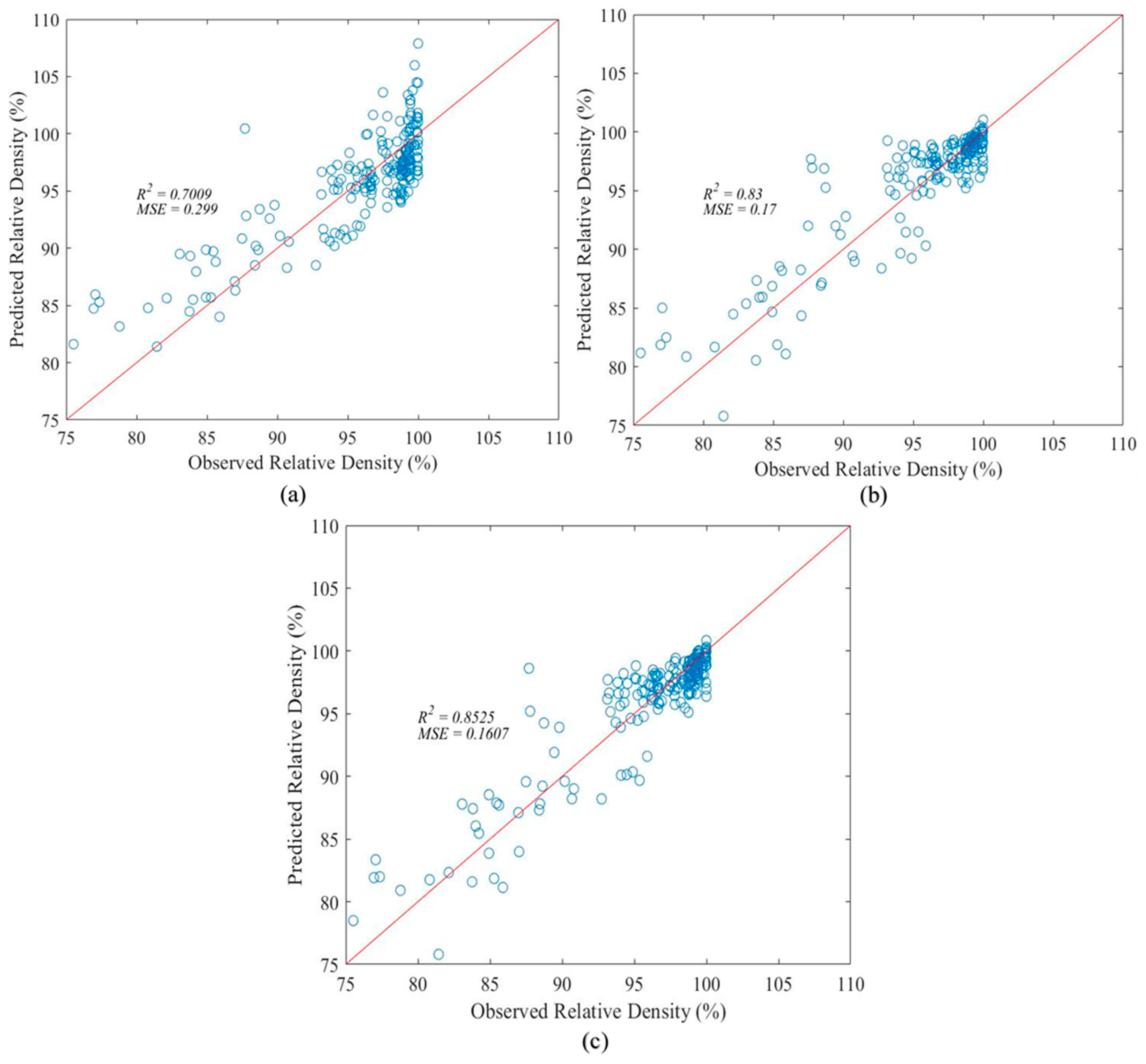
4.2. Analysis of Regression Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ISO/ASTM. ASTM Standard 52900; Additive Manufacturing—General Principles Terminology. ISO: Geneva, Switzerland, 2015. [Google Scholar]
- Baturynska, I.; Martinsen, K. Prediction of Geometry Deviations in Additive Manufactured Parts: Comparison of Linear Regression with Machine Learning Algorithms. J. Intell. Manuf. 2021, 32, 179–200. [Google Scholar] [CrossRef]
- Peng, T.; Chen, C. Influence of Energy Density on Energy Demand and Porosity of 316L Stainless Steel Fabricated by Selective Laser Melting. Int. J. Precis. Eng. Manuf. Green Technol. 2018, 5, 55–62. [Google Scholar] [CrossRef]
- Garg, A.; Tai, K.; Lee, C.H.; Savalani, M.M. A Hybrid M5′-Genetic Programming Approach for Ensuring Greater Trustworthiness of Prediction Ability in Modelling of FDM Process. J. Intell. Manuf. 2014, 25, 1349–1365. [Google Scholar] [CrossRef]
- Garg, A.; Tai, K.; Savalani, M.M. State-of-the-Art in Empirical Modelling of Rapid Prototyping Processes. Rapid Prototyp. J. 2014, 20, 164–178. [Google Scholar] [CrossRef]
- Mahamood, R.M.; Akinlabi, E.T. Processing Parameters Optimization for Material Deposition Efficiency in Laser Metal Deposited Titanium Alloy. Lasers Manuf. Mater. Process. 2016, 3, 9–21. [Google Scholar] [CrossRef]
- Averyanova, M.; Cicala, E.; Bertrand, P.; Grevey, D. Experimental Design Approach to Optimize Selective Laser Melting of Martensitic 17-4 PH Powder: Part I—Single Laser Tracks and First Layer. Rapid Prototyp. J. 2012, 18, 28–37. [Google Scholar] [CrossRef]
- Srivastava, M.; Maheshwari, S.; Kundra, T.; Rathee, S. Multi-Response Optimization of Fused Deposition Modelling Process Parameters of ABS Using Response Surface Methodology (RSM)-Based Desirability Analysis. Mater. Today Proc. 2017, 4, 1972–1977. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine Learning in Additive Manufacturing: State-of-the-Art and Perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Miranda, G.; Faria, S.; Bartolomeu, F.; Pinto, E.; Madeira, S.; Mateus, A.; Carreira, P.; Alves, N.; Silva, F.S.; Carvalho, O. Predictive Models for Physical and Mechanical Properties of 316L Stainless Steel Produced by Selective Laser Melting. Mater. Sci. Eng. A 2016, 657, 43–56. [Google Scholar] [CrossRef]
- Asilturk, I.; Kahramanli, H.; El Mounayri, H. Prediction of Cutting Forces and Surface Roughness Using Artificial Neural Network (ANN) and Support Vector Regression (SVR) in Turning 4140 Steel. Mater. Sci. Technol. 2013, 28, 980–986. [Google Scholar] [CrossRef]
- Desu, R.K.; Guntuku, S.C.; Aditya, B.; Gupta, A.K. Support Vector Regression Based Flow Stress Prediction in Austenitic Stainless Steel 304. Procedia Mater. Sci. 2014, 6, 368–375. [Google Scholar] [CrossRef] [Green Version]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O. Estimation of Superconducting Transition Temperature TC for Superconductors of the Doped MgB2 System from the Crystal Lattice Parameters Using Support Vector Regression. J. Supercond. Nov. Magn. 2015, 28, 75–81. [Google Scholar] [CrossRef]
- Pham, T.L.; Nguyen, N.D.; Nguyen, V.D.; Kino, H.; Miyake, T.; Dam, H.C. Learning Structure-Property Relationship in Crystalline Materials: A Study of Lanthanide–Transition Metal Alloys. J. Chem. Phys. 2018, 148, 204106. [Google Scholar] [CrossRef] [PubMed]
- Kauwe, S.K.; Rhone, T.D.; Sparks, T.D. Data-Driven Studies of Li-Ion-Battery Materials. Crystals 2019, 9, 54. [Google Scholar] [CrossRef] [Green Version]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine Learning Assisted Design of High Entropy Alloys with Desired Property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef] [Green Version]
- Goh, G.D.; Sing, S.L.; Yeong, W.Y. A Review on Machine Learning in 3D Printing: Applications, Potential, and Challenges. Artif. Intell. Rev. 2021, 54, 63–94. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, M.; Wu, Y.; Wang, M.; Gao, H. Machine Learning to Optimize Additive Manufacturing Parameters for Laser Powder Bed Fusion of Inconel 718. In Proceedings of the 9th International Symposium on Superalloy 718 & Derivatives: Energy, Aerospace, and Industrial Applications; No. 800; Springer: Cham, Switzerland, 2018; pp. 389–404. [Google Scholar] [CrossRef]
- Singh, A.; Cooper, D.E.; Blundell, N.J.; Gibbons, G.J.; Pratihar, D.K. Modelling of Direct Metal Laser Sintering of EOS DM20 Bronze Using Neural Networks and Genetic Algorithms. In Proceedings of the 37th International Matador 2012 Conference;International Matador Conference; Springer: London, UK, 2013; pp. 395–398. [Google Scholar]
- Tapia, G.; Elwany, A.H.; Sang, H. Prediction of Porosity in Metal-Based Additive Manufacturing Using Spatial Gaussian Process Models. Addit. Manuf. 2016, 12 Pt B, 282–290. [Google Scholar] [CrossRef]
- Imani, F.; Gaikwad, A.; Montazeri, M.; Rao, P.; Yang, H.; Reutzel, E. Layerwise In-Process Quality Monitoring in Laser Powder Bed Fusion. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 1, pp. 1–14. [Google Scholar] [CrossRef]
- Barrionuevo, G.O.; Ramos-Grez, J.A.; Walczak, M.; Betancourt, C.A. Comparative Evaluation of Supervised Machine Learning Algorithms in the Prediction of the Relative Density of 316L Stainless Steel Fabricated by Selective Laser Melting. Int. J. Adv. Manuf. Technol. 2021, 113, 419–433. [Google Scholar] [CrossRef]
- Lee, S.; Peng, J.; Shin, D.; Choi, Y.S. Data Analytics Approach for Melt-Pool Geometries in Metal Additive Manufacturing. Sci. Technol. Adv. Mater. 2019, 20, 972–978. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Tan, X.; Liu, E.; Tor, S.B. Process Parameter Optimization and Mechanical Properties for Additively Manufactured Stainless Steel 316L Parts by Selective Electron Beam Melting. Mater. Des. 2018, 147, 157–166. [Google Scholar] [CrossRef]
- Kamath, C.; El-Dasher, B.; Gallegos, G.F.; King, W.E.; Sisto, A. Density of Additively-Manufactured, 316L SS Parts Using Laser Powder-Bed Fusion at Powers up to 400 W. Int. J. Adv. Manuf. Technol. 2014, 74, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Spierings, A.B.; Herres, N.; Levy, G. Influence of the Particle Size Distribution on Surface Quality and Mechanical Properties in AM Steel Parts. Rapid Prototyp. J. 2020, 17. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.P.; Shin, G.H.; Brochu, M.; Kim, Y.J.; Yang, S.S.; Kim, K.T.; Yang, D.Y.; Lee, C.W.; Yu, J.H. Densification Behavior of 316L Stainless Steel Parts Fabricated by Selective Laser Melting by Variation in Laser Energy Density. Mater. Trans. 2016, 57, 1952–1959. [Google Scholar] [CrossRef] [Green Version]
- Greco, S.; Gutzeit, K.; Hotz, H.; Kirsch, B.; Aurich, J.C. Selective Laser Melting (SLM) of AISI 316L—Impact of Laser Power, Layer Thickness, and Hatch Spacing on Roughness, Density, and Microhardness at Constant Input Energy Density. Int. J. Adv. Manuf. Technol. 2020, 108, 1551–1562. [Google Scholar] [CrossRef]
- Leicht, A.; Rashidi, M.; Klement, U.; Hryha, E. Effect of Process Parameters on the Microstructure, Tensile Strength and Productivity of 316L Parts Produced by Laser Powder Bed Fusion. Mater. Charact. 2020, 159, 110016. [Google Scholar] [CrossRef]
- Larimian, T.; Kannan, M.; Grzesiak, D.; AlMangour, B.; Borkar, T. Effect of Energy Density and Scanning Strategy on Densification, Microstructure and Mechanical Properties of 316L Stainless Steel Processed via Selective Laser Melting. Mater. Sci. Eng. A 2020, 770, 138455. [Google Scholar] [CrossRef]
- Tucho, W.M.; Lysne, V.H.; Austbø, H.; Sjolyst-Kverneland, A.; Hansen, V. Investigation of Effects of Process Parameters on Microstructure and Hardness of SLM Manufactured SS316L. J. Alloys Compd. 2018, 740, 910–925. [Google Scholar] [CrossRef]
- Cherry, J.A.; Davies, H.M.; Mehmood, S.; Lavery, N.P.; Brown, S.G.R.; Sienz, J. Investigation into the Effect of Process Parameters on Microstructural and Physical Properties of 316L Stainless Steel Parts by Selective Laser Melting. Int. J. Adv. Manuf. Technol. 2014, 76, 869–879. [Google Scholar] [CrossRef] [Green Version]
- AlFaify, A.; Hughes, J.; Ridgway, K. Controlling the Porosity of 316L Stainless Steel Parts Manufactured via the Powder Bed Fusion Process. Rapid Prototyp. J. 2019, 25, 162–175. [Google Scholar] [CrossRef]
- Shi, W.; Wang, P.; Liu, Y.; Hou, Y.; Han, G. Properties of 316L Formed by a 400 W Power Laser Selective Laser Melting with 250 μm Layer Thickness. Powder Technol. 2020, 360, 151–164. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Yang, Y.; Xiao, D. Theoretical and Experimental Study on Surface Roughness of 316L Stainless Steel Metal Parts Obtained through Selective Laser Melting. Rapid Prototyp. J. 2016, 22, 706–716. [Google Scholar] [CrossRef]
- EOS GmbH. Large and Ultra-Fast 3D Printer with 4 Laser. Available online: https://www.eos.info/en/additive-manufacturing/3d-printing-metal/eos-metal-systems/eos-m-400-4 (accessed on 15 September 2021).
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Salim, I.; Hamza, A.B. Ridge Regression Neural Network for Pediatric Bone Age Assessment. Multimed. Tools Appl. 2021, 80, 30461–30478. [Google Scholar] [CrossRef]
- Schölkopf, B.; Vovk, V.; Luo, Z. ‘Kernel Ridge Regression’, in Empirical Inference; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Maalouf, M.; Homouz, D. Kernel Ridge Regression Using Truncated Newton Method. Knowledge-Based Syst. 2014, 71, 339–344. [Google Scholar] [CrossRef]
- Goswami, K.; Samuel, G.L. Support Vector Machine Regression for Predicting Dimensional Features of Die-Sinking Electrical Discharge Machined Components. Procedia CIRP 2021, 99, 508–513. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, M.; Lu, X. Support Vector Machine Regression Based Supercapacitor’s Dynamic Characteristics Model. In Proceedings of the 2017 International Conference on Consumer Electronics and Devices (ICCED), London, UK, 14–17 July 2017; pp. 27–30. [Google Scholar] [CrossRef]
- Loshin, D. The Practitioner’s Guide to Data Quality Improvement; Loshin, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Tidemann, A.; Høverstad, B.A.; Langseth, H.; Öztürk, P. Effects of Scale on Load Prediction Algorithms. IET Conf. Publ. 2013, 2013, 615. [Google Scholar] [CrossRef] [Green Version]
- Raj, S.; Kannan, S. Detection of Outliers in Regression Model for Medical Data. Int. J. Med. Res. Health Sci. 2017, 6, 50–56. [Google Scholar]
- Maalouf, M.; Barsoum, Z. Failure Strength Prediction of Aluminum Spot-Welded Joints Using Kernel Ridge Regression. Int. J. Adv. Manuf. Technol. 2017, 91, 3717–3725. [Google Scholar] [CrossRef]
- de Rooij, M.; Weeda, W. Cross-Validation: A Method Every Psychologist Should Know. Adv. Methods Pract. Psychol. Sci. 2020, 3, 248–263. [Google Scholar] [CrossRef]
- Brown, C.U.; Jacob, G.; Possolo, A.; Beauchamp, C.; Peltz, M.; Stoudt, M.; Donmez, A. The Effects of Laser Powder Bed Fusion Process Parameters on Material Hardness and Density for Nickel Alloy 625. NIST Adv. Manuf. Ser. 2018, 2018, 100–119. [Google Scholar]
- Yusuf, S.M.; Chen, Y.; Boardman, R.; Yang, S.; Gao, N. Investigation on Porosity and Microhardness of 316L Stainless Steel Fabricated by Selective Laser Melting. Metals 2017, 7, 64. [Google Scholar] [CrossRef] [Green Version]
- An, H.; Byon, Y.J.; Cho, C.S. Economic and Environmental Evaluation of a Brick Delivery System Based on Multi-Trip Vehicle Loader Routing Problem for Small Construction Sites. Sustainability 2018, 10, 1427. [Google Scholar] [CrossRef] [Green Version]



| Authors | Experimental Conditions | |||
|---|---|---|---|---|
| Machine | Powder | Fabricated Parts | Density/Porosity Measurement Method | |
| Kamath et al. [25] |
|
| Pillars of surface area 10 × 10 mm2. | Archimedes method and scanning electron microscope. |
| Spierings et al. [26] |
|
| Cubes of size 5 × 5 × 5 mm2. | Archimedes method. |
| Choi et al. [27] |
|
| Cubes of size 10 × 10 × 10 mm3. | Archimedes method. |
| Greco et al. [28] |
|
| Cubes of size 8 × 8 × 8 mm3. | Relative density was determined from an analytical model describing the parts dimensions, mass, and density of the material used. |
| Leicht et al. [29] |
|
| Rectangular prisms of 72 × 12 × 2.5 mm3. | Light optical microscopy micrographs. |
| Larimian et al. [30] |
|
|
| Scanning electron microscope images using ImageJ software. |
| Tucho et al. [31] |
| - | Cubes of size 10 × 10 × 10 mm3. | Scanning electron microscope images using ImageJ software. |
| Peng and Chen. [3] | Renishaw AM250. | - | Cubes of size 10 × 10 × 10 mm3. | Metallographic microscope (Leica DM2700P) after polishing the samples. |
| Cherry et al. [32] |
|
| Cubes of size 10 × 10 × 10 mm3. | In-house image analysis software. Microstructural analysis using a JEOL-35C scanning electron microscope. |
| AlFaify et al. [33] |
|
| Cubes of size10 × 10 × 10 mm3. | Archimedes method. |
| Shi et al. [34] |
|
| Specimen dimensions of 5 × 5 × 10 mm3. | Optical microscope images using Image J. |
| Wang et al. [35] |
|
| Cubes of size10 × 10 × 5 mm3. | Relative density was measured through the drainage method. |
| Sample No. | Power (W) | Speed (mm/s) | Hatch Distance (mm) | Relative Density (%) |
|---|---|---|---|---|
| 1 | 150 | 500 | 0.090 | 100.00 |
| 2 | 150 | 500 | 0.100 | 99.97 |
| 3 | 150 | 500 | 0.125 | 87.70 |
| 4 | 200 | 700 | 0.090 | 100.00 |
| 5 | 200 | 700 | 0.100 | 99.95 |
| 6 | 200 | 700 | 0.125 | 96.41 |
| 7 | 250 | 900 | 0.090 | 100.00 |
| 8 | 250 | 900 | 0.100 | 99.96 |
| 9 | 250 | 900 | 0.125 | 96.80 |
| 10 | 300 | 1100 | 0.090 | 100.00 |
| 11 | 300 | 1100 | 0.100 | 99.98 |
| 12 | 300 | 1100 | 0.125 | 97.50 |
| 13 | 230 | 950 | 0.090 | 99.93 |
| 14 | 330 | 800 | 0.120 | 100.00 |
| 15 | 330 | 950 | 0.090 | 100.00 |
| 16 | 200 | 800 | 0.110 | 97.72 |
| 17 | 200 | 950 | 0.090 | 98.93 |
| 18 | 230 | 900 | 0.110 | 98.51 |
| 19 | 230 | 1100 | 0.090 | 98.93 |
| 20 | 260 | 1100 | 0.100 | 99.30 |
| Symbols | Remarks |
|---|---|
| Coefficient vector in RR and KRR | |
| Random error vector in RR and KRR | |
| Regularization parameter in RR and KRR | |
| identity matrix in RR and KRR | |
| Tuning parameter in the KRR radial basis function () | |
| Tuning parameter in the KRR radial basis function | |
| Dual variable vector in KRR | |
| Slack variables in SVR | |
| Regularization parameter that adds a penalty in SVR | |
| Maximum error in SVR | |
| Lagrange multipliers in SVR |
| Model | Optimal Parameters | Accuracy | |
|---|---|---|---|
| R2 | MSE | ||
| RR | λ = 0.006 | 0.701 | 0.299 |
| SVR | γ = 0.4, ε = 0.05 | 0.830 | 0.170 |
| KRR | λ = 0.01, σ = 2.9 | 0.853 | 0.161 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulla, H.; Maalouf, M.; Barsoum, I.; An, H. Truncated Newton Kernel Ridge Regression for Prediction of Porosity in Additive Manufactured SS316L. Appl. Sci. 2022, 12, 4252. https://doi.org/10.3390/app12094252
Abdulla H, Maalouf M, Barsoum I, An H. Truncated Newton Kernel Ridge Regression for Prediction of Porosity in Additive Manufactured SS316L. Applied Sciences. 2022; 12(9):4252. https://doi.org/10.3390/app12094252
Chicago/Turabian StyleAbdulla, Hind, Maher Maalouf, Imad Barsoum, and Heungjo An. 2022. "Truncated Newton Kernel Ridge Regression for Prediction of Porosity in Additive Manufactured SS316L" Applied Sciences 12, no. 9: 4252. https://doi.org/10.3390/app12094252
APA StyleAbdulla, H., Maalouf, M., Barsoum, I., & An, H. (2022). Truncated Newton Kernel Ridge Regression for Prediction of Porosity in Additive Manufactured SS316L. Applied Sciences, 12(9), 4252. https://doi.org/10.3390/app12094252






