Research on Predicting Remain Useful Life of Rolling Bearing Based on Parallel Deep Residual Network
Abstract
:1. Introduction
2. Theoretical Background
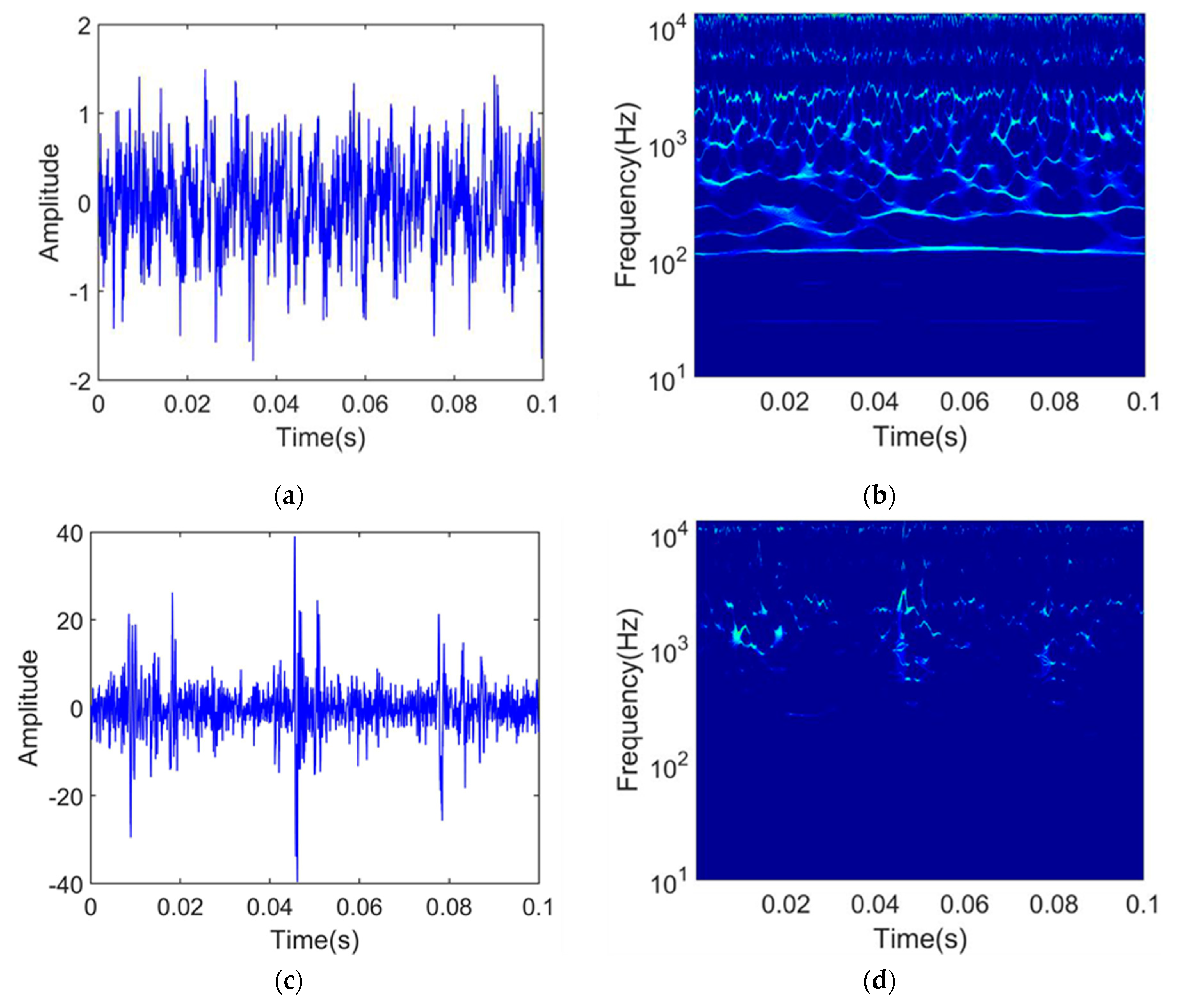
2.1. Synchrosqueezed Wavelet Transforms
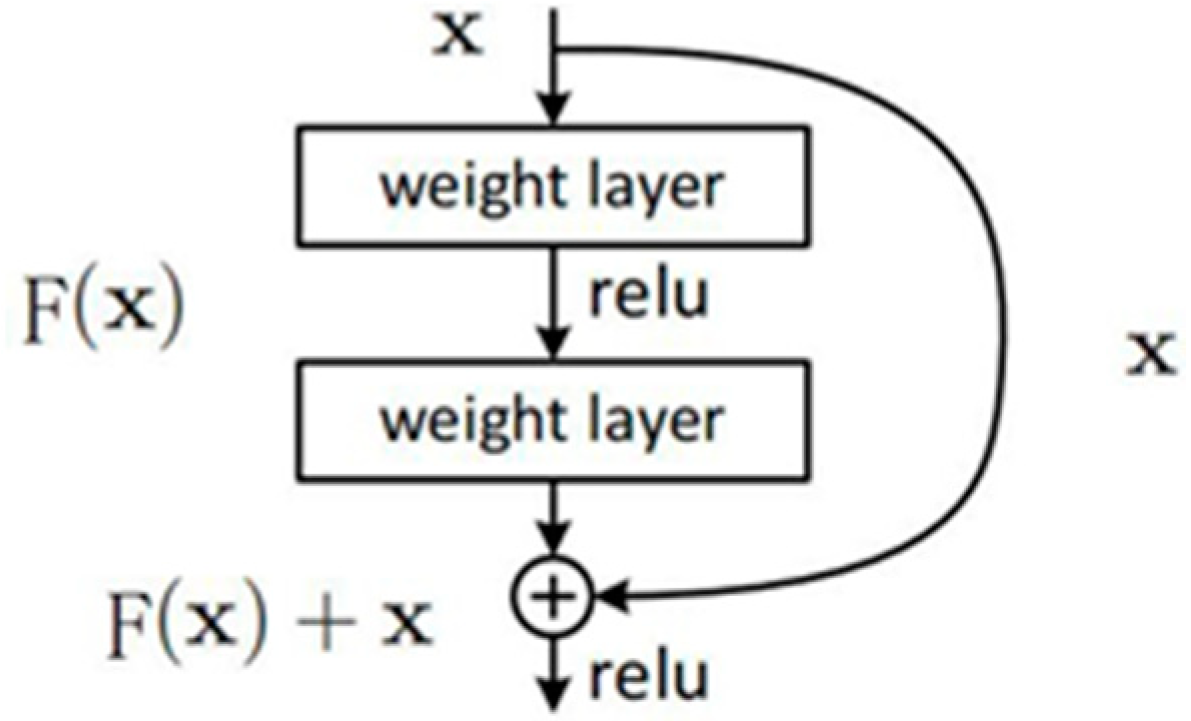
2.2. Deep Residual Convolutional Neural Networks
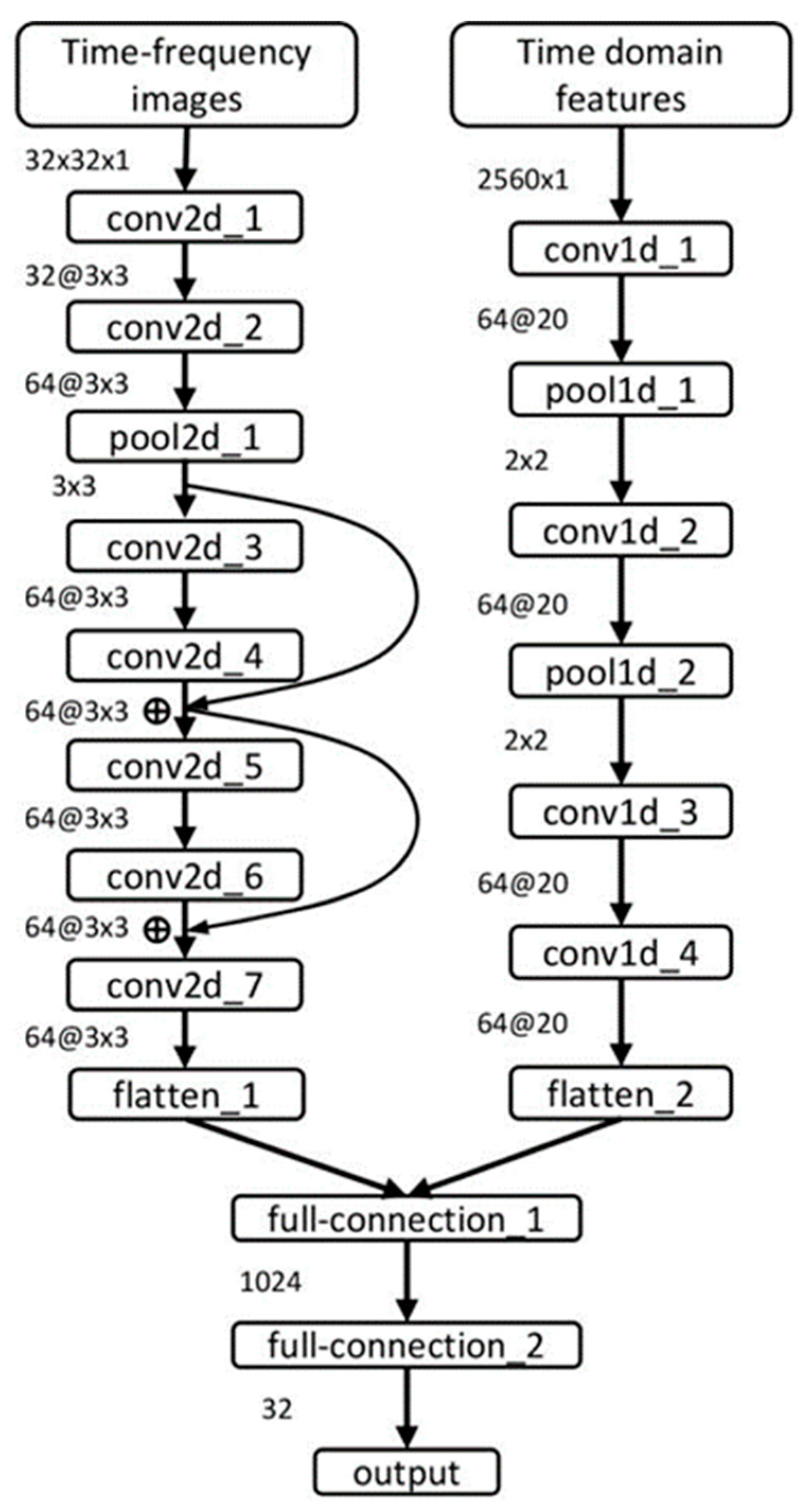
2.3. Parallel Network Structure
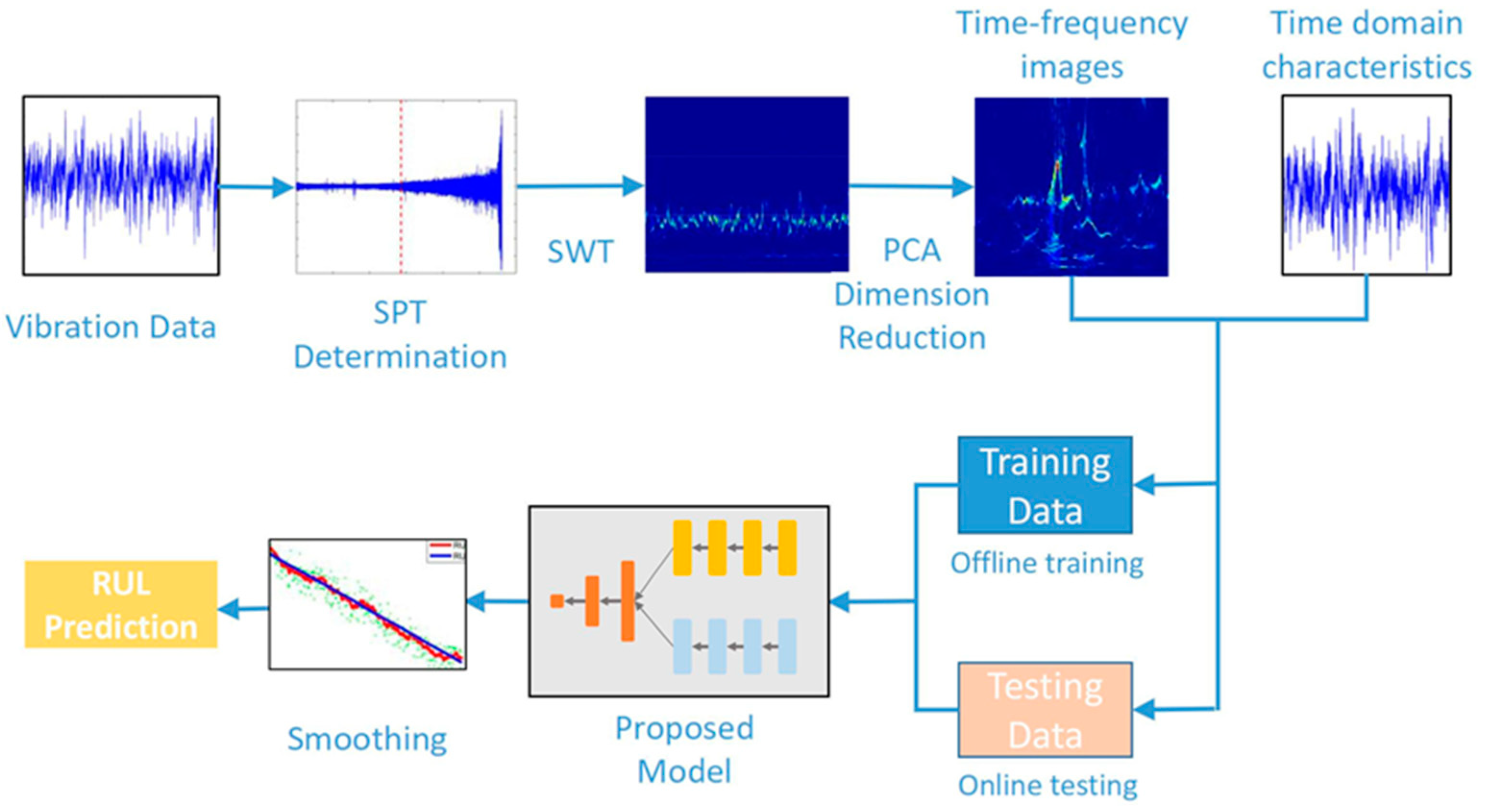
3. Proposed Method
3.1. Flow Chart
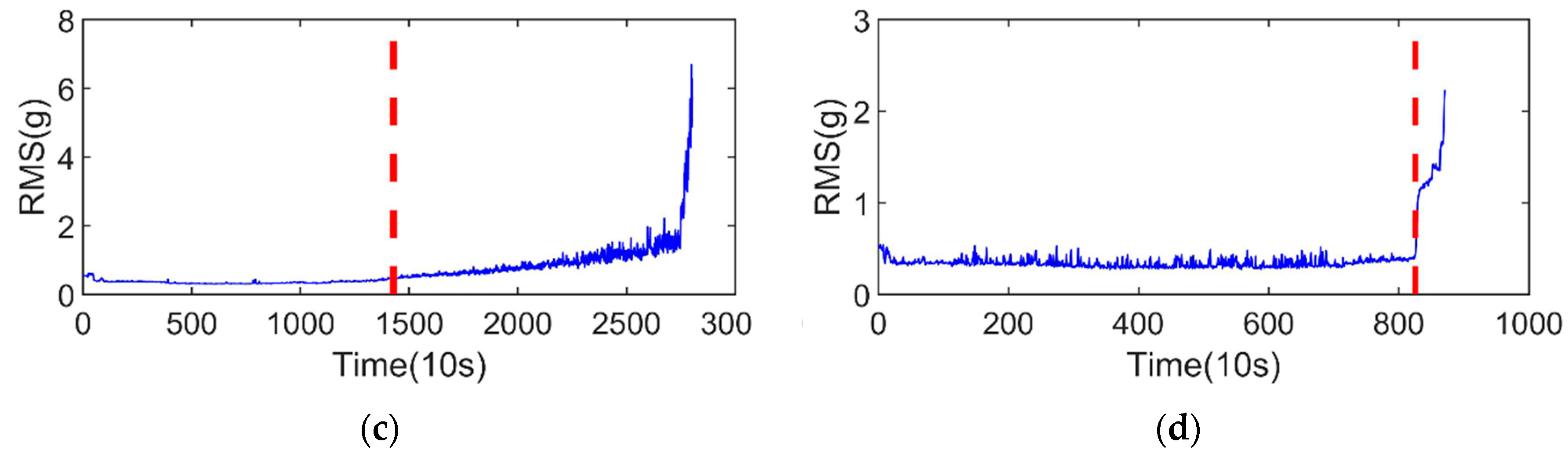
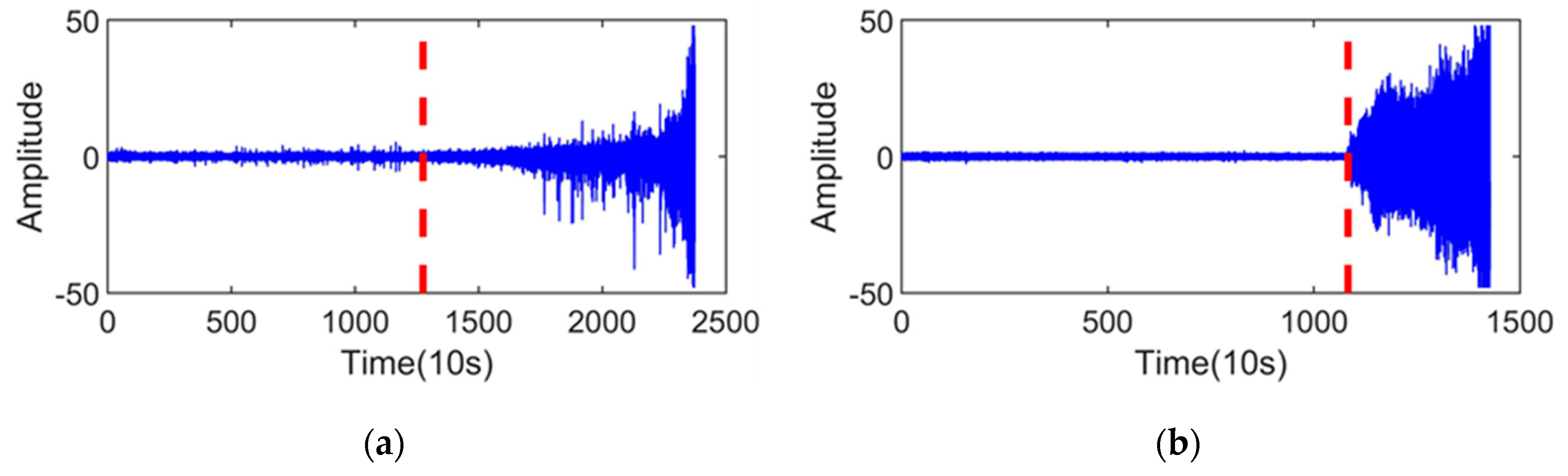
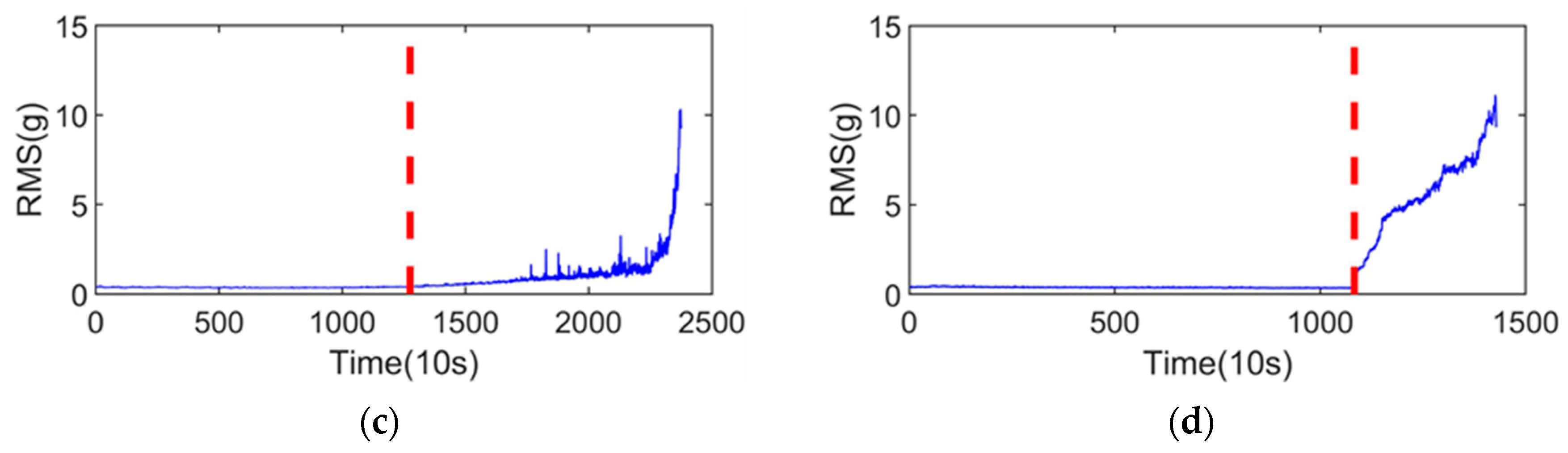
3.2. SPT Determination
3.3. Training Details of Neural Network Model
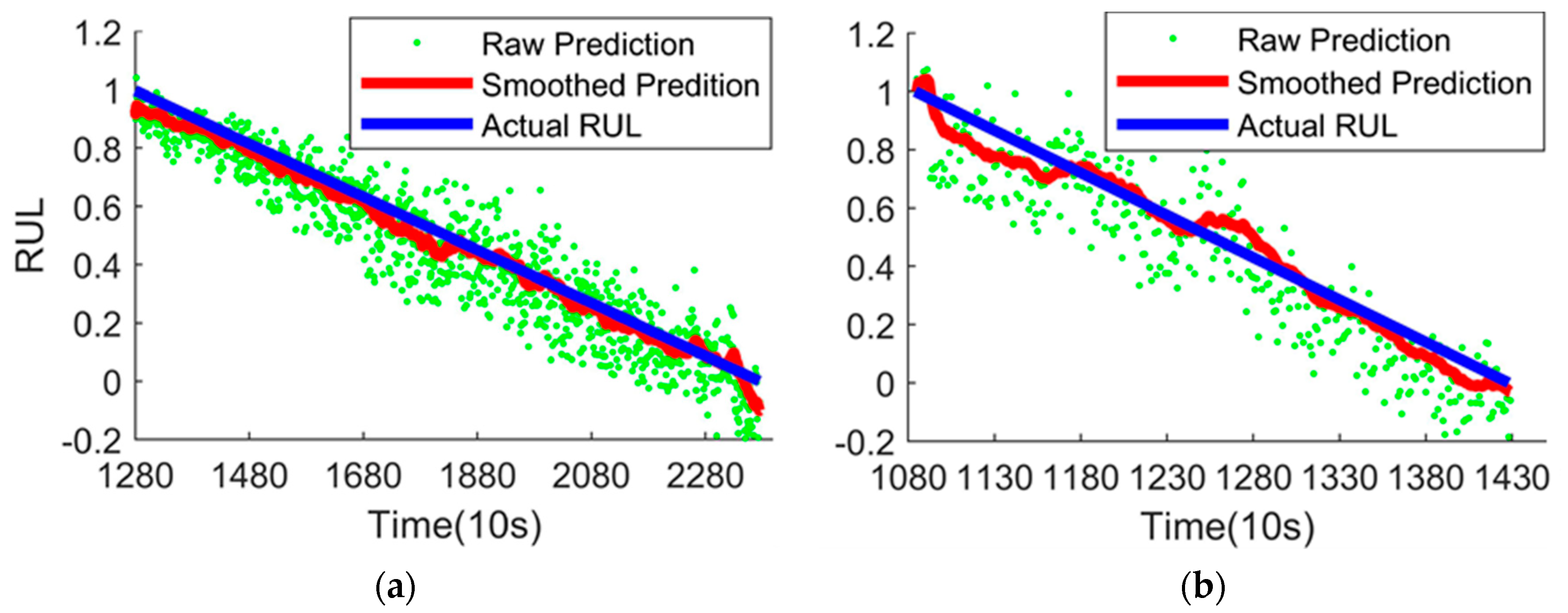
3.4. Smoothing
4. Experimental Study
4.1. Dataset Description
4.2. Experimental Process
4.3. Comparisons with Different Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.; Quan, Q.; Cai, K.Y. A profust reliability based approach to prognostics and health management. IEEE Trans. Rel. 2014, 63, 26–41. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.C.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Tian, Z.G.; Liao, H.T. Condition based maintenance optimization for multi-component systems using proportional hazards model. Reliab. Eng. Syst. Saf. 2011, 96, 581–589. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Liu, R.; Parmeshwaran, V. Residual life predictions from vibration-based degradation signals: A neural network approach. IEEE Trans. Ind. Electron. 2004, 51, 694–700. [Google Scholar] [CrossRef]
- Ali, J.B.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56, 150–172. [Google Scholar]
- Chen, X.; Xiao, H.; Guo, Y.; Kang, Q. A multivariate grey RBF hybrid model for residual useful life prediction of industrial equipment based on state data. Int. J. Wirel. Mob. Comput. 2016, 10, 90–96. [Google Scholar] [CrossRef]
- Loutas, T.H.; Roulias, D.; Georgoulas, G. Remaining useful life estimation in rolling bearings utilizing data-driven probabilistic E-support vectors regression. IEEE Trans. Rel. 2013, 62, 821–832. [Google Scholar] [CrossRef]
- Song, Y.; Liu, D.; Hou, Y.; Yu, J.; Peng, Y. Satellite lithium-ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm. Chin. J. Aeronaut. 2018, 31, 31–40. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Babu, G.S.; Zhao, P.; Li, X.L. Deep convolutional neural network based regression approach for estimation of remaining useful life. In Proceedings of the 21st International Conference on Database Systems for Advanced Applications, Dallas, TX, USA, 16–19 April 2016. [Google Scholar]
- Zhu, J.; Chen, N.; Peng, W. Estimation of bearing remaining useful life based on multiscale convolutional neural network. IEEE Trans. Ind. Electron. 2019, 66, 3208–3216. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Yang, B.; Liu, R.; Zio, E. Remaining useful life prediction based on a double-convolutional neural network architecture. IEEE Trans. Ind. Electron. 2019, 66, 9521–9530. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, X. Convolutional neural network based on attention mechanism and Bi-LSTM for bearing remaining life prediction. Appl. Intell. 2022, 52, 1076–1091. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, K.; Wu, J.; Zhu, H.; Lee, C.K.M. A deep learning-based two-stage prognostic approach for remaining useful life of rolling bearing. Appl. Intell. 2022, 52, 5880–5895. [Google Scholar] [CrossRef]
- Huang, R.; Xi, L.; Li, X.; Liu, R.; Qiu, H.; Lee, J. Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods. Mech. Syst. Singal Process. 2007, 21, 193–207. [Google Scholar] [CrossRef]
- Wang, X.; Wang, T.; Ming, A.; Han, Q.; Chu, F.; Zhang, W.; Li, A. Deep spatiotemporal convolutional-neural-network-based remaining useful life estimation of bearings. Chin. J. Mech. Eng. 2021, 34, 62–76. [Google Scholar] [CrossRef]
- Cao, Y.; Ding, Y.; Jia, M.; Tian, R. A novel temporal convolutional network with residual self-attention mechanism for remaining useful life prediction of rolling bearings. Reliab. Eng. Syst. Safe. 2021, 215, 107813. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the 13th International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ren, L.; Cheng, X.; Wang, X.; Cui, J.; Zhang, L. Multi-scale dense gate recurrent unit networks for bearing remaining useful life prediction. Future Gener. Comput. Sys. 2019, 94, 601–609. [Google Scholar] [CrossRef]
- Ahmad, W.; Khan, S.A.; Kim, J.M. A hybrid prognostics technique for rolling element bearings using adaptive predictive models. IEEE Trans. Ind. Electron. 2018, 65, 1577–1584. [Google Scholar] [CrossRef]
- Picking Loss Functions—A Comparison Between MSE, Cross Entropy and Hinge Loss. Available online: https://rohanvarma.me/Loss-Functions/ (accessed on 14 April 2022).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. ASME. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the 2012 IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012. [Google Scholar]


| The Proposed Method | Time–Frequency Features + CNN | Time Domain Features + CNN | SVR | ||
|---|---|---|---|---|---|
| Bearing1_3 | MAE | 0.09 | 0.12 | 0.15 | 0.14 |
| RMSE | 0.12 | 0.16 | 0.22 | 0.31 | |
| Bearing1_4 | MAE | 0.17 | 0.73 | 0.31 | 0.25 |
| RMSE | 0.23 | 0.26 | 0.28 | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Qiao, D.; Han, K.; Chen, X.; He, Z. Research on Predicting Remain Useful Life of Rolling Bearing Based on Parallel Deep Residual Network. Appl. Sci. 2022, 12, 4299. https://doi.org/10.3390/app12094299
Wang X, Qiao D, Han K, Chen X, He Z. Research on Predicting Remain Useful Life of Rolling Bearing Based on Parallel Deep Residual Network. Applied Sciences. 2022; 12(9):4299. https://doi.org/10.3390/app12094299
Chicago/Turabian StyleWang, Xingang, Dongkai Qiao, Kaizhong Han, Xiaohui Chen, and Ziqiu He. 2022. "Research on Predicting Remain Useful Life of Rolling Bearing Based on Parallel Deep Residual Network" Applied Sciences 12, no. 9: 4299. https://doi.org/10.3390/app12094299
APA StyleWang, X., Qiao, D., Han, K., Chen, X., & He, Z. (2022). Research on Predicting Remain Useful Life of Rolling Bearing Based on Parallel Deep Residual Network. Applied Sciences, 12(9), 4299. https://doi.org/10.3390/app12094299





