Single-Shot Compressed Imaging via Random Phase Modulation

Abstract

Compressed sensing (CS) provides an innovative framework for signal sampling, which enables accurate recovery of the sparse or compressible signal from a small set of linear measurements far fewer than the Nyquist rate in traditional signal processing. In compressed sensing, random modulation plays a key role, which can spread out the signal information more or less evenly across all locations. There are many modulation techniques, such as amplitude modulation, frequency modulation, phase modulation, spectrum modulation, and so on. Among these modulation techniques, phase modulation is vital due to the efficiency and convenience of modulation. In this paper, we review both the theoretical and application of compressed sensing and several compressed imaging systems using random phase modulation. First, we review the fundamentals of compressed sensing, dividing it into three parts: sparse representation, incoherent measurement, and nonlinear reconstruction algorithm. We then show how phase modulation can be applied to compressed sensing and compressed imaging, where the presentation can be divided into six main parts, corresponding to different aspects of phase modulation applied in compressed sensing or compressed imaging: (1) Fundamentals of compressed sensing. (2) Principles of phase modulation. (3) Single-shot compressed imaging with spatial-domain single random phase mask (CI-SSRPM). (4) Single-shot compressed imaging with a random convolution using a double random phase mask (CI-DRPM). (5) Single-shot compressed imaging with Fourier-domain single random phase mask (CI-FSRPM). (6) Single-shot compressed imaging with double random phase encoding (CI-DRPE).

1. Introduction

The Nyquist/Shannon theorem has been considered the doctrine of signal acquisition and processing since 1948, which asserts that an arbitrary band-limited signal can be accurately reconstructed from its samples with the sampling rate to be at least twice the bandwidth. One of the major drawbacks is that the Nyquist rate is so high that most of the applications require signal compression before storage or transmission, which takes too much time for signal sampling.

In 2006, compressed sensing (CS) was firstly proposed by Candès [1] and Donoho [2], considered a breakthrough in the signal processing community, aiming at reducing this high sampling rate. Compressed sensing (CS) provides an innovative framework for signal sampling, which enables accurate recovery of the sparse or compressible signal from a small set of linear measurements far fewer than the Nyquist rate in traditional signal processing.

In CS, randomness is exactly crucial because it can spread out the information of the signal more or less evenly across all locations, which is one key for CS to successfully recover from fewer measurements less than the Nyquist rate. In classical CS, the random Gaussian matrix (RGM) is the most popular measurement matrix due to its theoretical guarantees. However, the drawback of RGM is that it is impractical or too expensive for physical implementation, and other random modulation techniques must be introduced to realize random modulation.

CS theory is not only available to traditional imaging applications but also available in more complex cases, e.g., infrared imaging and terahertz imaging. The introduction of CS theory can help enhance the performance of various imaging systems in terms of high-quality reconstruction, low cost, small size and etc. From the aspect of physical realization, various modulation techniques existed, such as amplitude modulation, frequency modulation, phase modulation, spectrum modulation, and so on. Among these modulation techniques, phase modulation plays a vital role in the efficiency and convenience of phase modulation.

In 2009, Romberg [3] proposed a compressed imaging system by random convolution and that the convolution with a specific-designed random pulse followed by random subsampling was considered as a universal compressed sampling operator, which was equivalent to a random phase modulation in the Fourier-domain of the well-known 4-f system. In 2010, Rivenson et al. [4] proposed a single-exposure compressed imaging system by combining the well-known optical scheme of double random phase encoding (DRPE), which could be applied to overcome the resolution limit caused by both diffraction and geometrical limitation. In 2014, Wu et al. proposed a quasi-monochromatic thermo optical phase modulation compressed sensing imaging system, which overcomes the problem of collecting too much data due to high-resolution requirements in the imaging process [5]. In 2017, Liu et al. [6] proposed a single exposure compressed imaging system based on the conventional optical 4-f architecture with an RPM placed in the Fourier plane and a random coded aperture in the image plane for subsampling. In 2021, Li et al. proposed the correlation imaging of moving targets based on phase modulation. The spatial random phase modulator was introduced into the imaging optical path to modulate the three-dimensional spectrum data of the target, and then the detector was used to obtain the two-dimensional aliasing signal to realize the reconstruction by single exposure [7].

In this paper, both the theoretical and applications of compressed sensing and several compressed imaging systems using random phase modulation are reviewed. First, the fundamentals of compressed sensing are presented. Second, the principle of phase modulation is described. Finally, several strategies of compressed sensing and compressed imaging using random phase modulation are reviewed. The rest of the paper is organized as follows: In Section 2 and Section 3, the fundamentals of compressed sensing and the principles of phase modulation are both described. In Section 4, different schemes of compressed imaging using random phase modulation are presented, which include: (i) single-shot compressed imaging with spatial-domain single random phase mask (CI-SSRPM). (ii) Single-shot compressed imaging with a random convolution using a double random phase mask (CI-DRPM). (iii) Single-shot compressed imaging with Fourier-domain single random phase mask (CI-FSRPM). (iv) Single-shot compressed imaging with double random phase encoding (CI-DRPE). Section 5 is the conclusion.

2. Fundamentals of Compressed Sensing

In 2006, Compressed Sensing (CS) was firstly proposed by Donoho and Candès et al. Compared to the traditional Shannon–Nyquist sampling theorem, CS provides a new sampling framework for band-limited signals. As we all know, most signals in the real world are sparse or compressible in some bases or dictionary, which means that they may have a concise representation by selecting the appropriate transform domain or dictionary.

The success of CS relies on two properties: sparsity and incoherence. Sparsity is the inherent property of those signals. The information contained in the signal can be represented only with the help of a few significant components, as compared to the total length of the signal. Incoherence provides a guideline for the design of the measurement matrix, and performance guarantees for successful recovery of the signal from fewer measurements.

CS involves three major foundations: sparse representation, random measurement matrix, and nonlinear recovery algorithm.

2.1. Sparse Representation

In compressed sensing, the sparsity of the signal means that the signal can be represented on a suitable basis with fewer significant coefficients than the signal length. Examples of the bases include discrete Fourier transform (DFT), discrete cosine transform (DCT), discrete wavelet transform (DWT), etc.

In mathematical, the sparse representation of the signal can be expressed in the following form

$$\mathit{x}=\mathsf{\Psi }\mathsf{\alpha }=\left(\begin{array}{cccc}{\psi }_{11}& {\psi }_{12}& \cdots & {\psi }_{1N}\\ {\psi }_{21}& {\psi }_{22}& \cdots & {\psi }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\psi }_{N1}& {\psi }_{N2}& \cdots & {\psi }_{NN}\end{array}\right)\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_N\end{array}\right)=\left(\begin{array}{cccc}{\mathsf{\Psi }}_1& {\mathsf{\Psi }}_2& \cdots & {\mathsf{\Psi }}_N\end{array}\right)\left(\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_N\end{array}\right)={\displaystyle \sum _{i=1}^N{\mathsf{\Psi }}_i{\alpha }_i}$$

(1)

where $\mathsf{\Psi }$ is a sparsifying matrix, the size is $N\times N$, ${\psi }_i$ is the column of matrix $\mathsf{\Psi }$, ${\mathsf{\Psi }}_i$ is the $i$-th column, $i=1,2,\cdots ,N$, $\mathsf{\alpha }$ is the sparse coefficients whose has only $K$ non-zeros (i.e., sparsity) or significant entries with $K<<N$.

2.2. Measurement Matrix

Different from the Shannon sampling scheme, in compressed sensing, the subsampling measurements can be obtained via linear and incoherent projections corrupted by noise as follows

$$\begin{array}{cc}\mathit{y}& =\mathsf{\Phi }\mathit{x}+\mathit{e}=\left(\begin{array}{cccc}{\varphi }_{11}& {\varphi }_{12}& \cdots & {\varphi }_{1N}\\ {\varphi }_{21}& {\varphi }_{22}& \cdots & {\varphi }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\varphi }_{M1}& {\varphi }_{M2}& \cdots & {\varphi }_{MN}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_N\end{array}\right)+\left(\begin{array}{c}{e}_1\\ e_2\\ ⋮\\ e_M\end{array}\right)\\ & =\mathsf{\Phi }\mathsf{\Psi }\mathsf{\alpha }+\mathit{e}=\mathsf{\Theta }\mathsf{\alpha }+\mathit{e}\end{array}$$

(2)

where $\mathsf{\Phi }\in {ℝ}^{M\times N}$ is measurement matrix, $\mathsf{\Theta }$ is the sensing matrix and $\mathit{e}$ is the random additive noise.

Since the measurement process of CS is not adaptive, the measurement matrix is fixed and independent of the signal $\mathit{x}$, which means that the measurement matrix should be universal for any sparse or compressible signal. The effects of the measurement matrix are reflected in two aspects: On the one hand, a stable measurement matrix $\mathsf{\Phi }$ can preserve salient information in any $K$-sparse or compressible signal in a compressed sampling process; On the other hand, the measurement matrix plays a crucial role in the reconstruction process, a ‘good’ measurement matrix can clearly enhance the recovery performance for recovering $\mathit{x}$ only from the $M$ measurements $\mathit{y}$.

In order to ensure the successful recovery of a sparse signal from fewer measurements, CS theory indicates that if the Restricted Isometry Property (RIP [8]) is satisfied, i.e., the measurement matrix satisfies the $K$-order RIP of the parameter ${\delta }_K\in (0,1)$, if

$$\left(1-{\delta }_K\right)\Vert \mathsf{\alpha }{\Vert }_2^2\le \Vert \mathsf{\Theta }\mathsf{\alpha }{\Vert }_2^2\le \left(1+{\delta }_K\right)\Vert \mathsf{\alpha }{\Vert }_2^2$$

(3)

holds for all sparse vectors $\mathsf{\alpha }$ having no more than $K$ nonzero entries.

2.3. Nonlinear Recovery Algorithm

Once the measurements vector $\mathit{y}$ and measurement matrix $\mathsf{\Phi }$ are given, the way to find a signal $\mathit{x}$ in the class of interest so that $\mathit{y}=\mathsf{\Phi }\mathit{x}$ is complete or approximate is a problem that the reconstruction algorithm should solve, termed the sparse recovery algorithms in CS.

In recent years, there have been many sparse recovery algorithms proposed to recover a sparse signal from fewer incoherent measurements. These algorithms can be categorized into three main types: convex relaxation algorithms, non-convex optimization algorithms, and greedy algorithms.

2.3.1. L0-Norm Minimization Recovery

Intuitively, we can solve the problem in Equation (2) by ${\ell }_0$ norm minimization using the following optimization.

$$\begin{array}{l}\widehat{\mathit{x}}=\arg \underset{\mathit{x}}{\min }\Vert \mathit{x}{\Vert }_0 \\ \mathrm{s}.\mathrm{t}. \mathit{y}=\mathsf{\Phi }\mathit{x}=\mathsf{\Phi }\mathsf{\Psi }\mathsf{\alpha }\end{array}$$

(4)

Unfortunately, solving Equation (4) relies on an exhaustive search, which has combinatorial computational complexity. Therefore, the goal is to find a computationally feasible algorithm that can successfully recover the sparse signal $\mathit{x}$ from the measurement $\mathit{y}$.

2.3.2. L1-Norm Minimization Recovery

An alternative is to use ${\ell }_1$ norm and defined the ${\ell }_1$ norm of a vector $\Vert \mathit{x}{\Vert }_1$ as $\Vert \mathit{x}{\Vert }_1={\sum }_{n=1}^N|x(n)|$. Then the optimization problem solved can be rewritten as

$$\begin{gathered} \widehat{\mathit{x}}=\arg \underset{\mathit{x}}{\min }\Vert \mathit{x}{\Vert }_1 \\ \mathrm{s}.\mathrm{t}.\mathit{y}=\Phi \mathit{x}=\Phi \Psi \mathsf{\alpha } \end{gathered}$$

(5)

Due to the convexity of ${\ell }_1$ the norm, Equation (5) can be regarded as the convex relaxation version of Equation (4), which can be solved via linear programming, with the computational complexity polynomial over the length of the signal.

3. Principles of Phase Modulation

In optical sensing and imaging system, light modulation has the potential to exceed the diffract limit and achieve higher contrast in imaging; among various light modulation techniques, phase modulation has gained more attention than its amplitude modulation due to its notable sensitivity and close relation to spectrum, coherence and polarization of light, and so on. Moreover, phase modulation can be easily implemented using various optical devices, spatial light modulator (SLM), liquid crystal display (LCD) and so on, which makes its use more efficient and convenient.

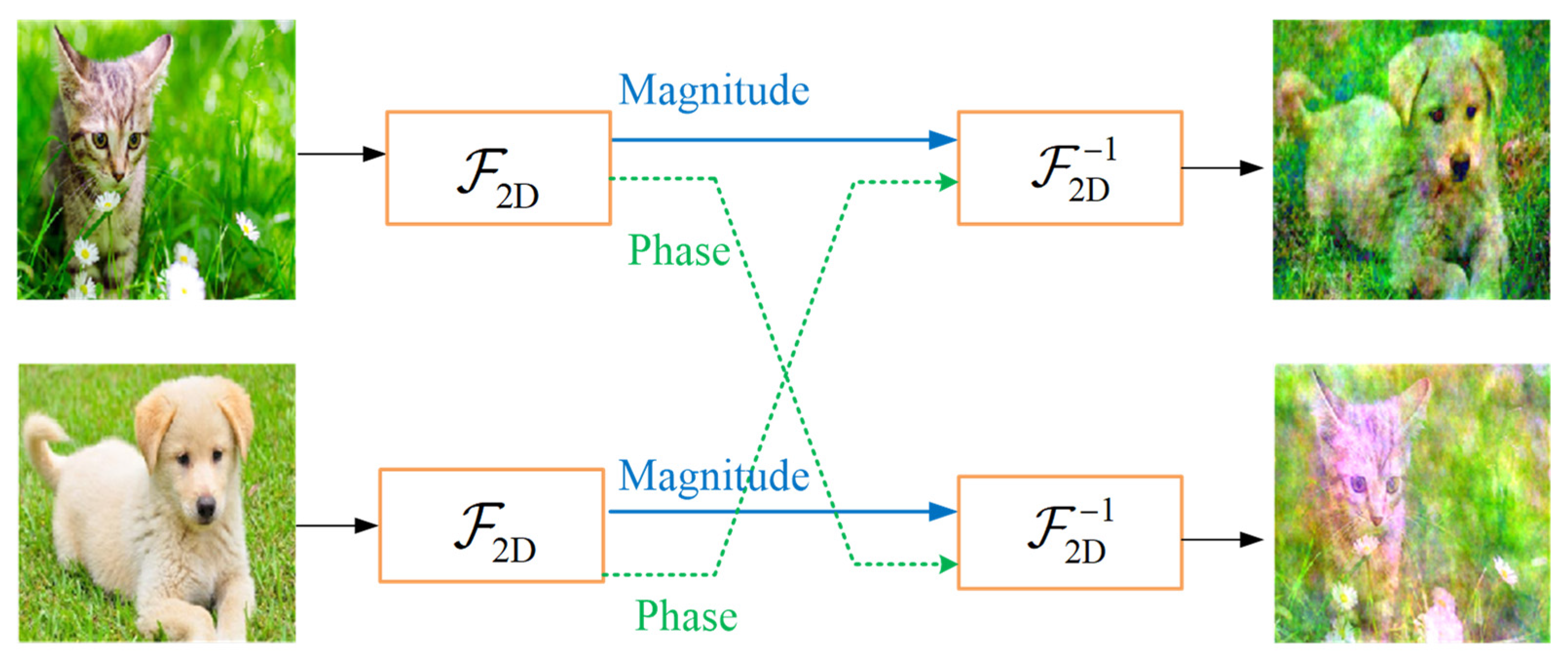
The phase component carries much more information than the amplitude component, such as the shape, depth, polarization, and so on. Therefore, phase plays a role in many applications, such as system encryption [9] or electro-optic conversion of microwave signals [10]. For example, as illustrated in Figure 1, exchange the Fourier phase of the two images and keep the amplitude unchanged, then the major contexts of both image exchange, which means that the Fourier phase contains the most amount of information about the image.

Phase modulation (PM) is the modulation technique that utilizes various optical devices to change the optical path difference (OPD) of an incident light to produce different phase delays [11]. Phase modulation can be achieved either by changing the refractive index or the thickness of an optical device, as indicated in the following equation

$$u_{\mathrm{out}}=u_{\mathrm{in}}\exp (-j\phi )$$

(6)

where $u_{\mathrm{in}}$ is the incident light, and $u_{\mathrm{out}}$ is the exit light, $\phi$ is the modulated phase of the optical device expressed by

$$\phi =2\pi n_{0}d/\lambda$$

(7)

where $d$ is the thickness of the devices or equivalently the thickness caused by the change of the refractive index, $n_0$ denotes the refractive index of the passing-through material and $\lambda$ is the wavelength of the incident light. The phase modulation can vary the direction or the shape of the wavefront of incident light.

4. Compressed Imaging Using Random Phase Modulation

The combination of random phase modulation and compressed sensing has been proposed and applied on many occasions, such as in various types of single-exposure imaging. Using them in imaging can not only overcome the problem of low resolution but also restore the possibility for the reconstruction of complex data or moving targets.

In this section, we briefly review four compressed imaging strategies using random phase modulation: (i) compressed imaging with spatial-domain single random phase mask (CI-SSRPM). (ii) Compressed imaging with double random phase mask (CI-DRPM). (iii) Compressed imaging with Fourier-domain single random phase mask (CI-FSRPM). (iv) Compressed imaging with double random phase encoding (CI-DRPE).

4.1. Single-Shot Compressed Imaging with Spatial-Domain Single Random Phase Mask (CI-SSRPM)

In this section, single-shot compressed imaging with spatial-domain single random phase mask (CI-SSRPM [12]) is presented. The optical setup is depicted in Figure 2. As illustrated in Figure 2, the random phase mask is attached to the middle between the two lenses $L_1$ and $L_2$. The object plane is at the position $z_1$ in front of the lens $L_1$, and the right side of the lens is a random phase mask with the phase distribution $\phi (r_{\phi })$. The right side of the phase mask is closely attached to the lens $L_2$, and the image plane is $z_2$ from the right side of the lens.

The optical field emitted by the object is focused by the lens $L_1$ and then randomly modulated by a random phase mask; the scattered field is then focused by the lens $L_2$. Finally, the complex field of the object reaches the CCD detection array behind the lens. The entire measurement process is achieved in a single exposure.

The advantage of this system is that all the required measurements can be obtained in a single exposure. The forward projection operator (i.e., measurement matrix) between the object point ${\mathit{r}}_o$ and the image point ${\mathit{r}}_i$ can be expressed as

$$\begin{array}{ll}u(r_i,r_o)& =K_0{\displaystyle \int \exp \left[j\frac{2\pi }{\lambda z_1}{(r_o-r_{\phi })}^2\right]}\times \exp \left[-j\frac{\pi }{\lambda f_{L_1}}{r}_{\phi }{}^2\right]\exp \left[j\phi (r_{\phi })\right]\times \\ & \exp \left[-j\frac{\pi }{\lambda f_{L_2}}{r}_{\phi }{}^2\right]\exp \left[j\frac{2\pi }{\lambda z_2}{(r_i-r_{\phi })}^2\right]d{r}_{\phi }\end{array}$$

(8)

where $\lambda$ denotes the wavelength of the incident light, $\phi ({\mathit{r}}_{\phi })$ denotes the random phase mask, $f_{L_1}$ and $f_{L_2}$ denotes the focal length of Lens $L_1$ and $L_2$, and $C$ denotes a multiplicative constant. Equation (8) defines the relationship between the object point and image point as integrated overall random phase mask pointing $\phi ({\mathit{r}}_{\phi })$. Such relation is spatial random and shift-variant due to the randomness of the phase mask.

The relation in Equation (9) can be discretized into the following form

$$\begin{array}{ll}{\mathsf{\Phi }}_{m,n}& =K_0{\displaystyle {\int }_{-L/2}^{L/2}\exp \left[j\frac{\pi }{\lambda z_1}{(n{\Delta }_o-\xi )}^2\right]}•\exp (-j\frac{\pi }{\lambda f_{L_1}}{\xi }^2)\exp \left[j\varphi (\xi )\right]\\ & •\exp \left[-j\frac{\pi }{\lambda f_{L_2}}{\xi }^2\right]\exp \left[j\frac{\pi }{\lambda z_2}{(m{\Delta }_i-\xi )}^2\right]d\xi \end{array}$$

(9)

where $-N/2\le n\le N/2-1,-M/2\le m\le M/2-1$. ${\Delta }_o$ and ${\Delta }_i$ are the pixel size of the object and the CCD.

As the element of the Gaussian matrix has too much freedom, which cannot be physically achieved or cost too much, some deterministic matrices [13] with fewer independent elements have important practical significance and are easy to implement to satisfy the specific distribution of optical phase mask (such as Toeplitz or Circulant distribution), which can be expressed as follows Equations (10)–(12):

$${\phi }_{\mathrm{Gauss}}=\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1N}\\ a_{21}& a_{22}& \cdots & a_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ a_{M1}& a_{M2}& \cdots & a_{MN}\end{array}\right)$$

(10)

$${\phi }_{\mathrm{Toeplitz}}=\left(\begin{array}{cccc}{a}_N& a_{N-1}& \cdots & a_1\\ a_{N+1}& a_N& \cdots & a_2\\ ⋮& ⋮& \ddots & ⋮\\ a_{N+M-1}& a_{N+M-2}& \cdots & a_M\end{array}\right)$$

(11)

$${\phi }_{\mathrm{Circulant}}=\left(\begin{array}{cccc}{a}_N& a_{N-1}& \cdots & a_1\\ a_1& a_N& \cdots & a_2\\ ⋮& ⋮& \ddots & ⋮\\ a_{N-1}& a_{N-2}& \cdots & a_N\end{array}\right)$$

(12)

The numerical experiments of CI-SSRPM are depicted in Figure 3. Lena image is chosen as the test image with the size 64 × 64. Daubechies 5 wavelet transform is chosen as the sparsifying basis. The subspace pursuit (SP [14]) algorithm is used as the recovery algorithm. The reconstruction quality is quantified using the signal-to-noise ratio (SNR) and shown in

Table 1. SNR of Lena image reconstruction with different number of measurements.

Phase Mask	Measurements	SNR (dB)
Gauss	2163	26.87
Gauss	2336	28.91
Gauss	2595	29.94
Toeplitz	2163	28.13
Toeplitz	2336	29.07
Toeplitz	2595	30.18
Circulant	2163	27.73
Circulant	2336	29.26
Circulant	2595	30.21

.

4.2. Single-Shot Compressed Imaging with Random Convolution Using Double Random Phase Mask (CI-DRPM)

In 2009, Romberg [4] proposed a compressed imaging system by random convolution, that the convolution with a specific-designed random pulse followed by random sub-sampling was considered as a universal compressed sampling operator, which was equivalent to implementing a random phase modulation in the Fourier-domain of the well-known 4-f system.

In Ref. [4], Romberg proposed a novel strategy for compressed sensing which utilizes random convolution as a universal and efficient random measurement operator. Such measurement operator is constructed by firstly convolved with a specific-designed pulse and successively by random sub-sampling. The random convolution for compressed sensing can be algebraically written as

$$\begin{array}{cc}{\mathit{x}}_{\Sigma }& =\mathit{x}\otimes \mathit{h}\\ & =N^{-1/2}{\mathit{F}}^{\mathrm{H}}\Sigma \mathit{F}\mathit{x}\\ & =\mathit{H}\mathit{x}\end{array}$$

(13)

where $\otimes$ denotes convolution operator, $\mathit{F}$ denotes the discrete Fourier matrix with entries $(F_{ij})={[{\exp }^{-j2\pi (i-1)(j-1)/N}]}_{0\le i,j\le N-1}$ and ${\mathit{F}}^{\mathrm{H}}$ denotes the inverse, and $\mathsf{\Sigma }$ is the Fourier transform version of pulse $\mathit{h}$ in the following form

$$\mathsf{\Sigma }=\mathit{F}\mathit{h}=\left[\begin{array}{cccc}{\sigma }_1& & & \\ & {\sigma }_2& & \\ & & \ddots & \\ & & & {\sigma }_N\end{array}\right]$$

(14)

where $\mathsf{\Sigma }$ is a diagonal matrix with the entries ${\sigma }_i (i=1,2,\cdots ,N)$ has a unit amplitude and random phases, which can be generated as follows:

$${\sigma }_i=\{\begin{array}{ll}\pm 1 \mathrm{with} \mathrm{equal} \mathrm{probability}\hfill & i=1\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & 2\le i<N/2\hfill \\ \pm 1 \mathrm{with} \mathrm{equal} \mathrm{probability}\hfill & i=N/2\hfill \\ {\sigma }_{N-i+2}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{N-i+2}\hfill & N/2+1\le i\le N\hfill \end{array}$$

(15)

The random demodulation (RD) method is often used for random subsampling. The image ${\mathit{x}}_{\Sigma }$ can be divided into blocks, and successively a measurement vector can be obtained by multiplying the entries in each block by a sequence of random signs and summing. Let $\Xi$ be a diagonal matrix with the entries independently drawn from ±1 Bernoulli distribution with equal probability, and $\mathit{P}\in {ℝ}^{M\times N}$ denotes an accumulate-and-dump subsampling operation that can be expressed as follows:

$$\mathit{P}=\left[\begin{array}{cccc}1 1 \cdots & & & \\ & 1 1 \cdots & & \\ & & \cdots & \\ & & & 1 1 \cdots \end{array}\right]$$

(16)

For simplicity, a renormalization factor is introduced into the random demodulation process, and finally, the random measurement vector can be algebraically rewritten as

$$\begin{array}{cc}{\mathit{y}}_{\Xi }& ={(M/N)}^{-1/2}\mathit{P}\mathsf{\Xi }{\mathit{x}}_{\mathsf{\Sigma }}\\ & =M^{-1/2}P\mathsf{\Xi }{\mathit{F}}^H\mathsf{\Sigma }\mathit{F}\mathit{x}\\ & =\mathsf{\Phi }\mathit{x}\\ & ={\mathcal{D}}_{\downarrow }\left(\mathit{x}\otimes \mathit{h}\right)\end{array}$$

(17)

where $\mathsf{\Phi }$ denotes the forward measurement operator (i.e., measurement matrix) in compressed sensing via random convolution followed by random demodulation.

The subsampling strategy of random convolution compressed sensing (RCCS) has several attractive advantages, such as universality, numerical structure, physically realizable, which can provide an excellent strategy to perform universal CS acquisition, fast reconstruction, and a simply equipped setup to record the compressed measurements in a single exposure. The scheme of RCCS is depicted in Figure 4.

As illustrated in Figure 4, an SLM coded with the pulse $\mathit{h}$ is placed in the Fourier domain, and another SLM with random sign entries in the image plane. Numerical results will be presented in the next subsection for comparison.

4.3. Single-Shot Compressed Imaging with Fourier-Domain Single Random Phase Mask (CI-FSRPM)

Figure 5 is a schematic diagram of a 2D image in a 4-f optical setup with a random phase modulated in the frequency domain. The first lens transforms the standard Lena image and is then followed by a phase modulation that may be performed by an SLM after another lens transforms back into the time domain. Finally, a low-resolution detector array records the measurements.

In Refs. [15,16], we proposed a novel compressed imaging using single random phase modulation in the Fourier domain. The optical setup of our proposed is depicted in Figure 6. As depicted in Figure 6, the system is based upon the architecture based on a 4-f optical setup. A phase mask that may be manipulated by an SLM placed in the frequency domain plays a crucial role in maintaining the amplitude of the Fourier transform of the original image unchanged; only the phase of the Fourier transforms of the image makes the type uniformly random delay point-wise. Such modulation can reduce the sampling burden in a spatial domain because the entire information is spread out in the spatial domain.

For a 2D image, the forward measurement operator of our proposed CI-FSRPM scheme can be expressed as

$$\Phi ={\mathcal{D}}_{\downarrow }{\mathit{ℱ}}_{2\mathrm{D}}^{-1}\left(\Sigma \odot {\mathit{ℱ}}_{2\mathrm{D}}(\cdot )\right)={\mathcal{D}}_{\downarrow }\mathit{ℳ}$$

(18)

where $\odot$ denotes Hadamard product. ${\mathit{ℱ}}_{2\mathrm{D}}$ and ${\mathit{ℱ}}_{2\mathrm{D}}^{-1}$ denote 2D Fourier transform and 2D inverse Fourier transform operator and matrix $\mathsf{\Sigma }$ is a $N\times N$ matrix whose entries are the (renormalized) 2D Fourier transform coefficients of $h$, i.e., $\mathsf{\Sigma }={\mathit{ℱ}}_{2\mathrm{D}}(h)$. Nevertheless, we first generate $\mathsf{\Sigma }$ at random by taking

$$\mathsf{\Sigma }=\left[\begin{array}{cccc}{\sigma }_{11}& {\sigma }_{12}& \cdots & {\sigma }_{1N}\\ {\sigma }_{21}& {\sigma }_{22}& \cdots & {\sigma }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{N1}& {\sigma }_{M2}& \cdots & {\sigma }_{NN}\end{array}\right]$$

(19)

where the entries $\left\{{\sigma }_{ij}\right\},i=1,\cdots ,N,j=1,\cdots ,N$ are unit magnitude complex numbers with random phases which means pure phase mask. Note that the entries of $\mathsf{\Sigma }$ must satisfy conjugate symmetric property for simplicity so that real object $\mathit{x}$ can still be real after performing the operator $\mathsf{\Phi }$.

Specifically, the entries $\mathsf{\Sigma }$ are generated as follows:

For $N$ even,

$${\sigma }_{ij}=\{\begin{array}{ll}\pm 1 \mathrm{with} \mathrm{equal} \mathrm{probability}\hfill & (i,j)\in \{(1,1),(1,N/2+1),(N/2+1,1),(N/2+1,N/2+1)\}\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & i=1,2\le j<N/2\hfill \\ {\sigma }_{i,N-j+2}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{i,N-j+2}\hfill & i=1,N/2+1\le j\le N\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & j=1,2\le i<N/2\hfill \\ {\sigma }_{N-i+2,j}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{N-i+2,j}\hfill & j=1,N/2+1\le i\le N\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & 2\le i<N/2,2\le j\le N\hfill \\ {\sigma }_{N-i+2,N-j+2}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{N-i+2,N-j+2}\hfill & N/2+1\le i\le N,2\le j\le N\hfill \end{array}$$

(20)

For $N$ odd,

$${\sigma }_{ij}=\{\begin{array}{ll}\pm 1 \mathrm{with} \mathrm{equal} \mathrm{probability}\hfill & (i,j)\in \{(1,1)\}\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & i=1,2\le j\le (N+1)/2\hfill \\ {\sigma }_{i,N-j+2}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{i,N-j+2}\hfill & i=1,(N+1)/2+1\le j\le N\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & j=1,2\le i<(N+1)/2\hfill \\ {\sigma }_{N-i+2,j}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{N-i+2,j}\hfill & j=1,(N+1)/2+1\le i\le N\hfill \\ \exp (j{\theta }_i),{\theta }_i\in (0,2\pi ] \mathrm{yields} \mathrm{uniform} \mathrm{distribution}\hfill & 2\le i<(N+1)/2,2\le j\le N\hfill \\ {\sigma }_{N-i+2,N-j+2}^{*},\mathrm{the} \mathrm{conjucate} \mathrm{of} {\sigma }_{N-i+2,N-j+2}\hfill & (N+1)/2+1\le i\le N,2\le j\le N\hfill \end{array}$$

(21)

And the adjoint operator can be constructed as

$${\Phi }^{\mathrm{H}}={\mathit{ℱ}}_{2\mathrm{D}}^{-1}\left({\Sigma }^{\mathrm{H}}\odot {\mathit{ℱ}}_{2\mathrm{D}}\left({\mathcal{D}}_{\uparrow }(\cdot )\right)\right)$$

(22)

where ${\mathsf{\Sigma }}^{\mathrm{H}}$ is the conjugate of $\mathsf{\Sigma }$, $𝒟$_↑ is the integral upsampling. Note that one advantage of the construction is that the modulation scheme $\mathit{ℳ}$ is orthogonal, i.e.,

$${\mathit{ℳ}}^{\mathrm{H}}\mathit{ℳ}={\mathit{ℱ}}_{2\mathrm{D}}^{-1}({\Sigma }^{\mathrm{H}}\odot {\mathit{ℱ}}_{2\mathrm{D}}({\mathit{ℱ}}_{2\mathrm{D}}^{-1}(\Sigma \odot {\mathit{ℱ}}_{2\mathrm{D}}(\cdot ))))=N\mathbb{I}$$

(23)

where $\mathbb{I}$ is the matrix with all entries equal to one.

In this section, numerical experiments are presented to verify the effectiveness of CI-DRPM and CI-FSRPM. The test environment is set with a 32-bit Windows7 operating system, the Intel (R) Core (TM) i5-2320 and 4-core processor, a basic frequency 3.00 GHz, an effective memory of 3.0 GB, and the test software Matlab2010a. Figure 7 shows the potential applications of random phase encoding in frequency domain simulation based on 4-f optical architecture. We create 1536 × 1536 original images using Lena and Phantom and take them using Figure 6 to achieve a random phase encoding and integral subsampling.

Figure 7a,b are standard images of Lena and Phantom, and Figure 7c,f are compressed measurements of Lena and Phantom images, respectively. The measurement size is 384 × 384; that is to say, the sampling rate is four in the horizontal and vertical directions. Figure 7d,e are the reconstruction results of Lena with the measurements shown in Figure 7c using iterative soft thresholding (IST [17]) algorithm and gradient projection sparse reconstruction (GPSR [18]) algorithm. The SNR is 29.84 dB and 29.68 dB. Figure 7g,h are the reconstruction results from measurements shown in Figure 7f using the IST and GPSR algorithm. The SNR is 39.87 dB and 39.62 dB. The sparse operators $\mathsf{\Psi }$ have chosen the Daubechies 10 wavelet of Rice University (rice wavelet toolbox, RWT) [19]. The wavelet scale is the same as 3.

In another numerical experiment, we compare our proposed method with Random Demodulation (RD) method proposed by Justin Romberg [16] and the RecPC method proposed by W. Yin [20]. The test images are Lena, Cameraman, and Phantom image; the image size is chosen into seven levels of 256 × 256, 512 × 512, 768 × 768, 1024 × 1024, 1280 × 1280, 1536 × 1536, and 1792 × 1792, the total downsampling rate is 1/8 (the reason for this rate selection is due to the hybrid measurements of RD method, which mean two low-resolution measurements, one is the measurement with random demodulation, another is a direct low-resolution version of the original image, both sampling rates are 1/16, with the amount to 1/8. For a fair comparison, while RecPC method uses random location downsampling, that is, in all positions, the uniform random decimation measurement value of the position. In this experiment, the sample rate for horizontal and vertical are 1/2 and 1/4, respectively. The test environment is a 32-bit window7 operating system, the processor is Intel (R) Core (TM) i5-2320 quad-core, the frequency is 3.00 GHz, available memory is 3.0 G, and we used Matlab2010a software. Numerical results are listed in

Table 2. Performance comparison of CI-DRPM, RecPC, and CI-FSRPM method.

Phantom	CI-DRPM		RecPC		CI-FSRPM
Subsampling Type	Integral Subsampling		Random Location		Integral Subsampling
Solver	tvqc_logbarrier		RecPF_Circ		IST		GPSR
Size	SNR/dB	Time/s	SNR/dB	Time/s	SNR/dB	Time/s	SNR/dB	Time/s
256 × 256	22.55	824	39.43	3.92	12.15	3.03	12.21	2.92
512 × 512	24.85	2629	39.90	11.99	23.38	8.78	23.41	10.47
768 × 768	26.81	6788	41.24	20.83	25.98	14.28	26.08	23.47
1024 × 1024	27.38	12,558	41.44	38.26	32.52	22.39	32.68	45.14
1280 × 1280	27.62	25,507	41.96	55.27	34.00	27.41	34.04	52.93
1536 × 1536	-	-	42.10	87.31	37.46	30.57	37.47	72.61
1792 × 1792	-	-	42.36	111.4	37.53	33.13	37.26	86.49
Cameraman	CI-DRPM		RecPC		CI-FSRPM
Subsampling Type	Integral Subsampling		Random Location		Integral Subsampling
Solver	tvqc_logbarrier		RecPF_Circ		IST		GPSR
Size	SNR/dB	Time/s	SNR/dB	Time/s	SNR/dB	Time/s	SNR/dB	Time/s
256 × 256	20.22	624.7	23.30	7.97	20.74	1.52	20.74	3.19
512 × 512	25.47	3033	32.12	20.35	29.74	3.85	29.73	6.53
768 × 768	26.88	6732	34.18	33.49	32.96	6.28	32.98	12.18
1024 × 1024	28.93	13,719	37.35	55.43	36.75	9.05	36.62	20.64
1280 × 1280	29.58	24,939	38.37	77.87	37.50	10.54	37.39	32.95
1536 × 1536	-	-	39.85	120.6	38.88	14.04	38.59	40.33
1792 × 1792	-	-	40.37	144.8	39.08	18.50	38.76	56.22
Lena	CI-DRPM		RecPC		CI-FSRPM
Subsampling Type	Integral Subsampling		Random Location		Integral Subsampling
Solver	tvqc_logbarrier		RecPF_Circ		IST		GPSR
Size	SNR/dB	Time/s	SNR/dB	Time/s	SNR/dB	Time/s	SNR/dB	Time/s
256 × 256	20.98	624.7	24.33	6.86	23.57	1.35	23.51	2.73
512 × 512	26.24	2838	32.35	19.43	32.00	3.17	32.02	5.72
768 × 768	28.33	6391	35.13	30.31	34.93	5.04	34.77	10.35
1024 × 1024	30.38	13,621	37.97	52.08	37.22	6.20	37.02	18.36
1280 × 1280	30.86	23,143	39.25	72.85	37.69	9.45	37.32	35.21
1536 × 1536	-	-	40.62	111.8	38.33	14.49	37.96	55.69
1792 × 1792	-	-	41.25	142.0	38.59	18.99	38.18	77.32

.

As depicted in Table 2, the CI-DRPM method proposed by Romberg with a random demodulator (RD) for subsampling using tvqc_logbarrier solver can only deal with 1280 × 1280 pixels; larger is impossible. Our proposed CI-FSRPM is superior to CI-DRPM in terms of image size, reconstruction time, and reconstruction quality. The reason is that our proposed CI-FSRPM performs in 2D form, which is more effective than CI-DRPM performs in 1D form. Although the RecPC method has the highest SNR (especially sparse gradient images, such as the Phantom images), the reason is the subsampling type is by random sampling with a random position rather than random demodulation, which severely limits its practical application.

4.4. Single-Shot Compressed Imaging with Double Random Phase Encoding (CI-DRPE)

In 2010, Rivenson et al. [15] proposed a single-exposure compressed imaging system by combining the well-known optical scheme of double random phase encoding (DRPE), which could be applied to overcome the resolution limit caused by both diffraction and geometrical limitation. The schematic of compressed imaging using double random phase encoding (CI-DRPE) is depicted in Figure 8. As shown in Figure 8, the image is randomly modulated with the two random phase masks (RPMs) placed in the input plane and the Fourier plane of the 4-f optical system.

The modulation scheme of CI-DRPE can be expressed as follows

$$\mathit{y}={\mathcal{D}}_{\downarrow }{\mathit{ℱ}}_{2\mathrm{D}}^{-1}{\Sigma }_{\mathrm{RPM}2}{\mathit{ℱ}}_{2\mathrm{D}}\left({\Sigma }_{\mathrm{RPM}1}\odot \mathit{x}\right)$$

(24)

where $\odot$ denotes Hadamard product. ${\mathsf{\Sigma }}_{\mathrm{RPM1}}=\exp (j{P}_1)$ and ${\mathsf{\Sigma }}_{\mathrm{RPM2}}=\exp (j{P}_2)$ denotes two random phase masks, both the size of $P_1$ and $P_2$ are the same as the image $\mathit{x}$, ${\mathcal{D}}_{\downarrow }$ denotes a random subsampling operator.

The Equation (21) can be reformulated as a universal measurement operator in matrix-vector form as follows

$$\mathit{y}={\mathcal{D}}_{\downarrow }{\mathit{F}}^{\mathrm{H}}{\mathsf{\Theta }}_{\mathrm{RPM}2}\mathit{F}{\mathsf{\Theta }}_{\mathrm{RPM}1}\mathit{x}$$

(25)

where ${\mathcal{D}}_{\downarrow }$ is the random subsampling operation, $\mathit{F}$ denote the discrete Fourier matrix (DFT) with size $N\times N$ ($N=n^2$) and ${\mathit{F}}^{\mathrm{H}}$ denotes its inverse, ${\mathsf{\Theta }}_{\mathrm{RPM1}}=\mathrm{diag}({\Sigma }_{\mathrm{RPM1}})$ and ${\mathsf{\Theta }}_{\mathrm{RPM2}}=\mathrm{diag}({\Sigma }_{\mathrm{RPM2}})$, i.e., ${\mathsf{\Theta }}_{\mathrm{RPM1}}$ take the elements of random phase mask ${\Sigma }_{\mathrm{RPM1}}$ on the diagonal, so as the ${\mathsf{\Theta }}_{\mathrm{RPM1}}$. $\mathit{x}$ denotes the vector rearranged the input image lexicographically, and $\mathit{y}$ denotes the compressed measurements. Note that the operation $\mathit{F}{\mathsf{\Theta }}_{\mathrm{RPM1}}$ in Equation (25) denotes random scrambling in the Fourier domain in the matrix form as:

$$\mathit{F}{\mathsf{\Theta }}_{\mathrm{RPM1}}=\left(\begin{array}{cccc}1& 1& \cdots & 1\\ 1& W_N& \cdots & W_N^{(N-1)}\\ ⋮& ⋮& \ddots & ⋮\\ 1& W_N^{(N-1)}& \cdots & W_N^{(N-1)(N-1)}\end{array}\right)\left(\begin{array}{cccc}{e}^{j2\pi p_1}& & & \\ & e^{j2\pi p_2}& & \\ & & \ddots & \\ & & & e^{j2\pi p_N}\end{array}\right)$$

(26)

where $W_N=\exp (j2\pi /N)$. The entries ${\left\{p_i\right\}}_{i=1}^N$ are drawn independently from a uniform distribution $[0,1)$, which leads to inter-column statistical independence for $\mathit{F}{\mathsf{\Theta }}_{\mathrm{RPM1}}$ and equivalence to the random Gaussian measurement operator. Numerical experiments are shown in Figure 9. In Figure 9, the parameters are set as follows: Cameramen image is selected as the test image, the size is 512 × 512, the subsampling rate is 0.5, the measurements are complex, the type of subsampling is random location. The sparsifying basis is RWT with a wavelet scale is 3. The performance of CI-DRPE under different subsampling rates is tested; the results are depicted in

Table 3. Performance test of CI-DRPE method with different subsampling rate.

Subsampling Rate	0.1	0.2	0.3	0.4	0.5
SNR/dB	17.88	25.05	27.60	29.43	31.18

. As shown in Table 3, we can find that the quality of the recovered image can be improved as the subsampling rate increases.

5. Conclusions

In this paper, we have demonstrated the effectiveness of several different compressive imaging methods using random phase modulation. The principles of compressive sensing theory and random phase modulation are presented. A brief review of the implementation of compressive imaging with different optical architectures is described. Numerical experiments demonstrate that compressive imaging together with random phase modulation can help in recovering the image from real-valued measurements or complex-valued measurements.

In summary, we have shown that random phase modulation can effectively enhance the performance of the compressive imaging method. We believe that random phase modulation combined with compressive sensing can further enhance the performance of three-dimensional imaging, video sensing, and phase retrieval, which will lead to new designs of optical setups and enable new applications.