A Comparative Energy and Economic Analysis of Different Solar Thermal Domestic Hot Water Systems for the Greek Climate Zones: A Multi-Objective Evaluation Approach
Abstract
1. Introduction
2. Material and Methods
2.1. Overall Configuration
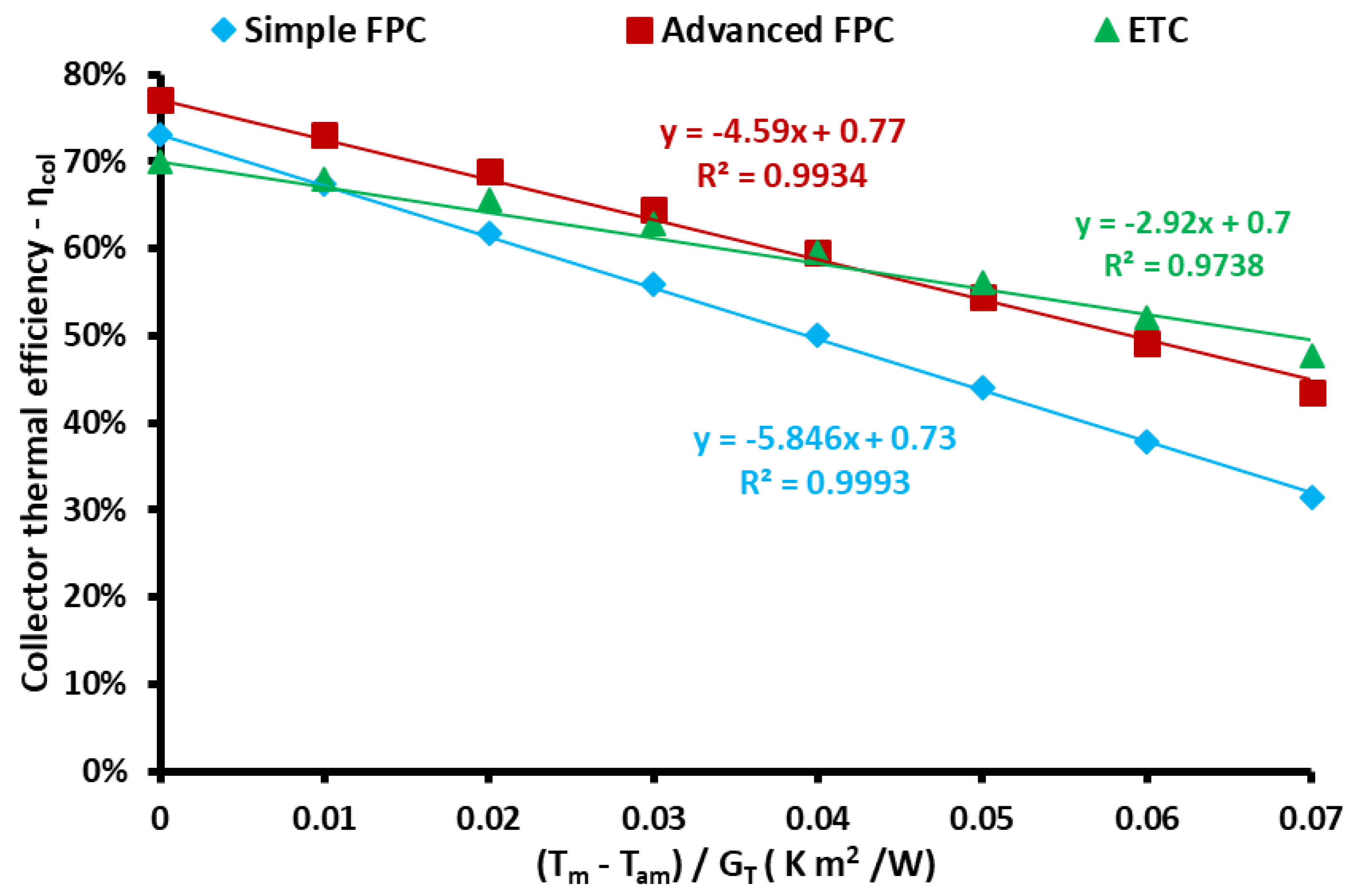
2.2. Solar Thermal Collectors
2.3. The F-Chart Method
2.4. Economic Evaluation
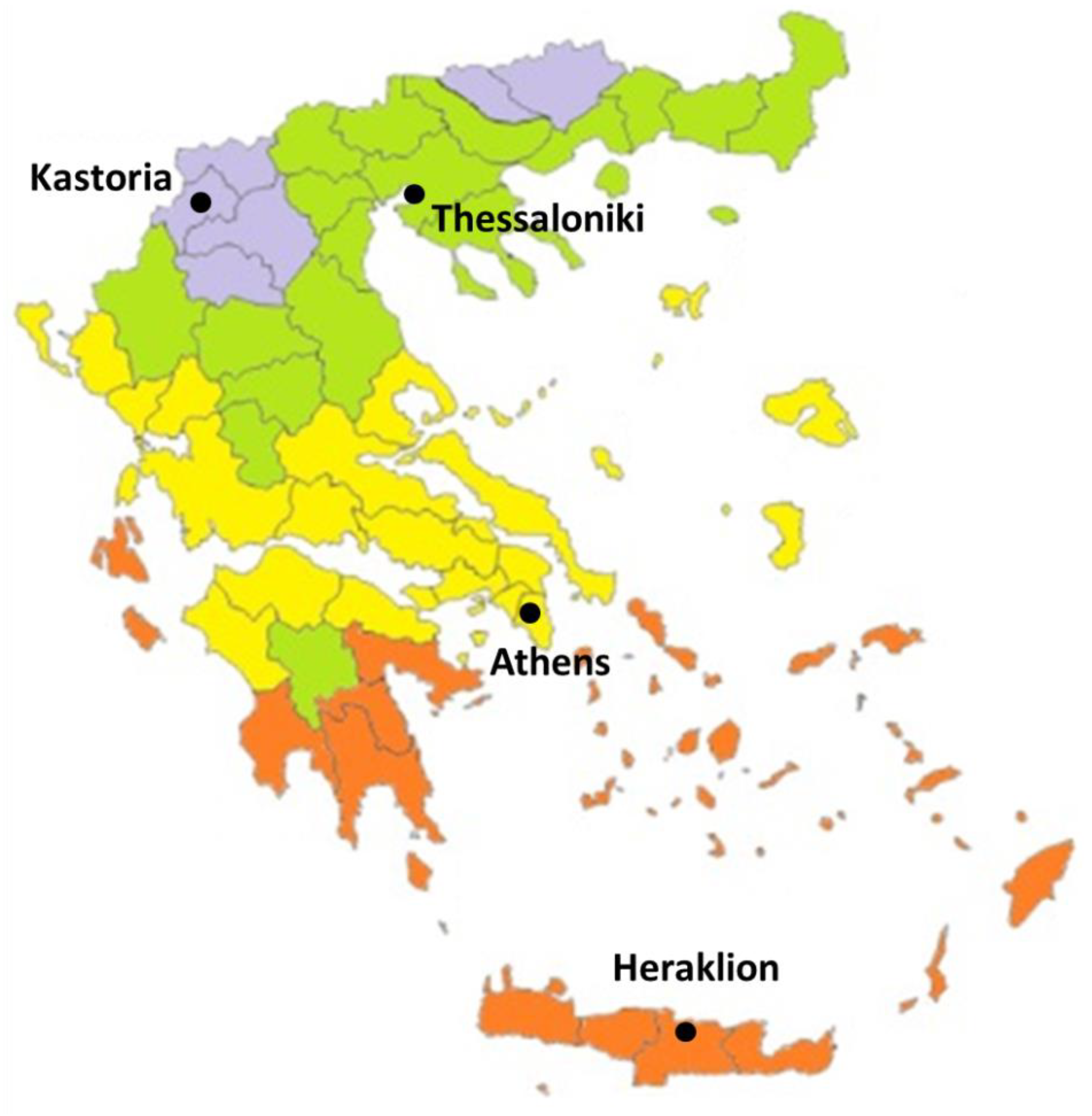
2.5. Weather Data
2.6. Followed Methodology
3. Results and Discussion
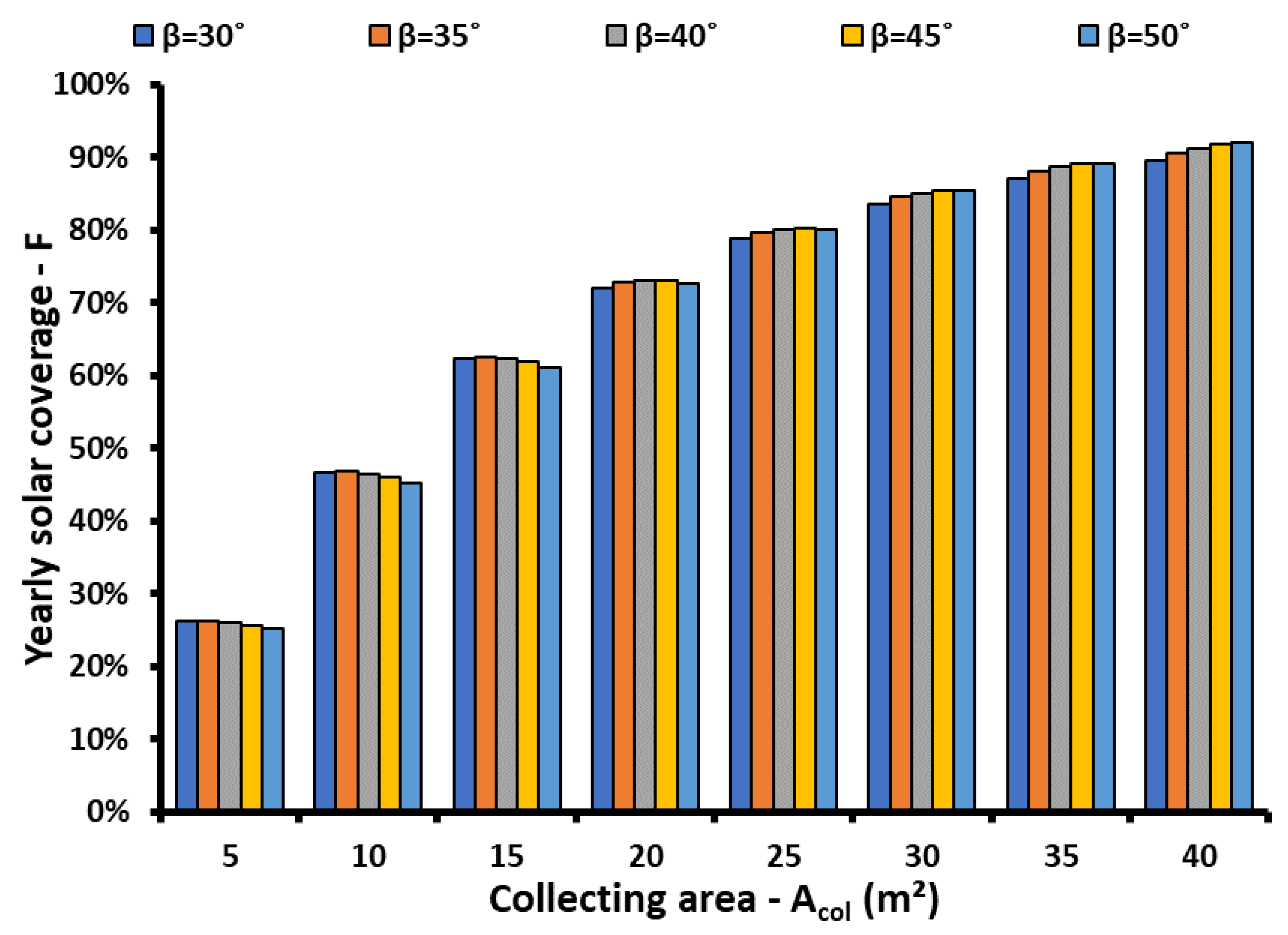
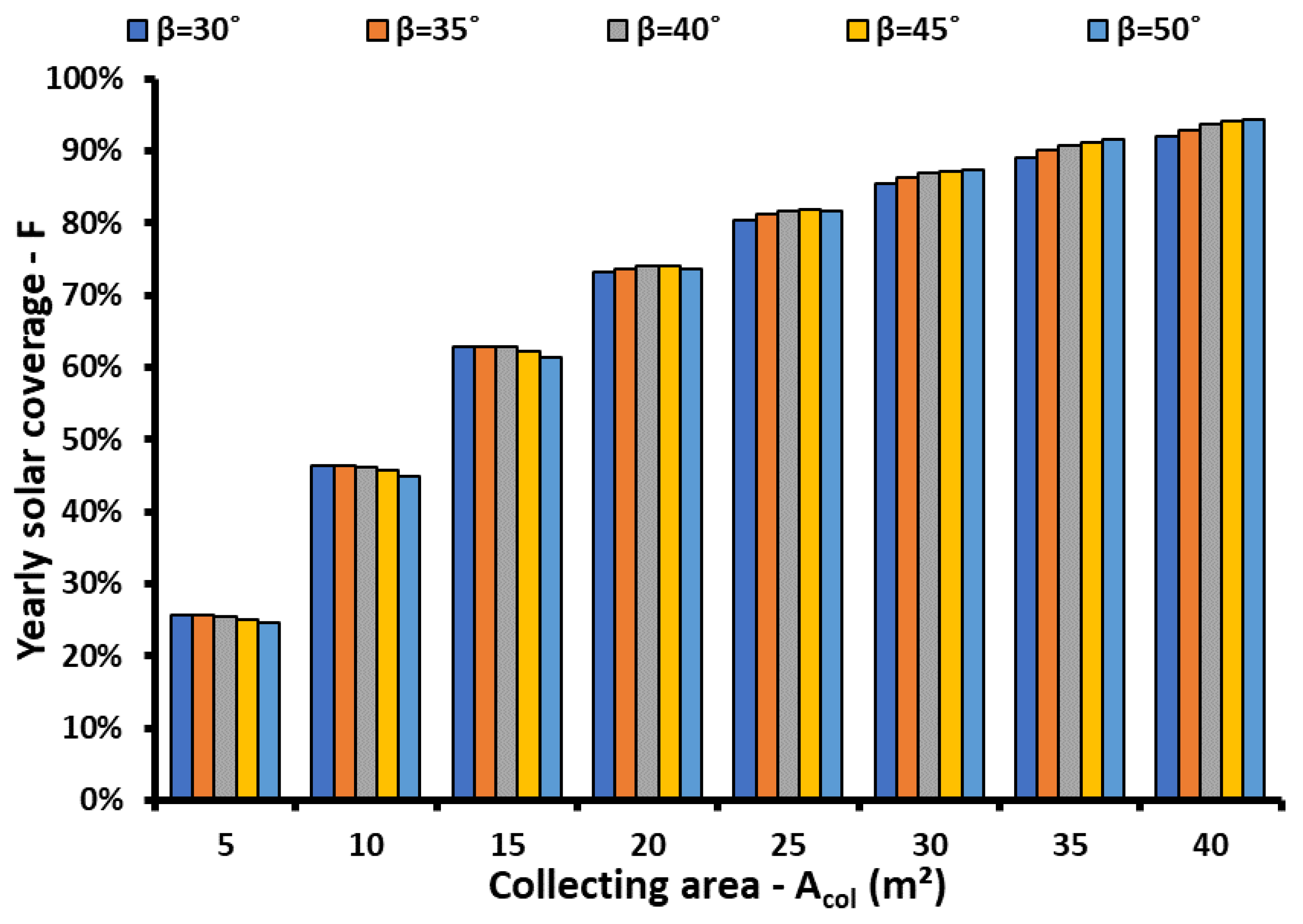
3.1. Parametric Analysis for the Climate Zone B—Athens
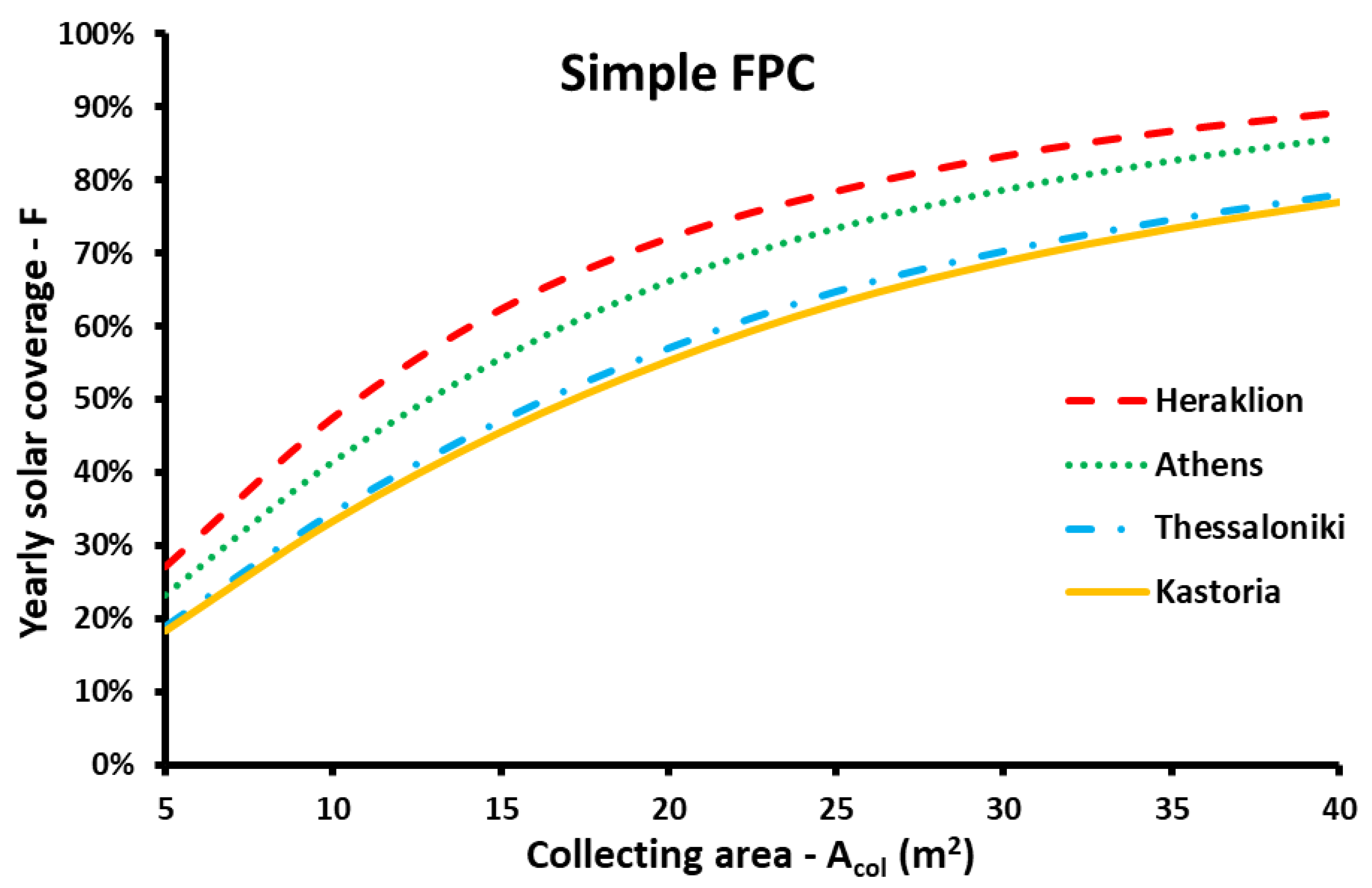
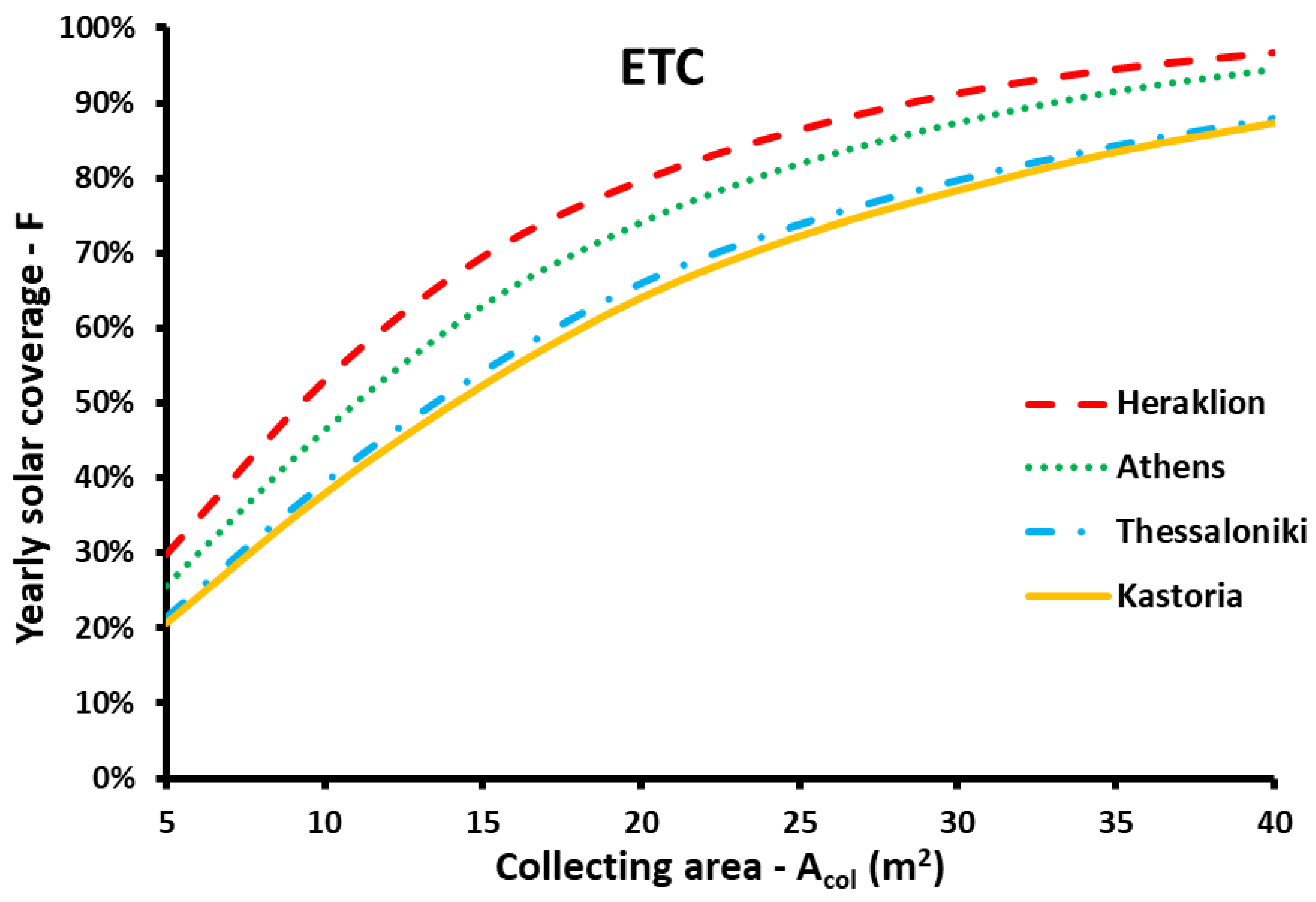
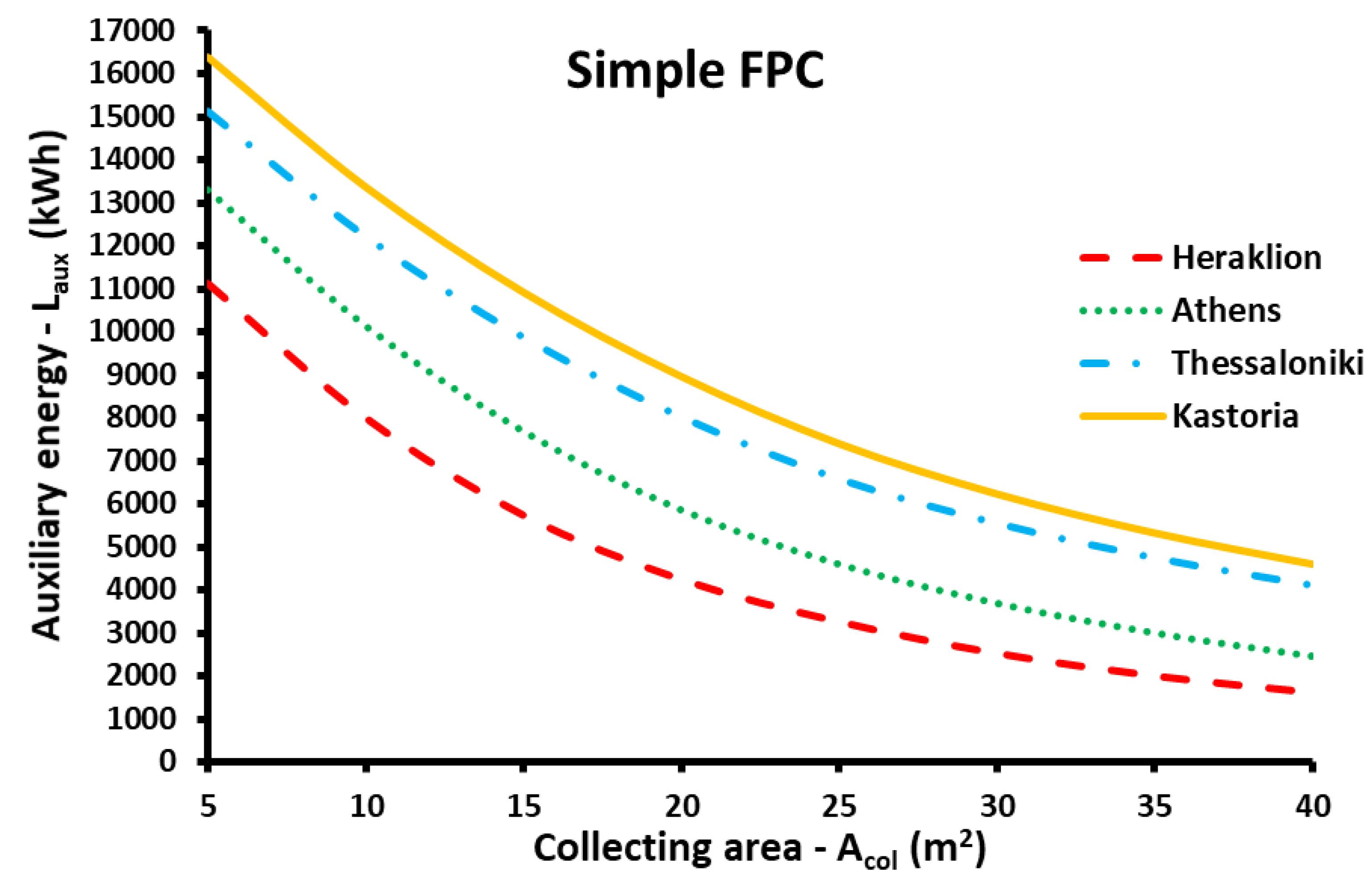
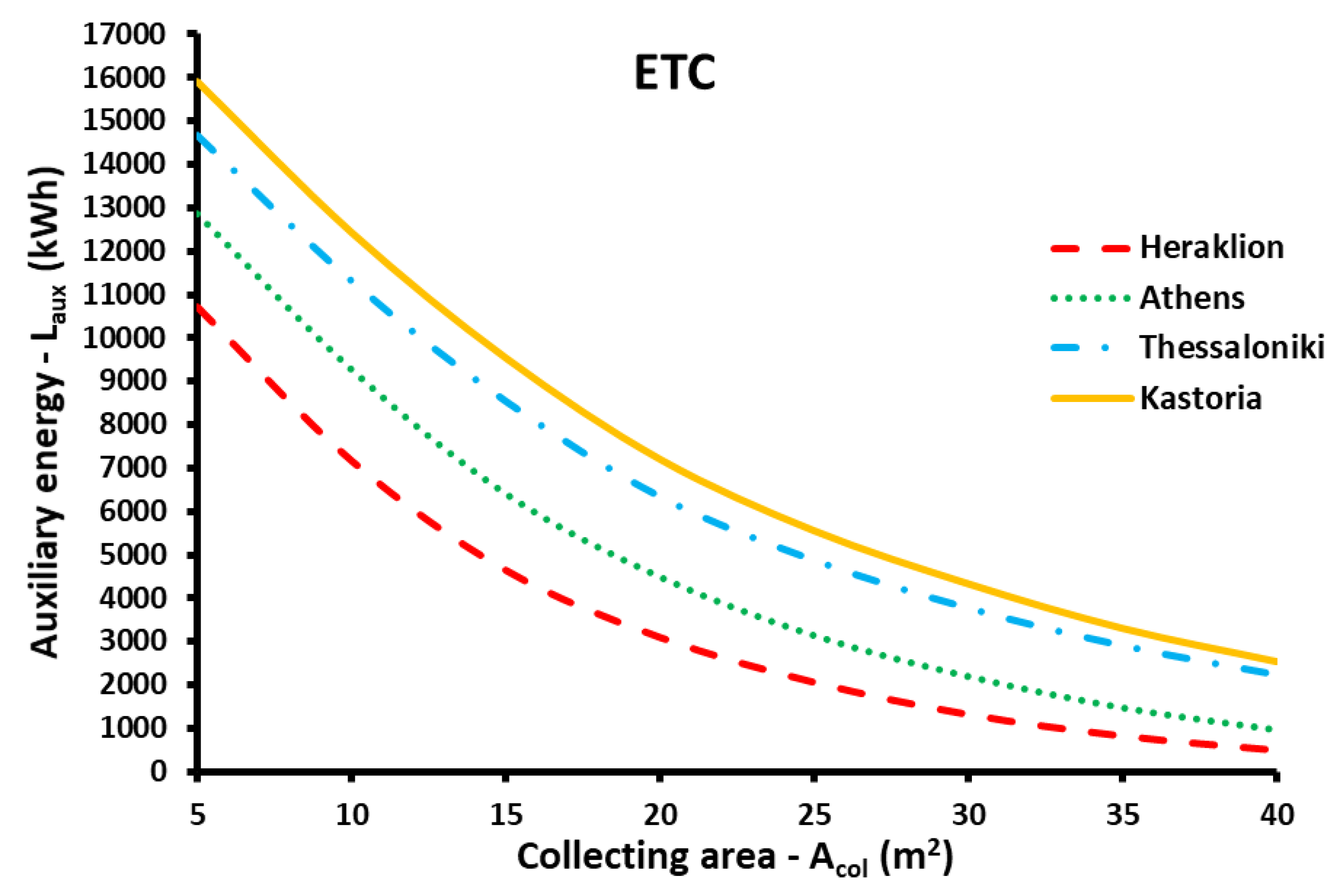
3.2. Comparison of the Energy Performance for Different Climate Zones
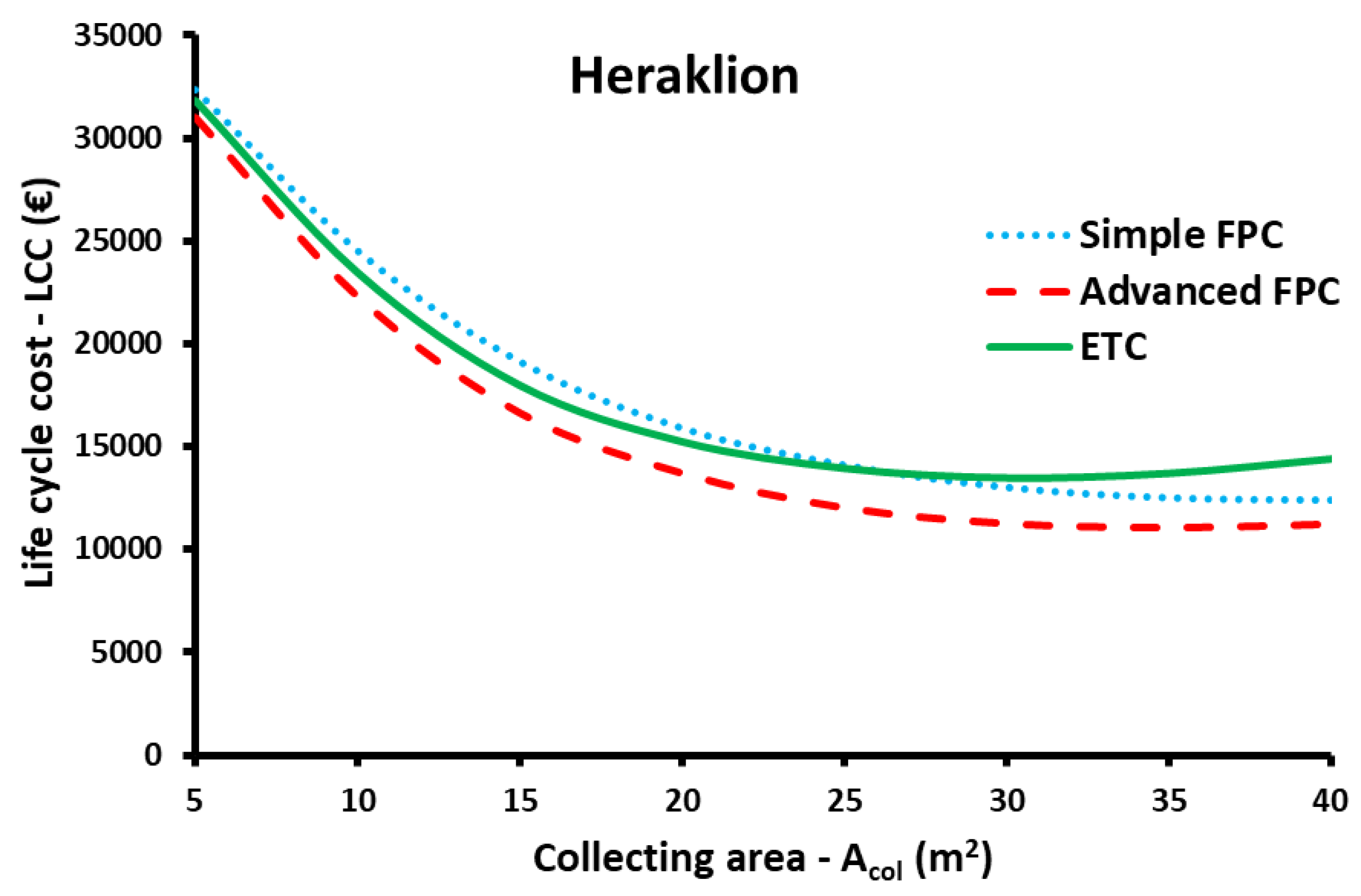
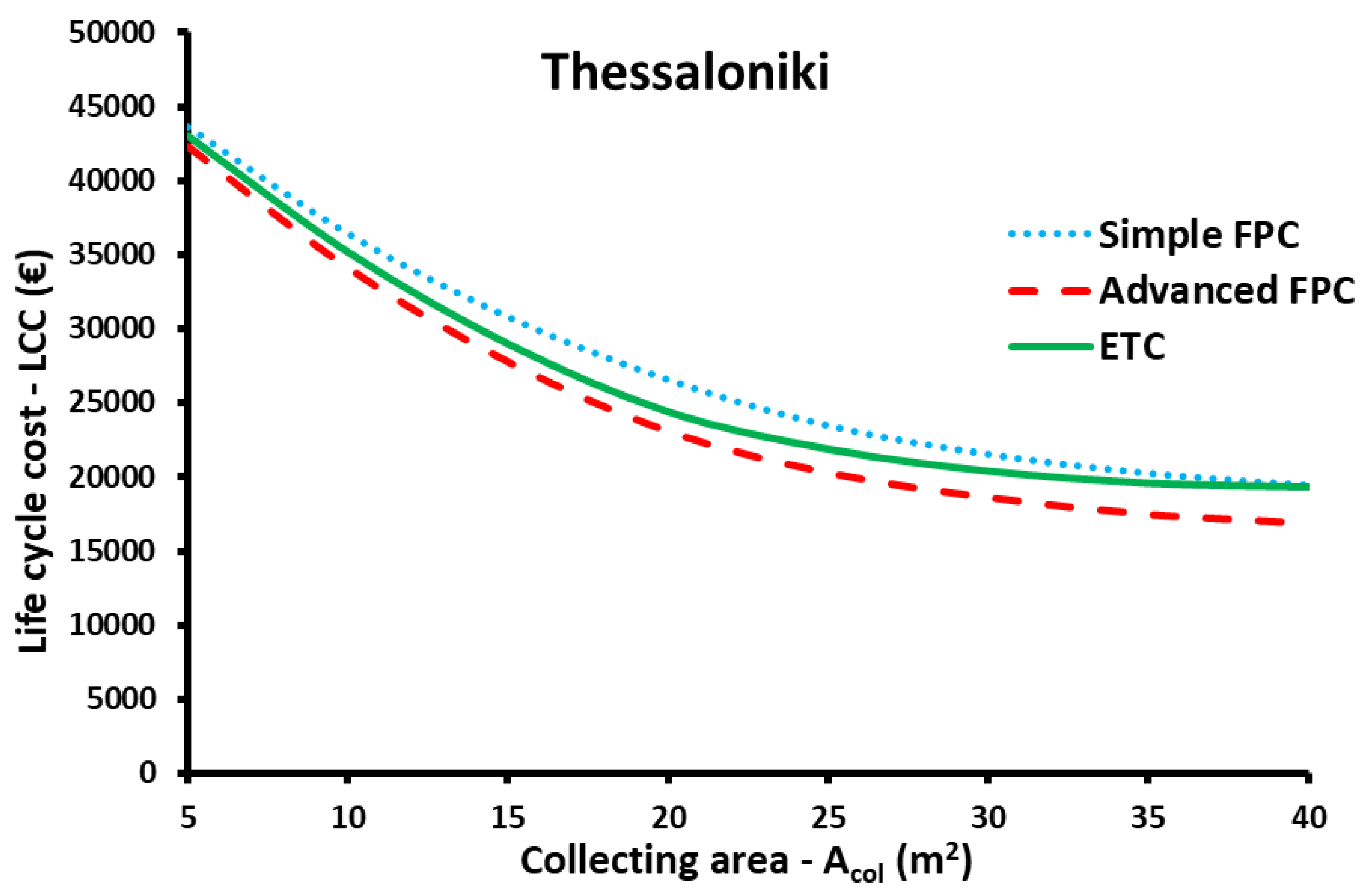
3.3. Economic Optimization
3.4. Multi-Objective Evaluation Procedure
4. Conclusions
- -
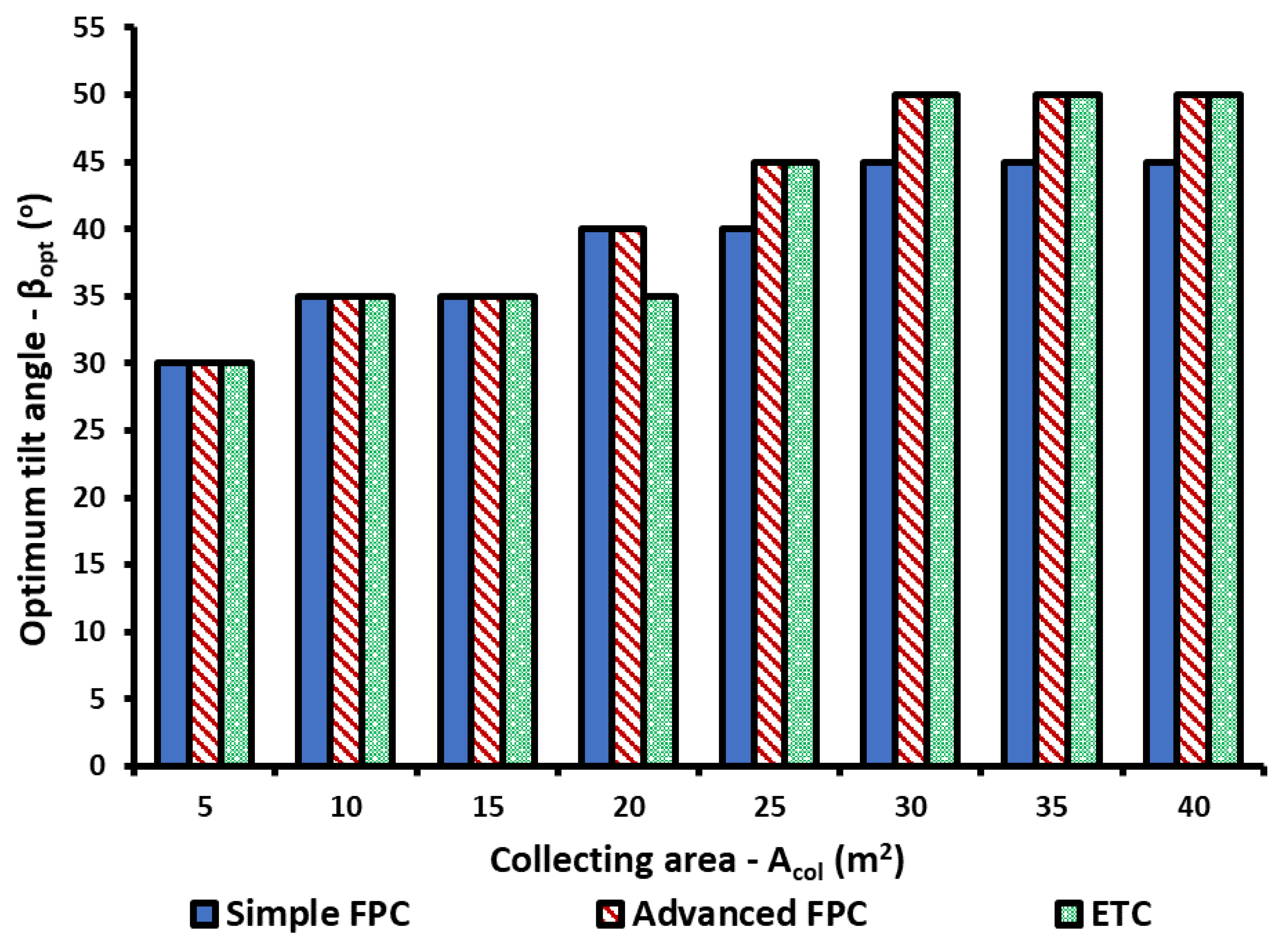
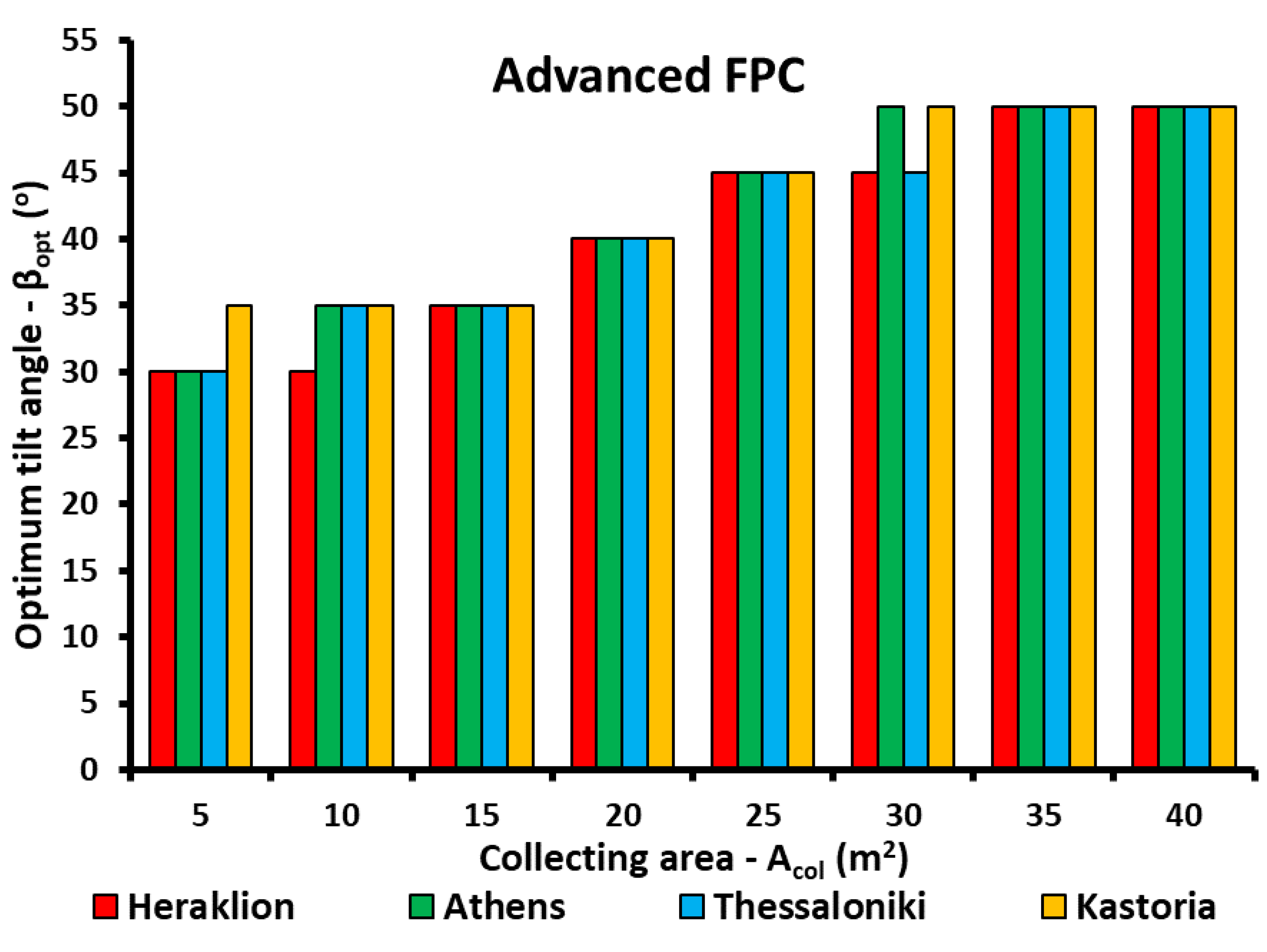
- Higher solar field area leads to higher solar coverage and also to a higher optimum tilt angle for all the solar technologies and locations.
- -
- In the parametric study, it was found that higher efficiency is found with ETC, while the advanced FPC has a bit lower, while the simple FPC has significantly lower performance than the other two choices.
- -
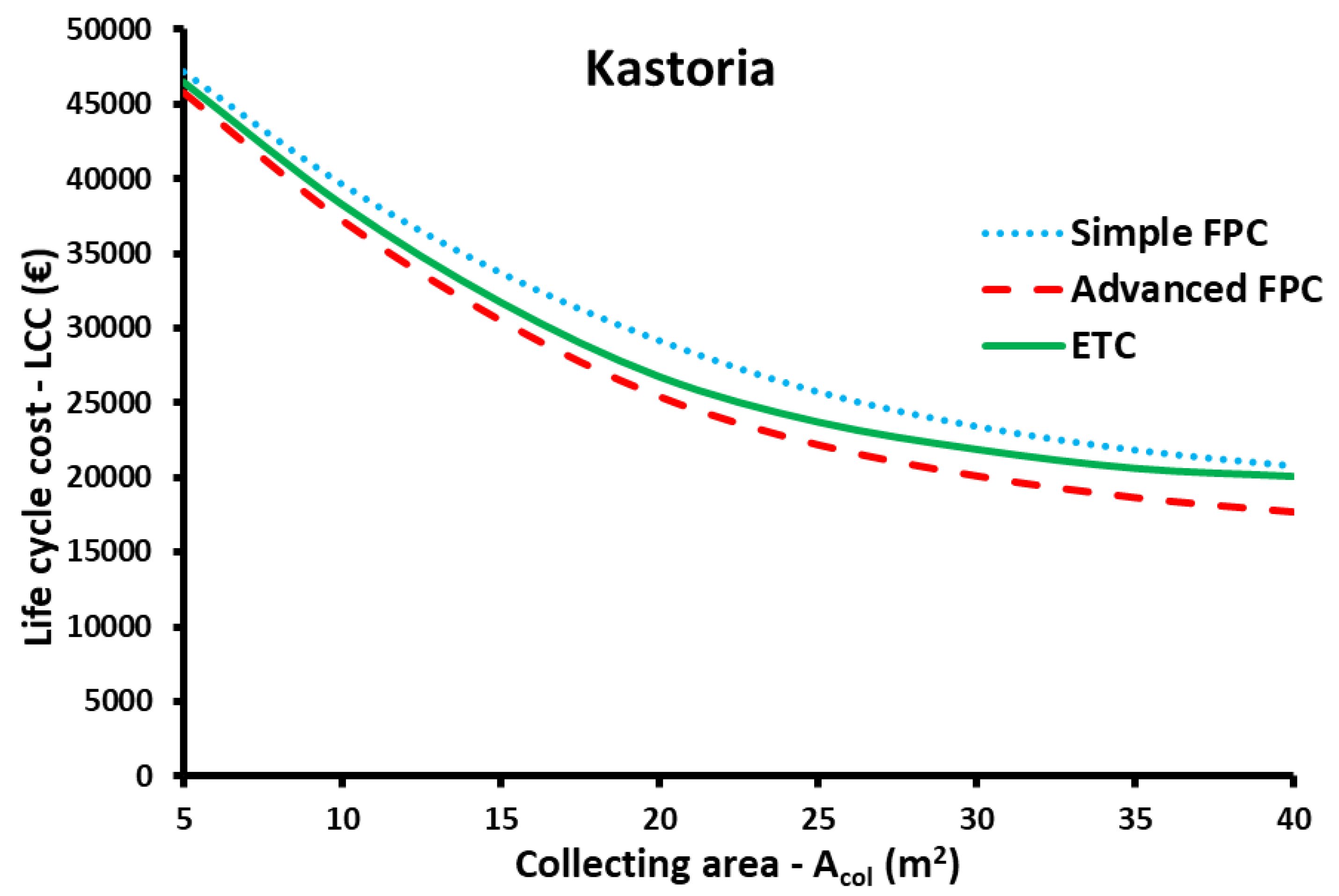
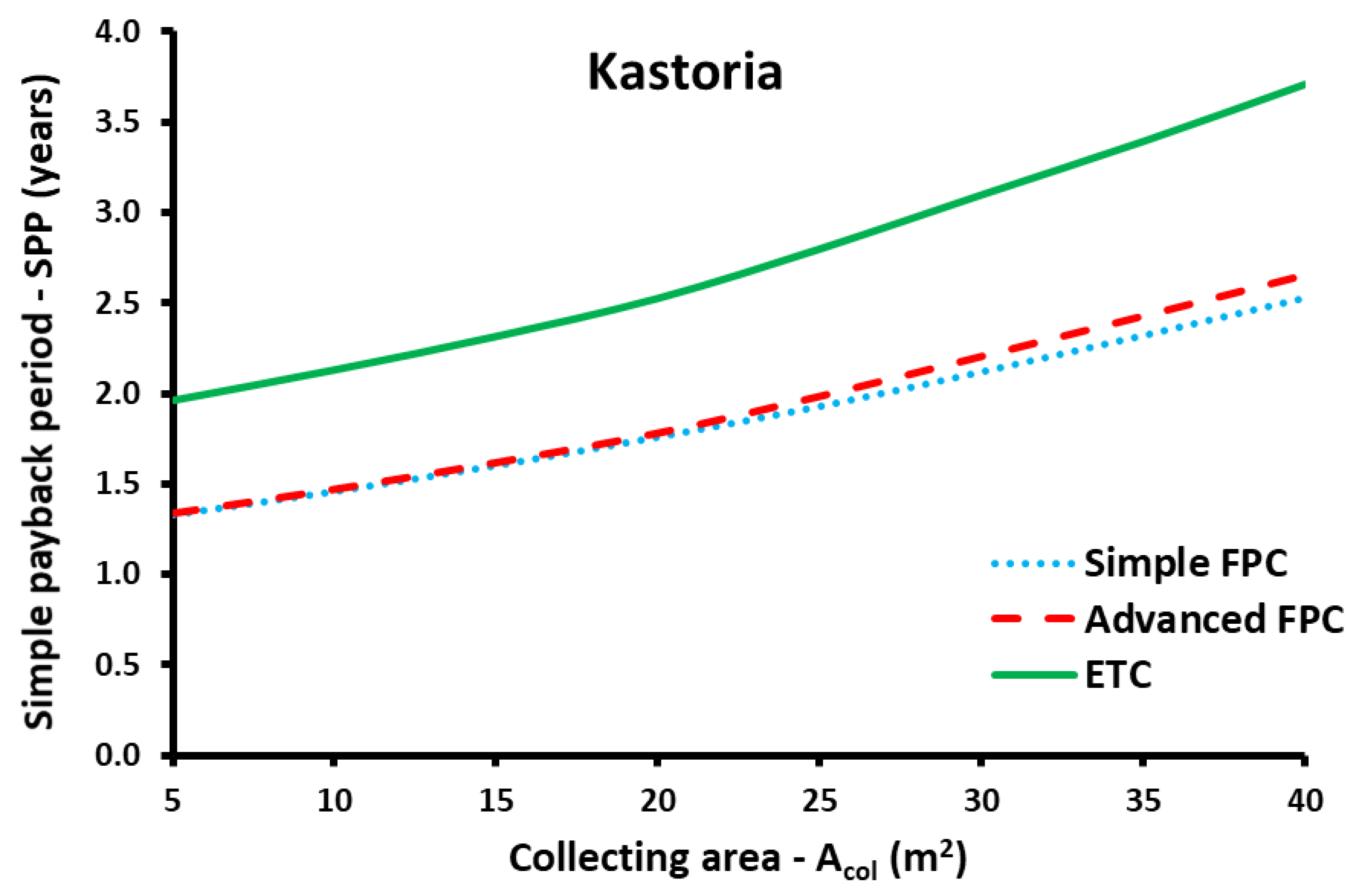
- The minimization of the LCC indicated that the advanced FPC is the best choice for all the locations. The LCC is 11,088 € for 35 m2 in Heraklion, 12,875 € for 40 m2 in Athens, 16,855 € for 40 m2 in Thessaloniki and 17,692 € for 40 m2 in Kastoria.
- -
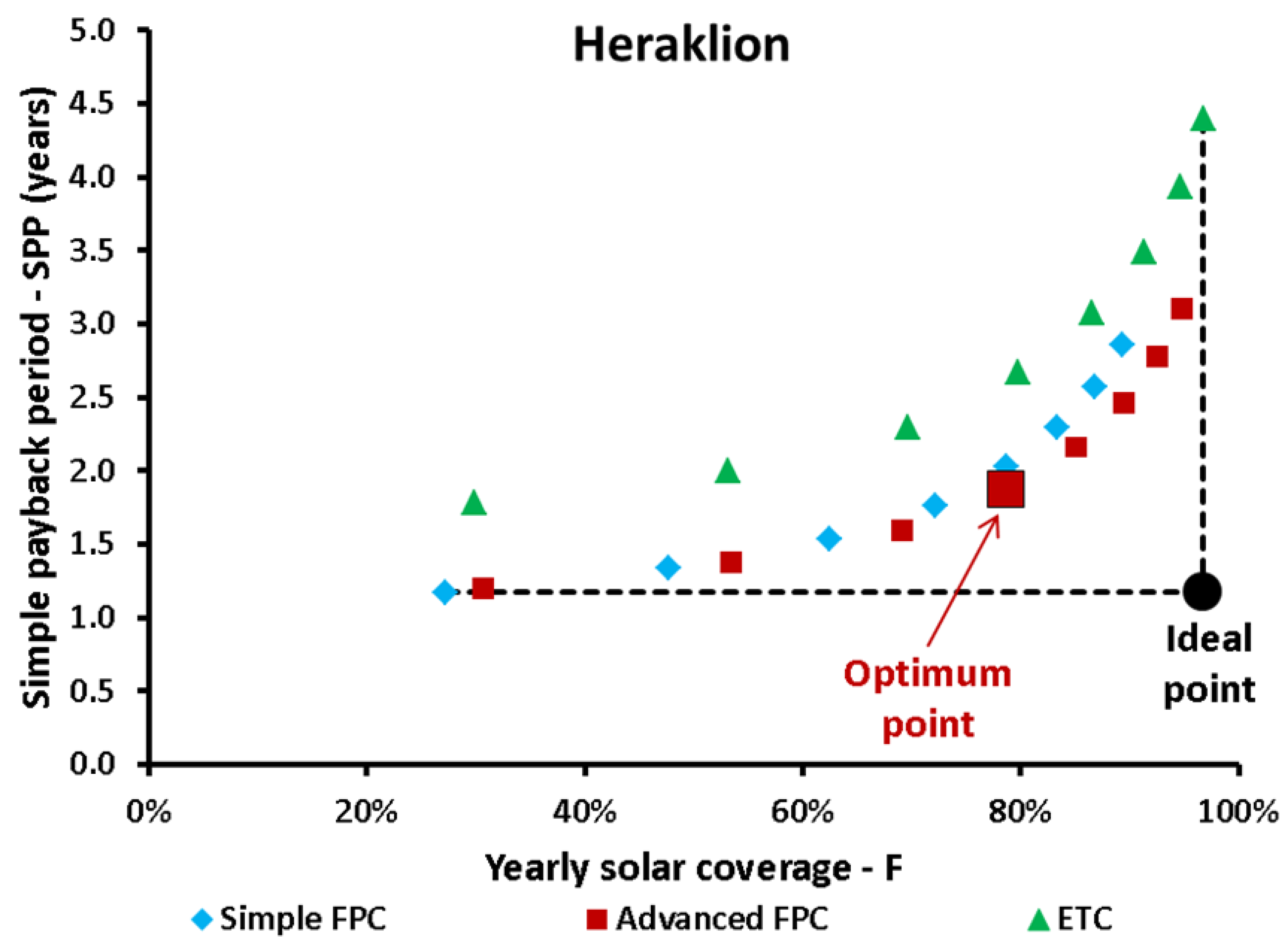
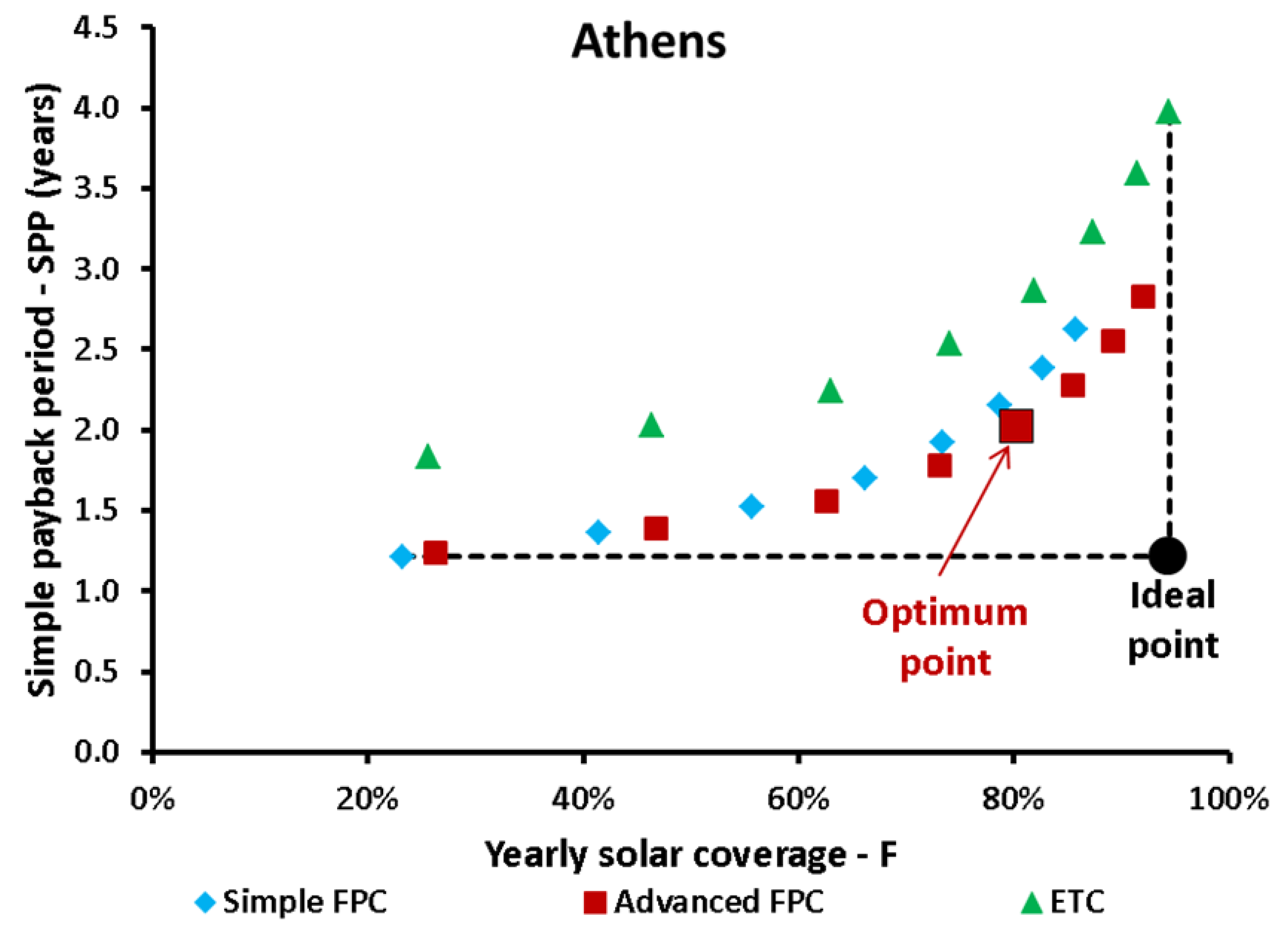
- According to the multi-objective optimization, the advanced FPC is again the optimal choice. For Heraklion, the 20 m2 leads to 78.59% solar coverage and 13,731 € LCC, for Athens, the 25 m2 leads to 80.25% solar coverage and 15,257 € LCC for Thessaloniki, the 25 m2 leads to 72.22% solar coverage and 20,257 € LCC, while for Kastoria, the 25 m2 leads to 78.67% solar coverage and 22,193 € LCC.
- -
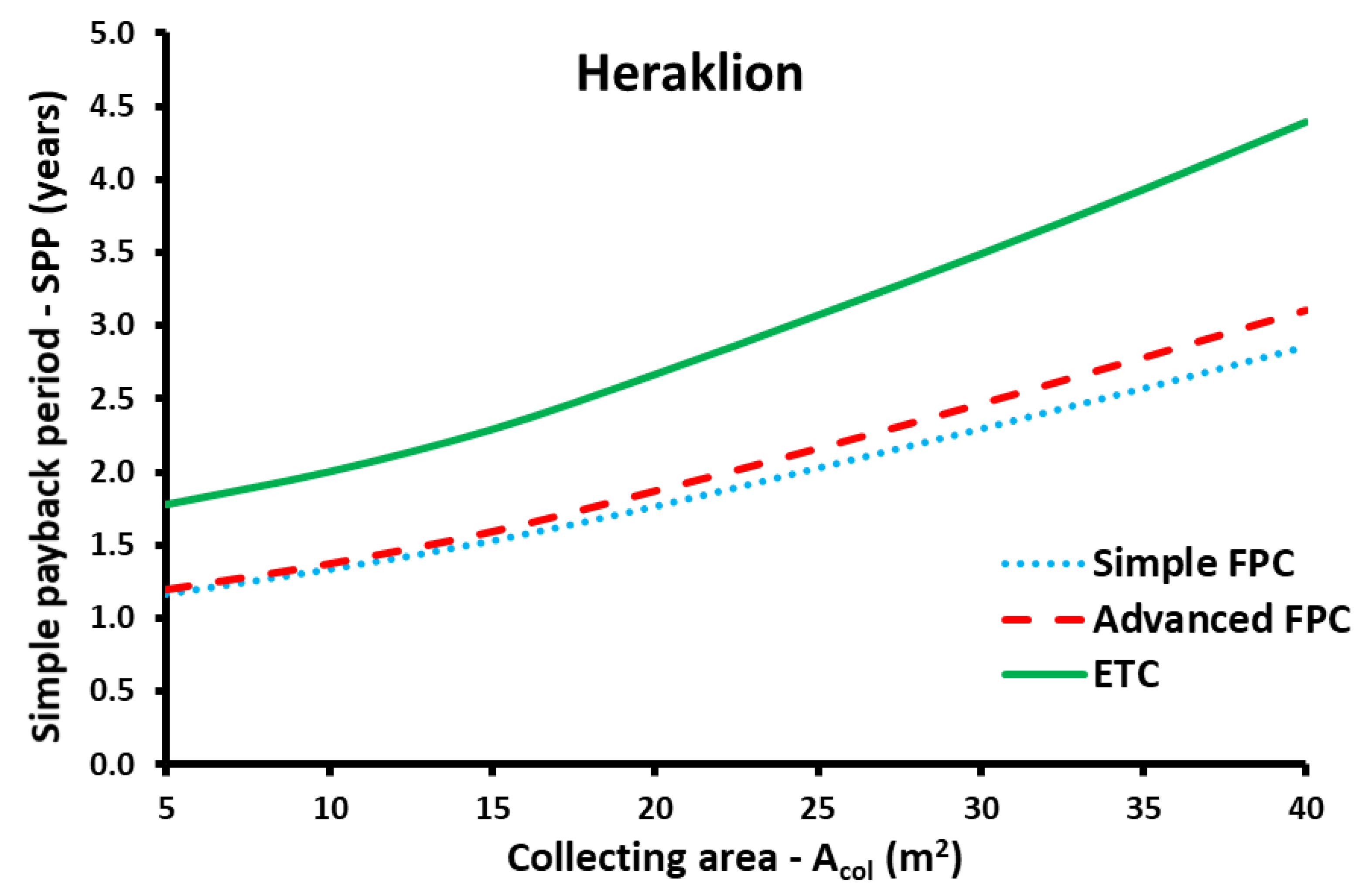
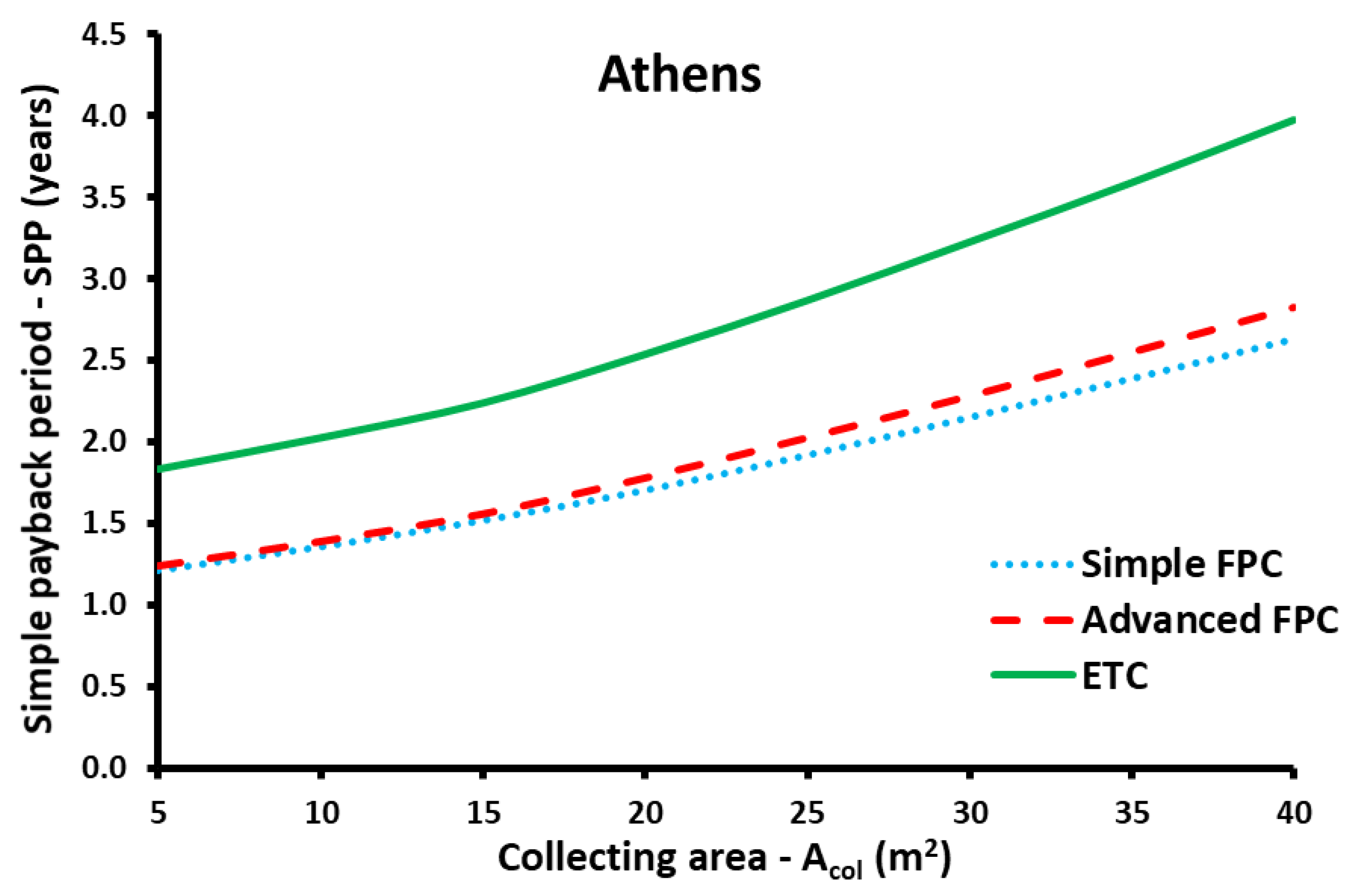
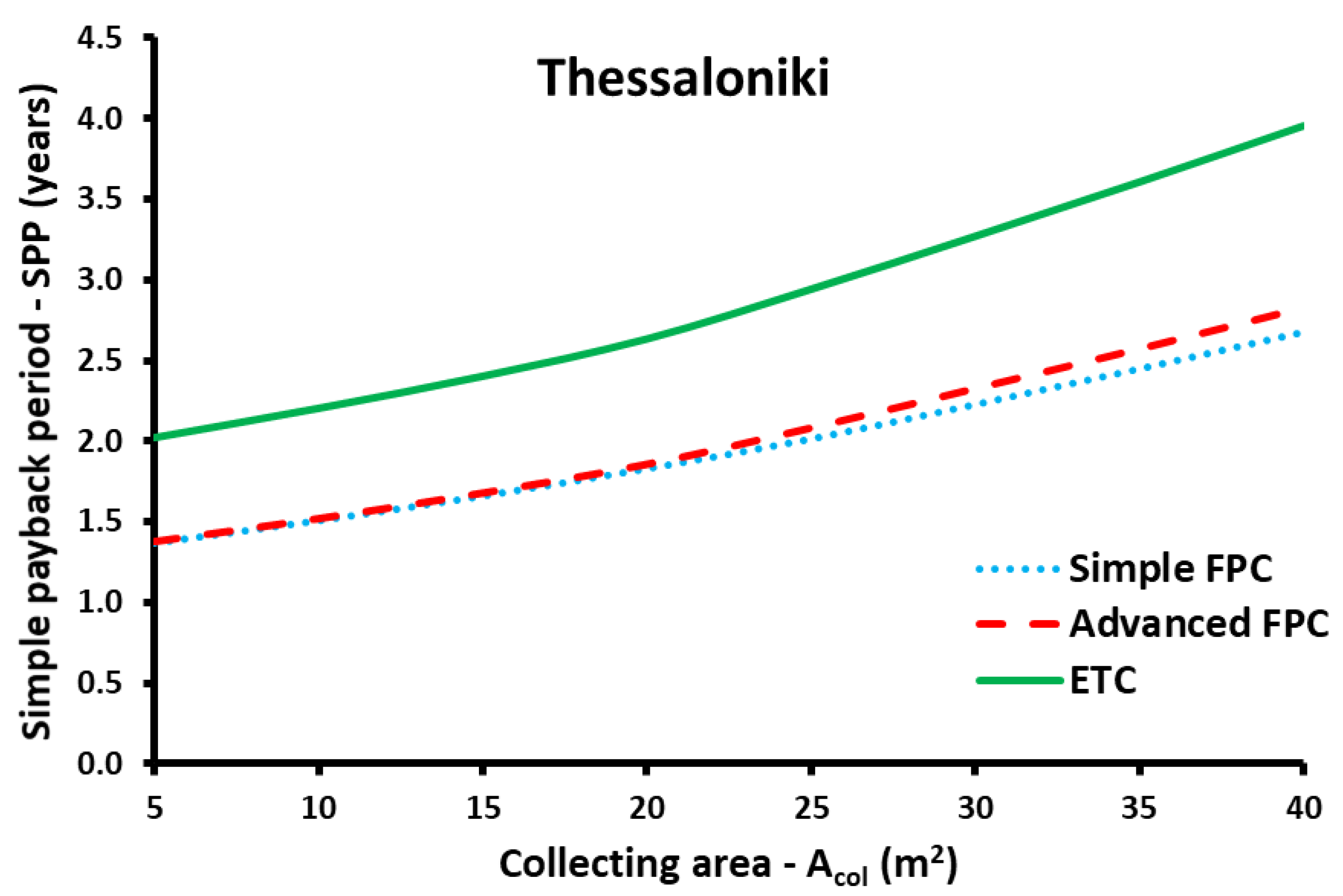
- The SPP period after the multi-objective optimization is found to be around 2 years; a promising value that indicates sustainable and viable assessment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Acol | Collecting area (m2) |
| a0 | Zero-order coefficient of the collector efficiency |
| a1 | First-order coefficient of the collector efficiency (W/m2K) |
| a2 | Second-order coefficient of the collector efficiency (W/m2K2) |
| cp | Specific heat capacity (J/kgK) |
| CFgain | Yearly economic gain—Cash flow (€) |
| C0 | Capital cost (€) |
| DD | Dimensionless distance in the multi-objective optimization |
| f | Monthly solar coverage |
| F | Yearly solar coverage |
| FR | Collector heat removal factor |
| FR΄ | System heat removal factor |
| GT | Incident solar irradiation on the tilted surface (W/m2) |
| H | Daily global solar energy on the horizontal surface (kWh/m2) |
| Hd | Daily diffuse solar energy on the horizontal surface (kWh/m2) |
| HT | Daily global solar energy on the tilted surface (kWh/m2) |
| kcol | Specific cost of the solar collectors (€/m2) |
| kel | Electricity cost (€/kWhel) |
| ktank | Specific cost of the tank (€/m3) |
| L | Load energy (kWh) |
| Laux | Auxiliary energy consumption (kWh) |
| Lu,sol | Part of the load covered by the sun (kWh) |
| LCC | Life cycle cost of the investment (€) |
| M | Lifetime of the project (years) |
| N | Days of the month |
| r | Discount factor |
| R2 | Approximation index |
| Rb | Ratio of the beam irradiation |
| SPP | Simple Payback Period (years) |
| Tam | Ambient temperature (°C) |
| Tam,m | Mean ambient temperature of the month (°C) |
| Tcold | Supply temperature from the grid (°C) |
| Tfluid | Operating fluid temperature (°C) |
| Thot | Desired temperature of the hot water (= 45 °C) |
| Tref | Reference temperature (= 100 °C) |
| Tw,m | Mean monthly water temperature from the grid (°C) |
| UL | Collector thermal loss coefficient (W/m2K) |
| Vtank | Storage tank volume (m3) |
| Vw | Daily hot water demand (m3/day) |
| X | Parameter for the calculation of the solar coverage |
| Y | Parameter for the calculation of the solar coverage |
| Greek Symbols | |
| β | Collector tilt angle (°) |
| βopt | Optimum collector tilt angle (°) |
| δ | Declination angle (°) |
| Δt | Time of the month (s) |
| ηcol | Collector thermal efficiency |
| ρ | Density (kg/m3) |
| ρg | Ground reflectance |
| (τα) | Optical efficiency |
| (τα)n | Optical efficiency for normal incident solar irradiation |
| φ | Location latitude (°) |
| ωs | Sunset hour angle (°) |
| ωs’ | Sunset hour angle for the tilted surface (°) |
| Subscripts and Superscripts | |
| max | Maximum value |
| min | Minimum values |
| Abbreviations | |
| DHW | Domestic Hot Water |
| ETC | Evacuated Tube Collectors |
| FPC | Flat Plate Collector |
References
- United Nations, Department of Economic and Social Affairs. Sustainable Development. 2021. Available online: https://sdgs.un.org/goals (accessed on 15 January 2022).
- Hannan, M.; Al-Shetwi, A.Q.; Ker, P.J.; Begum, R.; Mansor, M.; Rahman, S.; Dong, Z.; Tiong, S.; Mahlia, T.I.; Muttaqi, K. Impact of renewable energy utilization and artificial intelligence in achieving sustainable development goals. Energy Rep. 2021, 7, 5359–5373. [Google Scholar] [CrossRef]
- Benavente-Peces, C.; Ibadah, N. Buildings Energy Efficiency Analysis and Classification Using Various Machine Learning Technique Classifiers. Energies 2020, 13, 3497. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Cao, S.; Yang, H. Overview on hybrid solar photovoltaic-electrical energy storage technologies for power supply to buildings. Energy Convers. Manag. 2019, 187, 103–121. [Google Scholar] [CrossRef]
- Shirmohammadi, R.; Aslani, A.; Ghasempour, R.; Romeo, L.M.; Petrakopoulou, F. Techno-economic assessment and optimization of a solar-assisted industrial post-combustion CO2 capture and utilization plant. Energy Rep. 2021, 7, 7390–7404. [Google Scholar] [CrossRef]
- Ratajczak, K.; Michalak, K.; Narojczyk, M.; Amanowicz, Ł. Real Domestic Hot Water Consumption in Residential Buildings and Its Impact on Buildings’ Energy Performance—Case Study in Poland. Energies 2021, 14, 5010. [Google Scholar] [CrossRef]
- Abd-Ur-Rehman, H.M.; Al-Sulaiman, F.A. Optimum selection of solar water heating (SWH) systems based on their comparative techno-economic feasibility study for the domestic sector of Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 62, 336–349. [Google Scholar] [CrossRef]
- Dongellini, M.; Falcioni, S.; Morini, G.L. Dynamic Simulation of Solar Thermal Collectors for Domestic Hot Water Production. Energy Procedia 2015, 82, 630–636. [Google Scholar] [CrossRef][Green Version]
- Knudsen, S. Consumers’ influence on the thermal performance of small SDHW systems—Theoretical investigations. Sol. Energy 2002, 73, 33–42. [Google Scholar] [CrossRef]
- Nikolic, D.; Skerlic, J.; Radulovic, J.; Miskovic, A.; Tamasauskas, R.; Sadauskienė, J. Exergy efficiency optimization of photovoltaic and solar collectors’ area in buildings with different heating systems. Renew. Energy 2022, 189, 1063–1073. [Google Scholar] [CrossRef]
- Olfian, H.; Ajarostaghi, S.S.M.; Ebrahimnataj, M. Development on evacuated tube solar collectors: A review of the last decade results of using nanofluids. Sol. Energy 2020, 211, 265–282. [Google Scholar] [CrossRef]
- Khurana, H.; Majumdar, R.; Saha, S.K. Response Surface Methodology-based prediction model for working fluid temperature during stand-alone operation of vertical cylindrical thermal energy storage tank. Renew. Energy 2022, 188, 619–636. [Google Scholar] [CrossRef]
- Gorzin, M.; Hosseini, M.J.; Ranjbar, A.A.; Bahrampoury, R. Investigation of PCM charging for the energy saving of domestic hot water system. Appl. Therm. Eng. 2018, 137, 659–668. [Google Scholar] [CrossRef]
- Bilardo, M.; Fraisse, G.; Pailha, M.; Fabrizio, E. Design and experimental analysis of an Integral Collector Storage (ICS) prototype for DHW production. Appl. Energy 2020, 259, 114104. [Google Scholar] [CrossRef]
- Martorana, F.; Bonomolo, M.; Leone, G.; Monteleone, F.; Zizzo, G.; Beccali, M. Solar-assisted heat pumps systems for domestic hot water production in small energy communities. Sol. Energy 2021, 217, 113–133. [Google Scholar] [CrossRef]
- TOTEE 20701-3/2017; Technical Guidelines; Technical Chamber of Greece: Athens, Greece, 2017.
- Bellos, E.; Tzivanidis, C. Solar concentrating systems and applications in Greece—A critical review. J. Clean. Prod. 2020, 272, 122855. [Google Scholar] [CrossRef]
- Kaldellis, J.; El-Samani, K.; Koronakis, P. Feasibility analysis of domestic solar water heating systems in Greece. Renew. Energy 2005, 30, 659–682. [Google Scholar] [CrossRef]
- Tsilingiridis, G.; Martinopoulos, G. Thirty years of domestic solar hot water systems use in Greece-energy and environmental benefits—Future perspectives. Renew. Energy 2010, 35, 490–497. [Google Scholar] [CrossRef]
- Koroneos, C.J.; Nanaki, E.A. Life cycle environmental impact assessment of a solar water heater. J. Clean. Prod. 2012, 37, 154–161. [Google Scholar] [CrossRef]
- Martinopoulos, G.; Tsilingiridis, G.; Kyriakis, N. Identification of the environmental impact from the use of different materials in domestic solar hot water systems. Appl. Energy 2013, 102, 545–555. [Google Scholar] [CrossRef]
- Balaras, C.A.; Dascalaki, E.; Droutsa, P.; Kontoyiannidis, S. Hellenic renewable energy policies and energy performance of residential buildings using solar collectors for domestic hot water production in Greece. J. Renew. Sustain. Energy 2013, 5, 041813. [Google Scholar] [CrossRef]
- Antoniadis, C.N.; Martinopoulos, G. Optimization of a building integrated solar thermal system with seasonal storage using TRNSYS. Renew. Energy 2019, 137, 56–66. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Development of an analytical model for the daily performance of solar thermal systems with experimental validation. Sustain. Energy Technol. Assess. 2018, 28, 22–29. [Google Scholar] [CrossRef]
- TOTEE 20701-1/2017; Technical Guidelines; Technical Chamber of Greece: Athens, Greece, 2017.
- Beckman, W.A.; Klein, S.A.; Duffie, J.A. Solar Heating Design by the f-Chart Method; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Klein, S.; Beckman, W.; Duffie, J. A design procedure for solar heating systems. Sol. Energy 1976, 18, 113–127. [Google Scholar] [CrossRef]
- TOTEE 20701-2/2017; Technical Guidelines; Technical Chamber of Greece: Athens, Greece, 2017.
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A. Exergetic, energetic and financial evaluation of a solar driven absorption cooling system with various collector types. Appl. Therm. Eng. 2016, 102, 749–759. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Symeou, C.; Antonopoulos, K.A. Energetic, exergetic and financial evaluation of a solar driven absorption chiller—A dynamic approach. Energy Convers. Manag. 2017, 137, 34–48. [Google Scholar] [CrossRef]
- Gaglia, A.G.; Tsikaloudaki, A.G.; Laskos, C.M.; Dialynas, E.N.; Argiriou, A.A. The impact of the energy performance regulations’ updated on the construction technology, economics and energy aspects of new residential buildings: The case of Greece. Energy Build. 2017, 155, 225–237. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. Daily Insolation on Surfaces Tilted Toward the Equator. ASHRAE J. 1962, 3, 1962. [Google Scholar]
- Klein, S. Calculation of monthly average insolation on tilted surfaces. Sol. Energy 1977, 19, 325–329. [Google Scholar] [CrossRef]
- Georgousis, N.; Lykas, P.; Bellos, E.; Tzivanidis, C. Multi-objective optimization of a solar-driven polygeneration system based on CO2 working fluid. Energy Convers. Manag. 2021, 252, 115136. [Google Scholar] [CrossRef]
- DAPEEP, Residual Energy Mix 2020, June 2021. Available online: https://www.dapeep.gr (accessed on 15 January 2021).












| Collector Type | a0 (-) | a1 (W/m2K) | a2 (W/m2K2) |
|---|---|---|---|
| Simple FPC | 0.73 | 5.51 | 0.006 |
| Advanced FPC | 0.77 | 3.75 | 0.015 |
| Collector with evacuated tubes (ETC) | 0.70 | 1.80 | 0.020 |
| Collector Type | FR(τα) (-) | FRUL (W/m2K) | R2 (%) |
|---|---|---|---|
| Non-selective simple FPC | 0.73 | 5.85 | 99.93 |
| Selective advanced FPC | 0.77 | 4.59 | 99.34 |
| Collector with evacuated tubes (ETC) | 0.70 | 2.92 | 97.38 |
| Cities | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC | Year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Heraklion | 65.6 | 81.6 | 125 | 166.5 | 207.3 | 222.4 | 227.1 | 207.0 | 163.0 | 117.3 | 78.6 | 61.2 | 1722.6 |
| Athens | 63.3 | 77.7 | 118.9 | 152.7 | 190.4 | 207.4 | 214.5 | 198.6 | 156.0 | 111.1 | 68.1 | 54.4 | 1613.1 |
| Thessaloniki | 52.6 | 67.5 | 103.2 | 140.7 | 179.1 | 198.6 | 209.5 | 184.7 | 136.7 | 91.4 | 56.6 | 45.5 | 1466.1 |
| Kastoria | 57.6 | 71.3 | 111.2 | 141.1 | 173.6 | 201.8 | 206.3 | 185.5 | 138.5 | 97.0 | 60.0 | 47.7 | 1491.6 |
| Cities | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC | Year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Heraklion | 27.6 | 34.4 | 52.6 | 66.8 | 81.5 | 84.3 | 84.3 | 74.1 | 57.2 | 42.8 | 29.4 | 24.8 | 659.8 |
| Athens | 25.1 | 32.0 | 50.4 | 65.6 | 81.8 | 85.5 | 85.2 | 73.7 | 55.5 | 40.1 | 26.3 | 21.8 | 643.0 |
| Thessaloniki | 21.8 | 29.2 | 47.3 | 64.2 | 82.0 | 86.6 | 86.1 | 73.1 | 53.6 | 36.9 | 23.1 | 18.7 | 622.6 |
| Kastoria | 22.5 | 29.7 | 48.1 | 64.3 | 81.7 | 86.6 | 86.0 | 73.2 | 53.7 | 37.4 | 23.5 | 19.1 | 625.8 |
| β (ο) | 30 | 35 | 40 | 45 | 50 | β (ο) | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Zone A—Heraklion | Zone C—Thessaloniki | ||||||||||
| JAN | 3.09 | 3.19 | 3.27 | 3.34 | 3.38 | JAN | 2.69 | 2.80 | 2.90 | 2.98 | 3.04 |
| FEB | 3.77 | 3.85 | 3.89 | 3.92 | 3.93 | FEB | 3.28 | 3.37 | 3.43 | 3.47 | 3.49 |
| MAR | 4.60 | 4.60 | 4.58 | 4.54 | 4.47 | MAR | 3.89 | 3.91 | 3.91 | 3.89 | 3.85 |
| APR | 5.63 | 5.54 | 5.42 | 5.27 | 5.10 | APR | 4.85 | 4.79 | 4.71 | 4.60 | 4.47 |
| MAY | 6.23 | 6.04 | 5.83 | 5.60 | 5.33 | MAY | 5.51 | 5.37 | 5.22 | 5.03 | 4.83 |
| JUN | 6.64 | 6.40 | 6.14 | 5.85 | 5.54 | JUN | 6.09 | 5.91 | 5.70 | 5.47 | 5.22 |
| JUL | 6.67 | 6.45 | 6.20 | 5.92 | 5.62 | JUL | 6.31 | 6.14 | 5.93 | 5.70 | 5.45 |
| AUG | 6.53 | 6.39 | 6.21 | 6.00 | 5.77 | AUG | 5.98 | 5.87 | 5.74 | 5.57 | 5.38 |
| SEP | 5.99 | 5.96 | 5.90 | 5.81 | 5.68 | SEP | 5.15 | 5.15 | 5.12 | 5.07 | 4.98 |
| OCT | 4.80 | 4.87 | 4.92 | 4.94 | 4.92 | OCT | 3.87 | 3.95 | 4.01 | 4.04 | 4.05 |
| NOV | 3.80 | 3.92 | 4.02 | 4.09 | 4.14 | NOV | 2.89 | 3.00 | 3.09 | 3.16 | 3.22 |
| DEC | 3.02 | 3.13 | 3.23 | 3.31 | 3.36 | DEC | 2.44 | 2.56 | 2.66 | 2.74 | 2.80 |
| β (ο) | 30 | 35 | 40 | 45 | 50 | β (ο) | 30 | 35 | 40 | 45 | 50 |
| Zone B—Athens | Zone D—Kastoria | ||||||||||
| JAN | 3.17 | 3.29 | 3.40 | 3.48 | 3.54 | JAN | 2.99 | 3.13 | 3.24 | 3.33 | 3.40 |
| FEB | 3.73 | 3.82 | 3.88 | 3.93 | 3.94 | FEB | 3.50 | 3.59 | 3.66 | 3.71 | 3.73 |
| MAR | 4.47 | 4.49 | 4.48 | 4.45 | 4.40 | MAR | 4.23 | 4.26 | 4.26 | 4.24 | 4.20 |
| APR | 5.23 | 5.16 | 5.06 | 4.94 | 4.79 | APR | 4.87 | 4.81 | 4.72 | 4.62 | 4.49 |
| MAY | 5.80 | 5.65 | 5.47 | 5.27 | 5.05 | MAY | 5.34 | 5.21 | 5.06 | 4.88 | 4.69 |
| JUN | 6.29 | 6.09 | 5.86 | 5.61 | 5.34 | JUN | 6.18 | 6.00 | 5.79 | 5.55 | 5.30 |
| JUL | 6.40 | 6.21 | 5.99 | 5.75 | 5.48 | JUL | 6.22 | 6.04 | 5.84 | 5.62 | 5.37 |
| AUG | 6.37 | 6.25 | 6.09 | 5.91 | 5.69 | AUG | 6.00 | 5.90 | 5.76 | 5.60 | 5.41 |
| SEP | 5.85 | 5.84 | 5.80 | 5.73 | 5.62 | SEP | 5.23 | 5.23 | 5.20 | 5.14 | 5.06 |
| OCT | 4.69 | 4.79 | 4.85 | 4.89 | 4.89 | OCT | 4.14 | 4.23 | 4.29 | 4.33 | 4.34 |
| NOV | 3.41 | 3.53 | 3.64 | 3.72 | 3.77 | NOV | 3.09 | 3.21 | 3.32 | 3.40 | 3.46 |
| DEC | 2.83 | 2.95 | 3.06 | 3.15 | 3.22 | DEC | 2.58 | 2.70 | 2.81 | 2.90 | 2.97 |
| Heraklion | Athens | Thessaloniki | Kastoria | |||||
|---|---|---|---|---|---|---|---|---|
| Tam,m | Tw,m | Tam,m | Tw,m | Tam,m | Tw,m | Tam,m | Tw,m | |
| JAN | 12.1 | 14.7 | 8.7 | 11.3 | 5.3 | 8.2 | 2.2 | 4.2 |
| FEB | 12.2 | 14.2 | 9.3 | 10.9 | 6.8 | 7.9 | 3.4 | 5.0 |
| MAR | 13.5 | 14.8 | 11.2 | 11.8 | 9.8 | 9.2 | 6.9 | 7.5 |
| APR | 16.5 | 17.2 | 15.4 | 14.3 | 14.3 | 12.8 | 11.5 | 11.5 |
| MAY | 20.3 | 20.6 | 20.7 | 17.7 | 19.7 | 16.8 | 16.4 | 15.7 |
| JUN | 24.4 | 24.5 | 25.7 | 21.6 | 24.5 | 20.2 | 21.4 | 19.8 |
| JUL | 26.2 | 27.3 | 28.1 | 24.7 | 26.8 | 21.5 | 24.0 | 22.2 |
| AUG | 26.1 | 28.2 | 27.5 | 25.7 | 26.2 | 22.8 | 23.2 | 22.7 |
| SEP | 23.6 | 27.2 | 23.4 | 24.2 | 21.9 | 22.1 | 18.9 | 20.2 |
| OCT | 20.1 | 24.7 | 18.2 | 21.1 | 16.3 | 19.4 | 13.4 | 15.9 |
| NOV | 16.7 | 20.9 | 13.8 | 16.9 | 11.1 | 15.7 | 7.2 | 10.8 |
| DEC | 13.7 | 17.2 | 10.3 | 13.5 | 6.9 | 11.0 | 3.0 | 6.6 |
| Zone A—Heraklion | |||||
|---|---|---|---|---|---|
| Collector type | Acol (m2) | βopt (°) | F | LCC (€) | SPP (years) |
| Simple FPC | 40 | 50 | 89.37% | 12,383 | 2.85 |
| Advanced FPC | 35 | 50 | 92.55% | 11,088 | 2.78 |
| ETC | 30 | 50 | 91.35% | 13,480 | 3.49 |
| Zone B—Athens | |||||
| Collector type | Acol(m2) | βopt(°) | F | LCC (€) | SPP (years) |
| Simple FPC | 40 | 45 | 85.77% | 14,737 | 2.63 |
| Advanced FPC | 40 | 50 | 92.05% | 12,875 | 2.83 |
| ETC | 35 | 50 | 91.50% | 15,518 | 3.59 |
| Zone C—Thessaloniki | |||||
| Collector type | Acol(m2) | βopt(°) | F | LCC (€) | SPP (years) |
| Simple FPC | 40 | 50 | 77.97% | 19,405 | 2.68 |
| Advanced FPC | 40 | 50 | 85.09% | 16,855 | 2.83 |
| ETC | 40 | 50 | 87.98% | 19,329 | 3.95 |
| Zone D—Kastoria | |||||
| Collector type | Acol(m2) | βopt(°) | F | LCC (€) | SPP (years) |
| Simple FPC | 40 | 50 | 77.01% | 20,784 | 2.53 |
| Advanced FPC | 40 | 50 | 84.61% | 17,692 | 2.65 |
| ETC | 40 | 50 | 87.41% | 20,110 | 3.71 |
| City | Collector Type | Acol (m2) | βopt (°) | F (%) | LCC (€) | SPP (years) | CO2 Avoidance (kg/year) |
|---|---|---|---|---|---|---|---|
| Heraklion | Advanced FPC | 20 | 40 | 78.59 | 13,731 | 1.87 | 5854 |
| Athens | Advanced FPC | 25 | 45 | 80.25 | 15,257 | 2.03 | 6762 |
| Thessaloniki | Advanced FPC | 25 | 45 | 72.22 | 20,257 | 2.08 | 6573 |
| Kastoria | Advanced FPC | 25 | 45 | 70.67 | 22,193 | 1.99 | 6896 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellos, E.; Papavasileiou, L.; Kekatou, M.; Karagiorgas, M. A Comparative Energy and Economic Analysis of Different Solar Thermal Domestic Hot Water Systems for the Greek Climate Zones: A Multi-Objective Evaluation Approach. Appl. Sci. 2022, 12, 4566. https://doi.org/10.3390/app12094566
Bellos E, Papavasileiou L, Kekatou M, Karagiorgas M. A Comparative Energy and Economic Analysis of Different Solar Thermal Domestic Hot Water Systems for the Greek Climate Zones: A Multi-Objective Evaluation Approach. Applied Sciences. 2022; 12(9):4566. https://doi.org/10.3390/app12094566
Chicago/Turabian StyleBellos, Evangelos, Lydia Papavasileiou, Maria Kekatou, and Michalis Karagiorgas. 2022. "A Comparative Energy and Economic Analysis of Different Solar Thermal Domestic Hot Water Systems for the Greek Climate Zones: A Multi-Objective Evaluation Approach" Applied Sciences 12, no. 9: 4566. https://doi.org/10.3390/app12094566
APA StyleBellos, E., Papavasileiou, L., Kekatou, M., & Karagiorgas, M. (2022). A Comparative Energy and Economic Analysis of Different Solar Thermal Domestic Hot Water Systems for the Greek Climate Zones: A Multi-Objective Evaluation Approach. Applied Sciences, 12(9), 4566. https://doi.org/10.3390/app12094566







