MatNERApor—A Matlab Package for Numerical Modeling of Nonlinear Response of Porous Saturated Soil Deposits to P- and SH-Waves Propagation
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Scheme of One-Dimensional Horizontally Layered Soil System and Governing Equations of Motion
2.2. The Models of Elementary Volume of Saturated Soils
2.3. Nonlinear Hysteretic Model
2.4. Effect of Water Column on Incident Plane P-Waves
3. Implementation of the Algorithm
- Subset 1—a core of earthquake site response computing;
- Subset 2—a toolkit for calculating the bulk density of porous soil and various parameters of porous soil from velocity profiles for the Kik-net sites;
- Subset 3—a toolkit for calculating constrained moduli degradation curves above and under water table and creating an input file with a set of soil moduli degradation curves;
- Subset 4—a toolkit for calculating damping curves for P- and SH-wave cases;
- Subset 5—a toolkit for visualizing general and supplementary output;
- Subset 6—a toolkit for calculating theoretical reduction spectra for vertical components due to the water column of different thicknesses above the site, and simulating this reduction by a set of digital Butterworth bandpass filters and applying them to accelerograms.
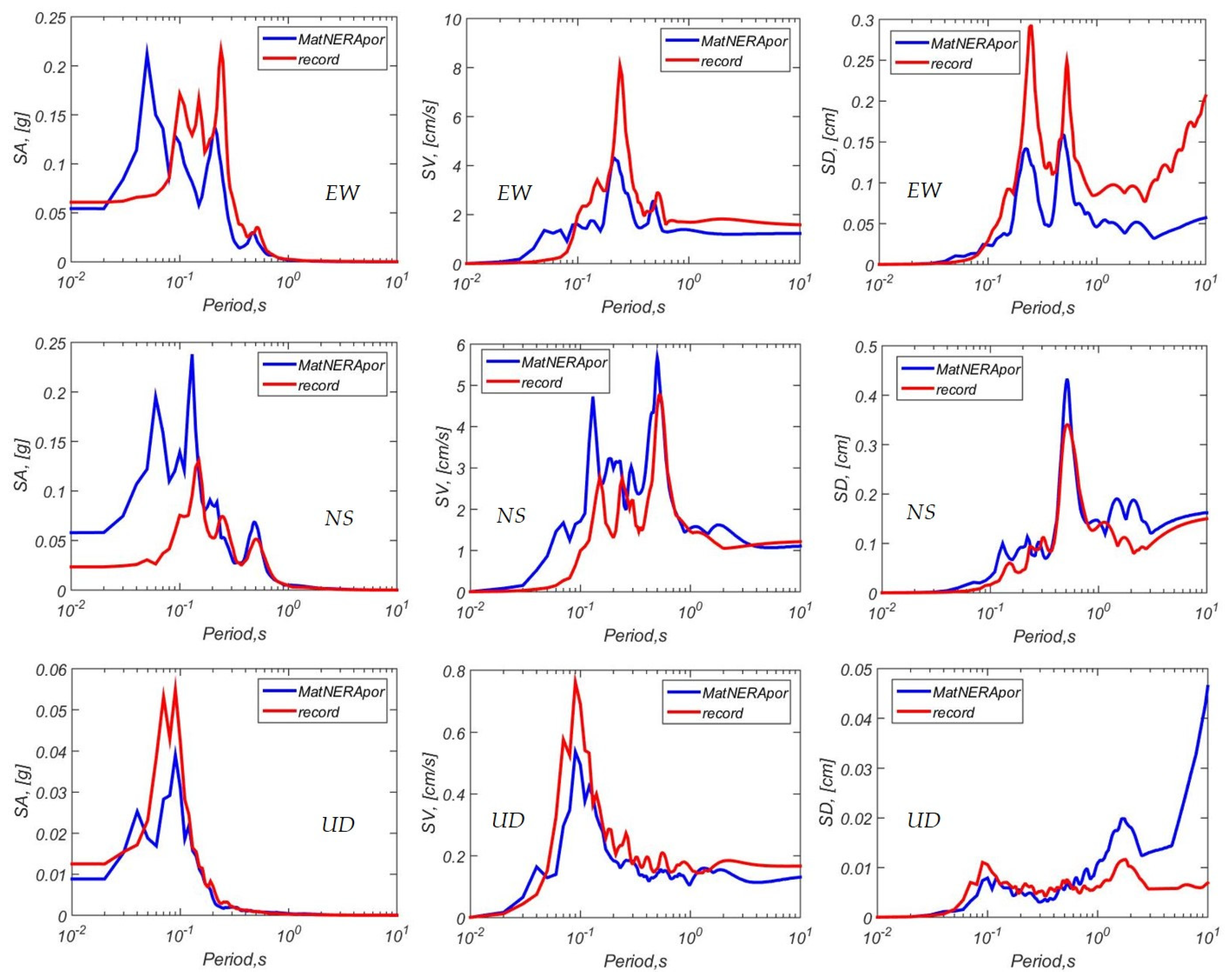
4. Approbation of the Algorithm with the Kik-Net Vertical Arrays Data
5. Calculation of Water Column Reduction Spectra Using the OBS Records Obtained in the Arctic
6. Conclusions
- (1)
- The algorithm MatNERApor and its Matlab implementation were introduced for numerical modeling of the nonlinear response of porous saturated soil deposits to P- and SH-waves vertical propagation. The presented algorithm is based on the NERA algorithm, but develops significantly, expanding its applicability to the cases of a porous saturated soil structure, propagation of P-waves instead of SH-waves and occurrence of soil deposits in the water area. In addition, many shortcomings of the software implementation of the original algorithm have been overcome. We added the ability to run the calculation for a set of input seismic signals, soil profiles, shear and constrained moduli reduction curves with subsequent averaging of the output response spectra. The source code can be further developed.
- (2)
- The package was tested and verified using the records at two sites of the Kik-net network: the TCGH15 site is characterized by sandy soils lying on the bedrock, and the KSRH10 site is characterized by clayey soils. The effect of the water column on the reduction of vertical motion spectra was demonstrated using the records of local earthquakes obtained by ocean bottom seismographs in the Laptev Sea in 2019–2020. The results of the calculations showed good agreement with the data obtained from real seismic records, which justifies the correctness of the theoretical basis of the presented algorithm and its software implementation.
- (3)
- The MatNERApor package has significant prospects for practical use. This is especially actual for sites located in the water area within the zones of continuous or sparse permafrost, as well as the massive release of bubble gas from bottom sediments, such as the Arctic shelf of Eastern Siberia. In this case, it is especially important to consider the complex structure of marine soils, i.e., their saturation with water, gas mixture and ice.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krylov, A.A.; Alekseev, D.A.; Kovachev, S.A.; Radiuk, E.A.; Novikov, M.A. Numerical Modeling of Nonlinear Response of Seafloor Porous Saturated Soil Deposits to SH-Wave Propagation. Appl. Sci. 2021, 11, 1854. [Google Scholar] [CrossRef]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; Report No. UCB/EERC-28 -72/12; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1972; 102p. [Google Scholar]
- Bardet, J.P.; Ichii, K.; Lin, C.H. EERA: A computer program for Equivalent Linear Earthquake Site Response Analysis of Layered Soils Deposits; University of Southern California: Los Angeles, CA, USA, 2000; 38 p. [Google Scholar]
- Kottke, A.R.; Rathje, E.M. Technical Manual for Strata; PEER Report 2008/10; Pacifc Earthquake Engineering Research Center College of Engineering, University of California: Berkeley, CA, USA, 2008; 100p. [Google Scholar]
- Bardet, J.P.; Tobita, T. NERA, A Computer Program for Nonlinear Earthquake Site Response Analyses of Layered Soil Deposits; University of Southern California: Los Angeles, CA, USA, 2001; 44p. [Google Scholar]
- Hashash, Y.M.A.; Musgrove, M.I.; Harmon, J.A.; Ilhan, O.; Xing, G.; Numanoglu, O.; Groholski, D.R.; Phillips, C.A.; Park, D. DEEPSOIL 7, User Manual; Board of Trustees of University of Illinois at Urbana-Champaign: Urbana, IL, USA, 2020; 170p, Available online: http://deepsoil.cee.illinois.edu/Publications.html (accessed on 22 February 2022).
- Matasovic, N. Seismic Response of Composite Horizontally-Layered Soil Deposits. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1993. [Google Scholar]
- Kramer, S.L.; Paulsen, S.B. Practical Use of Geotechnical Site Response Models. In Proceedings of the International Workshop on Uncertainties in Nonlinear Soil Properties and Their Impact on Modeling Dynamic Soil Response, University of California, Berkeley, Richmond, CA, USA, 18–19 March 2004; p. 10. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996; 653p. [Google Scholar]
- Papazoglou, A.J.; Elnashai, A.S. Analytical and field evidence of the damaging effect of vertical earthquake ground motion. Earthq. Eng. Struct. Dyn. 1996, 25, 1109–1137. [Google Scholar] [CrossRef]
- Gülerce, Z.; Abrahamson, N.A. Vector-valued probabilistic seismic hazard assessment for the effects of vertical ground motions on the seismic response of highway bridges. Earthq. Spectra 2010, 26, 999–1016. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Lui, H.-W. Site response analysis of vertical ground motion in consideration of soil nonlinearity. Soil Dyn. Earthq. Eng. 2017, 102, 124–136. [Google Scholar] [CrossRef]
- Yuan, R.-M.; Tang, C.-L.; Deng, Q.-H. Effect of the acceleration component normal to the sliding surface on earthquake-induced landslide triggering. Landslides 2015, 12, 335–344. [Google Scholar] [CrossRef]
- Shakhova, N.; Semiletov, I.; Sergienko, V.; Lobkovsky, L.; Yusupov, V.; Salyuk, A.; Salomatin, A.; Chernykh, D.; Kosmach, D.; Panteleev, G.; et al. The East Siberian Arctic Shelf: Towards further assessment of permafrost-related methane fluxes and role of sea ice. Phil. Trans. R. Soc. A. 2015, 373, 20140451. [Google Scholar] [CrossRef]
- Shakhova, N.; Semiletov, I.; Gustafsson, Ö.; Sergienko, V.; Lobkovsky, L.; Dudarev, O.; Tumskoy, V.; Grigoriev, M.; Mazurov, A.; Salyuk, A.; et al. Current rates and mechanisms of subsea permafrost degradation in the East Siberian Arctic Shelf. Nat. Commun. 2017, 8, 15872. [Google Scholar] [CrossRef]
- Shakhova, N.; Semiletov, I.; Chuvilin, E. Understanding the Permafrost–Hydrate System and Associated Methane Releases in the East Siberian Arctic Shelf. Geosciences 2019, 9, 251. [Google Scholar] [CrossRef] [Green Version]
- Towhata, I. Geotechnical Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2008; 684p. [Google Scholar] [CrossRef]
- Stewart, J.P.; Boore, D.M.; Seyhan, E.; Atkinson, G.M. NGA-West2 equations for predicting vertical-component PGA, PGV, and 5%-damped PSA from shallow crustal earthquakes. Earthq. Spectra 2016, 32, 1005–1031. [Google Scholar] [CrossRef]
- Beresnev, I.A.; Nightingale, A.M.; Silva, W.J. Properties of Vertical Ground Motions. Bull. Seismol. Soc. Am. 2002, 92, 3152–3164. [Google Scholar] [CrossRef]
- Li, C.; Hao, H.; Li, H.; Bi, K.; Chen, B. Modeling and Simulation of Spatially Correlated Ground Motions at Multiple Onshore and Offshore sites. J. Earthq. Eng. 2017, 21, 359–383. [Google Scholar] [CrossRef] [Green Version]
- Diao, H.; Hu, J.; Xie, L. Effect of seawater on incident plane P and SV waves at ocean bottom and engineering characteristics of offshore ground motion records off the coast of southern California, USA. Earthq. Eng. Eng. Vib. 2014, 13, 181–194. [Google Scholar] [CrossRef]
- Boore, D.M.; Smith, C.E. Analysis of earthquake recordings obtained from the seafloor earthquake measurement system (SEMS) instruments deployed off the coast of Southern California. Bull. Seismol. Soc. Am. 1999, 89, 260–274. [Google Scholar] [CrossRef]
- Frenkel, J. On the Theory of Seismic and Seismoelectric Phenomena in a Moist Soil. J. Phys. 1994, 111, 230–241, Republished in: J. Eng. Mech., 2005, 131, 879‒887. [Google Scholar] [CrossRef] [Green Version]
- Biot, M. Theory of propagation of elastic waves in a fluid-saturated porous solid. J. Acoust. Soc. Am. 1956, 28, 168–191. [Google Scholar] [CrossRef]
- Gassmann, F. Über die Elastizität poröser Medien. Viertel Nat. Ges. Zürich 1951, 96, 1–23. [Google Scholar]
- National Research Institute for Earth Science and Disaster Resilience (NIED). Available online: https://www.kyoshin.bosai.go.jp/ (accessed on 20 November 2021).
- Bardet, J.P. The damping of saturated poroelastic soils during steady-state vibrations. Appl. Math. Comput. 1995, 67, 3–31. [Google Scholar] [CrossRef]
- White, J.E. Underground Sound: Application of Seismic Waves. Methods Geochem. Geophys. 1983, 18, 253. [Google Scholar] [CrossRef]
- Avseth, P.; Mukerji, T.; Mavko, G. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk; United Kingdom at the University Press: Cambridge, UK, 2005; 359p. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media; United States of America by Cambridge University Press: New York, NY, USA, 2009; 511p. [Google Scholar] [CrossRef]
- Iwan, W.D. On a class of models for the yielding behavior of continuous and composite systems. J. Appl. Mech. ASME 1967, 34, 612–617. [Google Scholar] [CrossRef]
- Mróz, Z. On the description of anisotropic workhardening. J. Mech. Phys. Solids 1967, 15, 163–175. [Google Scholar] [CrossRef]
- Masing, G. Eigenspannungen and verfertigung beim messing. In Proceedings of the 2nd International Congress of Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. [Google Scholar]
- Elgamal, A.; He, L.C. Vertical earthquake ground motion records: An overview. J. Earthq. Eng. 2004, 8, 663–697. [Google Scholar] [CrossRef]
- Bozorgnia, Y.; Campbell, K.W. Vertical Ground Motion Model Using NGA-West2 database. Earthq. Spectra 2015, 32, 150414082519000. [Google Scholar] [CrossRef]
- Crouse, C.B.; Quilter, J. Seismic Hazard Analysis and Development of Design Spectra for Maul A Platform. In Proceedings of the Pacific Conference on Earthquake Engineering, Auckland, New Zealand, 20–23 November 1991; Vol. III, pp. 137–148. [Google Scholar]
- Bajaj, K.; Anbazhagan, P. Identification of Shear Modulus Reduction and Damping Curve for Deep and Shallow Sites: Kik-Net Data. J. Earthq. Eng. 2021, 25, 2668–2696. [Google Scholar] [CrossRef]
- Gardner, G.H.F.; Gardner, L.W.; Gregory, A.R. Formation velocity and density—The diagnostic basics for stratigraphic traps. Geophysics 1974, 39, 770–780. [Google Scholar] [CrossRef] [Green Version]
- Anbazhagan, P.; Uday, A.; Moustafa, S.S.R.; Al-Arifi, N.S.N. Correlation of densities with shear wave velocities and SPT N values. J. Geophys. Eng. 2016, 13, 320–341. [Google Scholar] [CrossRef] [Green Version]
- IRIS Wilber 3 system. Available online: https://ds.iris.edu/wilber3/ (accessed on 22 January 2022).
- Seed, H.B.; Idriss, I.M. Soil Moduli and Damping Factors for Dynamic Response Analysis; Report No. UCB/EERC-70/10; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1970; 48p. [Google Scholar]
- Sun, J.I.; Golesorkhi, R.; Seed, H.B. Dynamic Moduli and Damping Ratios for Cohesive Soils; Report No. UCB/EERC-88/15; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1988; 42p. [Google Scholar]
- Presnov, O.M. Mekhanika Gruntov: Uchebno-Metodicheskoe Posobie [Soil Mechanics: Teaching Aid]; Krasnoyarsk Siberian Federal University: Krasnoyarsk, Russia, 2012; 67p. (In Russian) [Google Scholar]
- Lomtadze, V.D. Inzhenernaya Geologiya. In Inzhenernaya Petrologiya [Engineering Geology. Engineering Petrology], (In Russian), 2nd ed.; USSR: Nedra, Leningrad, 1984; 509p. (In Russian) [Google Scholar]
- Krylov, A.A.; Ivashchenko, A.I.; Kovachev, S.A.; Tsukanov, N.V.; Kulikov, M.E.; Medvedev, I.P.; Ilinskiy, D.A.; Shakhova, N.E. The Seismotectonics and Seismicity of the Laptev Sea Region: The Current Situation and a First Experience in a Year-Long Installation of Ocean Bottom Seismometers on the Shelf. J. Volcanolog. Seismol. 2020, 14, 379–393. [Google Scholar] [CrossRef]
- Krylov, A.A.; Egorov, I.V.; Kovachev, S.A.; Ilinskiy, D.A.; Ganzha, O.Y.; Timashkevich, G.K.; Roginskiy, K.A.; Kulikov, M.E.; Novikov, M.A.; Ivanov, V.N.; et al. Ocean-Bottom Seismographs Based on Broadband MET Sensors: Architecture and Deployment Case Study in the Arctic. Sensors 2021, 21, 3979. [Google Scholar] [CrossRef]
- Bogoyavlensky, V.I.; Kishankov, A.V.; Kazanin, A.G. Permafrost, Gas Hydrates and Gas Seeps in the Central Part of the Laptev Sea. Dokl. Earth Sci. 2021, 500, 766–771. [Google Scholar] [CrossRef]
- Bogoyavlensky, V.; Kishankov, A.; Kazanin, A.; Kazanin, G. Distribution of permafrost and gas hydrates in relation to intensive gas emission in the central part of the Laptev Sea (Russian Arctic). Mar. Pet. Geol. 2022, 138, 105527. [Google Scholar] [CrossRef]












| Source: [26] | Calculated According to [38] | Calculated According to [39] | Source: [43,44] | Calculated by Equations (22) and (25) | ||||
|---|---|---|---|---|---|---|---|---|
| Depth to Top of Layer (m) | Vp, (m/s) | Vs, (m/s) | ρ bulk = f(Vp), (kg/m3) | ρ bulk = f(Vs), (kg/m3) | ρ dry = f(Vs), (kg/m3) | ρS, (kg/m3) | W = f(ρ, ρ dry) | ϕ = f(ρ dry, ρS) |
| 0 | 200 | 100 | 1164 | 1377 | 1272 | 2.66 | 0.08 | 0.52 |
| 3 | 1600 | 580 | 1958 | 2182 | 1786 | 2.66 | 0.22 | 0.33 |
| 22 * | 2120 | 980 | 2100 | 2504 | 1976 | 2.69 | 0.27 | 0.27 |
| Source: [26] | Calculated According to [38] | Calculated According to [39] | Source: [43,44] | Calculated by Equations (22) and (25) | ||||
|---|---|---|---|---|---|---|---|---|
| Depth to Top of Layer (m) | Vp, (m/s) | Vs, (m/s) | ρ bulk = f(Vp), (kg/m3) | ρ bulk = f(Vs), (kg/m3) | ρ dry = f(Vs), (kg/m3) | ρS, (kg/m3) | W = f(ρ, ρ dry) | ϕ = f(ρ dry, ρS) |
| 0 | 220 | 90 | 1921 | 1339 | 1246 | 2.74 | 0.07 | 0.55 |
| 1 | 590 | 130 | 1525 | 1475 | 1338 | 2.74 | 0.10 | 0.51 |
| 5 | 1500 | 210 | 1926 | 1972 | 1468 | 2.74 | 0.14 | 0.46 |
| 16 | 1500 | 300 | 1926 | 1836 | 1572 | 2.74 | 0.17 | 0.43 |
| 36 * | 3100 | 1400 | 2310 | 2749 | 2117 | 2.63 | 0.30 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krylov, A.A.; Kovachev, S.A.; Radiuk, E.A.; Roginskiy, K.A.; Novikov, M.A.; Samylina, O.S.; Lobkovsky, L.I.; Semiletov, I.P. MatNERApor—A Matlab Package for Numerical Modeling of Nonlinear Response of Porous Saturated Soil Deposits to P- and SH-Waves Propagation. Appl. Sci. 2022, 12, 4614. https://doi.org/10.3390/app12094614
Krylov AA, Kovachev SA, Radiuk EA, Roginskiy KA, Novikov MA, Samylina OS, Lobkovsky LI, Semiletov IP. MatNERApor—A Matlab Package for Numerical Modeling of Nonlinear Response of Porous Saturated Soil Deposits to P- and SH-Waves Propagation. Applied Sciences. 2022; 12(9):4614. https://doi.org/10.3390/app12094614
Chicago/Turabian StyleKrylov, Artem A., Sergey A. Kovachev, Elena A. Radiuk, Konstantin A. Roginskiy, Mikhail A. Novikov, Olga S. Samylina, Leopold I. Lobkovsky, and Igor P. Semiletov. 2022. "MatNERApor—A Matlab Package for Numerical Modeling of Nonlinear Response of Porous Saturated Soil Deposits to P- and SH-Waves Propagation" Applied Sciences 12, no. 9: 4614. https://doi.org/10.3390/app12094614
APA StyleKrylov, A. A., Kovachev, S. A., Radiuk, E. A., Roginskiy, K. A., Novikov, M. A., Samylina, O. S., Lobkovsky, L. I., & Semiletov, I. P. (2022). MatNERApor—A Matlab Package for Numerical Modeling of Nonlinear Response of Porous Saturated Soil Deposits to P- and SH-Waves Propagation. Applied Sciences, 12(9), 4614. https://doi.org/10.3390/app12094614










