Dynamic Analysis of the Seismo-Dynamic Response of Anti-Dip Bedding Rock Slopes Using a Three-Dimensional Discrete-Element Method
Abstract
:1. Introduction
2. Numerical Modeling Using 3D Discrete Elements
2.1. Overview
2.2. Setting the Dynamic Parameters
3. Dynamic Response of the Slope
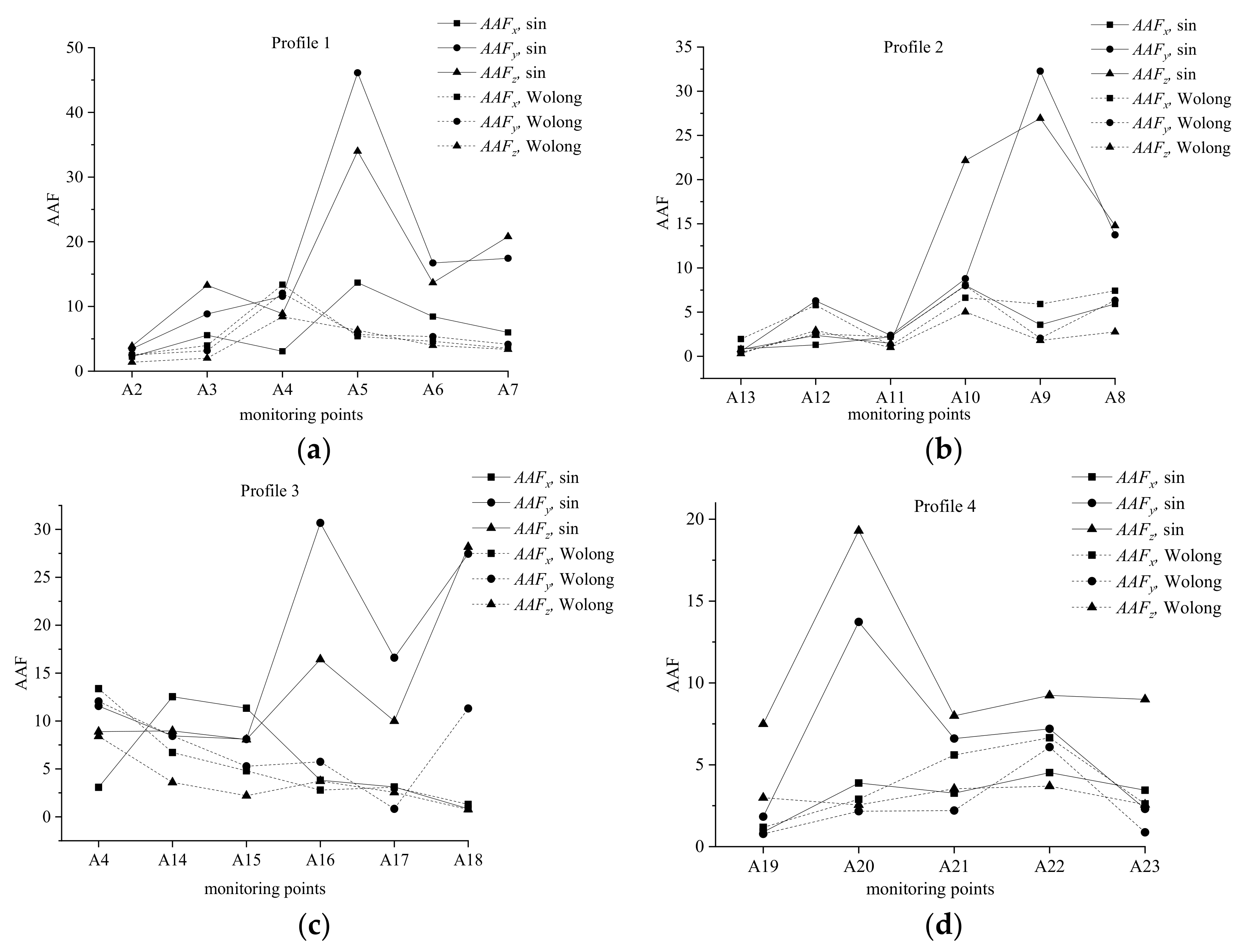
3.1. Analysis of the Amplification Effect
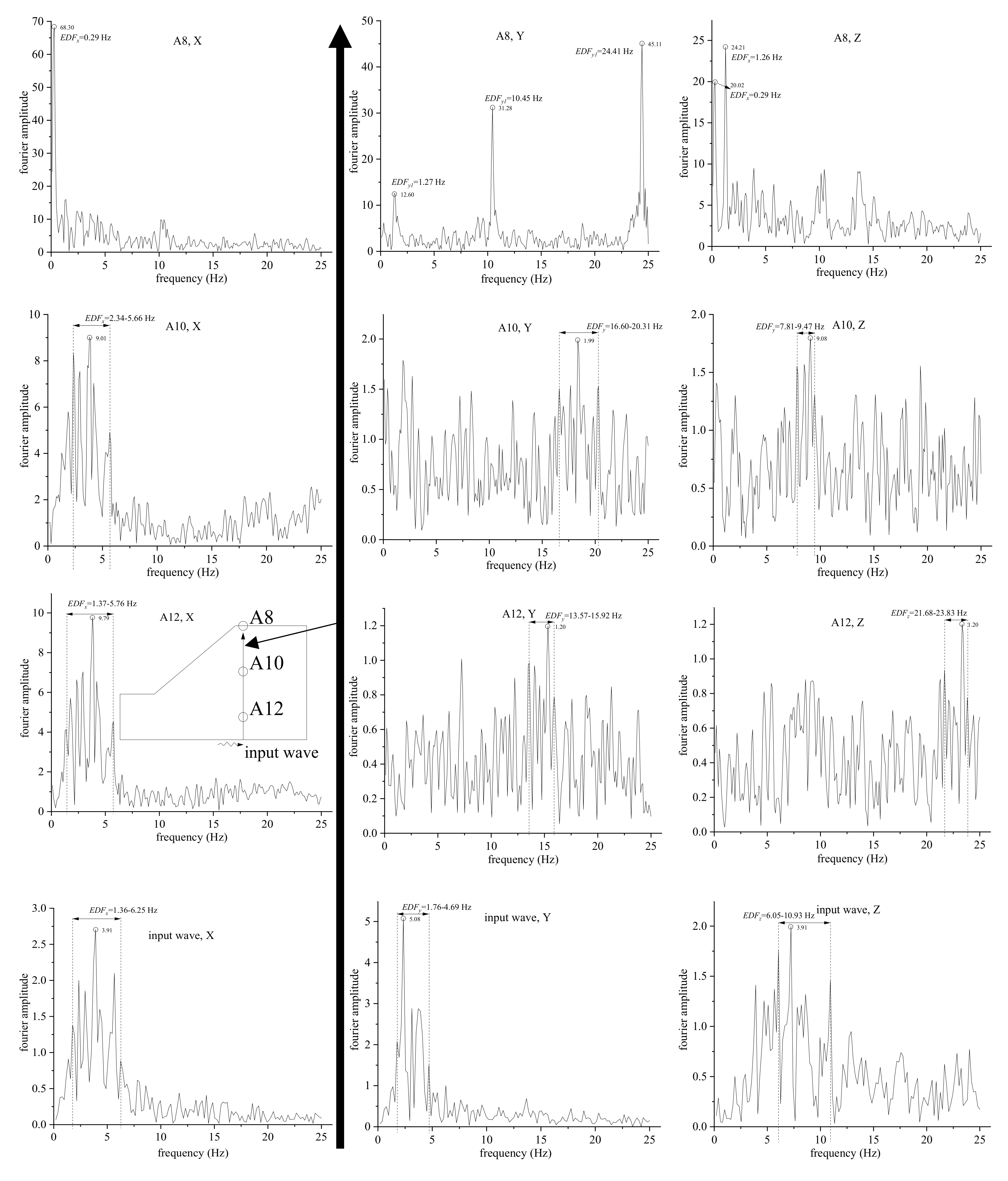
3.2. Fourier Spectra
4. Mechanism Responsible for Slope Failure under Seismic Action
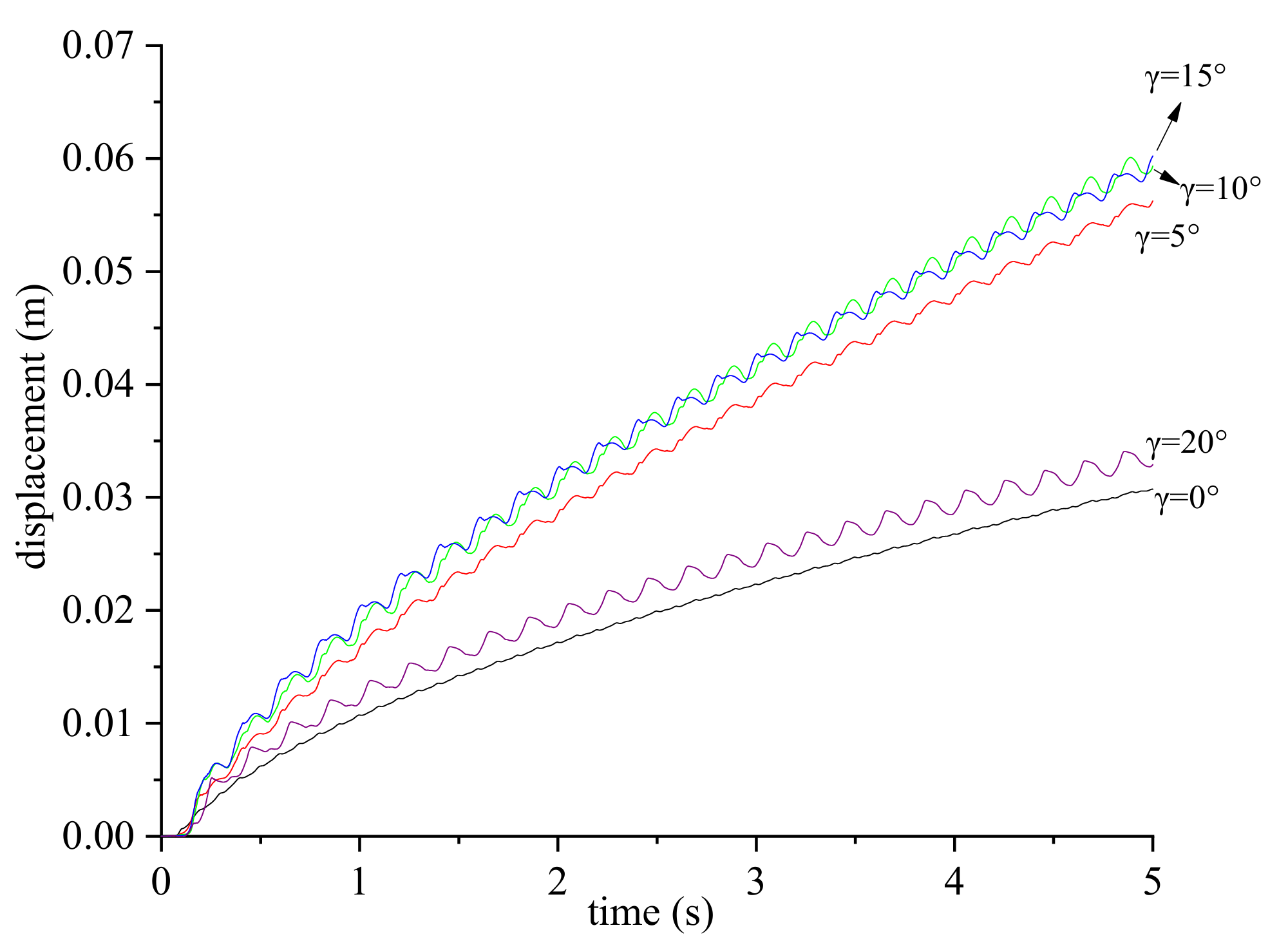
5. Permanent Displacement of the Slope
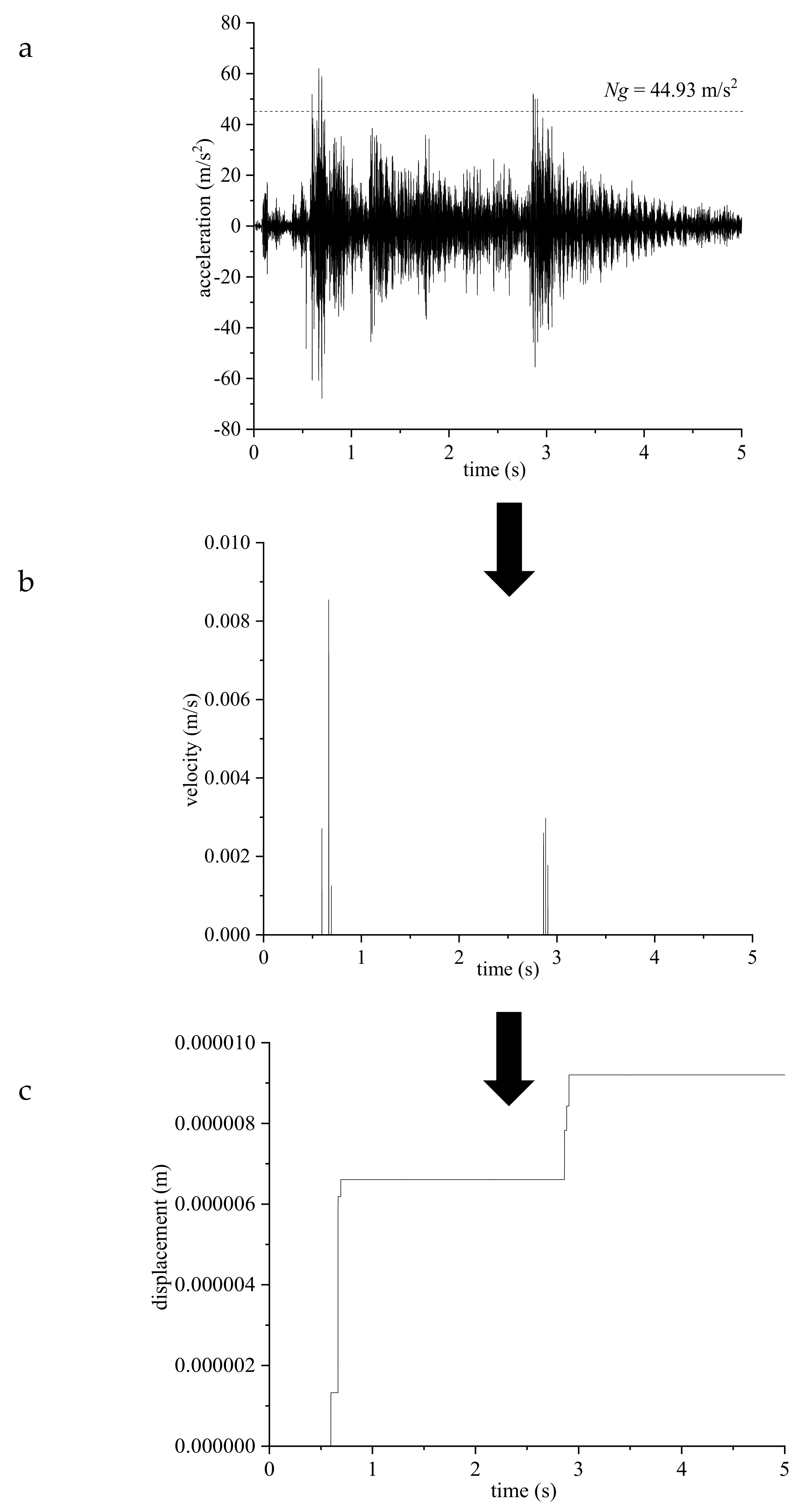
5.1. Newmark’s Method
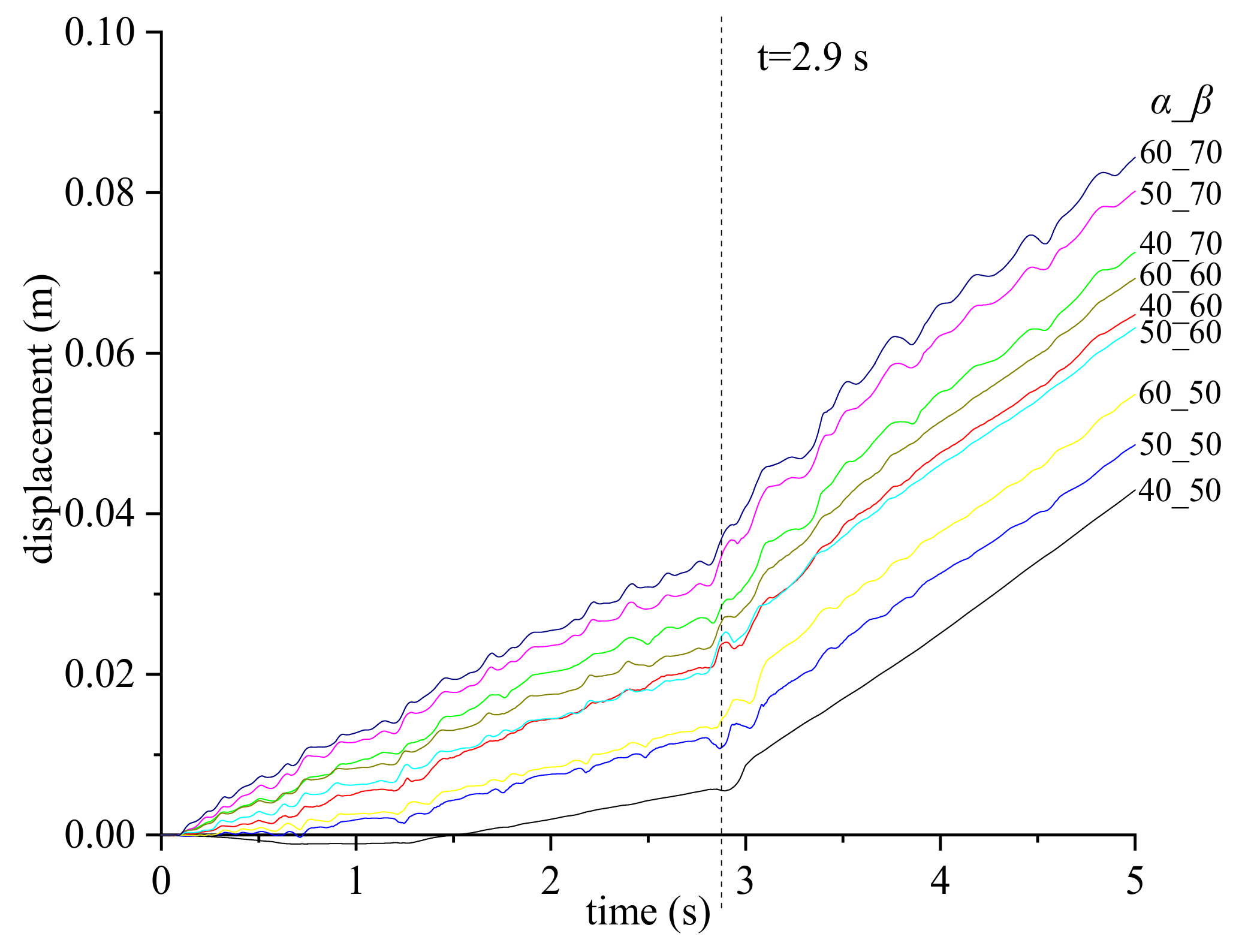
5.2. Displacements Calculated Using the 3D Discrete-Element Method
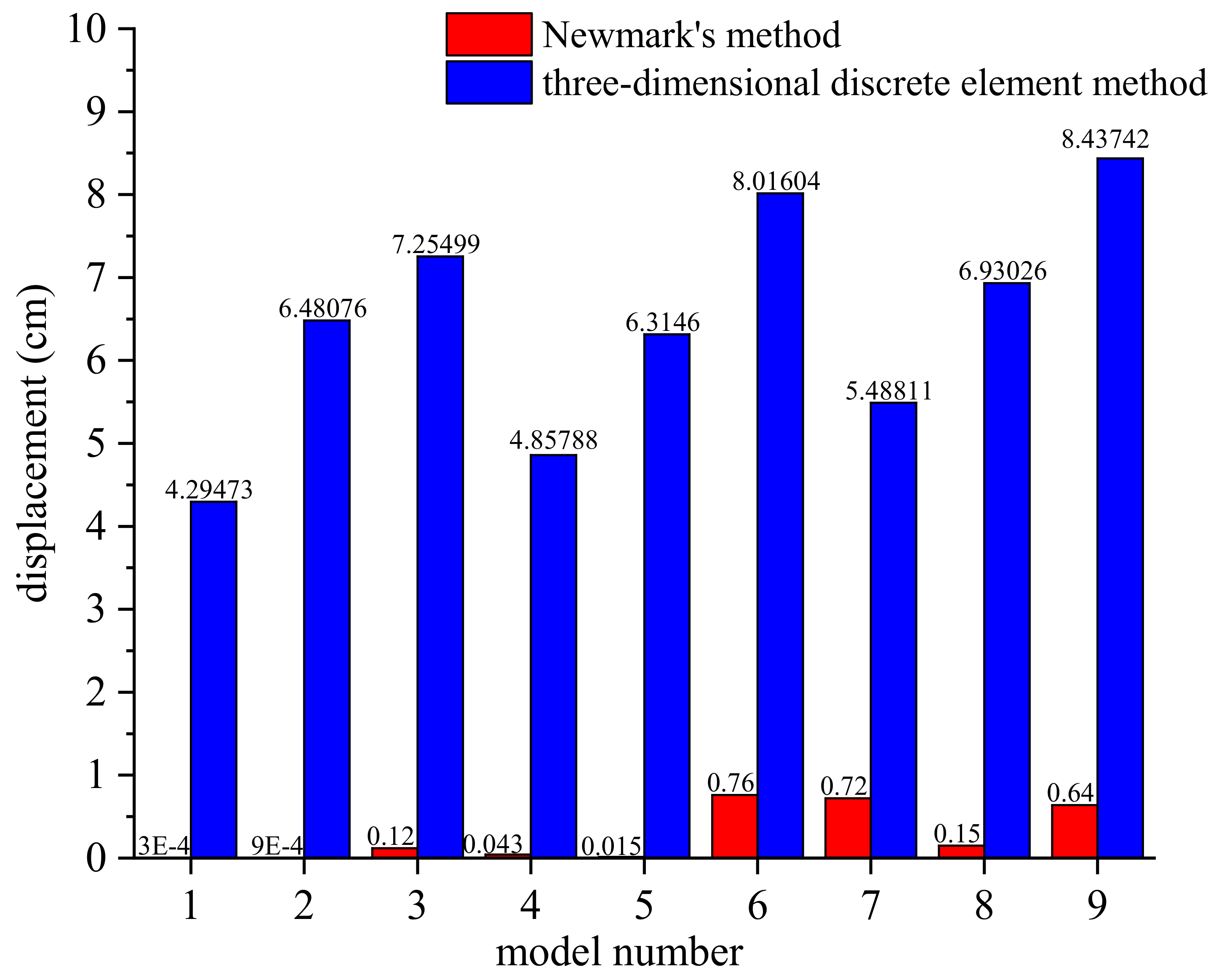
5.3. Comparison of Results and Discussion
- Compared with bedding slopes (or landslides), anti-dip bedding slopes are more stable under static conditions and have higher safety factors (SF). On the other hand, Newmark’s method is based on the assumption that sliding failure occurs with a straight failure surface. This is obviously contrary to the flexure toppling failure mode of anti-dip bedding rock slopes.
- Newmark’s method is based on a pseudo-static method and assumes that the geotechnical object can be regarded as a rigid, nondeforming body. In reality, the geotechnical object will deform and the 3D discrete-element method takes this into account. As a result, the displacement obtained using our method will be larger.
- Newmark’s method is based on the assumption that the problem can be treated in a single plane; the seismic waves and displacements are also considered to be in the same horizontal direction. In this paper, we consider the loading caused by the seismic waves in the X-, Y- and Z-directions. This means our model can account for 3D spatial effects that cannot be treated using a simple single-plane approach.
6. Conclusions
- When the slope is dynamically loaded using a 3D seismic wave, the 3D acceleration magnification coefficient of the slope is not very regular; there is also no sign of obvious ‘elevation’ and ‘appearance’ effects. Instead, it shows rhythmicity. The peak acceleration amplification effect is more significant under the action of sinusoidal waves. As the angle between the joint and slope trends increases, the amplification effect of the slope first decreases and then increases.
- As the seismic wave propagates within the slope, the amplitudes of the low-frequency parts of the seismic wave are generally amplified and the earthquake dominant frequency tends to decrease. The EDF in the Y-direction also diverges, forming 2 or 3 peaks.
- When subjected to seismic action, the slope starts to fail in the lower part of the slope and failure progresses from bottom to top. The failure surface is step-like, showing the characteristics of flexure toppling. When the angle between the joint and slope trends is nonzero, the failure surface becomes more irregular. Moreover, as this angle increases, the depth of the failure surface increases and the scope of the unstable part of the slope becomes wider.
- The permanent displacement of the slope increases as the slope and joint angles increase. Under the action of natural seismic waves, the displacement of the slope in the Y-direction develops slowly at first and then accelerates at a critical time Tc. As the angle between the joint and slope trends increases, the permanent displacement of the slope increases and then decreases.
- Newmark’s method only considers the action of seismic waves in one direction (i.e., the method is only useful for planar problems). The displacement results obtained using the method are much smaller than those obtained using the dynamic 3D discrete-element method. The results obtained using Newmark’s method are therefore overly conservative.
Author Contributions
Funding
Conflicts of Interest
References
- Goodman, R.E.; Bray, J.W. Toppling of Rock Slopes. In Proceedings of the Specialty Conference on Rock Engineering for Foundations and Slopes, Boulder, CO, USA, 15–18 August 1976; Volume 2, pp. 201–234. [Google Scholar]
- Aydan, Ö.; Kawamoto, T. The stability of slopes and underground openings against flexural toppling and their stabilisation. Rock Mech. Rock Eng. 1992, 25, 143–165. [Google Scholar] [CrossRef]
- Liu, C.H.; Jaksa, M.B.; Meyers, A.G. Improved analytical solution for toppling stability analysis of rock slopes. Int. J. Rock Mech. Min. Sci. 2008, 45, 1361–1372. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Zhang, H.; Sun, C. Theoretical and numerical study on the block-flexure toppling failure of rock slopes. Eng. Geol. 2019, 263, 105309. [Google Scholar] [CrossRef]
- Ding, B.; Han, Z.; Zhang, G.; Beng, X.; Yang, Y. Flexural Toppling Mechanism and Stability Analysis of an Anti-dip Rock Slope. Rock Mech. Rock Eng. 2021, 54, 3721–3735. [Google Scholar] [CrossRef]
- Alejano, L.R.; Gómez-Márquez, I.; Martínez-Alegría, R. Analysis of a complex toppling-circular slope failure. Eng. Geol. 2010, 114, 93–104. [Google Scholar] [CrossRef]
- Brideau, M.A.; Stead, D. Controls on block toppling using a three-dimensional distinct element approach. Rock Mech. Rock Eng. 2010, 43, 241–260. [Google Scholar] [CrossRef]
- Xue, Y.; Kong, F.; Yang, W.; Qiu, D.; Su, M.; Fu, K.; Ma, X. Main unfavorable geological conditions and engineering geological problems along Sichuan-Tibet railway. Chin. J. Rock Mech. Eng. 2020, 39, 445–468. [Google Scholar]
- Peng, J.B.; Cui, P.; Zhuang, J.Q. Challenges to engineering geology of Sichuan-Tibet railway. Chin. J. Rock Mech. Eng. 2020, 39, 2377–2389. [Google Scholar]
- Chinese Code GB 50011-2010, Code for Seismic Design of Buildings. Available online: https://www.doc88.com/p-3037442363978.html (accessed on 31 August 2018).
- Yagoda, B.G.; Hatzor, Y.H. A new failure mode chart for toppling and sliding with consideration of earthquake inertia force. In Proceedings of the 47th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013. [Google Scholar]
- Guo, S.; Qi, S.; Yang, G.; Zhang, S.; Saroglou, C. An analytical solution for block toppling failure of rock slopes during an earthquake. Appl. Sci. 2017, 7, 1008. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Ren, Z. A new method of assessing the stability of anti-dip bedding rock slopes subjected to earthquake. Bull. Eng. Geol. Environ. 2021, 80, 3693–3710. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, J.; Wu, J.; Yan, K. Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table. Rock Mech. Rock Eng. 2016, 49, 3243–3256. [Google Scholar] [CrossRef]
- Chen, C.-C.; Li, H.-H.; Chiu, Y.-C.; Tsai, Y.-K. Dynamic response of a physical anti-dip rock slope model revealed by shaking table tests. Eng. Geol. 2020, 277, 105772. [Google Scholar] [CrossRef]
- Ning, Y.; Zhang, G.; Tang, H.; Shen, W.; Shen, P. Process analysis of toppling failure on anti-dip rock slopes under seismic load in southwest China. Rock Mech. Rock Eng. 2019, 52, 4439–4455. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Wu, S.; Tang, H. Rock toppling failure mode influenced by local response to earthquakes. Bull. Eng. Geol. Environ. 2016, 75, 1361–1375. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, L.; Zhang, J.; Yang, C. Analysis of seismic stability of an obsequent rock slope using time–frequency method. Rock Mech. Rock Eng. 2019, 52, 3809–3823. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.; Chen, C.; Sun, C.; Ren, Z.; Zhang, W. Dynamic analysis of anti-dip bedding rock slopes reinforced by pre-stressed cables using discrete element method. Eng. Anal. Bound. Elem. 2021, 130, 79–93. [Google Scholar] [CrossRef]
- Itasca 3DEC-3 Dimensional Distinct Element Code, Version 5.2; Itasca Consulting Group: Minneapolis, MN, USA, 2019.
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. ASCE 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Chinese Code GB/T 17742-2020, The Chinese Seismic Intensity Scale. Available online: https://www.doc88.com/p-61773129398077.html (accessed on 27 August 2020).
- Rizzitano, S.; Cascone, E.; Biondi, G. Coupling of topographic and stratigraphic effects on seismic response of slopes through 2D linear and equivalent linear analyses. Soil Dyn. Earthq. Eng. 2014, 67, 66–84. [Google Scholar] [CrossRef]
- Yang, G.; Qi, S.; Wu, F.; Zhan, Z. Seismic amplification of the anti-dip rock slope and deformation characteristics: A large-scale shaking table test. Soil Dyn. Earthq. Eng. 2018, 115, 907–916. [Google Scholar] [CrossRef]
- Yang, G.; Ye, H.; Wu, F.; Qi, S.; Dong, J. Shaking table model test on dynamic response characteristics and failure mechanism of antidip layered rock slope. Chin. J. Rock Mech. Eng. 2012, 31, 2214–2221. [Google Scholar]
- Fan, G.; Zhang, J.J.; Fu, X. Dynamic response differences between bedding and count-tilt rock slopes with siltized intercalation. Chin. J. Geotech. Eng. 2015, 37, 692–699. [Google Scholar]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotech. 1965, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Jibson, R.W. Predicting earthquake-induced landslide displacements using Newmark’s sliding block analysis. Transp. Res. Record 1993, 1411, 9–17. [Google Scholar]
- Romeo, R. Seismically induced landslide displacements: A predictive model. Eng. Geol. 2000, 58, 337–351. [Google Scholar] [CrossRef]
- Xiao, K.; Li, H.; Liu, Y.; Xia, X.; Zhang, L. Study on deformation characteristics of bedding slopes under earthquake. Rock Soil Mech. 2007, 28, 1557–1564. (In Chinese) [Google Scholar]
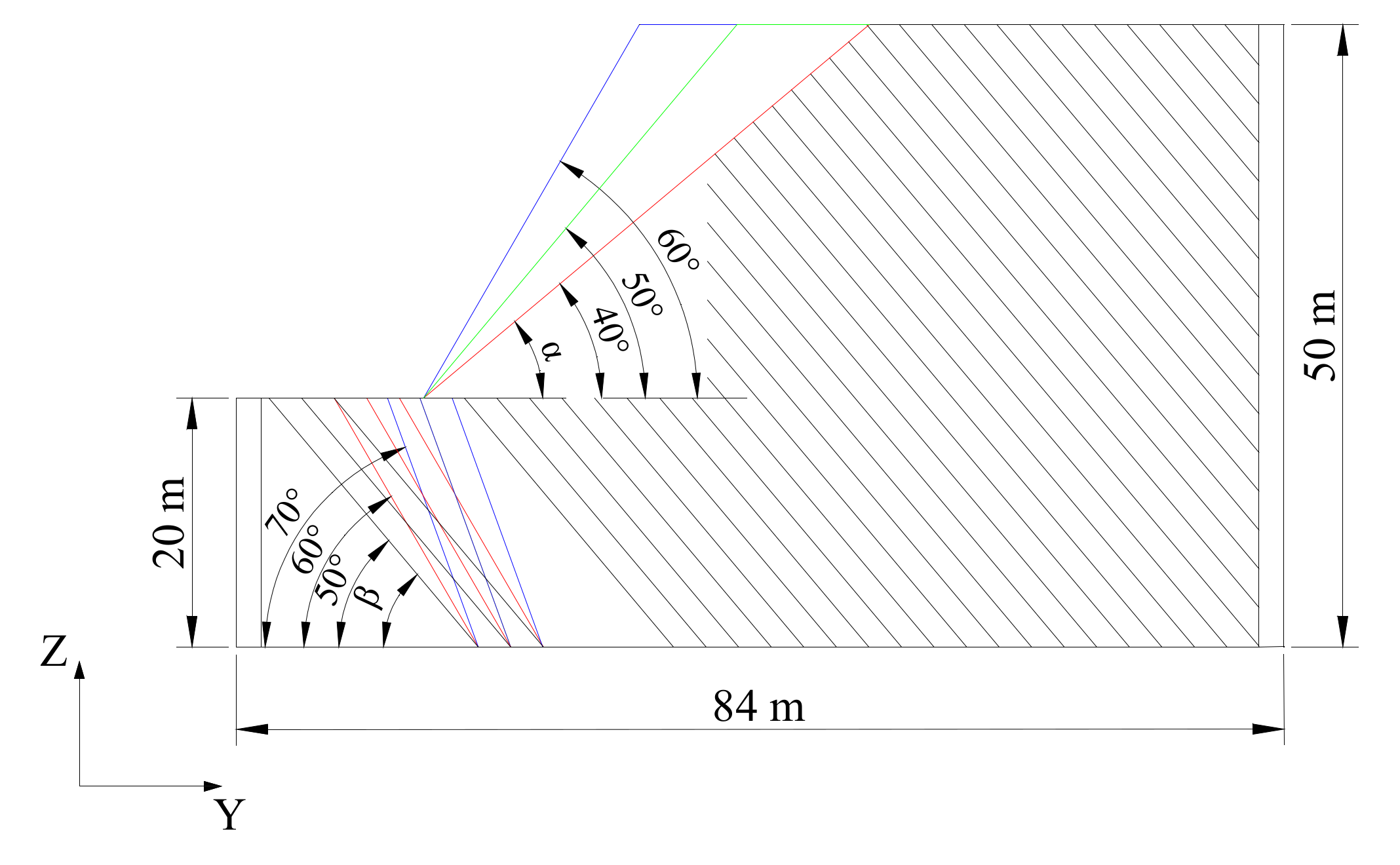
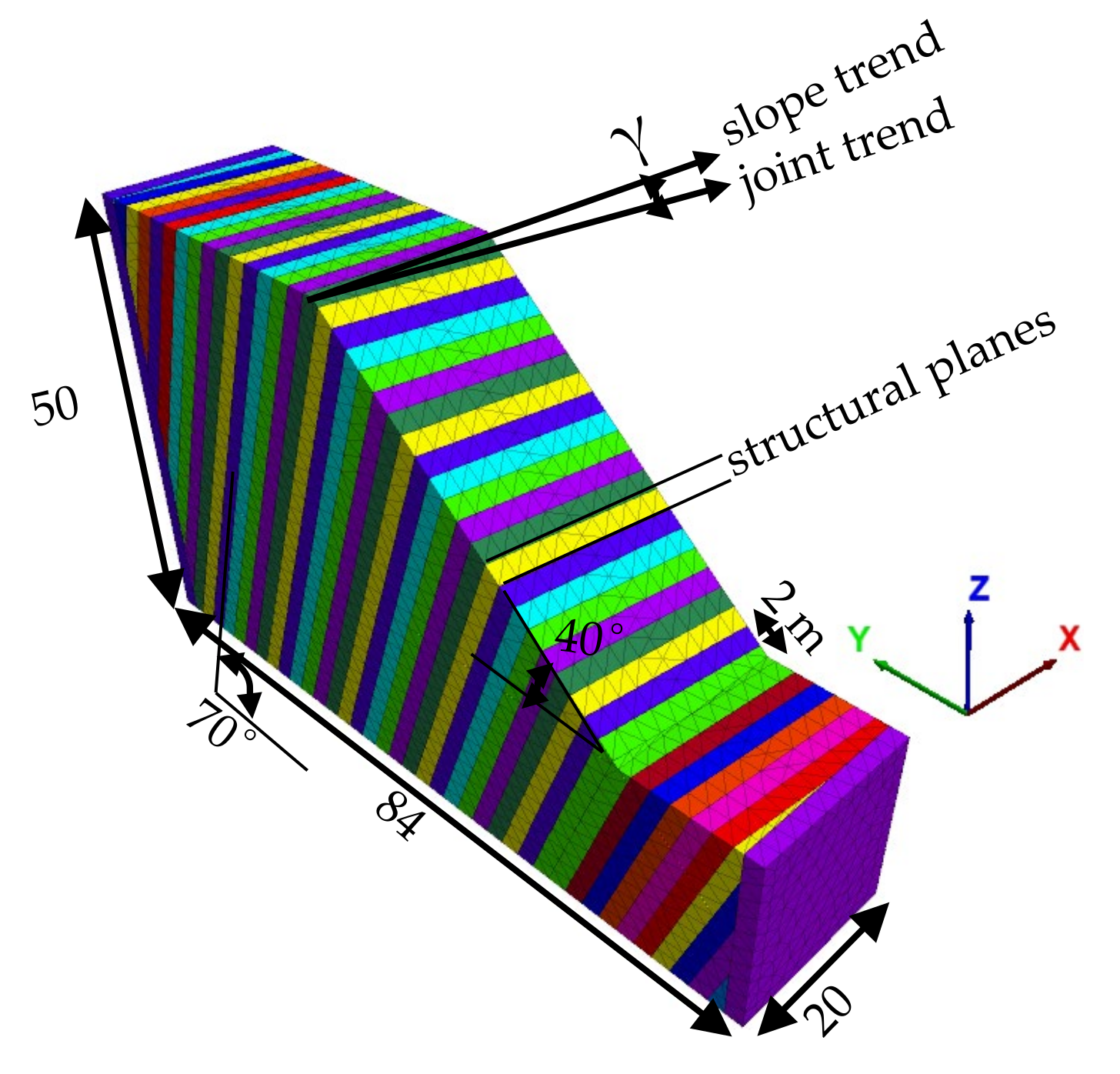
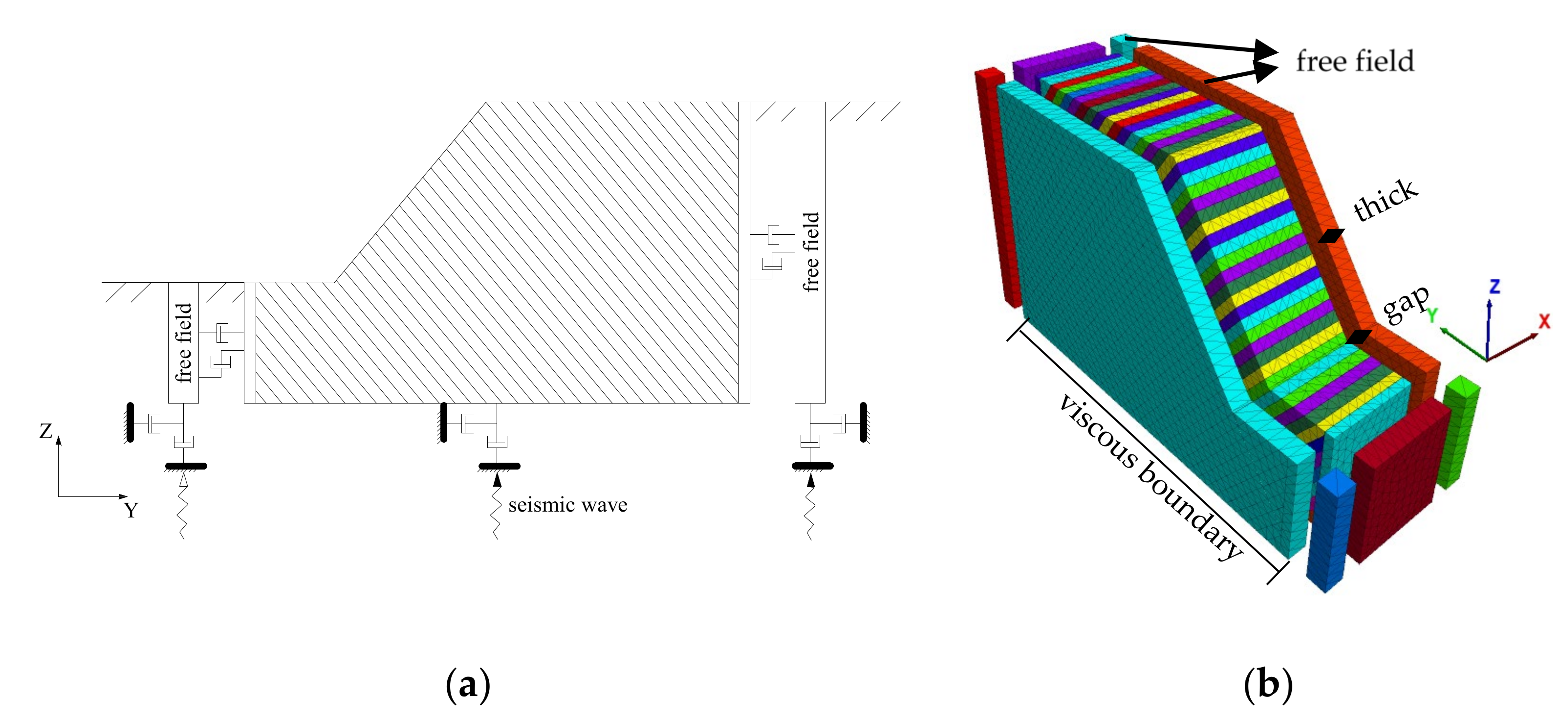

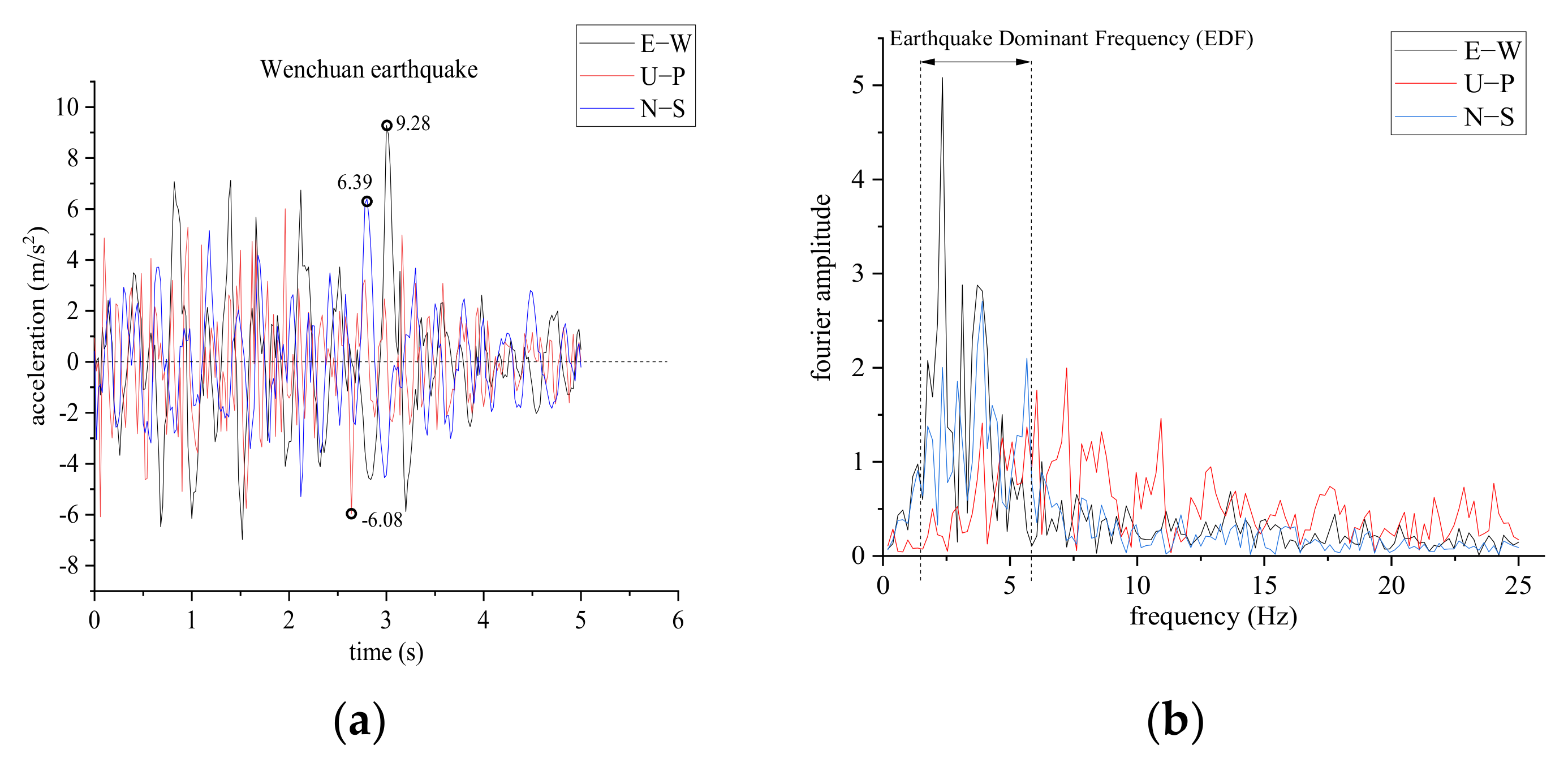





| Density (kN/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Friction Angle (°) | Tensile Strength (MPa) | Dilation Angle (°) | Normal Stiffness (GPa/m) | Tangential Stiffness (GPa/m) | |
|---|---|---|---|---|---|---|---|---|---|
| Rock mass | 25.97 | 10.5 | 0.25 | 1.5 | 45 | 0.5 | 0 | – | – |
| Structural planes | – | – | – | 0.24 | 32 | 0.001 | 0 | 58.33 | 19.44 |
| Model Number | α (°) | β (°) | SF | N (m/s2) | D (cm) |
|---|---|---|---|---|---|
| 1 | 40 | 50 | 7.88 | 5.77 | 0.00030 |
| 2 | 40 | 60 | 6.46 | 4.58 | 0.00090 |
| 3 | 40 | 70 | 3.99 | 2.51 | 0.12 |
| 4 | 50 | 50 | 5.66 | 5.55 | 0.043 |
| 5 | 50 | 60 | 4.07 | 3.66 | 0.015 |
| 6 | 50 | 70 | 2.71 | 2.04 | 0.76 |
| 7 | 60 | 50 | 3.95 | 5.11 | 0.72 |
| 8 | 60 | 60 | 2.70 | 2.94 | 0.15 |
| 9 | 60 | 70 | 2.02 | 1.77 | 0.64 |
| 1 | 40 | 50 | 7.88 | 5.77 | 0.00030 |
| 2 | 40 | 60 | 6.46 | 4.58 | 0.00090 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Chen, C.; Sun, C.; Wang, Y. Dynamic Analysis of the Seismo-Dynamic Response of Anti-Dip Bedding Rock Slopes Using a Three-Dimensional Discrete-Element Method. Appl. Sci. 2022, 12, 4640. https://doi.org/10.3390/app12094640
Ren Z, Chen C, Sun C, Wang Y. Dynamic Analysis of the Seismo-Dynamic Response of Anti-Dip Bedding Rock Slopes Using a Three-Dimensional Discrete-Element Method. Applied Sciences. 2022; 12(9):4640. https://doi.org/10.3390/app12094640
Chicago/Turabian StyleRen, Zhanghao, Congxin Chen, Chaoyi Sun, and Yue Wang. 2022. "Dynamic Analysis of the Seismo-Dynamic Response of Anti-Dip Bedding Rock Slopes Using a Three-Dimensional Discrete-Element Method" Applied Sciences 12, no. 9: 4640. https://doi.org/10.3390/app12094640






