HDPP: High-Dimensional Dynamic Path Planning Based on Multi-Scale Positioning and Waypoint Refinement
Abstract
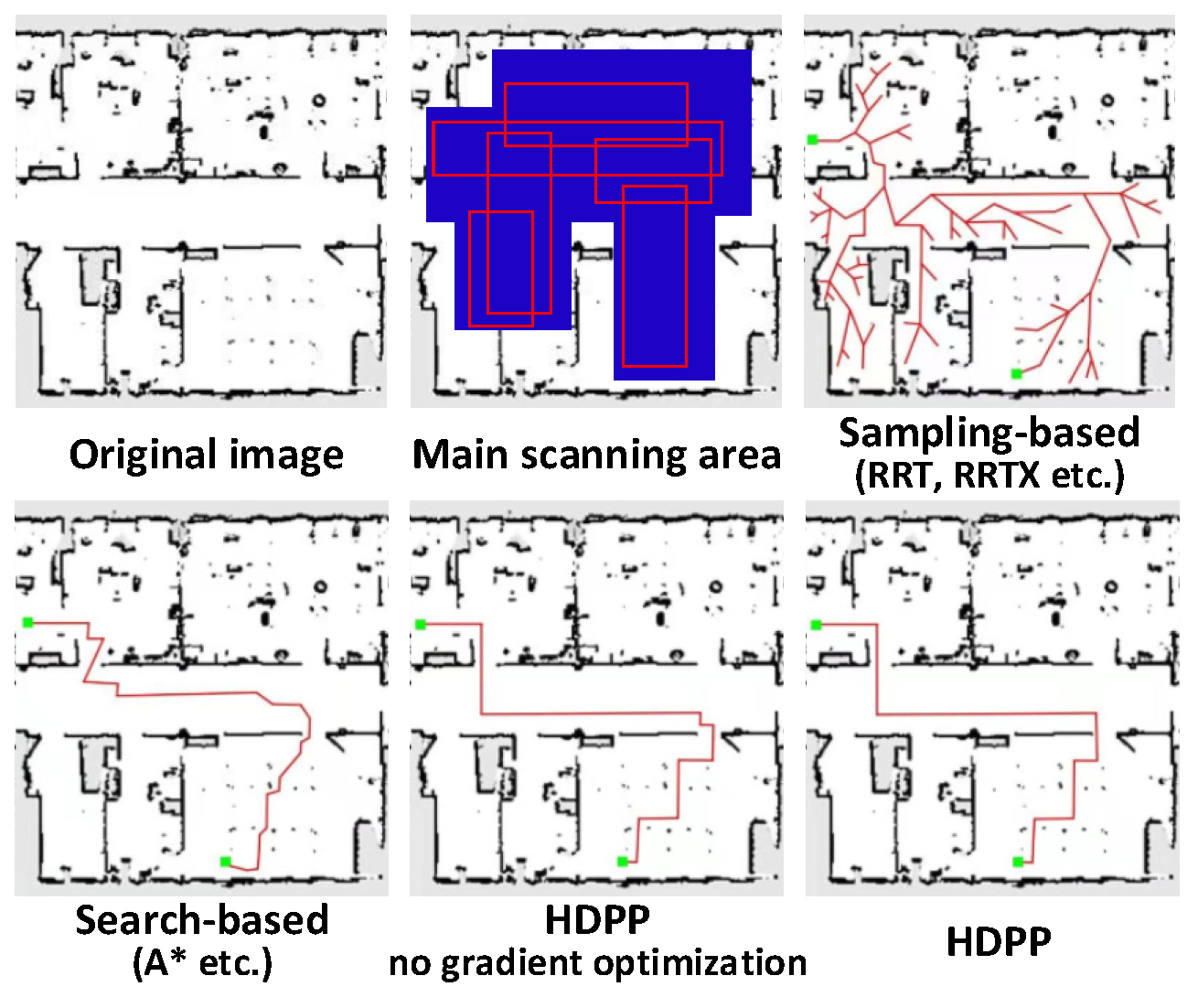
:1. Introduction
- A novel multi-scale positioning model of high-dimensional path planning is proposed to adaptively extract and learn multi-scale feature maps with multiple predictions, while dynamically refine them through fast positioning. The multi-scale strategy is used to improve the characterization ability of unknown environmental factors. The results demonstrate the superiority of our approach through comparison with state-of-the-art models;
- A patch selection and optimization scheme are proposed to dynamically find and divide category areas, and gradually eliminate insignificant waypoints for multi-degree-of-freedom planning;
- We balance the gradients of multi-category feature points to process obstacles and road segment edges at the same time to avoid over-optimizing one of them during the training phase, eliminating the redundancy and collapse of previous research planning methods;
- Extensive experiments conducted on both manually annotated and machine weakly labeled datasets demonstrate the effectiveness of the proposed approach. We have verified the effect of HDPP not only in high-dimensional space, but also in a planar simulation environment.
2. Related Work
2.1. Path Planning Methods
- Search-based. The research for search-based path planning has been studied broadly (for example, A*, Dijkstra, LPA* etc.) [16,21,22,23]. These algorithms are based on heuristic functions that calculate the prior loss at different locations on the map and thus search for the optimal path; but this is usually a static, flat search. Saleem et al. [21] propose a multi-heuristic framework to guide the search along the relevant classes for dynamic inspection. Elhoseny et al. [22] built an efficient, Bezier curve-based approach for the path planning in a dynamic field using a Modified Genetic Algorithm (MGA), which aims to boost the diversity of the generated solutions of the standard GA. Dang et al. [23] present a novel search-based strategy for autonomous graph-based exploration path planning in subterranean environments. These search-based methods break the limitations of being limited to static searches;
- Sampling-based. Similarly to search-based methods, sampling-based path planning also has been widely used (for example, RRT, RRT*, S-RRT) [17,24,25,26,27,28]. It uses an incremental method to build a search tree to gradually improve the resolution ability without setting any resolution parameters. This sampling-based strategy has a good effect on dynamic programming. Summers [24] propose a distributional, robust incremental sampling-based method—DR-RRT—for dynamic motion planning under uncertainty. Lai et al. [25] propose a novel framework—PDMP—that uses bijective and differentiable mappings or diffeomorphisms to transform sampling distributions of sampling-based motion planners. Some researchers use multilevel abstractions to solve motion planning problems involving high-dimensional state spaces and develop novel multilevel motion planning algorithms, which are called QRRT* and QMP* [26,27]. Those algorithms are proved to be probabilistically complete and almost-surely asymptotically optimal. Meanwhile, a learning method based on Monte-Carlo Tree Search is proposed to learn assignment orders for the variable-subsets [28]. The strategy can efficiently compute a set of diverse valid robot configurations for mode-switches within sequential manipulation tasks, which are waypoints for subsequent trajectory optimization or sampling-based motion planning algorithms;
- Reinforcement Learning-based. With the development of deep learning, many methods [29,30,31,32,33] have been proposed for robot’s path planning with reinforcement learning strategy (for example, Q-learning, Monte Carlo, DQN, C51, HER etc.). Chen et al. [30] propose a path planning and manipulating approach based on Q-learning, which can drive a cargo ship by itself without requiring any input from human experiences. STAPP [31]—a multi-agent reinforcement learning algorithm is proposed for multi-UAV target assignment and path planning (MUTAPP) based on a multi-agent deep deterministic policy gradient. Yan et al. [32] present a Deep Reinforcement Learning (DRL) approach for UAV path planning based on the global situation information. RLGWO [33]—a novel reinforcement learning based grey wolf optimizer algorithm is also proposed for unmanned aerial vehicles (UAVs) path planning.
2.2. Multi-Degree-of-Freedom Target Motion Planning
3. Materials and Methods
3.1. Problem Formulation
3.2. Multi-Scale Positioning for Waypoint Navigation
| Algorithm1. Multi-scale positioning for waypoint navigation |
| Input: (image of robot receptive field), (movement cost), ( for gait sequence, for gait sequence subscript, for overall number of action groups), (start point), (the planning result for start point) (the planning result for th iteration), (maximum iteration, which is 3000 in this paper), (Robot gait planning result after th iteration), , (the modular combination network including instance segmentation and position, and the network for patch-based selection and refining mentioned in Section 3.3), (the lower limit of the difference between the target prediction results) Output: Robot gait planning result after optimization /* INITIALIZATION */ 1: Initialize , ,, , , /* MULTISCALE FEATURE EXTRATION */ 2: while and do: 3: Get and fill the 4: two stream feature extraction pyramid 5: 6: while do: 7: 8: end while /* OPTIMIZATION */ 9: Optimize ∈ based on Equation (8)–(10) 10: Update and Extract /* INTEGRATION */ 11: for each do: 12: Update , 13: end for 14: end while 15: end 16: Integration (Parent, ). |
3.3. Patch-Based Selection and Refining of Waypoints
| Algorithm 2. Patch-based Selection and Refining |
| Input: (perturbation), (the number of patches), (the max number of patches), (the min number of patches), (the frequency of adding perturbation), (the threshold of decreasing perturbation), (maximum iteration), (the flag for increased classification area), (the flag for decreased classification area), (input image), (optimize method which returns new waypoints and the number of bounding boxes) Output: Classification result after optimization 1: , , , 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: |
3.4. Position Correction and Eliminate Camera Distortion
4. Experiment
4.1. Datasets
- High-dimensional Space Map Dataset. This is a data set we created. In the scene, we manually control the robotic arm to calibrate the position of the steering gear and perform image acquisition at a fixed frame rate. This data set is based on palletizing application scenarios, with a total of ten environments. Each environment contains 6 different specifications of obstacles (3 × 2, there are 3 shapes of obstacles, and each shape has 2 sizes). A single environment group consists of 600 training images, 100 verification images, and 100 test images. Obstacles of the same type are placed in different layouts. At the same time, we use robots with different degrees of freedom (as shown in Table 1) to complete the entire experiment in a reasonable time. We follow the original settings to independently train and evaluate each environment group. In addition, in order to increase the amount of data and provide a basis for more robust ablation experiments, we have performed data enhancement operations. We cropped multiple random blocks with a size of 64 × 64 from each map and randomly generated them in the dataset scene. We use 30 of the 10 scene maps to generate 1600 training and 300 validation maps randomly. At the same time, we also constructed 200 data for testing through mapping, so as to ensure that there is no overfitting caused by the occurrence of shared maps. The entire data set contains more than 6000 sets of data for robust detection, 1900 sets of data for modular detection, and more than 2000 sets of collected data for safety collision detection. We hope to achieve the purpose of feasibility experiment and robustness detection through this original high-dimensional spatial data set.
- Motion Planning Dataset [39]. This data set was selected by us as the data for qualitative experiments. The MP dataset is a collection of eight grid world environments with unique obstacle shapes created by Bhardwaj et al. Each environment group is composed of 800 training maps, 100 verification maps and 100 test maps, and obstacles of the same type are placed in different layouts. We resize the data set to the same size scene specification of the High-dimensional Space Map Dataset to provide data support for the feasibility of the experiment. The entire data set contains a total of 8000 sets of data. We hope to use this data set to provide a sufficient and objective test for the experimental conclusions.
4.2. Methods for Experiment
- Tangent Bug Algorithms [42]. This is a real-time path planning algorithm for detecting surrounding obstacles, also a variant of Bug1 and Bug2. Tangent Bug is different from the previous two algorithms. Only when the distance from the obstacle is 0, the characteristics of the obstacle are found to be different. The variable R is defined. As long as there is an obstacle within the distance R, it will be detected. Next, take the robot as a single point to detect whether there is an obstacle on the line between the current position and the target point, and respond to it. We adjusted the R parameters of Tangent Bug, introduced μ parameters, and calculated R according to the robot’s motion environment. Compared with the traditional method, this method has certain advantages in the real-time obstacle avoidance scene of the robotic arm. We hope to introduce this algorithm to compare the effect of HDPP at the obstacle avoidance level.
- SAIL (Summation-based incremental learning). High search efficiency is achieved by learning heuristic functions from demonstrations. Distinct from HDPP, SAIL uses hand-designed features to introduce prior information into the algorithm, such as the nodes of each target and nearest obstacle. We adjusted SAIL to adapt to the detection and planning of high-dimensional space and evaluated the effect of SAIL on the data set. We hope that this method can be used to compare the impact of introducing a priori information on preliminary path planning.
- Cuckoo Search Algorithm [43]. A parallel compact cuckoo search algorithm for three-dimensional path planning. The algorithm uses an improved cuckoo search based on compact parallel technology to find the target in a complex three-dimensional environment. Cuckoo search proposes a new parallel communication strategy that saves the memory of the robot. We train the encoder by treating the parallel search module as a black box function and optimizing it through the black box, while keeping other settings. We transformed the drone in the original application scenario of the algorithm into a multi-joint robot, which is consistent with the HDPP operating environment. And check the plan in a high-dimensional environment. This algorithm is often used in UAVs (unmanned aerial vehicle), underwater robots and other equipment, and has reference significance for high-dimensional space planning.
- Search-based [16,21,22,23]. We mainly choose Dijkstra’s Algorithm, A* and D* lite for experiment. These algorithms are representative of traditional path planning based on search strategy, which will find the optimal path by visiting and calculating map nodes and costs. However, the difference is that the search strategies of these three algorithms are constantly refined, and their performance has a progressive relationship.
- Sampling-based [17,24,25,26,27,28]. RRT and its improved algorithm—RRT*—are regarded as representative of sample-based path planning. For this strategy, the optimal path point was found by random sampling and added into the planned path tree. RRT* is improved on the basis of RRT, mainly by reselecting the parent node and rewiring operations.
- Reinforcement learning [29,30,31,32,33]. Classical Monte Carlo algorithm and DQN are transferred to the experiment to explore the effect of reinforcement learning ideas in high-dimensional space, especially for multi-degree-of-freedom objects. Since our data set is dynamic and variable, and time thresholds are designed to emphasize practical applications, underfitting or local optimality can be expected with this strategy of calculating returns by receiving continuous environmental feedback. Two of the most typical algorithms are introduced to test this judgment.
4.3. Implementation Details
4.4. Results of HDPP
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liu, J.; Kato, N. Networking and communications in autonomous driving: A survey. IEEE Commun. Surv. Tutor. 2018, 21, 1243–1274. [Google Scholar] [CrossRef]
- Jhaver, S.; Birman, I.; Gilbert, E.; Bruckman, A. Human-machine collaboration for content regulation: The case of reddit automoderator. ACM Trans. Comput. Human Interact. TOCHI 2019, 26, 1–35. [Google Scholar] [CrossRef]
- Bao, L.G.; Dang, T.G.; Anh, N.D. Storage assignment policy and route planning of agvs in warehouse optimization. In Proceedings of the 2019 International Conference on System Science and Engineering (ICSSE), Dong Hoi City, Quang Binh Province, Vietnam, 20–21 July 2019; pp. 599–604. [Google Scholar]
- Tsai, C.H.; Elibol, A.; Chong, N.Y. A UAV-UUV Transformative Housing for Minimal Logistics Underwater Exploration. In Proceedings of the 2021 18th International Conference on Ubiquitous Robots (UR), Jeju, Korea, 4–6 July 2021. [Google Scholar]
- Agrawal, A.; Verschueren, R.; Diamond, S.; Boyd, S. A rewriting system for convex optimization problems. J. Control. Decis. 2018, 5, 42–60. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Park, J.; Koltun, V. Open3D: A modern library for 3D data processing. arXiv 2018, arXiv:1801.09847. [Google Scholar]
- Lei, Z.; Han, S.; Bouferguène, A.; Taghaddos, H.; Hermann, U.; Al-Hussein, M. Algorithm for mobile crane walking path planning in congested industrial plants. J. Constr. Eng. Manag. 2015, 141, 05014016. [Google Scholar] [CrossRef]
- Sharma, N.; Thukral, S.; Aine, S.; Sujit, P.B. A virtual bug planning technique for 2D robot path planning. In Proceedings of the IEEE 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 5062–5069. [Google Scholar]
- Liu, J.; Yang, J.; Liu, H.; Tian, X.; Gao, M. An improved ant colony algorithm for robot path planning. Soft Comput. 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
- Chou, J.S.; Cheng, M.Y.; Hsieh, Y.M.; Yang, I.T.; Hsu, H.T. Optimal path planning in real time for dynamic building fire rescue operations using wireless sensors and visual guidance. Autom. Constr. 2019, 99, 1–17. [Google Scholar] [CrossRef]
- Ammirato, P.; Poirson, P.; Park, E.; Košecká, J.; Berg, A.C. A dataset for developing and benchmarking active vision. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1378–1385. [Google Scholar]
- Banino, A.; Barry, C.; Uria, B.; Blundell, C.; Lillicrap, T.; Mirowski, P.; Pritzel, A.; Chadwick, M.J.; Degris, T.; Modayil, J.; et al. Vector-based navigation using grid-like representations in artificial agents. Nature 2018, 557, 429–433. [Google Scholar] [CrossRef]
- Ummenhofer, B.; Zhou, H.; Uhrig, J.; Mayer, N.; Ilg, E.; Dosovitskiy, A.; Brox, T. Demon: Depth and motion network for learning monocular stereo. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5038–5047. [Google Scholar]
- Modares, J.; Ghanei, F.; Mastronarde, N.; Dantu, K. Ub-anc planner: Energy efficient coverage path planning with multiple drones. In Proceedings of the 2017 IEEE international conference on robotics and automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6182–6189. [Google Scholar]
- Fraccaro, M.; Rezende, D.; Zwols, Y.; Pritzel, A.; Eslami, S.A.; Viola, F. Generative temporal models with spatial memory for partially observed environments. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1549–1558. [Google Scholar]
- Zhou, K.; Yu, L.; Long, Z.; Mo, S. Local path planning of driverless car navigation based on jump point search method under urban environment. Future Internet 2017, 9, 51. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Dai, B.; Lin, Q.; Ye, G.; Liu, H.; Song, L. Learning to plan in high dimensions via neural exploration-exploitation trees. arXiv, 2019; arXiv:1903.00070. [Google Scholar]
- Wei, K.; Ren, B. A method on dynamic path planning for robotic manipulator autonomous obstacle avoidance based on an improved RRT algorithm. Sensors 2018, 18, 571. [Google Scholar] [CrossRef] [Green Version]
- Clifton, J.; Laber, E. Q-learning: Theory and applications. Annu. Rev. Stat. Its Appl. 2020, 7, 279–301. [Google Scholar] [CrossRef] [Green Version]
- Betancourt, M. A conceptual introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Saleem, M.S.; Sood, R.; Onodera, S.; Arora, R.; Kanazawa, H.; Likhachev, M. Search-based Path Planning for a High Dimensional Manipulator in Cluttered Environments Using Optimization-based Primitives. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8301–8308. [Google Scholar]
- Elhoseny, M.; Tharwat, A.; Hassanien, A.E. Bezier curve based path planning in a dynamic field using modified genetic algorithm. J. Comput. Sci. 2018, 25, 339–350. [Google Scholar] [CrossRef]
- Dang, T.; Mascarich, F.; Khattak, S.; Papachristos, C.; Alexis, K. Graph-based path planning for autonomous robotic exploration in subterranean environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 3105–3112. [Google Scholar]
- Summers, T. Distributionally robust sampling-based motion planning under uncertainty. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6518–6523. [Google Scholar]
- Lai, T.; Zhi, W.; Hermans, T.; Ramos, F. Parallelised diffeomorphic sampling-based motion planning. In Proceedings of the Conference on Robot Learning, Online, 11 January 2022; pp. 81–90. [Google Scholar]
- Orthey, A.; Toussaint, M. Rapidly-exploring quotient-space trees: Motion planning using sequential simplifications. arXiv 2019, arXiv:1906.01350. [Google Scholar]
- Orthey, A.; Akbar, S.; Toussaint, M. Multilevel motion planning: A fiber bundle formulation. arXiv 2020, arXiv:2007.09435. [Google Scholar]
- Ortiz-Haro, J.; Hartmann, V.N.; Oguz, O.S.; Toussaint, M. Learning efficient constraint graph sampling for robotic sequential manipulation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 4606–4612. [Google Scholar]
- Schmitt, P.S.; Wirnshofer, F.; Wurm, K.M.; Wichert, G.V.; Burgard, W. Planning reactive manipulation in dynamic environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 136–143. [Google Scholar]
- Chen, C.; Chen, X.Q.; Ma, F.; Zeng, X.J.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean. Eng. 2019, 189, 106299. [Google Scholar] [CrossRef]
- Qie, H.; Shi, D.; Shen, T.; Xu, X.; Li, Y.; Wang, L. Joint optimization of multi-UAV target assignment and path planning based on multi-agent reinforcement learning. IEEE Access 2019, 7, 146264–146272. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Towards real-time path planning through deep reinforcement learning for a UAV in dynamic environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Ichter, B.; Pavone, M. Robot motion planning in learned latent spaces. IEEE Robot. Autom. Lett. 2019, 4, 2407–2414. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Feng, C. DeepMapping: Unsupervised map estimation from multiple point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8650–8659. [Google Scholar]
- Ichter, B.; Harrison, J.; Pavone, M. Learning sampling distributions for robot motion planning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7087–7094. [Google Scholar]
- Kunz, T.; Reiser, U.; Stilman, M.; Verl, A. Real-time path planning for a robot arm in changing environments. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5906–5911. [Google Scholar]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Bhardwaj, M.; Choudhury, S.; Scherer, S. Learning heuristic search via imitation. In Proceedings of the Conference on Robot Learning, Online, October 2017; pp. 271–280. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Qassim, H.; Verma, A.; Feinzimer, D. Compressed residual-VGG16 CNN model for big data places image recognition. In Proceedings of the 2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–10 January 2018; pp. 169–175. [Google Scholar]
- Xu, Q.L.; Yu, T.; Bai, J. The mobile robot path planning with motion constraints based on Bug algorithm. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 2348–2352. [Google Scholar]
- Song, P.C.; Pan, J.S.; Chu, S.C. A parallel compact cuckoo search algorithm for three-dimensional path planning. Appl. Soft Comput. 2020, 94, 106443. [Google Scholar] [CrossRef]




| Degree of Freedom | Original | Removing Redundancy |
|---|---|---|
| 2-DOF Four-legged car | 37 | 14 |
| 3-DOF Robotic arm | 59 | 31 |
| 6-DOF Robotic arm | 93 | 56 |
| 10-DOF Robotic arm | 152 | 72 |
| High-Dimensional Space Map Dataset | |||
|---|---|---|---|
| Methods | OPT* | ACC* | TS* |
| Dijkstra’s Algorithm | 0 | 0.71 | 0.49 |
| A*—A-star algorithm | 0.13 | 0.93 | 0.58 |
| D* Lite | 0.59 | 0.77 | 0.38 |
| RRT—Rapidly-exploring Random Trees | 0.04 | 0.89 | 0.74 |
| RRT* | 0.16 | 0.87 | 0.81 |
| Bug Algorithms | 0.48 | 0.83 | 0.78 |
| Monte Carlo | 0.60 | 0.43 | 0.24 |
| DQN | 0.75 | 0.62 | 0.43 |
| Tangent Bug Algorithms | 0.56 | 0.89 | 0.81 |
| SAIL | 0.63 | 0.92 | 0.91 |
| Cuckoo Search Algorithm. | 0.48 | 0.93 | 0.94 |
| HDPP | 0.72 | 0.91 | 0.97 |
| Motion planning Dataset | |||
| Methods | OPT* | ACC* | TS* |
| Dijkstra’s Algorithm | 0 | 0.63 | 0.51 |
| A*—A-star algorithm | 0.14 | 0.91 | 0.45 |
| D* Lite | 0.58 | 0.74 | 0.49 |
| RRT—Rapidly-exploring Random Trees | 0.10 | 0.92 | 0.63 |
| RRT* | 0.12 | 0.94 | 0.57 |
| Bug Algorithms | 0.52 | 0.79 | 0.61 |
| Monte Carlo | 0.35 | 0.31 | 0.47 |
| DQN | 0.52 | 0.54 | 0.66 |
| Tangent Bug Algorithms | 0.60 | 0.79 | 0.77 |
| SAIL | 0.64 | 0.89 | 0.83 |
| Cuckoo Search Algorithm. | 0.46 | 0.90 | 0.94 |
| HDPP | 0.81 | 0.87 | 0.94 |
| Simulation Dataset | |||
| Methods | OPT* | ACC* | TS* |
| Dijkstra’s Algorithm | 0 | 0.60 | 0.55 |
| A*—A-star algorithm | 0.13 | 0.92 | 0.64 |
| D* Lite | 0.69 | 0.78 | 0.43 |
| RRT—Rapidly-exploring Random Trees | 0.11 | 0.89 | 0.79 |
| RRT* | 0.21 | 0.90 | 0.72 |
| Bug Algorithms | 0.48 | 0.84 | 0.78 |
| Monte Carlo | 0.65 | 0.60 | 0.57 |
| DQN | 0.87 | 0.84 | 0.68 |
| Tangent Bug Algorithms | 0.56 | 0.91 | 0.86 |
| SAIL | 0.62 | 0.91 | 0.93 |
| Cuckoo Search Algorithm. | 0.46 | 0.95 | 0.98 |
| HDPP | 0.83 | 0.93 | 0.99 |
| OPT* | Dataset 1 | Dataset 2 | Dataset 3 |
|---|---|---|---|
| MIN | 0.65 | 0.79 | 0.80 |
| MAX | 0.83 | 0.94 | 0.85 |
| AVG | 0.72 | 0.81 | 0.83 |
| ACC* | Dataset 1 | Dataset 2 | Dataset 3 |
| MIN | 0.79 | 0.67 | 0.77 |
| MAX | 1 | 0.91 | 1 |
| AVG | 0.91 | 0.87 | 0.93 |
| TS* | Dataset 1 | Dataset 2 | Dataset 3 |
| MIN | 0.92 | 0.93 | 0.93 |
| MAX | 1 | 1 | 1 |
| AVG | 0.97 | 0.94 | 0.99 |
| Stabilizing Gradient | √ | √ | ||||
| Gradient-based Location | √ | √ | ||||
| Patch Selection and Refining | √ | √ | √ | |||
| Eliminate camera distortion | √ | |||||
| Position correction | √ | √ | ||||
| 3-6 Robot | 0.83 | 0.87 | 0.69 | 0.71 | 0.73 | 0.94 |
| 2-2 Robot | 0.91 | 0.89 | 0.83 | 0.91 | 0.95 | 0.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ruan, X.; Huang, J. HDPP: High-Dimensional Dynamic Path Planning Based on Multi-Scale Positioning and Waypoint Refinement. Appl. Sci. 2022, 12, 4695. https://doi.org/10.3390/app12094695
Wang J, Ruan X, Huang J. HDPP: High-Dimensional Dynamic Path Planning Based on Multi-Scale Positioning and Waypoint Refinement. Applied Sciences. 2022; 12(9):4695. https://doi.org/10.3390/app12094695
Chicago/Turabian StyleWang, Jingyao, Xiaogang Ruan, and Jing Huang. 2022. "HDPP: High-Dimensional Dynamic Path Planning Based on Multi-Scale Positioning and Waypoint Refinement" Applied Sciences 12, no. 9: 4695. https://doi.org/10.3390/app12094695
APA StyleWang, J., Ruan, X., & Huang, J. (2022). HDPP: High-Dimensional Dynamic Path Planning Based on Multi-Scale Positioning and Waypoint Refinement. Applied Sciences, 12(9), 4695. https://doi.org/10.3390/app12094695






