Capacity Estimation Models of Primary Lithium Batteries during Whole Life Cycle of Underwater Vehicles
Abstract
:1. Introduction
2. Proposed Methods
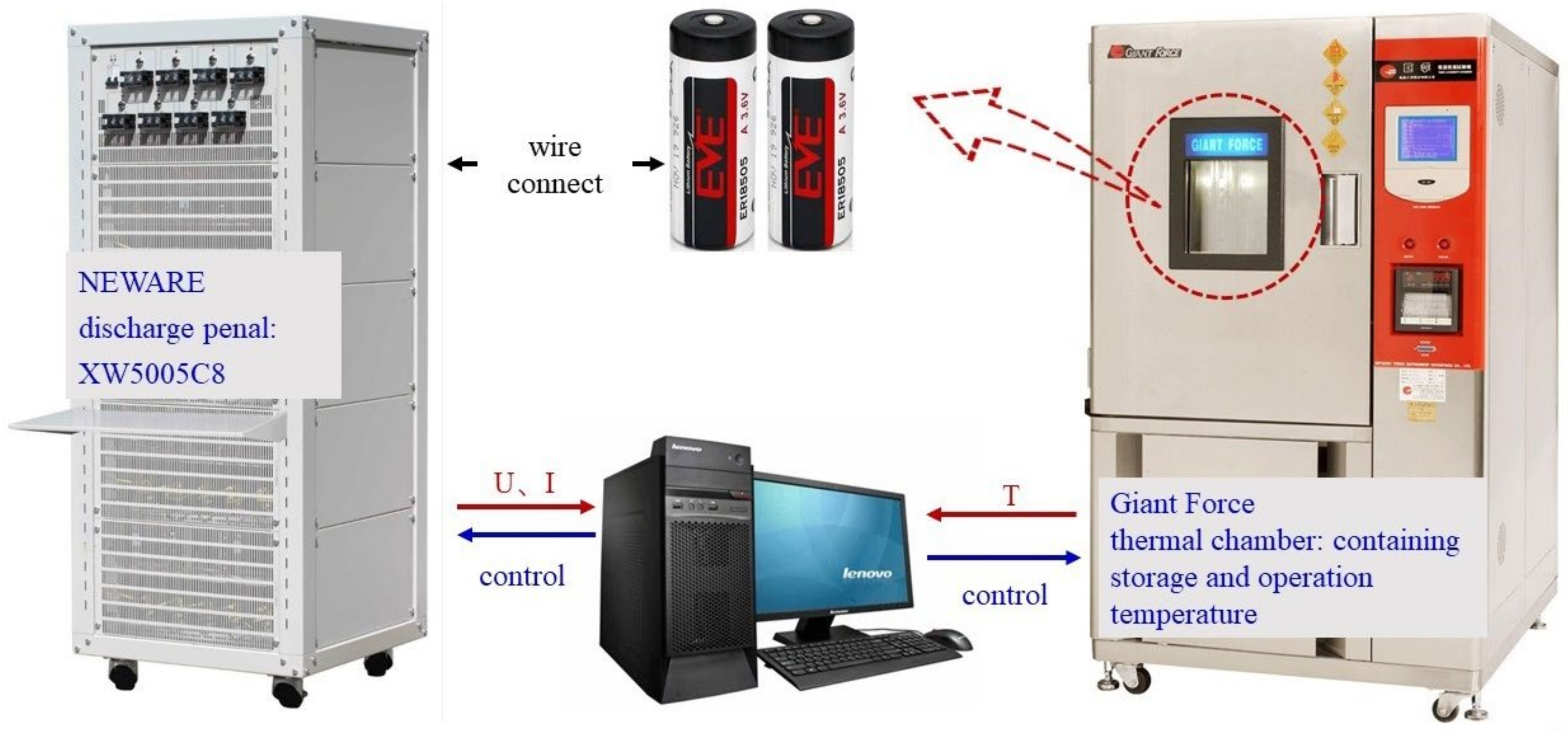
3. Experiment
4. Results and Discussion
4.1. Experiment Results
4.2. Capacity Estimation Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Sun, P.; Bai, P.; Chen, Z.; Su, H.; Yang, J.; Xu, K.; Xu, Y. A Lithium-Organic Primary Battery. Small 2020, 16, 201906462. [Google Scholar] [CrossRef]
- He, H.; Xing, R.; Zhang, X.; Sun, F.; Fan, J.; Xiong, R.; Cao, J.Y.; Yu, Q.Q.; He, H.W.; Sun, F.C. Critical review on the battery state of charge estimation methods for electric vehicle. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469, Erratum in IEEE Access 2018, 6, 1832–1843. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Zheng, F.D.; Jiang, J.C.; Sun, B.X.; Zhang, W.G.; Pecht, M. Temperature dependent power capability estimation of lithium-ion batteries for hybrid electric vehicles. Energy 2016, 113, 64–75. [Google Scholar] [CrossRef]
- Xing, Y.J.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Manane, Y.; Yazami, R. Accurate state of charge assessment of lithium-manganese dioxide primary batteries. J. Power Sources 2017, 359, 422–442. [Google Scholar] [CrossRef]
- Gou, L. Study on the Methods for Determining the Remaining Capacity of Lithium-Thionyl Chloride Primary Batteries. Master’s Thesis, South China Normal University, Guangdong, China, 2007. [Google Scholar]
- Hu, L.; Hu, X.S.; Che, Y.H.; Feng, F.; Lin, X.K.; Zhang, Z.Y. Reliable state of charge estimation of battery packs using fuzzy adaptive federated filtering. Appl. Energy 2020, 262, 114569. [Google Scholar] [CrossRef]
- He, H.W.; Zhang, X.W.; Xiong, R.; Xu, Y.L.; Guo, H.Q. Online model-based estimation of state of charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Smith, K.A.; Rahn, C.D.; Wang, C.Y. Model-based electrochemical estimation and constraint management for pulse operation of lithium ion batteries. IEEE Trans. Control Syst. Technol. 2010, 18, 654–663. [Google Scholar] [CrossRef]
- Ting, T.O.; Man, K.L.; Lim, E.G.; Leach, M. Tuning of Kalman Filter Parameters via Genetic Algorithm for State-of-Charge Estimation in Battery Management System. Sci. World J. 2014, 2014, 176052. [Google Scholar] [CrossRef] [Green Version]
- Lv, J.C.; Jiang, B.C.; Wang, X.L.; Liu, Y.R.; Fu, Y.C. Estimation of the State of Charge of Lithium Batteries Based on Adaptive Unscented Kalman Filter Algorithm. Electronics 2020, 9, 1425. [Google Scholar] [CrossRef]
- Tao, J.B.; Zhu, D.Y.; Sun, C.; Chu, D.F.; Ma, Y.L.; Li, H.B.; Li, Y.C.; Xu, T.X. A Novel Method of SOC Estimation for Electric Vehicle Based on Adaptive Particle Filter. Autom. Control Comput. 2020, 54, 412–422. [Google Scholar]
- Xu, J.; Ning, B.; Cao, B.G.; Wang, B.; Zou, Z.Y. Adaptive sliding mode observers for battery state estimation based on parameters identified online. Appl. Energy 2018, 153, 732–742. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Yang, H.; Sun, X.; An, Y.; Zhang, X.; Wei, T.; Ma, Y. Online parameters identification and state of charge estimation for lithium-ion capacitor based on improved cubature Kalman filter. J. Energy Storage 2019, 24, 100810. [Google Scholar] [CrossRef]
- Meng, J.H.; Cai, L.; Luo, G.Z.; Stroe, D.L.; Teodorescu, R. Lithium-ion battery state of health estimation with short-term current pulse test and support vector machine. Microelectron. Reliab. 2018, 88–90, 1216–1220. [Google Scholar] [CrossRef]
- Guo, P.Y.; Cheng, Z.; Yang, L. A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction. J. Power Sources 2019, 412, 442–450. [Google Scholar] [CrossRef]
- Hu, X.S.; Che, Y.H.; Lin, X.K.; Onori, S. Battery health prediction using fusion-based feature selection and machine learning. EEE Trans. Transp. Electrif. 2021, 7, 382–398. [Google Scholar] [CrossRef]
- Sun, Q.; Ye, X.; Li, H.; Li, W.; Yuan, R.; Zhai, G. Estimation of Lithium Primary Battery Capacity Based on Pulse Load Test. In Proceedings of the 2021 3rd International Conference on System Reliability and Safety Engineering, Virtual Conference, 19–21 October 2021. [Google Scholar]
- Zheng, Y.J.; Qin, C.; Lai, X.; Han, X.B.; Xie, Y. A novel capacity estimation method for lithium-ion batteries using fusion estimation of charging curve sections and discrete Arrhenius aging model. Appl. Energy 2019, 251, 113327. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Han, X.B.; Ouyang, M.G.; Lu, L.G.; Li, J.Q. A comparative study of commercial lithium ion battery cycle life in electric vehicle: Capacity loss estimation. J. Power Sources 2014, 268, 658–669. [Google Scholar] [CrossRef]
- Matsushima, T. Deterioration estimation of lithium-ion cells in direct current power supply systems and characteristics of 400-Ah lithium-ion cells. J. Power Sources 2009, 189, 847–854. [Google Scholar] [CrossRef]








| Test Method | Advantages | High-precision |
| Disadvantages | High-cost Long time-consuming | |
| Accuracy | Good | |
| Robustness | Poor | |
| Parameter-Based Method | Advantages | Simple Low computational-burden High real-time |
| Disadvantages | Sensitive to external environments, such as working environment and aging Require regular calibration of parameters Require precise equipment | |
| Accuracy | Poor | |
| Robustness | Good | |
| Ampere-Hour Integral Method | Advantages | Simple Low computational-burden High real-time |
| Disadvantages | Depends on the exact initial value Open-loop control Influenced by current drift, noise, and aging | |
| Accuracy | General | |
| Robustness | Good | |
| Model-BasedMethod | Advantages | High-precision Closed-loop control High real-time Well-adapted |
| Disadvantages | Require an accurate battery model High computational complexity | |
| Accuracy | Good | |
| Robustness | Good | |
| Data-Driven Method | Advantages | High precision Excellent nonlinearity |
| Disadvantages | High computational complexity Influence by data | |
| Accuracy | Good | |
| Robustness | Poor |
| Type | Nominal Capacity | Nominal Voltage | Nominal Current | Lower Cut-Off Voltage |
|---|---|---|---|---|
| ER48690 | 22 Ah | 3.6 V | 2.2 A | 3 V |
| K0 (Ah/d) | K25 (Ah/d) | K45 (Ah/d) | K54 (Ah/d) |
|---|---|---|---|
| 2.7 × 10−3 | 3.4 × 10−3 | 44.4 × 10−3 | 74.0 × 10−3 |
| MSE (Ah2) | RMSE (Ah) | Error (%) | |
|---|---|---|---|
| 45 °C | 0.077926 | 0.279153 | 1.12123 |
| 54 °C | 0.147483 | 0.384036 | 1.542495 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Lu, C.; Mao, Z.; Tian, W.; Zeng, L.; Li, M.; Zhang, J.; Li, B. Capacity Estimation Models of Primary Lithium Batteries during Whole Life Cycle of Underwater Vehicles. Appl. Sci. 2022, 12, 4761. https://doi.org/10.3390/app12094761
Chen P, Lu C, Mao Z, Tian W, Zeng L, Li M, Zhang J, Li B. Capacity Estimation Models of Primary Lithium Batteries during Whole Life Cycle of Underwater Vehicles. Applied Sciences. 2022; 12(9):4761. https://doi.org/10.3390/app12094761
Chicago/Turabian StyleChen, Peiyu, Chengyi Lu, Zhaoyong Mao, Wenlong Tian, Liteng Zeng, Mengjie Li, Jiming Zhang, and Bo Li. 2022. "Capacity Estimation Models of Primary Lithium Batteries during Whole Life Cycle of Underwater Vehicles" Applied Sciences 12, no. 9: 4761. https://doi.org/10.3390/app12094761
APA StyleChen, P., Lu, C., Mao, Z., Tian, W., Zeng, L., Li, M., Zhang, J., & Li, B. (2022). Capacity Estimation Models of Primary Lithium Batteries during Whole Life Cycle of Underwater Vehicles. Applied Sciences, 12(9), 4761. https://doi.org/10.3390/app12094761





